Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13 Solutions

Extra Questions for Class 10 Maths Surface Areas and Volumes with Answers

Extra Questions for Class 10 Maths Chapter 13 Surface Areas and Volumes. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

You can also download Class 10 Maths NCERT Solutions to help you to revise complete syllabus and score more marks in your examinations.

Surface Areas and Volumes Class 10 Extra Questions Very Short Answer Type

Question 1.
Vol. and surface area of a solid hemisphere are numerically equal. What is diameter of hemisphere ? [CBSE Delhi 2017]
Answer:
Vol. of hemisphere = S. A. of solid hemisphere 2 ,
⇒ \(\frac{2}{3}\)πr² = 3πr²
⇒ r = \(\frac{9}{2}\)
∴ diameter = 2r = 9 units

Question 2.
If the ratio of volume of two spheres is 1 : 8, then find the ratio of their surface area.
Answer:

Question 3.
A solid sphere of radius r is melted and recast into the shape of a solid cone of height r. Find the radius of the base of the cone.
Answer:

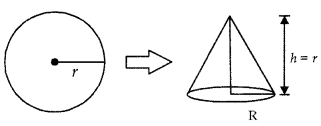
According to question,
Vol. of sphere = Vol. of cone
⇒ \(\frac{4}{3}\)πr³ = \(\frac{1}{3}\)πR²h
⇒ \(\frac{4}{3}\)πr³ = π × \(\frac{\mathrm{R}^2 \times r}{3}\)
⇒ R² = 4r²
∴ R = 2r

Question 4.
The diameter of sphere is 6 cm. It is melted and drawn into a wire of radius 1 mm. Find the length of wire.
Answer:

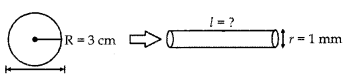
Radius of sphere (R) = 3 cm = 30 mm
Radius of wire (r) = 1 mm
Volume of sphere = Volume of wire
\(\frac{4}{3}\)πr³ = πr²l
\(\frac{1}{2}\)π × 30 × 30 × 30 = π × 1 × 1 × l
36000 mm = l
l = 3600 cm

Question 5.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm respectively is melted and recast into the form of a cone of base diameter 8 cm. Find height of the cone.
Answer:
Internal radius (r) = \(\frac{4}{3}\) = 2 cm
External radius (R) = \(\frac{8}{2}\) = 4 cm
Radius of cone (r1) = \(\frac{8}{2}\) = 4 cm
Height of cone = h
Outer volume – Inner volume = Volume of cone
⇒ \(\frac{4}{3}\)πR³ – \(\frac{4}{3}\)πr³ = \(\frac{1}{3}\)πr₁²h
⇒ 4[R³ – r³] = r₁²h
⇒ 4[4³ – 2³] = (4)²h
⇒ 4[64 – 8] = 16 h
⇒ \(\frac{4 \times 56}{16}\) = h
∴ h = 14 cm

Question 6.
If the area of the surface of sphere is 4π cm. Find the diameter of the sphere.
Answer:
Surface area of sphere = 4π
4πr² = 4π
r = 1
∴ Diameter = 2r = 2 × 1 = 2 cm

Question 7.
Find the volume and surf ace area of the largest cube that can be carved out of solid wooden sphere of radius 6√3 cm.

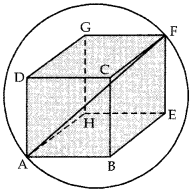
Answer:
For the largest cube (say ABCDEFGH) the diagonal of the cube (AF) must be along the diameter of the given sphere.
Length of diagonal of cube (AF)
= 2r = 2 × 6√3 = 12√3
If edge of the cube is a cm,
then diagonal AF= √3a
⇒ √3a = 12√3 ⇒ a = 12
∴ Volume of required cube
= a³ = (12)³ = 1728 cm³
Surface area of cube = 6a² = 6 × (12)²
= 864 cm²

Surface Areas and Volumes Class 10 Extra Questions Short Answer Type-1

Question 1.
Two cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.
Answer:
Let edge of the each cube be a cm.

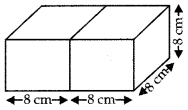
⇒ a³ = 64
⇒ a³ = (8)³
⇒ a = 8 cm
When two cubes are joined,
length of cuboid (1) = 2a = 2 × 8 = 16 cm
breadth (b) = a = 8 cm
height (h) = a = 8 cm
∴ Surface area of cuboid = 2 (lb + bh + Ih)
= 2 (16 × 8 + 8 × 8 + 16 × 8)
= 2 (128 + 64 + 128)
= 2 × 320
= 640 cm²

Question 2.
Find the length of the longest rod that can be kept in a room of dimensions 12 cm × 9 cm × 8 cm.
Answer:
Clearly, the longest rod can be kept only along the diagonal of cuboidal room.
∴ Length of the longest rod = Diagonal of cuboid

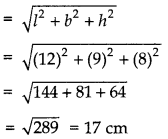
Question 3.
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 8 cm.
Answer:
For largest volume, the base of cone must be an inscribed circle in the face of the cube.
Diameter of base = Edge of cube = 8 cm

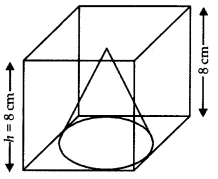
Radius (r) = \(\frac{8}{2}\) cm = 4 cm
and height of cone (h) = Edge of cone = 8 cm
Hence, volume of the largest cone = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 4 × 4 × 8 = \(\frac{2816}{21}\) = 134.09 cm³

Question 4.
A rectangular sheet of paper is 22 cm long and 12 cm wide. A cylinder is formed by rolling the paper along its length. Find the volume of cylinder.
Answer:
As illustrated in figure length (22 cm) of paper will become circumference of the base of cylinder and breadth of paper will become height of cylinder.

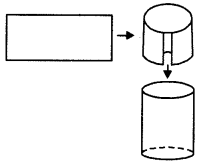
∴ 2πr = 22
⇒ r = \(\frac{1}{π}\) cm and h = 12 cm
Thus, volume of cylinder = πr²h
= π\(\left(\frac{11}{\pi}\right)^2\). 12 = \(\frac{121 \times 12}{\pi}\)
= \(\frac{121 \times 7 \times 12}{22}\) = 462 cm³

Question 5.
A toy is in the form of a cone mounted on a hemisphere of common base of radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy. [take π = \(\frac{22}{7}\)]
Answer:
Here, height of cone (h)
= Total height – Radius of hemisphere
= 31 – 7 = 24cm
im-9
Radius (r) = 7 cm
l = \(\sqrt{r^2+h^2}=\sqrt{7^2+24^2}\)
= \(\sqrt{49+576}\) = 25 cm
Total surface area = Lateral surface area of hemisphere + Lateral surface area of cone
= 2π² + πrl = πr (2r + l)
= \(\frac{22}{7}\) × 7 × (14 + 25)
= 22 × 39
= 858 cm²

Question 6.
The decorative block shown in fig. is made of two solids-a cube and a hemisphere. The base of the block is a cube with edge 5 cm and the hemisphere fixed on the-top has a diameter of 4.2 cm. Find the total surface area of the block. [take π = \(\frac{22}{7}\)]

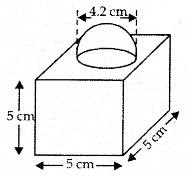
Answer:
Edge of cube (a) = 5 cm
∴ Total surface area of cube = 6a²
= 6(5)² = 150 cm²
Radius of hemisphere (r) = \(\frac{4.2}{2}\) = 2.1 cm
Surface area of block = {Total surface area of cube + Curved surface area of hemisphere} – base area of hemisphere
= {150 + 2πr²} – πr² = 150 + πr²
= 150 + \(\frac{22}{7}\) × 2.1 × 2.1
= 150 + 13.86 = 163.86 cm²

Question 7.
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and slant height of the conical portion is 53 m, find the area of the canvas needed tomake the tent. [Use π = \(\frac{22}{7}\)]
Answer:
Here radius (r) = 52.5 m
Height of cylinder (h) = 3 m
Slant height of cone (l) = 53 m

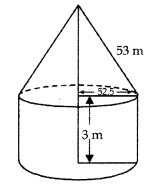
Area of canvas = Curved surface area of cylinder + Lateral surface area of cone
= 2πrh + πrl = πr(2h + l)
= \(\frac{22}{7}\) × 52.5 (2 × 3 + 53)
= 22 × 7.5 × 59
= 9735 m²

Surface Areas and Volumes Class 10 Extra Questions Short Answer Type-2

Question 1.
A hemispherical tank full of water is emptied by a pipe at the rate of 3\(\frac{4}{7}\) litres per second. How much time will it take to empty the tank? [CBSE 2019 (C)]
Answer:
Tank is in the form of hemisphere with

Diameter = 3 m
So, radius r = \(\frac{3}{2}\) m
Volume of the tank = \(\frac{2}{3}\)πr³

Now, it is given that,
tank is emptied at 3\(\frac{4}{7}=\frac{25}{7}\) litres per second 25
Time taken to empty \(\frac{25}{7}\) litres = 1 second
Time taken to empty 1 litre = 1 × \(\frac{7}{25}\) second
Time taken to empty \(\frac{99000}{28}\) litres = \(\frac{7}{25} \times \frac{99000}{28}\)
= \(\frac{693000}{700}\) = 990 sec

Question 2.
The \(\frac{3}{4}\) th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel. [CBSE 2017]
Answer:
\(\frac{3}{4}\) × Vol. of conical vessel = Vol. of cylindrical vessel

Question 3.
A metallic solid sphere of radius 10.5 cm is melted and recasted into smaller solid cones, each of radius 3.5 cm and height 3 cm. How many cones will be made? [CBSE 2017]
Answer:
Let the number of cones be n
Volume of solid sphere = Volume of ‘n’ solid cones
⇒ \(\frac{4}{3}\) π × 10.5 × 10.5 × 10.5
= n × \(\frac{1}{3}\) × π × 3.5 × 3.5 × 3
⇒ n = \(\frac{4 \times 10.5 \times 10.5 \times 10.5}{3.5 \times 3.5 \times 3}\)
∴ n = 126.

Question 4.
In figure, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of ₹ 500/sq. metre. (Use π = \(\frac{22}{7}\)) [CBSE Outside Delhi 2016]

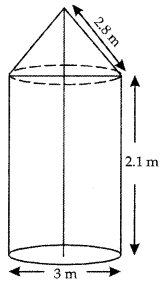
Answer:
Area of canvas = 2πrh + πrl = πr (2h + l)
= \(\frac{22}{7} \times \frac{3}{2}\)(2 × 2.1 + 2.8)
= \(\frac{22}{7} \times \frac{3}{2}\) × 7 = 33m²
Cost @ ₹ 500/m² = 33 × 500 = ₹ 16500

Question 5.
The radii of the circular ends of a bucket of height 15 cm are 14 cm and r cm (r < 14 cm). If the volume of bucket is 5390 cm³. Find the value of r. [Use π = \(\frac{22}{7}\)]
Answer:
Here, h = 15 cm
R = 14 cm
r = ?
Volume of bucket (frustum)
= 5390 cm³

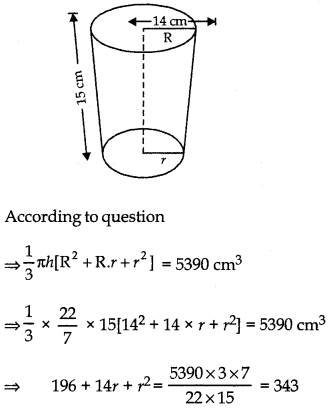
⇒ r² + 21r – 7r – 147 = 0
⇒ r(r + 21) -7 (r + 21) = 0
⇒ (r – 7)(r + 21) = 0
⇒ r = 7 cm
or r = -21 cm
∵ Radius cannot be (-ve)
∴ r =7 cm

Question 6.
How many coins 1.75 cm in diameter and of ) thickness 2 mm must be melted to form a cuboid of dimensions 11 cm × 10 cm × 7 cm?
Answer:
Let the radius and thickness of each coin be r and h respectively.
Then, r = \(\frac{1.75}{2}\) cm
h = 2 mm = \(\frac{2}{10}\) cm = 0.2 cm
Vol. of each coin = πr²h
[\(\frac{22}{7} \times \frac{1.75}{2} \times \frac{1.75}{2}\) x 0.2]cm³
For cuboid:
l = 11 cm, b = 10 cm and h = 7cm
∴ Volume of cuboid = l × b × h
= (11 × 10 × 7) cm³.
∴ Required no. of coins to be melted

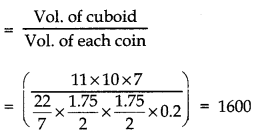
Question 7.
The cost of painting the total outer surface of a closed cylindrical oil tank at 60 paise per sq. cm is ₹ 237.60. The height of the tank is 6 times the radius of the base of the tank. Find height and radius of the tank. [Use π = \(\frac{22}{7}\)]
Answer:
Total cost of painting = ₹ 237.60
Rate of painting ₹ 0.60 per cm².
∴ Total surface area
= \(\frac{\text { Total cost }}{\text { Rate }}=\frac{237.60}{0.60}\) = 396 cm²

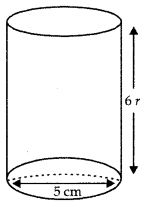
According to question,
∵ 2πr (r + h) = 396 cm²
⇒ 2 × \(\frac{22}{7}\) × r (r + 6r) = 396 cm² [h = 6r]
⇒ 2 × \(\frac{22}{7}\) × r × 7r = 396 cm²
⇒ 44r² = 396 cm²
⇒ r² = \(\frac{396}{44}\)cm² = 9 cm²
⇒ r = √9cm = 3cm
Hence, h = 6r = 6 × 3 = 18 cm
Height = 18 cm;
radius = 3 cm

Question 8.
A cone of maximum size is curved out from a cube of edge 14 cm. Find the surf ace area of the remaining solid after the cone is curved out. [CBSE Sample Paper-2017-18]
Answer:
Radius of cone = \(\frac{\text { edge of cube }}{2}=\frac{14}{2}\) cm = 7 cm
Height of cone = edge of cube = 14 cm
∴ Using Pythagoras Theorem:
l = \(\sqrt{7^2+14^2}\)
= \(\sqrt{49+196}=\sqrt{245}=7 \sqrt{5}\)
Surface area of remaining solid
= S.A. of cube – S.A. of circular base of cone + Lateral S.A. of cone
= 6a² – πr² + πrl
where a → edge of cube
r → radius & l → slant height of cone

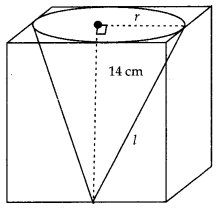
= 6 × 14 × 14 – \(\frac{22}{7}\) × 7 × 7 + \(\frac{22}{7}\) × 7 × 7√5
= 1176 – 154 + 154√3
= (1022 + 154√5) cm²

Question 9.
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. [Use π = \(\frac{22}{7}\)] [CBSE Outside Delhi 2016]
Answer:
Vol. of water in conical vessel = Vol. of water in cylinder vessel
⇒ \(\frac{1}{3}\)πr²h = πR²H
⇒ \(\frac{1}{3}\) × 5 × 5 × 24 = 10 × 10 × H
⇒ H = 2 cm
So water will rise by 2 cm in cylindrical vessel.

Question 10.
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3\(\frac{5}{9}\) cm. Find the diameter of the cylindrical vessel. [CBSE Outside Delhi 2016]
Answer:
Vol. of sphere =Vol. of water raised in cylinder
⇒ \(\frac{4}{3}\)π × 6 × 6 × 6 = π × r² × \(\frac{32}{9}\)
⇒ \(\sqrt{3 \times 3 \times 9}\) = r
⇒ r = 9
⇒ Diameter d = 2r = 2 × 9 = 18 cm

Question 11.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. [Use π = \(\frac{22}{7}\)] [CBSE Delhi 2016]
Answer:
Let the radius of base and height of the solid right circular cylinder be r cm and h cm, respectively. According to the question,
r + h = 37 …(1)
Total surface area = 1628 sq cm
2πr(r + h) = 1628 …(2)
From (1) and (2), we get
2πr(37) = 1628
\(\frac{2 \times 22}{7}\) × r × 37 =1628
⇒ r = \(\frac{44 \times 7}{2 \times 22}\)
⇒ r = 7 cm
Substituting the value of r in (1), we get
7 + h = 37
⇒ h = 30 cm

Now,
Volume of the cylinder = πr²h = \(\frac{22}{7}\) × 7 × 7 × 30
Hence the volume of the cylinder is 4,620 cm³.

Surface Areas and Volumes Class 10 Extra Questions Long Answer Type 1

Question 1.
A copper rod of diameter 1 cm and length 8 cm is drawn in to a wire of length 18 m of uniform thickness. Find the thickness of wire.
Or
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder. [CBSE SQP 2019 (Basic)]
Answer:
Radius of copper rod, (r) = \(\frac{\text { Diameter }}{2}=\frac{1}{2}\) cm
Length of copper rod, (h) = 8 cm
Let ‘t’ cm be thickness of wire into which rod is to be drawn.

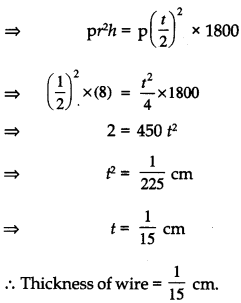
Or
Radius of sphere (r) = 4.2 cm
Radius of cylinder (R) = 6 cm
Let height of cylinder be H cm
Then, volume of sphere = volume of cylinder
⇒ \(\frac{4}{3}\)πr³ = pr²H
⇒ \(\frac{4}{3}\) × (4.2 × 4.2 × 4.2) = 6 × 6 × H
⇒ H = \(\frac{4 \times 1.4 \times 4.2 \times 4.2}{6 \times 6}\)
= 2.744 cm
∴ Height of cylinder is 2.744 cm.

Question 2.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14). [CBSE 2019]
Answer:
Volume of the bucket = 12308.8 cm³

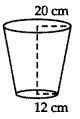
Let R = 20 cm, r = 12 cm
∴ V = \(\frac{\pi h}{3}\)(R² + r² + Rr)
∴ 12308.8 = \(\frac{3.14 \times h}{3}\)(400 + 144 + 240)
h = \(\frac{12308.8 \times 3}{3.14 \times 784}\) = 15 cm
Now, l² = h² + (R – r)²
= (15)² + (20 – 12)²
= 225 + 64 = 289
⇒ l = 17 cm
Surface area of metal sheet used
= πr² + πl(R – r)
π[r² + l(R + r)] = 3.14(144 + 17 × 32)
= 2160.32 cm²

Question 3.
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts. [CBSE Delhi 2017]
Answer:
Let r₁ r₂ be radii of smaller & larger part of cone with h₁ = 5cm, h₂ = 10 cm

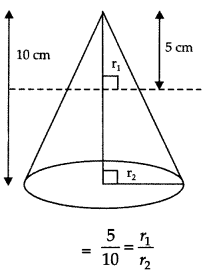
⇒ r₂ = 2r₁

Ratio of volumes of two parts

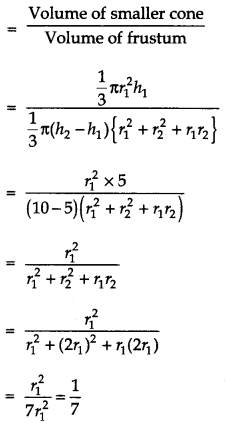
Reqd.Ratio = 1: 7

Question 4.
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park. Write your views on recycling of water. [CBSE 2017]
Answer:
Radius (R) of cylindrical tank = \(\frac{\text { diameter }}{2}\)
= \(\frac{2}{2}\) = 1 m
height (H) of cylindrical tank = 5 m
Let h be height of standing water in park of (l) length 25 m and (b) breadth = 20 m
Volume of water in cylindrical tank
= Volume of water in park ⇒ πr₂H = l × b × h
= \(\frac{22}{7}\) × 1 × 1 × 5 = 25 × 20 × h,

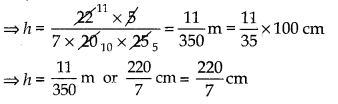
Question 5.
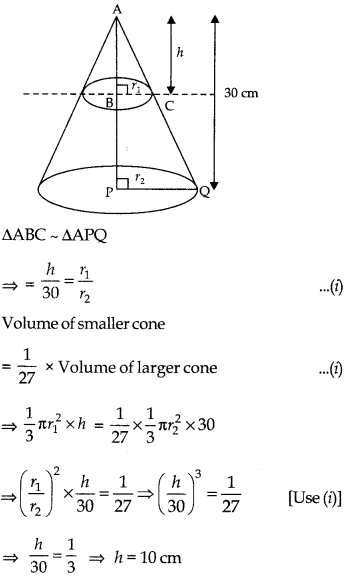
The height of a cone is 30 cm. From its topside a small cone is cut by a plane parallel to its base. If volume of smaller cone is \(\frac{1}{27}\) of the given cone, then at what height it is cut from its base? [CBSE 2017]
Answer:
Let plane parallel to the base passes through BC
let AB = h, B = r₁ cm, PQ = r₂ cm

Question 6.
An elastic belt is placed around the rim of a pulley of radius 5 cm. (figure). From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also find the shaded area. (Use π = 3.14 and √3 = 1.73) [CBSE 2016]

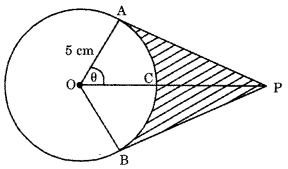
Answer:
Given OA = 5 cm
OP = 10 cm

We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, ΔOAP is a right-angled triangle.
∠OAP = 90°
Now, OP² = CA² + AP²
10² = 5² + AP²
AP² = 75
AP = 5√3 cm
Also, cos θ = \(\frac{\mathrm{OA}}{\mathrm{OP}}=\frac{5}{10}\)
⇒ cos θ = \(\frac{1}{2}\)
⇒ θ = 60°
Now, ∠AOF = ∠BOP = 600 (∵ ΔOAP ≅ ΔOBP)
⇒ ∠AOB = 120°
Length of the belt still in contact with the pulley
= Circumference of the circle – Length of the arc ACB
= 2πr – \(\frac{2 \pi r \theta}{360^{\circ}}\)
= 2 × 3.14 × 5 – 2 × 3.14 × 5 × \(\frac{120^{\circ}}{360^{\circ}}\)
= 2 × 3.14 × 5 × (1 – \(\frac{1}{3}\))
= 2 × 3.14 × 5 × \(\frac{2}{3}\)
= 20.93 cm (Approx)

Now, Area of ΔOAP
= \(\frac{1}{2}\) × AP × OA = \(\frac{1}{2}\) × 5√3 × 5 = \(\frac{25 \sqrt{3}}{2}\)cm²
Similarly, Area of ΔOBP = \(\frac{25 \sqrt{3}}{2}\)cm²
∴ Area of ΔOAP + Area of ΔOBP = 25√3 cm²
= 25 x 1.73 = 43.25 cm²
Area of sector OACB = \(\frac{120^{\circ}}{360^{\circ}}\) × 3.14 × (5)²
= \(\frac{1}{3}\) × 3.14 × 25 = 26.17 cm² (Approx.)
∴ Area of the shaded region
= ( Area of ΔOAP + Area of ΔOBP) – (Area of the sector OACB
= 43.25 cm² – 26.17 cm²)
= 17.08 cm² (Approx.)

Question 7.
A wooden toy is in the shape of a cone T mounted on a cylinder, , 1 as shown in figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted.red and white. Find the area to be painted by each of these colours. .
Answer:
For conical part:
Radius (R) = \(\frac{5}{2}\) = 2.5 cm
Height (H) = 6 cm
Slant height (l) = \(\sqrt{\mathrm{H}^2+\mathrm{R}^2}\)
= \(\sqrt{6^2+(2.5)^2}\)
= \(\sqrt{42.25}\) = 6.5 cm

For cylindrical part:
Radius (r) = 2 cm
Height (h) = (26 – 6) = 20 cm
Now, area to be painted red = (Curved surface area of the cone) + (Base area of the cone) – (Base area of cylinder)
= πRl + πR² – πr²
= π[Rl + R² – r²]
= \(\frac{22}{7}\) [2.5 × 6.5 + (2.5)² – (2)²]
= \(\frac{22}{7}\) [16.25 + 6.25 – 4]
= \(\frac{22}{7}\) × 18.50
= \(\frac{407}{7}\) = 58.14 cm²

Area to be painted white (Curved surface area of cylinder) + (Area of base of cylinder)
= 2πrh + πr² = πr [2h + r]
= \(\frac{22}{7}\) × 2 [2(20) + 2]
= \(\frac{44}{7}\) (42)
= 264 cm²

Question 8.
A bucket made up of metal sheet is in the form of a frustum of a cone. Its depth is 24 cm and the diameters of the top and bottom are 30 cm and 10 cm respectively. Find the cost of milk which can completely fill the bucket at the rate of ₹ 20 per litre and the cost of the metal sheet used, if it costs ₹ 10 per 100 cm². [Use π = 3.14]
Answer:
Here, depth (h) = 24 cm
Radius of top (R) = \(\frac{30}{2}\) = 15 cm
Radius of bottom (r) = \(\frac{10}{2}\) = 5 cm

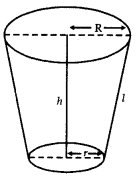
Slant height of frustum of cone
l = \(\sqrt{h^2+(\mathrm{R}-r)^2}\)
= \(\sqrt{24^2+(15-5)^2}\)
= \(\sqrt{576+100}=\sqrt{676}\)
= 26 cm

(i) Volume of the bucket = Volume of frustum of cone
= \(\frac{1}{3}\)πh(R² + r² + Rr)
= \(\frac{1}{3}\) × 3.14 × 24[15² + 5² + 15 × 5]
= 3.14 × 8[225 + 25 + 75] = 8164 cm³

Quantity of milk = \(\frac{8164}{1000}\)litre = 8.164 cm³
Cost of 1 litre milk = ₹ 20
∴ Cost of 8.164 litre milk = 8.164 × 20
= ₹ 163.28

(ii) Total surface area of bucket (excluding the upper end)
= πl(R + r) + πr²
= 3.14 × 26 (15 + 5) + 3.14 × 5²
= 1632.8 + 78.5
= 1711.3 cm²
Cost of 100 cm2 metal sheet = ₹ 10
∴ Cost of 1711.3 cm² metal sheet

Question 9.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
Answer:
Here, height of cylinder = Height of cone = h = 2.4 cm

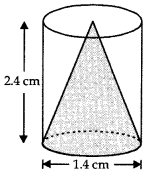
Radius of cylinder = Radius of base of cone = 1.4
r = \(\frac{1.4}{2}\) = 0.7 cm
Slant height of conical part (l) = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(0.7)^2+(2.4)^2}\)
= \(\sqrt{0.49+5.76}=\sqrt{6.25}\) = 2.5 cm
Total surface area of remaining solid = Curved surface area of cylinder + Curved surface area of cone + Base area of cylinder.
= 2πrh + πrl + πr² = πr [2h + l + r]
= \(\frac{22}{7}\) × 0.7 [2 × 2.4 + 2.5 + 0.7]
= 22 × 0.1 [4.8 + 3.2] = 2.2 × 8 = 17.6 cm²

Question 10.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm a conical cavity of the same height and same diameter is hollowed out. Find tiie total surface area of the remaining solid. [Take π = \(\frac{22}{7}\)]
Answer:

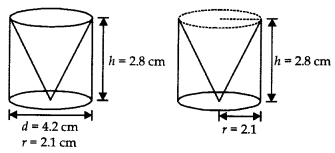
Radius of cone (r) = 2.1 cm, h = 2.8 cm
l = \(\sqrt{h^2+r^2}=\sqrt{(2.1)^2+(2.8)^2}\)
= \(\sqrt{4.41+7.84}=\sqrt{12.25}\) = 3.5 cm
Total surface area of solid = Curved surface area of cylinder + Area of base + Curved surface area of cone
= 2πrh + πr² + πrl = πr(2h + r + l)
= \(\frac{22}{7} \times \frac{21}{10}\) (2 × 28 + 21 + 3.5)= 73.92 cm²

Question 11.
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the government and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 m and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs ₹ 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? [Use π = \(\frac{22}{7}\)] [CBSE Outside Delhi 2016]
Answer:

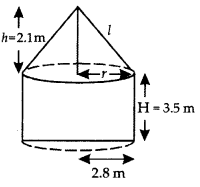
Slant height of cone (l) = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(2.1)^2+(2.8)^2}\) = 3.5 m
Amount of canvas required
= C.S.A. of cylinder + C.S.A. of cone
= 2πrH + πrl = πr(2H + l)
= \(\frac{22}{7}\) × 2.8 × (2 × 3.5 + 3.5)
= 22 × 0.4 (10.5)
= 92.4 m²
Cost of entire canvas @ ₹ 120 per m²
= 92.4 × 120 = ₹ 11088

Share of each school = \(\frac{11088}{\text { no. of schools }}=\frac{11088}{50}\)
= ₹ 221.76
Value of generosity, co-operation is generated out of this.

Surface Areas and Volumes Class 10 Extra Questions HOTS

Question 1.
A conical vessel of radius 6 cm and height 8 cm is completely filled with water. A sphere is lowered into the water and its size is such that when it touches the sides it is just immersed as shown in figure. What fraction of water flows out?
Answer:
Let r be the radius of sphere.

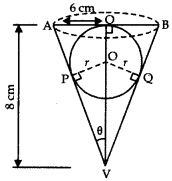
In right angled triangle AOV,

⇒ 5r = 24 – 3r
⇒ 8r = 24
⇒ r = 3 cm
∴ Volume of sphere = \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\) × π(3)³ = 36π
Fraction of water that overflows
= \(\frac{\text { Volume of sphere }}{\text { Volume of cone }}\)
= \(\frac{36 \pi}{\frac{1}{3} \pi(6)^2 \times 8}=\frac{3}{8}\)

Question 2.
A vessel in shape of an inverted cone is surmounted by a cylinder has a common radius of 7 cm. It was filled with liquid till it covered one third the height of the cylinder. If the height of each part is 9 cm and the vessel is turned upside down. Find the volume of the liquid and to what height will it reach in the cylindrical part.
Answer:
Here,
radius of cylinder = radius of cone (r) = 7 cm
Height of cone (h₁) = 9 cm

Let ‘h’ be height of water column in cylinder then according to as given
h = \(\frac{1}{3}\) × 9 = 3 cm
Volume of liquid in vessel = Volume of liquid in cone + Volume of liquid in cylinder to a height of 3 cm
= \(\frac{1}{3}\)πr²h₁ + πr²h
= \(\frac{1}{3}\)π(7)² × 9 × π × (7)² × 3
= π[147 + 147]
= \(\frac{22}{7}\) × 294 = 924 cm³
On turning upside down this 924 cm³ of liquid is poured in cylinder.
Let ‘H’ cm be the height to which liquid reaches in cylindrical vessel.
⇒ Volume of liquid column of height ‘H’ cm in cylinder = 924 cm3
⇒ π × (7)² × H = 924
⇒ H = \(\frac{924}{49 \pi}=\frac{924 \times 7}{49 \times 22}=\frac{42}{7}\) = 6 cm

Question 3.
The height of the cone is 30 cm. A small cone! is cut off at the top by a plane parallel to the base. If its volume be \(\frac{1}{27}\) of the given cone, at what height above the base is the section made?
Answer:
Small cone ADE be cut off at the top by the plane DE parallel to base BC.

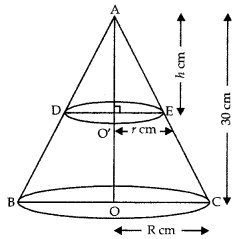
Let r, h be radius and height of small cone ADE. Also, R be the radius of larger cone.
Since ΔAO’E ~ ΔAOC,
∴ \(\frac{\mathrm{AO}^{\prime}}{\mathrm{AO}}=\frac{\mathrm{OE}}{\mathrm{OC}}\)
or \(\frac{r}{30}=\frac{r}{\mathrm{R}}\)
or r = \(\frac{h \mathrm{R}}{30}\) …….(1)

According to question,
Volume of smaller cone

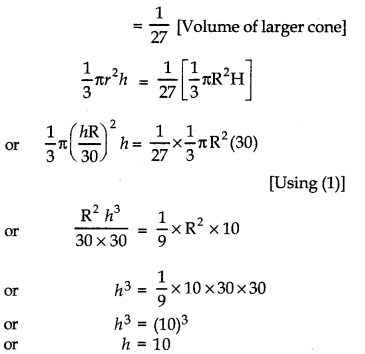
Question 4.
A tnilk tanker cylindrical in shape having ; diameters of 2 m and length 4.2 m supplies milk to the two booths in ratio of 3:2. One of the milk booths has a rectangular vessel having base area, 3.96 m² and other has cylindrical vessel having diameter 2 m. Find the level of milk in each of the vessel.
Answer:
Diameter of cylindrical milk tanker = 2 m
Radius of cylindrical milk tanker = 1 m
Length (height) of cylindrical milk tanker = 4.2 m
Volume of the tanker = πr²h
= \(\frac{22}{7}\) × (1)² × 4.2m³ = 13.2 m³

According to question,
[Volume of rectangular vessel]: [Volume of cylindrical vessel]
= 3:2
Volume of rectangular vessel
= (\(\frac{3}{5}\) × 13.2)m³
= 7.92 m³

and Volume of cylindrical vessel
= (\(\frac{2}{5}\) × 13.2)m³
= 5.28 m³
According to 1st condition,
Volume of rectangular vessel = 7.92 m³
or Area of base × Height = 7.92
or 3.96 × Height = 7.92
or Height = \(\frac{7.92}{3.96}\) = 2 m
According to 2nd condition,
Diameter of cylindrical vessel = 2 m
Radius of cylindrical vessel = \(\frac{2}{2}\) = 1 m
Volume of cylindrical vessel = 5.28 m³
πr²h = 5.28
or \(\frac{22}{7}\) × (1)² × h =5.28
or h = \(\frac{5.28 \times 7}{100 \times 22}\) = 168 m
Hence, height of rectangular vessel and cylindrical vessel are 2 m and 1.68 m respectively.

Multiple Choice Questions
Choose the correct option for each of the following:

Question 1.
The volume of the largest circular cone that can be cut out from a cube of edge 4.2 cm is:
(a) 9.7 cm³
(b) 77.6 cm³
(c) 58.2 cm³
(d) 19.4 cm³
Answer:
(d) 19.4 cm³

Question 2.
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is :
(a) 60 p cm²
(b) 68 p cm²
(c) 120 p cm²
(d) 136 p cm²
Answer:
(d) 136 p cm²

Question 3.
If the radii of circular ends of a frustum of a cone are 20 cm and 12 cm and its height is 6 cm, then the slant height of frustum (in cm) is:
(a) 10
(b) 8
(c) 12
(d) 15
Answer:
(a) 10

Question 4.
The radius of the base of a cylinder is doubled and the height remains unchanged, its curved surface area becomes:
(a) double
(b) three times
(c) half
(d) no change
Answer:
(a) double

Question 5.
If the surface area of a sphere is 144 p cm2, then its radius is:
(a) 6 cm
(b) 8 cm
(c) 12 cm
(d) 10 cm
Answer:
(a) 6 cm

Question 6.
A solid sphere of radius V is melted and recast into the shape of a solid cone of height V, then the radius of the base of the cone is:
(a) r
(b) 2r
(c) r²
(d) \(\frac{r}{2}\)
Answer:
(b) 2r

Question 7.
A metallic cube of edge 1 cm is drawn into a wire of diameter 4 mm, then the length of the wire is:
(a) 8:9
(b) 9:8
(c) 5:7
(d) 7:5
Answer:
(c) 5:7

Question 8.
A solid sphere of radius x cm is melted and cast into a shape of a solid cone of radius x cm. Then the height of the cone is:
(a) 3x cm
(b) x cm
(c) 4x cm
(d) 2x cm
Answer:
(c) 4x cm

Question 9.
The radii of bases of cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2:3 then ratio between the volume of cylinder to volume of cone is:
(a) 8: 9
(b) 9 : 8
(c) 5 : 7
(d) 7: 5
Answer:
(b) 9 : 8

Question 10.
If a cone is cut into two parts by a horizontal plane passing through the mid points of its axis, the ratio of the volumes of the upper part and the cone is :
(a) 1:2
(b) 1:4
(c) 1:6
(d) 1:8
Answer:
(d) 1:8

Question 11.
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that \(\frac{1}{8}\) space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is :
(a) 142296
(b) 142396
(c) 142496
(d) 142596
Answer:
(a) 142296

Question 12.
The diameter of a metallic sphere is 6 cm. It is melted and drawn into a wire of diameter 2 cm, then the length of the wire is:
(a) 12 cm
(b) 18 cm
(c) 36 cm
(d) 66 cm
Answer:
(c) 36 cm

Question 13.
A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter:
(a) r cm
(b) 2r cm
(c) h cm
(d) 2h cm
Answer:
(b) 2r cm

Question 14.
A metallic spherical shell of internal and exter¬nal diameters 4 cm and 8 cm, respectively is melted and recast into the form of a cone of base diameter 8 cm. The height of the cone is:
(a) 12 cm
(b) 14 cm
(c) 18 cm
(d) 21 cm
Answer:
(b) 14 cm

Question 15.
An iron sphere of radius 14 cm is melted. The number of spheres each of diameter 2 cm that can be made out of it are:
(a) 49
(b) 343
(c) 729
(d) 512
Answer:
(b) 343

Fill in the Blanks

Question 1.
If two identical cubes of side ‘a’ are joined end to end. Then the total surface area of resulting cuboid is ______.
Answer:
10a² sq.units

Question 2.
If a solid ball is exactly fitted inside a cubical box of side 2b. Then the volume of the ball is ______
Answer:
\(\frac{4}{3}\)πb³

Question 3.
The total surface area of a cuboid of dimensions l × l × b is ______.
Answer:
2l² + 4lb

Question 4.
The volume of right circular cylinder of base radius r and height 2r is ______.
Answer:
2πr³

Question 5.
When one solid ‘A’ is melted and recasted into another solid B, then the ______ of solid A and solid B is same.
Answer:
volumes

Question 6.
The total surface area of a cylinder of base radius r and height h is ______.
Answer:
2πr(r + h)

Question 7.
If the height of a cone is equal to diameter ‘d’ of its base, the volume of cone is ______.
Answer:
\(\frac{\pi d^3}{12}\)

Question 8.
Volume of a frustum of a cone of radii of circular base R and r and height h is ______.
Answer:
\(\frac{1}{3}\)πh(R² + r² + Rr)

Question 9.
The total surface area of a hemisphere of radius r is ______.
Answer:
3πr²

Question 10.
If the radius of a sphere is doubled, its volume becomes ______ times the volume of original sphere.
Answer:
Eight

Extra Questions for Class 10 Maths

NCERT Solutions for Class 10 Maths