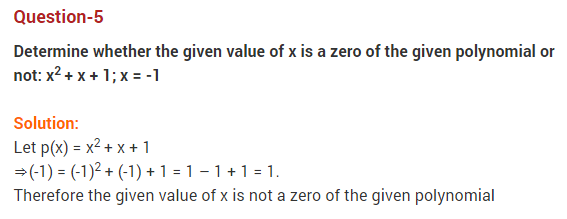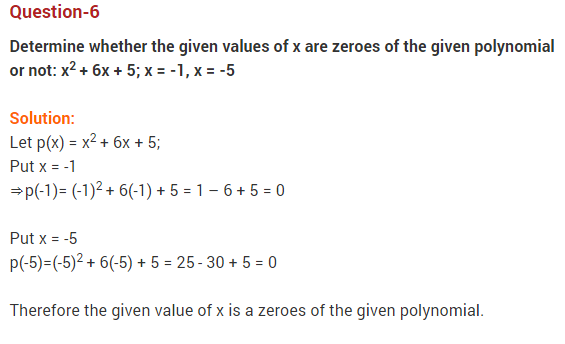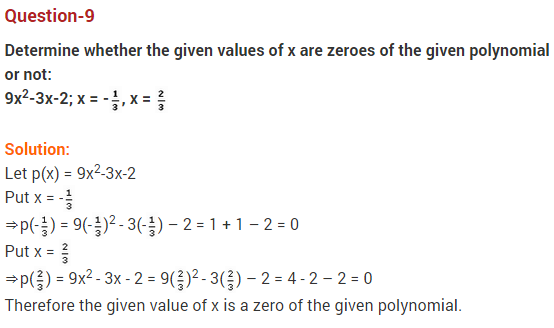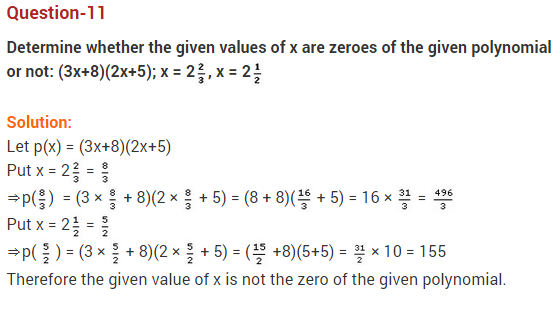Polynomials Class 10 Extra Questions Maths Chapter 2 with Solutions

Polynomials Class 10 Extra Questions Maths Chapter 2 with Answers

Extra Questions for Class 10 Maths Chapter 2 Polynomials. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

Polynomials Class 10 Extra Questions Very Short Answer Type

Question 1.
The graph of a quadratic polynomial x² – 3x – 4 is a parabola. Determine the opening of parabola.
Answer:
∵ In x² – 3x – 4, the Coefficient of x² is 1 and 1 > 0.
∴ The parabola opens upwards.

Question 2.
If p(x) = x² + 5x + 2, then find p(3) + p(2) + p(0).
Answer:
p(3) = 3² + 5(3)+ 2 = 26
p(2) = 2² + 5(2) + 2 = 16
p(0) = 0² + 5(0) + 2 = 2
⇒ p(3) + p(2) + p(0) = 26 + 16 + 2 = 44

Question 3.
The graph of y = p(x) is shown in the figure below. How many zeroes does p(x) have?

Answer:
Since, the curve (graph) of p(x) is intersecting the x-axis at three points, y = p(x) has 3 zeroes.

Question 4.
The coefficient of x and the constant term in a linear polynomial are 5 and – 3 respectively, find its zero.
Answer:
∵ The zero of a linear polynomial = – \(\frac{\text { Constant term }}{\text { Coefficient of } x}\)
∴ The zero of the given linear polynomial
= – \(\frac{(-3)}{5}=\frac{3}{5}\)

Question 5.
What is the value of p(x) = x² – 3x – 4 at x = -1 ?
Answer:
We have: p(x) = x² – 3x – 4
∴ P(- 1) = (- 1)² – {3(- 1)} – 4 = 1 + 3 – 4
= 0

Question 6.
If the polynomial p(x) is divisible by (x – 4) and 2 is a zero of p(x), then write the corresponding polynomial.
Answer:
Here, p(x) is divisible by (x – 4) and also 2 is a zero of p(x), therefore p(x) is divisible by (x – 4) and (x – 2)
Thus, the required polynomial p(x) = (x – 4) (x – 2) = x² – 6x + 8.

Question 7.
If (α – β), α, (α + β) are zeroes of the polynomial p(x) = 2x³ – 16x² + 15x – 2, then find the value of α
Answer:
Sum of zeroes = – \(\frac{\text { Coeff. of } x^2}{\text { Coeff. of } x^3}\)
⇒ (α – β), α, (α + β) = \(\frac{-(-16)}{2}\)
⇒ 3α = 8
⇒ α = \(\frac{8}{3}\)

Question 8.
What is the zero of 2x + 3?
Answer:
∵ The zero of a linear polynomial = – \(\frac{\text { Constant term }}{\text { Coefficient of } x}\)
∴ The zero of 2x + 3 = – \(\frac{3}{2}\)

Question 9.
Find the value of p for which the poloynomial x3 + 4×2 – px + 8 is exactly divisible by (x – 2).
Here p(x) = x³ + 4x² – px + 8
∵ (x – 2) divides p(x), exactly
⇒ P(2) = 0
⇒ (2)³ + 4 (2)² – p(2) + 8 = 0
2p = 32 ⇒ p = 16

Question 10.
If α and β are zereos of the polynomial 2x² – 5x + 7, then find the value of α^-1 + β^-1.
Answer:
Here p(x) = 2x² – 5x + 7
α, β are zeroes of p(x)

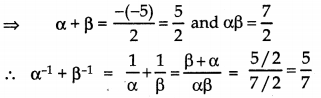
Question 11.
If p and q are the roots of ax² – bx + c = 0, a ≠ 0, then find the value of p + q.
Answer:
Here, p and q are the roots of ax² – bx + c = 0.
Sum of roots = \(\frac{-b}{a}\)
∴ p + q = \(\frac{-b}{a}\)

Question 12.
If – 1 is a zero of quadratic polynomial, p(x) = kx² – 5x – 4, then find the value of k.
Answer:
Here p(x) = kx² – 5x – 4
Since – 1 is a zero of p(x)
∴ P(- 1) = o
⇒ k (-1)² – 5(- 1) – 4 = 0
⇒ k + 5 – 4 = 0
⇒ k = – 1

Polynomials Class 10 Extra Questions Short Answer Type-1

Question 1.
Find the quadratic polynomial whose sum of zeroes is 8 and their product is 12. Hence find zeroes of polynomial.
Answer:
Let, α, β be zereos of polynomial.
Now, here α + β = 8, αβ = 12.
Required polynomial
p(x) = k{x² – (α + β) x + α β),
k is a constant.
⇒ p(x) = k{x² – 8x + 12}
In particular, taking k = 1
Reqd. polynomial = x² – 8x + 12
Now, p(x) = x² – 8x + 12
= x² – 6x – 2x + 12
= x(x – 6) – 2(x – 6)
= (x – 6) (x – 2)
∴ p(x) = o
⇒ x = 6, 2
Thus zeroes of polynomial are 6 and 2.

Question 2.
Check whether x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.
Answer:
Let p(x) = 3x⁴ + 5x³ – 7x² + 2x + 2,
g(x) = x² + 3x + 1
Next we divide p(x) by g(x).

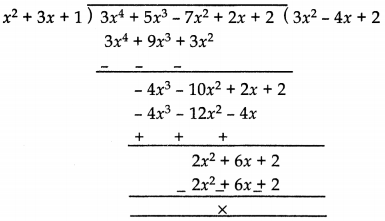
Using division algorithm
3x⁴ + 5x³ – 7x² + 2x + 2 = (x² + 3x + 1) (3x² – 4x + 2) + 0
= (x² + 3x + 1) (3x² – 4x + 2)
Clearly, as remainder is 0, so the divisor x² + 3x + 1 appear on R.H.S as factor of 3x⁴ + 5x³ 7x² + 2x + 2.

Question 3.
If one zero of the polynomial (a² + 9)x² + 13x + 6a is reciprocal of the other, find the value of a.
Answer:
Let α, \(\frac{1}{\alpha}\) be the zeroes of (a² + 9)x² + 13x + 6a

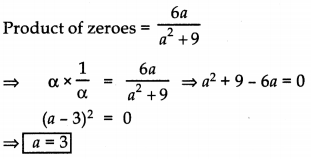
Question 4.
If α and β are zeroes of x² + 7x + 12, then find the value of \(\frac{1}{\alpha}+\frac{1}{\beta}\) – 2αβ
Answer:
Here α + β = – 7, αβ = 12

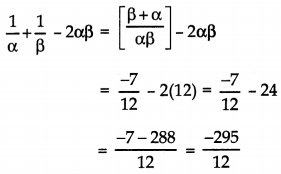
Question 5.
Find α^-1 + β^-1, if α and β are zereos of the polynomial 9x² – 3x – 2.
Answer:
Since α and β are zereos of p(x) = 9x² – 3x – 2

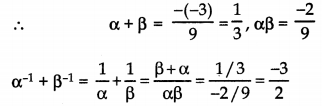
Question 6.
Find whether 2x³ – 1 is a factor of 2x⁵ + 10x⁴ + 2x² + 5x + 1 or not.
Answer:

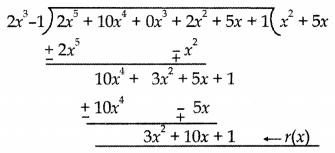
Since r(x) ≠ 0
∴ 2x³ – 1 is not a factor of given polynomial.

Question 7.
If α, β, γ are zeroes of the polynomial f(x) = x³ – 3x² + 7x – 12, then find the value of (αβ)^-1 + (βγ)^-1 + (γα)^-1.
Answer:

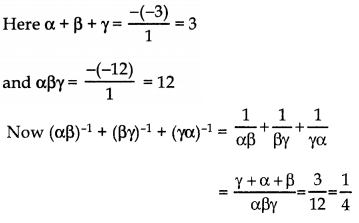
Question 8.
For what value of k is the polynomial x³ + kx² + 3x – 18 is exactly divisible by (x – 3).
Answer:
If p(x) = x³ + kx² + 3x – 18 is exactly divisible by (x – 3)
⇒ p(3) = 0 ⇒ (3)³ + k(3)² + 3(3) – 18 = 0
⇒ 9k = – 18 ⇒ k = – 2

Polynomials Class 10 Extra Questions Short Answer Type-2

Question 1.
Find all the zeroes of 2x⁴ – 13x³ + 19x² + 7x – 3, if you know that two of its zeroes are 2 + √3 and 2 – √3. [C.B.S.E. 2019]
Answer:
Given, x = (2 + √3) and x = (2 – √3) are zeroes of p(x) = 2x⁴ – 13x³ + 19x² + 7x – 3
∴ (x – (2 + √3)) (x – (2 – √3)) is factor of p(x).
⇒ (x – 2 – √3) (x – 2 + √3) is factor of p(x).
= (x – 2)² – (√5)²
= x² – 4x + 4 – 3
= x² – 4x + 1
Now, we divide p(x) by x² – 4x + 1

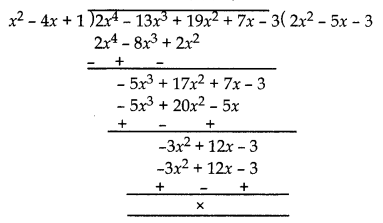
Now p(x) = (x² – 4x + 1) (2x² – 5x – 3)
∴ Other zeroes are given by
2x² – 5x – 3 = 0
⇒ 2x² – 6x + x – 3 = 0
⇒ 2x (x – 3) + 1 (x – 3) = 0
⇒ (2x + 1) (x – 3) = 0
⇒ 2x + 1 = 0 or x – 3 = 0
x = – \(\frac{1}{2}\), 3
∴ Zeroes of given polynomial are
– \(\frac{1}{2}\), 3, (2 + √3), (2 – √3)

Question 2.
Find all the zeroes of 2x⁴ – 3x³ – 3x² + 6x – 2, if it is given that two of its zeroes are 1 and \(\frac{1}{2}\). [CBSE 2019 (C) Set-B]
Answer:
Given: x = 1, x = \(\frac{1}{2}\) are zeroes of p(x) = 2x⁴ – 3x³ – 3x² + 6x – 2
∴ (x – 1) and (x – \(\frac{1}{2}\)) or (2x – 1) are factor of p(x).
⇒ (x – 1) (2x – 1) = 2x² – 3x + 1 is a factor of p(x).
Next, we divide p(x) by 2x² – 3x + 1.

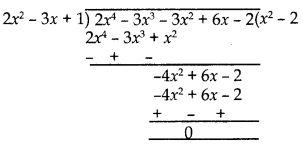
∴ p(x) = (2x² – 3x + 1) (x² – 2)
∴ Other zeroes are given by (x² – 2) = 0
⇒ x = ±√2
∴ Zeroes of p(x) are – √2, \(\frac{1}{2}\), 1, √2.

Question 3.
Find all zeros of the polynomial 3x³ + 10x² – 9x – 4, if one of its zero is 1. [CBSE 2019]
Answer:
Let p(x) = 3x³ + 10x² – 9x – 4
Since, 1 is a zero of p(x)
Therefore, (x – 1) is a factor of p(x)
Dividing p(x) by (x – 1), we have:

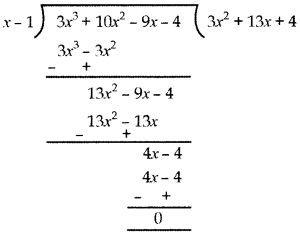
∴ By Division Algorithm,
p(x) = (3x² + 13x + 4)(x – 1)
Zeroes of p(x) are given by p(x) = 0
⇒ (3x² + 13x + 4)(x – 1) = 0
⇒ (3x² + 12x + x + 4)(x – 1) = 0
⇒ {3x(x + 4) + 1 (x + 4)}(x – 1) = 0
⇒ (x + 4 )(3x + 1) (x – 1) = 0
⇒ x + 4 = 0
or 3x + 1 = 0 or x – 1 = 0
⇒ x = – 4, – \(\frac{1}{3}\), 1
∴ Zeroes of p(x) are – 4, – \(\frac{1}{3}\), 1.

Question 4.
Divide the polynomial 3x³ – 6x² – 20x + 14 by the polynomial x² – 5x + 6 and verify the division algorithm. [CBSE Delhi 2016]
Answer:

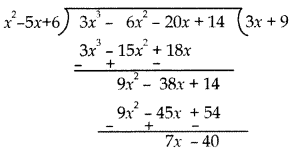
By division algorithm,
3x³ – 6x² – 20x + 14 = (x² – 5x + 6)(3x + 9) + (7x – 40)
or, p(x) = q(x) g(x) + r(x)

Question 5.
If α and β are the zeroes of a quadratic polynomial x² – x – 2 then find the value of \(\left(\frac{1}{\alpha}-\frac{1}{\beta}\right)\).
Answer:
Comparing x² – x – 2 with ax² + bx + c, we have a = 1, b = – 1, c = -2

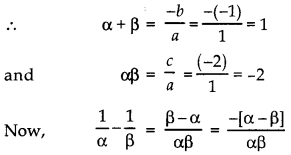
[∵ (α – β)² = (α + β)² – 4αβ
= (1)² – 4 (- 2) = 1 + 8 = 9
∴ α – β = √9
⇒ (α – β) = ± 3]

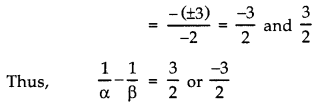
Question 6.
On dividing p(x) by a polynomial x – 1 – x², the quotient and remainder were (x – 2) and 3 respectively. Find p(x).
Answer:
Here,
dividend = p(x)
Divisor, g(x) = (x – 1 – x²)
Quotient, q(x) = (x – 2)
Remainder, r(x) = 3
∵ Dividend = [Divisor × Quotient] + Remainder
∴ P(x) = [g(x) × q(x)] + r(x)
= [(x – 1 – x²) (x – 2)] + 3
= [x² – x – x³ – 2x + 2 + 2x²] + 3
= 3x² – 3x – x³ + 2 + 3
= – x³ + 3x² – 3x + 5

Question 7.
Find the zeroes of the quadratic polynomial 5x² – 4 – 8x and verify the relationship between the zeroes and the coefficients of the polynomial.
Answer:
p(x) = 5x² – 4 – 8x = 5x² – 8x – 4
= 5x² – 10x + 2x – 4
= 5x(x – 2) + 2(x – 2)
= (x – 2) (5x + 2)
= 5(x – 2) (x + \(\frac{2}{5}\))
∴ Zeroes of p(x) are 2 and – \(\frac{2}{5}\)

Relationship Verification:

Polynomials Class 10 Extra Questions Long Answer Type 1

Question 1.
If the polynomial x⁴ + 2x³ + 8x² + 12x + 18 is divided by another polynomial x² + 5, the remainder comes out to be px + q. Find the values of p and q.
Answer:

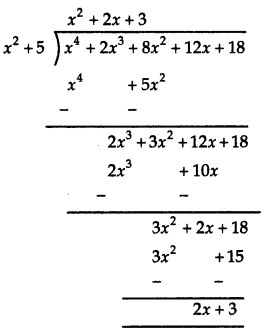
∴ Remainder = 2x + 3
Comparing 2x + 3 with px + q, we have
p = 2 and q = 3

Question 2.
If α, β, γ are the zeroes of p(x) = x³ – 7x² + 11x – 7 find the value of
(i) α² + β² + γ²
(ii) α³ + β³ + γ³
Answer:
Comparing p(x) = x³ – 7x² + 11x – 7 with standard cubic polynomial ax³ + bx² + cx + d, we have
a = 1, b = – 7, c = 11, d = – 7

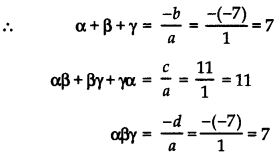
(i) Now, since (α + β + γ)² = α² + β² + γ² + 2(αβ + βγ + γα)
⇒ α² + β² + γ² = (α + β + γ)² – 2(αβ + βγ + γα)
= (7)² – 2(11) = 49 – 22 = 27

(ii) Since
α³ + β³ + γ³ – 3αβγ = (α² + β² + γ² – αβ – βγ – γα)
(α + β + γ)
= {(α + β + γ)² – 2(αβ + βγ + γα) – (αβ + βγ + γα)}(α + β + γ)
⇒ α³ + β³ + γ³ = {(α + β + γ)² – 3(αβ + βγ + γα)} (α + β + γ) + 3αβγ
= {7² – 3(11)} 7 + 3 × 7
= (49 – 33) 7 + 21
= 16 × 7 + 21 = 133.

Question 3.
Find the quadratic polynomial whose zeroes are 1 and – 3. Verify the relation between the coefficients and the zeroes of the polynomial.
Answer:
∵ The given zeroes are 1 and – 3.
∴ Sum of the zeroes = 1 + (- 3) = – 2
Product of the zeroes = 1 × (- 3) = – 3
A quadratic polynomial p(x) is given by
x² – (sum of the zeroes) x + (product of the zeroes)
∴ The required polynomial is
x² – (- 2)x + (-3)
⇒ x² + 2x – 3

Verification of relationship
∵ Sum of the zeroes = – \(\frac{\text { [coeff. of } x]}{\text { Coeff. of } x^2}\)
∴ 1 + (- 3) = \(\frac{-[2]}{1}\)
⇒ – 2 = – 2
i.e., LHS = RHS
⇒ The sum of zeroes is verified.
∵ Product of the zeroes = \(\frac{\text { [Constant term] }}{\text { Coefficient of } x^2}\)
∴ 1 × (- 3) = \(\frac{[-3]}{1}\)
⇒ – 3 = – 3
i.e., L.H.S. = R.H.S.
⇒ The product of zeroes is verified.

Question 4.
What must be added to 6x⁵ + 5x⁴ + 11x³ – 3x² + x + 1, so that the polynomial so obtained is exactly divisible by 3x² – 2x + 4?
Answer:

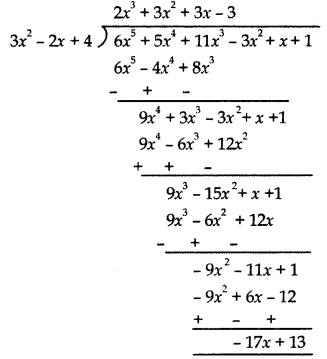
Therefore, we must add -(- 17x + 13),
i.e., 17x – 13.

Question 5.
Find the value of b for which the polynomial 2x³ + 9x² – x – b is divisible by 2x + 3.
Answer:

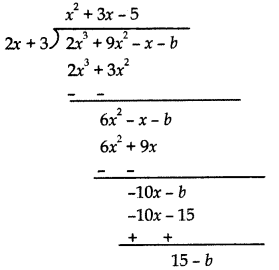
If the polynomial 2x³ + 9x² – x – b is divisible by 2x + 3, then the remainder must be zero.
So, 15 – b = 0
⇒ b = 15

Question 6.
Find the zeroes of a cubic polynomial p(x) = 3x³ – 5x² – 11x – 3 when it is given that product of two of its zeroes is -1.
Answer:
Here, p(x) = 3x³ – 5x² – 11x – 3
On comparing p(x) with ax³ + bx² + cx + d, we have;
a = 3, b = -5, c = -11, d = -3
Let α β γ be the zeroes of the given polynomial.

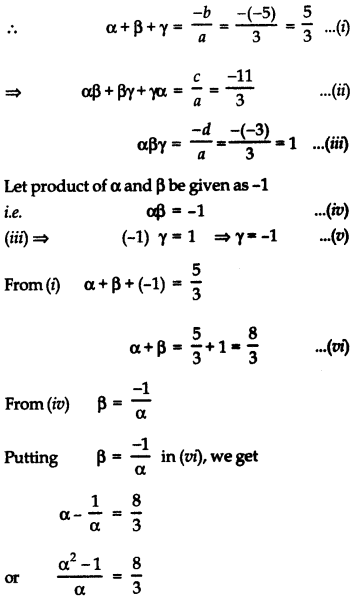
⇒ 3α² – 3 = 8α
⇒ 3α² – 8α – 3 = 0
⇒ 3α² – 9α + α – 3 = 0
⇒ 3α(α – 3) + 1 (α – 3) = 0
⇒ (α – 3) (3α + 1) = 0

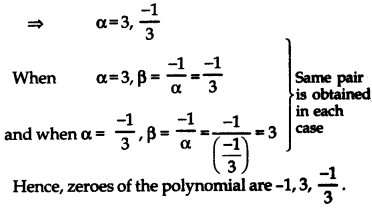
Polynomials Class 10 Extra Questions HOTS

Question 1.
If p and q are the zeroes of x² + px + q, then find the values of p and q.
Answer:
p, q are the zeroes of x² + px + q.
⇒ p + q = – p …………… (i)
and pq = q ……… (ii)
⇒ pq – q = 0
⇒ (p – 1)q = 0
⇒ either p = 1 or q = 0
When p = 1
⇒ 1 + q = – 1
⇒ q = – 2
When 9 = 0
⇒ p + 0 = – p
⇒ 2p = 0
⇒ p = 0
∴ p = 1, q = – 2 or p = q = 0.

Question 2.
If the zeroes of p(x) = ax³ + 3bx² + 3cx + d are in A.P., prove that 2b³ – 3abc + a²d = 0
Answer:
Let α β γ be zeroes of p(x) = ax³ + 3bx² + 3cx + d
But α, β, γ are in A.P.
So, take α = m – n, β = m, γ = m + n.

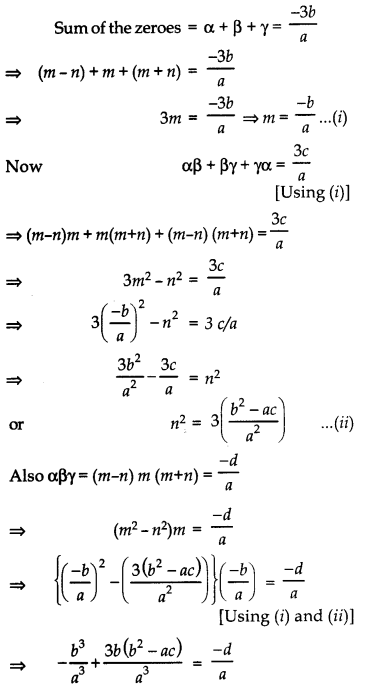
Multiplying throughout by a³, we get – b³ + 3b (b² – ac) = – a²d
⇒ – b³ + 3b³ – 3abc + a²d = 0
or 2b³ – 3abc + a²d = 0
Note: Three numbers are said to be in Arithmetic Progression (A.P.). If each number is obtained by adding a constant to the previous number e.g. 3, 7, 11 are in A.P. Generally we take three numbers in A.P. as a – d, a, a + d.
It would be discussed in detail in Second term.

Question 3.
Find a relation between p and q, if one zero of x² + px + q is 37 times the other.
Answer:
Let α, β be the zeroes of the polynomial
x² + px + q
then α + β = – p, αβ = q
α = 37β (given)
∴ α + β = – p
⇒ 38β = – p

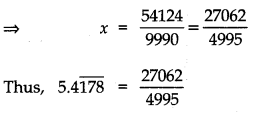
Multiple Choice Questions

Choose the correct option out of four given in each of the following:

Question 1.
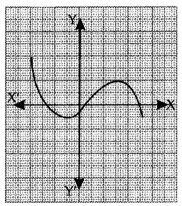
The graph of p(x) is shown alongside. The number of zeroes of p(x) are:

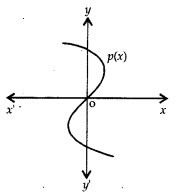
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(a) 1

Question 2.
If one zero of polynomial (k² + 16) x² + 13x + 8k is reciprocal of the other then k is equal to
(a) – 4
(b) +4
(c) 8
(d) 2
Answer:
(b) +4

Question 3.
If α and β are zeroes of the polynomial p(x) = x² + mx + n, then a polynomial whose zeroes are \(\frac{1}{\alpha}, \frac{1}{\beta}\) is given by
(a) nx² + mx + 1
(b) mx² + x + n
(c) x² + nx + m
(d) x² – mx + n
Answer:
(a) nx² + mx + 1

Question 4.
If the graph of y = p(x) does not cut the x-axis at any point, then polynomial has
(a) one zero
(b) two zeroes
(c) no zeroes
(d) infinite no. of zeroes
Answer:
(c) no zeroes

Question 5.
Sum of the zeroes of the polynomial p(x) = – 3x² + k is
(a) \(\frac{k}{3}\)
(b) \(\frac{-k}{3}\)
(c) 0
(d) k
Answer:
(c) 0

Question 6.
If x – 1 is a factor of p(x) = kx² – √2x + 1, then the value of k is
(a) √2 – 1
(b) – √2 + 1
(c) – 1 – √2
(d) 1 + √2
Answer:
(a) √2 – 1

Question 7.
Number of zeroes of a polynomial of degree n is
(a) equal to n
(b) less than n
(c) greater than n
(d) less than or equal to n
Answer:
(d) less than or equal to n

Question 8.
Zeroes of the polynomial p(x) = 2x² – 9 – 3x are
(a) 3, \(\frac{3}{2}\)
(b) –\(\frac{3}{2}\) , 3
(c) 2, 3
(d) 9, \(\frac{3}{2}\)
Answer:
(b) –\(\frac{3}{2}\) , 3

Question 9.
If (α – β), α, (α + β) are zeroes of the polynomial p(x) = 2x³ – 16x² + 15x – 2, value of α is
(a) 8
(b) 0
(c) \(\frac{3}{8}\)
(d) \(\frac{8}{3}\)
Answer:
(d) \(\frac{8}{3}\)

Question 10.
If n represents number of real zeroes for the polynomial ax3 + bx2 + cx + d then which of the following inequality is valid
(a) 0 < n < 3
(b) 0 < n < 3
(c) 0 < n < 3
(d) 0 < n < 3
Answer:
(c) 0 < n < 3

Question 11.
Number of quadratic polynomials having – 2 and – 5 as their two zeroes is :
(a) one
(b) two
(c) three
(d) infinite
Answer:
(d) infinite

Question 12.
If α, β, γ are zeroes of the polynomial p (x) such that α + β + γ = 2, αβ + βγ + γα = 5, αβγ = – 7, then p(x) is:
(a) x³ – 2x² + 5x – 7
(b) x³ + 2x² – 5x + 7
(c) x³ – 2x² – 5x – 7
(d) x³ – 2x² + 5x + 7
Answer:
(d) x³ – 2x² + 5x + 7

Question 13.
If the sum of products of zeroes taken two at a time of polynomial p(x) = x3 – 5×2 + cx + 8 is 2 then the value of c is
(a) 2
(b) – 2
(c) 8
(d) – 5
Answer:
(a) 2

Question 14.
The division algorithm states that given any polynomial p(x) and any non-zero polynomial g(x) there are polynomial q(x) and r(x) such that p(x) = g(x) q{x) + r(x), where r(x) is
(a) either = 0 or deg. r(x) < deg. g(x) (b) either = 0 or deg. r(x) > deg. g(x)
(c) a linear polynomial or deg. r(x) = deg. g(x)
(d) either = 0 or deg. r(x) < deg. g(x)
Answer:
(d) either = 0 or deg. r(x) < deg. g(x)

Question 15.
If divisor, quotient and remainder are x +
(a) 3x² + x + 1
(b) 3x² – x – 1
(c) 3x² + x – 1
(d) 3x² – x + 1
Answer:
(c) 3x² + x – 1

Fill in the blanks

Question 1.
The zeroes of the polynomial x² – 49 are ______________ .
Answer:
± 7

Question 2.
The quadratic polynomial, whose sum and product of zeroes are 4 and – 5 respectively is _____________ .
Answer:
k(x² – 4x – 5)

Question 3.
The value of the polynomial p(x) = 4x² – 7 at x = – 2 is _______________ .
Answer:
9

Question 4.
Product of zeroes of a polynomial p(x) = 6x² – 7x – 3 is _______________ .
Answer:
– \(\frac{1}{2}\)

Question 5.
If one zero of 3x² – 8x +2k + 1 is seven times the other, then k is _________________.
Answer:
\(\frac{2}{3}\)

Question 6.
The degree of the constant polynomial is _______________ .
Answer:
zero

Question 7.
A real number k is a zero of the polynomial p(x) if and only if _______________.
Answer:
p(k) = 0

Question 8.
The shape of the graph of a cubic polynomial is _______________ .
Answer:
not fixed

Question 9.
If α, β and γ are the zeroes of the cubic polynomial px³ + qx² + rx + s; a ≠ 0, then α + β + γ = ____________ , αβ + βγ + γα = _____________ and αβγ = ___________.
Answer:
\(\frac{-q}{p}, \frac{r}{p}, \frac{-s}{p}\)

Question 10.
The standard form of the polynomial x³ – x⁶ + x⁵ + 2x² – x⁴ – 5 is ______________ .
Answer:
x⁶ + x⁵ – x⁴ + x³ + 2x² – 5 or – 5 + 2x² + x³ – x⁴ + x⁵ – x⁶

You can also download Maths NCERT Solutions Class 10 to help you to revise complete syllabus and score more marks in your examinations.

Extra Questions for Class 10 Maths

NCERT Solutions for Class 10 Maths