NCERT Exemplar Class 6 Maths Chapter 2 Geometry are part of NCERT Exemplar Class 6 Maths. Here we have given NCERT Exemplar Class 6 Maths Solutions Chapter 2 Geometry.
NCERT Exemplar Class 6 Maths Solutions Chapter 2 Geometry
Question 1.
Number of lines passing through five points such that no three of them are collinear is
(A) 10
(B) 5
(C) 20
(D) 8
Solution:
(A) : Since, total number of points is 5 and we need two points to form a line.
∴ Total number of lines passing through the points is 5 × 2 = 10
Question 2.
The number of diagonals in a septagon is
(A) 21
(B) 42
(C) 7
(D) 14
Solution:
(D) : Since, the number of diagonals in
n(n – 3) a polygon
![]()
∵ Septagon has 7 sides, i.e., n = 7
∴ The number of diagonals in a septagon
![]()
Question 3.
Number of line segments in figure is
![]()
(A) 5
(B) 10
(C) 15
(D) 20
Solution:
(B) : The adjacent figure shows the line segments;
![]()
\(\overline{A B}, \overline{B C}, \overline{C D}, \overline{A C}, \overline{A D}, \overline{B D}, \overline{A E}, \overline{B E}, \overline{C E}, \overline{D E}\)
Thus, there are 10 line segments.
Question 4.
Measures of the two angles between hour and minute hands of a clock at 9 O’clock are
(A) 60°, 300°
(B) 270°, 90°
(c) 75°, 285°
(d) 30°, 330°
Solution:
(B) : We know that 1 minute = 6°
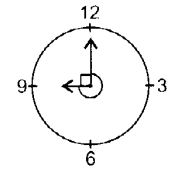
∴ The number of minutes between hour and minute hands of a clock at 9 O’ clock is 15 and 45.
∴ The required angles are 15 × 6° = 90° and 45 × 6° = 270°
Question 5.
If a bicycle wheel has 48 spokes, then the angle between a pair of two consecutive spokes is
![]()
![]()
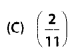
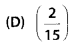
Solution:
(B) : A bicycle wheel has 48 spokes.
∴ The angle formed in circle is 360°.
∴ The angle between a pair of two consecutive
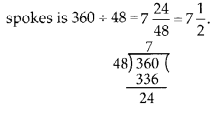
Question 6.
In the given figure, ∠XYZ cannot be written as
(A) ∠Y
(B) ∠ZXY
(C) ∠ZYX
(D) ∠XYP
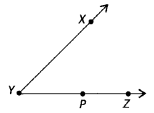
Solution:
(B) : In the given figure, the name of angles formed are
∠XYP, ∠XYZ, ∠PYX and ∠ZYX
Thus, ∠ZXY is not a correct option.
Question 7.
In the given figure, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of ∠BPY is
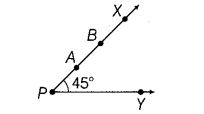
(A) greater than 45°
(B) 45°
(C) less than 45°
(D) 90°
Solution:
(B) : Since, the increase and decrease in the length of arms of an angle does not affect the angle made by them.
∴ ∠BPY = 45°
Question 8.
The number of angles in the given figure is
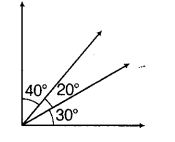
(A) 3
(B) 4
(C) 5
(D) 6
Solution:
(D) : The names of angles formed in the given figure are ∠AOB, ∠AOC, ∠AOD, ∠BOC, ∠BOD and ∠COD.
There are total 6 angles formed.
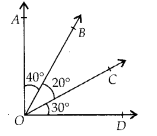
Question 9.
The number of obtuse angles in figure is
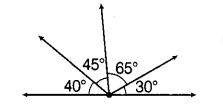
(A) 2
(B) 3
(C) 4
(D) 5
Solution:
(C) : The obtuse angles formed in the
given figure are
∠AOD = 20° + 45° + 65° = 130°
∠BOD = 45° + 65° = 110°, ∠COE = 65° + 30° = 95° and ∠BOE = 45° + 65° + 30° = 140°
Thus, there are total 4 obtuse angles formed.
Question 10.
The number of triangles in the given figure is
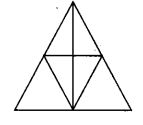
(A) 10
(B) 12
(C) 13
(D) 14
Solution:
(C) : We have,
The names of triangles formed in the given figure are
∆ABC, ∆ABD, ∆ADC, ∆AFG, ∆AEG, ∆AFE, ∆FGD, ∆EGD, ∆FED, ∆FBD, ∆DEC, ∆AFD, ∆AED
Question 11.
If the sum of two angles is greater than 180°, then which of the following is not possible for the two angles?
(A) One obtuse angle and one acute angle
(B) One reflex angle and one acute angle
(C) Two obtuse angles
(D) Two right angles
Solution:
(D) : Since, the sum of two right angles is 180°.
Question 12.
If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?
(A) One obtuse angle and one acute angle
(B) One right angle and one acute angle
(C) Two acute angles
(D) Two right angles
Solution:
(D) : Since, the sum of two right angles is 180°, which is a straight angle, not an obtuse angle.
Question 13.
A polygon has prime number of sides. Its number of sides i$ equal to the sum of the two least consecutive primes. The number of diagonals of the polygon is
(A) 4
(B) 5
(C) 7
(D) 10
Solution:
(B) : We have given, the number of sides of a polygon = Sum of the two least consecutive primes
= 2 + 3 = 5 [ ∵ 2 and 3 are the least consecutive prime numbers]
∴ The number of diagonals \(=\frac{n(n-3)}{2}\) , where
\(=\frac{5(5-3)}{2}=\frac{5 \times 2}{2}=5\)
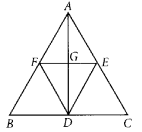
Question 14.
In the given figure, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is
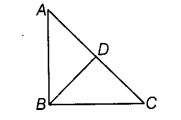
Solution:
(C) : ∵ We have, AB = BC and AD = BD = DC.
∴ ∆ ABD, ∆ BDC and ∆ ABC all are isosceles triangles.
∴ There are 3 isosceles triangles formed in the given figure.
Question 15.
In the given figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is
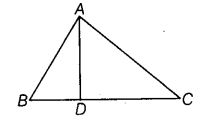
Solution:
(C) : We have, ∠BAC = 90° and AD ⊥ BC
∵ ∠BDA = ∠CDA = ∠BAC = 90°
∴ There are 3 right triangles formed in the given figure.
Question 16.
In the given figure, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆ PQR is
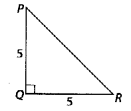
(A) a right triangle but not isosceles
(B) an isosceles right triangle
(C) isosceles but not a right triangle
(D) neither isosceles nor right triangle
Solution:
(B): We have, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm, which shows that in a triangle, two sides are equal and their included angle is 90°.
∴ ∆ PQR is an isosceles right triangle.
Directions: In questions 17 to 31, fill in the blanks to make the statements true.
Question 17.
An angle greater than 180° and less than a complete angle is called ____ .
Solution:
Reflex angle
Question 18.
The number of diagonals in a hexagon is _____ .
Solution:
9 : ∵ Number of diagonals \(=\frac{n(n-3)}{2}\) ,
where n = 6
\(=\frac{6(6-3)}{2}=\frac{6 \times 3}{2}=9\)
Question 19.
A pair of opposite sides of a trapezium are _____ .
Solution:
Parallel
Question 20.
In the given figure, points lying in the interior of the triangle PQR are ____, that in the exterior are ____ and that on the triangle itself are ____ .
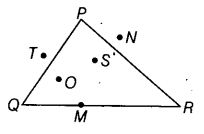
Solution:
O and S; T and N; P, Q, R and M
Question 21.
In the given figure, points A, B, C, D and E are collinear such that AB = BC = CD- DE. Then
![]()
(a) AD = AB + _____
(b) AD = AC +
(c) mid point of AEis
(d) mid point of CE is
(e) AE = ___ × AB
Solution:
(a) BD : AD = AB + BC + CD = AB + BD
(b) CD : AD = AB + BC+CD = AC + CD
(c) C : ∵ AB + BC = CD + DE
⇒ AC = CE
∴ Mid point of AE is C.
(d) D : ∵ CD = DE
∴ Mid point of CE is D.
(e) 4 : ∵ AB + BC + CD + DE = AE
⇒ AB + AB + AB + AB = AE
∴ 4 AB = AE
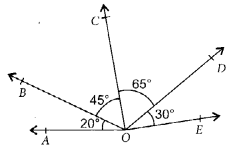
Question 22.
In the given figure.
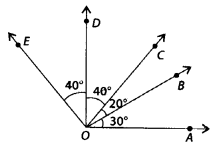
(a) ∠AOD is a/an ____ angle
(b) ∠COA is a/an ____ angle
(c) ∠AOE is a/an ____ angle
Solution:
(a) Right : ∠AOD = 30° + 20° + 40° = 90°
(b) Acute :∠COA = 20° + 30° = 50°
(c) Obtuse : ∠AOE = 40° + 40° + 20° + 30°
= 130°
Question 23.
The number of triangles in figure is _____. Their names are _____ .
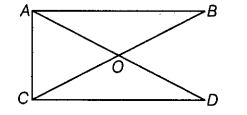
Solution:
5, ∆ AOB, ∆ AOC, ∆COD, ∆ CAB and ∆ ACD
Question 24.
Number of angles less than 180° in given figure is ____ and their names are ____.
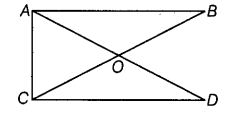
Solution:
12, ∠ABO, ∠BAO, ∠AOB, ∠BOD, ∠COD, ∠ODC, ∠OCD, ∠OCA, ∠CAO, ∠AOC, ∠BAC and ∠ACD.
Question 25.
The number of straight angles in given figure is ___ .
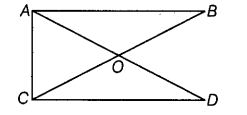
Solution:
4 : The number of straight angles in the given figure is 4.
Question 26.
The number of right angles in a straight angle is ____ and that in a complete angle is ____ .
Solution:
2, 4 : The number of right angles in a straight angle is 2 and that in a complete angle is 4.
Question 27.
The number of common points in the two angles marked in given figure is ____ .
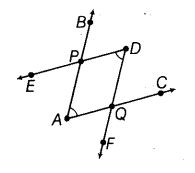
Solution:
Two : The two angles marked; ∠PAQ and ∠PDQ
∴ The number of common points are 2 and these are P and Q.
Question 28.
The number of common points in the two angles marked in given figure is ____ .
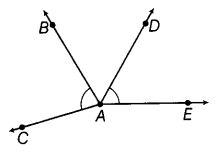
Solution:
One : The two angles marked; ∠CAB and ∠DAE.
∴ The number of common point is 1 and that is A.
Question 29.
The number of common points in the two angles marked in given figure
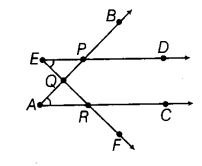
Solution:
Three : There are 3 common points in the two angles marked in the given figure and these are P, Q and R.
Question 30.
The number of common points in the two angles marked in the given figure is ______
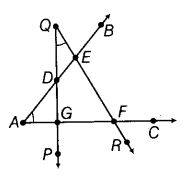
Four : The number of common points in the two angles marked in the given figure is 4 and these are E, D, G and F
Question 31.
The common part between the two angles BAC and DAB in given figure is ____.
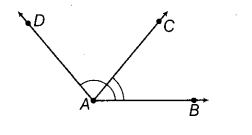
Solution:
Ray \(\overline{A B}\)
Directions: State whether the statements given in questions 32 to 41 are true (T) or false (F).
Question 32.
A horizontal line and a vertical line always intersect at right angles.
Solution:
True
Question 33.
If the arms of an angle on the paper are increased, the angle increases.
Solution:
False
If the arms of an angle on the paper are increasing or decreasing, it doesn’t affect the angle made by them.
Question 34.
If the arms of an angle on the paper are decreased, the angle decreases.
Solution:
False
If the arms of an angle on the paper are increasing or decreasing, it doesn’t affect the angle made by them.
Question 35.
If line PQ || line m, then line segment PQ || m
Solution:
True
Question 36.
Two parallel lines meet each other at some point.
Solution:
False
Two lines in a plane which do not meet even when produced indefinitely in either direction, are known as parallel lines.
Question 37.
Measures of ∠ABC and ∠CBA in given figure are the same.
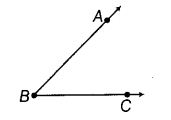
Solution:
True
∵ ∠ABC is same as ∠CBA.
Question 38.
Two line segments may intersect at two points.
Solution:
False
The intersecting point of any two line segments is only one.
Question 39.
Many lines can pass through two given points.
Solution:
False
∵ There is only one line which passes through two given points.
Question 40.
Only one line can pass through a given point.
Solution:
False
∵ There are infinite number of lines which passes through a given point.
Question 41.
Two angles can have exactly five points in common.
Solution:
False
∵ It can have any number of points.
Question 42.
Name all the line segments in given figure.
![]()
Solution:
The line segments are AB, BC, CD, DE, AC, AD, AE, BD, BE and CE
Question 43.
Name the line segments shown m given figure.
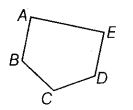
Solution:
The line segments are
AB, BC, CD, DE and EA
Question 44.
State the mid points of all the sides of given figure.
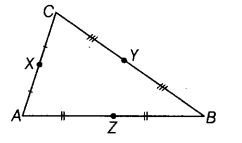
Solution:
X is a mid-point of AC,
Y is a mid-point of BC and
Z is a mid-point of AB.
Question 45.
Name the vertices and the line segments in given figure.
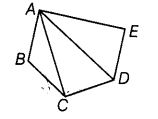
Solution:
The vertices are : A, B, C, D and E.
The line segments are : AB, BC, CD, DE, EA, AC and AD.
Question 46.
Write down fifteen angles (less than 180°) involved in given figure.
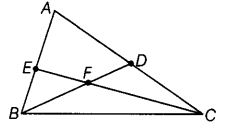
Solution:
The names of fifteen angles (less than 180°) involved in figure are :
∠AEC, ∠ADB, ∠EAD, ∠EFD, ∠EFB, ∠DFC, ∠FBC, ∠FCB, ∠BFC, ∠ABC, ∠ACB, ∠DCF, ∠FDC, ∠EBF and ∠BEF.
Question 47.
Name the following angles of given figure, using three letters:
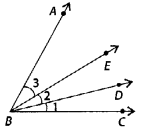
(a) ∠1
(b) ∠2
(c) ∠3
(d) ∠1 + ∠2
(e) ∠2 + ∠3
(f) ∠1 + ∠2 + ∠3
(g) ∠CBA – ∠1
Solution:
(a) ∠1 = ∠CBD
(b) ∠2 = ∠DBE
(c) ∠3 = ∠EBA
(d) ∠1 + ∠2 = ∠CBD + ∠DBE = ∠CBE
(e) ∠2 + ∠3 = ∠DBE + ∠EBA = ∠DBA
(f) ∠l + ∠2 + ∠3 = ∠CBD + ∠DBE + ∠EBA
= ∠CBA
(g) ∠CBA – ∠1 = ∠CBA – ∠CBD = ∠DBA
Question 48.
Name the points and then the line segments in each of the following figures:
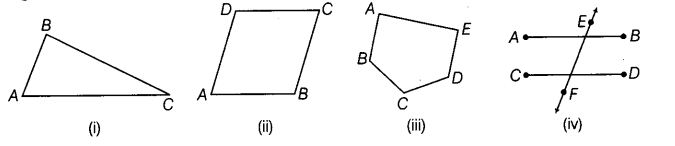
Solution:
(i) Name of the points ➝ A, B and C. Name of the line segments ➝ AB, BC and CA.
(ii) Name of the points ➝ A, B, C and D. Name of the line segments ➝ AB, BC, CD and DA.
(iii) Name of the points ➝ A, B, C, D and E. Name of the line segments ➝ AB, BC, CD, DE and EA.
(iv) Name of the points ➝ A, B, C, D, E and F.
Name of the line segments ➝ AB, CD and EF.
Question 49.
Which points in given figures, appear to be mid-points of the line segments? When you locate a mid-point, name the two equal line segments formed by it.
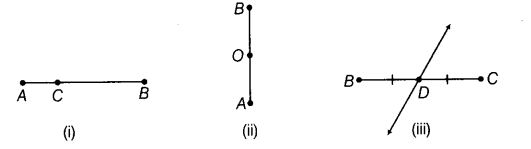
Solution:
(i) The given figure shows there is no mid-point.
(ii) The given figure shows that O is the mid-point of ZB and the name of the two equal line segments are AC and OB.
(iii) The given figure shows that D is the mid-point of BC and the name of the two equal line segments are BD and DC.
Question 50.
Is it possible for the same
(a) line segment to have two different lengths?
(b) angle to have two different measures?
Solution:
(a) No, it is not possible for the same line segment to have two different lengths.
(b) No, it is not possible for the same angle to have two different measures.
Question 51.
Will the measure of ∠ABC and of ∠CBD make measure of ∠ABD in given figure?
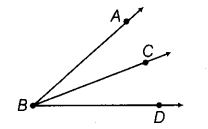
Solution:
Yes, ∵ ∠ABD = ∠ABC + ∠CBD
⇒ ∠ABD is the sum of ∠ABC and ∠CBD
Question 52.
Will the lengths of line segment AB and line segment BC make the length of line segment AC in given figure?
![]()
Solution:
Yes, ∵ the length of line segment AC is the sum of the lengths of line segment AB and BC.
Question 53.
Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate.
Solution:
Do it yourself.
Question 54.
Look at a given figure. Mark a point
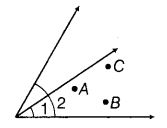
(a) A which is in the interior of both ∠1 and ∠2.
(b) B which is in the interior of only ∠1.
(c) Point C in the interior of ∠1.
Now, state whether points B and C lie in the interior of ∠2 also.
Solution:
Yes, the given figure shows that the points B and C lie in the interior of ∠2 also.
Question 55.
Find out the incorrect statement, if any, in the following : An angle is formed when we have
(a) two rays with a common end-point
(b) two line segments with a common end-point
(c) a ray and a line segment with a common end-point
Solution:
All the three statements (a), (b) and (c) are incorrect.
∵ The common initial point of two rays forms an angle.
Question 56.
In which of the following figures,
(a) perpendicular bisector is shown?
(b) bisector is shown?
(c) only bisector is shown?
(d) only perpendicular is shown?
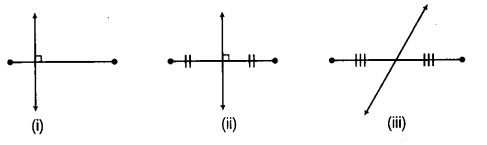
Solution:
(a) Figure (ii) shows the perpendicular bisector
(b) Figure (ii) and (iii) shows the bisector.
(c) Figure (iii) shows only the bisector.
(d) Figure (i) shows only the perpendicular.
Question 57.
What is common in the following figures (i) and (ii)?
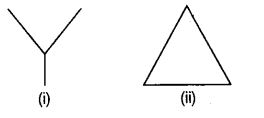
Is figure (i) that of triangle ? if not, why?
Solution:
Both the figures (i) and (ii) have 3 line segments.
No, Fig. (i) is not a triangle since the three line segments does not form a closed figure.
Question 58.
If two rays intersect, will their point of intersection be the vertex of an angle of which the rays are the two sides?
Solution:
Yes
Question 59.
In given figure,
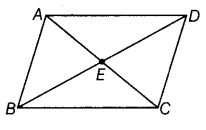
(a) name any four angles that appear to be acute angles.
(b) name any two angles that appear to be obtuse angles.
Solution:
(a) Acute angles : ∠ADE, ∠AEB, ∠ABE and ∠ECD.
(b) Obtuse angles : ∠BCD and ∠BAD.
Question 60.
In given figure,
![]()
(a) is AC + CB = AB ?
(b) is AB + AC= CB ?
(c) is AB + BC = CA ?
Solution:
(a) Yes, AC + CB = AB
(b) No, AB – AC = CB
(c) No, AB – BC = CA
Question 61.
In given figure
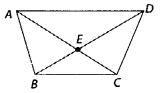
(a) What is AB + BC?
(b) What is AC – EC?
(c) What is BD – BE?
(d) What is BD – DE?
Solution:
(a) AE + EC = AC
(b) AC – EC = AE
(c) BD – BE = ED
(d) BD – DE = BE
Question 62.
Using the information given, name the right angles in each part of given figures.
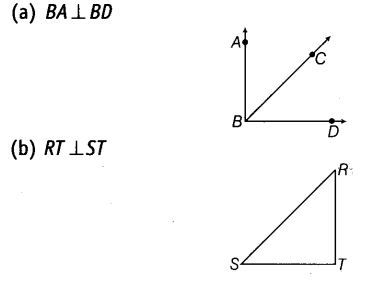
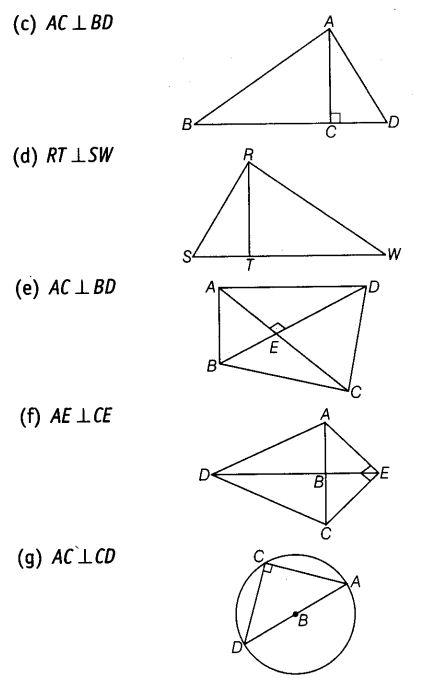
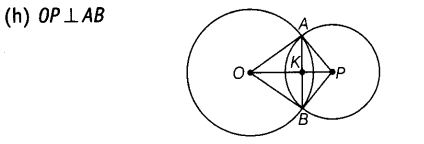
Solution:
(a) ∵ BA ⊥ BD,
∴ The right angle is ∠ABD
(b) ∵ RT ⊥ ST, ∴ The right angle is ∠RTS
(c) ∵ AC ⊥ BD,
∴ The right angles are ∠ACD and ∠ACB
(d) ∵ RS ⊥ RW,
∴ The right angle is ∠SRW
(e) ∵ AC ⊥ BD,
∴ The right angles are ∠AED, ∠AEB, ∠BEC and ∠CED
(f) ∵ AE ⊥ CE,
∴ The right angle is ∠AEC
(g) ∵ AC ⊥ CD,
∴ The right angle is ∠ACD
(h) ∵ OP ⊥ AB,
∴ The right angles are ∠AKO, ∠AKP, ∠BKO and ∠BKP.
Question 63.
What conclusion can be drawn from each part of given figures, if
(a) DB is the bisector of ∠ADC?
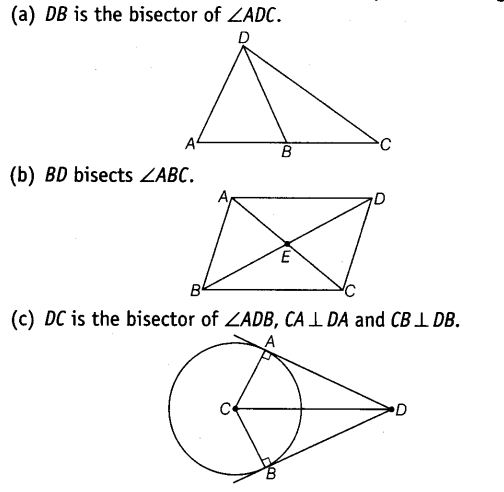
Solution:
(a) ∵ DB is the bisector of ∠ADC.
∴ ∠ADB = ∠CDB
(b) ∵ BD bisects ZABC.
∴ ∠ABD = ∠CBD
(c) ∵ DC is the bisector of ∠ADB,
CA ⊥ DA and CB ⊥ DB
∠ADC = ∠BDC, ∠CAD = ∠CBD = 90°
Question 64.
An angle is said to be trisected, if it is divided into three equal parts. If in a given figure, ∠BAC = ∠CAD = ∠DAE, how many trisectors are there for ∠BAE ?
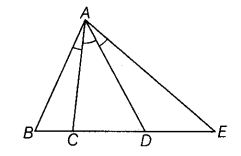
Solution:
We have given, ∠BAC = ∠CAD = ∠DAE
∴ There are two trisectors namely, AC and AD.
Question 65.
How many points are marked in given figure?
![]()
Solution:
Two points A and B are marked.
Question 66.
How many line segments are there in given figure?
![]()
Solution:
Only one line segment, AB is there.
Question 67.
In given figure, how many points are marked? Name them.
![]()
Solution:
Three points A, B and C are marked.
Question 68.
How many line segments are there in given figure? Name them.
![]()
Solution:
Three line segments, namely AB, BC and AC are there.
Question 69.
In given figure, how many points are marked? Name them.
![]()
Solution:
Four points A, B, C and D are marked.
Question 70.
In given figure how many line segments are there? Name them.
![]()
Solution:
Six line segments, namely AB, AC, AD, BC, BD and CD.
Question 71.
In given figure, how many points are marked? Name them.
![]()
Solution:
Five points are marked, namely A, B, D, E and C.
Question 72.
In given figure how many line segments are there? Name them.
![]()
Solution:
Ten line segments, namely AB, AD, AE, AC, BD, BE, BC, DE, DC and EC.
Question 73.
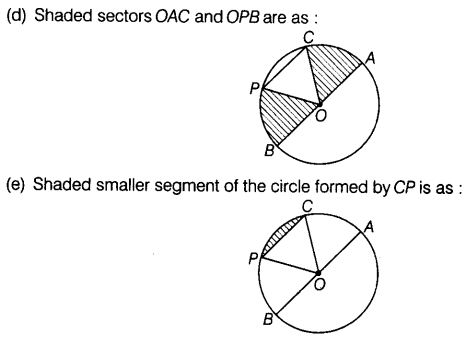
In given figure, O is the centre of the circle.
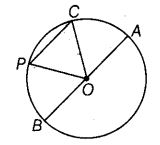
(a) Name all chords of the circle.
(b) Name all radii of the circle.
(c) Name a chord, which is not the diameter of the circle.
(d) Shade sectors OAC and OPB.
(e) Shade the smaller segment of the circle formed by CP.
Solution:
(a) Name of chords : PC and BA.
(b) Name of radii : PO, OC, OB and OA.
(c) PC is a chord which is not the diameter of the circle.
Question 74.
Can we have two acute angles whose sum is
(a) an acute angle? Why or why not?
(b) a right angle? Why or why not?
(c) an obtuse angle? Why or why not?
(d) a straight angle? Why or why not?
(e) a reflex angle? Why or why not?
Solution:
(a) Yes, ∵ the sum of two acute angles can be the acute angle.
E.g„ 30° and 40° are two acute angles and their sum = 30° + 40° = 70°, which is also an acute angle.
(b) Yes, ∵ the sum of two acute angles can be a right angle.
E.g., 30° and 60° are two acute angles and their sum = 30° + 60° = 90°, which is a right angle.
(c) Yes, ∵ the sum of two acute angles can be an obtuse angle.
E.g., 45° and 60° are two acute angles and their sum = 45° + 60° = 105°, which is an obtuse angle.
(d) No, ∵ the sum of two acute angles is always less than 180°.
(e) No, ∵ the sum of two acute angles is always less than 180°.
Question 75.
Can we have two obtuse angles whose sum is
(a) a reflex angle? Why or why not?
(b) a complete angle? Why or why not?
Solution:
(a) Yes, ∵ the sum of two obtuse angles is always greater than 180°.
E.g., 135° and 100° are two obtuse angles and their sum = 135° + 100° = 235°, which is greater than 180°.
(b) No, ∵ the sum of two obtuse angles is greater than 180° but less than 360°. In the above example, we can see that the sum of 135° and 100° i.e., 235° is greater than 180° but less than 360°.
Question 76.
Write the name of
(a) vertices
(b) edges, and
(c) faces of the prism shown in given figure.
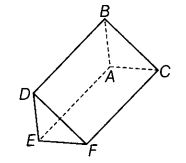
Solution:
(a) Vertices : A, B, C, D, E and F.
(b) Edges : AB, BC, AC, DF, FC, BD, EF, ED and AE.
(c) Faces : EACF, EDBA, ABC, DEF and DBCF.
Question 77.
How many edges, faces and vertices are there in a sphere?
Solution:
In a sphere, edges – 0, faces – 0 and vertices – 0.
Question 78.
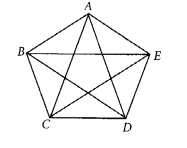
Draw all the diagonals of a pentagon ABCDE and name them.
Solution:
The diagonals of a pentagon ABCDE are AC, AD, BE, BD and EC
We hope the NCERT Exemplar Class 6 Maths Chapter 2 Geometry will help you. If you have any query regarding NCERT Exemplar Class 6 Maths Solutions Chapter 2 Geometry, drop a comment below and we will get back to you at the earliest.