NCERT Exemplar Class 10 Maths Chapter 9 Circles are part of NCERT Exemplar Class 10 Maths. Here we have given NCERT Exemplar Class 10 Maths Chapter 9 Circles.
NCERT Exemplar Class 10 Maths Chapter 9 Circles
Exercise 9.1
Choose the correct answer from the given four options:
Question 1
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is
(A) 3 cm
(B) 6 cm
(C) 9 cm
(D) 1 cm
Solution:
(B) Let O be the centre of two concentric circles C1 and C2, whose radii are r1 = 4 cm and r2 = 5 cm.
Now, we draw a chord AC of circle C2, which touches the circle Q at B.
Also, join OB, which is perpendicular to AC.
[∵ Tangent at any point of circle is perpendicular to radius through the point of contact]
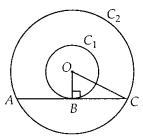
Now, in right angled ∆OBC,
OC2 = BC2 + BO2 [By Pythagoras theorem]
⇒ 52 = BC2 + 42
⇒ BC2 = 25 – 16 = 9
⇒ BC = 3 cm
∴ Length of chord AC = 2BC = 2 x 3 = 6 cm
Question 2
In figure, if ∠AOB = 125°, then ∠COD is equal to
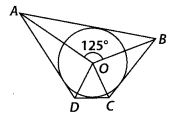
(A) 62.5°
(B) 45°
(C) 35°
(D) 55°
Solution:
(D) We know that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
⇒ ∠AOB + ∠COD = 180°
⇒ ∠COD = 180° – ∠AOB
= 180° – 125° = 55°
Question 3
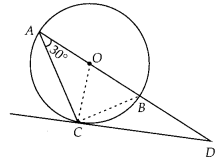
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
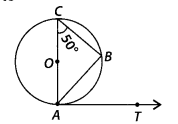
(A) 65°
(C) 50°
(B) 60°
(D) 40°
Solution:
(C) In figure, AOC is a diameter of the circle. We know that, diameter subtends an angle 90° at the circle.
So, ∠ABC = 90°
In ∆ACB,
∠A + ∠B + ∠C = 180° [Angle sum property]
⇒ ∠A + 90° + 50° = 180°
⇒ ∠A + 140° = 180°
⇒ ∠A = 180° – 140° = 40°
⇒ ∠A or ∠OAB = 40°
Since, AT is the tangent to the circle at point A. Therefore, OA is perpendicular to AT.
∠OAT = 90°
⇒ ∠OAB + ∠BAT =90°
On putting ∠OAB = 40°, we get
⇒ ∠BAT =90° -40° = 50°
Hence, the value of ∠BAT is 50°.
Question 4
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(A) 60 cm2
(B) 65 cm2
(C) 30 cm2
(D) 32.5 cm2
Solution:
(A) Firstly, draw a circle of radius 5 cm with centre O. P is a point at a distance of 13 cm from O. A pair of tangents PQ and PR are drawn.
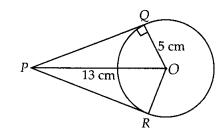
Thus, quadrilateral PQOR is formed.
∵ OQ ⊥ QP [since, QP is a tangent line]
In right angled ∆PQO,
OP2 = OQ2 + QP2
⇒ 132 = 52 + QP2
⇒ QP2 = 169 – 25 = 144
⇒ QP = 12 cm
Now, area of ∆OQP = \(\frac { 1 }{ 2 }\) x QP x QO
= \(\frac { 1 }{ 2 }\) x 12 x 5 = 30 cm2
∴ Area of quadrilateral PQOR = 2 x ar ∆OQP
= 2 x 30 = 60 cm2
Question 5
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XT and at a distance 8 cm from A is
(A) 4 cm
(B) 5 cm
(C) 6 cm
(D) 8 cm
Solution:
(D) First, draw a circle of radius 5 cm with centre O. A tangent XY is drawn at point A.
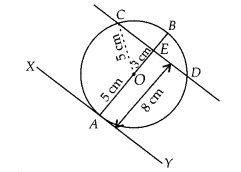
A chord CD is drawn which is parallel to XY and at a distance of 8 cm from A.
Now, ∠OAY = 90°
[ ∵ Tangent at any point of circle is perpendicular to the radius through the point of contact]
∠OAY +∠OED= 180°
[ ∵ Sum of cointerior angles is 180°]
⇒ ∠OED = 180° – 90° = 90°
Also, AE = 8 cm Join OC.
OC = 5 cm [Radius of circle]
OE = AE-OA = 8 – 5 = 3 cm
Now, in right angled ∆OEC,
OC2 = OE2 + EC2 [By Pythagoras theorem]
⇒ EC2 = OC2 – OE2
⇒ EC2 = 52 – 32
⇒ EC2 = 25 – 9 = 16
⇒ EC = 4 cm
Since, perpendicular from centre to the chord bisects the chord.
∴ CE = ED
⇒ CD = 2 x EC
⇒ CD = 2 x 4
⇒ CD = 8 cm
Question 6
In figure, ATis a tangent to the circle with centre O such that 07 = 4 cm and ∠OTA = 30°. Then AT is equal to
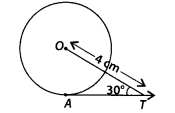
(A) 4cm
(B) 2cm
(C) 2√3cm
(D) 4√3cm
Solution:
(C) Join OA.
We know that, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
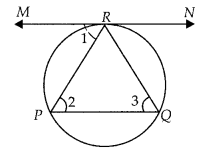
Question 7
In figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 500 with PQ, then ∠POQ is equal to
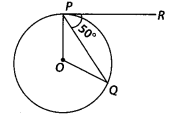
(A) 100°
(B) 80°
(C) 90°
(D) 75°
Solution:
(A) Given, ∠QPR = 50°
We know that, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠OPR = 90°
⇒ ∠OPQ + ∠QPR = 90°
⇒ ∠OPQ = 90° – 50° = 40° [ ∵ ∠QPR = 50°]
Now, OP = OQ = radius of circle
∴ ∠OQP = ∠OPQ = 40°
[Angles opposite to equal sides are equal]
In ∆OPQ,
∠O + ∠OPQ + ∠Q = 180° [Angle sum property]
⇒ ∠POQ = 180° – (40 + 40°)
= 180° – 80°
[∵ ∠OPQ = 40° = ∠Q]
⇒ ∠POQ = 100°
Question 8
In figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to
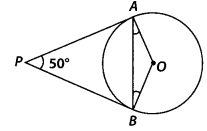
(A) 25°
(B) 30°
(C) 40°
(D) 50°
Solution:
(A) Given, PA and PB are tangent lines.
∴ PA = PB [∵ Length of tangents drawn from an external point to a circle is equal]
∠PBA = ∠PAB = θ (say)
In ∆PAB,
∠P + ∠A + ∠B = 180° [Angle sum property]
⇒ 50° + θ + θ= 180°
⇒ 20 = 180° – 50° = 130°
⇒ θ = 65°
Also, OA ⊥ PA
[∵ Tangent at any point of a circle is perpendicular to the radius through the point of contact]
∴ ∠PAO = 90°
⇒ ∠PAB + ∠BAO = 90°
⇒ 65° + ∠BAO = 90°
⇒ ∠BAO = 90° – 65° = 25°
⇒ ∠OAB = 25°
Question 9
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then length of each tangent is equal to

Solution:
(D) Let P be an external point and a pair of tangents is drawn from point P such that the angle between two tangents is 60°.
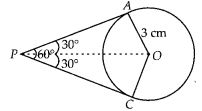
Join OA and OP.
Also, OP is a bisector line of ∠APC.
∴ ∠APO = ∠CPO = 30°
Also, OA ⊥ AP
[Tangent at any point of a circle is perpendicular to the radius through the point of contact.]
∴∠OAP = 90°
In right angled ∆OAP,
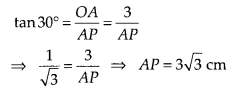
Hence, the length of each tangent is 3√3 cm.
Question 10
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to
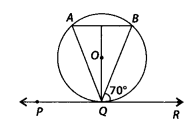
(A) 20°
(B) 40°
(C) 35°
(D) 45°
Solution:
(B) Given, AB ॥ PR
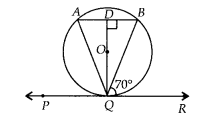
∴ ∠ABQ = ∠BQR = 70° [Alternate angles]
Also, QD is perpendicular to AB and QD bisects AB.
In ∆QDA and ∆QDB,
∠QDA = ∠QDB [90° each]
AD = BD
QD = QD [Common side]
∆ADQ ≅ ∆BDQ [by SAS congruency]
⇒ ∠QAD = ∠QBD [CPCT] …(i)
But ∠QBD = ∠ABQ = 70°
⇒ ∠QAD = 70° [From (i)]
Now, in ∆ABQ, ∠A + ∠B + ∠AQB = 180°. [Angle sum property]
⇒ ∠AQB = 180° – (70° + 70°) = 40°
Exercise 9.2
Write ‘True’ or ‘False’ and justify your answer in each of the following:
Question 1
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
Solution:
False
Since a chord AB subtends an angle of 60° at the centre of a circle.
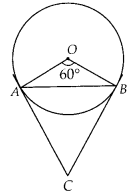
⇒ ∠AOB = 60°
As OA = OB = Radius of the circle
∠OAB = ∠OBA = 60°
[∵ Angles opposite to equal sides are equal]
The tangent at points A and B is drawn, which intersect at C.
We know, OA ⊥ AC and OB ⊥ BC.
∴ ∠OAC = 90° and ∠OBC = 90°
⇒ ∠OAB + ∠B AC = 90° and ∠OBA + ∠ABC = 90°
⇒ ∠BAC = 90° – 60° = 30° and ∠ABC = 90° – 60° = 30°
In ∆ABC,
∠BAC + ∠CBA + ∠ACB = 180°
[Angle sum property]
⇒ ∠ACB = 180° – (30° + 30°) = 120°
Question 2
The length of tangent from an external point on a circle is always greater than the radius of the circle.
Solution:
False
Because the length of tangent from an external point P on a circle may or may not be greater than the radius of the circle.
Question 3
The length of tangent from an external point P on a circle with centre O is always less than OP.
Solution:
True
PT is a tangent drawn from an external point P. Join OT
∵ OT ⊥ PT
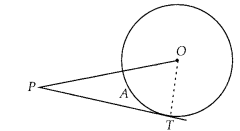
So, OTP is a right angled triangle formed.
In right angled triangle, hypotenuse is always greater than any of the two sides of the triangle.
∴ OP > PT or PT< OP
Question 4
The angle between two tangents to a circle may be 0°.
Solution:
True
This may be possible only when both tangent lines coincide or are parallel to each other.
Question 5
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = a√2.
Solution:
True
From point P, two tangents are drawn.
Given, OT = a
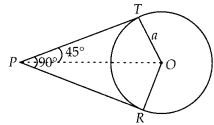
Also, line OP bisects the ∠RPT
∴ ∠TPO = ∠RPO = 45°
Also, OT ⊥ TP ⇒ ∠OTP = 90°
In right angled ∆OTP,
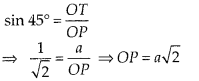
Question 6
If angle between two tangents drawn from a point P to a circle of radius a and centre 0 is 60°, then OP = a√3.
Solution:
False
From point P, two tangents are drawn.
Given, OT= a
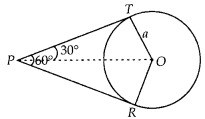
Also, line OP bisects the ∠RPT.
∴∠TPO = ∠RPO = 30°
Also, OT ⊥ PT
⇒ ∠OTP = 90°
In right angled ∆OTP,
sin 30° = \(\frac { OT }{ OP }\) ⇒ \(\frac { 1 }{ 2 }\) = \(\frac { a }{ OP }\)
⇒ OP = 2a
Question 7
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
Solution:
True
Let EAF be tangent to the circumcircle of ∆ABC.
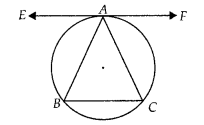
To prove: EAF ॥ BC
We have, ∠EAB = ∠ACB …(i)
[Angle between tangent and chord is equal to angle made by chord in the alternate segment]
Here, AB = AC
⇒ ∠ABC = ∠ACB …(ii)
From equation (i) and (ii), we get
∠EAB = ∠ABC
∵ Alternate angles are equal.
⇒ EAF ॥ BC
Question 8
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
Solution:
False
Given that PQ is any line segment and S1, S2, S3, S4, …….. circles touch the line segment PQ at a point A. Let the centres of the circles S1, S2, S3, S4, ……….. be C1, C2, C3, C4, ……… respectively.
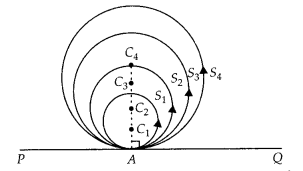
To prove: Centres of the circles lie on the perpendicular bisector of PQ.
Joining each centre of the circles to the point A on the line segment PQ by line segment i.e., C1A, C2A, C3A, C4A,… and so on.
We know that, if we draw a line from the centre of a circle to its tangent line, then the line is always perpendicular to the tangent line. But it does not bisect the line segment PQ.
Question 9
If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
Solution:
True
We draw two circles with centre C1 and C2 passing through the end points P and Q of a line segment PQ. We know that the perpendi-cular bisector of a chord of circle always passes through the centre of the circle.
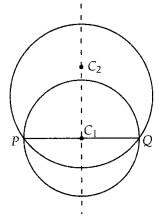
Thus, perpendicular bisector of PQ passes through C1 and C2 . Similarly, all the circle passing through the end points of line segment PQ, will have their centres on the perpendicular bisector of PQ.
Question 10
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
Solution:
True
To prove: BC = BD
Join BC and OC.
Given, ∠BAC = 30°
⇒ ∠BCD = 30°
[Angle between tangent and chord is equal to angle made by chord in the alternate segment]
∵ OC ⊥ CD and OA = OC = radius
⇒ ∠OAC = ∠OCA = 30°
∠ACD = ∠ACO + ∠OCD = 30° + 90° = 120°
In ∆ACD,
∠DAC + ∠ACD + ∠CDA = 180° [Angle sum property]
⇒ 30° + 120° + ∠CDA = 180°
⇒ ∠CDA = 180° – (30° + 120°) = 30°
∠CDA = ∠BCD
⇒ BC = BD
[∵ Sides opposite to equal angles are equal]
Exercise 9.3
Question 1
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
Solution:
Let C1 and C2 be the two circles having same centre O. AC is a chord which touches C1 at point D.
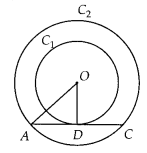
Join OD.
Also, OD ⊥ AC
∴ AD = DC = 4 cm
[Perpendicular line OD bisects the chord]
In right angled ∆AOD,
OA2 = AD2 + OD2 [By Pythagoras theorem]
⇒ OD2 = 52 – 42
⇒ OD2 = 25 – 16 = 9
⇒ OD = 3 cm
∴ Radius of the inner circle is OD = 3 cm
Question 2
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
Solution:
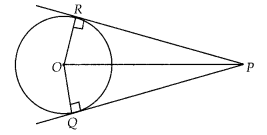
To prove: QORP is a cyclic quadrilateral.
Since, PR and PQ are tangents.
∴ OR ∠ PR and OQ ∠ PQ
⇒ ∠ORP = ∠OQP = 90°
Hence, ∠ORP + ∠OQP = 180°
Also, in quadrilateral QORP,
∠ORP + ∠OQP + ∠ROQ + ∠QPR = 360°
⇒ 180° + ∠ROQ + ∠QPR = 360°
⇒ ∠ROQ + ∠QPR = 180°
∵ If sum of opposite angles in quadrilateral is 180°, then the quadrilateral is cyclic.
⇒ QORP is cyclic quadrilateral.
Question 3
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
Solution:
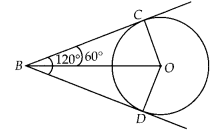
To prove: BO = 2BC
Given, ∠DBC = 120°
Join OC, OD and BO.
Since, BC and BD are tangents.
∴ OC ⊥ BC and OD ⊥ BD
We know, OB is the angle bisector of ∠DBC.
∴∠OBC = ∠DBO = 60°
In right angled ∆OBC,
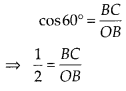
⇒ OB = 2 BC
Also, BC = BD
[Tangent drawn from external point to circle are equal]
OB = BC + BC
⇒ OB = BC + BD
Question 4
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of angle formed by tangents..
Solution:
Given, two tangents PQ and PR are drawn from an external points P to a circle with centre O.
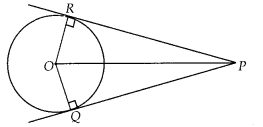
To prove: Centre of a circle touching two intersecting lines lies on the angle bisector of angle formed by tangents.
Construction: Join OR and OQ.
In ∆POR and ∆POQ,
∠PRO = ∠PQO = 90°
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
OR = OQ [Radii of same circle]
OP = OP [Common side]
∆ PRO ≅ ∆ PQO [RHS criterion]
Hence, ∠RPO = ∠QPO [By CPCT]
Thus, O lies on angle bisector of ∠RPQ.
Question 5
In figure, AB and CD are common tangents to two circles of unequal radii.
Prove that AB = CD.
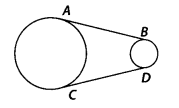
Solution:
Given, AB and CD are common tangents to two circles of unequal radii.
To prove : AB = CD
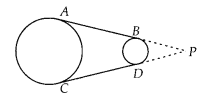
Construction: Extend AB and CD, to intersect at P.
PA = PC
[∵ Length of tangents drawn from an external point to a circle is equal]
Also, PB = PD
∴PA – PB = PC – PD
⇒ AB = CD
Question 6
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
Solution:
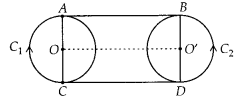
Join OO’
Since, OA = O’B [Given]
Also, ∠OAB = ∠O’BA = 90°
[Tangent at any point of a circle is perpendicular to the radius at the point of contact]
Since, perpendicular distance between two straight lines at two different points is same.
⇒ AB is parallel to OO’
Similarly, CD is parallel to OO’
⇒AB ॥ CD
Also, ∠OAB = ∠OCD = ∠O’BA = ∠O’DC = 90°
⇒ ABCD is a rectangle.
Hence, AB = CD.
Question 7
In figure, common tangents AB and CD to two circles intersect at E.
Prove that AB = CD.
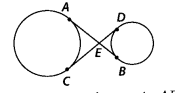
Solution:
Given, common tangents AB and CD to two circles intersecting at E.
To prove: AB = CD
∵ The length of tangents drawn from an external point to a circle is equal
∴ EB = ED and EA = EC
On adding, we get
EA + EB = EC + ED
⇒ AB = CD
Question 8
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Solution:
Given, chord PQ is parallel to tangent at R.
To prove : R bisects the arc PRQ.
∠1 = ∠2 [Alternate interior angles]
∠1 = ∠3 [Angle between tangent and chord is equal to angle made by chord in alternate segment]
⇒ ∠2 = ∠3
⇒ PR = QR [Sides opposite to equal angles are equal]
⇒ arc PR = arc QR
So, R bisects PQ.
Question 9
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
Solution:
To prove : ∠1 = ∠2
Let RQ be a chord of the circle. Tangents are drawn at the points R and Q.
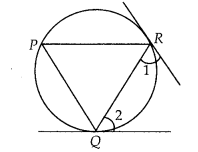
Let P be another point on the circle, then join PQ and PR.
Since, at point Q, there is a tangent.
∠2 = ∠P [Angles in alternate
segments are equal] Since, at point R, there is a tangent.
∴ ∠1 = ∠P [Angles in alternate segments are equal]
∴ ∠1 = ∠2 = ∠P
⇒ ∠1 = ∠2
Question 10
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Solution:
Given, AB is a diameter of the circle.
A tangent is drawn at point A.
Draw a chord CD parallel to tangent MAN.
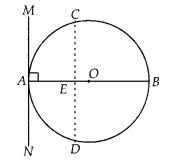
So, CD is a chord of the circle and OA is radius of the circle.
∴ ∠MAO = 90°
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
⇒ ∠CEO = ∠MAO [Corresponding angles]
∴ ∠CEO = 90°
Thus, OE bisects CD,
[Perpendicular from centre of circle to chord bisects the chord]
Similarly, diameter AB bisects all chords which are parallel to the tangent at the point A.
Exercise 9.4
Question 1
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
Solution:
Given, a hexagon ABCDEF circumscribes a circle.
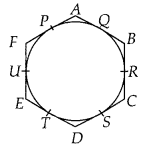
To prove : AB + CD + EF = BC + DE + FA
∵ AQ = AP
QB = BR
CS = CR
DS = DT
EU = ET
UF = FP
[Tangents drawn from an external point to a circle are equal]
AB + CD + EF = (AQ + QB) + (CS + SD) + (EU + UF) = (AP + BR) + (CR + DT) + (ET + FP)
= (AP + FP) + (BR + CR) + (DT + ET)
= AF + BC + DE
⇒ AB + CD + EF = AF + BC + DE
Question 2
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F respectively, prove that BD = s – b.
Solution:
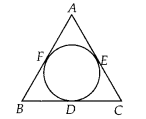
Given, BC = a, CA = b and AB = c
Since, tangents drawn from an external point to the circle are equal in length.
∴ BD = BF = x (say)
DC = CE = y (say)
and AE = AF = 2 (say)
Now, BC + CA + AB = a + b + c
⇒ (BD + DC) + (CE + EA) + (AF + FB) = a + b + c
⇒ (x + y) + (y + z) + (z + x) = a + b + c
⇒ 2(x + y + z) = 2s
[ ∵ 2s = a + b + c = perimeter of ∆ABC]
⇒ s = x + y + z
⇒ x = s – (y + z)
⇒ BD = s – b [∵ b = AE + EC = z + y]
Question 3
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of the triangle PCD.
Solution:
∵ Tangents from an external point to a circle are equal in length.
∴ CE = CA, DE = DB and PA = PB.
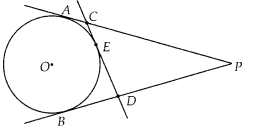
Perimeter of ∆PCD = PC + CD + PD
= PC + CE + ED + PD
= PC + CA + DB + PD
= PA + PB
= 2PA = 2 x 10 = 20 cm
Question 4
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
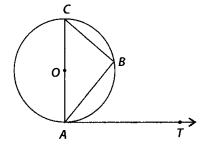
Solution:
Since, AC is a diameter line, so angle in semi-circle formed is 90°.
i.e., ∠ABC = 90°
In ∆ABC,
∠CAB + ∠ABC + ∠BCA = 180° [Angle sum property]
⇒ ∠CAB + ∠BCA = 180°-90° = 90° ,..(i)
Since, diameter of a circle is perpendicular to the tangent.
i.e., CA ⊥ AT
∴ ∠CAT = 90°
⇒ ∠CAB + ∠BAT =90° …(ii)
From equation (i) and (ii),
∠CAB + ∠ACB = ∠CAB + BAT
⇒ ∠ACB = ∠BAT
Question 5
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.
Solution:
Here, two circles are of radii OP = 3 cm and O’P = 4 cm.
These two circles intersect at P and Q.
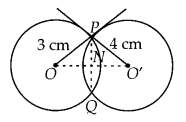
Here, OP and O’P are two tangents drawn at point P.
∠OPO’ = 90° [Tangent at any point of circle is perpendicular to radius through the point of contact]
Join OO’ and PQ such that OO’ and PQ intersect at point N.
In right angled ∆OPO’,
(OO’)2 = (OP)2 + (PO’)2 [By Pythagoras theorem]
⇒ (OO’)2 = (3)2 + (4)2 = 25
⇒ OO’ = 5 cm
Also, PN ⊥ OO’
Let ON = x, then NO’ = 5 – x
In right angled ∆ONP,
(OP)2 = (ON)2 + (NP)2 [By Pythagoras theorem]
⇒ (NP)2 = 32 – x2 = 9 – x2 …(i)
and in right angled ∆PNO’,
(PO’)2 = (PN)2 + (NO’)2 [By Pythagoras theorem]
⇒ (4)2 = (PN)2 + (5 – x)2
⇒ (PN)2 = 16- (5 -x)2 …(h)
From equation (i) and (ii),
9 -x2 = 16 – (5 -x)2
⇒ 7 + x2 – (5 – x)2 = 0
⇒ 7 + x2 -(25 + x2 – 10x) = 0
⇒ 10x = 18
∴ x = 1.8
Again, in right angled ∆OPN,
OP2 = (ON)2 + (NP)2 [By Pythagoras theorem]
⇒ 32= (1.8)2 + (NP)2
⇒ (NP)2 = 9 – 3.24 = 5.76
⇒ NP = 2.4
∴ Length of common chord,
PQ = 2PN = 2 x 2.4 = 4.8 cm
Question 6
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC.
Solution:
Let O be the centre of the given circle. Suppose, the tangent at P meets BC at Q. Join BP.
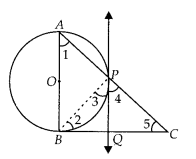
To prove: BQ = QC
∠ABC = 90° [Given]
In ∆ABC, ∠1 + ∠5 = 90° [Angle sum property, ∠ABC = 90°]
∠3 = ∠1 [Angle between tangent and the chord equals angle made by the chord in alternate segment]
⇒ ∠3 + ∠5 = 90° …(i)
Also, ∠APB = 90° [Angle in semi-circle]
∠APB + ∠BPC = 180°
∴ 90° + ∠3 + ∠4 = 180°
⇒ ∠3 + ∠4 = 90° …(ii)
From equations (i) and (ii), we get ∠3 + ∠5 = ∠3 + ∠4
⇒ ∠5 = ∠4
⇒ PQ = QC [Sides opposite to equal angles are equal]
Also, QP = QB
[tangents drawn from an external point to a circle are equal]
⇒ QB = QC
⇒ PQ bisects BC.
Question 7
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
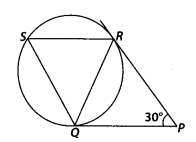
Solution:
PQ and PR are two tangents drawn from an external point P.
∴ PQ = PR
[Lengths of tangents drawn from an external point to a circle are equal]
⇒ ∠PQR = ∠QRP
[Angles opposite to equal sides are equal]
Now, in ∆PQR,
∠PQR + ∠QRP + ∠RPQ = 180° [Angle sum property]
⇒ ∠PQR + ∠PQR + 30° = 180°
⇒ 2∠PQR = 180° – 30° = 150°
[∵ ∠PQR = ∠QRP]
⇒ ∠PQR = 75°
Since, SR ॥ QP
∠SRQ = ∠RQP = 75° [Alternate interior angles]
Also, ∠PQR = ∠QSR = 75° [Angles in alternate segment]
In ∆QRS,
∠Q + ∠R + ∠S = 180° [Angle sum property]
⇒ ∠Q = 180° – (75° + 75°) = 30°
∴ ∠RQS = 30°
Question 8
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°.The tangent at C intersects extended AB at a point D. Prove that BC = BD.
Solution:
Given, AB is a diameter and AC is a chord of circle with centre O, ∠BAC = 30°
To prove : BC = BD
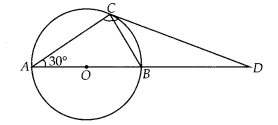
Join BC
∠BCD = ∠CAB [Angles in alternate segment]
∠CAB = 30° [Given]
∠BCD = 30° …(i)
∠ACB = 90° [Angle in semi-circle]
In ∆ABC,
∠A + ∠B + ∠C = 180° [Angle sum property]
30° + ∠CBA + 90° = 180°
⇒ ∠CBA = 60°
Also, ∠CBA + ∠CBD = 180° [Linear pair]
⇒ ∠CBD = 180° – 60° = 120°
[∵ ∠ CBA = 60°]
Now, in ACBD,
∠CBD + ∠BDC + ∠DCB = 180°
⇒ 120° + ∠BDC + 30° = 180°
⇒ ∠BDC = 30° …(ii)
From (i) and (ii),
∠BCD = ∠BDC
⇒ BC = BD
[Sides opposite to equal angles are equal]
Question 9
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Solution:
Let mid-point of an arc AMB be M and TMT’ be the tangent to the circle.
Join AB, AM and MB.
Since arc AM = arc MB =3 Chord AM = Chord MB
In ∆AMB, AM = MB
⇒ ∠MAB = ∠MBA …(i)
[Sides opposite to equal angles are equal]
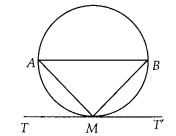
Since, TMT’ is a tangent line.
∴ ∠AMT = ∠MBA [Angles in alternate segments are equal]
= ∠MAB [from equation (i)]
But ∠AMT and ∠MAB are alternate angles, which is possible only when AB ॥ TMT
Hence, the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Question 10
In figure, the common tangent, AB and CD to two circles with centres O and O’ intersect at E. Prove that the points O, E, O’ are collinear.
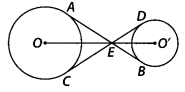
Solution:
Join AO, OC and O’D, O’B.
Now, in ∆EO’D and ∆EO’B,
O’D = O’B
O’E = O’E
ED = EB
[Tangents drawn from an external point to the circle are equal in length]
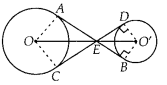
∴ EO’D ≅ ∆ EO’B [By SSS congruence criterion]
⇒ ∠O’ED = ∠O’EB …(i)
i.e., O’E is the angle bisector of ∠DEB.
Similarly, OE is the angle bisector of ∠AEC. Now, in quadrilateral DEBO’.
∠O’DE = ∠O’BE = 90°
[CED is a tangent to the circle and O’D is the radius, i.e., O’D ⊥ CED]
⇒ ∠O’DE + ∠O’BE = 180°
∴ ∠DEB + ∠DO’B = 180°
[∵ DEBO’ is cyclic quadrilateral] …(ii)
Since, AB is a straight line.
∴ ∠AED + ∠DEB = 180°
⇒ ∠AED + 180° – ∠DO’B = 180° [from (ii)]
⇒ ∠AED = ∠DO’B …(iii)
Similarly, ∠AED = ∠AOC …(iv)
Again from eq. (ii), ∠DEB = 180° – ∠DO’B
Dividing by 2 on both sides, we get
So, OEO’ is straight line.
Hence, O, E and O’ are collinear.
Question 11
In figure, O is the centre of a circle of radius 5 cm, T is a point such that 07= 13 cm and 07 intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.
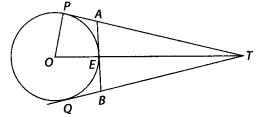
Solution:
OP is perpendicular to PT.
∴ In ∆OPT,
OT2 = OP2 + PT2
⇒ PT2 = OT2 – OP2
⇒ PT2 = (13)2 – (5)2 = 169 – 25 = 144
⇒ PT= 12 cm
Since, the length of pair of tangents from an external point T is equal.
∴ QT= 12 cm
Now, TA = PT – PA
⇒ TA = 12 -PA …(i)
and TB = QT – QB
TB = 12 – QB …(ii)
Also, PA = AE and QB = EB …(iii) [Pair of tangents]
∴ ET = OT – OE [∵ OE = 5 cm = radius]
⇒ ET = 13 – 5
⇒ ET = 8 cm
Since, AB is a tangent and OE is the radius.
∴OE ⊥ AB
⇒ ∠OEA = 90°
∴ ∠AET = 180° – ∠OEA [Linear pair]
⇒ ∠AET = 90°
Now, in right angled ∆AET,
(AT)2 = (AE)2 + (ET)2 [by Pythagoras theorem]
⇒ (12 – PA)2 = (PA)2 + (8)2
⇒ 144 + (PA)2 – 24 PA = (PA)2 + 64
⇒ 24 PA = 80

Question 12
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, Find ∠CBA.
Solution:
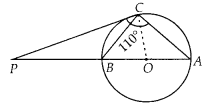
Join OC. Here, OcC is the redius.
Since, tangent at any point of a circle is – perpendicular to the radius through the point of contact.
∴ OC ⊥ PC
Now, ∠PCA = 110° [Given]
⇒ ∠PCO + ∠OCA = 110°
⇒ 90° + ∠OCA = 110°
⇒ ∠OCA = 20°
∵ OC = OA = radius of circle
∴ ∠OCA = ∠OAC = 20°
[Sides opposite to equal angles are equal]
Since, PC is a tangent,
∠BCP = ∠CAB = 20° [Angles in alternate segment]
In ∆PAC,
∠P + ∠C + ∠A = 180°
∠P = 180° – (∠C + ∠A)
= 180°-(110°+ 20°)
= 180° – 130° = 50°
In ∆PBC,
∠BPC + ∠PCB + ∠CBP = 180°
⇒ 50° + 20° + ∠PBC = 180°
⇒ ∠PBC = 180° – 70°
⇒ ∠PBC = 110°
Since, ABP is a straight line.
∴ ∠PBC + ∠CBA = 180°
⇒ ∠CBA = 180° – 110° = 70°
Question 13
if an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
Solution:
Join OB, OC and OA.
In ∆ABO and ∆ACO,
AB = AC [Given]
BO = CO [Radii of same circle]
AO = AO [Common side]
∴ ∆ABO ≅ ∆ACO [By SSS congruence criterion]
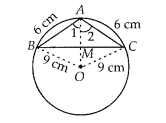
⇒ ∠1 = ∠2 [CPCT]
Now, in ∆ABM and ∆ACM,
AB = AC [Given]
∠1 = ∠2 [proved above]
AM = AM [Common side]
∴ ∆AMB ≅ ∆AMC [By SAS congruence criterion]
⇒ ∠AMB = ∠AMC [CPCT]
Also, ∠AMB + ∠AMC = 180° [Linear pair]
⇒ ∠AMB = 90°
We know that a perpendicular from the centre of circle bisects the chord.
So, OA is a perpendicular bisector of BC.
Let AM = x, then OM = 9 – x [ ∵ OA = radius = 9 cm]
In right angledd ∆AMC,
AC2 = AM2 + MC2
[By Pythagoras theorem]
⇒ MC2 = 62 – x2 …(i)
In right angle ∆OMC,
OC2 = OM2 + MC2 [By Pythagoras theorem]
⇒ MC2 = 92 – (9 – x)2
From equation (i) and (ii),
62 – x2 = 92 – (9 – x)2
⇒ 36 – x2 = 81 – (81 + x2 – 18x)
⇒ 36 = 18x
⇒ x = 2
∴ AM = 2 cm
From equation (ii),
MC2 = 92 – (9 – 2)2
⇒ MC2 = 81 – 49 = 32
⇒ MC = 4√2 cm
∴ BC = 2 MC = 8√2 cm
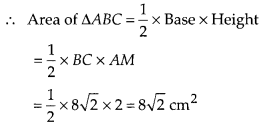
Fience, the required area of ∆ABC is 8√2 cm2.
Question 14
1 is a point at a distance 13 cm from the centre 0 of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Solution:
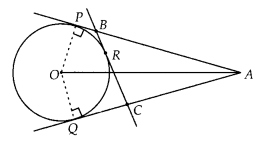
OP ⊥ AP
∴ ∠OPA = 90°
[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
In ∆OAP,
OA2 = OP2 + PA2
⇒ 132 = 52 + PA2
⇒ PA = 12 cm
Now, perimeter of ∆ABC = AB + BC + CA
= AB + BR + RC + CA
= (AB + BR) + (RC + CA)
= (AB + BP) + (CQ + CA)
[ ∵ BR = BP, RC = CQ i.e., tangents from external point to a circle are equal]
= AP + AQ
= 2AP [∵ AP = AQ]
= 2 x 12 = 24 cm
Hence, the perimeter of ∆ABC = 24 cm.
We hope the NCERT Exemplar Class 10 Maths Chapter 9 Circles will help you. If you have any query regarding NCERT Exemplar Class 10 Maths Chapter 9 Circles, drop a comment below and we will get back to you at the earliest.