NCERT Exemplar Class 10 Maths Chapter 8 Introduction to Trigonometry and Its Applications are part of NCERT Exemplar Class 10 Maths. Here we have given NCERT Exemplar Chapter 8 Introduction to Trigonometry and Its Applications.
NCERT Exemplar Class 10 Maths Chapter 8 Introduction to Trigonometry and Its Applications
Exercise 8.1
Choose the correct answers from the given four options:
Question 1
If cos A = \(\frac { 4 }{ 5 }\) , then the value of tanA is

Solution:
(B) Given, cosA = \(\frac { 4 }{ 5 }\)
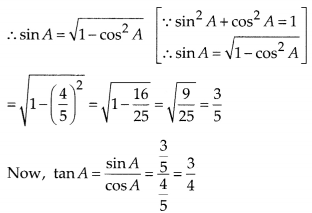
Question 2
If sin A = \(\frac { 1 }{ 2 }\), then the value of cot A ¡s

Solution:
Given, sin A = \(\frac { 1 }{ 2 }\)
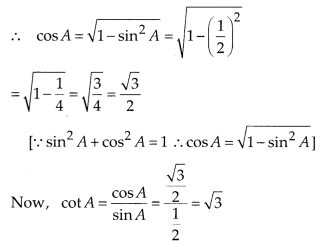
Hence, the required value of cotA is √3.
Question 3
The value of the expression [cosec (75° + θ) – sec (15° – θ) – tan (55° + θ) + cot (35° – θ)] is
(A) -1
(B) θ
(C) 1
(D) \(\frac { 3 }{ 2 }\)
Solution:
(B) Given, cosec(75° + θ) – sec(15° – θ) – tan (55° + θ) + cot(35° – θ)
= cosec [9θ° – (15° – θ)] – sec (15° – θ) – tan(55° + θ) + cot[90° – (55° + θ)]
= sec(15° – θ) – sec(15° – θ) – tan(55° + θ) + tan(55° + θ) [ ∵ cosec (9θ° – θ) = seeθ and cot (9θ° – θ) = tanθ]
= 0
Hence, the required value of the given expression is 0.
Question 4
Given that sinθ = \(\frac { a }{ b }\), then cos0 is equal to
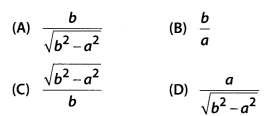
Solution:
(C) Given, sin θ = \(\frac { a }{ b }\) [ ∵ sin2θ + cos2θ = 1]
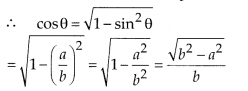
Question 5
If cos (α + β) = 0, then sin (α – β) can be reduced to
(A) cos β
(B) cos 2β
(C) sin α
(D) sin 2α
Solution:
(B) Given, (α + β) = 0 = cos90° [∵cos90° = 0]
α + β = 90°,
α = 90° – β
Now, sin(α – β ) = sin(90° – β – β ) [From eq. (i)]
=sin(90° – 2β)
= cos2 ( sin(90° – 2β)
= cos2β [∵ sin(90° – θ) cosθ]
Hence, sin(α – β) can be reduced to cos 2β
Question 6
The value of (tan 1° tan2° tan3° … tan89°) is
(A) 0
(B) 1
(C) 2
(D) \(\frac { 1 }{ 2 }\)
Solution:
(B) tan1° tan2° tan3° … tan89° =tan1° tan2° tan3° … tan44° (1)
tan(90° – 44°) … tan(90° – 3°) tan(90° – 2°) tan(90° – 1°)
= tan1° tan2° tan3° … tan44° (1). cot44° … cot3°. cot2°. cot1° . tan(90° – θ) cotθ]
= tan1° tan2° tan3° … tan44° (1)
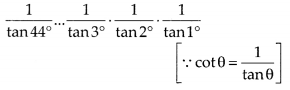
= 1
Question 7
If cos 9α = sina and 9α < 90°, then the value of tan5α is
(A) \(\frac { 1 }{ \sqrt { 3 } }\)
(B) √3
(C) 1
(D) 0
solution:
(C) Given, cosα = sina and 9α < 90° i.e.,
α is an acute angle.
sin(90° – 9α) = sinα [ ∵ cosA = sin(90° – A)
⇒ 90° – 9α = α
⇒ α = 9°
∴ tan5α = tan(5 x 9°) = tan45° = 1
[ ∵ tan45° = 1]
Question 8
If ∆ABC is right angled at C, then the value of cos (A+B) is

Solution:
(A) We know that, in ∆ABC,
Sum of three angles = 180°
i.e., ∠A + ∠B + ∠C = 180°
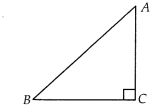
But the triangle is right angled at C i.e.,
∠C = 90° [givenl
∴ ∠A + ∠B + 90° = 180°
⇒ A + B = 90° [ ∵ ∠A = A and ∠A = B ]
∴ cos(A + B) = cos90° = 0
Question 9
If sinA + sin2A = 1, then the value of the expression (cos2A + cos4A) is
(A) 1
(B) \(\frac { 1 }{ 2 }\)
(C) 2
(D) 3
solution:
(A) Given, sinA + sin2A = 1
= sinA – 1 – sin2A – cos2A [ ∵ sin2θ + cos2θ =1 )
∵ cos2A = 1 – sin2A
On squaring both sides, we get
sin2A = cos4A
⇒ 1 – cos2A = cos4A
⇒ cos2A + cos4A = 1
Question 10
Given that sinα = \(\frac { 1 }{ 2 }\) and cosβ = \(\frac { 1 }{ 2 }\), then the value of (α+ β)
(A) 0°
(B) 30°
(C) 60°
(D) 90°
solution:
Given,
sinα = \(\frac { 1 }{ 2 }\) = sin30° [ ∵ sin30°= \(\frac { 1 }{ 2 }\)]
⇒ α = 30°
and cosβ \(\frac { 1 }{ 2 }\) = sin60°
⇒ β = 60°
∴ α + β = 30° + 60° = 90°
Question 11
The value of the expression
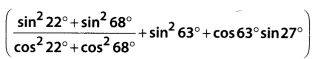
is
(A) 3
(B) 2
(C) 1
(D) 0
Solution:
(B) Given,
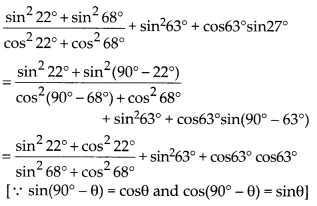
= \(\frac { 1 }{ 1 }\) + (sin263°+cos263°) [∵ sin2θ +cos2θ= 1]
= 1 + 1 = 2
Question 12
lf 4tanθ = 3, then \((\frac { 4sin\theta -cos\theta }{ 4sin\theta +4cos\theta } )\) is equal to

Solution:
(C) Given, 4 tanθ = 3
tanθ = 1

Question 13
lf sinθ – cosθ = 0, then the value of (sin4θ + cos4θ) is

Solution:
Given, sinθ – cosθ = 0
Question 14
sin (45° + θ ) – cos (45° – θ) is equal ta
(A) 2cosθ
(B) 0
(C) 2sinθ
(D) 1
Solution:
(B) sin(45° + θ) – cos(45° – θ)
= cos[90° – (45° + θ) 1 – cos(45° – θ)[ ∵ cos(90° – θ) = sinθ]
= cos(45° – θ) – cos(45° – θ) = 0
Question 15
A pole 6m high casts a shadow 2√3 m long on the ground, then the Sun’s elevation is
(A) 600
(B) 45°
(C) 30°
(D) 90°
Solution:
Let BC = 6 m be the height of the pole and AB = 2√3m be the length of the shadow on the ground.
Let the Sun’s elevation be θ.
Hence, the Sun’s elevation is 600.
Exercise 8.2
Write ‘True’ or ‘False’ and justify your answer in each of the following:
Question 1
![]()
Solution:
True
Question 2
The value of the expression (cos2 23° – sin2 67°) is positive.
Solution:
False
cos223° – sin267°
= (cos23° – sin67°) (cos23° + sin67°)
[∵ (a2 – b2) – (a – b)(a + b)]
= [cos23° – sin(90° – 23°)] (cos23° + sin67°)
= (cos23° – cos23°) (cos23° + sin67°) [∵ sin(90° – 0) = cos0]
= 0 . (cos23° + sin67°) = 0
which neither positive nor negative.
Question 3
The value of the expression (sin 80°- cos 80°) is negative.
Solution:
False
We know,
sinθ is increasing when, 0° ≤ θ ≤ 90°
and cos0 is decreasing when, 0° ≤ θ ≤ 90°
∴ sin80° – cos80° > 0 [positive]
Note : You will study about increasing and decreasing functions in higher classes.
Question 4
\(\sqrt { (1-{ cos }^{ 2 }\theta ){ sec }^{ 2 }\theta } =\quad tan\theta \)
Solution:
True
Question 5
If cosA + cos2A = 1, then sin2A + sin4A= 1.
Solution:
True
∵cosA+ cos2A = 1
⇒ cosA= 1 – cos2A = sin2A [ ∵ sin2A + cos2A = 1]
⇒ cos2A= sin4A
⇒ 1 – sin2A = sin4A [ ∵ cos2A = 1 – sin2A]
⇒ sin2A + sin4A = 1
Question 6
(tan θ + 2) (2 tan θ + 1) = 5 tan θ + sec2θ .
Solution:
False
(tanθ + 2)(2tanθ+ 1)
= 2tan2θ+ 4 tanθ + tanθ+ 2
= 2(sec2θ – 1) + 5tanθ + 2 [∵ sec2θ – tan2θ = 1]
= 2sec2θ +5tanθ
Question 7
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
Solution:
False
To understand the fact of this question, consider the following example
(i) A tower 2√3 m high casts a shadow 2 m long on the ground, then the Sun’s elevation is 60°
In ∆ABC, tanθ =\(\frac { BC }{ AB } =\quad \frac { 2\sqrt { 3 } }{ 2 } \)
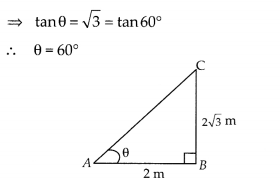
(ii) The A same height of tower casts a shadow 4 m more from preceding point, then the Sun’s elevation is 30°
In ∆PBC, CB
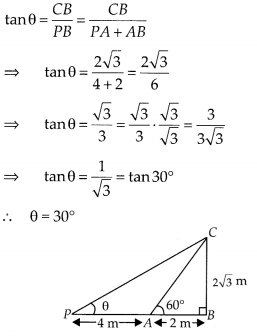
Hence, we conclude from above two examples that if the length of the shadow of a tower is increasing, then the angle of elevation of the Sun is decreasing
Question 8
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
Solution:
False
From figure, we observe that, a man standing on a platform at point P, 3 m above the surface of a lake observes a cloud at point C. Let the height of the cloud from the surface of the platform is h.
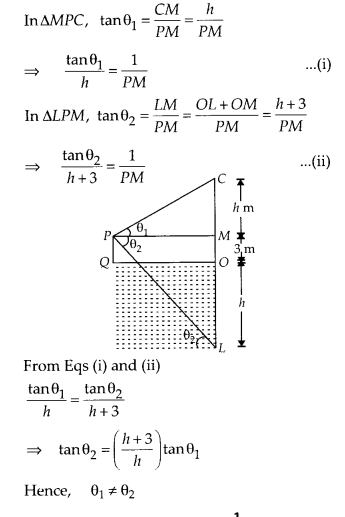
Question 9
The value of 2sinθ can be a + \(\frac { 1 }{ a } \) , where a is a positive number, and a≠ 1.
Solution:
False
Let a = 2, then a+ \(\frac { 1 }{ a } \)=2+\(\frac { 1 }{ 2 } \) = \(\frac { 5 }{ 2 } \)
If 2sinθ = a+ \(\frac { 1 }{ a } \),then a
2sinθ = \(\frac { 5}{ 2 } \)
⇒ sinθ = \(\frac { 5}{ 4 } \) = 1.25
Which is not possible [∵ sin θ ≤ 1 ]
Question 10
cos θ =\(\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2ab } \)
where a and b are two distinct numbers such that ab > 0.
Solution:
False
(a+b)² > 0
⇒ a² + b² > 2ab
⇒ \(\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2ab } >1\)
⇒ cosθ = cosθ > 1
[ ∵ cosθ =\(\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2ab }\) ]
Which is not possible. [ ∵ -1 ≤ cos θ ≤ 1]
Hence, cosθ ≠ \(\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2ab }\)
Question 11
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
Solution:
False
Case (i): Let the height of the tower is h In ∆ABC, let BC = x m
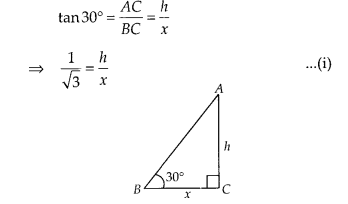
Case (ii): By condition, the height of the tower is doubled i.e., PR = 2h,
In ∆PQR, tan θ = \( \frac { PR }{ QR } =\frac { 2h }{ x } \)
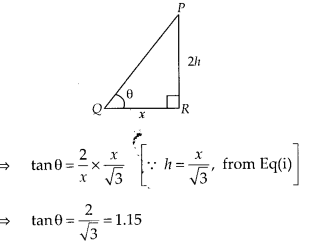
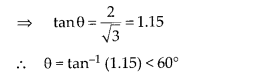
Hence, the required angle is not doubled.
Note : Teacher should explain about inverse functions for the given solution
Question 12
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
Solution
True
Case(i): Let the height of a tower be h and the distance of the point of observation from its foot is x.
In ∆ABC,
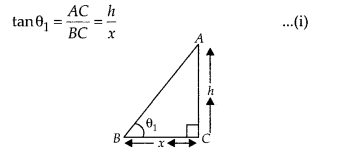
Case (ii): Now, the height of a tower increased
by 10% = h + 10% of h= h + h* \(\frac { 10 }{ 100 } =\frac { 11h }{ 100 } \)
and the distance of the point of observation from its foot = x + 10% of x
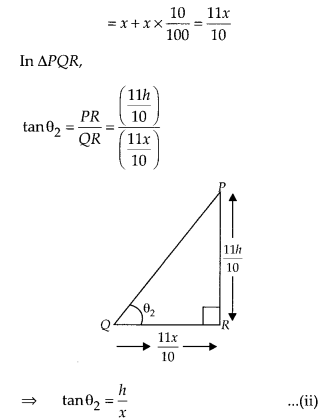
From Eqs. (i) and (ii), we get tan θ1 = tan θ2 ⇒ θ1 = θ2
Hence, the required angle of elevation of its top remains unchanged.
Exercise 8.3
Prove the following (from Q.1 to Q.7):
Question 1
![]()
Solution:
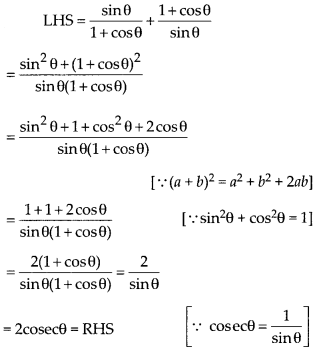
Question 2
![]()
Solution:
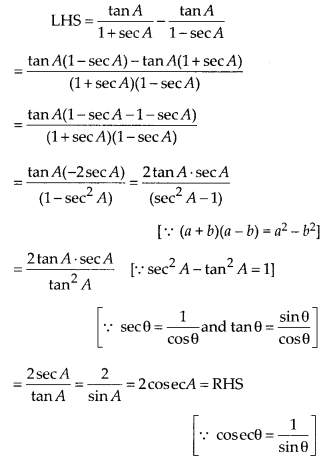
Question 3
If tanA = \(\frac { 3 }{ 4 }\) , then sinA cosA = \(\frac { 12 }{ 25 }\) .
Solution:
Given tanA = \(\frac { 3 }{ 4 }\) = \(\frac { P }{ B }\) = \(\frac { Perpendicular }{ Base }\)
LetP = 3k and B = 4k
By Pythagoras theorem,
H2 = P2 + B2 – (3k)2+ (4k)2
= 9k2 + 16k2 = 25k2
⇒ H = 5k [since, side cannot be negativel
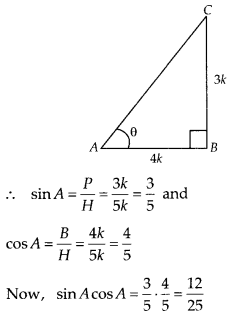
Question 4
(sin α + cos α) (tan α + cot α) = sec α + cosec α
Solution:
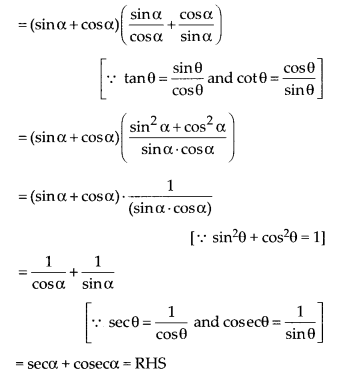
Question 5
(√3 +1)(3 – cot 30°) = tan3 60° – 2 sin 60°
Solution:
RHS = tan60° – 2sin60°
= (√3)3 – 2 x \(\frac { \sqrt { 3 } }{ 2 }\)
= 3√3 – √3 = 2√3
LHS = (√3 +1)(3 – cot 30°) = (√3 + 1)(3 – √3)
= (√3 +1 )√3 (√3 – 1)
= √3[(√3)2 – 1)] = √3(3-1) = 2√3
LHS = RHS
Question 6
tan θ + tan (90° – θ) = sec θ sec (90° – θ)
Solution:
LHS = tanθ + tan(90° – θ)
= tanθ + cotθ [ ∵ tan(90° – θ) = cotθ]

Question 7
Find the angle of elevation of the sun when the shadow of a pole h metres high is √3 h metres long.
Solution:
Let the angle of elevation of the Sun is θ.
Given, height of pole = h m
Now, in ∆ABC,
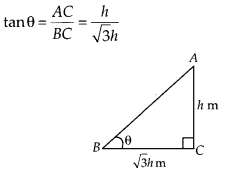
⇒ tanθ = \(\frac { \sqrt { 1 } }{ 3 }\) ⇒ tan30° ⇒ θ = 30°
Hence, the angle of elevation of the Sun is 30°.
Question 8
If √3 tan θ = 1, then find the value of sin2θ – cos2 θ.
Solution:
Given that, √3tanθ = 1
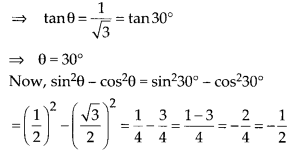
Question 9
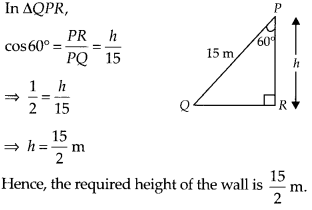
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
Solution:
Given, height of the ladder = 15 m
Let the height of the vertical wall = h
Because, and the ladder makes an angle of 60° with the wall i.e., θ = 60°
In ∆QPR,
Question 10
Simplify (1 + tan2θ) (1 – sinθ) (1 + sinθ)
Solution:
(1 + tan20)(1 – sinθ)(1 + sinθ)
= (1 + tan2θ)(1- sin2θ) [∵ (a – b)(a + b) = a2 – b2]
= sec2θ . cos2θ
[ ∵ 1 + tan2θ = sec2θ and cos2θ + sin2θ = 1]
= \(\frac { 1 }{ { cos }^{ 2 }\theta }\) .cos2 θ
= 1 [ ∵ sec θ = \(\frac { 1 }{ cos\theta }\) ]
Question 11
If 2sin2θ – cos2θ = 2, then find the value of θ.
Solution:
Given, 2sin2θ – cos2θ = 2
⇒ 2sin2θ – (1 – sin2θ) = 2 [∵ sin2θ + cos2θ = 1]
⇒ 2sin2θ + sin2θ – 1 = 2
⇒ 3sin2θ = 3
⇒ sin2θ = 1
⇒ sinθ = 1 = sin90° [ ∵ sin90° = 1]
∴ θ = 90°
Question 12
Show that
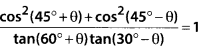
Solution:

Question 13
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
Solution:
Let the angle of elevation of the top of the tower from the eye of the observer is θ
Given that, AB = 22m, PQ = 1.5 m = MB and QB = PM = 20.5 m
⇒ AM = AB – MB
= 22 – 1.5 = 20.5 m
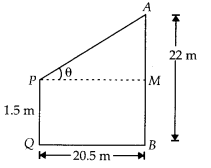
Now, in ∆APM,
tanθ = \(\frac { AM }{ PM } =\frac { 20.5 }{ 20.5 }=1\)
⇒ tanθ = tan45°
∴ θ = 45°
Hence, the required angle of elevation of the top of the tower from the eye of the observer is 45°.
Question 14
Show that tan4θ + tan2θ = sec4θ – sec2θ.
Solution:
LHS = tan4θ + tan2θ
= tan2θ(tan2 +1)
= tan2θ .sec2θ [ ∵ sec2θ = tan2θ + 1]
=(sec2 θ -1) .sec2θ [ ∵ tan2θ = sec2θ – 1]
= sec4θ – sec2θ= RHS
Exercise 8.4
Question 1
If cosecθ + cotθ = p, then prove that cosθ = \(\frac { { { P }^{ 2 } }-1 }{ { P }^{ 2 }+1 }\)
Solution:
Given, cosecθ + cotθ = p

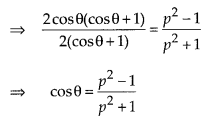
Question 2
Prove that \(\sqrt { { sec }^{ 2 }\theta +{ cosec }^{ 2 }\theta }\) = tanθ + cot θ
Solution:

Question 3
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
Solution:
Let the height of the tower be h.
Also, SR = x m,
Given that, QS = 20 m
√PQR = 30°
and √PSR = √PQR + 15°
= 30° +15°
= 45°
Now, in ∆PSR,
tan 45° = \(\frac { PR }{ SR }\) = \(\frac { h }{ x }\)
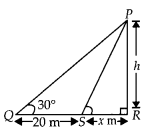

Hence, the required height of tower is 10(√3 + 1)m.
Question 4
If 1 + sin2θ = 3sinθ cosθ, then prove that tanθ = 1 or \(\frac { 1 }{ 2 }\) .
Solution:
Given, 1 + sin2θ = 3sinθ cosθ
Dividing both sides by sin2θ
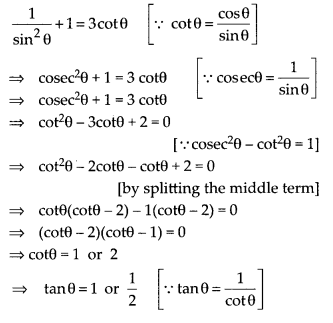
Question 5
Given that sinθ + 2cosθ = 1, then prove that 2sinθ – cosθ = 2.
Solution:
Given. sinθ + 2cosθ = 1
On squaring both sides, we get (sinθ + 2cosθ)2 = 1
⇒ sin2θ + 4cos2θ + 4sinθ cosθ = 1
⇒ (1 – cos2θ) + 4(1 – sin2θ) + 4sinθ cosθ = 1 [∵ sin2θ + cos2θ = 1]
⇒ 1 – cos2θ + 4 – 4sin2θ + 4sinθ cosθ = 1
⇒ – cos2θ – 4sin2θ + 4sinθ cosθ = -4
⇒ 4sin2θ + cos2θ – 4sinθ cosθ = 4
⇒ (2sinθ – cosθ)2 = 4
[ ∵ a2 + b2 – 2ab = (a – b)2]
⇒ 2sinθ – cosθ = 2
Question 6
The angle of elevation of the top of a tower from two points distant s and f from its foot are complementary. Prove that the height of the tower is √st.
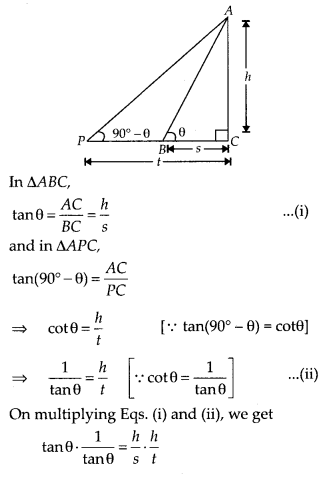
Solution:
Let the height of the tower is It. and ∠ABC = θ
Given that, BC = s, PC = t
and angle of elevation on both positions are complementary.
i.e., ∠APC = 90° – θ
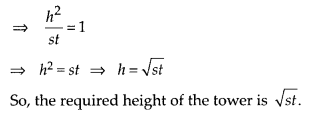
Question 7
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
Solution:
Let the height of the tower be h and RQ = x m
Given that, PR = 50 m and ∠SPQ = 30°, ∠SRQ = 60°
Hence, the required height of towcr is 25√3 m.
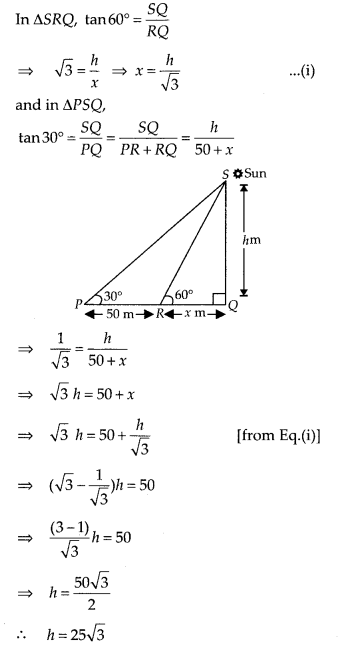
Question 8
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β , respectively. Prove that the height of the tower is ( \(\frac { htan\alpha }{ tan\beta -tan\alpha }\))
Solution:
Let the height of the tower be h and OR = x m
Given height of flag staff = h = FP
and ∠PRO = α , ∠FRO = β
Now, in ∆PRO,
Hence the required height of the tower is \(\frac { htan\alpha }{ tan\beta -tan\alpha }\)
Question 9
If tanθ + secθ = l, then prove that sec = \(\frac { { l }^{ 2 }+1 }{ 2l }\)
Solution:
Given, tanθ + secθ = l …..(i)
[multiply by (secθ – tanθ) on numerator and denominator to LHS]
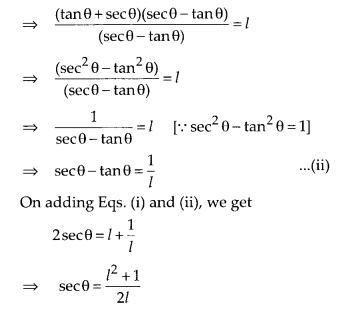
Question 10
If sinθ + cosθ = p and secθ + cosecθ = q, then prove that q(p2 – 1) = 2p.
Solution:
Given that, sinθ + cosθ = p …(i)
and secθ + cosecθ = q
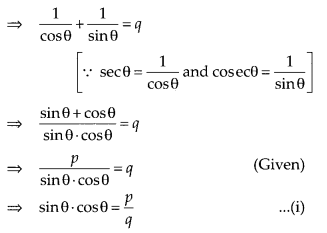
Since, sinθ + cosθ = p
On squaring both sides, we get
(sinθ +cosθ)2 = p2
(sin2θ + cos2θ) + 2sinθ cosθ = p2
[ ∵ (a + b)2 a2 + 2ab + b2]
1 + 2sinθ cosθ =p2 [∵ 2sin26 + cos2θ = 1]
= 1 + 2. \(\frac { p }{ q }\) = p2 [fromEq(i)1
= q + 2p = p2q = 2p ⇒ p2q – q
⇒ q(p2 – 1) – 2p
Question 11
If a sinθ + b cosθ = c, then prove that acosθ – bsinθ = \(\sqrt { { a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 } }\).
Solution:
Given that, a sinθ + b cosθ = c
On squaring both sides,
(a2 sinθ + cosθ b)2 = c2
asin2θ + b2 cos2θ + 2absinθ cosθ = c2
[ (x + y)2= x2 + 2xy + y2]
⇒ a2(1 – cos2θ) + b2( 1 – sin2θ) + 1ab sinθ . cosθ
= c2
⇒ a2 – a2 cos2θ + b2 – b2 sin2θ + 2absinθ . cosθ
= c2
⇒ a2 + b2 – c2 = a2cos2θ + 1)2sin2θ – 2absinθ . cosθ
⇒ a2 + b2 – c2 = (acosθ – bsinθ)2
[ ∵ a2 + b2 – 1ab = (a – b)2 ]
⇒ acosθ – bsinθ = \(\sqrt { { a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 } }\).
Question 12
Prove that
![]()
Solution:
On multiplying by (sec θ – tan θ) on numerator and denominator

Question 13
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
Solution:
Let distance between the two towers = AB = xm
and height of the other tower = PA = h m
Given, height of the tower = QB = 30 m, ∠QAB = 60° and ∠PBA = 30°
Now, in ∆QAB,
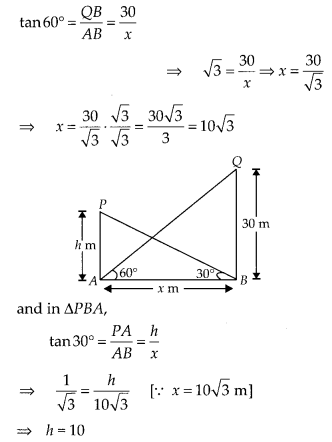
Hence, the required distance and height are 10√3 m and 10 m, respectively.
Question 14
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
Solution:
Let the distance between the two objects is x m and CD = y m
Given that, ∠BAX = α = ∠ABD and
∠CAX = β = ∠ACD [Alternate angle]
and height of tower, AD = h m
Now, in ∆ACD,

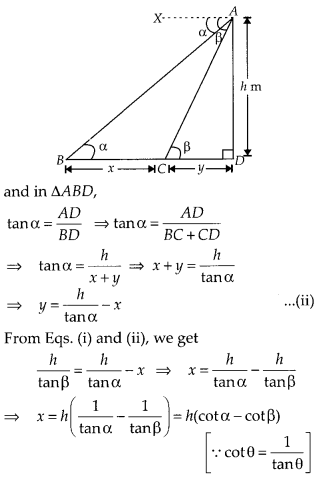
Which is the required distance between the two objects.
Question 15
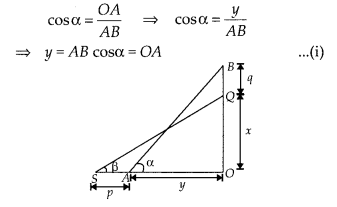
A ladder rests against a vertical wall at an inclination α to the horizontal. Its foot is pulled away from the wall through a distance p so that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal. Show that \( \frac { p }{ q } =\frac { cos\beta -cos\alpha }{ sin\alpha -sin\beta }\)
Solution:
Let OQ = x and OA = y
Given, BQ = q, SA = p
and AB = SQ = Length of ladder
Also, ∠BAO = α and ∠QSO = β
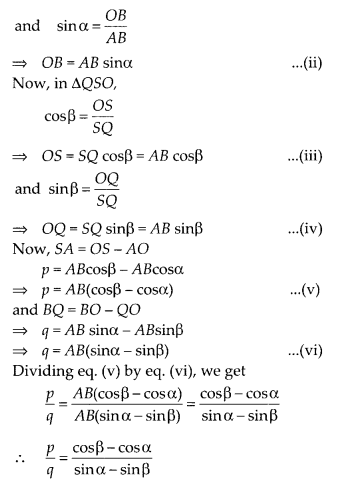
Question 16
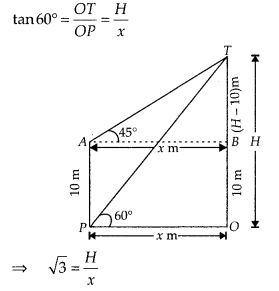
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
Solution:
Let the height the vertical tower be
OT = H m and OP = AB = xm
Given that, AP = 10 m
and ∠TPO = 60°, ∠TAB = 45°
Now, in ∆TPO,
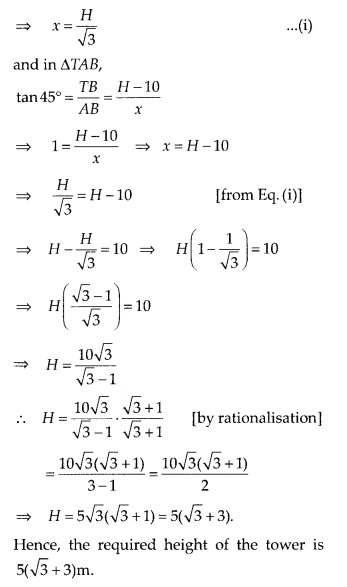
Question 17
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h (1 + tan α cot β) metres.
Solution:
Let the height of the other house = OQ = Hm and OB = MW = xm
Given, height of the first house = WB = h = MO
and ∠QWM = α, ∠OWM = β = ∠WOB [Alternate angle]
Now, ∆WOB,
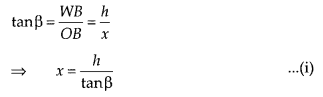
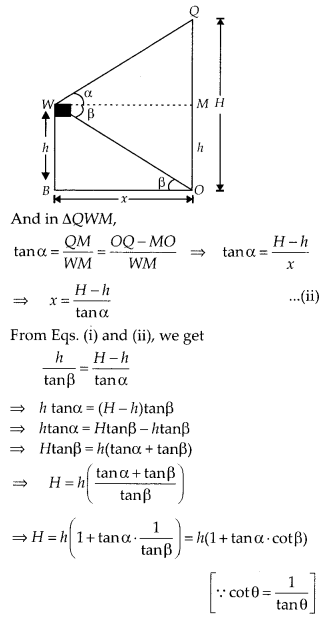
Hence, the required height of the other house is h(1 + tanα. cotβ)
Question 18
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30°, respectively. Find the height of the balloon above the ground.
Solution:
Let the height of the balloon from above the ground is H m and OP = W2 R = W1 Q = x m
Given, height of lower window from the ground = W2P = 2 m = OR
Height of upper window from the lower window = W1W2 = 4m = QR
∴ BQ = OB – (QR + RO)
= H – (4 + 2)
= H – 6
∠BW1Q = 30° and
∠BW2R = 60°
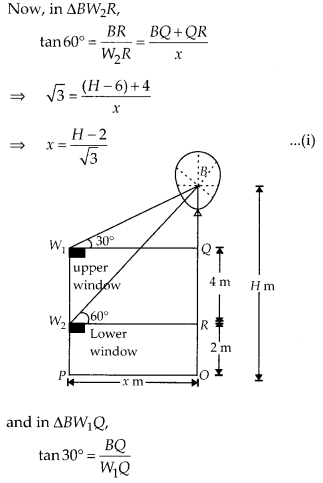
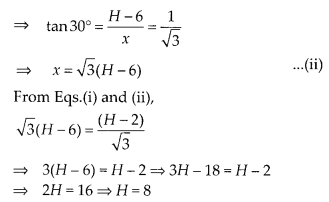
So, the required height is 8 m.
Hence, the required height of the balloon from the ground is 8 m.
We hope the NCERT Exemplar Class 10 Maths Chapter 8 Introduction to Trigonometry and Its Applications will help you. If you have any query regarding NCERT Exemplar Chapter 8 Introduction to Trigonometry and Its Applications, drop a comment below and we will get back to you at the earliest.