NCERT Exemplar Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables are part of NCERT Exemplar Class 10 Maths. Here we have given NCERT Exemplar Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables.
NCERT Exemplar Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables
Exercise 3.1
Choose the correct answer from the given four options:
Question 1
Graphically, the pair of equations
6x – 3y + 10 = 0
2x – y + 9 = 0
represents two lines which are
(A) intersecting at exactly one point.
(B) intersecting at exactly two points.
(C) coincident.
(D) parallel.
Solution:
(D) The given equations are 6x – 3y + 10 = 0
⇒ 2x – y + \(\frac { 10 }{ 3 }\) = 0 …(i)
and 2x – y + 9 = 0 … (ii)
Now, table for 2x – y + \(\frac { 10 }{ 3 }\) = 0,
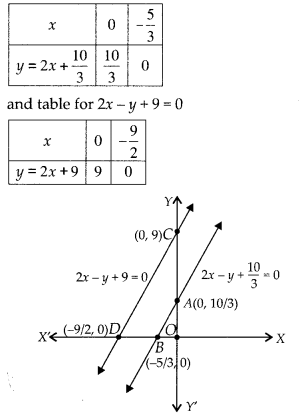
Hence, the pair of equations represent two parallel lines.
Question 2
The pair of equations x + 2y + 5 = 0 and -3x – 6y + 1 =0 have
(A) a unique solution
(B) exactly two solutions
(C) infinitely many solutions
(D) no solution Milim
Solution:
(D) We have,
x + 2y + 5 = 0 and -3x – 6y + 1 = 0
Here, a1= 1, b1 = 2, C1 = 5 and a2 = -3, b3 = -6, C2 = 1
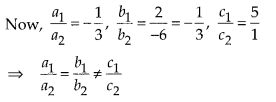
So, the pair of equations have no solution.
Question 3
If a pair of linear equations is consistent, then the lines will be
(A) parallel
(B) always coincident
(C) intersecting or coincident
(D) always intersecting
Solution:
(C) A pair of linear equations is consistent if these exists a solution.
i.e., intersecting (one solution) or coincident (infinite solution) lines are consistent.
Question 4
The pair of equations y = 0 and y = -7 has
(A) one solution
(B) two solutions
(C) infinitely many solutions
(D) no solution
Solution:
(D) The given pair of equations are y = 0 and y = -7.
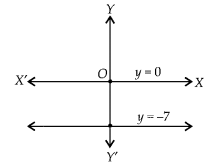
Since from the graph, both lines are parallel. So, they have no solution.
Question 5
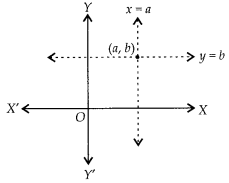
The pair of equationsx= a and y=b graphically represents lines which are
(A) parallel
(B) intersecting at (b, a)
(C) coincident
(D) intersecting at (a, b)
Solution:
(D) Graphically x = a represents a line parallel to y-axis at a distance a unit from y-axis and y = b represents a line parallel to x-axis at a distance b unit from x-axis.
∴ The pair of equations x = a and y = b represents lines which are intersecting at (a, b) as shown below.
Question 6
For what value of Ar, do the equations 3x-y+8 = 0 and 6x – ky = -16 represent coincident lines?
(A) 1/2
(B) -1/2
(C) 2
(D) -2
Solution:
(C) Given equations of lines are 3x – y + 8 = 0 and 6x – ky + 16 = 0
Here, a1 = 3, b1 = -1, c1 = 8 and a2 = 6, b2 = -k, c2 = 16
Since, condition for coincident lines is
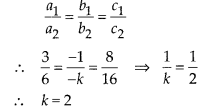
Question 7
If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of Ac is

Solution:
(C) Given equation of lines are
3x + 2ky -2 = 0 and 2x + 5y + 1 = 0
Here a1 =3 ,b1 = 2k, C1 = -2 and a2 = 2,b2 = 5,c2 = 1
Since condition for parallel lines is
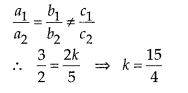
Question 8
The value of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 will have infinitely many solutions is
(A) 3
(B) -3
(B) -12
(D) no value
Solution:
(D) The given equations of lines are cx – y = 2 and 6x – 2y = 3
⇒ cx – y – 2 = 0 and 6x – 2y – 3 = 0
Here, a1 = c, b1= -1, c1 = -2 and a2 = 6, b2 = -2, C2 = -3
Since, condition for infinitely many solutions is
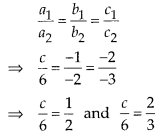
⇒ c = 3 and c = 4
Since, c has different values.
So, there exists no value of c for which given equations have infinitely many solutions.
Question 9
One equation of a pair of dependent linear equations is -5x + 7y = 2. The second equation can be
(A) 10x +14y + 4 = 0
(B) -10x – 14y + 4 = 0
(C) -10x + 14y + 4 = 0
(D) 10x – 14y = -4
Solution:
(D) Given equation of line is -5x + 7y – 2 = 0
Compare with a1x + b1y + C1 = 0, we get a1 = -5, b1 = 7, c1 = -2
Since condition for dependent linear equation is
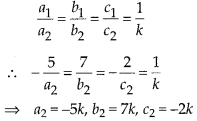
where, k is any arbitrary constant.
Substituting k = 2, then
a2 = -10, b2 = 14 and C2 = -4
∴ The required equation of line becomes – 10x + 14y – 4 = 0
⇒ 10x – 14y + 4 = 0
⇒ 10x – 14y = -4
Question 10
A pair of linear equations which has a unique solution x = 2 andy = -3 is
(A) x + y = -1 and 2x – 3y = -5
(B) 2x + 5y = -11 and 4x + 10y = -22
(C) 2x – y= 1 and 3x + 2y = 0
(D) x – 4y – 14 = 0 and 5x – y – 13 = 0
Solution:
(B), (D) For option (A),
L.H.S. = x + y = 2 + (-3) = -1 = R.H.S.
and
L.H.S. = 2x – 3y = 2(2) -3(-3) = 4 + 9 = 13 ≠ R.H.S.
∴ does not satisfy the equation.
For option (B),
L.H.S. = 2x + 5y = 2(2) + 5(-3)
= 4 – 15 = -11 = R.H.S.
and L.H.S. = 4x + 10y = 4(2) + 10(-3)
= 8-30 = -22 = R.H.S.
Since x = 2, y = -3 satisfy the equations in option (B).
∴ x = 2, y = -3 is a unique solution of these equations.
For option (C)
L.H.S. = 2x – y = 2(2) – (-3) = 4 + 3 = 7 ≠ R.H.S. and
L.H.S. = 3x + 2y = 3(2) + 2(-3) = 6 – 6 = 0 = R.H.S.
∴ x = 2, y = -3 does not satisfy the equation. For option (D)
L.H.S. = x-4y-14 = 2-4 (-3)-14 = 2+ 12 – 14
= 14 – 14 = 0 = R.H.S.
and L.H.S. = 5x – y – 13 = 5(2) – (-3) – 13
= 10+ 3 – 13 = 0 = R.H.S.
∴ x = 2,y = -3 satisfy the equations in option (D)
Question 11
If x = a and y = b is the solution of the equations x – y = 2 and x + y = 4, then the values of a and b are, respectively
(A) 3 and 5
(B) 5 and 3
(C) 3 and 1
(D) -1 and -3
Solution:
(C) Since x = a and y = b is the solution of the equations x – y = 2 and x + y = 4, so
a – b = 2 … (i)
and a + b = 4 … (ii)
On adding (i) and (ii), we get
2a = 6 ⇒ a = 3
Substitute value of a in equation (i)
⇒ 3 – b = 2
⇒ b = 1
Question 12
Aruna has only ₹1 and ₹2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is ₹75, then the number of ₹ 1 and ₹2 coins are, respectively
(A) 35 and 15
(B) 35 and 20
(C) 15 and 35
(D) 25 and 25
Solution:
(D) Let the number of ₹1 coins = x and number of ₹2 coins = y According to the condition,
x + y = 50 … (i)
Also, (x x 1) + (y x 2) = 75
⇒ x + 2y = 75 … (ii)
On subtracting (i) from (ii), we get
y = 75 – 50 = 25
When y = 25, then from (i),
x = 25
Question 13
The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present ages, in years of the son and the father are, respectively
(A) 4 and 24
(B) 5 and 30
(C) 6 and 36
(D) 3 and 24
Solution:
(C) Let the present age of father is x year and the present age of son is y year.
According to the statement,
(x + 4) = 4(y + 4)
⇒ x – 4y = 12 …..(i)
and x = 6y …(ii)
Substituting the value of x from (ii) in (i), we get 2y = 12
⇒ y = 6 When y = 6, then from (ii), x = 36
Hence, present age of father is 36 year and age of son is 6 year.
Exercise 3.2
Question 1
Do the following pair of linear equations have no solution? Justify your answer.
(i) 2x + 4y = 3; 12y+6x = 6
(ii) x = 2y; y = 2x
(iii) 3x + y-3 = 0; 2x + \(\frac { 2 }{ 3 }\) y = 2
Solution:
(i) Yes. Given pair of linear equations are
2x + 4y = 3 and 12y + 6x = 6
⇒ 2x + 4y – 3 = 0 and 12y + 6x – 6 = 0
Here, a1 = 2, b1 = 4, c1 = -3
a2 = 6, b2 = 12, c2 = -6
So, the given pair of linear equations has no solution.
(ii) No. Given pair of linear equations are x – 2y = 0 and 2x – y = 0
Here, a1 = 1 ,b1 = -2, c1 = 0
a2 = 2, b2 = -1, c2 = 0
So, the given pair of linear equations has unique solution.
(iii) No. Given pair of linear equations are
3x + y – 3 = 0 and 2x + \(\frac { 2 }{ 3 }\) y = 2
Here a1 = 3, b1 = 1, c1 = -3
and a2 = 2, b2 = \(\frac { 2 }{ 3 }\) , c2 = -2
So, the given pair of linear equations is coincident and having infinitely many solutions.
Question 2
Do the following equations represent a pair of coincident lines? Justify your answer.
(i) 3x + \(\frac { 1 }{ 7 }\) y = 3; 7x + 3y = 7
(ii) -2x – 3y = 1; 6y + 4x = -2
(iii) \(\frac { x }{ y }\) +y + \(\frac { 2 }{ 5 }\) = 0; 4x + 8y + \(\frac { 5 }{ 16 }\) = 0
Solution:
(i) No. Given pair of linear equations are
So, the given pair of linear equations has unique solution.
(ii) Yes. Given pair of linear equations are -2x – 3y – 1 = 0 and 6y + 4x + 2 = 0
Here, a1= -2, b1 = -3, c1 = -1
and a2 = 4, b2 = 6 , c2 = 2
So, the given pair of linear equations is coincident.
(iii) No. Given pair of linear equations are
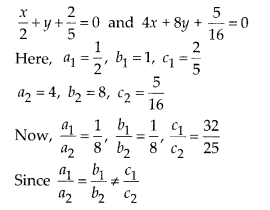
So, the given pair of linear equations has no solution.
Question 3
Are the following pair of linear equations consistent? Justify your answer.
(i) -3x – 4y = 12; 4y + 3x = 12
(ii) \(\frac { 3 }{ 5 }\)x – y = \(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 5 }\)x – 3y = \(\frac { 1 }{ 6 }\)
(iii) 2ax + by = a; 4ax + 2by-2a = 0; a,b ≠ 0
(iv) x + 3y = 11; 2(2x + 6y) = 22
Solution:
(i) No. Given pair of linear equations are
-3x – 4y – 12 = 0 and 3x + 4y – 12 = 0
Here, a1 = -3, b1 = -4, c1 = -12
a2 = 3, b2 = 4, c2 = -12
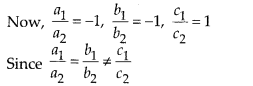
So, the pair of linear equations has no solution, i.e., inconsistent.
(ii) Yes. Given pair of linear equations arc
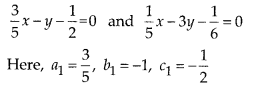
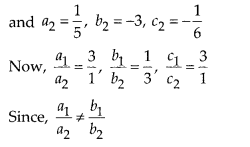
So, the given pair of linear equations has unique solution, i.e. consistent.
(iii) Yes. Given pair of linear equations are
2ax + by – a = 0 and
4ax + 2by – 2a = 0
Here, a1 = 2a, b1 = b, c1 = -a
a2 = 4a, b2 = 2h, c2 = -2a
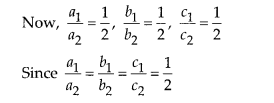
So, the given pair of linear equations has infinitely many solutions i.e. consistent.
(iv) No. Given pair of linear equations are
x + 3y – 11 = 0 and 2x + 6y – 11 =0
Here, a1 = 1 ,b1 = 3, c 1 = -11
and a2 = 2, b2 = 6, c2 = -11
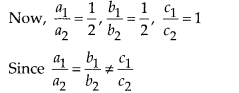
So, the pair of linear equation have no
solution i.e. inconsistent.
Question 4
For the pair of equations λx + 3y = -7 and 2x + 6y = 14 to have infinitely many solutions, the value of λ should be 1. Is the statement true? Give reasons.
Solution:
No. Given pair of linear equations are
λx + 3y + 7 = 0 and 2x + 6y – 14 = 0
Here, a1 = λ, b1 = 3, c1 = 7;
a2 = 1, b2 = 6, c2 = -14
For infinitely many solutions,
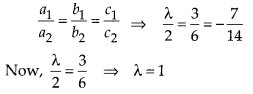
![]()
Since λ = 1 does not have a unique value So, for no value of λ, the given pair of linear equations have infinitely many solutions.
Question 5
For all real values of c, the pair of equations x – 2y = 8 and 5x – 10y = c have a unique solution. Justify whether it is true or false.
Solution:
False
Given pair of linear equations are x – 2y – 8 = 0 and 5x – 10y – c = 0
Here, a1 = 1, b1 = -2, c1 = -8
a2 = 5, b2 = -10, c2= -c
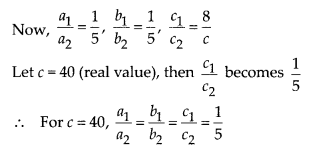
Thus, for c = 40, the system of linear equations has infinitely many solutions.
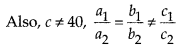
Thus, for c ≠ 40 the system of equations does not have any solution.
Hence, for any value of c, the system of linear equations does not have a unique solution.
Question 6
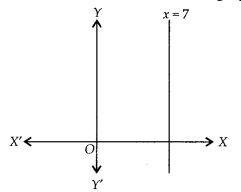
The line represented by x = 7 is parallel to the x-axis. Justify whether the statement is true or not.
Solution:
False
Since x = 7 is a line parallel to y-axis and perpendicular to x-axis (as shown in graph).
Exercise 3.3
Question 1
For which values(s) of λ , do the pair of linear equations λx + y = λ2 and x + λy = 1 have
(i) no solution ?
(ii) infinitely many solutions ?
(iii) a unique solution ?
Solution:
The given pair of linear equations are
λx + y = λ2 and x + λy = 1
⇒ λx + y – λ2 = 0 and x + λy – 1 = 0
Here, a1 = λ, b1 = 1, c1 = -λ2
and a2 = 1, b2 = λ, c2 = -1
(i) For no solution,
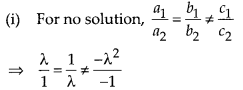
⇒ λ2 -1 = 0 and λ (λ – 1) = 0
⇒ λ = 1, -1 and λ ≠ 0,1
Thus, for λ = -1 system of equations have no solution.
(ii) For infinitely many solutions,
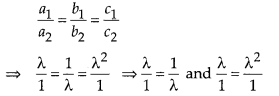
⇒ λ2 -1 = 0 and λ(λ -1) = 0
⇒ λ = 1, -1 and λ = 1, 0
Thus, for λ = 1 system of equations have infinitely many solutions.
(iii) For a unique solution,
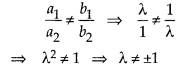
So, all real values of λ except ±1.
Question 2
For which value (s) of k will the pair of equations kx + 3y = k – 3, 12x + ky = k have no solution?
Solution:
Given pair of linear equation is
kx + 3y = k – 3 ⇒ kx + 3y – (k – 3) = 0 … (i)
and 12x + ky = k ⇒ 12x + ky -k = 0 … (ii)
On comparing with ax + by + c = 0, we get
a1 = k,b1 = 3 and c1 = -(k – 3) [from (i)]
a2 = 12, b2 = k and C2 = -k [from (ii)]
For no solution,
\(\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } \neq \frac { { c }_{ 1 } }{ { c }_{ 2 } }\)
⇒ \(\frac { k }{ 12 } =\frac { 3 }{ k } \neq \frac { -(k-3) }{ -k }\)
Taking first two parts, we get
\(\frac { k }{ 12 } =\frac { 3 }{ k }\)
⇒ k2 = 36
⇒ k = ±6
Taking last two parts, we get
\(\frac { 3 }{ k } \neq \frac { k-3 }{ k }\)
⇒ 3k = k(k – 3)
⇒ 3k – k(k – 3) ≠ 0
⇒ k(3 – k + 3) ≠ 0
⇒ k( 6 -k)i ≠ 0
⇒ k ≠ 0 and k ≠ 6
Hence, required value of k for which the given pair of linear equations have no solution is -6.
Question 3
For which values of a and b will the following pair of linear equations have infinitely many solutions?
x + 2y= 1
(a – b)x + (a + b)y = a + b – 2
Solution:
Given pair of linear equations are
x + 2y = 1 ⇒ x + 2y – 1 = 0 … (i)
and (a – b)x + (a + b)y = a + b – 2
⇒ (a – b)x + (a + b)y – (a + b – 2) = 0 …(ii)
On comparing with ax + by + c = 0, we get
a1 = 1, b1 = 2 and C1 = -1 [from (i)]
a2 = (a- b), b2 = (a + b) and c2 = -(a + b – 2) [from (ii)]
For infinitely many solutions,
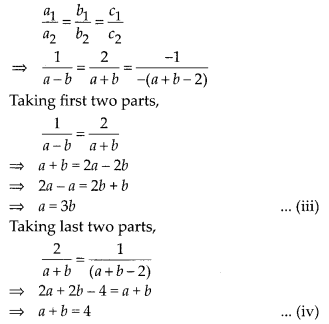
Now, put the value of a from eq. (iii) in eq. (iv), we get
3b + b = 4
⇒ 4b = 4
⇒ b = 1
Put the value of b in eq. (iii), we get a = 3 x 1 ⇒ a = 3
So, the value (a, b) = (3,1) satisfies all the parts.
Hence, required values of a and b are 3 and 1 respectively for which the given pair of linear equations has infinitely many solutions.
Question 4
Find the value(s) of p in (i) to (iv) and p and q in (v) for the following pair of equations:
(i) 3x – y – 5 = 0 and 6x – 2y – p = 0, if the lines represented by these equations are parallel.
(ii) -x + py = 1 and px – y = 1, if the pair of equations has no solution.
(iii) -3x + 5y = 7 and 2px – 3y = 1, if the lines represented by these equations are intersecting at a unique point.
(iv) 2x + 3y – 5 = 0 and px – 6y – 8 = 0, if the pair of equations has a unique solution.
(v) 2x + 3y = 7 and 2px + py = 28 – qy, if the pair of equations have infinitely many solutions.
Solution:
(i) Given pair of linear equations are
3x – y – 5 = 0 … (i)
and 6x – 2y – p = 0 … (ii)
On comparing with ax + by + c = 0, we get
a1 = 3, b1 = -1 and c1 = -5 … [from (i)]
a2 = 6,b2 = -2, c2 = -p … [from (ii)]
Since, the lines represented by these equations are parallel, then
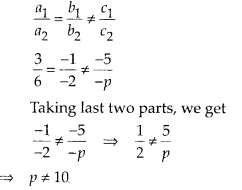
Hence, the given pair of linear equations are parallel for all real values of p except 10.
(ii) Given pair of linear equation are
-x + py – 1 = 0 …(i)
px – y – 1 = 0 …(ii)
On comparing with ax + by + c = 0, we get
a1 = -1, b1 = p and c1 = -1 [from (i)]
a2 = p, b2 = -1 and c2 = -1 [from (ii)]
Since, the pair of linear equations has no solution i.e. both lines are parallel to each other.
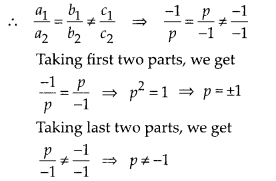
Hence, the given pair of linear equations has no solution for p = 1.
(iii) Given, pair of linear equations are
-3x + 5y – 7 = 0 … (i)
2px – 3y – 1 = 0 … (ii)
On comparing with ax + by + c = 0, we get
a1 = -3, b1 = 5 and c1 = -7 [from (i)]
a2 = 2p, b2 = -3 and c2 = -1 [from (ii)]
Since, the lines are intersecting at a unique point, i.e. it has a unique solution.
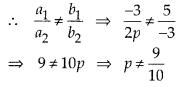
Hence, the lines represented by these equations are intersect ng at a unique point for all real values of p except \(\frac { 9 }{ 10 }\) .
(iv) Given pair of linear equations are
2x + 3y – 5 = 0 … (i)
px – by – 8 = 0 … (ii)
On comparing with ax + by + c = 0, we get
a1 = 2, b1 = 3 and c1 = -5 [from (i)]
a2 = p,b2 = -6 and c2 = -8 [from (ii)]
Since, the pair of linear equations has a unique solution,
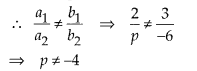
Hence, the pair of linear equations has a unique solution for all values of p except -4.
(v) Given pair of linear equation are 2x + 3y = 7
⇒ 2x + 3y – 7 = 0 … (i)
2px + py = 28 – qy
⇒ 2px + (p + q)y – 28 = 0 … (ii)
On comparing with ax + by + c = 0, we get
a1 = 2,b1 = 3 and c1 = -7 [from (i)]
a2 = 2p, b2 = (p + q) and c2 = -28 [from (ii)]
Since, the pair of equations has infinitely many solutions, i.e. both lines are coincident.
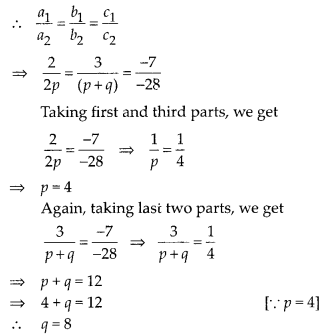
Here, we see that the value of p = 4 and q = 8 satisfies all three parts.
Hence, the pair of equations has infinitely many solutions for the values of p = 4 and q = 8.
Question 5
Two straight paths are represented by the equations x – 3y = 2 and -2x + 6y = 5. Check whether the paths cross each other or not.
Solution:
Given linear equations are x-3y-2 = 0 … (i)
and -2x + 6y – 5 = 0 … (ii)
On comparing both the equations with ax + by + c = 0, we get
a1 = 1, b1 = -3 and c1 = -2 [from (i)]
a2= -2, b2 = 6 and c2 = -5 [from (ii)]
![]()
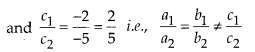
Thus, lines are parallel.
Hence, two straight paths represented by the given equations never cross each other, because they are parallel to each other.
Question 6
Write a pair of linear equations which has the unique solution x = -1, y = 3. How many such pairs can you write?
Solution:
Condition for the pair of system to have unique solution :
\(\frac { { a }_{ 1 } }{ { a }_{ 2 } } \neq \frac { { b }_{ 1 } }{ { b }_{ 2 } }\)
Let the equations are a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0
Since, x = -1 and y = 3 is the unique solution of these two equations, then
a1(-1) + b1( 3) + c1 = 0
⇒ -a1 + 3b1 + c1 = 0 ……(i)
and a2(-1) + b2(3) + c2 = 0
⇒ -a2 +3b2 + c2 = 0 …….(ii)
So, many values of a1, a2, b1, b2, c1 and c2 satisfy the eq. (i) and eq. (ii).
Hence, infinitely many pairs of linear equations are possible.
Question 7
If 2x + y = 23 and 4x – y = 19, find the values of 5y – 2x and \(\frac { y }{ x }\) – 2.
Solution:
Given equation are
2x + y = 23 …(i)
and 4x – y = 19 … (ii)
On adding both equations, we get
6x = 42 ⇒ x = 7
Put the value of x in eq. (i), we get
2(7) + y = 23 ⇒ 14 + y = 23
⇒ y = 23 – 14 ⇒ y = 9
We have, 5y – 2x = 5 x 9 – 2 x 7 = 45 – 14 = 31
![]()
Hence, the values of (5y – 2x) and ( \(\frac { y }{ x }\) – 2) are 31 and \(\frac { -5 }{ 7 }\) respectively.
Question 8
Find the values of x and y in the following rectangle (see figure).
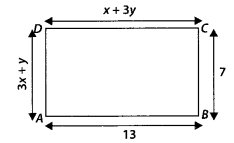
Solution:
By property of rectangle,
Lengths are equal i.e., CD = AB
⇒ x + 3y = 13 …(i)
Breadth are equal i.e., AD = BC
⇒ 3x + y = 7 …(ii)
On multiplying eq. (ii) by 3 and then subtracting eq. (i), we get
8x = 8
⇒ x = 1
On putting x = 1 in eq.(i), we get
3y = 12 ⇒ y = 4
Hence, the required values of x and y are 1 and 4, respectively.
Question 9
Solve the following pairs of equations : 1
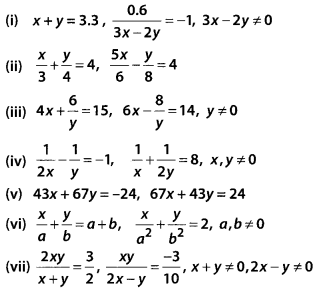
Solution:
Given pair of linear equations are x + y = 3.3 …(i)
and \(\frac { 0.6 }{ 3x – 2y}\) = -1
⇒ 0.6 = -3x + 2y
3x – 2y = -0.6 …(ii)
Now, multplying eq. (i) by 2 and then adding with eq. (ii), we get 5x = 6
⇒ x = \(\frac { 6 }{ 5 }\) = 1.2
Now, put the value of x in eq. (i), we get 1.2 + y = 3.3
⇒ y = 3.3-1.2 ⇒ y = 2.1
Hence, the required values of x and y are 1.2 and 2.1, respectively.
(ii) Given, pair of linear equations are
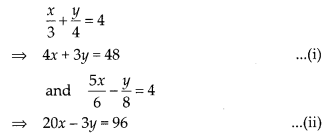
Now, adding eq. (i) and eq. (ii), we get
24x = 144 ⇒ x = 6
Now, put the value of x in eq. (i), we get
4 x 6 + 3y = 48
⇒ 3y = 48 – 24
⇒ 3y = 24
⇒ y = 8
Hence, the required values of x and y are 6 and 8, respectively.
(iii) Given pair of linear equations are
4x + \(\frac { 6 }{ y }\) = 15 ……….(i)
and 6x – \(\frac { 8 }{ y }\)= 14 ………….. (ii)
Let u = \(\frac { 1 }{ y }\), then above equations become
4x + 6u = 15 …(iii)
and 6x – 8u = 14 …(iv)
On multiplying eq. (iii) by 8 and eq. (iv) by 6 and then adding both of them, we get
68x = 204
⇒ x = 3
Now, put the value of x in eq. (iii), we get
4 x 3 + 6u = 15
⇒ 6M = 15 – 12
⇒ 6u = 3
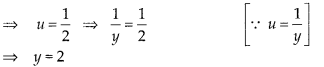
Hence, the required values of x and y are 3 and 2, respectively.
(iv) Given pair of linear equations are
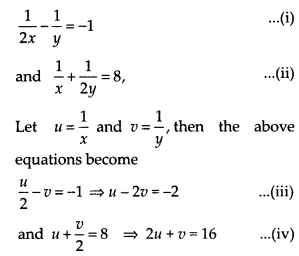
On multiplying eq. (iv) by 2 and then adding with eq. (iii), we get
5u = 30
⇒ u = 6
Now, put the value of u in eq. (iv), we get
2 x 6 + ν = 16
⇒ ν = 16 – 12 = 4 ⇒ ν = 4
∴ x = \(\frac { 1 }{ u }\) = \(\frac { 1 }{ 6 }\) and y = \(\frac { 1 }{ v }\) = \(\frac { 1 }{ 4 }\)
Hence, the required values of x and y are \(\frac { 1 }{ 6 }\) and \(\frac { 1 }{ 4 }\), respectively.
(v) Given pair of linear equations are
43x + 67y = -24 …(i)
and 67x + 43y = 24 …(ii)
On multiplying eq. (i) by 43 and eq. (ii) by 67 and then subtracting both of them, we get
{(67)2 – (43)2}x = 24(67 + 43)
⇒ (67 + 43)(67 – 43)x = 24 x 110 [ ∵ (a2 – b2) = (a – b)(a + b)]
⇒ 110 x 24x = 24 x 110
⇒ x = 1
Now, put the value of x in eq. (i), we get
43 x 1 + 67y = -24
⇒ 67y = -24 – 43
⇒ 67y = -67
⇒ y = -1
Hence, the required values of x and y are 1 and -1, respectively.
(vi) Given pair of linear equations are
\(\frac { x }{ a }\) + \(\frac { y }{ b }\) = a + b …(i)
and \( \frac { x }{ { a }^{ 2 } } +\frac { y }{ { b }^{ 2 } } =\quad 2\)
On multiplying eq. (i) by \(\frac { 1 }{ a }\) and then subtracting from eq. (ii), we get
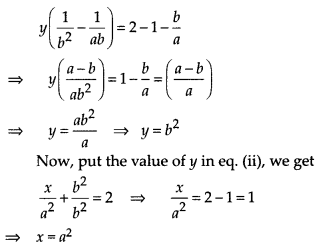
Hence, the required values of x and y are a2 and b2, respectively.
(vii) Given pair of equations are
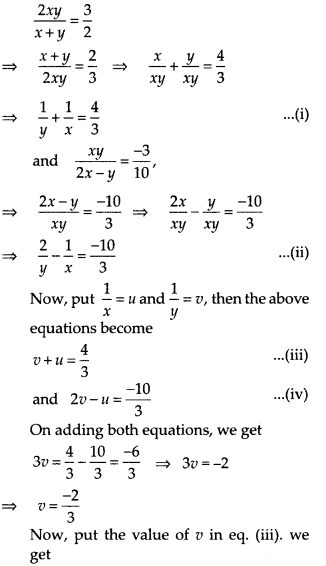
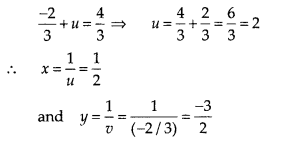
Hence, the required values of x and y are \(\frac { 1 }{ 2 }\) and \(\frac { -3 }{ 2 }\) , respectively.
Question 10
Find the solution of the pair of equations
\(\frac { x }{ 10 } +\frac { y }{ 5 } -1=0\) and \(\frac { x }{ 8 } +\frac { y }{ 6 } = 15\). Hence, find λ, if y = λx + 5.
Solution:
Given pair of equations are
\(\frac { x }{ 10 } +\frac { y }{ 5 } -1=0\)
⇒ x + 2y – 10 = 0 …(i)
⇒ x + 2y = 10
and \(\frac { x }{ 8 } +\frac { y }{ 6 } = 15\)
⇒ 3x + 4y = 360 …(ii)
On multiplying eq. (i) by 2 and then subtracting from eq. (ii), we get
(3x + 4y) – (2x + 4y) = 360 – 20 ⇒ x = 340
Put the value of x in eq. (i), we get 340 + 2y = 10
⇒ 2y = 10 – 340 = -330
⇒ y = -165
Now, y = λx + 5
Put the values of x and y in above relation, we get
-165 = λ(340) + 5
⇒ 340λ = -170
⇒ λ = \(-\frac { 1 }{ 2 }\)
Hence, the solution of the pair of equations are x = 340, y = -165 and the required value of λ is \(-\frac { 1 }{ 2 }\).
Question 11
By the graphical method, find whether the following pair of equations are consistent or not. If consistent, solve them.
(i) 3x + y + 4 = 0,6x – 2y + 4 = 0
(ii) x – 2y =6, 3x – 6y = 0
(iii) x + y = 3, 3x + 3y = 9
Solution:
(i) Given pair of equations are
3x + y + 4 = 0
and 6x – 2y + 4 = 0 …(ii)
On comparing with ax + by + c = 0, we get
a1 = 3, b1 = land c1 = 4 [from, (i)]
a2 = 6, b2 = -2 and c2 = 4 [from (ii)]
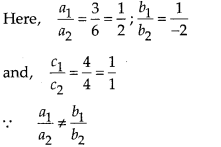
So, the given pair of linear equations are intersecting at one point, therefore these lines have unique solution.
Hence, given pair of linear equations are consistent.
We have, 3x + y + 4 = 0
⇒ y = -4 – 3x
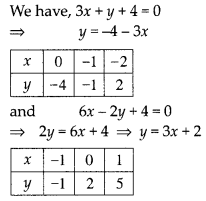
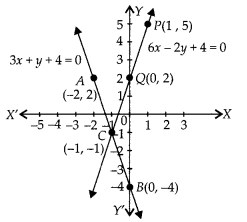
Plotting the points B(0, -4) and A(-2, 2), we get the straight line AB, Plotting the points Q(0,2) and P(1, 5), we get the straight line PQ. The lines AB and PQ intersect at C (-1, -1).
(ii) Given pair of equation is x – 2y = 6 …(i)
and 3x – 6y = 0 …(ii)
On comparing with ax + by + c = 0, we get
a1 = 1 ,b1 = -2 and c1 = -6 [from (i)]
a2 = 3, b2 = -6 and c2 = 0 [from (ii)]
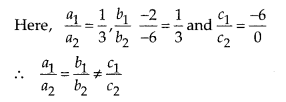
Hence, the lines represented by the given equations are parallel. Therefore, it has no solution. So, the given pair of lines is inconsistent.
(iii) Given pair of equation are
x + y = 3
⇒ x + y- 3 = 0 …(i)
and 3x + 3y = 9
⇒ 3x + 3y – 9 = 0 …(ii)
On comparing with ax + by + c = 0, we get
a1 = 1, b1 = 1 and c1 = -3 [from (i)]
a2 = 3, b2 = 3 and c2 = -9 [from (ii)]
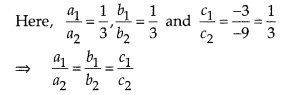
So, the given pair of lines is coincident. Therefore, these lines have infinitely many solutions. Hence, the given pair of linear equations are consistent.
Now, x + y = 3 ⇒ y = 3 – x
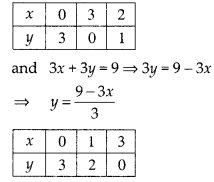
Plotting the points we get the graph of lines.
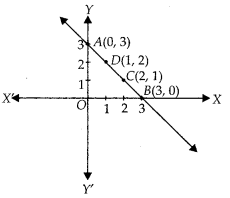
We observe that the lines represented by (i) and (ii) are coincident.
Question 12
Draw the graph of the pair of equations 2x + y = 4 and 2x- y = 4. Write the vertices of the triangle formed by these lines and the y-axis. Also, find the area of this triangle?
Solution:
Table for line 2x + y = 4
⇒ y = 4 – 2x
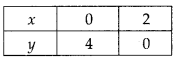
and table for line 2x – y = 4 ⇒ y = 2x – 4
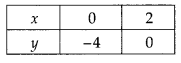
Graphical representation of both lines are as follows :
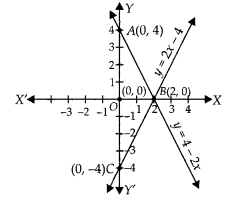
Here, both lines and y-axis form ∆ABC Hence, the vertices of a ∆ABC are A(0, 4), B(2, 0) and C(0, – 4)
∴ Required area of ∆ABC = 2 x Area of ∆AOB = 2 x \(\frac { 1 }{ 2 }\) x 4 x 2 = 8sq units
Hence, the required area of the triangle is 8 sq units.
Question 13
Write an equation of a line passing through the point representing solution of the pair of linear equations x + y = 2 and 2x – y = 1. How many such lines can we find?
Solution:
Given pair of linear equation are
x + y – 2 = 0 …(i)
and 2x – y – 1 = 0 …(ii)
On comparing with ax + by + c = 0, we get
a1 = 1, b1 = 1 and c1 = -2 [from (i)]
a2 = 2, b2 = -1 and c2 = -1 [from (ii)]
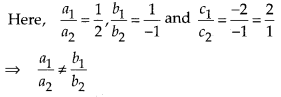
So, both lines intersect at a point. Therefore, the pair of equations has a unique solution. Hence, these equations are consistent.
Now, x + y = 2 ⇒ y = 2 – x
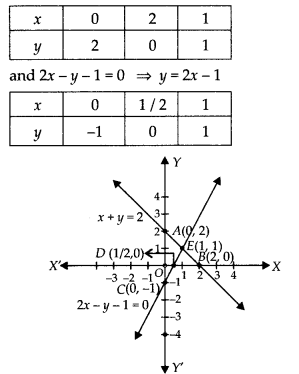
The given lines intersect at E(1,1) Hence, infinite lines can pass through the intersection point of linear equations x + y = 2 and 2x – y = 1 i.c., E( 1, 1) like as y = x, 2x + y = 3, x + 2y = 3 so on.
Question 14
If (x + 1) is a factor of 2x3 + ax2 + 2bx + 1, then find the values of a and b given that 2a – 3b = 4.
Solution:
Given that, (x + 1) is a factor of f(x) = 2x3 + ax2 + 2bx + 1, then f(-1) = 0
[if (x + a) is a factor of f(x) = ax2 + bx + c, then f(-a) = 0]
⇒ 2(-1)3 + a(-1)2 + 2b (-1) + 1 = 0
⇒ -2 + a – 2b + 1 = 0
⇒ a – 2b – 1 = 0 …(i)
Also, 2a – 3b = 4
⇒ 3b = 2a – 4
⇒ b = (\(\frac { 2a – 4 }{ 3 }\) )
Now, put the value of b in eq. (i), we get
a – 2(\(\frac { 2a – 4 }{ 3 }\)) – 1 = 0
⇒ 3a – 2(2a – 4) – 3 = 0
⇒ 3a – 4a + 8 – 3 = 0
⇒ -a + 5 = 0
⇒ a = 5
Now, put the value of a in eq.(i), we get 5 – 2b – 1 = 0
⇒ 2b = 4
⇒ b = 2
Hence, the required values of a and b are 5 and 2, respectively.
Question 15
The angles of a triangle are x, y and 40°. The difference between the two angles x and y is 30°. Find x and y.
Solution:
Given that x, y and 40° are the angles of a triangle.
∴ x + y + 40° = 180°
[since, the sum of all the angles of a triangle is 180°]
⇒ x + y = 140° …(i)
Also, x-y = 30° …(ii)
On adding (i) and (ii), we get
2x =170°
⇒ x = 85°
On putting x = 85° in (i), we get
85° + y = 140°
⇒ y = 55°
Hence, the required values of x and y are 85° and 55°, respectively.
Question 16
Two years ago, Salim was thrice as old as his daughter and six years later, he will be four years older than twice her age. How old are they now?
Solution:
Let Salim and his daughter’s age be x year and y year, respectively.
Now, by first condition,
Two years ago, Salim was thrice as old as his daughter.
i. e., x – 2 = 3(y – 2)
⇒x – 2 = 3y – 6
⇒ x – 3y = -4 …(i)
And by second condition,
Six years later, salim will be four years older than twice her age.
x + 6 = 2(y + 6) + 4
⇒ x + 6 = 2y + 12 + 4
⇒ x -2y = 16 – 6
⇒ x – 2y = 10 …(ii)
On subtracting eq.(i) from eq.(ii) we get y = 14
Put the value of y in eq.(ii), we get
x – 2 x 14 = 10
⇒ x = 10 + 28
⇒ x = 38
Hence, Salim and his daughter’s age are 38 years and 14 years, respectively.
Question 17
The age of the father is twice the sum of the ages of his two children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father.
Solution:
Let the present age (in year) of father and his two children be x, y and z years, respectively.
Now by given condition, x = 2(y + z) …(i)
and after 20 years, (x + 20) = (y + 20) + (z + 20)
⇒ y + z + 40 = x + 20
⇒ y + z = x – 20
On putting the value of (y + z) in eq.(i), we get the present age of father
x = 2(x – 20)
∴ x = 2x – 40 ⇒ x = 40
Hence, the father’s age is 40 years.
Question 18
Two number are in the ratio 5 : 6, If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers.
Solution:
Let the two numbers be x and y.
Then, by first condition,
Ratio of these two numbers = 5 : 6
x : y = 5 : 6
⇒ \(\frac { x }{ y }\) = \(\frac { 5 }{ 6 }\)
⇒ y = \(\frac { 6x }{ 5 }\) ……(i)
and by second condition,
If, 8 is subtracted from each of the numbers, then ratio becomes 4 : 5
⇒ \(\frac { x – 8 }{ y – 8 }\) = \(\frac { 4 }{ 5 }\)
⇒ 5x – 40 = 4y – 32
⇒ 5x – 4y = 8 …(ii)
Now, put the value of y from eq. (i) in eq. (ii) we get
5x – 4(\(\frac { 6x }{ 5 }\) ) = 8
⇒ 25x – 24x = 40
⇒ x = 40
Put the value of x in eq. (i) we get
y = \(\frac { 6 }{ 5 }\) x 40 = 6 x 8 = 48
Hence, the required numbers are 40 and 48.
Question 19
There are some students in the two examination halls A and B. To make the number of students equal in each hall, 10 students are sent from A to 8. But if 20 students are sent from B to A, the number of students in A becomes double the number of students in B. Find the number of students in the two halls.
Solution:
Let the number of students in halls A and B are x and y respectively.
Now, by given condition, x – 10 = y + 10
⇒ x – y = 20 …(i)
and (x + 20) = 2(y – 20)
⇒ x – 2y = -60 ……(ii)
On subtracting eq.(ii) from eq.(i) we get
(x – y) – (x – 2y) = 20 + 60
x – y – x + 2y = 80
⇒ y = 80
On putting y = 80 in eq. (i) we get
x – 80 = 20 ⇒ x = 100
Hence, 100 students are in hall A and 80 students are in hall B.
Question 20
A shopkeeper gives books on rent for reading. She takes a fixed charge for the first two days, and an additional charge for each day thereafter. Latika paid ₹22 for a book kept for six days, while Anand paid ₹16 for the book kept for four days. Find the fixed charges and the charge for each extra day.
Solution:
Let fixed charge for the first two day is ₹ x and additional charge for each day thereafter is ₹ y Now by first condition,
Latika paid ₹ 22 for a book kept for six days i.e.,
x + 4y = 22 …(i)
and by second condition,
Anand paid ₹16 for a book kept for four days i.e.,
x + 2y = 16 …(ii)
Now, subtracting eq. (ii) from eq.(i), we get
2y = 6
⇒ y = 3
On putting the value of y in eq.(ii), we get
x + 2 x 3 = 16
⇒ x = 16 – 6 = 10
Hence, the fixed charge = ₹ 10
and the charge for each extra day = ₹ 3
Question 21
In a competitive examination, one mark is awarded for each correct answer while 1/2 mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly?
Solution:
Let the number of correct answers be x then the number of wrong answers be (120 – x) Then, by given condition,
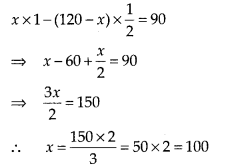
Hence, Jayanti answered correctly 100 questions.
Question 22
The angles of a cyclic quadrilateral ABCD are ∠A = (6x + 10)°, ∠B = (5x)°, ∠C = (x + y)° and ∠D = (3y – 10)°. Find x and y and hence the values of the four angles.
Solution:
We know that, by property of cyclic quadrilateral,
Sum of opposite angles = 180°
∠A + ∠C = (6x + 10)° + (x + y)° = 180° [ ∵ ∠A = (6x + 10)°, ∠C = (x + y)°, given]
⇒ 7x + y = 170 …(i)
and ∠B + ∠D = (5x)° + (3y – 10)° = 180° [∵ ∠B = (5x)°, ∠D = (3y – 10)°, given]
⇒ 5x + 3y = 190
On multiplying eq. (i) by 3 and then subtracting eq. (ii) from them, we get
3 x (7x + y) – (5x + 3y) = 510° – 190°
⇒ 21x + 3y – 5x – 3y = 320°
⇒ 16x = 320°
⇒ x = 20°
On putting x = 20° in eq. (i), we get
7 x 20 + y = 170°
⇒ y = 170° – 140°
⇒ y = 30°
∴ ∠A = (6x + 10)° = 6 x 20° + 10° = 120° + 10° = 130°
∠B = (5x)° = 5 x 20° = 100°
∠C = (x + y)° = 20° + 30° = 50°
∠D = (3y – 10)° = 3 x 30° – 10°
= 90° – 10° = 80°
Hence, the required values of x and y are 20° and 30°, respectively and the values of the four angles i.e., ∠A, ∠B, ∠C, and ∠D are 130°, 100°, 50° and 80°, respectively.
Exercise 3.4
Question 1
Graphically, solve the following pair of equations:
2x + y = 6 and 2x – y + 2 = 0
Find the ratio of the areas of the two triangles formed by the lines representing these equations with the x-axis and the lines with the y-axis.
Solution:
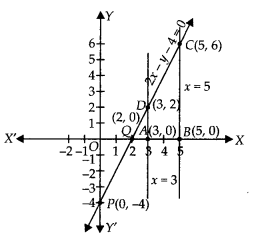
Given equations are 2x + y = 6 and 2x – y + 2 = 0
Table for equation 2x + y = 6
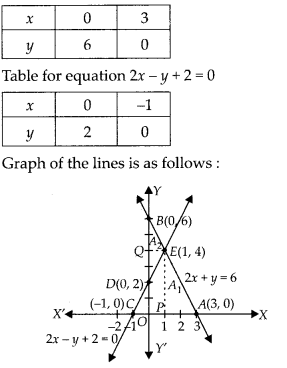
Hence, the pair of equations intersect graphically at point E(1, 4), i.e., x = 1 and y = 4
Let A1 and A2 represent the areas of ∆ACE and ∆BDE, respectively.
Now, A1 = Area of ∆ACE = \(\frac { 1 }{ 2 }\) x AC x PE
= \(\frac { 1 }{ 2 }\) x 4 x 4=8 2
and A2 = Area of ∆ BDE = \(\frac { 1 }{ 2 }\) x BD x QE
= \(\frac { 1 }{ 2 }\) x 4 x 1 = 2
∴ Required Ratio = A1 : A2 = 8 : 2 = 4 : 1
Question 2
Determine, graphically, the vertices of the triangle formed by the lines y = x, 3y = x and x + y = 8
Solution:
Given linear equations are
y = x, 3y = x and x + y = 8
Table for line y = x,
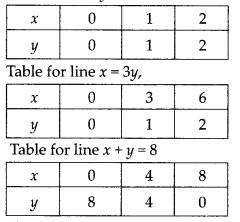
Plotting the points we get the graph of given lines.
We see that lines y = x and 3y = x intersecting the line x + y = 8 at Q and D, respectively.
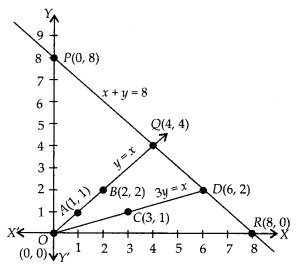
So, ∆OQD is formed by these lines. Hence the vertices of the ∆OQD are O(0, 0), Q(4, 4) and D(6, 2).
Question 3
Draw the graphs of the equations x = 3, x = 5 and 2x – y – 4 = 0. Also find the area of the quadrilateral formed by the lines and the x-axis.
Solution:
Given equation of lines 2x – y – 4 = 0, x = 3 and x = 5
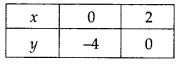
Plotting the points (0, -4) and (2, 0) and join these points we get the graph of 2x – y – 4 = 0.
Draw the lines x = 3 and x = 5.
Now, from the graph ABCD is the quadrilateral formed by given lines and x – axis.
∴ Area of quadrilateral ABCD = \(\frac { 1 }{ 2 }\) x (distance between parallel lines) x (sum of parallel sides)
= \(\frac { 1 }{ 2 }\) x AB x (AD + BC) = \(\frac { 1 }{ 2 }\) x 2 x (2 + 6)
[∵ AB = OB – OA = 5-3 = 2, AD = 2 and BC = 6]
= 8 sq. units
Hence, the required area of the quadrilateral formed by the lines and the x-axis is 8 sq. units.
Question 4
The cost of 4 pens and 4 pencils boxes is ₹100. Three times the cost of a pen is ₹15 more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and a pencil box.
Solution:
Let the cost of a pen be ₹ x
and the cost of a pencil box be ₹y
Then, by given condition,
4x + 4y = 100
⇒ x + y = 25 …(i)
and 3x = y + 15
⇒ 3x – y = 15 …(ii)
On adding eq. (i) and eq. (ii), we get
4x = 40
⇒ x = 10
By substituting x = 10 in eq. (i), we get
y = 25 – 10 = 15
Hence, the cost of a pen and a pencil box are ₹10 and ₹15, respectively.
Question 5
Determine, algebraically, the vertices of the triangle formed by the lines
3x – y = 3, 2x – 3y = 2 and x + 2y = 8
Solution:
Given equation of lines are 3x-y = 3 …(i)
2x – 3y = 2 …(ii)
and x + 2y = 8 …(iii)
Let lines (i), (ii) and (iii) represent the sides of a ∆ABC i.e., AB, BC and CA, respectively.
On solving lines (i) and (ii), we will get the intersecting point B
On multiplying eq. (i) by 3 and then subtracting eq. (ii) from it, we get
(9x – 3y) – (2x – 3y) = 9 – 2
⇒ 7x = 7
⇒ x = 1
On putting the value of x in eq. (i), we get
3 x 1 – y = 3
⇒ y = 0
So, the coordinates of point or vertex B are (1, o)
On solving lines (ii) and (iii), we will get the intersecting point C
On multiplying eq.(iii) by 2 and then subtracting, eq.(ii) from it, we get
(2x + 4y) – (2x – 3y) = 16 – 2
⇒ 7y = 14
⇒ y = 2
On putting the value of y in eq. (iii), we get
x + 2 x 2 = 8 ⇒ x = 8 – 4
⇒x = 4
Hence, the coordinates of point or vertex C are (4,2).
On solving lines (iii) and (i), we will get the intersecting point A
On multiplying in eq.(i) by 2 and then adding eq. (iii), we get
(6x – 2y) + (x + 2y) = 6 + 8
⇒ 7x = 14
⇒ x = 2
On putting the value of x in eq.(i), we get
3 x 2 – y = 3
⇒ y = 6 – 3
⇒ y = 3
So, the coordinate of point or vertex A is (2, 3)
Hence, the vertices of the ∆ABC formed by the given lines are A(2, 3), B( 1, 0) and C(4, 2).
Question 6
Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hour, if she travels 2 km by rickshaw, and the remaining distance by bus. On the other hand, if she travels 4 km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.
Solution:
Let the speed of the rickshaw and the bus are x km/h and y km/h, respectively. Now, time taken to travel 2 km by rickshaw,
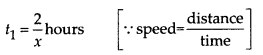
and time taken to travel remaining distance
i.e., (14 – 2) = 12 km by bus, t2 = \(\frac { 12 }{ y }\)hours
By first condition, t1 + t2 = \(\frac { 1 }{ 2 }\)
⇒ \(\frac { 2 }{ x }\) + \(\frac { 12 }{ y }\) = \(\frac { 1 }{ 2 }\) …(i)
Now, time taken to travel 4 km by rickshaw,
t3 = \(\frac { 4 }{ x }\) hours
and time taken to travel remaining distance i.e., (14 – 4) = 10 km by bus,
t4 = \(\frac { 10 }{ y }\) hours
By second condition, t3 + t4 = \(\frac { 1 }{ 2 }\) + \(\frac { 9 }{ 60 }\) = \(\frac { 1 }{ 2 }\) + \(\frac { 3 }{ 20 }\)
⇒ \(\frac { 4 }{ x }\) + \(\frac { 10 }{ y }\) = \(\frac { 13 }{ 20 }\) ……..(ii)
Let \(\frac { 1 }{ x }\) = u and \(\frac { 1 }{ y }\) = ν, then eq.(i) and eq.(ii) becomes
2u + 12ν = \(\frac { 1 }{ 2 }\) ….(iii)
and 4u + 10ν = \(\frac { 13 }{ 20 }\) ……(iv)
On multiplying eq. (iii) by 2 and then subtracting eq. (iv) from it, we get
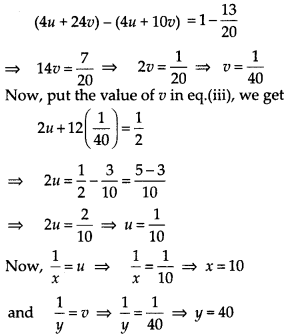
Hence, the speed of rickshaw and the bus are 10 km/h and 40 km/h, respectively.
Question 7
A person, rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream.
Solution:
Let the speed of the stream be v km/h Given that, speed of a person rowing in still water = 5 km/h
The speed of a person rowing in downstream = (5 + ν ) km/h
and the speed of a person has rowing in upstream = (5 – ν ) km/h
Now, the person takes time to cover 40 km downstream,

Hence, the speed of the stream is 2.5 km/h.
Question 8
A motorboat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream.
Solution:
Let the speed of the motorboat in still water and the speed of the stream are u km/h and ν km/h, respectively
Then, downstream speed of motorboat = (u + ν) km/h
And upstream speed of motorboat = (u – ν) km/h
Time taken to travel 30 km upstream,

By first condition, t1 + t2 = 7 hours
⇒ \(\frac { 30 }{ u-\nu } +\frac { 28 }{ u+\nu } =7\)
Now, time taken to travel 21 km upstream,
t3 = \(\frac { 21 }{ u-\nu }\)hours
And time taken to travel 21 km downstream,
t4 = \(\frac { 21 }{ u+\nu }\)hours
By second condition, t4 + t3 = 5 hours
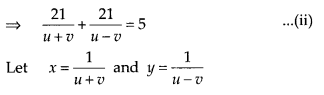
Eq. (i) and eq. (ii) becomes,
30x + 28y = 7 …………(iii)
and 21x + 21y = 5
⇒ x + y = \(\frac { 5 }{ 21 }\) ………(iv)
Now, multiplying in eq.(iv) by 28 and then subtracting from eq.(iii), we get
(30x – 28y) – (28x + 28y) = 7 – \(\frac { 140 }{ 21 }\)
⇒ 2x = 7 – \(\frac { 20 }{ 3 }\)
⇒ 2x = \(\frac { 1 }{ 3 }\)
⇒ x = \(\frac { 1 }{ 6 }\)
On putting the value of x in eq.(iv), we get
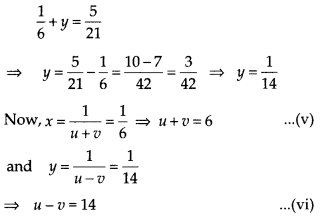
Now, adding eq. (v) and eq. (vi), we get 2u = 20 ⇒ u = 10
On putting the value of u in eq. (v), we get
10 + ν = 6 ⇒ ν = -4
Hence, the speed of the motorboat in still water is 10 km/h and the speed of the stream 4 km/h.
Question 9
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number.
Solution:
Let the two-digit number = 10x + y
Case I: Multiplying the sum of the digits by 8
and then subtracting 5 = two-digit number
⇒ 8 x (x + y) – 5 = 10x + y
⇒ 8x + 8y – 5 = 10x + y
⇒ 2x-7y = -5 …(i)
Case II : Multiplying the difference of the digits by 16 and then adding 3 = two-digit number
⇒ 16 x (x – y) + 3 = 10x+ y
⇒ 16x – 16y + 3 = 10x + y
⇒ 6x – 17y = -3 …(ii)
Now, multiplying eq.(i) by 3 and then subtracting from eq.(ii) we get
(6x – 17y) – (6x – 21y) = – 3 – (- 15)
⇒ 4y=12
⇒ y = 3
Now, put the value of y in eq. (i), we get
2x – 7 x 3 = -5
⇒ 2x = 21 – 5 = 16 ⇒ x = 8
Hence, the required two-digit number
= 10x + y
= 10 x 8 + 3 = 80 + 3 = 83
Question 10
A railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket. One reserved first class ticket from the stations. A to 8 costs ₹2530. Also, one reserved first class ticket and one reserved first class half ticket from A to 8 costs ₹3810. Find the full first class fare from station A to 8 and also the reservation charges for a ticket.
Solution:
Let the cost of full and half first class fare be ₹x and ₹ \(\frac { x }{ 2 }\) respectively and reservation charges be ₹ y per ticket.
Case I : The cost of one reserved first class ticket from the stations A to B = ₹2530
⇒ x + y = 2530 …….(i)
Case II : The cost of one reserved first class ticket and one reserved first class half ticket from stations A to B = ₹3810
⇒ x + y + \(\frac { x }{ 2 }\) + y = 3810
⇒ \(\frac { 3x }{ 2 }\)+ 2y = 3810
⇒ 3x + 4y = 7620 …(ii)
Now, multiplying eq. (i) by 4 and then subtracting from eq. (ii), we get
(3x + 4y) – (4x + 4y) = 7620 – 10120
⇒ -x = -2500
⇒x = 2500
On putting the value of x in eq.(i), we get
2500 + y = 2530
⇒ y = 2530 – 2500
⇒ y = 30
Hence, full first class fare from stations A to B is ₹2500 and the reservation charge for the ticket is ₹30.
Question 11
A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, thereby, getting a sum ₹1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got ₹1028. Find the cost price of the saree and the list price (price before discount) of the sweater.
Solution:
Let the cost price of the saree and the list price of the sweater be ₹x and ₹y, respectively.
Case I : sells a saree at 8% profit + Sells a
sweater at 10% discount = ₹1008
⇒ (100 + 8)% of x + (100 – 10)% of y = 1008
⇒ 108% of x+ 90% of y = 1008
⇒ 1.08x + 0.9 y = 1008 …(i)
Case II: Sold the saree at 10% profit + Sold the sweater at 8% discount = ₹1028
⇒ (100 + 10)% of x + (100 – 8)% of y = 1028
⇒ 110% of x + 92% of y = 1028
⇒ 1.1x + 0.92y = 1028 …(ii)
On putting the value of y from eq.(i), into eq. (ii), we get
1.1 x 0.92( \(\frac { 1008 – 1.08x }{ 0.9 }\))
⇒ 1.1 x 0.9x + 927.36 – 0.9936x = 1028 x 0.9
⇒ 0.99x – 0.9936x = 925.2 – 927.36
⇒ -0.0036x =-2.16
∴ x = \(\frac { 2.16 }{ 0.0036 }\) = 600
On putting the value of x in eq. (i), we get
1.08 x 600+ 0.9y= 1008
⇒ 648 + 0.9y = 1008
⇒ 0.9y = 1008 – 648
⇒ 0.9y = 360
⇒ y = \(\frac { 360 }{ 0.9 }\) = 400
Hence, the cost price of the saree and the list price (price before discount) of the sweater are ₹600 and ₹400, respectively.
Question 12
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received ₹1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received ₹20 more as annual interest. How much money did she invest in each scheme?
Solution:
Let the amount of investments in schemes A and B be ₹ x and ₹ y, respectively.
Case I: Interest at the rate of 8% per annum on scheme A + Interest at the rate of 9% per annum on scheme B = ₹1860
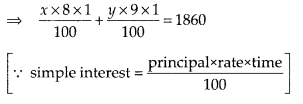
⇒ 8x + 9y = 186000 …(i)
Case II: Interest at the rate of 9% per annum on scheme A + Interest at the rate of 8% per annum on scheme B = ₹ 1860 + ₹20
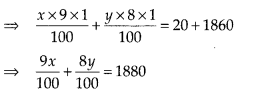
⇒ 9x + 8y= 188000 …(ii)
On multiplying eq. (i) by 9 and eq. (ii) by 8 and then subtracting them, we get
(72x + 81y) – (72x + 64y) = 9 x 186000 – 8 x 188000
⇒ 17y = 1000[(9 x 186) – (8 x 188)] = 1000(1674 – 1504) = 1000 x 170
17y = 170000 ⇒ y =10000
On putting the value of y in eq.(i), we get
8x + 9 x 10000 = 186000
⇒ 8x = 186000 – 90000
⇒ 8x = 96000
⇒ x = 12000
Hence, she invested ₹ 12000 and ₹ 10000 in two schemes A and B respectively.
Question 13
Vijay had some bananas, and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 bananas and the second lot at the rate of ₹ 1 per banana, and got a total of ₹ 400. If he had sold the first lot at the rate of ₹1 per banana and the second lot at the rate of ₹ 4 for 5 bananas, his total collection would have been ₹ 460. Find the total number of bananas he had.
Solution:
Let the number of bananas in lots A and B be x and y respectively
Case I: Cost of the first lot at the rate of ₹ 2 for 3 bananas + Cost of the second lot at the rate of ₹1 per banana = ₹ 400
⇒ \(\frac { 2 }{ 3 }\)x + y = 400
⇒ 2x + 3y = 1200 …(i)
Case II: Cost of the first lot at the rate ₹1 per banana + Cost of the second lot at the rate of ₹4 for 5 bananas = Amount received
⇒ x + \(\frac { 4 }{ 5 }\)y = 460
⇒ 5x + 4y = 2300 …(ii)
On multiplying in eq. (i) by 4 and eq. (ii) by 3 and then subtracting them, we get
(8x + 12y) – (15x + 12y) = 4800 – 6900
⇒ – 7x = – 2100
⇒ x = 300
Now, put the value of x in eq.(i), we get
2 x 300 + 3y = 1200
⇒ 600 + 3y = 1200
⇒ 3y = 1200 – 600
⇒ 3y = 600
⇒ y = 200
∴ Total number of bananas = Number of bananas in lot A + Number of bananas in lot B = x + y = 300 + 200 = 500
Hence, he had 500 bananas.
We hope the NCERT Exemplar Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables will help you. If you have any query regarding NCERT Exemplar Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables, drop a comment below and we will get back to you at the earliest.