NCERT Exemplar Class 10 Maths Chapter 10 Constructions are part of NCERT Exemplar Class 10 Maths. Here we have given NCERT Exemplar Class 10 Maths Chapter 10 Constructions.
NCERT Exemplar Class 10 Maths Chapter 10 Constructions
Exercise 10.1
Choose the correct answer from the given four options:
Question 1
To divide a line segment AB in the ratio 5 : 7, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is
(A) 8
(B) 10
(C) 11
(D) 12
Solution:
(D) We know that, to divide a line segment AB in the ratio m : n, first draw a ray AX which makes an acute angle ∠BAX, then marked m + n points at equal distance on AX. Here, m = 5,n = 7
So, minimum number of these points = m + n = 5 + 7 = 12
Question 2
To divide a line segment AB in the ratio 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1, A2, A3,…. are located at equal distances on the ray AX and the point B is joined to
(A) A12
(B) A11
(C) A10
(D) A9
Solution:
(B) Here, minimum 4 + 7 = 11 points are located at equal distances on the ray AX, and then B is joined to last point A11.
Question 3
To divide a line segment AB in the ratio 5:6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the points A1, A2, A3,… and B1, B2, B3,… are located at equal distances on ray AX and BY, respectively. Then the points joined are
(A) A5 and B6
(B) A6 and B5
(C) A4 and B5
(D) A5 and B4
Solution:
(A) Given, a line segment AB and we have to divide it in the ratio 5 : 6.
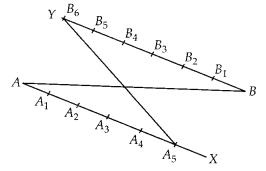
Steps of construction:
1. Draw a ray AX making an acute ∠BAX.
2. Draw a ray BY parallel to AX by making ∠ABY equal to ∠BAX.
3. Now, locate the points A1, A2, A3, A4 and A5 (m = 5) on AX and B1, B2, B3, B4, B5 and B6 (n = 6) such that all the points are at equal distance from each other.
4. Join B6A5.
Question 4
To construct a triangle similar to a given ∆ABC with its sides \(\frac { 3 }{ 7 }\) of the corresponding sides of ∆ABC, first draw a ray BX such that ∠CBX is an acute angle and X lies on the opposite side of A with respect to BC. Then locate points B1, B2, B3,… on BX at equal distances and next step is to join
(A) B10 to C
(B) B3 to C
(C) B7 to C
(D) B4 to C
Solution:
(C) Here, we locate points B1, B2, B3, B4, B5, B6 and B7 on BX at equal distance and in next step join the last point B7 to G.
Question 5
To construct a triangle similar to a given ∆ABC with its sides \(\frac { 8 }{ 5 }\) of the corresponding sides 5 of ∆ABC draw a ray BX such that ∠CBX is an acute angle and X is on the opposite side of A with respect to BC. The minimum number of points to be located at equal distances on ray BX is
(A) 5
(B) 8
(C) 13
(D) 3
Solution:
(B) To construct a triangle similar to a given triangle, with its sides \(\frac { m }{ n }\) of the n corresponding sides of given triangle the minimum number of points to be located at equal distance is equal to the greater of m and n in \(\frac { m }{ n }\). Here, \(\frac { m }{ n }\) = \(\frac { 8 }{ 5 }\)
So, the minimum number of point to be located at equal distance on ray BX is 8.
Question 6
To draw a pair of tangents to a circle which are inclined to each other at an angle of 60°, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be
(A) 135°
(B) 90°
(C) 60°
Solution:
(D) The angle between them should be 120° because in that case the figure formed by the intersection point of pair of tangent, the two end points of those two radii (at which tangents are drawn) and the centre of the circle is a quadrilateral.
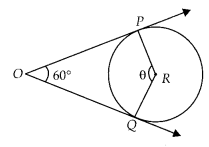
From figure it is quadrilateral,
∠POQ + ∠PRQ = 180°
[ ∵ sum of opposite angles are 180°]
∴ 60° + θ = 180°
θ = 120°
Hence, the required angle between them is 120 .
Exercise 10.2
Write True or False and give reasons for your answer in each of the following:
Question 1
By geometrical construction, it is possible to divide a line segment in the ratio \(\sqrt { 3 } :\frac { 1 }{ \sqrt { 3 } }\).
Solution:
True
Given, ratio = \(\sqrt { 3 } :\frac { 1 }{ \sqrt { 3 } }\)
∴ Required ratio = 3 : 1
[multiply √3 in each term]
So, \(\sqrt { 3 } :\frac { 1 }{ \sqrt { 3 } }\) can be simplified as 3 : 1 and 3 as well as 1 both are positive integer.
Hence, the geometrical construction is possible to divide a line segment in the ratio 3 : 1.
Question 2
To construct a triangle similar to a given ∆ABC with its sides \(\frac { 7 }{ 3 }\) of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B1, B2, ……., B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C’ is drawn parallel to B3C where C’ lies on BC produced. Finally, line segment A’C’ is drawn parallel to AC.
Solution:
False
Steps of construction:
1. Draw a line segment BC with suitable length.
2. Taking B and C as centres draw two arcs of suitable radii intersecting each other at A.
3. Join BA and CA. ∆ABC is the required triangle.
4. From B draw any ray BX downwards making an acute angle CBX.
5. Locate seven points B1, B2, b3, …. B7 on BX such that BB1 = B1B2 = B1B3 = B3B4 = B4B5 = B5B6 = B6B7.
6. Join B3C and from B7 draw a line B7C’ ॥ B3C intersecting the extended line segment BC at C’.
7. From point C’ draw C’A’ ॥ CA intersecting the extended line segment BA at A’.
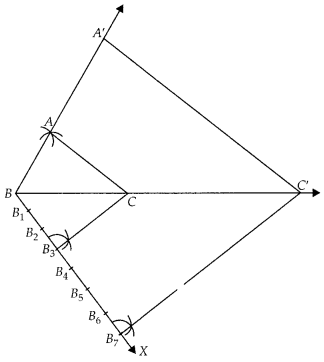
Then ∆A’BC’ is the required triangle whose sides are \(\frac { 7 }{ 3 }\) of the corresponding sides of ∆ABC.
Given that, segment B6C’ is drawn parallel to B3C. But from our construction is never possible that segment B6C’ is parallel to B3C because the similar triangle A’BC’ has its sides \(\frac { 7 }{ 3 }\) of the corresponding sides of triangle ABC. So, B7C’ is parallel to B3C.
Question 3
A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of 3 cm from the centre.
Solution:
False
Since, the radius of the circle is 3.5 cm
i.e., r = 3.5 cm and a point P situated at a distance of 3 cm from the centre
i.e., d = 3 cm.
We see that r > d
i. e., a point P lies inside the circle. So, no tangent can be drawn to a circle from a point lying inside it.
Question 4
A pair of tangents can be constructed to a circle inclined at an angle of 170°.
Solution:
True
Since, the angle between the pair of tangents is always greater than 0 but less than 180°. Hence, we can draw a pair of tangents to a circle inclined at an angle at 170°.
Exercise 10.3
Question 1
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3 : 5.
Solution:
Steps of construction :
1. Draw a line segment AB = 7 cm.
2. Draw a ray AX, making an acute ∠BAX.
3. Along AX, mark 3 + 5 = 8 points
A1, A2, A3, A4, A5, A6, A7, A8 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A6A7 = A7A8
4. Join A8B.
5. From A3, draw A3P ॥ A8B meeting AB at P.
[by making an angle equal to ∠BA8A at A3]
Then, P is the point on AB which divides it in the ratio 3 : 5.
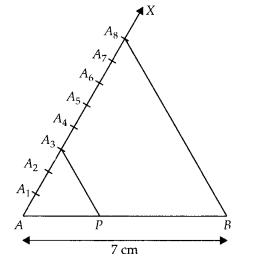
Justification:
Let AA1 = A1A2 = A2A3 = A3A4 = ……… = A7A8 = x
In ∆ABA8, we have
A3P ॥ A8B
\(\therefore \quad \frac { AP }{ PB } =\frac { A{ A }_{ 3 } }{ { A }_{ 3 }{ A }_{ 8 } } =\frac { 3x }{ 5x } =\frac { 3 }{ 5 }\)
Hence, AP : PB = 3 : 5
Question 2
Draw a right triangle ABC in which BC= 12 cm, AB = 5 cm and ∠B = 90°. Construct a triangle similar to it and of scale factor \(\frac { 2 }{ 3 }\) . Is the new triangle also a right triangle?
Solution:
Steps of construction :
1. Draw a line segment BC = 12 cm.
2. From B draw a line AB = 5 cm which makes right angle at B.
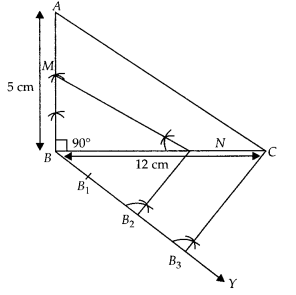
3. Join AC, ∆ABC is the given right triangle.
4. From B draw an acute ∠CBY downwards.
5. On ray BY, mark three points B1, B2 and B3, such that BB1 = B1B2 = B2B3.
6. Join B3C.
7. From point B2 draw B2N ॥ B3C intersect BC at N.
8. From point N draw NM ॥ CA intersect BA at M. ∆MBN is the required triangle. ∆MBN is also a right angled triangle at B.
Question 3
Draw a triangle ABC in which BC = 6 cm, CA = 5 cm and AB = 4 cm. Construct a triangle similar to it and of scale factor \(\frac { 5 }{ 3 }\) .
Solution:
Steps of construction :
1. Draw a line segment BC = 6 cm.
2. Taking B and C as centres, draw two arcs of radii 4 cm and 5 cm intersecting each other at A.
3. Join BA and CA. ∆ABC is the required triangle.
4. From B, draw any ray BX downwards making at acute angle ∠CBX
5. Mark five points B1, B2, B3, B4 and B5 on BX, such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
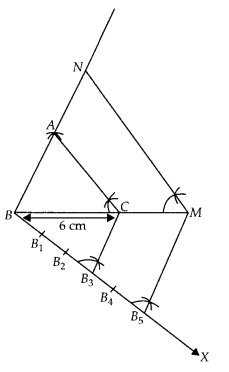
6. Join B3C and from B5 draw B5M ॥ B3C intersecting the extended line segment BC at M.
7. From point M draw MN ॥ CA intersecting the extended line segment BA at N.
Then, ∆NBM is the required triangle
whose sides is equal to \(\frac { 5 }{ 3 }\) of the corresponding sides of the ∆ABC.
Hence, ∆NBM is the required triangle.
Question 4
Construct a tangent to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
Solution:
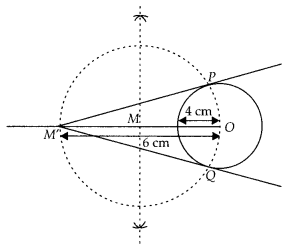
Given, a point M’ is at a distance of 6 cm from the centre of a circle of radius 4 cm.
Steps of construction:
1. Draw a circle of radius 4 cm. Let centre of this circle is O.
2. Join OM’ and bisect it. Let M be mid-point of OM’.
3. Taking M as centre and MO as radius draw a circle to intersect circle (0, 4) at two points, P and Q.
4. Join PM’ and QM’. PM’ and QM’ are the required tangents from M’ to circle C(0, 4).
Exercise 10.4
Question 1
Two line segments AB and AC include an angle of 600 where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = \(\frac { 3 }{ 4 }\)AB and AQ = \(\frac { 1 }{ 4 }\)AC. Join P and Q and measure the length PQ.
Solution;
Given that AB = 5cm and AC = 7cm
Mso, AP = \(\frac { 3 }{ 4 }\)AB and AQ = \(\frac { 1 }{ 4 }\)AC …(i)
From equation (i)
AP = \(\frac { 3 }{ 4 }\).AB = \(\frac { 3 }{ 4 }\) x 5 = \(\frac { 15 }{ 4 }\)cm
Then,
PB = AB – AP = 5 – \(\frac { 15 }{ 4 }\) = \(\frac { 20 – 15 }{ 4 }\) = \(\frac { 5 }{ 4 }\)cm
[ ∵ P is any point on the AB]
∴ AP : PB = \(\frac { 15 }{ 4 }\): \(\frac { 5 }{ 4 }\)= AP : PB = 3 : 1
i.e., scale factor of line segment AB is \(\frac { 3 }{ 1 }\)
Again from equation (i),
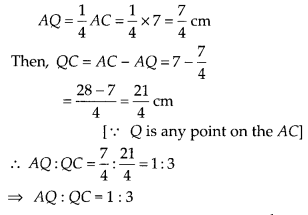
i.e., scale factor of line segment AC is \(\frac { 1 }{ 3 }\).
Steps of construction:
1. Draw a line segment AB = 5 cm.
2. Now draw a ray AZ making an acute ∠BAZ = 60°.
3. With A as centre and radius equal to 7 cm draw an arc cutting the line AZ at C.
4. Draw a ray AX, making an acute ∠BAX.
5. Along AX, mark 1 + 3 = 4 points A1, A2, A3 and A4 such that AA1 = A1A2 = A2A3 = A3A4.
6. Join A4B.
7. From A3 draw A3P ॥ A4B meeting AB at P.
[by making an angle equal to ∠AA4B]
Then, P is the point on AB which divides it in the ratio 3 : 1.
So, AP : PB = 3 : 1.
8. Draw a ray AY, making an acute ∠CAY.
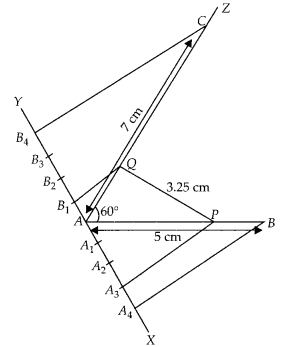
9. Along AY, mark 3 + 1=4 points B1, B2, B3 and B4. Such that AB1 = B1B2 = B2B3 = B3B4.
10. Join B4C.
11. From B1 draw B1Q॥ B4C meeting AC at Q.
[by making an angle equal to ∠AB4C]
Then, Q is the point on AC which divides it in the ratio 1 : 3.
So, AQ : QC = 1 : 3
12. Finally, join PQ and its measurement is 3.25 cm.
Question 2
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD’C’ similar to ∆BDC with scale factor \(\frac { 4 }{ 3 }\) . Draw the line segment D’A’ parallel to DA where A’ lies on extended side BA. Is A’BC’D’ a parallelogram?
Solution:
Steps of construction :
1. Draw a line segment AB = 3 cm.
2. Now, draw a ray by making an acute ∠ABY = 60°.
3. With B as centre and radius equal to 5 cm draw an arc cut the point Con BY.
4. Again draw a ray AZ making an acute ∠ZAX’ = 60°.
[∵ BY ॥ AZ, ∴ YBX’ = ZAX’ = 60°]
5. With A as centre and radius equal to 5 cm draw an arc cut the point D on AZ.
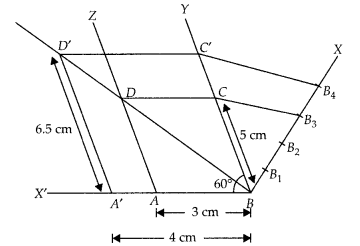
6. Now, join CD and finally make a parallelogram ABCD.
7. Join BD, which is a diagonal of parallelogram ABCD.
8. From B draw any ray BX downwards making an acute ∠CBX.
9. Locate 4 points B1, B2, B3, B4, on BX, such that BB1 = B1B2 = B2B3 = B3B4.
10. Join B3C and from B4 draw a line B4C’ ॥ B3C intersecting the extended line segment BC at C.
11. From point C’ draw C’D’ ॥ CD intersecting the extended line segment BD at D’. Then, ∆D’BC’ is the required triangle whose sides are \(\frac { 4 }{ 3 }\) of the corresponding sides of ∆DBC.
12. Now draw a line segment D’A’ parallel to DA, where A’ lies on extended side BA i.e., a ray BX’.
13. Finally, we observe that A’BC’D’ is a parallelogram in which A’D’ = 6.5 cm A’B = 4 cm and ∠A’BD’ = 60° divide it into triangles BC’D’ and A’BD’ by the diagonal BD’.
Question 3
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Solution:
Given, two concentric circles of radii 3 cm and 5 cm with centre O. We have to draw pair of tangents from point P on outer circle to the other.
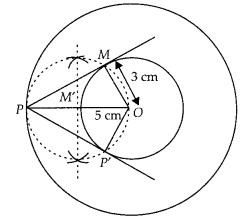
Steps of construction:
1. Draw two concentric circles with centre O and radii 3 cm and 5 cm.
2. Taking any point P on outer circle. Join OP.
3. Bisect OP, let M’ be the mid-point of OP.
Taking M’ as centre and OM’ as radius draw a circle dotted which cuts the inner circle at M and P’.
4. Join PM and PP’. Thus, PM and PP’ are the required tangents.
5. On measuring PM and PP’, we find that PM = PP’ = 4 cm.
Actual calculation :
In right angle ∆OMP, ∠PMO = 90°
PM2 = OP2 – OM2
[by Pythagoras theorem i.e. (hypotenuse)2 = (base)2 + (perpendicular)2]
⇒ PM2 = (5)2 – (3)2
= 25 – 9 = 16
⇒ PM = 4 cm
Hence, the length of both tangents is 4 cm
Question 4
Draw an isosceles triangle ABC in which AB = AC = 6 cm and BC = 5 cm. Construct a triangle PBR similar to ABC in which PB = 8 cm. Also justify the construction.
Solution:
Let ∆PQR and ∆ABC are similar triangles, then its scale factor between the corresponding side is \(\frac { PQ }{ AB }\) = \(\frac { 8 }{ 6 }\) = \(\frac { 4 }{ 3 }\)
Steps of construction:
1. Draw a line segment BC = 5 cm.
2. Construct OQ the perpendicular bisector of line segment BC meeting BC at P’.
3. Taking B and C as centres draw two arcs of equal radius 6 cm intersecting each other at A.
4. Join BA and CA. So, ∆ABC is the required isosceles triangle.
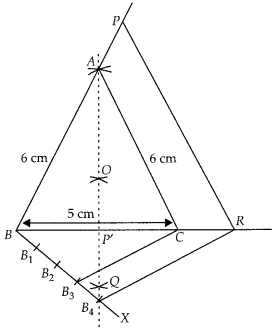
5. From B, draw any ray BX making an acute ∠CBX.
6. Locate four points B1, B2, B3 and B4 on BX such that BB1 = B1B2 = B2B3 = B3B4.
7. Join B3C and from B4 draw a line B4R ॥ B3C intersecting the extended line segment BC at R.
8. From point R, draw RP ॥ CA meeting BA produced at P.
Then, ∆ PBR is the required triangle.
Justification:
∵ B4R ॥ B3C (by construction)
![]()

Question 5
Draw a triangle ABC in which AB = 5 cm, BC= 6cm and ∠ABC= 60°. Construct a triangle similarto ABC with scale factor \(\frac { 5 }{ 7 }\) . Justify the construction.
Solution:
Steps of construction:
1. Draw a line segment AB = 5 cm.
2. From point B, draw ∠ABY = 60° on which take BC = 6 cm.
3. Join AC, ∆ABC is the required triangle.
4. From A, draw any ray AX downwards making an acute angle ∠BAX
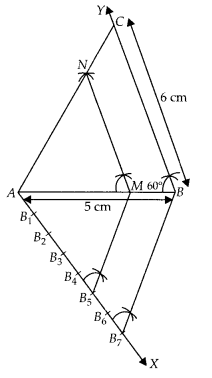
5. Mark 7 points B1, B2, B3, B4, B5, B6 and B7 on AX, such that AB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6= B6B7.
6. Join B7B and from B5 draw B5M ॥ B7B intersecting AB at M.
7. From point M draw MN ॥ BC intersecting AC at N. Then, ∆AMN is the required triangle whose sides are equal to \(\frac { 5 }{ 7 }\) of the corresponding sides of the ∆ABC.
Justification:
Here, B5M ॥ B7B (by construction)
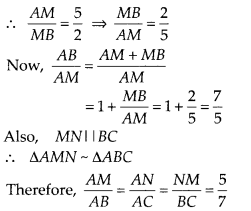
Question 6
Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60°. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents. wgiil In order to draw the pair of tangents, we follow the following steps
Solution:
Steps of construction:
1. Take a point O on the plane of the paper and draw a circle of radius OA = 4 cm.
2. Produce OA to B such that OA = AB = 4 cm.
3. Taking A as the centre draw a circle of radius AO = AB = 4 cm.
Suppose it cuts the circle drawn in step 1 at P and Q.
4. Join BP and BQ to get desired tangents.
Justification:
In ∆OAP, we have
OA = OP = 4 cm (Radius)
Also, AP = 4 cm
(∵ Radius of circle with centre A)
∴ ∆OAP is equilateral
⇒ ∠PAO = 60° ⇒ ∠BAP = 120°
In ∆BAP, we have
BA = AP and ∠BAP = 120°
∴ ∠ABP = ∠APB = 30° ⇒ ∠PBQ = 60°
Question 7
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to ∆ABC with scale factor \(\frac { 3 }{ 2 }\). Justify the construction. Are the two triangles congruent? Note that all the three angles and two sides of the two triangles are equal.
Solution:
Steps of construction :
1. Draw a line segment BC = 6 cm.
2. Taking B and C as centres, draw two arcs of radii 4 cm and 9 cm intersecting each other at A.
3. Join BA and CA. ∆ABC is the required triangle.
4. From B, draw any ray BX downwards making an acute angle ∠CBX
5. Mark three points B1, B2, B3, on BX, such that BB1 = B1B2 = B2B3.
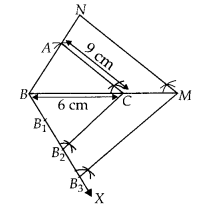
6. Join B2C and from B3 draw B3M ॥ B2C intersecting BC at M.
7. From point M, draw MN ॥ CA intersecting the extended line segment BA to N.
Then ∆NBM is the required triangle whose sides are equal to \(\frac { 3 }{ 2 }\) of the ∆ABC .
Justification:

The two triangles are not congruent because, if two triangles are congruent, then they have same shape and same size. Here, all the three angles are same but three sides are not same i.e, one side is different.
We hope the NCERT Exemplar Class 10 Maths Chapter 10 Constructions will help you. If you have any query regarding NCERT Exemplar Class 10 Maths Chapter 10 Constructions, drop a comment below and we will get back to you at the earliest.