Motion Class 9 Extra Questions Science Chapter 8
Extra Questions for Class 9 Science Chapter 8 Motion
Motion Class 9 Extra Questions Very Short Answer Questions
Question 1.
The phenomenon of motion was placed on a sound scientific footing by two scientists. Write their names.
Answer:
Galileo Galilei and Isaac Newton.
Question 2.
Are rest and motion absolute or relative terms?
Answer:
They are relative terms.
Question 3.
Suppose a ball is thrown vertically upwards from a position P above the ground. It rises to the highest point Q and returns to the same point P. What is the net displacement and distance travelled by the ball?
Answer:
Displacement is zero. Distance is twice the distance between position P and Q.
Question 4.
Which speed is greater: 30 m/s or 30 km/h?
Answer:
30 m/s
Question 5.
What do you mean by 2 m/s2?
Answer:
The velocity of the body increases by 2 m/s after every second.
Question 6.
Can uniform linear motion be accelerated?
Answer:
No
Question 7.
Define one radian.
Answer:
It is the angle which is subtended at the centre by an arc having a length equal to the radius of the circle.
Question 8.
What is the relation between linear velocity and angular velocity?
Answer:
Linear velocity = Angular velocity × Radius of circular path.
Question 9.
Give an example when we infer the motion indirectly.
Answer:
We infer the motion of air by observing the movement of dust particles or leaves and branches of trees, or simply by feeling the blowing air on our face.
Question 10.
What is essential to describe the position of an object?
Answer:
We need to specify a reference point called the origin.
Question 11.
What is the simplest type of motion?
Answer:
Motion in a straight line.
Question 12.
What indicates the motion of the earth?
Answer:
The phenomenon like day and night indicates the motion of the earth.
Question 13.
If the displacement of a body is zero, is it necessary that the distance coyered by it is also zero?
Answer:
No. When the body comes back to the same position after travelling a distance, its displacement is zero though it has travelled some distance.
Question 14.
Can the displacement be greater than the distance travelled by an object?
Answer:
No, it is always either equal to or less than the distance travelled by the object.
Question 15.
When do the distance and displacement of a moving object have the same magnitude?
Answer:
The magnitude of distance and displacement of a moving object are same when the object moves along the same straight line in the same fixed direction.
Question 16.
Does the speedometer of a car measure its average speed?
Answer:
No. It measures its instantaneous speed.
Question 17.
A body is moving with a velocity of 10 m/s. If the motion is uniform, what will be the velocity after 10 s?
Answer:
As the motion is uniform, the velocity remains 10 m/s after 10 s.
Question 18.
Can a body have constant speed but variable velocity?
Answer:
Yes, e.g. a body in uniform circular motion has constant speed but due to the change in the direction of motion, its velocity changes at every point.
Question 19.
When is the acceleration taken as negative?
Answer:
Acceleration is taken as negative if it is in the direction opposite to the direction of velocity.
Question 20.
What is uniform acceleration?
Answer:
Acceleration of an object is said to be uniform if it travels in a straight line and its velocity increases or decreases by equal amounts in equal intervals of time.For example, motion of a freely falling body.
Question 21.
Give an example of non-uniform acceleration.
Answer:
A car is travelling along a straight road increases its speed by unequal amounts in equal intervals of time.
Question 22.
How are the distances travelled by an object related to the time taken when an object travels equal distances in equal intervals of time?
Answer:
In this case, distance travelled by the object is directly proportional to the time taken.
Question 23.
What would be acceleration of a body if its velocity-time graph is a line parallel to the time axis?
Answer:
Zero, as the body possesses uniform velocity.
Question 24.
Is the motion of a body uniform or accelerated if it goes round the sun with constant speed in a circular orbit?
Answer:
It is accelerated, as its velocity changes due to change in direction.
Motion Class 9 Extra Questions Short Answer Questions-I
Question 1.
Give an example of a body which may appear to be moving for one person and stationary for the other.
Answer:
The passengers in a moving bus observe that the trees, buildings as well as the people on the roadside appear to be moving backwards. Similarly, a person standing on the roadside observes that the bus (along with its passengers) is moving in forward direction. But, at the same time, each passenger in a moving bus or train observes, his fellow passengers sitting and not moving. Thus, we can tell that motion is relative.
Question 2.
How can we describe the location of an object?
Answer:
To describe the position of an object we need to specify a reference point called the origin.
For example, suppose that a library in a city is 2 km north of the railway station. We have specified the position of the library with respect to the railway station i.e., in this case, the railway station acts as the reference point.
Question 3.
What do you mean by average speed? What are its units?
Answer:
Average speed is defined as the average distance travelled per unit time and is obtained by dividing the total distance travelled by the total time taken.
The unit of average speed is the same as that of the speed, that is, ms-1.
Question 4.
What is the difference between uniform velocity and non-uniform velocity?
Answer:
Uniform velocity: An object with uniform velocity covers equal distances in equal intervals of time in a specified direction, e.g., an object moving with speed of 40 kmh-1 towards west has uniform velocity.
Non-uniform velocity: When an object covers unequal distances in equal intervals of time in a specified direction, or if the direction of motion changes, it is said to be moving with a non-uniform or variable velocity, e.g., revolving fan at a constant speed has variable velocity.
Question 5.
What do you understand by instantaneous velocity?
Answer:
Instantaneous velocity is the velocity of a body at any particular instant during its motion. For example, the instantaneous velocity of a motorcycle at a particular instant is 40 kmh-1 if it is moving at 40 kmh-1 at that particular instant. It is measured by the speedometers on the vehicles.
Question 6.
What is negative acceleration?
Answer:
If the velocity of a body decreases with time, then its final velocity is less than the initial velocity and thus its acceleration is negative. Negative acceleration is called retardation or deceleration. For example, when brakes are applied to a moving truck, its velocity gradually decreases. In other words, it is under retardation.
Question 7.
How will the equations of motion for an object moving with a uniform velocity change? [NCERT Exemplar]
Answer:
Acceleration a = 0, v = u
So, the equations of motion will become
s = ut
v2 – u2 = 0
Question 8.
Express average velocity when the velocity of a body changes at a non-uniform rate and a uniform rate.
Answer:
When the velocity of a body changes at a non-uniform rate, its average velocity is found by dividing the net displacement covered by the total time taken.
i.e., Average velocity = \(\frac{\text { Net displacement }}{\text { Total time taken }}\)
In case the velocity of a body changes at a uniform rate, then the average velocity is given by the arithmetic mean of initial velocity and final
i.e., Average velocity = \(\frac{\text { Initial velocity + Final velocity }}{2}\)
Question 9.
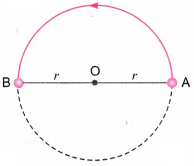
A particle is moving in a circular path of radius r. What would be the displacement after half a circle?
Answer:
Displacement = AB
= Shortest distance between initial and final positions
= r + r = 2r
Motion Class 9 Extra Questions Short Answer Questions-II
Question 1.
Differentiate between distance and displacement.
Answer:

Question 2.
What are the uses of a distance-time graph?
Answer:
The various uses of a distance-time graph are as follows:
- It tells us about the position of the body at any instant of time.
- From the graph, we can see the distance covered by the body during a particular interval of time.
- It also gives us information about the velocity of the body at any instant of time.
Question 3.
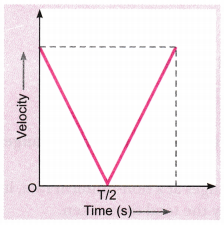
Draw a velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height. [NCERT Exemplar]
Answer:
During upward motion, acceleration = -g and during downward motion acceleration = + g. Times of upward and downward motion is equal. Also initial and final velocities are equal to \(\left(g \frac{T}{2}\right)\).
Question 4.
The data regarding the motion of two different objects P and Q is given in the following table. Examine them carefully and state whether the motion of the objects is uniform or non-uniform.

Answer:
We can see that the object P covers a distance of 10 m in every fifteen minutes. In other words, it covers equal distance in equal interval of time. So, the motion of object P is uniform. On the other hand, the object Q covers 7 m from 9:30 am to 9:45 am, 4 m from 9:45 am to 10:00 am, and so on. In other words, it covers unequal distance in equal interval of time. So, the motion of object Q is non-uniform.
Question 5.
How will you show that the slope of displacement-time graph gives velocity of the body ?
Answer:
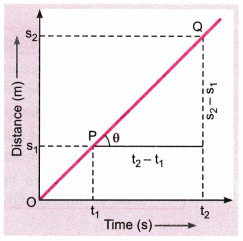
The adjoining figure shows the displacement-time graph for a body moving with uniform velocity. Clearly, it covers distance s1 and s2 at times t1 and t2 respectively.
Slope of line PQ = tanθ = \(\frac{Q R}{P R}\)
= \(\frac{s_{2}-s_{1}}{t_{2}-t_{I}}=\frac{\text { Displacement }}{\text { Time }}\)
As \(\frac{\text { Displacement }}{\text { Time }}\) is velocity, so the slope of the distance-time graph gives velocity of the body.
Question 6.
What are the characteristics of distance-time graph for an object moving with a non-uniform speed?
Answer:
The characteristics of distance-time graph for a non-uniform speed are:
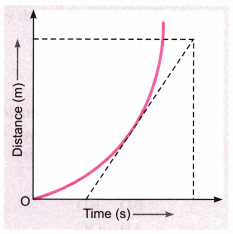
- It is always a curve (parabola).
- The speed of the moving object at any point is given by the slope of the tangent to the curve at that point.
Question 7.
Given below is the velocity-time graph for the motion of the car. What does the nature of the graph show ? Also find the acceleration of the car.
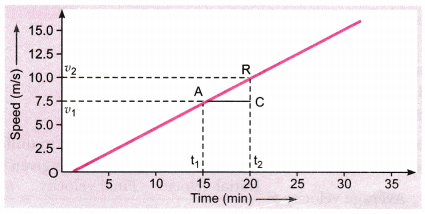
Answer:
The nature of the graph shows that velocity changes by equal amounts in equal intervals of time. For a uniformly accelerated motion, velocity-time graph is always a straight line.
As we know, acceleration is equal to the slope of the graph
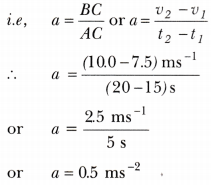
Motion Class 9 Extra Questions Long Answer Questions
Question 1.
With the help of a graph, derive the relation v = u + at.
Answer:
Consider the velocity-time graph of an object that moves under uniform acceleration as shown in the figure (u ≠ 0).
From this graph, we can see that initial velocity of the object (at point A) is u and then it increases tow (at point B) in time t. The velocity changes at a uniform rate a. As shown in the figure, the lines BC and BE are drawn from point B on the time and the velocity axes respectively, so that the initial velocity is represented by OA, the final velocity is represented by BC and the time interval t is represented by OC. BD = BC – CD, represents the change in velocity in time interval t.
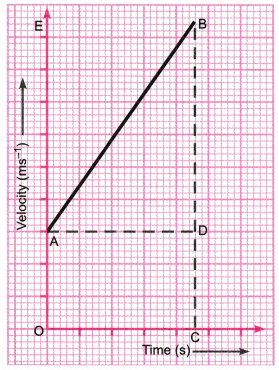
If we draw AD parallel to OC, we observe that
BC = BD + DC = BD + OA
Substituting, BC with v and OA with u,
we get
v = BD + u
or BD = v – u …(1)
Thus, from the given velocity-time graph, the acceleration of the object is given by
a = \(\frac{\text { Change in velocity }}{\text { Time taken }}\)
= \(\frac{B D}{A D}=\frac{B D}{O C}\)
Substituting, OC with t, we get
a = \(\frac{\mathrm{BD}}{t}\) or BD= at …..(2)
From equations (1) and (2),
we have
v – u = at or v = u + at
Question 2.
Deduce the following equations of motion:
(i) s = ut + \(\left(\frac{1}{2}\right)\)at2
(ii) v2 = u2 + 2as
Answer:
(i) Consider a body which starts with initial velocity u and due to uniform acceleration a, its final velocity becomes v after time t. Then, its average velocity is given by

Question 3.
Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between 4th and 5th seconds. [NCERT Exemplar]
Answer:
Using the equation of motion s = ut + \(\frac{1}{2}\) at2
Distance travelled in 5 seconds, s = u × 5 + \(\frac{1}{2}\)a × 5 2
or s = 5u + \(\frac{25}{2}\)a
Similarly, distance travelled in 4 seconds, s’ = 4u + \(\frac{1}{4}\)a
Distance travelled in the interval between 4th and 5th seconds
= (s – s’) = (u + \(\frac{9}{2}\) a)m
Question 4.
Two stones are thrown vertically upwards simultaneously with their initial velocities u] and w2 respectively. Prove that the heights reached by them would be in the ratio of \(u_{1}^{2} : u_{2}^{2}\).
(Assume upward acceleration is —g and downward acceleration to be +g). [NCERT Exemplar]
Answer:

Question 5.
The driver of train A travelling at a speed of 54 kmh-1 applies brakes and retards the train uniformly. The train stops in 5 seconds. Another train B is travelling on the parallel with a speed of 36 kmh-1. Its driver applies the brakes and the train retards uniformly; train B stops in 10 seconds. Plot speed-time graphs for both the trains on the same axis. Which of the trains travelled farther after the brakes were applied?
Answer:
For train A, the initial velocity,
u = 54 kmh-1 = 54 × \(\frac{5}{18}\) = 15 ms– 1
Final velocity, v = 0 and time, t = 5 s
For train B, u = 36 kmh– 1 = 36 × \(\frac{5}{18}\) = 10 ms– 1
v = 0; t = 10 s
Speed-time graph for train A and B are shown in the figure.
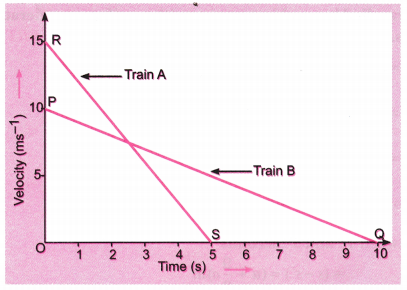
Distance travelled by train A
= Area under straight line graph RS
= Area of ∆ORS
= \(\frac{1}{2}\) × OR × OS = \(\frac{1}{2}\) × 15 ms– 1 × 5 s = 37.5 m
Distance travelled by train B = Area under PQ = Area of ∆OPQ
= \(\frac{1}{2}\) × OP × OQ = \(\frac{1}{2}\) × 10 ms-1 × 10 s = 50 m
Thus, train B travelled farther after the brakes were applied.
Numericals
Question 1.
Study the speed-time graph of a body given here and answer the following questions:
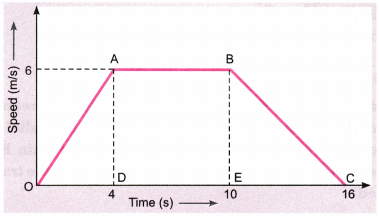
(a) What type of motion is represented by OA?
(b) What type of motion is represented by AB?
(c) What type of motion is represented by BC?
(d) Find out the acceleration of the body.
(e) Calculate the retardation of the body.
(f) Find out the distance travelled by the body from A to B.
Answer:
(a) OA is a straight line graph between speed and time, and it is sloping upward from O to A. Therefore, the graph line OA represents uniform acceleration.
(b) AB is a straight line graph between speed and time, which is parallel to the time axis (x-axis).
So, AB represents uniform speed. There is no acceleration from A to B.
(c) BC is a straight line graph between speed and time which is sloping downwards from B to C. Therefore, BC represents uniform retardation or negative acceleration.
(d) Acceleration of the body as we see from graph line OA represents it. So, the slope of velocity-time graph OA will give the acceleration of the body. Thus,
Acceleration = Slope of line OA = AD/OD
We have, AD = 6 m/s, and OD = 4 s
So, acceleration = \(\frac{6 \mathrm{m} / \mathrm{s}}{4 \mathrm{s}}\) = 1.5 m/s
(e) The slope of line graph BC represents the retardation of the body.
So, retardation = Slope of line BC = BE/EC
We have, BE = 6m/s, EC = 16 – 10 = 6s
Retardation = \(\frac{6 \mathrm{m} / \mathrm{s}}{4 \mathrm{s}}\) = 1m/s2
(f) Distance travelled from A to B = Area under the line AB and the time axis
= Area of rectangle DABE = DA × DE
Here, DA = 6 m/s and DE = 10 – 4 = 6 s
Distance travelled from A to B = 6 × 6 = 36m
Question 2.
The graph given below shows the positions of a body at different times. Calculate the speed of the body as it moves from
(i) A to B
(ii) B to C and
(iii) C to D.
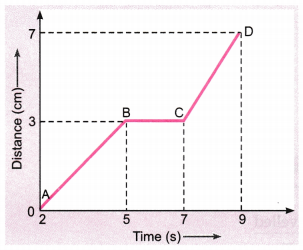
Answer:
(i) The distance-time graph represents the line AB which shows the speed of the body. So,
Speed = \(\frac{\text { Distance }}{\text { Time }}=\frac{3 \mathrm{cm}}{(5-2) \mathrm{s}}\) = 1 cm/s
(ii) The distance-time graph shows that the body is at rest between graph line B to C, it means no movement. So speed is zero i.e.,
Speed = \(\frac{\text { Distance }}{\text { Time }}=\frac{0}{(7-5) \mathrm{s}}=\frac{0}{2 \mathrm{s}}\) = 0
(iii) The distance-time graph represents the line CD which shows the speed of the body. So,
Speed = \(\frac{\text { Distance }}{\text { Time }}=\frac{(7-3) \mathrm{cm}}{(9-7) \mathrm{s}}=\frac{4 \mathrm{cm}}{2 \mathrm{s}}\) = 2 cm/s
Question 3.
Distance travelled by a train and time taken by it is shown in the following table, (i) Plot distance-time graph. (ii) What is the average speed of the train? (iii) When is the train travelling at the highest speed? (iv) At what distance does the train slow down? (v) Calculate the speed of the train between 10:40 AM to 11:00 AM.

Answer:
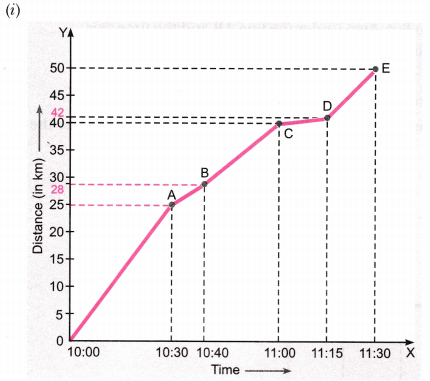

(iii) We know, speed = slope of distance-time graph. The greater the slope, the greater is the speed.
From the graph, it is clear that slope of distance-time graph is maximum between 10:00 AM to 10:30 AM, so the train was travelling at the highest speed during this interval of time.
(iv) The part CD of the graph has minimum slope, so the train had minimum speed between 11:00 AM and 11:15 AM. Thus, the train had slowed down between 40 km and 42 km.
(v) Speed between 10:40 AM to 11:00 AM = \(\frac{\text { Distance }}{\text { Time }}=\frac{(40-28) \mathrm{km}}{20 \mathrm{min}}=\frac{12 \mathrm{km}}{\frac{20}{60} \mathrm{h}}\) = 36 kmh-1
Question 4.
The velocity-time graph shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds. [NCERT Exemplar]
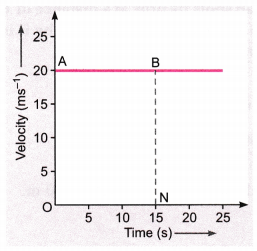
Answer:
(i) Since velocity is not changing acceleration is equal to zero. [a = \(\frac{\Delta v}{\Delta t}\) = 0]
(ii) Reading the graph, velocity = 20 ms-1 (constant)
(iii) Distance covered in 15 seconds = Area of ABNO
= v × t
= 20 × 15 = 300 m
Question 5.
A body starts to slide over a horizontal surface with an initial velocity of 0.5 m/s. Due to friction, its velocity decreases at the rate 0.05 m/s2. How much time will it take for the body to stop?
Answer:
Initial velocity, u = 0.5 m/s
Final velocity, v= 0
Acceleration, a = -0.05 m/s2
Now, from the first equation of the motion,
v = u + at
or, 0 = 0.5 + (- 0.05t) ⇒ 0.5 = 0.05t,
∴ t = 0.5/0.05 = 10 s
Thus, the body will take 10 s to stop.
Question 6.
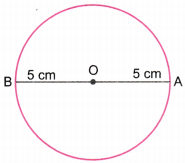
A particle moves in a circle with O as centre and AO = OB = 5 cm, as radius, as shown in the figure. It starts from A. Calculate:
(a) the distance covered, and
(b) the displacement, when it reaches B.
Answer:
(a) Distance covered = π × OA = π × 5 = 5π cm
(b) Displacement = 2 × OB
= 2 × 5 = 10 cm along AB
Question 7.
A body travels along a circular path of radius 70 m. After travelling half a revolution in 20 s, find the
(i) average velocity,
(ii) average speed.
Answer:


Question 8.
A cheetah is the fastest land animal and can achieve a peak velocity of 100 km/h up to distances less than 500 m. If a cheetah spots its prey at a distance of 100 m, what is the minimum time it will take to get its prey, if the average velocity attained by it is 90 km/h?
Answer:
Average velocity = 90 km/h = \(\frac{90 \mathrm{km}}{1 \mathrm{h}}\)
= \(\frac{90 \times 1000 \mathrm{m}}{60 \times 60 \mathrm{s}}\) = 25 ms-1
Also, Average velocity = \(\frac{\text { Displacement }}{\text { Time taken }}\)
∵ Cheetah moves in a straight line displacement is equal to 100 m.
Therefore, time taken = \(\frac{100}{25}\) = 4 s
Question 9.
The brakes applied to a car produce an acceleration of 6 ms-2 in the opposite direction to the motion. If the car takes 2s to stop after the application of brakes, calculate the distance it travels during this time.
Answer:
We have been given
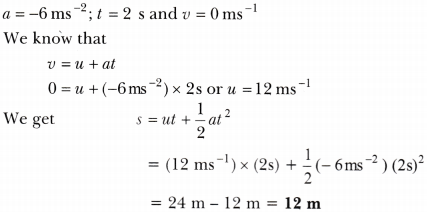
Thus, the car will move 12 m before it stops after the application of brakes.
Question 10.
A car starts from rest and moves along the x-axis with constant acceleration 5 ms-2 for 8 seconds. If it then continues with constant velocity, what distance will the car cover in 12 seconds since it started from the rest? [NCERT Exemplar]
Answer:
Initial velocity ,u = 0
Using s = ut + \(\frac{1}{2}\)at2
The distance travelled in first 8s,
s1 = 0 + \(\frac{1}{2}\) × 5 × 82 = 160 m
At this point the velocity, v = u + at
= 0 + 5 × 8 = 40 ms-1
So, the distance covered in last four seconds
s2 = 40 × 4 = 160 m
Hence, total distance, s = s1 + s2
= 160 m + 160 m = 320 m
Question 11.
A motorcyclist drives from A to B with a uniform speed of 30 kmh-1 and returns back with a speed of 20 kmh-1. Find its average speed. [NCERT Exemplar]
Answer:
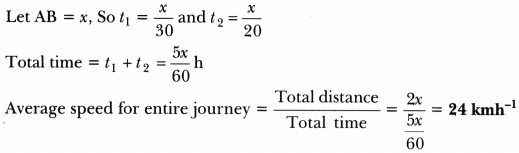
Question 12.
An object is dropped from rest at a height of 150 m and simultaneously another object is dropped from rest at a height 100 m. What is the difference in their heights after 2 s if both the objects drop with same accelerations? How does the difference in heights vary with time? [NCERT Exemplar]
Answer:
Initial difference in height = (150 – 100) m = 50 m
Distance travelled by first body in 2 s = h1 = 0 + \(\frac{1}{2}\) g(2)2 = 2g
Distance travelled by another body in 2 s = h2 = 0 + \(\frac{1}{2}\) g(2)2 = 2g
After 2 s, height at which the first body will be = h1‘ = 150 – 2g
After 2 s, height at which the second body will be = h’2 = 100 – 2g
Thus, after 2 s, difference in height = 150 – 2g – (100 – 2g) = 50 m = initial difference in height Thus, difference in height does not vary with time.
Question 13.
An object starting from rest travels 20 m in first 2s and 160 m in next 4s. What will be the velocity after 7s from the start? [NCERT Exemplar]
Answer:
s1 = ut + \(\frac{1}{2}\) at2 or 20 = 0 + \(\frac{1}{2}\)a(2)2 or a = 10ms-2
v = u + at = 0 + (10 × 2) = 20 ms-1
s2 = 160 = vt’ + \(\frac{1}{2}\)a'(t’)2 = (20 × 4) + (\(\frac{1}{2}\)a’ × 16) ⇒ a’ = 10ms-2
Since accelerations is the same, we have v’ = 0 + (10 × 7) =70 ms-1
Question 14.
An electron moving with a velocity of 5 × 104 ms-1 enters into a uniform electric field and acquires a uniform acceleration of 104 ms-2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover in this time? [NCERT Exemplar]
Answer:
Given initial velocity, u = 5 × 104 ms-1
and acceleration, a = 104ms-2
(i) Final velocity = v = 2u = 2 × 5 × 104ms-1 = 10 × 104ms-1
To find t, use v = u + at
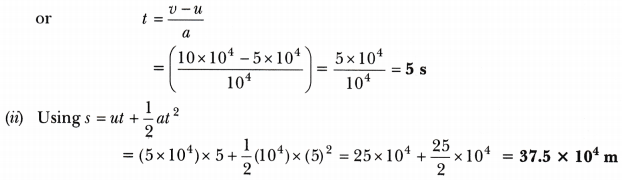
Motion Class 9 Extra Questions HOTS (Higher Order Thinking Skills)
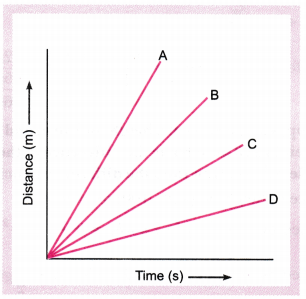
Question 1.
Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown in figure. Which car is the slowest?
Answer:
Speed = Slope of distance-time graph. The smaller the slope, the smaller is the speed.
From the figure, slope is minimum for car D. So, D is the slowest car.
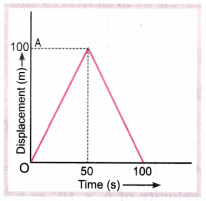
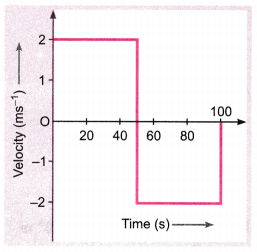
Question 2.
A girl walks along a straight path to drop a letter in the letterbox and comes back to her initial position. Her displacement-time graph is shown in figure. Plot a velocity-time graph for the same. [NCERT Exemplar]
Answer:
Velocity from 0 to 50 s is v1 = \(\frac{\Delta s}{\Delta t}=\frac{100-0}{50-0}\) = 2 ms-1
At 50 – 0
Velocity from 50 s to 100 s, v2 = \(\frac{\Delta s}{\Delta t}=\frac{0-100}{100-50}\) = – 2 ms-1
Accordingly the velocity-time graph is shown in figure below.
Question 3.
Suppose a squirrel is moving at a steady speed from the base of a tree towards some nuts. It then stays in the same position for a while, eating the nuts, before returning to the tree at the same speed. A graph can be plotted with distance on the x-axis and the time on y-axis.
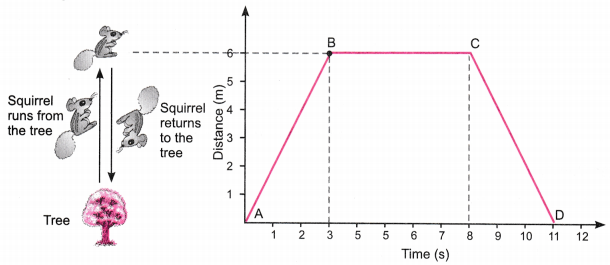
Observe the graph carefully and answer the following questions.
(i) Which part of the graph shows the squirrel moving away from the tree?
(ii) Name the point on the graph which is 6 m away from the base of the tree.
(iii) Which part of the graph shows that the squirrel is not moving?
(iv) Which part of the graph shows that the squirrel is returning to the tree?
(v) Calculate the speed of the squirrel from the graph during its journey.
Answer:
(i) Part AB
(ii) Part B
(iii) Part BC
(iv) Part CD
(v) Total distance travelled = 6m + 6m=12m
Time = 11 s.
Speed = \(\frac{\text { Total distance }}{\text { Time }}=\frac{12}{11}\) = 1.09m/s.
Question 4.
The table given below shows distance (in cm) travelled by bodies A, B and C. Read this data carefully and answer the following questions.
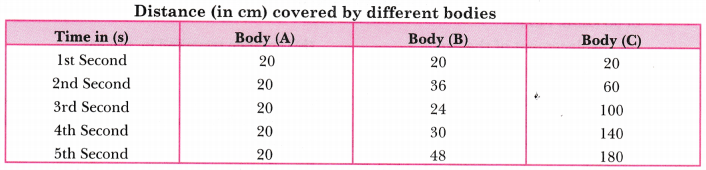
(i) Which of the bodies is moving with
(a) constant speed?
(b) constant acceleration?
(c) non-uniform acceleration?
(ii) Which of the bodies covers
(a) maximum distance in 3rd second?
(b) minimum distance in 3rd second?
Answer:
(i) (a) Body A (b) Body C (c) Body B
(ii) (a) Body C. Total distance travelled = 100 – 60 = 40 cm
(b) Body B. Total distance travelled = 24 – 36 = (-) 12 cm
The negative sign implies decceleration.