Free PDF Download of CBSE Class 10 Maths Chapter 7 Coordinate Geometry Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Coordinate Geometry MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 7 Coordinate Geometry
1. The distance of the point P(2, 3) from the x-axis is
(a) 2
(b) 3
(c) 1
(d) 5
Answer/ Explanation
Answer: b
Explaination: Reason: The distance from x-axis is equal to its ordinate i.e., 3
2. The distance between the point P(1, 4) and Q(4, 0) is
(a) 4
(b) 5
(c) 6
(d) 3√3
Answer/ Explanation
Answer: b
Explaination: Reason: The required distance = \(\sqrt{(4-1)^{2}+(0-4)^{2}}=\sqrt{9+16}=\sqrt{25}=5\)
3. The points (-5, 1), (1, p) and (4, -2) are collinear if
the value of p is
(a) 3
(b) 2
(c) 1
(d) -1
Answer/ Explanation
Answer: d
Explaination: Reason: The points are collinear if area of Δ = 0
= \(\frac{1}{2}\)[-5(p + 2) +l(-2 -1) + 4(1 – p)] – 0
⇒ -5 p -10-3 + 4-4p = 0
⇒ -9p = +9
∴ p = -1
4. The area of the triangle ABC with the vertices A(-5, 7), B(-4, -5) and C(4, 5) is
(a) 63
(b) 35
(c) 53
(d) 36
Answer/ Explanation
Answer: c
Explaination: Reason: Area of ΔABC = \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\)[-5(-5 – 5) -4(5 – 7) + 4(7 – (-5))] = \(\frac{1}{2}\)[-5(-10) -4(-2) + 4(12)]
= \(\frac{1}{2}\)[50 + 8 + 48] = \(\frac{1}{2}\) × 106 = 53 sq. units
5. The distance of the point (α, β) from the origin is
(a) α + β
(b) α² + β²
(c) |α| + |β|
(d) \(\sqrt{\alpha^{2}+\beta^{2}}\)
Answer/ Explanation
Answer: d
Explaination: Reason: Distance of (α, β) from origin (0, 0) = \(\sqrt{(\alpha-0)^{2}+(\beta-0)^{2}}=\sqrt{\alpha^{2}+\beta^{2}}\)
6. The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is
(a) 11
(b) 22
(c) 33
(d) 21
Answer/ Explanation
Answer: a
Explaination: Reason: Required area= \(\frac{1}{2}\)[1(3 + 4) -2(-4 – 2) -3(2 – 3)]
= \(\frac{1}{2}\)[7 + 12 + 3]
= \(\frac{1}{2}\) × 22 = 11
7. The line segment joining the points (3, -1) and (-6, 5) is trisected. The coordinates of point of trisection are
(a) (3, 3)
(b) (- 3, 3)
(c) (3, – 3)
(d) (-3,-3)
Answer/ Explanation
Answer: b
Explaination: Reason: Since the line segment AB is trisected

8. The line 3x + y – 9 = 0 divides the line joining the points (1, 3) and (2, 7) internally in the ratio
(a) 3 : 4
(b) 3 : 2
(c) 2 : 3
(d) 4 : 3
Answer/ Explanation
Answer: a
Explaination: Reason: Let the line 3x + y – 9 = 0 divide the line segment joining A(l, 3) ad B(2, 7) in the ratio K : 1 at point C.

9. The distance between A (a + b, a – b) and B(a – b, -a – b) is
Answer/ Explanation
Answer: c
Explaination:
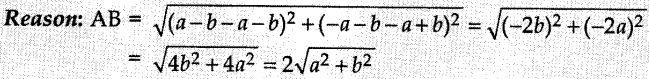
10. If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5) and R(-2, 3), then the value of ‘a’ is
(a) 12
(b) -6
(c) -12
(d) -4
Answer/ Explanation
Answer: c
Explaination:

11. If the distance between the points (x, -1) and (3, 2) is 5, then the value of x is
(a) -7 or -1
(b) -7 or 1
(c) 7 or 1
(d) 7 or -1
Answer/ Explanation
Answer: d
Explaination: Reason: We have \(\sqrt{(x-3)^{2}+(-1-2)^{2}}=5\)
⇒ (x – 3)² + 9 = 25
⇒ x² – 6x + 9 + 9 = 25
⇒ x² -6x – 7 = 0
⇒ (x – 7)(x + 1) = 0
⇒ x = 7 or x = -1
12. The points (1,1), (-2, 7) and (3, -3) are
(a) vertices of an equilateral triangle
(b) collinear
(c) vertices of an isosceles triangle
(d) none of these
Answer/ Explanation
Answer: b
Explaination: Reason: Let A(1, 1), B(-2, 7) and C(3, 3) are the given points, Then, we have

13. The coordinates of the centroid of a triangle whose vertices are (0, 6), (8,12) and (8, 0) is
(a) (4, 6)
(b) (16, 6)
(c) (8, 6)
(d) (16/3, 6)
Answer/ Explanation
Answer: d
Explaination: Reason: The co-ordinates of the centroid of the triangle is

14. Two vertices of a triangle are (3, – 5) and (- 7,4). If its centroid is (2, -1), then the third vertex is
(a) (10, 2)
(b) (-10,2)
(c) (10,-2)
(d) (-10,-2)
Answer/ Explanation
Answer: c
Explaination: Reason: Let the coordinates of the third vertex be (x, y)
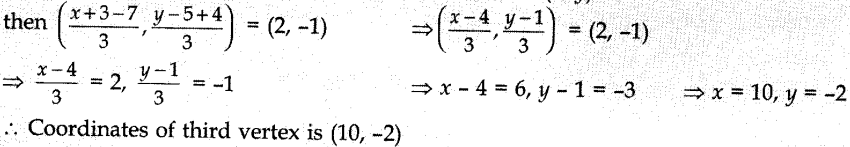
15. The area of the triangle formed by the points A(-1.5, 3), B(6, -2) and C(-3, 4) is
(a) 0
(b) 1
(c) 2
(d) 3/2
Answer/ Explanation
Answer: a
Explaination: Reason: Area of ΔABC = \(\frac{1}{2}\) [-1.5(-2 – 4) + 6(4 – 3) + (-3) (3 + 2)] = \(\frac{1}{2}\) [9 + 6 – 15] = 0. It is a straight line.
16. If the points P(1, 2), B(0, 0) and C(a, b) are collinear, then
(a) 2a = b
(b) a = -b
(c) a = 2b
(d) a = b
Answer/ Explanation
Answer: a
Explaination: Reason: Area of ΔPBC = 0
⇒ \(\frac{1}{2}\)[1(0 – b) + 0(6 – 1) + a(2 – 0)] = 0
⇒ \(\frac{1}{2}\)[-6 + 2a] = 0
⇒ -b + 2a = 0
∴ 2a = b
We hope the given MCQ Questions for Class 10 Maths Coordinate Geometry with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 7 Coordinate Geometry Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.