We have given these Important Questions for Class 10 Science Chapter 10 Light Reflection and Refraction to solve different types of questions in the exam. Previous Year Questions & Important Questions of Light Reflection and Refraction Class 10 Science Chapter 10 will help the students to score good marks in the board examination.
Important Questions of Light Reflection and Refraction Class 10 Science Chapter 10
Question 1.
The laws of reflection hold true for
(a) plane mirrors only
(b) concave mirrors only
(c) convex mirrors only
(d) all reflecting surface
Answer:
(d) The laws of reflection holds true for all reflecting surface.
Question 2.
List four characteristics of the images formed by plane mirrors. (Delhi 2015, AI2011)
Answer:
Characteristics of the image formed by a plane mirror are
(i) imagedistanceissameasthatofobjectdistance
(ii) image formed is virtual and erect
(iii) image formed is of the same size as that of the object
(iv) image formed is laterally inverted (left appears right and right appears left).
Question 3.
State the two laws of reflection of light. (Delhi 2011)
Answer:
Laws of reflection of light states that
(i) The angle of incidence is equal to the angle of reflection.
(ii) The incident ray, the reflected ray and the normal to the mirror at the point of incidence all lie in the same plane.
Question 4.
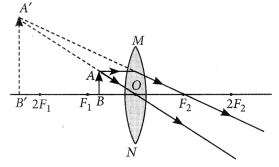
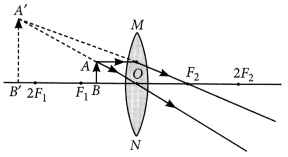
When an object is kept within the focus of a concave mirror, an enlarged image is formed behind the mirror. This image is
(a) real
(b) inverted
(c) virtual and inverted
(d) virtual and erect (2020)
Answer:
(d) When an object is placed between the principal focus and pole of a concave mirror, an enlarged virtual and erect image is formed behind the mirror.
Question 5.
What is the magnification of the images formed by plane mirrors and why? (Delhi 2015)
Answer:
Magnification of images formed by plane mirrors is unity because for plane mirrors, the size of the image formed is equal to that of the object.
Question 6.
Draw a labelled ray diagram to show the path of the reflected ray corresponding to an incident ray of light parallel to the principal axis of a convex mirror. Mark the angle of incidence and angle of reflection on it. (AI 2019)
Answer:
Question 7.
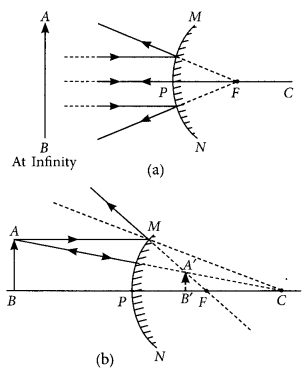
If the image formed by a spherical mirror for all positions of the object placed in front of it is always erect and diminished , what type of mirror is it? Draw a labelled ray diagram to support your answer. (2018)
Answer:
If the image formed by a spherical mirror is always erect and diminished then it is convex mirror.
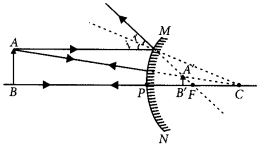
Question 8.
An object is placed at a distance of 30 cm in front of a convex mirror of focal length 15 cm. Write four characteristics of the image formed by the mirror. (Delhi 2017)
Answer:
Four characteristics of the image formed by the given convex mirror are :
(i) Virtual
(ii) Erect
(iii) Diminished
(iv) Image is always formed behind the mirror between pole and focus.
Question 9.
An object is placed at a distance of 12 cm in front of a concave mirror of radius of curvature 30 cm. List four characteristics of the image formed by the mirror. (Delhi 2017)
Answer:
Radius of curvature (R) = 30 cm, object distance is 12 cm in front of the mirror. Thus we can say that object is placed between focus and pole. Four characteristics of the image formed by die given concave mirror when object is placed between pole and focus are:
(i) Virtual
(ii) Erect
(iii) Enlarged
(iv) Image is formed behind the mirror
Question 10.
A ray of light is incident on a convex mirror as shown. Redraw the diagram and complete the path of this ray after reflection from the mirror. Mark angle of incidence and angle of reflection on it. (Delhi 2016)
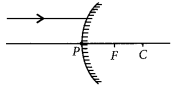
Answer:
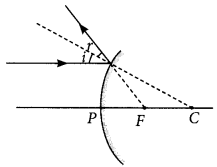
Question 11.
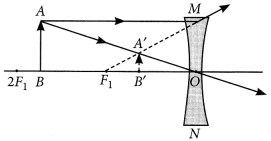
Name the type of mirrors used in the design of solar furnaces. Explain how high temperature is achieved by this device. (AI 2016)
Answer:
Concave mirrors are used in the designing of solar furnaces.
When a solar furnace is placed at the focus of a large concave mirror, it focuses a parallel beam of light on the furnace. Therefore, a high temperature is attained at the point after some time.
Question 12.
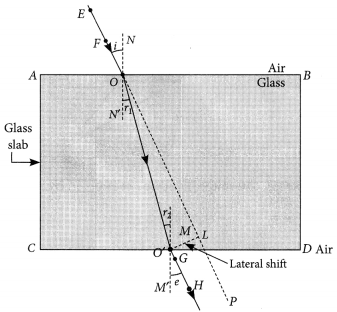
“The magnification produced by a spherical mirror is -3”. List four informations you obtain from this statement about the mirror/ image. (AI 2016)
Answer:
Negative sign of magnification indicates that the image is real and inverted. Since the image is real and inverted, the mirror is concave and magnification of -3 indicates that the image is magnified.
Question 13.
AB and CD, two spherical mirrors, from parts of a hollow spherical ball with its centre at O as shown in the diagram. If arc AB = \(\frac { 1 }{ 2 }\) arc CD, what is the ratio of their focal lengths? State which of the two mirrors will always form virtual image of an object placed in front of it and why? (Foreign 2016)
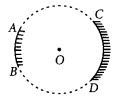
Answer:
Focal length of a mirror is given by
Focal length = \(\frac { Radius of curvature }{ 2 }\)
Since both the mirrors have same radius of curvature, therefore focal length of the two mirrors will be same, i.e.,
\(\frac { f_1 }{ f_2 }\) = \(\frac { 1 }{ 1 }\)
Since virtual image is always formed by convex mirror. The mirror AB will always form virtual image.
Question 14.
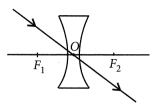
List two properties of the images formed by convex mirrors. Draw ray diagram in support of your answer. (Foreign 2016)
Answer:
Convex mirrors always form diminished, virtual and erect images.
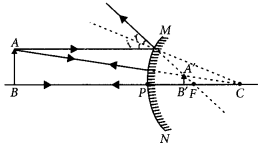
Question 15.
The linear magnification produced by a spherical mirror is +3. Analyse this value and state the (i) type of mirror and (ii) position of the object with respect to the pole of the mirror. Draw a ray diagram to show the formation of image in this case. (Foreign 2016)
Answer:
Positive value of the magnification indicates that image is virtual and erect.
(i) Since the image is magnified, the mirror is concave.
(ii) The object is between pole and focus of the mirror as shown
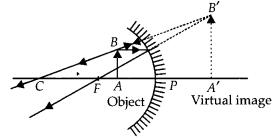
The image produced in second case will be real and inverted.
Question 16.
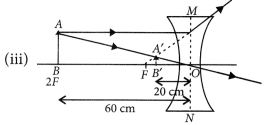
List four specific characteristics of the images of the objects formed by convex mirrors. (Delhi 2015)
Answer:
Refer to answer 8
Question 17.
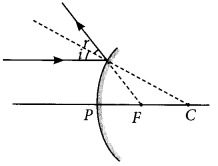
Draw a ray diagram to show the path of the reflected ray corresponding to an incident ray which is directed towards the principal focus of a convex mirror. Mark on it the angle of incidence and the angle of reflection. (Delhi 2014)
Answer:
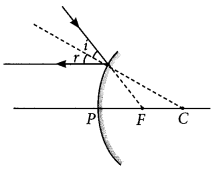
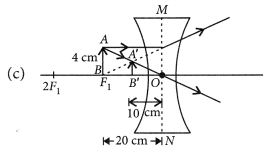
Question 18.
Draw a ray diagram to show the path of the reflected ray corresponding to an incident ray which is directed parallel to the principal axis of a convex mirror, Mark on it the angle of incidence and the angle of reflection. (Delhi 2014)
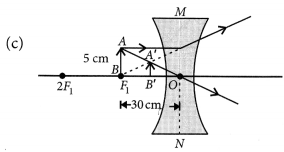
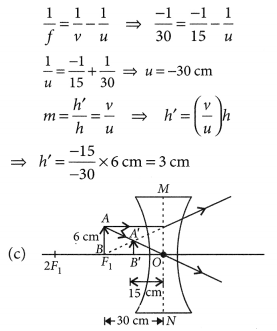
Answer:
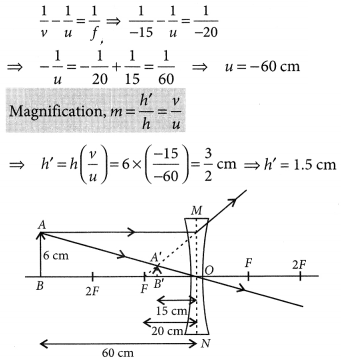
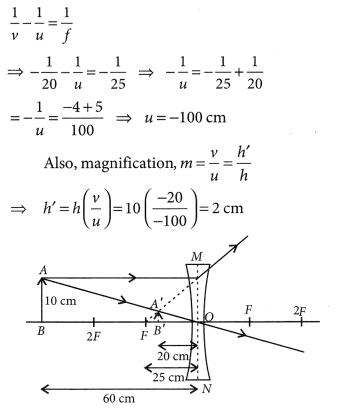
Refer to answer 6
Question 19.
Draw a ray diagram to show the path of the reflected ray corresponding to an incident ray of light parallel to the principal axis of a concave mirror. Mark the angle of incidence and angle of reflection on it. (Delhi 2014)
Answer:
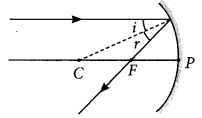
Question 20.
List two possible ways in which a concave mirror can produce a magnified image of an object placed in front of it. State the difference if any between these two images. (AI2014)
Answer:
A concave mirror can produce a magnified image of an object when object is placed:
(1) In between its pole and its focus
(2) In between its focus and its centre of curvature.
Difference,between these two images:
The image produced in first case will be virtual and erect.
The image produced in second case will be real and inverted.
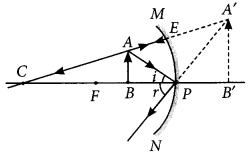
Question 21.
The image formed by a concave mirror is observed to be virtual, erect and larger than the object. Where should the position of the object be relative to the mirror? Draw ray diagram to justify your answer. (AI 2014)
Answer:
The position of the object should be between P and F
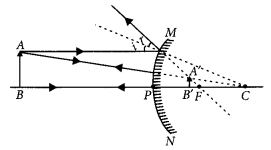
Question 22.
The linear magnification produced by a spherical mirror is +1/3. Analysing this value state the (i) type of mirror and (ii) position of the object with respect to the pole of the mirror. Draw any diagram to justify your answer. (AI 2014, Foreign 2014)
Answer:
(i) Convex mirror
(ii) Between infinity and the pole of the mirror.
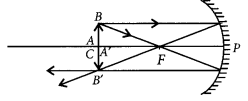
Question 23.
The linear magnification produced by a spherical mirror is -1. Analysing this value state the (i) type of mirror and (ii) position of the object with respect to the pole of the mirror. Draw any diagram to justify your answer. (Foreign 2014)
Answer:
(i) Concave mirror because the image is real, inverted.
(ii) Object is placed at C.
Question 24.
The linear magnification produced by a spherical mirror is -1/5. Analysing this value state the (i) type of spherical mirror and (ii) the position of the object with respect to the pole of the mirror. Draw ray diagram to justify your answer. (Foreign 2014)
Answer:
(i) Concave mirror
(ii) Object is placed beyond C.
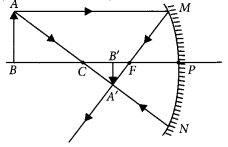
Question 25.
Draw ray diagrams for the following cases when a ray of light:
(i) passing through centre of curvature of a concave mirror is incident on it.
(ii) parallel to principal axis is incident on convex mirror.
(iii) is passing through focus of a concave mirror incident on it. (2020)
Answer:
(i) Ray of light passing through centre of curvature of concave mirror, after reflection
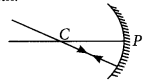
(ii) Ray of light parallel to the principal axis is incident on a convex mirror after reflection appear to diverge from the principal focus of a convex mirror.
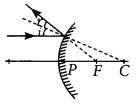
(iii) Ray of light passing through focus of a concave mirror after reflection will emerge parallel
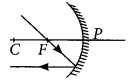
Question 26.
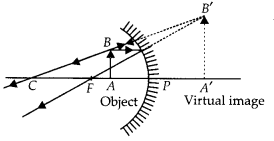
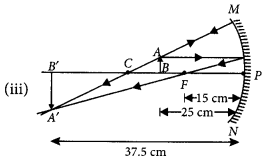
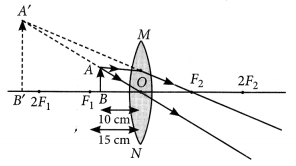
A concave mirror is used for image formation for different positions of an object. What inferences can be drawn about the following when an object is placed at a distance of 10 cm from the pole of a concave mirror of focal length 15 cm?
(a) Position of the image
(b) Size of the image
(c) Nature of the image
Draw a labelled ray diagram to justify your inferences. (2020)
Answer:
Given, f = -15 cm, u = -10 cm.
Thus the object is placed between the principal focus and pole of the mirror.
(a) The position of the image will be behind the mirror.
(b) The size of the image will be highly enlarged.
(c) The nature of the image will be virtual and erect.
Question 27.
A concave mirror has a focal length of 20 cm. At what distance from the mirror should a 4 cm tall object be placed so that it forms an image at a distance of 30 cm from the mirror? Also calculate the size of the image formed. (AI 2019)
Answer:
Given f = -20 cm v = -30 cm u = ?
Using \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
\(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) – \(\frac { 1 }{ v }\) = \(\frac { 1 }{ -20 }\) – \(\frac { 1 }{ -30 }\) = \(\frac { -3+2 }{ 60 }\)
⇒ u = -60 cm
∴ Object placed at 60 cm from the mirror.
Also magnification, m = \(\frac { h’ }{ h }\) = \(\frac { -v }{ u }\)
⇒ h’ = \(\frac { -(-30) }{ -60 }\) × 4 = -2 cm
∴ The size of the image is 2 cm.
Question 28.
The image of a candle flame placed at a distance of 30 cm from a mirror is formed on a screen placed in front of the mirror at a distance of 60 cm from its pole. What is the nature of the mirror? Find its focal length. If the height of the flame is 2.4 cm, find the height of its image. State whether the image formed is erect or inverted. (Delhi 2017)
Given:
Object distance, u = – 30 cm, image size, h’ = ?
Image distance, v = – 60 cm,
Object size ,h = 2.4 cm,
Focal length, f = ?
Using mirror formula,
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u} \quad \text { or } \quad \frac{1}{f}=\frac{-1-2}{60}=\frac{-3}{60}=-\frac{1}{20}\)
or f = – 20 cm
Hence, focal length is 20 cm
Also, magnification, m = \(\frac { h’ }{ h }\) = \(\frac { -v }{ u }\)
or, m = \(\frac { (-60)}{ (-30) }\) = -2 or \(\frac { h’ }{ h }\) = -2
h’ = – 2 × 2.4 = – 4.8 cm
As the image formed is real, therefore the mirror is concave.
The height of the image is 4.8 cm.
The image formed is enlarged and inverted.
Question 29.
An object 4 cm in height, is placed at 15 cm in front of a concave mirror of focal length 10 cm. At what distance from the mirror should a screen be placed to obtain a sharp image of the object. Calculate the height of the image. (Delhi 2017)
Answer:
Given : object distance, u = -15 cm,
object height, h = 4 cm, focal length f = -10 cm;
Image distance, v = ?
Using mirror formula,
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f} \Rightarrow \frac{1}{v}+\frac{1}{(-15)}=\frac{1}{-10} \Rightarrow \frac{1}{v}=\frac{1}{15}-\frac{1}{10}\)
or \(\frac{1}{v}=\frac{10-15}{150}=\frac{-5}{150}=\frac{-1}{30}\) or v = -30
In order to obtain a sharp image of the object on the screen, screen should be placed at a distance of 30 cm in front of the mirror.
Also, magnification, m = \(\frac{h^{\prime}}{h}=\frac{-v}{u}\)
or \(\frac{h^{\prime}}{4}=-\frac{(-30)}{(-15)}\) or h’ = \(\frac { -(30)×4 }{ (15) }\) = -2 × 4
or h’ = -8 cm
Thus, the height of the image is 8 cm.
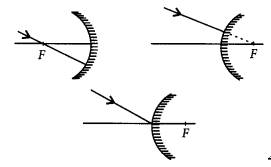
Question 30.
Draw the following diagram in which a ray of light is incident on a concave/convex mirror, on your answer sheet. Show the path of this ray, after reflection, in each case.
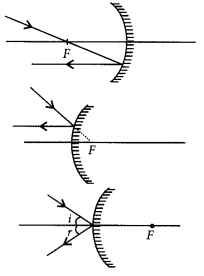
Answer:
The path of the rays are shown in figure.
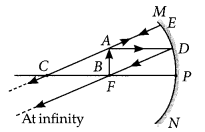
Question 31.
The image of an object formed by a mirror is real, inverted and is of magnification -1. If the image is at a distance of 40 cm from the mirror, where is the object placed? Where would the image be if the object is moved 20 cm towards the mirror? State reason and also draw ray diagram for the new position of the object to justify your answer. (AI 2016)
Answer:
Since the image formed by the mirror is real and inverted, therefore the mirror is concave and magnification of the mirror will be
m = –\(\frac { v }{ u }\) ⇒ -1 = –\(\frac { v }{ u }\) ⇒ v = u
i.e., object and image both are formed at the centre of curvature, i.e., 40 cm from the mirror.
Now, if the object is moved 20 cm towards the mirror, the object will be at the focus of the mirror and therefore the image will be formed at infinity.
Question 32.
The image formed by a spherical mirror is real, inverted and its magnification is -2. If the image is at a distance of 30 cm from the mirror, where is the object placed? Find the focal length of the mirror. List two characteristics of the image formed if the object is moved 10 cm towards the mirror. (AI 2016)
Answer:
Since the image formed is real and inverted, the mirror is concave.
Magnification, m = \(\frac { -v }{ u }\) ⇒ -2 = \(\frac { -v }{ u }\) ⇒ v = 2u
Now, if v = – 30 cm then u = – 15 cm
As focal length of the mirror is
f = \(\frac{u v}{u+v}=\frac{-15 \times-30}{-15-30}=f=\frac{450}{-45}\) = -10 cm
If the object is shifted 10 cm towards the mirror, then the object is between principal focus and the optical centre and the image formed will be virtual and erect.
Question 33.
If the image formed by mirror for all positions of the object placed in front of it is always virtual and diminished, state the type of the mirror. Draw a ray diagram in support of your answer. Where are such mirrors commonly used and why? (Foreign 2016, AI 2015)
Answer:
Refer to answer 7.
Convex mirrors are widely used as rear view mirrors in cars, motorcycles etc. It produces an erect image that is smaller in size than the object hence giving a wide view.
Question 34.
To construct a ray diagram we use two rays of light which are so chosen that it is easy to determine their directions after reflection from the mirror. Choose these two rays and state the path of these rays after reflection from a concave mirror. Use these two rays to find the nature and position of the image of an object placed at a distance of 15 cm from a concave mirror of focal length 10 cm. (Delhi 2015, AI 2012)
Answer:
We use two rays of light, one passing through the centre of curvature of a concave mirror, and another is parallel to the principal axis. After reflection, the ray passing through the centre of a concave mirror is reflected back along the same path and the ray parallel to the principal axis will pass through the principal focus.
u = -15 cm, f= -10 cm
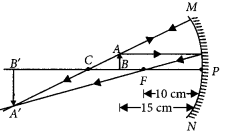
From ray diagram, v = -30 cm, i.e., beyond C Nature of image is real, inverted and magnified.
Question 35.
Draw a ray diagram to show the path of the reflected ray in each of the following cases. A ray of light incident on a convex mirror :
(a) strikes at its pole making an angle 0 from the principal axis.
(b) is directed towards its principle focus.
(c) is pardllel to its principal axis. (Foreign 2015)
Answer:
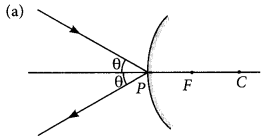
(b) Refer to answer 17.
(c) Refer to answer 6.
Question 36.
A spherical mirror produces an image of magnification -1 on a screen placed at a distance of 50 cm from the mirror.
(a) Write the type of mirror.
(b) Find the distance of the image from the object.
(c) What is the focal length of the mirror?
(d) Draw the ray diagram to show the image formation in this case. (Delhi 2014, AI 2014)
Answer:
(a) Concave mirror
(b) Magnification, m = –\(\frac { v }{ u }\) or v = u
∴ Distance of the image from the object is, v – u = 0
(c) As the image is formed at centre of curvature i.e., v = R.
∴ focal length of the mirror, f = \(\frac { -50 }{ 2 }\) = -25 cm
(d) Refer to answer 23(ii).
Question 37.
A spherical mirror produces an image of magnification -1 on a screen placed at a distance of 40 cm from the mirror.
(i) Write type of mirror.
(ii) What is the nature of the image formed?
(iii) How far is the object located from the mirror?
(iv) Draw the ray diagram to show the image formation in this case. (Delhi 2014)
Answer:
(i) This is a concave mirror.
(ii) The image is real and inverted and of same size.
(iii) As m = – 1
∴ m = –\(\frac { v }{ u }\) ⇒ -1 = \(\frac { -v }{ u }\) ⇒ u = v
Hence, object is located at centre of curvature i.e., at distance of 40 cm from the pole of the mirror,
(iv) Refer to answer 23(ii).
Question 38.
A spherical mirror produces an image of magnification -1.0 on a screen placed at a distance of 30 cm from the pole of the mirror.
(i) Write the type of mirror in this case.
(ii) What is the focal length of the mirror?
(iii) What is the nature of the images formed?
(iv) Draw the ray diagram to show the image formation in this case. (Delhi 2014)
Answer:
(i) The mirror is concave mirror.
(ii) Distance the image from the mirror = – 30 cm
Magnification, m = \(\frac { -v }{ u }\)
Here m = – 1 and v = – 30 cm
-1 = –\(\frac { (-30) }{ u }\)
∴ u = – 30 cm
As v = u, object is placed at centre of curvature. Therefore, focal length of the mirror,
f = \(\frac { -30 }{ 2 }\) = – 15 cm
(iii) Image formed is real and inverted and of the same size of the object.
(iv) Refer to answer 23(ii).
Question 39.
A student wants to project the image of a candle flame on a screen 48 cm in front of a mirror by keeping the flame at a distance of 12 cm from its pole.
(a) Suggest the type of mirror he should use.
(b) Find the linear magnification of the image produced.
(c) How far is the image from its object?
(d) Draw ray diagram to show the image formation in this case. (AI 2014)
Answer:
(a) Concave mirror
(b) Linear magnification,
m = \(\frac { -v }{ u }\) = \(\frac { -(-48) }{ -12 }\) = -4
(c) The distance between the image and the object
= 48 – 12 = 36 cm
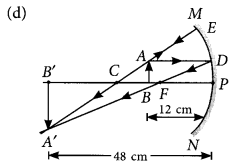
Question 40.
A student wants to obtain an erect image of an object using a concave mirror of 12 cm focal length. What should be the range of distance of the candle flame from the mirror? State the nature and size of the image he is likely to observe. Draw a ray diagram to show the image formation in this case. (Foreign 2014)
Answer:
To obtain an erect image, the object is placed in between pole and the focus of the concave mirror. So range of distance of the candle llame from the mirror is in between 12 cm.
Nature of the image = Virtual and erect.
Size of the image = Enlarged
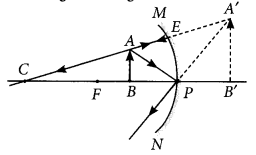
Question 41.
A student wants to obtain an erect image of a candle flame using a concave mirror of focal length 15 cm. What should be the range of distance of the candle flame from the mirror?
State the nature and size of the image he is likely to observe. Draw a ray diagram to show the image formation in this case. (Foreign 2014)
Answer:
To obtain an erect image of an object, the object should be placed in between pole and focus. Range of distance of the candle flame from the mirror is in between 15 cm.
Nature of the image = Virtual and erect
Size of the image = Enlarged
For ray diagram, refer to answer 40.
Question 42.
A student has a concave mirror of 20 cm focal length and he wants to see an erect image of his face in the mirror. What should be the range of distance of the mirror from his face? State the nature and size of the image he is likely to observe. Draw a ray diagram to justify your answer. (Foreign 2014)
Answer:
Focal length of a concave mirror = 20 cm Range will be in between 20 cm.
Nature of the image = Virtual and erect
Size of the image = Enlarged
For ray diagram, refer to answer 40.
Question 43.
Mention the types of mirrors used as (i) rear view mirrors, (ii) shaving mirrors. List two reasons to justify your answer in each case. (Delhi 2013, Delhi 2012)
Answer:
(i) Convex mirror is used as rear view mirror because
(a) it gives erect image.
(b) it gives diminished image thus provides wider view of traffic behind the vehicle.
(ii) Concave mirror is used as shaving mirror because
(a) it gives erect image when mirror is close to the face.
(b) it gives enlarged image of the face so that a person can shave safely.
Question 44.
Calculate the magnification of the image of an object placed perpendicular to the principal axis of a concave mirror of focal length 15 cm. The object is at a distance of 20 cm from the mirror. (Delhi 2013)
Answer:
Given, focal length of concave mirror,
f = -15 cm
Object distance, u = -20 cm
Image distance, v = ?
Using mirror formula,
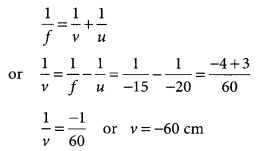
Using magnification formula,
m = –\(\frac { v }{ u }\) = -(\(\frac { -60 }{ -20 }\)) or m = -3
So, the magnification, m = -3.
Question 45.
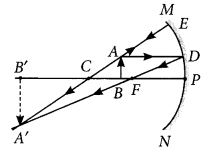
To construct ray diagram we use two light rays which are so chosen that it is easy to know their directions after reflection from the mirror. List these two rays and state the path of these rays after reflection. Use these rays to locate the image of an object placed between centre of curvature and focus of a concave mirror. (AI2012)
Answer:
A ray parallel to the principal axis, after reflection, will pass through the principal focus in case of a concave mirror or appear to diverge from the principal focus in case of a convex mirror.
A ray passing through the centre of a curvature of a concave mirror or directed in the direction of the centre of curvature of a convex mirror, after reflection, is reflected back along the same path. The light rays come back along the same path because the incident rays fall on the mirror along the normal to the reflecting surface.
Question 46.
State the types of mirrors used for (i) headlights and (ii) rear view mirrors, in motorcycles. Give reason to justify your answer in each case. (AI 2012)
Answer:
(i) Concave mirrors are used in headlights of cars to get powerful beams of light.
(ii) Convex mirrors are used as rear-view mirrors of vehicle to get a wider field of view and and erect image of traffic behind.
Question 47.
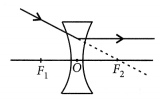
An object is placed between infinity and the pole of a convex mirror. Draw a ray diagram and also state the position, the relative size and the nature of the image formed. (AI 2011)
Answer:
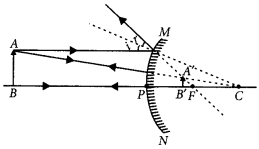
Position: Image is formed between pole and principal focus of the mirror.
Relative size : Image formed is diminished.
Nature : Image formed is virtual and erect.
Question 48.
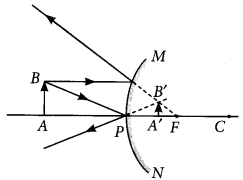
With the help of a ray diagram explain why a convex mirror is preferred for rear view mirrors in the motor cars. (Foreign 2011)
Answer:
Convex mirror is preferred for rear view mirrors in motor cars because no matter where the object is located in front of convex mirror, it always gives erect and diminished image of the object, so that driver is able to see the large traffic view in small area and the image is erect. This can be interpreted from the following diagram.
Question 49.
An object 4.0 cm in size, is placed 25.0 cm in front of a concave mirror of focal length 15.0 cm.
(i) At what distance from the mirror should a screen be placed in order to obtain a sharp image?
(ii) Find the size of the image.
(iii) Draw a ray diagram to show the formation of image in this case. (2020)
Answer:
(i) Given, h = 4 cm,
u = -25 cm (concave mirror), f = -15 cm
Using mirror formula,
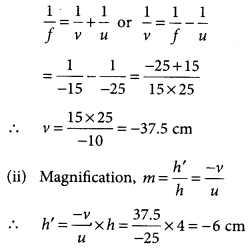
Thus, the image is real and inverted.
Question 50.
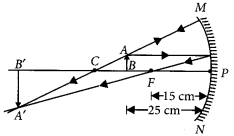
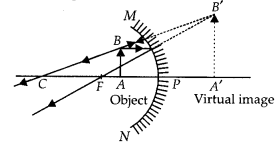
(a) A concave mirror of focal length 10 cm can produce a magnified real as well as virtual image of an object placed in front of it. Draw ray diagrams to justify this statement,
(b) An object is placed perpendicular to the principal axis of a convex mirror of focal length 10 cm. The distance of the object from the pole of the mirror is 10 cm. Find the position of the image formed. (2020)
Answer:
(a) A magnified real image is produced in a concave mirror when the object is placed between principal focus and centre of curvature.
A magnified virtual image is produced in a concave mirror when the object is placed between the pole and the principle focus of the mirror.
(b) Given, f = +10 cm (convex mirror) and u = -10 cm
From mirror formula,
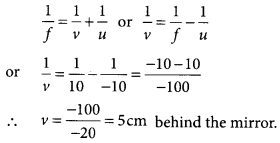
Question 51.
(a) A security mirror used in a big showroom has radius of curvature 5 m. If a customer is standing at a distance of 20 m from the cash counter, find the position, nature and size of the image formed in the security mirror.
(b) Neha visited a dentist in his clinic. She observed that the dentist was holding an instrument fitted with a mirror. State the nature of this mirror and reason for its use in the instrument used by dentist. (2020)
Answer:
(a) Given radius of curvature of the mirror,
R = 5 m
∴ Focal length, f = R/2 = 2.5 m (convex mirror) and u = -20 m
From mirror formula,
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u} \text { or } \frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
= \(\frac{1}{2.5}-\frac{1}{-20}=\frac{-20-2.5}{-20 \times 2.5}\)
∴ v = 2.22 m
Thus, the image is formed 2.22 m behind the mirror. The image is diminished, virtual and erect.
(b) Concave mirrors are used by dentist. Dentist use it as it is a converging mirror and when used at close range forms a highly enlarged, virtual and erect image of the object.
Question 52.
(a) To construct a ray diagram we use two rays which are so chosen that it is easy to know their directions after reflection from the mirror. Use these two rays and draw ray diagram to locate the image of an object placed between pole and focus of a concave mirror.
(b) A concave mirror produces three times magnified image on a screen. If the objects placed 20 cm in front of the mirror, how far is the screen from the object? (Delhi 2017)
Answer:
(a) Two lights rays whose path of reflection are priorly known are :
(i) When the incident ray passes through the centre of curvature of a concave mirror, it gets reflected in the same path.
(ii) When the ray is incident obliquely to the principal axis, towards the pole of mirror, it gets reflected back by making equal angles with the principal axis (laws of reflections).
Suppose an object is placed between focus and pole of the concave mirror. Then by using the above two rays, the image of the object can be located as
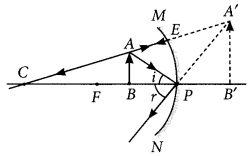
Image formed is virtual, erect, magnified and it is formed behind the mirror.
(b) Given : Magnification, m = – 3
Object distance, u = – 20 cm
Magnification, m = \(\frac { -v }{ u }\) or -3 = \(\frac { -v }{ -20 }\)
or v = -60 cm
The screen is placed in front of the mirror at a distance of 60 cm from the pole.
Thus, the screen is placed 40 cm (= 60 cm – 20 cm) away from the object.
Question 53.
(a) If the image formed by a mirror for all positions of the object placed in front of it is always diminished, erect and virtual, state the type of the mirror and also draw a ray diagram to justify your answer. Write one use such mirrors are put to and why?
(b) Define the radius of curvature of spherical mirrors. Find the nature and focal length of a spherical mirror whose radius of curvature is +24 cm. (AI2017)
Answer:
(a) If the image formed by a mirror for all positions of the object placed in front of it is always diminished, erect and virtual then the mirror is convex mirror.
The ray diagrams for the formation of image by a convex mirror for the first position when the object is at infinity and the second position when the object is at a finite distance from the mirror are shown.
Use of Convex Mirrors
Convex mirrors are commonly used as rear-view (wing) mirrors in vehicles because they always give an erect, though diminished image. Also, they have a wider field of view as they are curved outwards. Thus, convex mirrors enable the driver to view a large area.
(b) Radius of Curvature: The radius of the sphere of which the reflecting surface of a spherical mirror forms a part, is called the radius of curvature of the mirror. It is represented by the letter R.
∵ The radius of curvature is equal to twice the focal length.
∴ R = 2f
If R = +24 cm ∴ f = \(\frac { R }{ 2 }\) = \(\frac { 24 }{ 2 }\) = 12 cm
Since the radius of curvature is positive, the mirror is convex mirror. Hence the nature of the image is virtual and erect.
Question 54.
(a) Define the following terms in the context of spherical mirrors:
(i) Pole
(ii) Centre of curvature
(iii) Principal axis
(iv) Principal focus
(b) Draw ray diagrams to show the principal focus of a
(i) Concave mirror (ii) Convex mirror
(c) Consider the following diagram in which M is a mirror and P is an object and Q is its magnified image formed by the mirror.
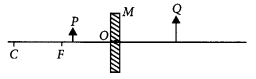
State the type of the mirror M and one characteristic property of the image Q. (Delhi 2016)
Answer:
(a) (i) Pole : The centre of the reflecting surface of a spherical mirror is a point called the pole. It lies in the surface of the mirror and its represented by the letter P.
(ii) Centre of curvature: The reflecting surface of a spherical mirror is a part of a sphere which has a centre. This point is called the centre of curvature of spherical mirror and is represented by the letter C.
(iii) Principal axis : An imaginary line passing through the pole and the centre of curvature of a spherical mirror and normal to the mirror at its pole is called principal axis.
(iv) Principal focus : Incident rays parallel to principal axis, after reflection either converge to as appear to diverge from a fixed point on the principal axis known as principal focus of the spherical mirror.
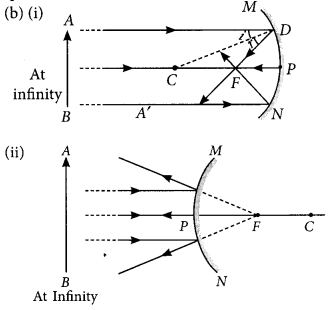
(c) The object is placed between focus and pole of the mirror and a magnified image is formed behind the mirror.
∴ The mirror is concave and image formed is virtual and erect.
Question 55.
It is desired to obtain an erect image of an object, using concave mirror of focal length of 12 cm.
(i) What should be the range of distance of a , object placed in front of the mirror?
(ii) Will the image be smaller or larger than the object? Draw ray diagram to show the formation of image in this case.
(iii) Where will the image of this object be, if it is placed 24 cm in front of the mirror? Draw ray diagram for this situation also to justify your answer.
Show the positions of pole, principal focus and the centre of curvature in the above ray diagrams. (AI2016)
Answer:
Given : focal length of the concave mirror f = 12 cm
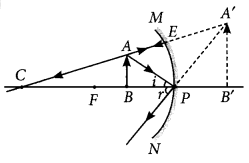
(i) If the object is placed between the pole and focus of the concave mirror, then the image formed is virtual and erect. Iheretore, the range of distance of the object should be 0 < u <. 12 cm.
(ii) The image formed will be enlarged as shown below.
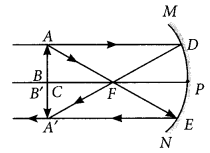
(iii) If the object is placed 24 cm in front of the mirror i.e., at the centre of the curvature then the image will also be formed at the centre of the curvature.
Question 56.
Suppose you have three concave mirrors A, B and C of focal lengths 10 cm, 15 cm and 20 cm. For each concave mirror you perform the experiment of image formation for three values of object distances of 10 cm, 20 cm and 30 cm. By giving reason, answer the following:
(a) For the three object distances, identify the mirror/mirrors which will form an image of magnification -1.
(b) Out of the three mirrors, identify the mirror which would be preferred to be used for shaving purposes/make up.
(c) For the mirror B draw ray diagram for image formation for object distances 10 cm and 20 cm. (Foreign 2016)
Answer:
Given fa = 10 cm, fb = 15 cm, fc = 20 cm
ua = 10 cm, ub = 20 cm, uc = 30 cm
(a) Magnification of -1 implies that size of image is same as that of object or image is formed at the same distance as of the object. This is the case when the object distance, u = 2f, i.e., when the object is at the centre of the curvature.
For fa, ub and for fb, uc, we get magnification – 1.
(b) Concave mirror forms virtual, erect and magnified image when the object is between focus and pole of the mirror, i.e., direct distance should be less than the focal length of the mirror.
For object distance 10 cm, mirrors of focal length fb = 15 cm and fc = 20 cm can be used.
Question 57.
A student has focused the image of a candle flame on a white screen using a concave mirror. The situation is a given below:
Length of fhe flame = 1.5 cm
Focal length of the mirror = 12 cm
Distance of flame from the mirror = 18 cm
If the flame is perpendicular to the principal axis of the mirror, then calculate the following:
(a) Distance of the image from the mirror
(b) Length of the image
If the distance between the mirror and the flame is reduced to 10 cm, then what would be observed on the screen? Draw ray diagram to justify your answer from this situation. (Foreign 2015)
Answer:
Given: focal length of the concave mirror, f = – 12 cm
Length of the flame, h = 1.5 cm
Distance of flame from the mirror, u = -18 cm
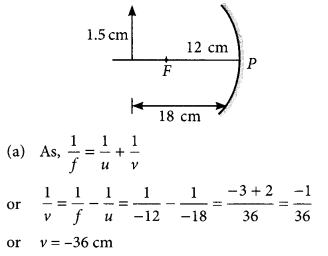
(b) Let h’ be the length of the image.
∵ Magnification, m = \(\frac { h’ }{ h }\) = \(\frac { -v }{ u }\)
∴ h’ = \(\frac{-v \times h}{u}=\frac{-(-36) \times 1.5}{-18}\) = -3 cm
If the distance between the mirror and the flame is reduced to 10 cm, then
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}=\frac{1}{-12}-\frac{1}{-10}=\frac{1}{60}\)
∴ v = 60 cm
Hence, image is formed behind the mirror.
Question 58.
A student wants to project the image of a candle flame on the walls of school laboratory by using a mirror.
(a) Which type of mirror should he use and why?
(b) At what distance in terms of focal length ‘f’ of the mirror should he place the candle flame so as to get the magnified image on the wall?
(c) Draw a ray diagram to show the formation of image in this case.
(d) Can he use this mirror to project a diminished image of the candle flame on the same wall? State ‘how’ if your answer is ‘yes’ and ‘why not’ if your answer is ‘no’ (Delhi 2014)
Answer:
(a) He should use concave mirror to get image of candle flame on the walls of school laboratory. Because concave mirror is a converging mirror and produce real image.
(b) He should place the candle flame in between centre of curvature C and principal focus F of the mirror to get the magnified image on the wall.
(d) Yes, he can use concave mirror to project a diminished image of the candle flame on the same wall. He has to place the candle flame beyond centre of curvature to get diminished image.
Question 59.
Define the following terms in case of a concave mirror:
(a) Pole
(b) Radius of curvature
(c) Principal axis
(d) Principal focus
Suppose you want to observe an erect image of a candle flame using a concave mirror of focal length 20 cm. State the range of distance of the candle flame from the mirror. List two other characteristics of the observed image. Draw a ray diagram to show the formation of image in this case. (Delhi 2013)
Answer:
(a) Refer to answer 54(a) (i).
(b) Refer to answer 53(b).
(c) Refer to answer 54(a) (iii).
(d) Refer to answer 54(a) (iv).
If we want to get an erect image of a candle flame using concave mirror of focal length 20 cm, then we must place the object between a pole and focus of the mirror. If u is the image distance, then 0 < u < 20 cm
Other two characteristics of the observed image are
(i) Image is virtual and erect
(ii) Image is enlarged
The ray diagram for this situation can be drawn as follows:
Question 60.
List the sign conventions for reflection of light by spherical mirrors. Draw a diagram and apply these conventions in the determination of focal length of a spherical mirror which forms a three times magnified real image of an object placed 16 cm infront of it. (Delhi 2012)
Answer:
Sign Convention for Reflection by Spherical Mirrors : While dealing with the reflection of light by spherical mirrors, we shall follow a set of sign conventions called the New Cartesian Sign Convention, the conventions are as follows:
(i) The object is always placed to the left of the mirror. This implies that the light from the object falls on the mirror from the left-hand side.
(ii) All distances parallel to the principal axis are measured from the pole of the mirror.
(iii) All the distances measured to the right of the origin (along + x-axis) are taken as positive while those measured to the left of the origin (along – x-axis) are taken as negative.
(iv) Distances measured perpendicular to and above the principal axis (along +y-axis) are taken as positive.
(v) Distances measured perpendicular to and below the principal axis (along-y-axis) are taken as negative.
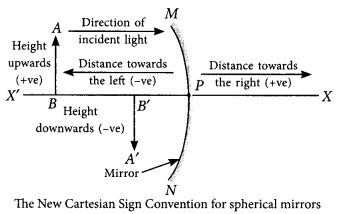
Given that m = -3 (real image), u = -16 cm
Magnification, m = \(\frac { -v }{ u }\)

Question 61.
List the new Cartesian sign convention for reflection of light by spherical mirrors. Draw a diagram and apply these conventions for calculating the focal length and nature of a spherical mirror which forms a 1/3 times magnified virtual image of an object placed 18 cm in front of it. (AI 2012)
Answer:
Refer to answer 60.
Given that m = +\(\frac { 1 }{ 3 }\) (virtual image), u = -18 cm
Magnification, m = –\(\frac { v }{ u }\)
\(\frac { 1 }{ 3 }\) = \(\frac { -v }{ -18 }\) ⇒ v = 6 cm
mirror formula \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
\(\frac { 1 }{ 6 }\) – \(\frac { 1 }{ 18 }\) = \(\frac { 1 }{ f }\) ⇒ \(\frac { 3-1 }{ 18 }\) = \(\frac { 1 }{ f }\) ⇒ f = 9 cm
As the value of focal length is positive, the mirror used is convex mirror.
Question 62.
Name the type of mirror used in the following situations
(i) Headlights of a car
(ii) Rear-view mirror of vehicle
(iii) Solar furnace
Support your answer with reason. (Foreign 2012)
Answer:
(i) Refer to answer 46(i).
(ii) Refer to answer 46(ii).
(iii) Concave mirrors are used in solar furnaces to concentrate sunlight to produce heat.
Question 63.
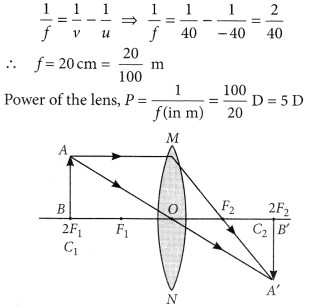
What is meant by power of a lens? (Delhi 2015)
Answer:
Power is the degree of convergence or divergence of light rays achieved by a lens.
It is defined as the reciprocal of its focal length.
i.e., P = \(\frac { 1 }{ f }\)
Question 64.
An object is placed at a distance of 15 cm from a convex lens of focal length 20 cm. List four characteristics (nature, position, etc.) of the image formed by the lens. (AI2017)
Answer:
Given : Object distance, u = – 15 cm
Focal length, f = + 20 cm
Using lens formula, As |u| < |f|
The object is placed between F and optical centre of lens.
Thus, the four characteristics of the image formed by the convex lens are:
(i) Erect
(ii) Virtual
(iii) Enlarged image,
(iv) Image is formed on the same side of the lens as the object.
Question 65.
What is meant by power of a lens? What does its sign (+ve or -ve) indicate? State its S.I. unit related to focal length of a lens. (Delhi 2016)
Answer:
Refer to answer 63.
Positive sign (+) of power indicates that lens is convex and negative sign (-) of power indicates that lens is concave.
If focal length (f) is expressed in metres, then, power is expressed in dioptres. The SI unit of power is dioptre. Thus, 1 dioptre is the power of lens whose focal length is 1 metre. 1 D = 1 m-1
Question 66.
The refractive indices of glass and water with respect to air are 3/2 and 4/3 respectively. If speed of light in glass is 2 × 108 m/s, find the speed of light in water. (AI 2016)
Answer:
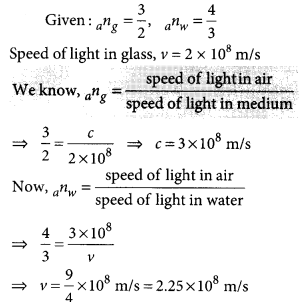
Question 67.
The absolute refractive indices of glass and water are 4/3 and 3/2 respectively. If the speed of light in glass is 2 × 108 m/s, calculate the speed of light in (i) vacuum, (ii) water. (AI 2015)
Answer:
Given that: ng = \(\frac { 4 }{ 3 }\), nw = \(\frac { 3 }{ 2 }\), vg = 2 × 108 m/s
Absolute refractive index of a medium, nm = \(\frac { c }{ v }\)
where, c is the speed of light in vacuum and v is the speed of light in medium.
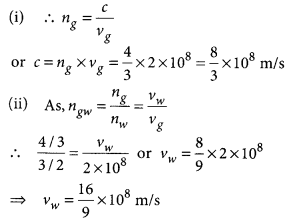
Note: The values given in question are not correct as the speed of light in vacuum is 3 × 108 m/s
Question 68.
“A ray of light incident on a rectangular glass slab immersed in any medium emerges parallel to itself.” Draw labelled ray diagram to justify the statement”. (Delhi 2013)
Answer:
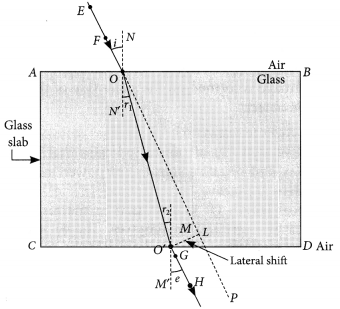
Question 69.
The absolute refractive indices of glass and water are 1.5 and 1.33 respectively. In which medium does light travel faster? Calculate the ratio of speeds of light in the two media. (Delhi 2013 C)
Answer:
Given : refractive index of glass, ng = 1.5
Refractive index of water, nw = 1.33
Since, refractive index of medium,

For glass ng = \(\frac { c }{ v_g }\) ……… (i)
For water nw = \(\frac { c }{ v_w }\) ……… (ii)
Since velocity of light in medium is inversely proportional to its refractive index, the light will travel faster in optically rarer medium i.e., water.
Dividing (i) by (ii),
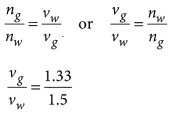
So, the ratio of vg and vw is 1.33 : 1.5.
Question 70.
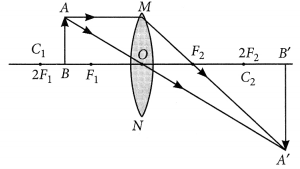
To construct a ray diagram we use two light rays which are so chosen that it is easy to know their directions after refraction from the lens. List these two rays and state the path of these rays after refraction. Use these two rays to locate the image of an object placed between ‘f’ and ‘2f’ of a convex lens. (Foreign 2012)
Answer:
The two rays are :
(i) A ray of light from the object, parallel to the principal axis, after refraction from a convex lens, passes through the principal focus on the other side of the leps and in case of concave lens, a ray appears to diverge from the principal focus located on the same side of the lens.
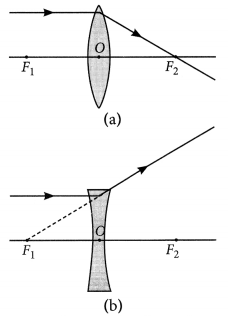
(ii) A ray of light passing through the optical centre of a lens will emerge without any deviation.
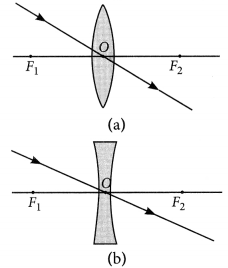
When object is placed between F and 2F.
Question 71.
(a) Water has refractive index 1.33 and alcohol has refractive index 1.36. Which of the two medium is optically denser? Give reason for your answer.
(b) Draw a ray diagram to show the path of a ray of light passing obliquely from water to alcohol.
(c) State the relationship between angle of incidence and angle of refraction in the above case. (2020)
Answer:
(a) Here, alcohol is optically denser medium as its refractive index is higher than that of water. When we compare the two media, the one with larger refractive index is called the optically denser medium than the other as the speed of light is lower in this medium.
(b) Since light is travelling from water (rarer medium) to alcohol (denser medium), it slows down and bends towards the normal.
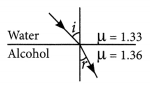
where i = angle of incidence and r = angle of refraction.
(c) According to Snell’s law,
\(\frac{\sin i}{\sin r}=\frac{\mu_{\text {alcohol }}}{\mu_{\text {water }}}=\frac{1.36}{1.33}\) = 1.0225
∴ sin i = 1.0225 × sin r
Question 72.
The refractive index of a medium V with respect to a medium ‘y’ is 2/3 and the refractive index of medium ‘y’ with respect to medium ‘z’ is 4/3. Find the refractive index of medium ‘z with respect to medium V. If the speed of light in medium ‘x’ is 3 × 108 m s-1, calculate the speed of light in medium ‘y’. (2020)
Answer:
Given, refractive index of medium x with respect to y,
yµx = \(\frac { 2 }{ 3 }\)
Refractive index of medium y with respect to z,
zµy = \(\frac { 4 }{ 3 }\)
∴ Refractive index of medium x with respect to z,
zµx = yµx . zµy = \(\frac { 2 }{ 3 }\) × \(\frac { 4 }{ 3 }\) = \(\frac { 8 }{ 9 }\)
∴ Refractive index of medium z with respect to x,
xµy = \(\frac { 1 }{ ^zµ_x }\) = \(\frac { 9 }{ 8 }\)
Now speed of light in x = 3 × 108 m/s
Speed of light in y, vy = ?
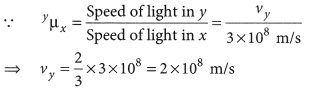
⇒ vy = \(\frac { 2 }{ 3 }\) × 3 × 108 = 2 × 108 m/s
Question 73.
A real image 2/3rd of the size of an object is formed by a convex lens when the object is at a distance of 12 cm from it. Find the focal length of the lens. (AI 2019)
Answer:
Given, h’ = \(\frac { 2 }{ 3 }\)h, u = -12 cm

∴ Focal length of the convex lens = 4.8 cm
Question 74.
State the laws of refraction of light. Explain the term absolute refractive index of a medium’ and write an expression to relate it with the speed of light in vaccum. (2018)
Answer:
(a) Laws of refraction of light:
(i) The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane.
(ii) The ratio of sine of angle of incidence to the sine of the angle of refraction is constant, for the light of a given colour and for the given pair of media.
This law is also known as Snell’s law of refraction.
\(\frac { sin i }{ sin r }\) = constant,
where i is the angle of incidence and r is the angle of refraction.
This constant value is called refractive index of the second medium with respect to the first when the light travels from first medium to second medium.
⇒ constant = n21 = \(\frac { v_1 }{ v_2 }\) ∴\(\frac { sin i }{ sin r }\) = \(\frac { v_1 }{ v_2 }\)
If n is the absolute refractive index of the medium, c is the velocity of light in vacuum and v is the speed of light in a given medium, then n = cl v.
Question 75.
What is meant by power of a lens? Write its SI unit. A student uses a lens of focal length 40 cm and another of -20 cm. Write the nature and power of each lens. (2018)
Answer:
Refer to answer 65.
Given that: Focal length of lens A, fA = +40 cm
Focal length of lens B, fB = -20 cm
Lens A is converging. Lens B is diverging.
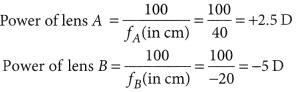
Question 76.
Draw ray diagrams to show the formation of three times magnified (a) real, and (b) virtual image of an object by a converging lens. Mark the positions of O, F and 2F in each diagram. (AI 2017)
Answer:
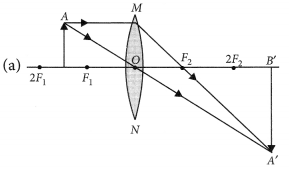
(b) Ray diagrams of an object placed between F1 and optical centre O of lens can be drawn as follows:
(i) The image formed is virtual and erect.
(ii) Image is formed in front of the lens.
(iii) Image formed is enlarged.
Question 77.
(a) Draw a diagram to show the refraction of light through a glass slab and mark angle of refraction and the lateral shift suffered by a ray of light while passing through the slab.
(b) If the refractive index of glass for light going from air to glass is 3/2, find the refractive index of air for light going from glass to air. (Delhi 2016)
Answer:
(a) Refer to answer 68.
(b) Refractive index of glass w.r.t air is 3
gna = \(\frac { 3 }{ 2 }\)
Now, refractive index of air w.r.t glass will be
ang = \(\frac { 1 }{ _gn_a }\) = \(\frac { 1 }{ (3/2) }\) = \(\frac { 2 }{ 3 }\)
Question 78.
The image of an object formed by a lens is of magnification -1. If the distance between the object and its image is 60 cm, what is the focal length of the lens? If the object is moved 20 cm towards the lens, where would the image be formed? State reason and also draw a ray diagram in support of your answer. (AI2016)
Answer:
Magnification of -1 indicates that the image is real and inverted and is of the same size as of the object. The object must be at 2f and image also at 2f on the other side.
Total distance between image and object
Also 4f = 60 cm ⇒ f = 15 cm
If object is moved 20 cm towards the lens, then the object will be between focus and optical centre of the lens and image formed will be virtual and erect and on the same side of the lens.
Question 79.
(a) Define focal length of a spherical lens.
(b) A divergent lens has a focal length of 30 cm. At what distance should an object of height 5 cm from the optical centre of the lens be placed so that its image is formed 15 cm away from the lens? Find the size of the image also.
(c) Draw a ray diagram to show the formation of image in the above situation. (AI 2016)
Answer:
(a) Distance between the optical centre and the focus of the lens is known as the focal length of the lens.
(b) Given f = -30 cm, v = -15 cm, h = 5 cm From the lens formula,
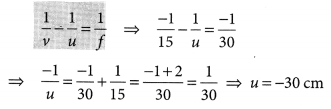
Object should be placed 30 cm from the optical centre.
Also m = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\) ⇒ h’ = h(\(\frac { v }{ u }\))
or h’ = 5 × \(\frac { -15 }{ -30 }\) = 2.5 cm
Size of image formed is 2.5 cm
Question 80.
If the image formed by a lens for all positions of the object placed in front of it is always virtual, erect and diminished, state the type of the lens. Draw a ray diagram in support of your answer. If the numerical value of focal length of such a lens is 20 cm, find its power in new cartesian sign conventions. (Foreign 2016)
Answer:
Concave lens always forms virtual, erect and diminished image for all positions of the object.
Focal length of the concave lens
f = -20 cm = \(\frac { -20 }{ 100 }\) m
Power of the lens, P = \(\frac { 1 }{ f(in m) }\) = \(\frac { -100 }{ 20 m }\) = -5D
Question 81.
State the laws of refraction of light. If the speed of light in vacuum is 3 × 108 m/s, find the absolute refractive index of a medium in which light travels with a speed of 1.4 × 108 m/s. (Foreign 2015)
Answer:
Laws of refraction: Refer to answer 74.
The speed of light in vacuum = 3 × 108 m/s
The speed of light in a medium = 1.4 × 108 m/s
∴ Absolute refractive index
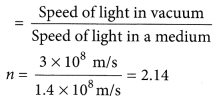
Question 82.
State the laws of refraction of light. If the speed of light in vacuum is 3 × 108 m s-1, find the speed of light in a medium of absolute refractive index 1.5. (Delhi 2014, AI 2014)
Answer:
Refer to answer 74.
The speed of light in vacuum = 3 × 108 m/s
Absolute refractive index =1.5
∴ The speed of light in a medium

Question 83.
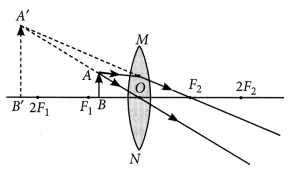
The image of a candle flame placed at a distance of 40 cm from a spherical lens is formed on a screen placed on the other side of the lens at a distance of 40 cm from the lens. Identify the type of lens and write its focal length. What will be the nature of the image formed if the candle flame is shifted 25 cm towards the lens? Draw a ray diagram to justify your answer. (Foreign 2014)
Answer:
Given : u = -40 cm, v = 40 cm
\(\frac{1}{f}=\frac{1}{40}+\frac{1}{40}=\frac{2}{40}\) ⇒ f = 20 cm
Type of lens : Convex lens
Focal length = 20 cm
Nature of the image will be virtual and erect if the candle flame is shifted 25 cm towards the lens.
Question 84.
An object of height 6 cm is placed perpendicular to the principal axis of a concave lens of focal length 5 cm. Use lens formula to determine the position, size and nature of the image if the distance of the object from the lens is 10 cm. (Delhi 2013)
Answer:
Focal length of given concave lens, f= – 5 cm
Distance, u = -10 cm, object size, h = 6 cm
Image distance, v = ?
Using lens formula, \(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\)
\(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}=\frac{1}{-5}+\frac{1}{-10}=\frac{-3}{10}\)
v = –\(\frac { 10 }{ u }\) = -3.33 cm
So, the image is located 3.33 cm from the lens. Magnification (m) of lens is given by
m = \(\frac { v }{ u }\) = \(\frac{-\frac{10}{3}}{-10}=\frac{1}{3}\) = 0.33
m is positive implies that image is virtual and erect. Also, magnitude of m is less than one implies that image is diminished.
Since m = \(\frac { v }{ u }\) = \(\frac { h’ }{ h }\) ⇒ \(\frac { 1 }{ 3 }\) = \(\frac { h’ }{ 6 }\) or h’ = 2 cm
Question 85.
Draw ray diagram to show the path of the refracted ray in each of the following cases. A ray of light incident on a concave lens
(i) is parallel to its principal axis, (ii) is passing through its optical centre and (iii) is directed towards its principal focus. (Delhi 2013 C)
Answer:
(i) A ray of light incident on a concave lens is parallel to its principal axis, the diagram can be drawn as follows:
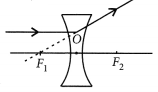
The refracted ray appears to pass through focus on the same side of the lens.
(ii) If a ray of light incident on a concave lens is passing through its optical centre then the refracted ray will go without deviation.
(iii) If a ray of light incident on a concave lens is directed towards its principal axis then it will go parallel to principal axis.
Question 86.
What is the principle of reversibility of light? Show that the incident of light is parallel to the emergent ray of light when light falls obliquely on a side of a rectangular glass slab. (AI 2011)
Answer:
Principle of reversibility of light states that the light will follow exactly the same path if the direction is reversed.
Using Snell’s law of refraction, \(\frac{\sin i}{\sin r_{1}}=\frac{\sin e}{\sin r_{2}}\)
Since r1 = r2, so i = e
so PQ is parallel to RS.
So, we conclude that incident ray is parallel to the emergent ray.
Question 87.
What is understood by lateral displacement of light? Illustrate it with the help of a diagram. List any two factors on which the lateral displacement in a particular substance depends. (Foreign 2011)
Answer:
When a ray of light is incident obliquely on a parallel sided glass slab, the emergent ray shifts laterally. The perpendicular distance between the direction of the incident ray and emergent ray is called lateral shift.
Diagram : Refer to answer 68.
Tire factors on which the lateral displacement depends are:
(i) thickness of the refracting material.
(ii) the refractive index of the material.
Question 88.
Draw a ray diagram in each of the following cases to show the formation of image, when the object is placed:
(i) between optical centre and principal focus of a convex lens.
(ii) anywhere in front of a concave lens.
(iii) at 2F of a convex lens.
State the signs and values of magnifications in the above mentioned cases (i) and (ii). (2020)
Answer:
(i) When an object is placed between Fj and optical centre, O of a convex lens, it forms a virtual and erect image. The ray diagram for this situation can be drawn as follows:
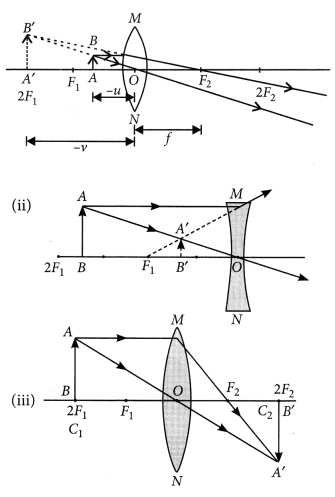
In case (i), the magnification, m is given by,
m = \(\frac { v }{ u }\) = \(\frac { -v }{ -u }\) = positive
i.e., the image formed virtual and erect.
In case (ii), the magnification,
m = \(\frac { v }{ u }\) = \(\frac { -v }{ -u }\) = positive
i.e., the image formed is virtual and erect.
Question 89.
(a) Define the following terms :
(i) Power of lens
(ii) Principal focus of a concave mirror
(b) Write the relationship among the object distance (u), image distance (v) and the focal length (f) of a
(i) Spherical lens
(ii) Spherical mirror
(c) An object is placed at a distance of 10 cm from optical centre of a convex lens of focal length 15 cm. Draw a labelled ray diagram to show the formation of image in this case. (2020)
Answer:
(a) (i) Refer to answer 63.
(ii) Refer to answer 54(a)(iv).
(b) (i) for a spherical lens, according to lens formula,
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\)
where f is the focal length of the lens, v is the image distance and u is the object distance.
(ii) For a spherical mirror, according to mirror formula,
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\)
where f is the focal length of the mirror, v is the image distance and u is the object distance.
(c) Given focal length, f = +15 cm (convex lens) and u = -10 cm
Question 90.
Rishi went to a palmist to show his palm. The palmist used a special lens for this purpose.
(i) State the nature of the lens and reason for its use.
(ii) Where should the palmist place/hold the lens so as to have a real and magnified image of an object?
(iii) If the focal length of this lens is 10 cm, the lens is held at a distance of 5 cm from the palm, use lens formula to find the position and size of the image. (2020)
Answer:
(i) The lens used here is a convex lens and it is used as a magnifying glass because at close range, i.e., when the object is placed between optic centre and principal focus it forms an enlarged, virtual and erect image of the object.
(ii) When this lens is placed such that the object is between the centre of curvature and the principal focus, the palmist obtain a real and magnified image.
(iii) Given focal length, f = 10 cm and u = -5 cm According to lens formula,
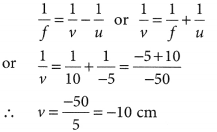
Thus, the image will be formed at 10 cm on the same side of the palm and the size of the image will be enlarged.
Question 91.
An object is placed at a distance of 60 cm from a concave lens of focal length 30 cm.
(i) Use lens formula to find the distance of the image from the lens
(ii) List four characteristics of the image (nature, position, size, erect/inverted) formed by the lens in this case
(iii) Draw ray diagram to justify your answer of pair (ii) . (Delhi 2019)
Answer:
(i) Given, f = -30 cm, u = -60 cm, v = ?
Using lens formula,
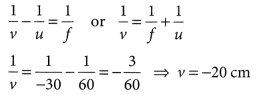
(ii) (a) The image is virtual in nature.
(b) The image is formed at a distance of 20 cm on the left from the concave lens.
(c) Magnification, m = \(\frac { v }{ u }\)
Here, v = – 20 cm; u = – 60 cm
So, m = \(\frac { 20 }{ 60 }\) = \(\frac { 1 }{ 3 }\) = + 0.3
Since value of magnification is less than 1, therefore, the image is diminished.
(d) The plus sign for the magnification shows that the image is erect.
Question 92.
(a) A 5 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 20 cm. The distance of the object from the lens is 30 cm. Find the position, nature and size of the image formed.
(b) Draw a labelled ray diagram showing object distance, image distance and focal length in the above case. (AI 2019)
Answer:
(a) Given, h = 5 cm, f = 20 cm, u = -30 cm
Using lens formula, \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
\(\frac{1}{v}=\frac{1}{u}+\frac{1}{f}=\frac{1}{-30}+\frac{1}{20}=\frac{-2+3}{60}=\frac{1}{60}\)
⇒ v = 60 cm
Now, magnification, m = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\)
⇒ h’ = \(\frac { v }{ u }\) × h = \(\frac {60 }{ -30 }\) × 5 = -10 cm
Hence, the image formed at 60 cm, which is real and magnified.
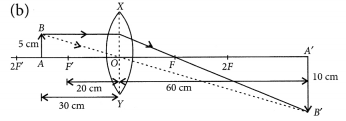
Question 93.
Analyse the following observation table showing variation of image distance (v) with object distance (u) in case of a convex lens and answer the questions that follows, without doing any calculations :
| S. No. | Object distance u (cm) | Image distance v (cm) |
| 1 | -90 | + 18 |
| 2 | -60 | + 20 |
| 3 | -30 | + 30 |
| 4 | -20 | + 60 |
| 5 | – 18 | + 90 |
| 6 | – 10 | + 100 |
(a) What is the focal length of the convex lens? Give reason in support of your answer.
(b) Write the serial number of that observation which is not correct. How did you arrive at this conclusion?
(c) Take an appropriate scale to draw ray diagram for the observation at S. No. 4 and the approximate value of magnification. (Delhi 2017)
Answer:
(a) When an object placed at 2F from a convex lens, then its image is formed on the other side of the lens at the same distance from the lens. Thus from S. No.(3) we can say that.
f = v/2 ⇒ f = \(\frac {30}{ 2 }\) = + 15 cm
Thus, the focal length is + 15 cm.
(b) In this case S.No. (6) is incorrect as the object distance is between focus and pole, for such case, the image formed is virtual and on the same side as the object, hence image distance is negative.
(c) The approximate value of magnification for object distance -20 cm and image distance +60 cm is -3
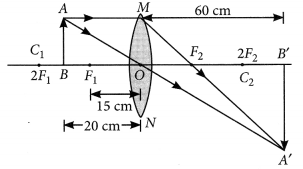
Question 94.
Analyse the following observation table showing variation of image-distance (v) with object-distance (u) in case of a convex lens and answer the questions that follow without doing any calculations.
| S. No. | Object Distance w(cm) | Image Distance v(cm) |
| 1 | -100 | +25 |
| 2 | -60 | +30 |
| 3 | -40 | +40 |
| 4 | -30 | +60 |
| 5 | -25 | +100 |
| 6 | -15 | +120 |
(a) What is the focal length of the convex lens? Give reason to justify your answer.
(b) Write the serial number of the observation which is not correct. On what basis have you arrived at this conclusion?
(c) Select an appropriate scale and draw a ray diagram for the observation at S. No. 2. Also find the approximate value of magnification. (AI 2017)
Answer:
(a) When an object is placed at 2F from the convex lens, then its image is formed on the other side of the lens at the same distance from the lens. Thus from S.No. (3), we can say that
∴ f = \(\frac {v}{ 2 }\) = \(\frac {40}{ 2 }\) = 20 cm
(b) In this case, S. No. (6) is incorrect as the object distance is between focus and optical centre for such cases, the image formed is virtual and image distance is negative.
The approximate value of magnification for object distance -60 cm and image distance +30 cm is -1/2.
Question 95.
(a) Draw a ray diagram to show the formation of image by a convex lens when an object is placed in front of the lens between its optical centre and principal focus.
(b) In the above ray diagram mark the object distance (u) and the image distance (v) with their proper sign (+ve or -ve as per the new Cartesian sign convention) and state how these distances are related to the focal length (f) of the convex lens in this case.
(c) Find the power of a convex lens which forms a real and inverted image of magnification -1 of an object placed at a distance of 20 cm from its optical centre. (Delhi 2016)
Answer:
(a) Refer to answer 88(i).
(b) The lens formula is given as
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
(c) Magnification of the lens is given by
m = \(\frac { v }{ u }\) ⇒ -1 = \(\frac { -v }{ 20 }\) [u = -20 cm]
∴ v = 20 cm
As v = u then
∴ f = \(\frac { 20 }{ 2 }\) cm = 10 cm = 0.1 m
Power of the lens, P = \(\frac { 1 }{ f(in m) }\) D = \(\frac { 1}{ 0.1 }\) D = 10 D
Question 96.
(a) Draw a ray diagram to show the formation of image by a concave lens when an object is placed in front of it.
(b) In the above diagram mark the object distance (u) and the image distance (v) with their proper sign (+ve or -ve as per the new Cartesian sign convention) and state how these distances are related to the focal length (/) of the concave lens in this case.
(c) Find the nature and power of a lens which forms a real and inverted image of magnification -1 at a distance of 40 cm from its optical centre. (Delhi 2016)
Answer:
(a) Refer to answer 88(ii).
(b) The lens formula is given by
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
(c) Since, the nature of the image is real and inverted therefore the lens is convex.
Now magnification of the lens is
m = \(\frac { v }{ u }\) ⇒ -1 = \(\frac { v }{ u}\) ⇒ v = -u
Now, from lens formula,
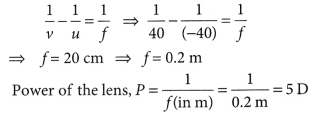
Question 97.
(a) Define optical centre of a spherical lens.
(b) A divergent lens has a focal length of 20 cm. At what distance should an object of height 4 cm from the optical centre of the lens be placed so that its image is formed 10 cm away from the lens. Find the size of the image also.
(c) Draw a ray diagram to show the formation of image in above situation. (AI 2016)
Answer:
(a) Optical centre is the central part of the lens through which a ray of light passes without suffering any deviation. It is usually represented by the letter O.
(b) Given f = – 20 cm, h = 4 cm, v = – 10 cm
From lens formula,
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1 }{ u }\) = \(\frac { -1 }{ 10 }\) + \(\frac { 1 }{ 20 }\) ⇒ u = -20 cm
Also, magnification of the lens,
m = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\) ⇒ h’ = \(\frac { 10 }{ 20 }\) × 4 ⇒ h’ = 2 cm
Question 98.
(a) Define focal length of a divergent lens.
(b) A divergent lens has a focal length of 30 cm forms the image of an object of size 6 cm on the same side as the object at a distance of 15 cm from its optical centre. Use lens formula to determine the distance of the object from the lens and the size of the image formed.
(c) Draw a ray diagram to show the formation of image in the above situation. (AI 2016)
Answer:
(a) Distance between the principal focus and the optical centre is known as the focal length of the lens.
(b) Given, f = -30 cm, v = -15 cm, h = 6 cm
Now, from lens formula,
Question 99.
At what distance from a concave lens of focal length 20 cm a 6 cm tall object be placed so as to obtain its image at 15 cm from the lens? Also calculate the size of the image formed. Draw a ray diagram to justify your answer for the above situation and label it. (Foreign 2016)
Answer:
Focal length of concave lens, f = -20
cm Height of the object, h = 6 cm
Image distance, v = -15 cm
From lens formula,
Question 100.
At what distance from a concave lens of focal length 25 cm a 10 cm tall object be placed so as to obtain its image at 20 cm from the lens. Also calculate the size of the image formed. Draw a ray diagram to justify your answer for the above situation and label it. (Foreign 2016)
Answer:
Focal length of concave lens f = – 25 cm
Image distance, v = -20 cm
Height of the object, h = 10 cm
Now, from lens formula,
Question 101.
“A convex lens can form a magnified erect as well as magnified inverted image of an object placed in front of it”. Draw ray diagram to justify this statement stating the position of the object with respect to the lens in each case. An object of height 4 cm is placed at a distance of 20 cm from a concave lens of focal length 10 cm. Use lens formula to determine the position of the image formed. (Delhi 2015)
Answer:
Magnified erect image:
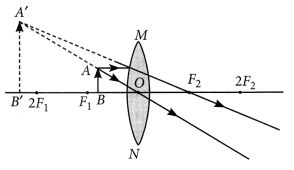
Magnified inverted image:
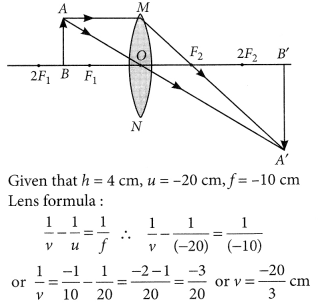
Given that h = 4 cm, u = -20 cm, f = -10 cm
Lens formula:
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) ∴ \(\frac { 1 }{ v }\) – \(\frac { 1 }{ (-20) }\) = \(\frac { 1 }{ (-10) }\)
or \(\frac{1}{v}=\frac{-1}{10}-\frac{1}{20}=\frac{-2-1}{20}=\frac{-3}{20}\) or v = \(\frac { -20 }{ 3 }\) cm
Question 102.
The image of a candle flame placed at a distance of 30 cm from a spherical lens is formed on a screen placed on the other side of the lens at a distance of 60 cm from the optical centre of the lens. Identify the type of lens and calculate its focal length. If the height of the flame is 3 cm, find the height of its image. (Delhi 2015)
Answer:
Given that u = -30 cm, v = 60 cm, h = 3 cm
Lens Formula:
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) ∴ \(\frac { 1 }{ 60 }\) – \(\frac { 1 }{ (-30) }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac{1+2}{60}=\frac{1}{f}=\frac{3}{60}=\frac{1}{20}\) or f = 20 cm
As focal length is positive, hence lens is convex lens.
Magnification, m = \(\frac { v }{ u }\) = \(\frac { h’ }{ h }\)
∴ \(\frac { 60 }{ -30 }\) = \(\frac { h’ }{ 3 }\) or h’ = \(\frac { -60×3 }{ 30 }\) = -6 cm
⇒ The height of image is 6 cm and negative sign shows that the image is real and inverted.
Question 103.
(a) State the laws of refraction of light. Explain the term absolute refractive index of a medium and write an expression to relate it with the speed of light in vacuum.
(b) The absolute refractive indices of two media A and B are 2.0 and 1.5 respectively. If the speed of light in medium B is 2 × 108 m/s, calculate the speed of light in
(i) vacuum
(ii) medium A (Delhi 2015)
Answer:
(a) Refer to answer 74.
(b) Given that nA = 2.0, nA = 1.5, vA = 2 × 108 m/s
(i) nB = \(\frac { c }{ v_B }\), where c is the speed of light in vacuum
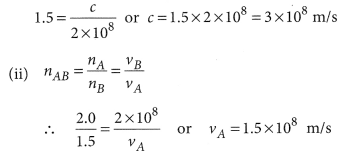
Question 104.
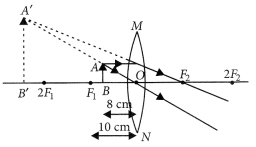
What is meant by power of a lens? Define its S.I. unit.
You have two lenses A and B of focal lengths + 10 and -10 cm respectively. State the nature and power of each lens. Which of the two lenses will form a virtual and magnified image of an object placed 8 cm from the lens? Draw a ray diagram to justify your answer. (AI 2015)
Answer:
Refer to answer 65.
Given that:
Focal length of lens A, fA = +10 cm
Focal length of lens B, fB = -10 cm
Lens A is convex lens . Lens B is concave lens,
Power of lens A = \(\frac { 100 }{ f_A(in cm) }\) = \(\frac { 100 }{ 10 }\) = +10 D
Power of lens B = \(\frac { 100 }{ f_B(in cm) }\) = \(\frac { 100 }{ -10 }\) = -10 D
Lens A will form a virtual and magnified image.
Question 105.
One half of a convex lens of focal length 10 cm is covered with a black paper. Can such a lens produce an image of a complete object placed at a distance of 30 cm from the lens? Draw a ray diagram to justify your answer.
A 4 cm tall obj ect is placed perpendicular to the principal axis of a concave lens of focal length 20 cm. The distance of the object from the lens is 15 cm. Find the nature, position and size of the image. (AI 2015)
Answer:
Yes, the lens will produce an image of complete object.
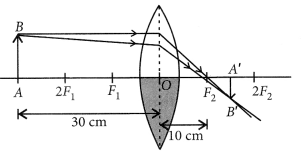
Given that h = 4 cm, f = 20 cm, u = -15 cm
Lens formula: = \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
∴ \(\frac { 1 }{ v }\) – \(\frac { 1 }{ (-15) }\) = \(\frac { 1 }{ 20 }\) or \(\frac { 1 }{ v }\) = \(\frac { 1 }{ 20 }\) – \(\frac { 1 }{ 15 }\) = \(\frac { -1 }{ 60 }\)
⇒ v = -60 cm
Magnification, m = \(\frac { v }{ u }\) = \(\frac { -60 }{ -15 }\) = 4
Nature of image: Virtual, erect and enlarged Position of image : In front of lens 60 cm from the lens
Size of image : Four times of object, i.e.,
(4 × 4) cm = 16 cm
Question 106.
What is meant by the power of a lens ? What is its S.I. unit ? Name the type of lens whose power is positive. The image of an object formed by a lens is real, inverted and of the same size as the object. If the image is at a distance of 40 cm from the lens, what is the nature and power of the lens? Draw ray diagram to justify your answer. (Foreign 2015)
Answer:
Refer to answer 65.
Convex lens has positive power. Since the image of an object formed by a lens is real, inverted and of the same size as the object.
Given: Size of object = Size of image and h’ = -h
∴ Magnification, m = \(\frac { h’ }{ h}\) = \(\frac { -h }{ h}\) = -1
∴ -1 = \(\frac { v }{ u}\) or v = -u
Focal length of the lens,
Question 107.
(a) Explain the following terms related to spherical lenses:
(i) optical centre
(ii) centres of curvature
(iii) principal axis (iv) aperture
(v) principal focus (vi) focal length
(b) A converging lens has focal length of 12 cm. Calculate at what distance should the object be placed from the lens so that it forms an image at 48 cm on the other side of the lens. (AI 2014)
Answer:
(a) (i) Optical centre : The centre point of a lens is known as the optical centre. It always lies inside the lens. A light beam passing through the optical centre without any deviation.
(ii) Centre of curvature : It is defined as the centre of the sphere of which the lens is originally a part of. Because the spherical lens consists of two spherical surfaces, the lens has two centre of curvature.
(iii) Principal axis : A straight line passing through the optical centre and principal focus of a spherical lens. This line is called the principal axis.
(iv) Aperture : The diameter of the reflecting surface of spherical lens is called its aperture.
(v) Principal focus : A number of rays parallel to the principal axis are falling on a lens.
These rays, after refraction from the lens, are appearing to converge to or diverge from a point on the principal axis. This point on the principal axis is called the principal focus of the lens.
(vi) Focal length: The distance between the optical centre and the principal focus of a spherical lens is called the focal length. It is represented by the letter f.
(b) Given f = 12 cm, v = 48 cm, u = ?
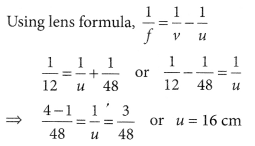
Question 108.
(i) Explain the following terms related to spherical lenses
(a) Centres of curvature (b) Principal axis
(c) Optical centre (d) Principal focus
(ii) At what distance from a concave lens of focal length 20 cm, should a 6 cm tall object be placed so that it forms an image at 15 cm from the lens? Also determine the size of the image formed. (AI 2014)
Answer:
(i) Refer to answer 107(a).
(ii) Refer to answer 99.
Question 109.
What is meant by power of a lens? Name and define its S.I. unit.
One student uses a lens of focal length +50 cm and another of -50 cm. State the nature and find the power of each lens. Which of the two lenses will always give a virtual and diminished image irrespective of the position of the object? (Foreign 2014)
Answer:
Refer to answer 65.
A convex lens has the focal length +50 cm.
∴ power = \(\frac { 1 }{ f }\) = \(\frac { +100 }{ 50 }\) = +2 D
A concave lens has the focal length -50 cm.
∴ power = \(\frac { 1 }{ f }\) = \(\frac { -100 }{ 50 }\) = -2 D
Concave lens always gives a virtual, erect and diminished image irrespective of the position of the object.
Question 110.
(a) State the laws of refraction of light. Give an expression to relate the absolute refractive index of a medium with speed of light in vacuum.
(b) The refractive indices of water and glass with respect to air are 4/3 and 3/2 respectively. If the speed of light in glass is 2 × 108 m s-1, find the speed of light in (i) air, (ii) water. (Delhi 2013)
Answer:
(a) Refer to answer 74.
(b) Refer to answer 66.
Question 111.
The image of a candle flame placed at a distance of 45 cm from a spherical lens is formed on a screen placed at a distance of 90 cm from the lens. Identify the type of lens and calculate its focal length. If the height of the flame is 2 cm, find the height of its image. (Delhi 2012)
Answer:
Given that u = -45 cm, v = +90 cm, h = 2 cm
(as the image is formed on the screen, the image is real and hence image is formed by convex lens on the other side of the lens).
Type of the lens used : Convex lens
Lens formula
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
∴ \(\frac{1}{90}-\frac{1}{(-45)}=\frac{1}{f}=\frac{3}{90}\) or f = 30 cm
Focal length, f = 30 cm
Magnification, m = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\)
∴ \(\frac { h’ }{ 2 }\) = \(\frac { 90 }{ -45 }\) or h’ = -4 cm
⇒ height of image = 4 cm (inverted)
Question 112.
State the law of refraction of light that defines the refractive index of a medium with respect to the other. Express it mathematically. How is reffactive index of any medium ‘A’ with respect to a medium ‘B’ related to the speed of propagation of light in two media A and A? State the name of this constant when one medium is vacuum or air.
The refractive indices of glass and water with respect to vacuum are 3/2 and 4/3 respectively. If the speed of light in glass is 2 × 108 m/s, find the speed of light in (i) vacuum, (ii) water. (Delhi 2012)
Answer:
Refer to answer 74 and 66.
Question 113.
A 4 cm tall object is placed perpendicular to the principal axis of convex lens of focal length 24 cm. The distance of the object from the lens is 16 cm. Find the position, size and nature of the image formed, using the lens formula. (AI 2012, Foreign 2012)
Answer:
Given that :u = -16 cm, f = 24 cm, h = 4 cm
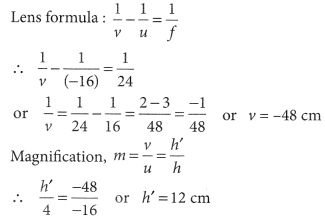
Nature of image : virtual and erect, enlarged
Question 114.
With the help of a ray diagram state what is meant by refraction of light. State Snell’s law for refraction of light and also express it mathematically.
The refractive index of air with respect to glass is 2/3 and the refractive index of water with respect to air is 4/3. If the speed of light in glass is 2 × 108 m/s, find the speed of light in (a) air, (b) water. (AI 2012)
Answer:
When travelling obliquely from one medium to another, the direction of propagation of light in the second medium changes. This phenomenon is known as refraction of light.
The ratio of sine of angle of incidence to the sine of the angle of refraction is constant, for the light of a given colour and for the given pair of media. This law is also known as snell’s law of refraction.
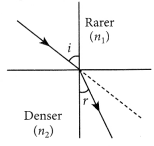
\(\frac { sin i }{ sin r }\) = constant,
Where i is the angle of incidence and r is the angle of refraction.
Given that: nag = 2/3, nwa = 4/3, vg = 2 × 108 m/s
(a) Refer to answer 66.
(b) Va = nga × vg
= \(\frac { 1 }{ n_{ag} }\) × Vg = \(\frac { 3 }{ 2 }\) × 2 × 108 = 3 × 108 m/s
Question 115.
List the sign conventions that are followed in case of refraction of light through spherical lenses. Draw a diagram and apply these conventions in determining the nature and focal length of a spherical lens which forms three times magnified real image of an object placed 16 cm from the lens. (Foreign 2012)
Answer:
For lenses, we follow sign convention, similar to one used for spherical mirrors. We apply the rules for signs of distances, except that all measurements are taken from the optical centre of the lens.
For sign convention of mirror : refer to answer 60.
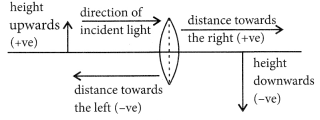
u = -16 cm, m = -3 (real)
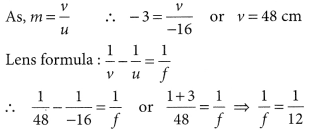
or f = 12 cm
Spherical lens is convex lens or converging lens of focal length 12 cm.
Question 116.
(a) What is meant by ‘power of a lens?’
(b) State and define the S.I unit of power of a lens.
(c) A convex lens of focal length 25 cm and a concave lens of focal length 10 cm are placed in close contact with each other. Calculate the lens power of this combination. (AI 2011)
Answer:
(a) Refer to answer 63.
(b) Refer to answer 65.
(c) Power of convex lens of focal length 25 cm is
p1 = \(\frac { 100 }{ 25(in m) }\) = 4 D
Power of concave lens of focal length 10 cm is 100
p2 = \(\frac { 100 }{ -10(in m) }\) = -10 D
∴ Power of the combination = P = P1 + P2
∴ P = 4 – 10 = -6D
Question 117.
(a) Under what condition with a glass lens placed in a transparent liquid become invisible.
(b) Describe and illustrate with a diagram, how we should arrange two converging lenses so that a parallel beam of light entering one lens emerges as a parallel beam after passing through the second lens.
(c) An object is placed at a distance of 3 cm from a concave lens of focal length 12 cm. Find the (i) position and (ii) nature of the image formed. (Foreign 2011)
Answer:
(a) If the refractive index of glass lens is equal to the refractive index of liquid then the glass lens placed in a transparent liquid will become invisible.
(b) Suppose we have two converging lens of focal lengths f1 and f2. We will keep the two converging lens at a distance of f1 +f2 so that a parallel beam of light entering one lens emerges as a parallel beam after passing through the second lens.
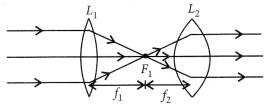
Here the focus of the two lenses should coincide,
(c) (i) Focal length of concave lens, f = -12 cm
Object distance, u = -3 cm Image distance, v = ?
Using lens formula,
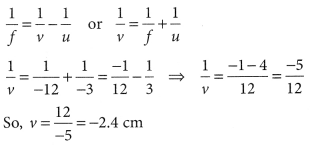
So, the image is formed at 2.4 cm from the concave lens.
(ii) Using magnification formula,
m = \(\frac { v }{ u }\) = \(\frac { -2.4 }{ -3 }\) = + 0.8
Since m is +ve and magnitude of m is less than 1, so the image formed is virtual and diminished.