Get access to Class 12 Maths Important Questions Chapter 12 Linear Programming, Linear Programming Class 12 Important Questions with Solutions Previous Year Questions will help the students to score good marks in the board examination.
Linear Programming Class 12 Important Questions with Solutions Previous Year Questions
Question 1.
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is ₹ 100 and that on a bracelet is ₹ 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximise the profit? It is being given that at least one of each must be produced. (Delhi 2017)
Answer:
Let number of necklaces and bracelets produced by firm per day be x and y, respectively.
Clearly, x ≥ 0, y ≥ 0
∵ Total number of necklaces and bracelets that the firm can handle per day is atmost 24.
∴ x + y ≤ 24
Since it takes one hour to make a bracelet and half an hour to make a necklace and maximum number of hours available per day is 16.
∴ \(\frac{1}{2}\)x + y ≤ 16
⇒ x + 2y ≤ 32
Let Z be the profit function.
Then, Z = 100x + 300y
∴ The given LPP reduces to
Maximise Z = 100x + 300y subject to,
x + y ≤ 24
x + 2y ≤ 32
and x, y ≥ 0
Question 2.
Two tailors A and B, earn ₹ 300 and ₹ 400 per day respectively. A can stitch 6 shirts and 4 pairs of trousers while B can stitch 10 shirts and 4 pairs of trousers per day. To find how many days should each of them work and if it is desired to produce at least 60 shirts and 32 pairs of trousers at a minimum labour cost, formulate this as an LPP. (All India 2017 )
Answer:
The given data can be summarised as follows

Let tailor A and tailor B works for x days and y days, respectively.
Then, x ≥ 0, y ≥ 0
v Minimum number of shirts = 60
6x + 10y ≥ 60 ⇒ 3x + 5y ≥ 30
Minimum number of trousers = 32
4x+ 4y ≥ 32 ⇒ x + y ≥ 8
Let Z be the total labour cost.
Then, Z = 300x + 400y
So, the given LPP reduces to Z = 300x + 400y
x ≥ 0, y ≥ 0, 3x + 5y ≥ 30 and x + y ≥ 8
Question 3.
Solve the following LPP graphically:
Minimise Z = 5x + 10y subject to the constraints
x + 2y ≤ 120
x + y ≥ 60,
x – 2y > 0 and x, y ≥ 0 (Delhi 2017)
Answer:
Our problem is to minimise
Z = 5x + 10y … (i)
Subject to constraints
x + 2y ≤ 120 …(ii)
x + y ≥ 60 …(iii)
x – 2y ≥ 0 … (iv)
and x ≥ 0, y ≥ 0
Table for line x + 2y = 120 is

Put (0, 0) in the inequality x + 2y ≤ 120, we get
0 + 2x ≤ 120
⇒ 0 ≤ 120 (which is true)
So, the half plane is towards the origin. Secondly, draw the graph of the line x + y = 60
![]()
On putting (0, 0) in the inequality x + y ≥ 60, we get
0 + 0 ≥ 60 ⇒ 0 ≥ 60 (which is false)
So, the half plane is away from the origin.
Thirdly, draw the graph of the line x – 2y = 0.
![]()
On putting (5, 0) in the inequality x – 2y ≥ 0, we get
5 – 2 × 0 ≥ 0 ⇒ 5 ≥ 0 (which is true)
Thus, the half plane is towards the X-axis. Since, x, y ≥ 0
∴ The feasible region lies in the first quadrant.
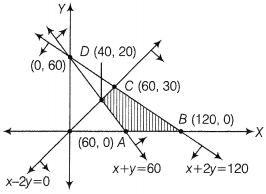
Clearly, feasible region is ABCDA.
On solving equations x – 2y = 0 and x + y = 60,
we get D(40,20) and on solving equations
x -2y = 0 and x + 2y = 120, we get C (60, 30). The corner points of the feasible region are A (60, 0), B (120, 0), C (60, 30) and D (40, 20). The values of Z at these points are as follows
| Corner point | Z = 5x + 10y |
| A (60, 0) | 300 (minimum) |
| 8(120,0) | 600 |
| C (60, 30) | 600 |
| D (40, 20) | 400 |
Clearly, the minimum value of Z is 300 at the points (60, 0)
Question 4.
Maximise and minimise Z = x + 2y subject to the constraints
x + 2 y ≥ 100
2x – y ≤ 0
2x+ y ≤ 200
x, y ≥ 0
Solve the above LPP graphically. (All India 2017)
Answer:
Our problem is to minimise and maximise
Z = x + 2y ……(i)
Subject to constraints,
x + 2y ≥ 100 ………..(ii)
2x – y ≤ 0 ………..(iii)
2x + y ≤ 200 ……..(iv)
and x ≥ 0, y ≥ 0 ……….(v)
Table for line x + 2y = 100 is
| x | 0 | 100 |
| y | 50 | 0 |
So, the line x + 2y = 100 is passing through the points (0, 50) and (100, 0).
On putting (0, 0) in the inequality x + 2y ≥ 100, we get
0 + 2 × 0 ≥ 100
⇒ 0 ≥ 100 (which is false)
So, the half plane is away from the origin.
Table for line 2x – y = 0 is
| x | 0 | 10 |
| y | 0 | 20 |
So, the line 2x – y = 0 is passing through the points (0, 0) and (10, 20).
On putting (5, 0) in the inequality 2x – y ≤ 0, we get
2 × 5 – 0 ≤ 0
⇒ 10 ≤ 0 (which is false)
So, the half plane is towards Y-axis.
Table for line 2x + y = 200 is
| x | 0 | 100 |
| y | 200 | 0 |
So, the line 2x + y = 200 is passing through the points (0, 200) and (100, 0).
On putting (0, 0) in the inequality 2x + y ≤ 200, we get
2 × 0 + 0 ≤ 200
⇒ 0 ≤ 200 (which is true)
So, the half plane is towards the origin.
Also, x, y ≥ 0.
So, the region lies in the I quadrant.
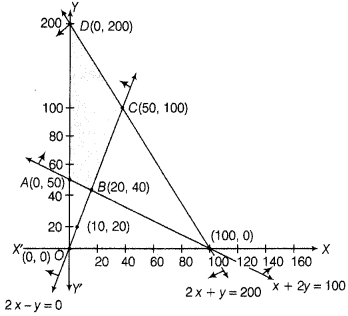
Clearly, feasible region is ABCDA.
On solving equations 2x – y = 0 and x + 2y = 100, we get B(20, 40).
Again, solving the equations 2x – y = 0 and 2x + y = 200, we get C(50, 100).
The comer points of the feasible region are
A(0, 50), B(20, 40), C(50, 100) and D(0, 200).
The values of Z at corner points are given below:
| Comer points | Z = x + 2y |
| A(0, 50) | Z = 0 + 2 × 50 = 100 |
| B(20, 40) | Z = 20 + 2 × 40 = 100 |
| C(50, 100) | Z = 50 + 2 × 100 = 250 |
| O(0, 200) | Z = 0 + 2 × 200 = 400 |
The maximum value of Z is 400 at 0(0, 200) and the minimum value of Z is 100 at all the points on the line segment joining A(0, 50) and B(20, 40).
Question 5.
A manufacturer has employed 5 skilled men and 10 semi-skilled men and makes two models A and B of an article. The making of one item of model A requires
2 h work by a skilled man and 2 h work by a semi-skilled man. One item of model B requires 1 h by a skilled man and 3 h by a semi-skilled man. No man is expected to work more than 8 h per day. The manufacturer profit on an item of model A is t 15 and on an items of model B is ? 10. How many of items of each models should be made per day in order to maximize daily profit? Formulate the above LPP and solve it graphically and find the maximum profit. (Delhi 2019)
Answer:
Let the company produce x items of A model and y items of B model.
Maximize profit is P = 15x + 10y
Now, total time spent by 5 skilled men = 2x + y
and it should be less than 40.
∴ 2x + y ≤ 40 …(i)
Also, the total time spent by 10 semi-skilled men = 2x + 3y and it should be less than 80.
∴ 2x + 3y ≤ 80 …(ii)
Also, x ≥ 0 and y ≥ 0
Now, our problem is to maximise Z = 15x + 10y
Subject to the constraints
2x + y ≤ 40
2x+ 3y ≤ 80
and x, y ≥ 0
Let us draw all the 4 lines on the graph and find the common area.
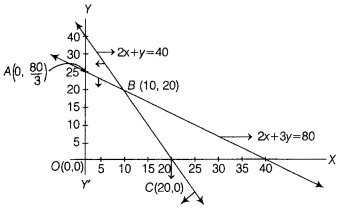
From above we get the region OABC is the feasible region with A (o, \(\frac{80}{3}\)) B(10, 20), C(20, 0), O(0, 0)
Since, the feasible is a bounded region, we can check the profit function at all the vertices to find the maxima.
At point A : Z = 15(0) + 10
At point B : Z = 15(10) + 10(20) = 350
At point C : Z = 15(20) + 10(0) = 300
At point O : Z = 15(0) +10(0) = 0
Thus, the maxima lies at point B having coordinates x = 10 and y = 20 and the maximum profit = ₹ 350.
Hence, the manufacturer should makes 10 items of A model and 20 items of B model for maximum profit of ₹ 350.
Question 6.
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of type B requires 1 g of silver and 2 g of gold. The company can use at the most 9 g of silver and 8 g of gold. If each unit of type A brings a profit of ₹ 40 and that of type B ₹ 50, find the number of units of each type that the company should produce to maximize profit. Formulate the above LPP and solve it graphically and also find the maximum profit. (All India 2019, CBSE 2018C)
Answer:
Let number of goods A = x units,
and number of goods B = y units
Now, the given LPP is to maximise profit:
P = 40x + 50y
Subject to following constraints
3x + y ≤ 9
x + 2y ≤ 8
and x ≥ 0, y ≥ 0
To solve this LPP, we first draw the following lines
3x + y – 9 and x + 2y = 8
The line 3x + y = 9 meets the coordinate axes at A(3, 0) and B(0, 9). Join these points to obtain the line represented by 3x + y = 9.
The line x + 2y = 8 meets the coordinate axes at C(8, 0) and D(0, 4). Join these points to obtain the line represented by x + 2y = 8.
Clearly, x ≥ 0and y ≥ 0represents the first quadrant.
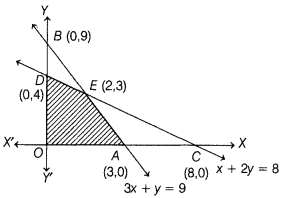
Thus, the shaded region in figure is the feasible region of the LPP. The coordinates of the comer points of this region are 0(0, 0), A (3, 0), E(2,3) and 0(0, 4), where the point E (2, 3) is obtained by solving 3x + y = 9 and x + 2y = 8 simultaneously.(1) The value of the objective function P = 40x + 50y at the corner points of the feasible region are given in the following table:
| Points (x, y) | Value of the objective function P = 40x + 50y |
| 0(0, 0) | P = 40 × 0 + 50 × 0 = 0 |
| A (3,0) | P = 40 × 3 + 50 × 0 = ₹ 120 |
| E (2, 3) | P = 40 × 2 + 50 × 3 = ₹ 230 |
| D (0, 4) | P = 40 × 0 + 50 × 4 = ₹ 200 |
Clearly, P is maximum at x = 2 and y = 3
∴ The maximum value of P is ₹ 230.
Question 7.
A factory manufactures two types of screws A and B, each type requiring the use of two machines, an automatic and a hand-operated. It takes 4 min on the automatic and 6 min on the hand-operated machines to manufacture a packet of screw ‘A’ while it takes 6 min on the automatic and 3 min on the hand-operated machine to manufacture a packet of screw ‘B’. Each machine is available for atmost 4 h on any day. The manufacturer can sell a packet of screw A’ at a profit of 70 paise and screw ‘B’ at a profit of U.
Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and find the maximum profit. (CBSE 2010)
Answer:
Let x be the number of packets of screw ‘A and y be the number of packets of screw ‘B’. Then, we have the following table from the given data.

Now, the mathematical model of the given problem is
Maximize Z = 0.7x + y
Subject to the constraints,
4x + 6y ≤ 240
or 2x + 3y ≤ 120 …(i)
6x + 3y ≤ 240
or 2x + y ≤ 80 …(ii)
and x, y ≥ 0 …(iii)
Now let us draw the graph of inequalities (i) to (iii).
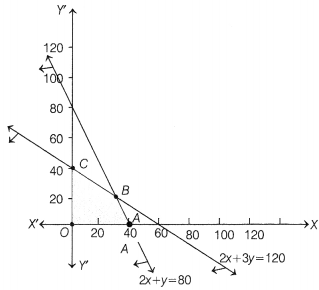
Clearly, the feasible region is the shaded region, whose comer points are O, A, B and C.
The coordinates of 0, A and C are (0, 0), (40,0) and (0, 40) respectively.
Let us find the coordinates of B which is the intersection point of 2x + y = 80 and 2x + 3y = 120.
On solving these two equations, we get x = 30 and y = 20
Thus, the coordinates of B are (30, 20).
Now, let us find the value of Z at corner points, as shown in the following table.
| Comer Points | Value of Z = 0.7x + y |
| O(0,0) | 0 |
| A (40,0) | 28 |
| B (30, 20) | 41 ← maximum |
| C (0, 40) | 40 |
We find that maximum value of Z is 41 at B (30, 20).
Hence, the manufacturer should produce 30 packets of screw A and 20 packets of screw B to get a maximum profit of ₹ 41.
Question 8.
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 h and that of second machine is 9 h per day. Each unit of product A requires 3 h on both machines and each unit of product B requires 2 h on first machine and 1 h on second machine. Each unit of product A is sold at a profit of ₹ 7 and B at a profit of ₹ 4. Find the production level per day for maximum profit graphically. (Delhi 2016)
Answer:
Let the manufacturer produces x units of product A and y units of product B.
Let us construct the following table.

Here, total profit Z = 7x + 4y
So, our problem is to maximise Z = 7x + 4y …(i)
Subject to the constraints,
3x + 2y ≤ 12
3x + y ≤ 9
and x ≥ 0, y ≥ 0
Now, consider the given inequations as equations
3x + 2y = 12 … (ii)
3x + y = 9 …(iii)
Table for line 3x + 2y = 12 or y = \(\frac{12-3 x}{2}\) is
| x | 0 | 4 |
| Y | 6 | 0 |
It passes through the points (0, 6) and (4, 0).
On putting (0, 0) in the inequality 3x + 2y ≤ 12, we get
0 + 0 ≤ 12
⇒ 0 ≤ 12 [true]
So, the half plane is towards the origin.
Table for line 3x + y = 9 or y = 9 – 3x is
| x | 0 | 3 |
| y | 9 | 0 |
It passes through the points (0, 9) and (3, 0).
On putting (0, 0) in the inequality 3x + y ≤ 9, we get
0+ 0 ≤ 9
⇒ 0 ≤ 9 [true]
So, the half plane is towards the origin.
Also, x ≥ 0 and y ≥ 0, so the region lies in 1st quadrant.
Now, on subtracting Eq. (iii) from Eq. (ii), we get
(3x + 2y) – (3x + y) = 12- 9
⇒ y = 3
Now, 3x = 12 – 2y = 12 – 2 × 3 = 6 ⇒ x = 2
Thus, the point of intersection is B(2, 3).
The graph of above inequations is shown below

Here, we see that OABC is the required feasible region, whose comer points are 0(0,0), A(3, 0), B(2,3) and C(0,6).
The values of Z at these comer points are as follows
| Comer points | Z = 7x + 4y |
| O(0, 0) | Z = 0 + 0 = 0 |
| A(3, 0) | Z = 7 × 3 + 0 = 21 |
| B(2, 3) | Z = 7 × 2 + 4 × 3 = 26 (maximum) |
| C(0, 6) | Z = 7 × 0 + 4 × 6 = 24 |
Hence, for maximum profit, the manufacturer should produce 2 units of product A and 3 units of product B.
Question 9.
A retired person wants to invest an amount of ₹ 50000. His broker recommends investing in two types of bonds A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least ₹ 20000 in bond A’ and at least ₹ 10000 in bond ‘B’. He also wants to invest at least as much in bond A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns. (All Indio 2016)
Answer:
Let the amounts invested by the person in bonds A and B are respectively, ₹ x and ₹ y.
Our problem is to maximise
Z = 10% of x + 9% of y or Z = 0.1x + 0.09y
Subject to constraints, x + y = 50000
x ≥ y or x – y ≥ 0
x ≥ 20000 and y ≥ 10000
Now, consider the given inequations as equations
x + y = 50000 …(i)
x – y = 0 …….(ii)
x = 20000 …(iii)
and y = 10000 …(iv)
The table for line x + y = 50000 is
| x | 0 | 50000 |
| y | 50000 | 0 |
∴ It passes through the points (0, 50000) and (50000, 0).
The table for line x – y = 0 is
| x | 0 | 20000 |
| Y | 0 | 20000 |
∴ It passes through the points (0, 0) and (20000, 20000).
On putting (10000, 0) in the inequality x ≥ y,
we get 10000 ≥ 0 (true)
So, the half plane is towards the X-axis.
The line x = 20000 is perpendicular to the X-axis.
On putting (0, 0) in the inequality x ≥ 20000, we cet
0 ≥ 20000 (false)
So, the half plane is away from the origin.
The line y = 10000 is perpendicular to the Y-axis.
On putting (0, 0) in the inequality y ≥ 10000, we get
0 ≥ 10000 (false)
So, the half plane is away from the origin.
Now, draw the graph of given system of inequalities as shown below.
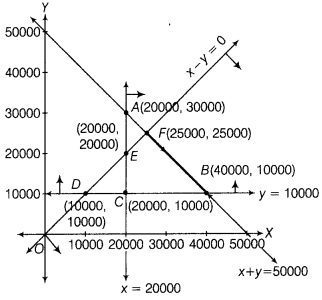
From the graph, it is clear that feasible region lies on the line segment BF. The corner points of feasible region are B (40000,10000) and F(25000, 25000).
The values of Z at comer points are given below:
| Comer Points | Z = 0.1x + 0.09y |
| B (40000,10000) | Z = 01 × 40000 + 0.09 × 10000 = 4900 (maximum) |
| P (25000, 25000) | Z = 02 × 25000 + 0.09 × 25000 = 4750 |
Hence, to get a maximum returns, he has to invest ₹ 40000 in bond A and ₹ 10000 in bond B.
Question 10.
There are two types of fertilisers A and B’. A’ consists of 12% nitrogen and 5% phosphoric acid whereas B’ consists of 4% nitrogen and 5% phospheric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If‘A’ costs 110 per kg and B’ costs ? 8 per kg , then graphically determine how much of each type of fertiliser should be used so that the nutrient requirements are met at a minimum cost? (All India 2016)
Answer:
Let the farmer uses x kg of fertiliser A and y kg of fertiliser B. The given data can be summarised as follows

The inequations thus formed based on the given problem are as follows:
\(\frac{12 x}{100}+\frac{4 y}{100}\) ≥ 12
⇒ 12x+ 4y ≥ 1200
⇒ 3x + y ≥ 300
Also, \(\frac{5 x}{100}+\frac{5 y}{100}\) ≥ 12
⇒ 5x+ 5y ≥ 1200
⇒ x + y ≥ 240
and x ≥ 0, y ≥ 0
Let Z be the total cost of the fertilisers. Then,
Z = 10x+ 8 y
The LPP can be stated mathematically as Minimise Z = lOx + 8y
Subject to constraints 3x + y ≥ 300, x + y ≥ 240, x ≥ 0,y ≥ 0
To solve the LPP graphically, let us convert the inequations into equations as follows :
3x + y = 300 …(i)
x + y = 240 …..(ii)
Table for line 3x + y = 300 is
| x | 0 | 100 |
| y | 300 | 0 |
So, it passes through (0, 300) and (100, 0).
On putting (0,0) in the inequality 3x + y ≥ 300, we get 3(0) + 0 ≥ 300 ⇒ 0 ≥ 300 (which is false)
So, the half plane is away from origin (1)
Table for line x + y = 240 is
| x | 0 | 240 |
| y | 240 | 0 |
So, it passes through (240, 0) and (0, 240).
On putting (0, 0) in x + y ≥ 240, we get 0 + 0 ≥ 240 (which is false)
So, the half plane is away from origin.
Also, x ≥ 0 and y ≥ 0, so the region lies in 1st quadrant.
The graph of inequations is shown below
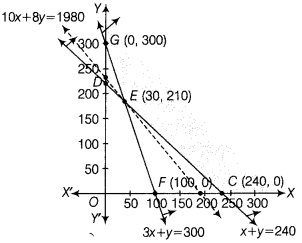
The shaded region GEC represents the feasible region of given LPP and it is unbounded.
On solving Eqs. (i) and (ii), we get x = 30 and y = 210
So, the point of intersection is B(30, 210).
| Comer points | Value of Z = 10x + 8y |
| G(0, 300) | 2400 |
| C (240,0) | 2400 |
| E (30, 210) | 1980 (minimum) |
From the table, we find that 1980 is the minimum value of Z at E (30, 210). Since, the region is unbounded, therefore, 1980 may or may not be the minimum value of Z. For this we have to check that the open half plane 10x + 8y < 1980 has any point common or not with the feasible region. Since, it has no point in common with the feasible region. So, the minimum value of Z is obtained at £(30, 210) and the miniumum value of Z is 1980. So, the farmer should use 30 kg of fertiliser A and 210 kg of fertiliser B.
Question 11.
In order to supplement daily diet, a person wishes to take X and Y tablets. The contents (in milligrams per tablet) of iron, calcium and vitamins in X and Y are given as below:

The person needs to supplement at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamins. The price of each tablet of X and Y is ₹ 2 and ₹ 1, respectively. How many tablets of each type should the person take in order to satisfy the above requirement at the minimum cost? Make an LPP and solve graphically. (Foreign 2016)
Answer:
Let the person takes x tablets of type X and Y
tablets of type Y.
According to the given conditions, we have
6x + 2y ≥ 18 3x + y ≥ 9
3x + 3y ≥ 21 = x + y ≥ 7
2x + 4y ≥ 16x+ 2y ≥ 8
Let Z be the total cost of tablets.
Then, Z = 2x + y
Hence, the given LPP is Minimise Z = 2x + y
Subject to constraints 3x + y ≥ 9, x + y ≥ 7.
x+ 2y ≥ 8and x,y ≥ 0
To solve graphically, let us convert the inequations into equations.
3x + y = 9, x + y = 7.
x + 2y = 8, x = 0, y = 0
Table for line 3x + y = 9 is
| x | 0 | 3 |
| y | 9 | 0 |
So, it passes through (0, 9) and (3, 0).
On putting (0, 0) in 3x+ y ≥ 9, we get
0 + 0 ≥ 9 (which is false)
So, the half plane is away from origin.
Table for line x + y = 7 is
| x | 0 | 7 |
| y | 7 | 0 |
So, it passes through (0, 7) and (7, 0).
Also, the half plane of x + y ≥ 7 is away from origin.
Table for line 2x + y = 8 is
| x | 0 | 4 |
| y | 8 | 0 |
So, it passes through (0, 8) and (4, 0).
Also, the half plane of 2x + y ≥ 8 is away from origin.
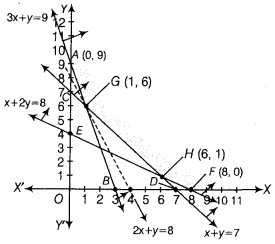
The shaded region AGHF represents the feasible region of the given LPP.
The point of intersection of the lines 3x + y = 9 and x + y= 7 is G(1, 6).
Also, the point of intersection of the lines x + y = 7 and x + 2y = 8 is H(6,1).
The comer points of the feasible region are A(0,9), G(1, 6), H(6, 1) and F(8, 0).
The values of the objective function at these points are given in the following table :
| Comer Points | Value of Z = 2x + y |
| A(0,9) | 2 × 0 + 9 = 9 |
| G(1,6) | 2 × 1 + 6 = 8 (minimum) |
| H(6,1) | 2 × 6 + 1 = 13 |
| F(8,0) | 2 × 8 + 0 = 16 |
From the table, we find that 8 is the minimum value of Z at G(1, 6). Since, the region is unbounded, therefore, 8 may or may not be the minimum value of Z. For this we have to check, that the open half plane 2x + y < 8 has any point common or not with the feasible region.
Since, it has no point in common with the feasible region. So, Z is minimum at G(1, 6) and the minimum value of Z is 8. Hence, the person should take 1 tablet of type X and 6 tablets of type Y in order to meet the requirements at the minimum cost.
Question 12.
A manufacturer produces nuts and bolts. It take 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of ₹ 24 per package on nuts and ₹ 18 per package on bolts. How many package of each should be produced each day so as to maximise his profit, if he operates his machines for at most 10 hours a day? Make an LPP and solve it graphically. (All India 2015C)
Answer:
Let x and y respectively denotes the number of packages of nuts and bolts manufactured by the manufacturer. Then, given data can be summarised in tabular form as follows.

The required LPP is
Maximize Z = 24x + 18y
Subject to constraints
2x + 3y ≤ 10, 3x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Let us consider the inequalities as equation,
2x + 3y = 10 …(i)
and 3x + 2y = 10 …(ii)
Table for line 2x + 3y = 10 is
| x | 0 | 5 |
| y | 10/3 | 0 |
So, it passes through (0, 10/3) and (5, 0).
On putting (0, 0) in the inequality 2x + 3 ≤ 10, we get 2(0) + 3(0) ≤ 10
⇒ 0 ≤ 10 (which is true)
So, the half plane is towards the origin.
Table for line 3x + 2y = 10 is 10/3
| x | 0 | 10/3 |
| y | 5 | 0 |
So, it passes through (0, 5) and (10/3, 0)
On putting (0, 0) in the inequality 3x + 2y ≤ 0, we get
3 (0) + 2 (0) = 10
⇒ 0 ≤ 10 (which is true)
So, the half plane is towards the origin.
On solving Eq. (i) and Eq. (ii), we get
x = 2 and y = 2
So, the intersection point is (2, 2).
The graphical representation of the system of inequation is given below.
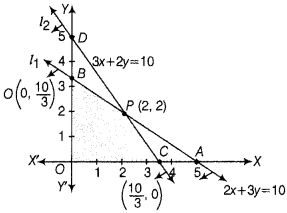
The feasible region is OCPB and the comer points are 0(0,0), B(0, \(\frac{10}{3}\)), C(\(\frac{10}{3}\), o) and P(2,2).
| Comer Points | Value of Z = 24x + 18y |
| O(0, 0) | 0 |
| C(\(\frac{10}{3}\), 0) | 80 |
| P(2, 2) | 84 (Maximum) |
| B(0, \(\frac{10}{3}\)) | 60 |
Thus, profit will be maximum, when 2 packages of nuts and 2 packages of bolts are manufactured.
Question 13.
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below
2x+ 4y ≤ 8; 3x + y ≤ 6
x + y ≤ A; x ≥ 0, y ≥ 0. (Delhi 2015)
Answer:
We have the following LPP,
Maximise, Z = 2x + 5y
Subject to the constraints
2x + 4y ≤ 8 or x + 2y ≤ 4
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
Now, considering the inequations as equations, we get
x + 2y = 4 …(i)
3x + y = 6 …(ii)
and x + y = 4 …(iii)
Table for line x + 2y = 4 is
| x | 4 | 0 |
| y | 0 | 2 |
So, the line passes through (4, 0) and (0, 2).
On putting (0, 0) in the inequality x + 2y ≤ 4, we get
0 + 0 ≤ 4 [which is true]
So, the half plane is towards the origin.
Table for line 3x + y = 6 is
| x | 2 | 0 |
| y | 0 | 6 |
So, the line passes through (2, 0) and (0, 6).
On putting (0, 0) in the inequality 3x + y ≤ 6, we get
0 + 0 ≤ 6 [which is true]
So, the half plane is towards the origin. CD
Table for line x + y = 4 is
| x | 4 | 0 |
| y | 0 | 4 |
On putting (0, 0) in the inequality x + y ≤ 4, we get
0 + 0 ≤ 4 [which is true]
So, the half plane is towards the origin.
Also, x ≥ 0, y ≥ 0, so the region lies in the 1st quadrant.
The graphical representation of the above system of inequations is given below
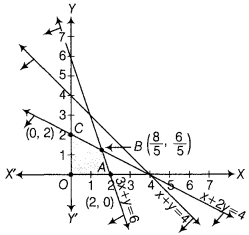
Clearly, the feasible region is OABCO.
The intersection point of lines (i) and (ii) is B(\(\frac{8}{5}, \frac{6}{5}\))
Thus, the corner points are
0(0, 0),A(2, 0), B(\(\frac{8}{5}, \frac{6}{5}\)),C(0, 2).
The values of Z at corner points are as follows:
| Corner Points | Z = 2x + 5y |
| 0(0,0) | Z = 0 + 0 = 0 |
| A (2, 0) | Z = 2 × 2 + 5 × 0 = 4 |
| B(\(\frac{8}{5}, \frac{6}{5}\)) | Z = 2 × \(\frac{8}{5}\) + 5 × \(\frac{6}{5}=\frac{46}{5}\) = 9.2 |
| C(0, 2) | Z = 2 x 0 + 5 x 2 = 10 (maximum) |
Hence, the maximum value of Z is 10.
Question 14.
A company manufactures three kinds of calculators: A B and C in its two factories I and II. The company has got an order for manufacturing at least 6400 calculators of kind A 4000 of kind B and 4800 of kind C. The daily output of factory I is of 50 calculators of kind A 50 calculators of kind B and 30 calculators of kind C. The daily output of factory II is of 40 calculators of kind A 20 of kind B and 40 of kind C. The cost per day to run factory I is ₹ 12000 and of factory II is ₹ 15000. How many days do the two factories have to be in operation to produce the order with the minimum cost? Formulate this problem as an LPP and solve it graphically. All India 2015
Answer:
Let factory (I) run for x days and factory (II) run fory days. Then,
Total cost (in ₹) = 12000x + 15000y and our problem is to
Minimise Z = 12000x + 15000y
Subject to the constraints
50x + 40y ≥ 6400 or 5x + 4y ≥ 640
50x + 20y ≥ 4000 or 5x + 2y ≥ 400
30x+ 40y ≥ 4800 or 3x + 4y ≥ 480
x ≥ 0 and y ≥ 0
Now, considering the inequations as equations, we get
5x + 4y = 640 …(i)
5x + 2y = 400 …(ii)
3x + 4y = 480 …(iii)
Table for line 5x + 4y = 640 is
| x | 128 | 0 |
| y | 0 | 160 |
So, the line passes through the points (128, 0) and (0, 160).
On putting (0, 0) in the inequality 5x + 4y ≥ 640, we get
0 + 0 ≥ 640 [which is false]
So, the half plane is away from the origin.
Table for line 5x + 2y = 400 is
| x | 80 | 0 |
| y | 0 | 200 |
So, the line passes through the points (80, 0) and (0, 200).
On putting (0, 0) in the inequality 5x + 2y ≥ 400, we get
0 + 0 ≥ 400 [which is false]
So, the half plane is away from the origin.
Table for line 3x + 4y = 480 is
| x | 160 | 0 |
| y | 0 | 120 |
So, the line passes through the points (160, 0) and (0, 120).
On putting (0, 0) in the inequality 3x + 4y ≥ 480, we get
0 + 0 ≥ 480 [which is false]
So, the half plane is away from the origin.
Also, x ≥ 0 and y ≥ 0, so the feasible region lies in the first quadrant.
The point of intersection of lines (i) and (iii) is (80, 60) and lines (i) and (ii) is (32, 120).
The graphical representations of the above system of inequations is given below
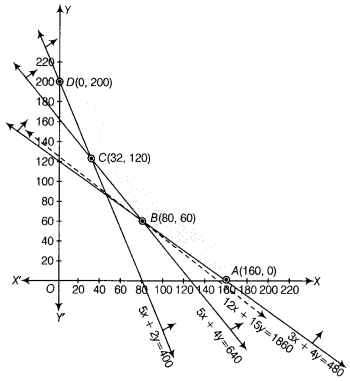
Clearly, feasible region is ABCD (shaded region), whose comer points are 4(160,0), B (80, 60), C (32,120) and D(0, 200).
The values of Z at comer points are as follows:
| Comer Points | Z = 12000x + 15000y |
| 4(160, 0) | Z = 12000 × 160 + 0 = 1920000 |
| B(80, 60) | Z = 12000 × 80 + 15000 × 60 = 1860000 (minimum) |
| C(32, 120) | Z = 12000 × 32 + 15000 × 120 = 2184000 |
| D(0, 200) | Z = 0 + 15000 × 200 = 3000000 |
In the table, we find that minimum value of Z is 1860000, occur at the point B(80, 60).
But we can’t say that it is a minimum value of Z as region is unbounded.
Therefore, we have to draw the graph of the inequality 12000x + 15000y < 1860000
or 12x + 15y < 1860
From the figure, we see that the open half plane represented by 12x + 15y < 1860 has no point in common with feasible region. Thus, the minimum value of Z is ₹ 1860000 attained at the point (80, 60). Hence, factory (I) should run for 80 days and factory (II) should run for 60 days to get a minimum cost.
Question 15.
Maximise Z = 8x + 9y subject to the constraints given below:
2x + 3y ≤ 6 3x – 2y ≤ 6
y ≤ 1; x,y ≥ 0. (Foreign 2015)
Answer:
We have the following LPP,
Maximise Z = 8x + 9y
Subject to the constraints
2x + 3y ≤ 6
3x – 2y ≤ 6
y ≤1 and x, y ≥ 0
Now, considering the inequations as equations, we get
2x + 3y = 6 …………(i)
3x – 2y = 6 ………(ii)
and y = 1 …(iii)
Table for line 2x + 3y = 6 is
| x | 3 | 0 |
| y | 0 | 2 |
So, it passes through the points, (3, 0) and (0, 2).
On putting (0,0) in the inequality 2x + 3y ≤ 6, we get
0 ≤ 6 [which is true]
So, the half plane is towards the origin.
Table for line 3x – 2y = 6 is
| x | 2 | 0 |
| y | 0 | -3 |
So, it passes through the points (2,0) and (0,-3).
On putting (0,0) in the inequality 3x – 2y ≤ 6, we get
0 ≤ 6 [which is true]
So, the half plane is towards the origin. (1)
The line y = 1 is perpendicular to Y-axis.
On putting (0,0) in the inequality y ≤ 1,
we get 0 ≤ 1 [which is true]
So, the half plane is towards the origin.
Also, x ≥ 0, y ≥ 0, so the feasible region lies in the first quadrant.
The point of intersection of Eqs. (i) and (ii) is and Eqs.(i) \(\frac{30}{13}, \frac{6}{13}\) Eqs. (ii) and (iii) is (\(\frac{8}{3}\), 1) and Eqs. (i) and (iii) is (\(\frac{3}{2}\), 1)
The graphical representation of the above system of inequations is given below
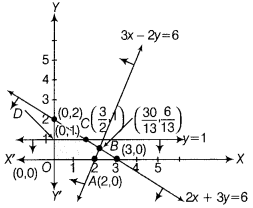
Clearly, feasible region is OABCDO, whose corner points are 0(0, 0), A(2, 0), B(\(\frac{30}{13}, \frac{6}{13}\)), C(\(\frac{3}{2}\), 1) and D(0, 1).
The values of Z at comer points are as follows:
| Corner points | Z = 8x + 9y |
| 0(0,0) | Z = 0 + 0 = 0 |
| A(2,0) | Z = 8 × 2 + 0 = 16 |
| B\left(\frac{30}{13}, \frac{6}{13}\right) | Z = 8 × \(\frac{30}{13}+\frac{9 \times 6}{13}=\frac{294}{13}\) = 22.62 (maximum) |
| C(\(\), 1) | Z = 8 × \(\frac{3}{2}\) + 1 = 13 |
| D(0,1) | Z = 0 + 9 × 1 = 9 |
In the table, we find that maximum value of Z is 22.62, when x = \(\frac{30}{13}\) and y = \(\frac{6}{13}\)
Question 16.
One kind of cake requires 200 g of flour and 25 g of fat, another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat, assuming that there is no shortage of the other ingredients used in making the cakes. Make it as an LPP and solve it graphically. (Delhi 2015C; All India 2014C, 2011C)
Answer:
We can write the given data in tabular form as follows:
| Cake | Flour | Fat |
| I kind | 200 g | 25g |
| II kind | 100 g | 50 g |
| Availability | 5 kg or 5000 g | 1 kg or 1000 g |
Suppose the number of cakes of I kind be x and II kind be y.
Then, required LPP is max (Z) = x + y
Subject to the constraints
200x + 100y ≤ 5000 ⇒ 2x + y ≤ 50 …(i)
[dividing both sides by 100]
25x + 50y ≤ 1000 ⇒ x + 2y ≤ 40 …(ii)
[dividing both sides by 25]
and x ≥ 0, y ≥ 0
Let us consider the inequalities as equations, we get
2x + y = 50 …(iii)
and x + 2y = 40 …(iv)
Table for line 2x + y = 50 is
| x | 25 | 0 |
| y | 0 | 25 |
So, it passes through the points (25, 0) and (0, 50).
On putting (0,0) in the inequality 2x + y < 50, we get
0 ≤ 50 [which is true]
So, the half plane is towards the origin.
Table for line x + 2y = 40 is
| x | 40 | 0 |
| y | 0 | 20 |
So, it passes through the points (40, 0) and (0,20).
On putting (0,0) in the inequality x+ 2y < 40, we get
0 ≤ 40 [which is true]
So, the half plane is towards the origin.
On solving Eqs. (iii) and (iv), we get the intersection point is (20, 10).
Now, on drawing all the inequalities on a graph paper, we get the feasible region OAEDO, which is bounded.
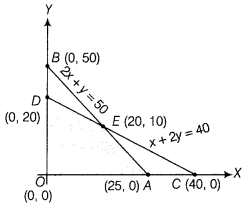
The corner points of feasible region are
0(0, 0), ,4(25, 0), 0(0, 20) and £'(20,10), respectively.
The values of Z at the comer points are as follows:
| Corner points | Value of Z = x + y |
| 0 (0, 0) | Z = 0 + 0 = 0 |
| A(25, 0) | Z = 25 + 0 = 25 |
| D (0, 20) | Z = 0 + 20 = 20 |
| E(20, 10) | Z = 20 + 10 = 30 (maximum) |
From the table, maximum number of cakes is 30, which has 20 cakes of 1st kind and 10 cakes of IInd kind.
Question 17.
A dealer in rural area wishes to purchase a number of sewing machines. He has only ₹ 5760 to invest and has space for atmost 20 items for storage. An electronic sewing machine cost ₹ 360 and a manually operated sewing machine ₹ 240. He can sell an electronic sewing machine at a profit of ₹ 22 and a manually operated sewing machine at a profit of ₹ 18. Assuming that he can sell all the items that he can buy, how should he invest his money in oder to maximise his profit? Make it as an LPP and solve it graphically. (Delhi 2014,2009C; All India 2009)
Answer:
Let the dealer purchased x electronic sewing machines and y manually operated sewing machines.
Now, we can constmct the following table

Then, given LPP is maximise, Z = 22x + 18y
Subject to constraints, x + y ≤ 20
360x + 240y ≤ 5760 or 3x + 2y ≤ 48
x ≥ 0, y ≥ 0
Let us consider the inequalities as equations, we get
x + y = 20 …(ii)
3x + 2y = 48 …(iii)
and x = 0, y = 0 …(iv)
Table for line x + y = 20 is
| x | 0 | 20 |
| y | 20 | 0 |
So, it passes through the points (0, 20) and (20, 0). On putting (0, 0) in the inequality x + y < 20, we get
0 + 0 ≤ 20 ⇒ 0 ≤ 20 [which is true]
So, the half plane is towards the origin.
Table for line 3x + 2y = 48 is
| x | 0 | 16 |
| y | 24 | 0 |
So, it passes through the points (0, 24) and (16, 0). On putting (0, 0) in the inequality 3x + 2y ≤ 48, we get
0 ≤ 48 [which is true]
So, the half plane is towards the origin.
On solving Eqs. (ii) and (iii), we get x = 8 and y = 12
So, the point of intersection of the lines (ii) and (iii) is (8,12). Also, x ≥ 0 and y ≥ 0, so the feasible region lies in the first quadrant.
Now, on drawing all the inequalities on a graph paper and we get the feasible region OABCO, which is bounded.
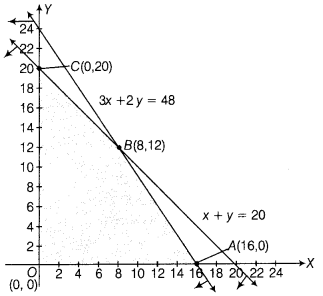
The corner points of the feasible region are 0(0, 0), A(16, 0), B(8,12) and C(0, 20).
The values of Z at corner points are as follows:
| Corner Points | Z = 22x + 18y |
| O(0, 0) | Z = 22(0) +18(0) = 0 |
| A(16, 0) | Z = 22 × 16 + 0= 352 |
| B(8, 12) | Z = 22 × 8 + 18 × 12 = 392 (maximum) |
| C(0, 20) | Z = 22 × 0 + 18 × 20 = 360 |
From the table, maximum value of Z = ₹ 392 at point B(8,12).
Hence, dealer should purchased 8 electronic and 12 manually operated sewing machines to get maximum profit.
Question 18.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours of fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of t 80 on each piece of type A and ₹ 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week? (All India 2014)
Answer:
Let the number of pieces of two types of teaching aids A and B be x and y, respectively.
We can write the given data in tabular form as follows:
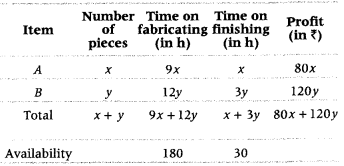
Thus, the required LPP is
Maximise, Z = 80x +120y …(i)
Subject to constraints
9x + 12y ≤ 180
x + 3y ≤ 30
x ≥ 0, y ≥ 0
Let us consider the inequalities as equations, we get
9x + 12y = 180
or 3x + 4y = 60 ……….(ii)
x + 3y = 30 … (iii)
and x = 0,y = 0 … (iv)
Table for line 3x + 4y = 60 is
| x | 0 | 20 |
| y | 15 | 0 |
So, it passes through the points (0, 15) and (20, 0).
On putting (0, 0) in the inequality 9x + 12y ≤ 180, we get
9(0) + 12(0) ≤ 180
⇒ 0 ≤ 180 [which is true]
So, the half plane is towards the origin.
Table for line x + 3y = 30 is
| x | 0 | 30 |
| y | 10 | 0 |
So, it passes through the points (0,10) and (30,0).
On putting (0, 0) in the inequality x + 3y ≤ 30,
we get 0 + 3(0) ≤ 30
⇒ 0 ≤ 30 [which is true]
So, the half plane is towards the origin.
Also, x ≥ 0 and y ≥ 0
Thus, the feasible region lies in the first quadrant. On solving Eqs. (ii) and (iii), we get x = 12
and y = 6
So, the point of intersection is (12, 6).
The graphical representation of the above system of inequations is given below
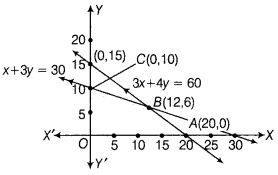
From graph, feasible region is OABCO, whose comer points are O(0, 0), A(20, 0), B (12, 6) and C(0,10).
The values of Z at corner points are as follows:
| Corner Points | Value 0f Z = 80x + 120y |
| O(0, 0) | Z = 80(0) + 120(0) = 0 |
| A(20, 0) | Z = 80(20) + 120(0) = 1600 |
| B(12, 6) | Z = 80(12) + 120(6) = 1680 (maximum) |
| C(0, 10) | Z = 80(0) + 120(10) = 1200 |
From the table, the maximum value of Z is ₹ 1680.
Hence, 12 pieces of type A and 6 pieces of type B should be manufactured per week to get a maximum profit of ₹ 1680 per week.
Question 19.
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 h on the grinding/cutting machine and 3 h on the sprayer to manufacture a pedestal lamp. It takes 1 h on the grinding/cutting machine and 2 h on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 h and the grinding/cutting machine for at most 12 h. The profit from the sale of a lamp is ? 25 and that from a shade is ₹ 15. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Formulate an LPP and solve it graphically. (Foreign 2014)
Answer:
Let the cottage industry manufacture x pedestal lamps and y wooden shades.
Therefore, x ≥ 0 and y ≥ 0.
The given information can be written in Labular form as given below

Then, the required LPP is
Maximise, Z = 25x + 15y
Subject to constraints
2x + y ≤ 12
3x + 2y ≤ 20
x ≥ 0, y ≥ 0 [non-negative constraints]
Let us consider the inequalities as equations, we get
2x + y = 12 …(i)
3x + 2y = 20 …(ii)
Table for 2x + y = 12 is
| x | 0 | 6 |
| y | 12 | 0 |
So, it passes through the points (0, 12) and (6, 0).
On putting (0,0) in inequality 2x + y ≤ 12 we get
2(0) + 0 ≤ 12 ⇒ 0 ≤ 12 [which is true]
So, the half plane is towards the origin.
Table for 3x + 2y = 20 is
| x | 0 | 20/3 |
| y | 10 | 0 |
So, it passes through the points (0,10) and (20/3,0).
On putting (0,0) in inequality 3x + 2y < 20, we get
3 (0) + 2 (0) ≤ 20⇒ 0 ≤ 20 [which is true]
So, the half plane is towards the origin.
Also, x ≥ 0, y ≥ 0, so the feasible region lies in first quadrant.
On solving Eqs. (i) and (ii), we get x = 4 and y = 4
So, the intersection point is (4, 4)
The graphical representation of the above system of inequations is given below
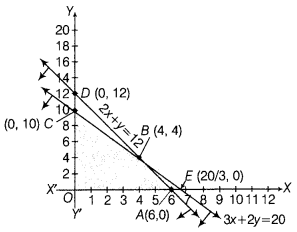
From graph, the feasible region is OABCO, whose comer points are 0(0,0), ,4(6,0), ,6(4,4) and C(0,10).
The values of Z at the corner points are as follows:
| Corner Points | Value of Z = 25x + 15y |
| O(0, 0 ) | Z = 25(0) + 15(0) = 0 |
| A(6, 0) | Z = 25(6) + 15(0) = 150 |
| B(4, 4) | Z = 25 (4) + 15 (4) = 160 (maximum) |
| C(0, 10) | Z = 25(0)+ 15 (10) = 150 |
From table, maximum value of Z is 160 at B(4, 4). Hence, the manufacturer should produce 4 pedestal lamps and 4 wooden shades daily to get maximum profit.
Question 20.
A decorative item dealer deals in two items A and B. He has ₹ 15000 to invest and a space to store at the most 80 pieces. Item A costs him ₹ 300 and item B costs him ₹ 150. He can sell items A and B at respective, profits of ₹ 50 and ₹ 28. Assuming he can sell all he buys, formulate the linear programming problem in order to maximise his profit and solve it graphically. (Delhi 2012C)
Answer:
Let the number of items of the type A and B be x and y, respectively.
Then the required LPP is
Maximise Z = 50x + 28y
Subject to the constraints,
x + y ≤ 80, 300x + 150y ≤ 15000
or 2x + y ≤ 100, x ≥ 0, y ≥ 0
Let us consider the inequalities as equations, we get
x + y = 80 …………..(i)
2x + y = 100 …………..(ii)
Table for line x + y = 80 is
| x | 0 | 80 |
| y | 80 | 0 |
So, it passes through the points (0, 80) and (80, 0).
On putting (0, 0) in the inequality x + y ≤ 80, we get
0+ 0 ≤ 80
⇒ 0 ≤ 80 (which is true)
So, the half plane is towards the origin.
Table for line 2x + y = 100
| x | 0 | 50 |
| y | 100 | 0 |
So, it passes through the points (0, 100) and (50,0)
On putting (0, 0) in the inequility 2x + y ≤ 100, we get
2(0) + 0 ≤ 100
⇒ 0 ≤ 100 (which is true)
So, the half plane is towards the origin.
On solving Eqs. (i) and (ii), we get x = 20 and y = 60 (1)
So, the point of intersection is (20,60).
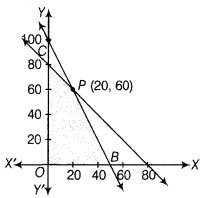
The feasible region is OBPC whose corner points are 0(0,0), 5(50,0), P(20,60) and C(0, 80).
| Corner Points | Value of Z = 50x + 28y |
| 0(0, 0) | 0 |
| C(0, 80) | 2240 |
| P(20,60) | 2680 (Maximum) |
| B(50, 0) | 2500 |
From the above table, the maximum value of Z is 2680 at P(20, 60), i.e. when 20 items of type A and 60 items of type B are purchased and sold. He get maximum profit.
Question 21.
A manufacturer produces nuts and bolts.
It takes 1 h of work on machine A and 3 h on machine B to produce package of nuts. It takes 3 h on machine A and 1 h on machine B to produce a package of bolts. He earns a profit of ₹ 17.50 per package : on nuts and ₹ 7 per package on bolts. How many packages of each should be produced each day so as to maximise his profits, if he operates his machines for atmost 12 h a day? Formulate above as a Linear Programming Problem (LPP) and solve it graphically. (Delhi 2012,2009C)
Answer:
Let x and y respectively denotes the number of packages of nuts and bolts manufactured by the manufacturer. Then, given data can be summarised in tabular form as follows.

The required LPP is
Maximize Z = 24x + 18y
Subject to constraints
2x + 3y ≤ 10, 3x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Let us consider the inequalities as equation,
2x + 3y = 10 …(i)
and 3x + 2y = 10 …(ii)
Table for line 2x + 3y = 10 is
| x | 0 | 5 |
| y | 10/3 | 0 |
So, it passes through (0, 10/3) and (5, 0).
On putting (0, 0) in the inequality 2x + 3 ≤ 10, we get 2(0) + 3(0) ≤ 10
⇒ 0 ≤ 10 (which is true)
So, the half plane is towards the origin. (1)
Table for line 3x + 2y = 10 is 10/3
| x | 0 | 0/3 |
| y | 5 | 0 |
So, it passes through (0, 5) and (10/3, 0)
On putting (0, 0) in the inequality 3x + 2y ≤ 0, we get
3 (0) + 2 (0) = 10
⇒ 0 ≤ 10 (which is true)
So, the half plane is towards the origin.
On solving Eq. (i) and Eq. (ii), we get
x = 2 and y = 2
So, the intersection point is (2, 2).
The graphical representation of the system of inequation is given below.

The feasible region is OCPB and the comer points are 0(0,0), B(0, \(\frac{10}{3}\)), C(\(\frac{10}{3}\), o) andP(2,2).
| Comer Points | Value of Z = 24x + 18y |
| O(0, 0) | 0 |
| C(\(\frac{10}{3}\), 0) | 80 |
| P(2, 2) | 84 (Maximum) |
| B(0, \(\frac{10}{3}\)) | 60 |
Thus, profit will be maximum, when 2 packages of nuts and 2 packages of bolts are manufactured.
Hint: Let the manufacturer produces x packages of nuts and y packages of bolts.
The required LPP is Maximize Z = 17.50x + 7y Subject to constraints x + 3y ≤ 12 3x + y ≤ 12 and x,y ≥ 0
[The manufacturer should produce 3 packages of nuts and 3 packages of bolts each day for maximum profit = ₹ 73.50]
Question 22.
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 1 hours on machine B to produce a package of nuts while it takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ₹ 2.50 per package of nuts and ₹ 1.00 per package of bolts. How many packages of each type should he produce each day so as to maximise his profit, if he operates his machines for at most 12 hours a day? Formulate this problem as a linear programming problem and solve it graphically. (All India 2012C)
Answer:
Let x and y respectively denotes the number of packages of nuts and bolts manufactured by the manufacturer. Then, given data can be summarised in tabular form as follows.

The required LPP is
Maximize Z = 24x + 18y
Subject to constraints
2x + 3y ≤ 10, 3x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Let us consider the inequalities as equation,
2x + 3y = 10 …(i)
and 3x + 2y = 10 …(ii)
Table for line 2x + 3y = 10 is
| x | 0 | 5 |
| y | 10/3 | 0 |
So, it passes through (0, 10/3) and (5, 0).
On putting (0, 0) in the inequality 2x + 3 ≤ 10, we get 2(0) + 3(0) ≤ 10
⇒ 0 ≤ 10 (which is true)
So, the half plane is towards the origin. (1)
Table for line 3x + 2y = 10 is 10/3
| x | 0 | 5 |
| y | 10/3 | 0 |
So, it passes through (0, 5) and (10/3, 0)
On putting (0, 0) in the inequality 3x + 2y ≤ 0, we get
3 (0) + 2 (0) = 10
⇒ 0 ≤ 10 (which is true)
So, the half plane is towards the origin.
On solving Eq. (i) and Eq. (ii), we get
x = 2 and y = 2
So, the intersection point is (2, 2).
The graphical representation of the system of inequation is given below.

The feasible region is OCPB and the comer points are 0(0,0), B(0, \(\frac{10}{3}\)), C(\(\frac{10}{3}\), o) andP(2,2).
| Comer Points | Value of Z = 24x + 18y |
| O(0, 0) | 0 |
| C(\(\frac{10}{3}\), 0) | 80 |
| P(2, 2) | 84 (Maximum) |
| B(0, \(\frac{10}{3}\)) | 60 |
Thus, profit will be maximum, when 2 packages of nuts and 2 packages of bolts are manufactured.
Hint: Let the manufacturer produces x packages of nuts and y packages of bolts.
The required LPP is Maximize Z = 2.5x + y Subject to constraints x + 3y ≤ 12 3x + y ≤ 12 and x, y ≥ 0
[The manufacturer should produce 3 packages of nuts and 3 packages of bolts each day for maximum profit = ₹ 10.5]
Question 23.
A dietician wishes to mix two types of foods in such a way that the vitamin contents of mixture contains atleast 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C, while food II contains 1 unit per kg of vitamin. A and 2 units per kg of vitamin C. It costs ₹ 5 per kg to purchase food I and ₹ 7 per kg to purchase food II. Find the minimum cost of such a mixture. Formulate above as an LPP and solve it graphically. (All India 2012)
Answer:
The given data can be put in the tabular form as follows

Suppose the diet contains x kg of food I and y kg of food II.
Then, the required LPP is minimise (Z) = 5x + 7y
Subject to constraints 2x + y ≥ 8, x + 2y ≥ 10 and x ≥ 0, y ≥ 0
| x | 0 | 4 |
| y | 8 | 0 |
So, it passes through the points (0, 8) and (4, 0). On putting (0,0) in the inequality 2x + y ≥ 8, we get
0 ≥ 8 [which is false]
So, the half plane is away from the origin.
Table for line x + 2y = 10 is
| x | 10 | 0 |
| y | 0 | 5 |
So, it passes through the points (10, 0) and (0, 5).
On putting (0,0) in the inequality x + 2y ≥ 10, we get
0 ≥ 10 [which is false]
So, the half plane is away front the origin.
Also, x, y ≥ 0, so the feasible region lies in the first quadrant.
On solving Eq. (i) and Eq. (ii), we get x = 2 and y = 4
So, these lines intersect at P (2, 4).
The graphical representation of the system of inequations given below
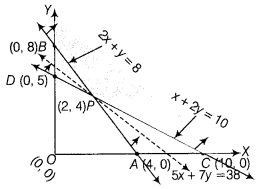
From the graph, the feasible region is BPC which is unbounded.
The values of Z at corner points are as follows:
| Corner Points | Value of Z = 5x + 7y |
| C(10,0) | Z = 5(10) + 7(0) = 50 |
| P (2, 4) | Z = 5(2) + 7(4) = 10 + 28 = 38 (minimum) |
| B(0, 8) | Z = 5(0) + 7(8) = 0 + 56 = 56 |
From table, the minimum value of Z is 38.
As the feasible region is unbounded, therefore 38 may or may not be the minimum value of Z. For this, we draw a dotted graph of the inequality 5x + 7y < 38 and check whether the resulting half plane has point in common with the feasible region or not.
It can be seen that the feasible region has no common point with 5x + 7y < 38.
Hence, the minimum cost is ₹ 38, when x = 2 and y = 4.
Question 24.
A dietician wishes to mix two types of foods in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C. Food II contains 1 unit per kg of vitamin A and 2 units per kg of vitamin C. It costs ₹ 50 per kg to purchase food I and ₹ 70 per kg to purchase food II. Formulate the problem as a linear programming problem to minimise the cost of such mixture and find the minimise cost graphically. (Delhi 2011C)
Answer:
The given data can be put in the tabular form as follows

Suppose the diet contains x kg of food I and y kg of food II.
Then, the required LPP is minimise (Z) = 5x + 7y
Subject to constraints 2x + y ≥ 8, x + 2y ≥ 10 and x ≥ 0, y ≥ 0
| x | 0 | 4 |
| y | 8 | 0 |
So, it passes through the points (0, 8) and (4, 0). On putting (0,0) in the inequality 2x + y ≥ 8, we get
0 ≥ 8 [which is false]
So, the half plane is away from the origin.
Table for line x + 2y = 10 is
| x | 10 | 0 |
| y | 0 | 5 |
So, it passes through the points (10, 0) and (0, 5).
On putting (0,0) in the inequality x + 2y ≥ 10, we get
0 ≥ 10 [which is false]
So, the half plane is away front the origin.
Also, x, y ≥ 0, so the feasible region lies in the first quadrant.
On solving Eq. (i) and Eq. (ii), we get x = 2 and y = 4
So, these lines intersect at P (2, 4).
The graphical representation of the system of inequations given below

From the graph, the feasible region is BPC which is unbounded.
The values of Z at corner points are as follows:
| Corner Points | Value of Z = 5x + 7y |
| C(10,0) | Z = 5(10) + 7(0) = 50 |
| P (2, 4) | Z = 5(2) + 7(4) = 10 + 28 = 38 (minimum) |
| B(0, 8) | Z = 5(0) + 7(8) = 0 + 56 = 56 |
From table, the minimum value of Z is 38.
As the feasible region is unbounded, therefore 38 may or may not be the minimum value of Z. For this, we draw a dotted graph of the inequality 5x + 7y < 38 and check whether the resulting half plane has point in common with the feasible region or not.
It can be seen that the feasible region has no common point with 5x + 7y < 38.
Hence, the minimum cost is ₹ 38, when x = 2 and y = 4.
Hint: Suppose the diet contains x kg of food I and y kg of food II.
Then, the required LPP is minimise (Z) = 50x + 70y
Subject to contraints
2x+ y ≥ 8, x+ 2y ≥ 10 and x ≥ 0,y ≥ 0
[The minimum cost of the mixture is X 380, when the mixture contains 2 kg of food I and 4 kg of food II]
Question 25.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 h of machine time and 3 h of craftman’s time in its making, while a cricket bat takes
3 h of machine time and 1 h of craftman’s time. In a day, the factory has the availability of not more than 42 h of machine time and 24 h of craftman’s time. If the profits on a racket and a bat are ₹ 20 and ₹ 10 respectively, then find the number of tennis rackets and cricket bats that the factory must manufacture to earn the maximum profit. Make it as an LPP and solve it graphically. (Delhi 2011)
Answer:
The given data can be put in the tabular form as follows

Suppose the diet contains x kg of food I and y kg of food II.
Then, the required LPP is minimise (Z) = 5x + 7y
Subject to constraints 2x + y ≥ 8, x + 2y ≥ 10 and x ≥ 0, y ≥ 0
| x | 0 | 4 |
| y | 8 | 0 |
So, it passes through the points (0, 8) and (4, 0). On putting (0,0) in the inequality 2x + y ≥ 8, we get
0 ≥ 8 [which is false]
So, the half plane is away from the origin.
Table for line x + 2y = 10 is
| x | 10 | 0 |
| y | 0 | 5 |
So, it passes through the points (10, 0) and (0, 5).
On putting (0,0) in the inequality x + 2y ≥ 10, we get
0 ≥ 10 [which is false]
So, the half plane is away front the origin.
Also, x, y ≥ 0, so the feasible region lies in the first quadrant.
On solving Eq. (i) and Eq. (ii), we get x = 2 and y = 4
So, these lines intersect at P (2, 4).
The graphical representation of the system of inequations given below

From the graph, the feasible region is BPC which is unbounded.
The values of Z at corner points are as follows:
| Corner Points | Value of Z = 5x + 7y |
| C(10,0) | Z = 5(10) + 7(0) = 50 |
| P (2, 4) | Z = 5(2) + 7(4) = 10 + 28 = 38 (minimum) |
| B(0, 8) | Z = 5(0) + 7(8) = 0 + 56 = 56 |
From table, the minimum value of Z is 38.
As the feasible region is unbounded, therefore 38 may or may not be the minimum value of Z. For this, we draw a dotted graph of the inequality 5x + 7y < 38 and check whether the resulting half plane has point in common with the feasible region or not.
It can be seen that the feasible region has no common point with 5x + 7y < 38.
Hence, the minimum cost is ₹ 38, when x = 2 and y = 4.
Hint: Let x be the number of tennis rackets and y be the cricket bats produced in one day in the factory.
The required LPP is
maximise (Z) = 20x + 10y Subject to constraints
1.5x + 3y ≤ 42 3x + y ≤ 24
and x ≥ 0, y ≥ 0
[For maximum profit of X 200, 4 tennis rackets and 12 cricket bats must be produced.]
Question 26.
A merchant plans to sell two types of personal computers, a desktop model and a portable model that will cost ₹ 25000 and ₹ 40000, respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit, if he does not want to invest more than ₹ 70 lakh and his profit on the desktop model is ₹ 4500 and on the portable model is ₹ 5000. Make an LPP and solve it graphically. (All India 2011)
Answer:
Let the merchant stocks x desktop computers and y portable computers. Now, let us construct the following table according to given data.

Then, the required LPP is maximise,
Z = 4500x + 5000y ……..(i)
Subject to constraints,
x + y ≤ 250
25000x + 40000y ≤ 7000000
or 5x + 8y ≤ 1400 [dividing both sides by 5000]
and x ≥ 0, y ≥ 0 ……..(1)
On considering the inequalities as equations, we get
x + y = 250 ………..(ii)
and 5x + 8y = 1400 …………..(iii)
Table for line x + y = 250 is
| x | 0 | 250 |
| y | 250 | 0 |
So, this line passes through the points (0, 250) and (250, 0).
On putting (0,0) in the inequality x + y ≤ 250, we get
0 ≤ 250 [which is true]
So, the half plane is towards the origin. (1)
Table for line 5x + 8y = 1400 is
| x | 280 | 0 |
| y | 0 | 175 |
So, this line passes through the points (280, 0) and (0, 175).
On putting (0,0) in 5x + 8y ≤ 1400, we get
⇒ 0 ≤ 1400 [which is true]
So, the half plane is towards the origin.
Also, x, y ≥ 0, so the feasible region lies in the first quadrant.
On solving Eqs. (ii) and (iii), we get x = 200 and y = 50
So, the intersection point is E(200, 50).
The graphical representation of the system of inequations as given below
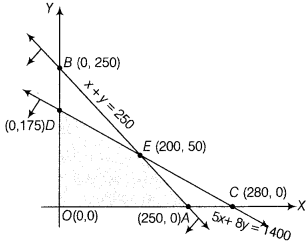
The comer points of the feasible region are O(0, 0), A (250, 0), E (200, 50) and D (0,175).
The values of Z at comer points are as follows:
| Corner Points | Value of z = 4500x + 5000 y |
| O(0,0) | Z = 4500(0) + 5000 (0) = 0 |
| A (250, 0) | Z = 4500(250) + 5000(0) = 1125000 |
| E (200, 50) | Z = 4500(200) + 5000(50) = 1150000 (maximum) |
| D (0,175) | Z = 4500(0) + 5000(175) = 875000 |
From the table, maximum value of Z is 1150000 at E (200,50).
Hence, the profit is maximum, i.e. ₹ 1150000, when 200 desktop computers and 50 portable computers are stocked.
Question 27.
A dealer deals in two items A and B. He has ₹ 15000 to invest and a space to store atmost 80 pieces. Item A costs him ₹ 300 and item B costs him ₹ 150. He can sell items A and B at profits of ₹ 40 and ₹ 25, respectively. Assuming that he can sell all that he buys, formulate the above as a linear programming problem for maximum profit and solve it graphically. (Delhi 2010C)
Answer:
He sell 20 items of type A and 60 items of type B. Maximum profit = ₹ 2300
Question 28.
A small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is atmost 24. It takes 1 h to make a ring and 30 min to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is ₹ 300 and that on a chain is ₹ 190, then find the number of rings and chains that should be manufactured per day so as to earn the maximum profit. Make it as an LPP and solve it graphically. (Delhi 2010)
Answer:
Let the firm manufactures x gold rings and y chains per day. The given data can be written in tabular form as follows:
| Items | Time taken | Profit (in₹) |
| Gold rings (x) | 1 h | 300 |
| Chains (y) | 30 min = 1/2 h | 190 |
| atmost 24 | atmost 16 h |
The required LPP is maximise,
Z = 300x + 190y
Subject to constraints
x + y ≤ 24
x + -y ≤ 16 or 2x + y ≤ 32
and x ≥ 0, y ≥ 0
On considering the inequalities as equations.
we get
x + y = 24 . ..(i)
and 2x + y = 32 ………….(ii)
Table for line x + y = 24 is
| x | 0 | 24 |
| y | 24 | 0 |
So, it passes through (0, 24) and (24, 0).
On putting (0, 0) in the inequality x + y ≤ 24, we get
0 ≤ 24 (which is true)
So, the half plane is towards the origin, (1)
Again, table for line 2x + y = 32 is
| x | 0 | 16 |
| y | 32 | 0 |
So, it passes through (0, 32) and (16, 0).
On putting (0, 0) in the inequality 2x + y ≤ 32 we get
0 ≤ 32 (which is true)
So, the half plane is towards the origin.
On solving Eq. (i) and Eq. (ii), we get x = 8 andy = 16
So, the point of intersection is B(8, 16)
The graphical representation of the system of inequations is given below
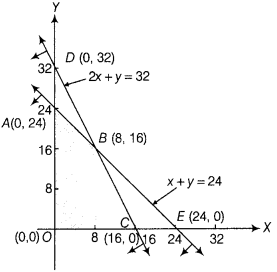
From the graph, OABCO is the feasible region which is bounded. The comer points are 0 (0, 0), A (0, 24), B (8, 16) and C (16, 0).
The values of z at corner points are as follows:
| Corner points | Value of Z = 300x + 190y |
| 0(0,0) | Z =300(0) + 190(0) = 0 |
| A( 0,24) | Z = 300(0) + 190(24) = 4560 |
| B(8,16) | Z= 300(8) + 190(16) = 5440 (maximum) |
| C(16,0) | Z = 300(16) + 190(0) = 4800 |
From the table, maximum value of z is 5440 at B(8, 16).
Hence, The manufacturer earns the maximum profit ₹ 5440, when he manufactures 8 gold rings and 16 chains per day.
Question 29.
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weight 1 kg and 1 \(\frac{1}{2}\) kg each, respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the hooks of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically. (All India 2010C)
Answer:
Let number of books of two types be x and y, respectively.
The required LPP is maximise Z = x + y
Subject to constraints
6x + 4y ≤ 96 or 3x + 2y ≤ 48
x + – y ≤ 21 or 2x + 3y ≤ 42 2
and x, y ≥ 0
On considering the inequalities as equations, we get
3x + 2y = 48 …(i)
2x + 3y = 42 …(ii)
Table for line 3x + 2y = 48 is
| x | 0 | 16 |
| y | 24 | 0 |
So, it passes through (0, 24) and (16, 0).
On putting (0, 0) in 3x + 2y ≤ 48, we get 0 + 0 ≤ 48
⇒ 0 ≤ 48 (which is true)
So, the half plane is towards the origin.
Table for 2x + 3y = 42 is
| x | 0 | 21 |
| y | 14 | 0 |
So, it passes through (0, 14) and (21, 0).
On putting (0, 0) in 2x+ 3y ≤ 42, we get 0 + 0 ≤ 42
⇒ 0 ≤ 42 (which is true)
So, the half plane is towards the origin.
On solving Eqs. (i) and (ii), we get x = 12 and y = 6
Thus, the point of intersection is (12 6).
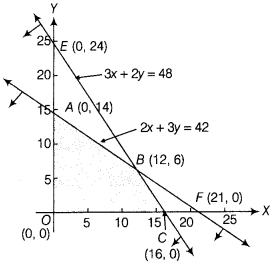
From the graph, OABCD is the feasible region which is bounded.
The corner points are 0(0, 0), A(0, 14) 5(12, 6) and C(16, 0).
The values of Z at comer points are as follows.
| Corner points | Value of Z = x + y |
| O(0, 0) | Z = 0 + 0 = 0 |
| A( 0, 14) | Z = 0 + 14 = 14 |
| B(12, 6) | Z = 12 + 6 = 18 (maximum) |
| C(16, 0) | Z = 16 + 0 = 16 |
From the table, the maximum value of Z is 18 at B(12, 6).
Hence, The maximum number of books is 18 and number of books of I type is 12 and books of II type is 6.
Question 30.
One kind of cake requires 300 g of flour and 15 g of fat, another kind of cake requires 150 g of flour and 30 g of fat. Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 g of fat, assuming that there is no shortage of other ingredients used in making the cakes. Make it as an LPP and solve it graphically. (All India 2010)
Answer:
The maximum number of cakes is 30 in which number of cake of first kind of cakes is 20 and second kind is 10.