Important Questions for Class 12 Chemistry Chapter 2 Solutions Class 12 Important Questions
Solutions Class 12 Important Questions Very Short Answer Type
Question 1.
Differentiate between molarity and molality of a solution. (All India 2010)
Answer:
The distinction between molarity and molality.
Molarity : It is the number of moles of solute dissolved in 1 litre of solution. It is temperature dependent.
M = \(\frac{\omega \times 1000}{\text { mol.mass } \times V}\)
Molality : It is the number of moles of solute dissolved in 1 kg of the solvent.
m = \(\frac{\omega \times 1000}{M_{2} \times W}\)
The relationship between molarity and molality is
m = \(\frac{\mathrm{M}}{d-\frac{\mathrm{MM}_{2}}{1000}}\)
When molality = molarity, we get,
1 = \(\frac{1}{d-\frac{\mathrm{MM}_{2}}{1000}}\) or d – \(\frac{\dot{\mathrm{MM}}_{2}}{1000}\) = 1
∴ d = \(1+\frac{\mathrm{MM}_{2}}{1000}\)
Molarity is temperature dependent while molarity is not.
For very dilute solution, the factor MM2/1000 can be neglected in comparison to 1.
Hence molality will be same to molarity when density d = 1.
Molality is independent of temperature, whereas molarity is a function of temperature because volume depends on temperature and mass does not.
Question 2.
What type of semiconductor is obtained when silicon is doped with arsenic? (Delhi 2010)
Answer:
n-type semiconductor.
Question 3.
What is meant by ‘reverse osmosis’? (All India 2011)
Answer:
If a pressure higher than the osmotic pressure is applied on the solution, the solvent will flow from the solution into the pure solvent through semipermeable membrane. This process is called reverse osmosis (R.O.).
Question 4.
What are isotonic solutions? (Delhi 2014)
Answer:
An isotonic solution is a kind of solution with the same salt concentration as blood and cells. Those solutions which are exerting same osmotic pressure under similar conditions (For example 0.9% NaCl solution by mass volume is Isotonic with human blood).
Question 5.
Some liquids on mixing form ‘azeotropes’. What are ‘azeotropes’? (Delhi 2014)
Answer:
The liquid mixture having a definite composition and boiling like a pure liquid without change in composition is called as azeotrope.
Question 6.
What type of intermolecular attractive interaction exists in the pair of methanol and acetone? (Delhi 2014)
Answer:
Solute-solvent dipolar interactions exist in the pair of methanol and acetone.
Question 7.
Out of BaCl2 and KCl, which one is more effective in causing coagulation of a negatively charged colloidal Sol? Give reason. (Delhi 2015)
Answer:
BaCl2 is more effective in causing coagulation because it has double +ve charge than K+.
Solutions Class 12 Important Questions Short Answer Type – I [SA-I]
Question 8.
Differentiate between molality and molarity of a solution. What is the effect of change in temperature of a solution on its molality and molarity? (Delhi 2009)
Answer:
Distinction between molarity and molality.
Molarity : It is the number of moles of solute dissolved in 1 litre of solution. It is temperature dependent.
M = \(\frac{\omega \times 1000}{\text { mol.mass } \times V}\)
Molality : It is the number of moles of solute dissolved in 1 kg of the solvent.
m = \(\frac{\omega \times 1000}{M_{2} \times W}\)
The relationship between molarity and molality is
m = \(\frac{\mathrm{M}}{d-\frac{\mathrm{MM}_{2}}{1000}}\)
When molality = molarity, we get,
1 = \(\frac{1}{d-\frac{\mathrm{MM}_{2}}{1000}}\) or d – \(\frac{\dot{\mathrm{MM}}_{2}}{1000}\) = 1
∴ d = \(1+\frac{\mathrm{MM}_{2}}{1000}\)
Molarity is temperature dependent while molarity is not.
For very dilute solution, the factor MM2/1000 can be neglected in comparison to 1.
Hence molality will be same to molarity when density d = 1.
Molality is independent of temperature, whereas molarity is a function of temperature because volume depends on temperature and mass does not.
Question 9.
Non-ideal solutions exhibit either positive or negative deviations from Raoult’s law. What are these deviations and why are they caused? Explain with one example for each type. (Delhi 2010)
Answer:
Non-ideal solutions exhibit Negative deviation from Raoult’s law : For any composition of the non-ideal solution, the partial vapour pressure of each component and total vapour pressure of the solution is less than expected from Raoult’s law. Such solutions show negative deviation.
Example : Mixture of CHCl3 and acetone.
Non-ideal solutions show positive deviations from Raoult’s law on mixing of two volatile components of the solution.
Example : Mixture of acetone and benzene solutions show positive deviation,
Question 10.
Define the terms, ‘osmosis’ and ‘osmotic pressure’.
What is the advantage of using osmotic pressure as compared to other colligative properties for the determination of molar masses of solutes in solutions? (All India 2010)
Answer:
Osmosis : The net spontaneous flow of the solvent molecules from the solvent to the solution or from a less concentrated solution to a more concentrated solution through a semipermeable membrane is called osmosis.
Osmotic pressure : The minimum excess pressure that has to be applied on the solution to prevent the entry of the solvent into the solution through the semipermeable membrane is called the osmotic pressure.
The osmotic pressure method has the advantage that it uses molarities instead of molalities and it can be measured at room temperature.
Question 11.
A 1.00 molal aqueous solution of trichloroacetic acid (CCl3COOH) is heated to its boiling point. The solution has the boiling point of 100.18°C. Determine the van’t Hoff factor for trichloroacetic acid. (Kb for water = 0.512 K kg mol-1) (Delhi 2012)
Answer:
As ΔTb= iKbm
(100.18 – 100) °C = i × 0.512 K kg mol-1 × 1 m
0.18 K = i × 0.512 K kg mol-1 × 1 m
∴ i = 0.3
Question 12.
Define the following terms :
(i) Mole fraction
(ii) Isotonic solutions
(iii) van’t Hoff factor
(iv) Ideal solution (Delhi 2012)
Answer:
(i) Mole fraction : Mole fraction is the ratio of number of moles of one component to the total number of moles in a mixture.
(ii) Isotonic solution : Two solutions having same osmotic pressure at a given temperature are called Isotonic solutions.
(iii) van’t Hoff factor : van’t Hoff factor is expressed as :
i = \(\frac{\text { normal molar mass }}{\text { abnormal molar mass }}\)
(iv) Ideal solution : The solution which obeys Raoult’s law under all conditions is known as an ideal solution.
Question 13.
Explain why aquatic species are more comfortable in cold water rather than in warm water. (Comptt. Delhi 2012)
Answer:
Aquatic species need dissolved oxygen for breathing. As solubility of gases decreases with increase of temperature, less oxygen is available in summer in the lake. Hence the aquatic species feel more comfortable in winter (low temperature) when the solubility of oxygen is higher.
Question 14.
State Raoult’s law. How is it formulated for solutions of non-volatile solutes? (Comptt. Delhi 2012)
Answer:
Raoult’s Law : Raoult’s Law states that “for a solution of volatile liquids, the partial vapour of each component in the solution is directly proportional to its mole fraction”.
Thus for component 1 : p1 = p10 X1
where [p10 is vapour pressure of pure component 1]
For component 2 : p2 = P20 X2
According to Dalton’s law of partial pressure
PTotal = P2 + P2 ⇒ PT = p1 0X1 + p2 0X2
⇒ PT = p1 0(1 – X2) + p2 0X2
⇒ PT = p1 0+ (p2 0 – p1 0)X2
Question 15.
State Henry’s law and mention two of its important applications. (Comptt. All India 2012)
Answer:
Henry’s law : Henry’s law states that “The partial pressure of the gas in vapour phase is proportional to the mole fraction of the gas in the solution “, Applications of Henry’s law :
- To increase the solubility of CO2 in soft drinks and soda water, the bottle is sealed under high pressure.
- To avoid a dangerous medical condition called bends, scuba divers use oxygen diluted with less soluble helium gas.
Question 16.
Why do gases nearly always tend to be less soluble in liquids as the temperature is raised? (Comptt. All India 2012)
Answer:
This is because the dissolution of gas in liquid is an exothermic process. The solubility should decrease with increase in temperature.
Question 17.
18 g of glucose, C6H12O6 (Molar mass – 180 g mol-1) is dissolved in 1 kg of water in a sauce pan. At what temperature will this solution boil? (Kb for water = 0.52 K kg mol-1, boiling point of pure water = 373.15 K) (Delhi 2013)
Answer:
We know that :
Elevation of boiling point ∆Tb
\(\frac{\mathrm{W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}}} \times \frac{100 \times \mathrm{K}_{\mathrm{b}}}{\mathrm{wt} . \text { of solvent }}\)
Given: WB = 18 g
MB = Formula of glucose is C6H12O6
= 6 × 12 + 12 + 6 × 16 = 180
Wt. of solvent = 1 kg or 1000 g,
Kb = 0.52 K kg mol-1
Hence, ∆Tb = \(\frac{18 g}{180} \times \frac{1000 \times 0.52}{1000 g}\) = 0.52 K
∴B.P of the solution = 373.15 + 0.052
= 373.202 K
Question 18.
An aqueous solution of sodium chloride freezes below 273 K. Explain the lowering in freezing points of water with the help of a suitable diagram. (Comptt. Delhi 2013)
Answer:
An aqueous solution of sodium chloride freezes below 273 K because vapour pressure g of the solution is g less than that of the pure solvent.
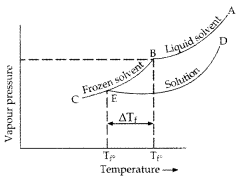
Question 19.
Derive expression for Raoult’s law when the solute is non-volatile. (Comptt. Delhi 2013)
Answer:
Raoult’s law : Raoult’s law states that “for a solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction”.
Thus for component 1 : p1 = p10X1
where [p10 is vapour pressure of pure component 1]
For component 2 : p2 = p20X2
ccording to Dalton’s law of partial pressure
PTotal = P1 + P2 ⇒ PT = p10X1 + p20X2
⇒ PT = p10( 1 – X2) + p20X2
∴ PT = p10 + (p20 – p10)X2
Question 20.
Calculate the mass of compound (molar mass = 256 g mol-1) to be dissolved in 75 g of benzene to lower its freezing point by 0.48 K (Kf = 5.12 K kg mol-1). (Delhi 2014)
Answer:
Given : ∆Tf = 0.48 K, W1 = 75g,
M2 = 256 g mol-1 W2 =?
Using formula, W2 = \(\frac{\mathrm{M}_{2} \times \mathrm{W}_{1} \times \Delta \mathrm{T}_{f}}{1000 \times \mathrm{K}_{f}}\)
= \(\frac{256 \times 75 \times 0.48}{1000 \times 5.12}\) = 1.8 g
Question 21.
Define an ideal solution and write one of its characteristics. (Delhi 2014)
Answer:
Those solutions which are obeying Raoult’s law are called ideal solutions. An ideal solution is a solution in which no volume change and no enthalpy change takes place on mixing the solute and the solvent in any proportion.
Characteristic of an ideal solution :
There will be no change in enthalpy ∆Hmix = 0,
∆Vmix = 0, ∆Pmix = 0
Question 22.
State Henry’s law. What is the effect of temperature on the solubility of a gas in a liquid? (Delhi 2014)
Answer:
Henry’s law : Henry’s law states that, “The solubility of a gas in a liquid at a particular temperature is directly proportional to the pressure of the gas in equilibrium with the liquid at that temperature.” Solubility of gas decreases with increase of temperature at the same pressure.
Question 23.
State Raoult’s law for the solution containing volatile components. What is the similarity between Raoult’s law and Henry’s law? (Delhi 2014)
Answer:
Raoult’s law : “In a solution, the vapour pressure of a component at a given temperature is equal to the mole fraction of that component in the solution multiplied by the vapour pressure of that component in pure state.”
Similarity between Raoult’s law and Henry’s law is that the partial pressure or vapour pressure of the volatile component (gas) is directly proportional to the mole fraction of that component in the solution.
Question 24.
How is the vapour pressure of a solvent affected when a non-volatile solute is dissolved in it? (Comptt. Delhi 2014)
Answer:
The vapour pressure of a solvent decreases when a non-volatile solute is dissolved in it because some solvent molecules are replaced by the molecules of solute.
Question 25.
Differentiate between molarity and molality of a solution. How can we change molality value of a solution into molarity value? (Comptt. Delhi 2014)
Answer:
The distinction between molarity and molality.
Molarity : It is the number of moles of solute dissolved in 1 litre of solution. It is temperature dependent.
M = \(\frac{\omega \times 1000}{\text { mol.mass } \times V}\)
Molality : It is the number of moles of solute dissolved in 1 kg of the solvent.
m = \(\frac{\omega \times 1000}{M_{2} \times W}\)
The relationship between molarity and molality is
m = \(\frac{\mathrm{M}}{d-\frac{\mathrm{MM}_{2}}{1000}}\)
When molality = molarity, we get,
1 = \(\frac{1}{d-\frac{\mathrm{MM}_{2}}{1000}}\) or d – \(\frac{\dot{\mathrm{MM}}_{2}}{1000}\) = 1
∴ d = \(1+\frac{\mathrm{MM}_{2}}{1000}\)
Molarity is temperature dependent while molarity is not.
For very dilute solution, the factor MM2/1000 can be neglected in comparison to 1.
Hence molality will be same to molarity when density d = 1.
Molality is independent of temperature, whereas molarity is a function of temperature because volume depends on temperature and mass does not.
Molarity (M) and Molality (m) relationship :
∵ Molarity is M moles of solute present in 1000 mL solution
If density of solution is d g mL-1, then
Mass of solution = 1000 d g
Mass of solute = MM2
(M2 is molar mass of solute)
∴ Mass of solvent = 1000 d – MM2 g
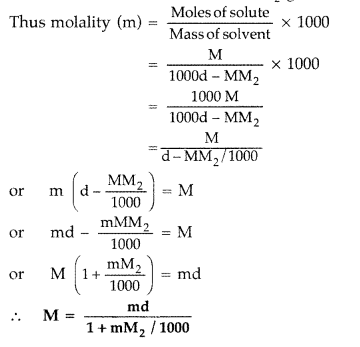
Question 26.
What is meant by positive deviations from Raoult’s law? Give an example. What is the sign of ∆mixH for positive deviation? (Delhi 2015)
Answer:
In positive deviations, the partial vapour pressure of each component A and B of a solution and the total pressure of the solution is higher than the vapour pressure calculated from Raoult’s law. For example, Water and Ethanol.
In case of positive deviations, ∆mixH > 0 (Positive)
Question 27.
Define azeotropes. What type of azeotrope is formed by positive deviation from Raoult’s law? Given an example. (Delhi) 2015
Answer:
Azeotropes : Liquid mixture which distills without change in compositions are called azeotropic mixtures or Azeotropes.
In positive deviations from Raoult’s law, minimum boiling point azeotropic mixture is formed. For example, 95% ethanol + 5% water.
Question 28.
(i) On mixing liquid X and liquid Y, volume of the resulting solution decreases. What type of deviation from Raoult’s law is shown by the resulting solution? What change in temperature would you observe after mixing liquids X and Y?
(ii) What happens when we place the blood cell in water (hypotonic solution)? Give reason. (All India 2015)
Answer:
(i) Volume decreases by mixing X and Y. It shows negative deviations from Raoult’s law. There will be rise in temperature. (∆Hmix < 0)
(ii) Blood cell will swell due to osmosis as water enters the cell.
Question 29.
Define osmotic pressure of a solution. How is the osmotic pressure related to the concentration of a solute in a solution? (Comptt. Delhi 2015)
Answer:
Osmotic pressure : It is the external pressure which is applied on the side solution which is sufficient to prevent the entry of the solvent through semi-permeable membrane.
According to the Boyle-van’t Hoff Law, the osmotic pressure (π) of a dilute solution is directly proportional to its molar concentration provided temperature is constant.
π ∝ C (At constant temperature)
π ∝ CT (At constant concentration)
π = CRT (R = Solution constant)
or, π = \(\frac{n}{v} \mathrm{RT}\)
Question 30.
Define the following terms :
(i) Mole fraction (x)
(ii) Molality of a solution (m) (Comptt. All India 2015)
Answer:
(i) Mole fraction : Mole fraction of a constituent is the fraction obtained by dividing number of moles of that constituent by the total number of moles of all the constituents present in the solution. It is denoted by ‘x’.
Example : x1 = \(\frac{\text { No. of moles of } x_{1}}{\text { Total no. of moles }}=\frac{n x_{1}}{n x_{1}+n x_{2}}\)
(ii) Molality of a solution : Molality of a solution is defined as the number of moles of the solute dissolved in 1000 grams (1 kg) of the solvent. It is denoted by’m’.
m = \(\frac{w \times 1000}{\mathrm{M} \times \mathrm{W}}\)
Where w = Weight of solute in grams
M = Molecular mass of solute
W = Weight of solvent in grams
Question 31.
(i) Gas (A) is more soluble in water than Gas
(B) at the same temperature. Which one of the two gases will have the higher value of KH (Henry’s constant) and why?
(ii) In non-ideal solution, what type of deviation shows the formation of maximum boiling azeotropes? (All India 2016)
Answer:
(i) Gas (B) will have higher value of KH (Henry’s constant) than Gas (A) at the same temperature because lesser the solubility of a gas in a given solvent, higher will be the value of KH for a gas.
KH = \(\frac{\text { Partial pressure of gas }}{\text { Mole fraction of gas in the solution }}\)
(ii) Negative deviations from Raoult’s law show the formation of maximum boiling azeotropes.
Question 32.
What is osmotic pressure? Why it is a colligative property? (Comptt Delhi 2016)
Answer:
The excess pressure applied on solution side to stop the process of osmosis. Because it depends upon the number of solute particles but not on their nature.
Question 33.
Define osmotic pressure. How is osmotic pressure related to the concentration of a solute in a solution? (Comptt. All India 2016)
Answer:
Osmotic pressure is the measure of excess pressure applied on solution side to stop the process of osmosis. Osmotic pressure is directly proportional to the conentration of solute in solution π ∝ c
Question 34.
Define the following terms: (Delhi 2017)
(i) Colligative properties
(ii) Molality (m)
Answer:
(i) Colligative properties. All those properties which depend on the number of solute particles irrespective of the nature of solute are called as colligative properties.
(ii) Molality (m). Number of moles of solute dissolved per kg of the solvent.
Question 35.
Define the following terms:
(i) Abnormal molar mass
(ii) van’t Hoff factor (i) (Delhi 2017)
Answer:
(i) Abnormal molar mass. If the molar mass calculated by using any of colligative properties tends to be different than theoretically expected molar mass, it is called abnormal molar mass.
(ii) van’t Hoff factor (i). Extent of dissociation or association or ratio of the observed colligative property to calculated colligative property.
i = \(\frac{\text { Observed colligative property }}{\text { Theoretical colligative property }}\)
Question 36.
Define the following terms:
(i) Ideal solution
(ii) Molarity (M) (Delhi 2017)
Answer:
(i) Ideal solution: The solution that obeys Raoults ’ Law over the entire range of concentration.
(ii) Molarity is the number of moles of solute dissolved per litre of solution or
M = \(\frac{w_{b} \times 1000}{\mathrm{M}_{b} \times \mathrm{Volume}(\mathrm{mL})}\)
Question 37.
Explain why on addition of 1 mol of glucose to 1 litre of water, the boiling point of water increases. (Comptt. Delhi 2017)
Answer:
(a) Glucose is a non-volatile solute, therefore, addition of glucose to water lowers the vapour pressure of water as a result of which boiling point of water increases.

i.e. nH2O = 27.78 mol
No. of moles of CO2
\(\frac{n \mathrm{CO}_{2}}{27.78}\) = 1.515 × 10-3
i.e. nCO2 = 42.08 × 10-3 moles = 0.042 mol
Solutions Class 12 Important Questions Short Answer Type – II [SA – II]
Question 38.
100 mg of a protein is dissolved in just enough water to make 10.0 mL of solution. If this solution has an osmotic pressure of 13.3 mm Hg at 25°C, what is the molar mass of the protein?
(R = 0.0821 L atm mol-1 K-1 and 760 mm Hg = 1 atm.) (Delhi & All India 2009)
Answer:
Given :
w = 100 mg = 0.100 = 0.1 g,
V = 10.0 mL = 0.01 L
π = 13.3 mm Hg = \(\frac{13.3}{760}\) atm,
T = 25°C = 25 + 273 = 298 K
R = 0.0821 L atm mol-1 K-1, M = ?
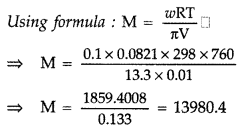
∴ Molar mass, M = 13980.4 g mol-1
Question 39.
Calculate the freezing point depression expected for 0.0711 m aqueous solution of Na2S04. If this solution actually freezes at – 0.320°C, what would be the value of Van’t Hoff factor? (Ky for water is 1.86°C mol-1) (Delhi 2009)
Answer:
Given : Molality, m = 0.0711 m
ΔTf = – 0.320°C Kf = 1.86°C f = ?
Substituting these values in the formula, we get
ΔTf = i Kf m or i = \(\frac{\Delta \mathrm{T}_{f}}{\mathrm{K}_{f} \mathrm{m}}\)
or i = \(\frac{-0.320}{1.86 \times 0.0711}=\frac{-0.320}{0.132246}\) = -2.4
Question 40.
A solution prepared by dissolving 1.25 g of oil of winter green (methyl salicylate) in 99.0 g of benzene has a boiling point of 80.31°C. Determine the molar mass of this compound. (B.P. of pure benzene = 80.10°C and Kb for benzene = 2.53°C kg mol-1) (Delhi 2010)
Answer:
Given : w2 = 1.25 g, w1 = 99 g
ΔTb = 80.31 – 80.10°C = 0.21°C
Kb = 2.53°C kg mol-1
According to the formula :
M2 = \(\frac{1000 \mathrm{K}_{b} w_{2}}{w_{1} \Delta \mathrm{T}_{b}}\)
Substituting these values in the formula, we get
M2 = \(\frac{1000 \times 2.53 \times 1.25}{99 \times 0.21}=\frac{3162.5}{20.79}\)
= 152 g mol-1
Question 41.
A solution of glycerol (C3H8O3; molar mass = 92 g mol-1) in water was prepared by dissolving some glycerol in 500 g of water. This solution has a boiling point of 100.42 °C. What mass of glycerol was dissolved to make this solution? Kb for water = 0.512 K kg mol-1. (Delhi 2010)
Answer:
Given : M2 = 92 g mol-1 w1 = 500g
ΔTb = 100.42°C – 100°C = 0.42°C
Kb = 0.512 K kg mol-1
Substituting above values in the formula
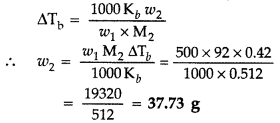
Question 42.
What mass of NaCl (molar mass = 58.5 g mol-1) must be dissolved in 65 g of water to lower the freezing point by 7.5°C? The freezing point depression constant, Kf, for water is 1.86 K kg mol-1. Assume van’t Hoff factor for NaCl is 1.87. (All India 2010)
Answer:
Given : M2 = 58.5 g mol-1 w1 = 65 g
ΔTf = 7.5 °C K, = 1.86 Kf kg mol-1 i = 1.87
Substituting these values in the formula

∴ Mass of NaCl to be dissolved, w2 = 8.199 g
Question 43.
What mass of ethylene glycol (molar mass = 62.0 g mol-1) must be added to 5.50 kg of water to lower the freezing point of water from 0° C to -10.0° C? (K, for water = 1.86 K kg mol-1)? (All India 2010)
Answer:
According to the formula :
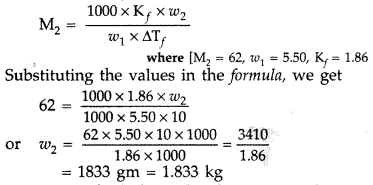
∴ Mass of ethylene glycol, w2 = 1.833 kg
Question 44.
15 g of an unknown molecular substance was dissolved in 450 g of water. The resulting solution freezes at -0.34° C. What is the molar mass of the substance?
(Kf for water = 1.86 K kg mol-1). (All India 2010)
Answer:
Given : w2 = 15 g, w1 = 450 g
ΔTf = -0.34°C CKf = 1.86 K kg mol-1 M2 =?
Substituting these values in the formula
M2 = \(\frac{1000 \times \mathrm{K}_{f} w_{2}}{w_{1} \Delta \mathrm{T}_{f}}\)
∴ M2 = \(\frac{1000 \times 1.86 \times 15}{450 \times 0.34}\)
or M2 = \(\frac{27900}{153}\) = 182.53
2 153
∴ Molar mass of the substance, M2 = 182.53 g
Question 45.
What mass of NaCl must be dissolved in 65.0 g of water to lower the freezing point of water by 7.5°C? The freezing point depression constant (Kf) for water is 1.86°C/m. Assume van’t Hoff factor for NaCl is 1.87. (Molar mass of NaCl = 58.5 g) (All India 2011)
Answer:
Given : M2 = 58.5 g mol-1 w1 = 65 g
ΔTf = 7.5 °C K, = 1.86 Kf kg mol-1 i = 1.87
Substituting these values in the formula

∴ Mass of NaCl to be dissolved, w2 = 8.199 g
Question 46.
Calculate the amount of KCl which must beadded to 1 kg of water so that the freezing point is depressed by 2K. (Kf for water = 1.86 K kg mol-1) (Delhi 2012)
Answer:
Since one mol of KCl gives 2 mole particles,
the value of i = 2, ΔTf, = 2K, Kf = 1.86 kg mol-1
Applying equation, ΔTf = iKf
m = \(\frac{\Delta \mathrm{T}_{f}}{i \mathrm{K}_{f}}=\frac{2}{2 \times 1.86}=\frac{1}{1.86}\) = 0.54 mol kg-1
∴ 0.54 mole of KC1 should be added to 1 kg of water
Molar mass of KCl = 39 + 35.5 = 74.5 g
∴ Amount of KCl = 0.54 × 74.5 g = 40.05 g
Question 47.
A solution of glycerol (C3H8O3) in water was prepared by dissolving some glycerol in 500 g of water. This solution has a boiling point of 100.42 °C while pure water boils at 100 °C. What mass of glycerol was dissolved to make the solution? (Delhi 2012)
Answer:
ΔTb = (100.42 – 100)°C = 0.42°C or 0.42 K
ΔTb = Kb m
0.42 = 0.512 × \(\frac{\mathrm{W}_{2}}{92} \times \frac{1000}{500}\)
W2 = \(\frac{0.42 \times 92 \times 500}{0.512 \times 1000}=\frac{4.83}{0.128}\) = 37.7 g
where W2 is the weight of the solute.
Question 48.
15.0 g of an unknown molecular material was dissolved in 450 g of water. The resulting solution was found to freeze at -0.34 °C. What is the molar mass of this material? (Kf for water = 1.86 K kg mol-1) (Delhi 2012)
Answer:
As ΔTf = Kf × m
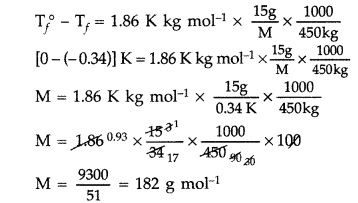
∴ Molar mass of material, M = 182 g mol-1
Question 49.
A solution containing 30 g of non-volatile solute exactly in 90 g of water has a vapour pressure of 2.8 kPa at 298 K. Further 18 g of water is added to this solution. The new vapour pressure becomes 2.9 kPa at 298 K. Calculate
(i) the molecular mass of solute and
(ii) vapour pressure of water at 298 K. (Comptt. Delhi 2012)
Answer:
For a very dilute solution
Since \(\frac{\mathrm{P}^{\circ}-\mathrm{P}}{\mathrm{P}^{\circ}}=\frac{\mathrm{W}_{\mathrm{B}} \times \mathrm{M}_{\mathrm{A}}}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}}\)
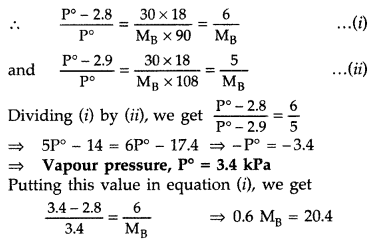
∴ Molecular mass, MB = 34 g/mol
Question 50.
If N2 gas is bubbled through water at 293K, how many millimoles of N2 gas would dissolve in 1 litre of water? Assume that N2 exerts a partial pressure of 0.987 bar. Given that Henry’s law constant for N2 at 293K is 76.48 k bar. (Comptt. All India 2012)
Answer:

∴ In millimoles 7.16 × 10-4 × 1000 = 0.716 m mol
Question 51.
The partial pressure of ethane over a saturated solution containing 6.56 × 10-2 g of ethane is 1 bar. If the solution contains 5.0 × 10-2 g of ethane, then what will be the partial pressure of the gas? (Comptt. All India 2012)
Answer:
Applying the Henry’s law, m = KH × p
In first case, 6.56 × 10-2 = KH × 1
KH = 6.56 × 10-2 g bar-1
Putting the value of KH in the second case, we get
5 × 10-2 g = 6.56 × 10-2 g bar-1 × p
∴ p = \(\frac{5 \times 10^{-2}}{6.56 \times 10^{-2} \mathrm{g} \mathrm{bar}}\) = 0.762 bar
Question 52.
Determine the osmotic pressure of a solution prepared by dissolving 2.5 × 10-2 g of K2SO4 in 2L of water at 25° C, assuming that it is completely dissociated.
(R = 0.0821 L atm K-1 mol-1, Molar mass of K2SO4 = 174 g mol-1). (Delhi 2013)
Answer:
We know, π = iCRT ⇒ π = \(\frac{i \mathrm{n} \mathrm{RT}}{\mathrm{V}}\)
⇒ π = i × \(\frac{w}{M} \times \frac{1}{V} R T\)
Given : w = 2.5 × 10-2 g = 0.025 g
V = 2L, T = 25°C = 298 K
M = K2SO4 = 2 × 39 + 32 + 4 × 16 = 174 g mol-1
K2SO4 = dissociates completely as K2SO4 → 2K+ + SO42-
∴ Ions produced = 3 i.e., i = 3
Hence, π = 3 × \(\frac{0.025 \mathrm{g}}{174 \mathrm{g} \mathrm{mol}^{-1}} \times \frac{1}{2 \mathrm{L}}\) × 0.0821 L atm K-1 mol-1 × 298 K
∴ π = 527 × 10-3 atm
Question 53.
The partial pressure of ethane over a saturated solution containing 6.56 × 10-2 g of ethane is 1 bar. If the solution were to contain 5.0 × 10-2 g of ethane, then what will be the partial pressure of the gas? (Comptt. Delhi 2013)
Answer:
Applying the Henry’s law, m = KH × p
In first case, 6.56 × 10-2 = KH × 1
KH = 6.56 × 10-2 g bar-1
Putting the value of KH in the second case, we get
5 × 10-2 g = 6.56 × 10-2 g bar-1 × p
∴ p = \(\frac{5 \times 10^{-2}}{6.56 \times 10^{-2} \mathrm{g} \mathrm{bar}}\) = 0.762 bar
Question 54.
Some ethylene glycol, HOCH2CH2OH, is added to your car’s cooling system along with 5 kg of water. If the freezing point of a water-glycol solution is -15.0°C, what is the boiling point of the solution?
(Kb = 0.52 K kg mol-1 and Kf = 1.86 K kg mol-1 for water) (Comptt. Delhi 2014)
Answer:
Given : ΔTf = 0 – (-15) = +15° C, w1 = 5 kg = 5000 g
Kf = 1.86 K kg mol-1 Kb = 0.52 K kg mol-1
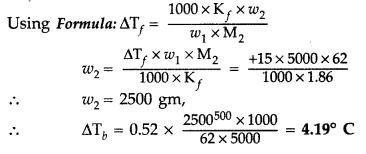
Question 55.
3.9 g of benzoic acid dissolved in 49 g of benzene shows a depression in freezing point of 1.62 K. Calculate the Van’t Hoff factor and predict the nature of solute (associated or dissociated).
(Given : Molar mass of benzoic acid = 122 g mol-1, Kf for benzene = 4.9 K kg mol-1) (Delhi 2015)
Answer:
ΔTf = iKf × m
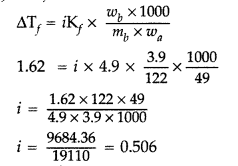
As i < 1, therefore solute gets associated
Question 56.
A solution is prepared by dissolving 10 g of non-volatile solute in 200 g of water. It has a vapour pressure of 31.84 mm Hg at 308 K. Calculate the molar mass of the solute.
(Vapour pressure of pure water at 308 K = 32 mm Hg) (All India 2015)
Answer:

Question 57.
45 g of ethylene glycol (C2H6O2) is mixed with 600 g of water. Calculate
(i) the freezing point depression and
(ii) the freezing point of the solution
(Given : Kf of water = 1.86 K kg mol-1) (Comptt. Delhi 2015)
Answer:
(i) Given : w = 45 g, W = 600 g,
Kf = 1.86 K kg mol-1, Δ Tf = ?
Using the formula for freezing point depression,
ΔTf = \(\mathrm{K}_{f} \frac{w \times 1000}{m \times \mathrm{W}}\)
m of ethylene glycol (C2H6O2)
= 2 × 12 + 6 × 1 + 2 × 16
= 24 + 6 + 32 = 62 g mol-1
Substituting above values in formula,
ΔTf = \(\frac{1.86 \mathrm{K} \mathrm{kg} \mathrm{mol}^{-1} \times 45 \mathrm{g} \times 1000 \mathrm{g} \mathrm{kg}^{-1}}{62 \mathrm{g} \mathrm{mol}^{-1} \times 600 \mathrm{g}}\)
= \(\frac{837}{372}\)
∴ ΔTf = 2.25 K
(ii) ΔTf = Tf0 – Tf
Where, Tf0 = Freezing point of pure water
⇒ Tf = 273.15 – 2.25 K
∴ Tf = 270.9 K (Freezing point of the solution)
Question 58.
A 5 percent solution (by mass) of cane-sugar (M.W. 342) is isotonic with 0.877% solution of substance X. Find the molecular weight of X. (Comptt. All India 2015)
Answer:
Given : W (mass) of cane-sugar = 5% means 5 g
Molar mass of cane-sugar (M) = 342 g mol-1
Mass of isotonic substance X
= 0.877% means 0.877 g
Molar mass of X = ?
Using formula,
\(\frac{\mathrm{W}_{\text { canesugar }}}{\mathrm{M}_{\text { cane sugar }}}=\frac{\mathrm{W}_{\mathrm{X}}}{\mathrm{M}_{\mathrm{X}}} \quad \Rightarrow \frac{5 \mathrm{g}}{342 \mathrm{g} \mathrm{mol}^{-1}}=\frac{0.877 \mathrm{g}}{\mathrm{M}_{\mathrm{X}}}\)
or Mx = \(\frac{0.877 \mathrm{g} \times 342 \mathrm{g} \mathrm{mol}^{-1}}{5 \mathrm{g}} \Rightarrow \frac{299.934 \mathrm{g} \mathrm{mol}^{-1}}{5 \mathrm{g}}\)
∴ Mx = 59.9 ≈ 60 g mol-1
Question 59.
Calculate the boiling point of solution when 4 g of MgSO4 (M =120 g mol-1) was dissolved in 100 g of water, assuming MgSO4 undergoes complete ionization.
(Kb for water = 0.52 K kg mol-1) (All India 2016)
Answer:
Since MgS04 is an ionic compound, so undergoes complete ionisation in the following way:
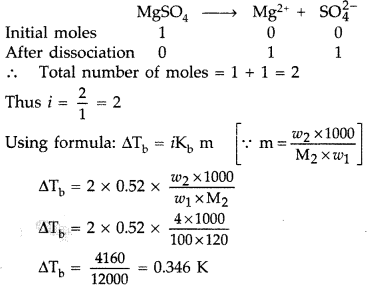
Boiling point of water = 373.15 K
Tb= Tb° + ΔTb = 373.15 K + 0.346 K
= 373.496 K
Question 60.
Calculate the mass of a non-volatile solute (molecular mass 40) which should be dissolved in 114 g octane to reduce the vapour pressure to 80%. (Comptt. Delhi 2016)
Answer:
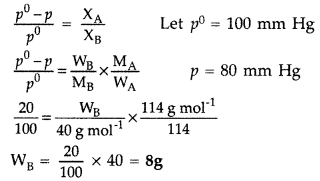
Question 61.
An aqueous solution of 2 percent non-volatile solute exerts a pressure of 1.004 bar at the boiling point of the solvent. What is the molecular mass of the solute?
[Vapour pressure of water = 1.013 bar] (Comptt. All India 2016)
Answer:
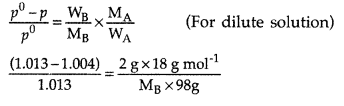
MB = \(\frac{2 \times 18 \times 1.013}{0.009 \times 98}\) g mol-1
MB = 41.3 g mol-1
Question 62.
A 10% solution (by mass) of sucrose in water has freezing point of 269.15 K. Calculate the freezing point of 10% glucose in water, if freezing point of pure water is 273.15 K.
Given: (Molar mass of sucrose = 342 g mol-1) (Molar mass of glucose = 180 g mol-1) (Delhi 2017)
Answer:
Molality (m) = \(\frac{w \times 100}{\mathrm{W} \times \mathrm{M}}\)
Given:
Molar mass of sucrose
= C12H22O11 = 12 × 12 + 22 + 11 × 16 = 342
10% solution (by mass) of sucrose in water means 10 g of sucrose is present in (100 – 10)
= 90 g of water
10% solution of sucrose means, w = 10 g
Mass of water, W = 90 g
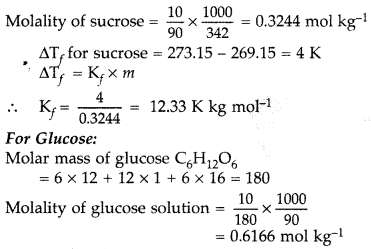
∴ ΔTf for glucose = 12.33 × 0.6166 = 7.60 K (approx.)
∴ Freezing point of 10% glucose solution
= (273.15 – 7.60) K = 265.55 K
Question 63.
The vapour pressure of pure liquids A and B at 400 K are 450 and 700 mmHg respectively. Find out the composition of liquid mixture if total vapour pressure at this temperature is 600 mmHg. (Comptt. Delhi 2017)
Answer:


Solutions Class 12 Important Questions Long Answer Type (LA)
Question 64.
(a) Define the following terms :
(i) Mole fraction (ii) Van’t Hoff factor
(b) 100 mg of a protein is dissolved in enough water to make 10.0 mL of a solution. If this solution has an osmotic pressure of 13.3 mm Hg at 25°C, what is the molar mass of protein?
(R = 0.0821 L atm mol-1 K-1 and 760 mm Hg = 1 atm) (All India 2009)
Answer:
(a) (i) Mole fraction : Mole fraction of a constituent is the fraction obtained by dividing number of moles of that constituent by the total number of moles of all the constituents present in the solution. It is denoted by ‘x’.
Example :
xi = \(\frac{\text { No. of moles of } x_{1}}{\text { Total no. of moles }}=\frac{n x_{1}}{n x_{1}+n x_{2}}\)
(ii) Van’t Hoff factor : It is the ratio of the observed colligative property to the theoretical value. It is denoted by ‘i’.
i = \(\frac{\text { Observed colligative property }}{\text { Theoretical colligative property }}\)
(b) Given :
w = 100 mg = 0.100 = 0.1 g,
V = 10.0 mL = 0.01 L
π = 13.3 mm Hg = \(\frac{13.3}{760}\) atm,
T = 25°C = 25 + 273 = 298 K
R = 0.0821 L atm mol-1 K-1, M = ?
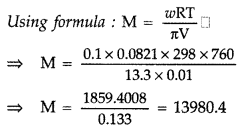
∴ Molar mass, M = 13980.4 g mol-1
Question 65.
(a) What is meant by :
(t) Colligative properties (ii) Molality of a solution (b) What concentration of nitrogen should be present in a glass of water at room temperature? Assume a temperature of 25° C, a total pressure of 1 atmosphere and mole fraction of nitrogen in air of 0.78.
[KH for nitrogen = 8.42 × 10-7 M/mm Hg] (All India 2009)
Answer:
(a) (i) Colligative properties : Those properties of ideal solutions which depend only on the number of particles of the solute dissolved in a definite amount of the solvent and do not depend on the nature of solute are called colligative properties.
(ii) Molality of a solution : Molality of a solution is defined as the number of moles of the solute dissolved in 1000 grams (1 kg) of the solvent. It is denoted by’m’.
m = \(\frac{w \times 1000}{\mathrm{M} \times \mathrm{W}}\)
Where
‘w = Weight of solute in grams
M = Molecular mass of solute
W = Weight of solvent in grams
(b) Given :
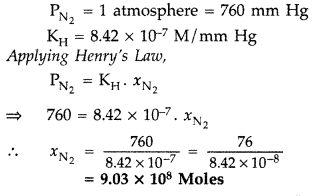
Question 66.
(a) Differentiate between molarity and molality for a solution.
How does a change in temperature influence their values?
(b) Calculate the freezing point of an acqueous solution containing 10.50 g of MgBr2 in 200 g of water. (Molar mass of MgBr2 = 184 g) (Kf for water = 1.86 K kg mol-1) (Delhi 2011)
Answer:
(a) Distinction between molarity and molality.
Molarity : It is the number of moles of solute dissolved in 1 litre of solution. It is temperature dependent.
M = \(\frac{\omega \times 1000}{\text { mol.mass } \times V}\)
Molality : It is the number of moles of solute dissolved in 1 kg of the solvent.
m = \(\frac{\omega \times 1000}{M_{2} \times W}\)
The relationship between molarity and molality is
m = \(\frac{\mathrm{M}}{d-\frac{\mathrm{MM}_{2}}{1000}}\)
When molality = molarity, we get,
1 = \(\frac{1}{d-\frac{\mathrm{MM}_{2}}{1000}}\) or d – \(\frac{\dot{\mathrm{MM}}_{2}}{1000}\) = 1
∴ d = \(1+\frac{\mathrm{MM}_{2}}{1000}\)
Molarity is temperature dependent while molarity is not.
For very dilute solution, the factor MM2/1000 can be neglected in comparison to 1.
Hence molality will be same to molarity when density d = 1.
Molality is independent of temperature, whereas molarity is a function of temperature because volume depends on temperature and mass does not.
(b) Since MgBr2 is an ionic compound, so undergoes complete dissociation

Question 67.
(a) Define the terms osmosis and osmotic pressure. Is the osmotic pressure of a solution a colligative property? Explain.
(b) Calculate the boiling point of a solution prepared by adding 15.00 g of NaCl to 250.0 g of water.
(Kb for water = 0.512 K kg mol-1, Molar mass of NaCl = 58.44 g) (Delhi 2011)
Answer:
Osmosis : The net spontaneous flow of the solvent molecules from the solvent to the solution or from a less concentrated solution to a more concentrated solution through a semipermeable membrane is called osmosis.
Osmotic pressure : The minimum excess pressure that has to be applied on the solution to prevent the entry of the solvent into the solution through the semipermeable membrane is called the osmotic pressure.
The osmotic pressure method has the advantage that it uses molarities instead of molalities and it can be measured at room temperature.
(b) Since NaCl is an ionic compound so undergoes complete dissociation.
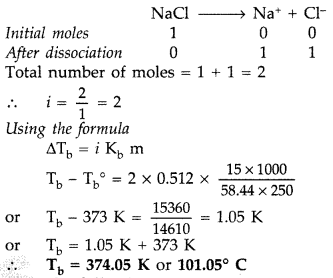
Question 68.
(a) State the following :
(i) Henry’s law about partial pressure of a gas in a mixture.
(ii) Raoult’s law in its general form in reference to solutions.
(b) A solution prepared by dissolving 8.95 mg of a gene fragment in 35.0 mL of water has an osmotic pressure of 0.335 torr at 25°C. Assuming the gene fragment is a non-electrolyte, determine its molar mass. (All India 2011)
Answer:
(a) (i) Henry’s law : “The solubility of a gas in a liquid at a particular temperature is directly proportional to the pressure of the gas in equilibrium with the liquid at that temperature.”
Applications of Henry’s law :
• In the production of carbonated beverages which are prepared under high pressure.
• Deep sea divers depend upon compressed air for their oxygen supply.
(ii) Raoult’s law : For a solution of volatile liquids the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.
P = P°x
Non-ideal solution shows positive and negative deviations from Raoult’s law.
Positive deviation from Raoult’s law : The total vapour pressure for any solution is greater than the corresponding ideal solution of same composition. Such behaviour is called positive deviation.
Example : Mixtures of ethanol + cyclohexane
Mixture of acetone + carbon disulphide
Negative deviation from Raoult’s law: When the total vapour pressure will be less than corresponding vapour pressure, then it is termed as negative deviation.
Example : Chloroform + Benzene Chloroform + Diethylether
(b) Given : w2 = 8.95 mg = 8.95 × 10-3 g
V = 35 mLπ = 0.335 torr
T = 25°C = 298 K M2 = ?
Substituting all the values in the given formula
π = CRT
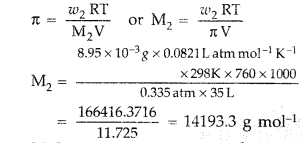
∴ Molar mass, M2 = 1.42 × 104 g mol-1
Question 69.
(a) Differentiate between molarity and molality in a solution. What is the effect of temperature change on molarity and molality in a solution?
(b) What would be the molar mass of a compound if 6.21 g of it dissolved in 24.0 g of chloroform form a solution that has a boiling point of 68.04°C. The boiling point of pure chloroform is 61.7°C and the boiling point elevation constant, Kb for chloroform is 3.63°C/m. (Delhi 2011)
Answer:
(a) Distinction between molarity and molality.
Molarity : It is the number of moles of solute dissolved in 1 litre of solution. It is temperature dependent.
M = \(\frac{\omega \times 1000}{\text { mol.mass } \times V}\)
Molality : It is the number of moles of solute dissolved in 1 kg of the solvent.
m = \(\frac{\omega \times 1000}{M_{2} \times W}\)
The relationship between molarity and molality is
m = \(\frac{\mathrm{M}}{d-\frac{\mathrm{MM}_{2}}{1000}}\)
When molality = molarity, we get,
1 = \(\frac{1}{d-\frac{\mathrm{MM}_{2}}{1000}}\) or d – \(\frac{\dot{\mathrm{MM}}_{2}}{1000}\) = 1
∴ d = \(1+\frac{\mathrm{MM}_{2}}{1000}\)
Molarity is temperature dependent while molarity is not.
For very dilute solution, the factor MM2/1000 can be neglected in comparison to 1.
Hence molality will be same to molarity when density d = 1.
Molality is independent of temperature, whereas molarity is a function of temperature because volume depends on temperature and mass does not.
(b) Given : w2 = 6.21 g, w1 = 24 g
ΔTb = Tb – T°b = 68.04 – 61.7 °C
= 6.34 °C
Kb = 3.63 °C/m, M2 = ?
Substituting all these values in formula given below
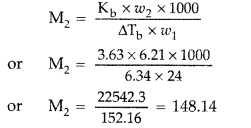
∴ Molar mass of the compound, M = 148.14 g mol-1
Question 70.
(a) Define the following terms :
(i) Mole fraction (ii) Ideal solution
(b) 15.0 g of an unknown molecular material is dissolved in 450 g of water. The resulting solution freezes at – 0.34°C. What is the molar mass of the material?
(Kf for water = 1.86 K kg mol-1) (All India 2011)
Answer:
(a) (i) Mole fraction : Mole fraction is the ratio of number of moles of one component to the total number of moles in a mixture.
XA = \(\frac{n_{\mathrm{A}}}{n_{\mathrm{A}}+n_{\mathrm{B}}}\), XB = \(\frac{n_{\mathrm{B}}}{n_{\mathrm{A}}+n_{\mathrm{B}}}\)
(ii) Ideal solution : The solution which obeys Raoult’s law under all conditions is known as an ideal solution.
(b) ΔTf = Kf m
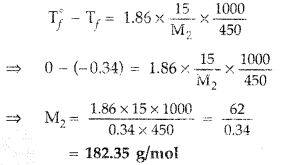
Question 71.
(a) Explain the following :
(i) Henry’s law about dissolution of a gas in a liquid
(ii) Boiling point elevation constant for a solvent
(b) A solution of glycerol (C3H8O3) in water was prepared by dissolving some glycerol in 500 g of water. This solution has a boiling point of 100.42°C. What mass of glycerol was dissolved to make this solution?
(Kb for water = 0.512 K kg mol-1) (All India 2011)
Answer:
(a) (i) Henry’s law : The law states “that at a constant temperature, the solubility of a gas in a liquid is directly proportional to the pressure of the gas.”
(ii) Boiling point elevation constant for a solvent or molal elevation constant may be defined as the elevation in the boiling point when the molality of the solution is unity.
(b) ΔTb = (100.42 – 100)°C = 0.42°C or 0.42 K
ΔTb = Kb m
0.42 = 0.512 × \(\frac{\mathrm{W}_{2}}{92} \times \frac{1000}{500}\)
W2 = \(\frac{0.42 \times 92 \times 500}{0.512 \times 1000}=\frac{4.83}{0.128}\) = 37.7 g
where W2 is the weight of the solute.
Question 72.
(a) State Raoult’s law for a solution containing volatile components. How does Raoult’s law become a special case of Henry’s law?
(b) 1.00 g of a non-electrolyte solute dissolved in 50 g of benzene lowered the freezing point of benzene by 0.40 K. Find the molar mass of the solute. (Kf for benzene = 5.12 K kg mol-1) (All India 2013)
Answer:
Raoult’s law: For a solution of volatile liquids the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.
P = P°x
Non-ideal solution shows positive and negative deviations from Raoult’s law.
(i) Positive deviation from Raoult’s law : The total vapour pressure for any solution is greater than the corresponding ideal solution of same composition. Such behaviour is called positive deviation.
Example : Mixtures of ethanol + cyclohexane Mixture of acetone + carbon disulphide
(ii) Negative deviation from Raoult’s law : When the total vapour pressure will be less than corresponding vapour pressure, then it is termed as negative deviation.
Example : Chloroform + Benzene
Chloroform + Diethvlether
According to Raoult’s law PA = PA° × xA
According to Henry’s law PA = KH × xA
Thus both laws are identical and differ by their proportionality constants.
(b) We know that M2 = \(\frac{1000 \mathrm{K}_{f} w_{2}}{w_{1} \mathrm{DT}_{f}}\)
Given : w2 = 1.0 g, w1 = 50 g, ΔTf = 0.40
Kf = 5.12 K kg mol-1
∴ M2 = \(\frac{1000 g \mathrm{kg}^{-1} \times 5.12 \mathrm{kg} \mathrm{mol}^{-1} \times 1.0 \mathrm{g}}{50 \mathrm{g} \times 0.40 \mathrm{K}}\)
= 256 g mol-1
Question 73.
(a) Define the following terms :
(i) Ideal solution (ii) Azeotrope
(iii) Osmotic pressure
(b) A solution of glucose (C6H12O6) in water is labelled as 10% by weight. What would be the molality of the solution?
(Molar mass of glucose = 180 g mol-1) (All India 2013)
Answer:
(a) (i) Ideal solution : An ideal solution is that which obeys Raoult’s law and in which the intermolecular interactions between the different components are of same magnitude as that is found in pure components.
(ii) Azeotrope : It is a type of liquid mixture having a definite composition and boiling like a pure liquid, (distills without change in compositions)
(iii) Osmotic pressure : The minimum excess pressure that has to be applied on the solution to prevent the entry of the solvent into the solution through semi- permeable membrane is called osmotic pressure.
(b) 10% of glucose means 10 g of solute in 100 g of solvent
∴ Mass of solute = 10 g
Mass of solvent = 100 – 10 = 90 g
= \(\frac{90}{1000}\) kg
Molar mass of glucose = 180 g mol-1
No. of moles of \(\frac{10}{100}=\frac{1}{18}\) mole
∴ Molarity = \(\frac{\text { No. of moles of solute }}{\text { mass of solvent in } \mathrm{kg}}\)
= \(\frac{1}{18} \times \frac{1000}{90}=\frac{100}{162}\)
= 0.67 mol kg-1 = 0.6 m
Question 74.
(a) The vapour pressures of benzene and toluene at 293 K are 75 mm Hg and 22 mm Hg respectively. 23.4 g of benzene and 64.4 g of toluene are mixed. If the two form an ideal solution, calculate the mole fraction of benzene in the vapour phase assuming that the vapour pressures are in equilibrium with the liquid mixture at this temperature.
(b) What is meant by +ve and -ve deviations from Raoult’s law and how is the sign of AH solution related to +ve and -ve deviations from Raoult’s law?
(Comptt. All India 2013)
Answer:
(a) Given : Mass of benzene = 23.4 g
Molar mass of benzene = C6H6
= 12 × 6 + 6 = 78g mol-1
Mass of toluene = 64.4 g
Molar mass of toluene = C6H5CH3
= 12 × 7 + 8 = 92g mol-1
Moles of Benzene = \(\frac{23.4}{78}\) = 0.3 mole
Moles of toluene = \(\frac{64.4}{92}\) = 0.7 mole
Vapour pressure of benzene, PB = xB × P
= 0.3 × 75 = 22.5 mm
Vapour pressure of toluene, PT = xT × P
= 0.7 × 22 = 15.4 mm
Total vapour pressure = 22.5 + 15.4
= 37.9 mm
∴ Mole fraction of benzene = \(\frac{22.5}{37.9}\) = 0.59
(b) +ve and -ve deviations :
Raoult’s law: For a solution of volatile liquids the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.
P = P°x
Non-ideal solution shows positive and negative deviations from Raoult’s law.
(i) Positive deviation from Raoult’s law : The total vapour pressure for any solution is greater than the corresponding ideal solution of same composition. Such behaviour is called positive deviation.
Example : Mixtures of ethanol + cyclohexane Mixture of acetone + carbon disulphide
(ii) Negative deviation from Raoult’s law : When the total vapour pressure will be less than corresponding vapour pressure, then it is termed as negative deviation.
Example : Chloroform + Benzene
Chloroform + Diethvlether
According to Raoult’s law PA = PA° × xA
According to Henry’s law PA = KH × xA
Thus both laws are identical and differ by their proportionality constants.
If it is higher, the solution exhibits positive deviation and if it is low, it exhibits negative deviation from Raoult’s law.
For positive deviation ΔmixH = +ve
For negative devation ΔmixH = -ve
Question 75.
(a) A 5% solution (by mass) of cane-sugar in water has freezing point of 271 K. Calculate the freezing point of 5% solution (by mass) of glucose in water if the freezing point of pure water is 273.15 K.
[Molecular masses : Glucose C6H12O6 : 180 amu; Cane-sugar C12H22C11 : 342 amu]
State Henry’s law and mention two of its important applications. (Comptt. All India 2013)
Answer:
Molality of sugar solution
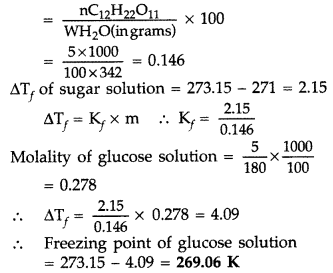
(b) Henry’s law : Henry’s law states that, “The solubility of a gas in a liquid at a particular temperature is directly proportional to the pressure of the gas in equilibrium with the liquid at that temperature.”
Solubility of gas decreases with increase of temperature at the same pressure.
Question 76.
(a) Define the following terms :
(i) Molarity
(ii) Molal elevation constant (Kb)
(b) A solution containing 15 g urea (molar mass = 60 g mol-1) per litre of solution in water has the same osmotic pressure (isotonic) as a solution of glucose (molar mass = 180 g mol-1) in water. Calculate the mass of glucose present in one litre of its solution. (All India 2014)
Answer:
(a) (i) Molarity is the number of moles of solute dissolved in one litre of solution.
(ii) Molal elevation constant may be defined as the elevation in boiling point when the molality of solution is unity i.e. 1 mole of solute is dissolved in 1 kg of the solvent.
(b) For urea, concentration = \(\frac{15}{60}\) moles/lt.
For glucose, concentration = \(\frac{w}{180}\) moles/lt.
∵ Solutions are isotonic
∴ \(\frac{w}{180}=\frac{15}{60}\) ∴ w = \(\frac{15 \times 180}{60}\) = 45 g
Question 77.
(a) What type of deviation is shown by a mixture of ethanol and acetone? Give reason.
(b) A solution of glucose (molar mass = 180 g mol-1) in water is labelled as 10% (by mass). What would be the molality and molarity of the solution?
(Density of solution = 1.2 g mL-1) (All India 2014)
Answer:
(a) Since acetone is nearly non-polar in nature and ethanol is polar in nature therefore, no interaction occurs between acetone and ethanol, the number of molecules increases, which shows positive deviation.
(b) 10% glucose means 10 g in 100 g solution or, 90 g of water = 0.090 kg of water
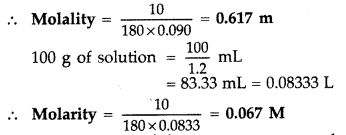
Question 78.
(a) What is van’t Hoff factor? What types of values can it have if in forming the solution, the solute molecules undergo
(i) Dissociation? (ii) Association?
(b) How many mL of a 0.1 M HCl solution are required to react completely with 1 g of a mixture of Na2CO3 and NaHCO3 containing equimolar amounts of both?
(Molar mass : Na2CO3 = 106 g, NaHCO3 = 84 g) (Comptt. All India 2014)
Answer:
(a) (i) Van’t Hoff factor : It is defined as the ratio of the experimental value of the colligative property to the calculated value of the colligative property .
i = \(\frac{\text { Experimental value }}{\text { Calculated value }}\)
If there is dissociation of the solute in the solution, the Van’t Hoff factor T’ will be greater than one i.e. i > 1.
It means observed colligative property will be greater than calculated value.
(ii) Association : If there is association of solute in the solution, the Van’t Hoff factor ‘f’ will be less than one i.e. i < 1. Thus, observed colligative property will be less than the calculated value.
(b) Calculation of no. of moles of the components in the mixture
Suppose Na2CO3 in the mixture = x g
∴ NaHCO3 in the mixture = (1 – x) g
Molar mass of Na2CO3 = 106 g mol-1
Molar mass of NaHCO3 = 84 g mol-1
∴ Moles of Na2CO3 = \(\frac{x}{106}\)
and Moles of NaHCO3 = \(\frac{1-x}{84}\)
As the mixture contains equimolar amounts of both
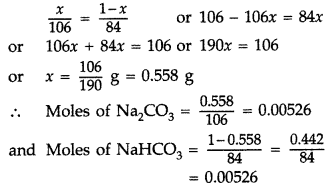
No. of moles of HCl required
Na2CO3 + 2HCl → 2NaCl + H2O + CO2
NaHCO3 + HCl → NaCl + H2O + CO2
1 mole of Na2CO3 requires HC1 = 2 moles
∴ 0.00526 mole of Na2CO3 requires HCl
= 0.00526 × 2 = 0.01052 mole
Similarly, 0.00526 mole of NaHCO3 requires
HCl = 0.00526
∴ Total HCl required = 0.01052 + 0.00526 = 0.01578 moles
Thus 0.1 mole of HCl is present in 1000 mL of HCl
∴ 0.01578 mole of HCl present in 1000 mL
= \(\frac{1000}{0.1}\) × 0.01578 = 157.8 mL
Question 79.
(a) Define
(i) Mole fraction (Hi) Raoult’s law
(b) Assuming complete dissociation, calculate the expected freezing point of a solution prepared by dissolving 6.00 g of Glauber’s salt, Na2SO4.10H2O in 0.100 kg of water. (Kf for water = 1.86 K kg mol-1, Atomic masses : Na = 23, S = 32, O = 16, H = 1) (Comptt. All India 2014)
Answer:
(a) (i) Mole fraction : Mole fraction is the ratio of number of moles of one component to the total number of moles in a mixture.
(ii) Molality of a solution : Molality of a solution is defined as the number of moles of the solute dissolved in 1000 grams (1 kg) of the solvent. It is denoted by’m’.
m = \(\frac{w \times 1000}{\mathrm{M} \times \mathrm{W}}\)
Where
‘w = Weight of solute in grams
M = Molecular mass of solute
W = Weight of solvent in grams
(ii) Raoult’s law : For a solution of volatile liquids the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution.
P = P°x
Non-ideal solution shows positive and negative deviations from Raoult’s law.
Positive deviation from Raoult’s law : The total vapour pressure for any solution is greater than the corresponding ideal solution of same composition. Such behaviour is called positive deviation.
Example : Mixtures of ethanol + cyclohexane
Mixture of acetone + carbon disulphide
Negative deviation from Raoult’s law: When the total vapour pressure will be less than corresponding vapour pressure, then it is termed as negative deviation.
Example : Chloroform + Benzene Chloroform + Diethylether
(b) Since Na2SO4.10H2O is an ionic compound, so undergoes complete dissociation.
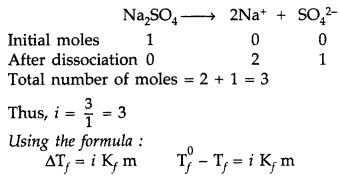
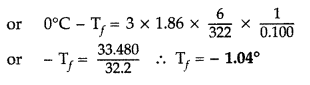
Question 80.
Calculate the freezing point of solution when 1.9 g of MgCl2 (M = 95 g mol-1) was dissolved in 50 g of water, assuming MgCl2 undergoes complete ionization.
(Kf for water = 1.86 K kg mol-1)
(b) (i) Out of 1 M glucose and 2 M glucose, which one has a higher boiling point and why?
(ii) What happens when the external pressure applied becomes more than the osmotic pressure of solution? (Delhi 2016)
Answer:
(a) Since MgCl2 is an ionic compound, so it undergoes complete dissociation.
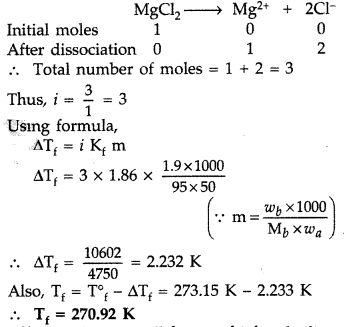
(b)
(i) 2M glucose will have a higher boiling point than 1M glucose because elevation in boiling point is a colligative property which depends upon the number of particles in the solution which is more in the case of 2M glucose solution.
(ii) When the external pressure applied becomes more than the osmotic pressure of the solution, then the solvent will flow from the solution into the pure solvent through the semi-permeable membrane. The process is called reverse osmosis (RO).
Question 81.
(a) When 2.56 g of sulphur was dissolved in 100 g of CS2, the freezing point lowered by 0.383 K. Calculate the formula of sulphur (Sx).
(Kf for CS2 = 3.83 K kg mol-1, Atomic mass of Sulphur = 32 g mol-1)
(b) Blood cells are isotonic with 0.9% sodium chloride solution. What happens if we place blood cells in a solution containing
(i) 1.2% sodium chloride solution?
(ii) 0.4% sodium chloride solution?(Delhi 2016)
Answer:
(a) Given: wb = 2.56 g wa = 100 g = 0.1 kg
ΔTf = 0.383 K Kf= 3.83 K kg mol-1
Atomic mass of sulphur = 32 g mol-1
Mb = ?
Using formula,
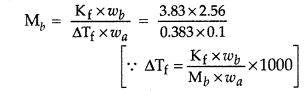
∴ Mb = 256 g mol-1
Hence the no. of atoms present in one molecule of sulphur = \(\frac{256}{32}\) = 8
∴ the formula is S8.
(b) (i) If RBCs are placed in contact with 1.2% NaCl solution, then the osmotic pressure of 1.2% NaCl becomes higher than that of RBCs due to which water present inside the cells moves into the NaCl solution which results in shrinkage of RBCs.
(ii) Reverse process will take place if RBCs are kept in contact with 0.4% NaCl solution which has less osmotic pressure ’ due to which water moves into RBCs and they will swell.
Question 82.
(a) A 10% solution (by mass) of sucrose in water has a freezing point of 269.15 K. Calculate the freezing point of 10% glucose in water if the freezing point of pure water is 273.15 K.
Given: (Molar mass of sucrose = 342 g mol-1) (Molar mass of glucose = 180 g mol-1)
(b) Define the following terms:
(i) Molality (m)
(ii) Abnormal molar mass (All India 2017)
Answer:
(a) Molality (m) = \(\frac{w \times 100}{\mathrm{W} \times \mathrm{M}}\)
Given:
Molar mass of sucrose
= C12H22O11 = 12 × 12 + 22 + 11 × 16 = 342
10% solution (by mass) of sucrose in water means 10 g of sucrose is present in (100 – 10)
= 90 g of water
10% solution of sucrose means, w = 10 g
Mass of water, W = 90 g
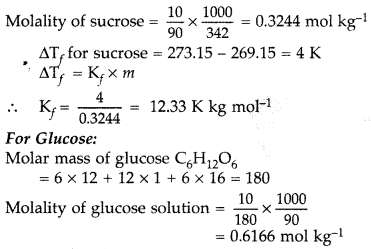
∴ ΔTf for glucose = 12.33 × 0.6166 = 7.60 K (approx.)
∴ Freezing point of 10% glucose solution
= (273.15 – 7.60) K = 265.55 K
(b) (i) Molality (m): Number of moles of solute dissolved per kg of the solvent.
(ii) Abnormal molar mass: If the molar mass calculated by using any of the colligative properties comes to be different than theoretically expected molar mass.
Question 83.
(a) 30 g of urea (M = 60 g mol-1) is dissolved in 846 g of water. Calculate the vapour pressure of water for this solution if vapour pressure of pure water at 298 K is 23.8 mm Hg.
(b) Write two differences between ideal solutions and non-ideal solutions. (All India 2017)
Answer:
(a) Given:
Urea (W) = 30 g; H2O (W) = 846 g

(b)
| Ideal Solution | Non- Ideal solution |
| (i) They obey Raoult’s law over the enitre range of concentration. | (i) They do no obey Raoult’s law over the entire range of concentration |
| (ii) Neither the heat is evolved or absorbed during dissolution | (ii) Heat is evolved or absorbed during dissolution |
| (iii) Δmix H = 0 Δmix V = 0 |
(iii) Δmix H is not equal to 0. ΔmixV is not equal to 0. |
Question 84.
(a) Explain why on addition of 1 mol glucose to 1 litre water the boiling point of water increases.
(b) Henry’s law constant for CO2 in water is 1.67 × 108 Pa at 298 K. Calculate the number of moles of CO2 in 500 ml of soda water when packed under 2.53 × 105 Pa at the same temperature. (Comptt. All India 2017)
Answer:
(a) Glucose is a non-volatile solute, therefore, addition of glucose to water lowers the vapour pressure of water as a result of which boiling point of water increases.

i.e. nH2O = 27.78 mol
No. of moles of CO2
\(\frac{n \mathrm{CO}_{2}}{27.78}\) = 1.515 × 10-3
i.e. nCO2 = 42.08 × 10-3 moles = 0.042 mol
Question 85.
(a) Define the following terms :
(i) Ideal solution (ii) Osmotic pressure
(b) Calculate the boiling point elevation for a solution prepared by adding 10 g CaCl2 to 200 g of water, assuming that CaCl2 is completely dissociated.
(Kb) for water = 0.512 K kg mol-1; Molar mass of CaCl2 = 111 g mol-1) (Comptt. All India 2017)
Answer:
(a) (i) Ideal solution : The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions.
(ii) The minimum excess pressure that has to be applied on the solution to prevent the entry of the solvent into the solution through the semipermeable membrane is called the osmotic pressure.
