Important Questions for Class 10 Maths Chapter 7 Coordinate Geometry
Coordinate Geometry Class 10 Important Questions Very Short Answer (1 Mark)
Question 1.
Find the distance of the point (-3, 4) from the x-axis. (2012OD)
Solution:
B(-3, 0), A (-3, 4)
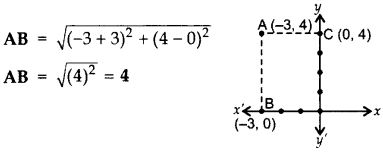
Question 2.
If the points A(x, 2), B(-3, 4) and C(7, -5) are collinear, then find the value of x. (2014D)
Solution:
When the points are collinear,
x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) = 0
x(-4 – (-5)) + (-3)(-5 – 2) + 7(2 – (-4)) = 0
x(1) + 21 + 42 = 0
x + 63 = 0 ∴ x = -63
Question 3.
For what value of k will k + 9, 2k – 1 and 2k + 7 are the consecutive terms of an A.P.? (2016OD)
Solution:
As we know, a2 – a1 = a3 – a2
2k – 1 – (k + 9) = 2k + 7 – (2k – 1)
2k – 1 – k – 9 = 2k + 7 – 2k + 1
k – 10 = 8 ∴ k = 8 + 10 = 18
Question 4.
In which quadrant the point P that divides the line segment joining the points A(2, -5) and B(5,2) in the ratio 2 : 3 lies? (2011D)
Solution:

Question 5.
ABCD is a rectangle whose three vertices are B(4, 0), C(4, 3) and D(0, 3). Calculate the length of one of its diagonals. (2014OD)
Solution:
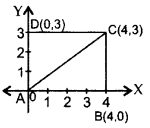
AB = 4 units
BC = 3 units
AC2 = AB2 + BC2 …[Pythagoras’ theorem
= (4)2 + (3)2
= 16 + 9 = 25
∴ AC = 5 cm
Question 6.
In the figure, calculate the area of triagle ABC (in sq. units). (2013D)
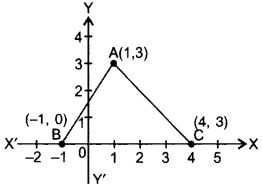
Solution:
Area of ∆ABC = \(\frac{1}{2}\) × base × corr, altitude
= \(\frac{1}{2}\) × 5 × 3 = 7.5 sq.units
Coordinate Geometry Class 10 Important Questions Short Answer-I (2 Marks)
Question 7.
Find a relation between x and y such that the point P(x, y) is equidistant from the points A (2, 5) and B (-3, 7). (2011D)
Solution:
Let P (x, y) be equidistant from the points A (2, 5) and B (-3, 7).
∴ AP = BP …[Given
AP2 = BP2 …[Squaring both sides
(x – 2)2 + (y – 5)2 = (x + 3)2 + (y – 7)2
⇒ x2 – 4x + 4 + y2 – 10y + 25
⇒ x2 + 6x + 9 + y2 – 14y + 49
⇒ -4x – 10y – 6x + 14y = 9 +49 – 4 – 25
⇒ -10x + 4y = 29
∴ 10x + 29 = 4y is the required relation.
Question 8.
Find the relation between x and y if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear. (2015OD)
Solution: When points are collinear,
∴ Area of ∆ABC = 0
= (x1 (y2 – y3) + x2(y3 – y1) + x3(y1 – y2)) = 0
= x (7 – 5) – 5 (5 – y) -4 (y – 7) = 0
= 2x – 25 + 5y – 4y + 28 = 0
∴ 2x + y + 3 = 0 is the required relation.
Question 9.
Find the ratio in which the point P\(\left(\frac{3}{4}, \frac{5}{12}\right)\) divides the line segment joining the points A\(\left(\frac{1}{2}, \frac{3}{2}\right)\) and B(2, -5). (2015D)
Solution:
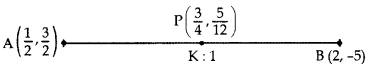
Let P divide AB in the ratio of K : 1.
Applying section formula,
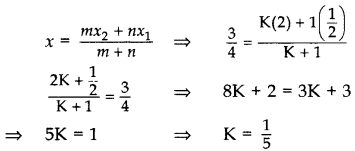
∴ Required ratio = 1 : 5
Question 10.
Find the ratio in which y-axis divides the line segment joining the points A(5, -6), and B(-1, -4). Also find the coordinates of the point of division. (2016D)
Solution:
![]()
Let AC: CB = m : n = k : 1.
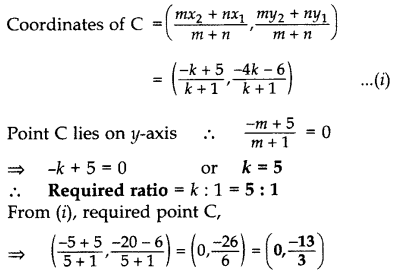
Question 11.
Let P and Q be the points of trisection of the line segment joining the points A (2, -2) and B (-7, 4) such that P is nearer to A. Find the coordinates of P and Question (2016D)
Solution:
![]()
AP : PB = 1 : 2
Coordinates of P are:

Question 12.
Three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of fourth vertex. (2011D)
Solution:
Let A(-1, 0), B(3, 1), C(2, 2) and D(x, y) be the vertices of a parallelogram ABCD taken in order. Since, the diagonals of a parallelogram bisect each other.
∴ Coordinates of the mid-point of AC = Coordinates of the mid-point of BD
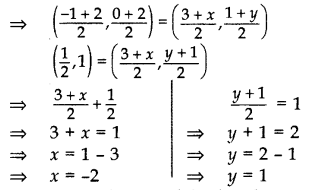
Hence, coordinates of the fourth vertex, D(-2, 1).
Question 13.
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, -5) is the mid point of PQ, then find the coordinates of P and Question (2017OD)
Solution:
![]()
We know that at y-axis coordinates of points are (0, y) and at x-axis (x, 0).
Let P(0, b) and Q(a,0)
Mid point of PQ = (2, -5) …[Given
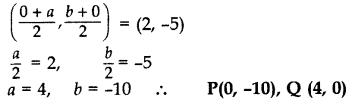
Question 14.
Determine the ratio in which the line 3x + y – 9 = 0 divides the segment joining the points (1, 3) and (2, 7). (2011D)
Solution:
Suppose the line 3x + y – 9 = 0 divides the line segment joining A(1, 3) and B(2, 7) in the ratio k : 1 at point C.
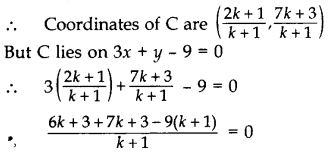
⇒ 6k + 3 + 7k + 3 – 9k – 9 = 0
⇒ 4k – 3 = 0
⇒ 4k = 3 ∴ k = 8
So, the required ratio is 3 : 4 internally.
Question 15.
If A(4, 3), B(-1, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y. (2015OD)
Solution:
We have A(4, 3), B(-1, y) and C(3, 4). In right angled triangle ABC,
(BC)2 = (AB)2 + (AC)…. [Pythagoras theorem
⇒ (-1 – 3)2 + (y – 4)2 = (4 + 1)2 + (3 – y)2 + (4 – 3)2 + (3 – 4)2 …(using distance formula
⇒ (-4)2 + (y2 – 8y + 16)
⇒ (5)2 + (9 – 6y + y2) + (1)2 + (-1)2
⇒ y2 – 8y + 32 = y2 – 6y + 36 = 0
⇒ -8y + 6y + 32 – 36
⇒ -2y – 4 = 0 ⇒ -2y = 4
∴ y = -2
Question 16.
If A(5, 2), B(2, -2) and C(-2, t) are the vertices of a right angled triangle with ∠B = 90°, then find the value of t. (2015D)
Solution:
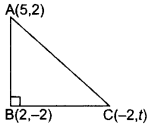
ABC is a right angled triangle,
∴ AC2 = BC2 + AB2 …(i)… (Pythagoras theorem
Using distance formula,
AB2 = (5 – 2)2 + (2 + 2)
= 25
BC2 = (2 + 2)2 + (t + 2)2
= 16 + (t + 2)2
AC2 = (5 + 2)2 + (2 – t)2
= 49 + (2 – t)2
Putting values of AB2, AC2 and BC2 in equation (i), we get
49 + (2 – t)2 = 16 + (t + 2)2 + 25
∴ 49 + (2 – t)2 = 41 + (t + 2)2
⇒ (t + 2)2 – (2 – t)2 = 8
⇒ (t2 + 4 + 4t – 4 – t2 + 4t) = 8
8t = 8 ⇒ t = 1
Question 17.
Find the area of the triangle whose vertices are (1, 2), (3, 7) and (5, 3).(2011OD)
Solution:
Area of Triangle
= \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3 (y1 – y2)]
= \(\frac{1}{2}\)(1(7 – 3) + 3(3 – 2) + 5(2 – 7)]
= \(\frac{1}{2}\)[4 + 3 + 5(-5)] = \(\frac{18}{2}\) = 9 sq. unit
Question 18.
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at B. Find the value of p. (2015OD)
Solution:
Similar to Question 16, Page 102.
Question 19.
Prove that the points (7, 10), (-2, 5) and (3, -4) are the vertices of an isosceles right triangle. (2013D)
Solution:
Let A (7, 10), B(-2, 5), C(3, -4) be the vertices of a triangle.
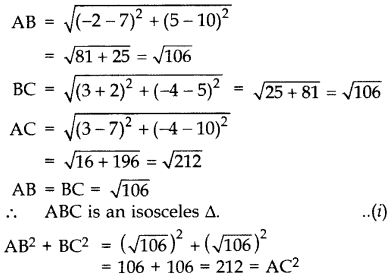
… [By converse of Pythagoras theorem
∆ABC is an isosceles right angled triangle. …(ii) From (i) & (ii), Points A, B, C are the vertices of an isosceles right triangle.
Coordinate Geometry Class 10 Important Questions Short Answer-II (3 Marks)
Question 20.
Find that value(s) of x for which the distance between the points P(x, 4) and Q(9, 10) is 10 units. (2011D)
Solution:
PQ = 10 …Given
PQ2 = 102 = 100 … [Squaring both sides
(9 – x)2 + (10 – 4)2 = 100…(using distance formula
(9 – x)2 + 36 = 100
(9 – x)2 = 100 – 36 = 64
(9 – x) = ± 8 …[Taking square-root on both sides
9 – x = 8 or 9 – x = -8
9 – 8 = x or 9+ 8 = x
x = 1 or x = 17
Question 21.
Find the value of y for which the distance between the points A (3,-1) and B (11, y) is 10 units. (2011OD)
Solution:
AB = 10 units … [Given
AB2 = 102 = 100 … [Squaring both sides
(11 – 3)2 + (y + 1)2 = 100
82 + (y + 1)2 = 100
(y + 1)2 = 100 – 64 = 36
y + 1 = ±6 … [Taking square-root on both sides
y = -1 ± 6 ∴ y = -7 or 5
Question 22.
The point A(3, y) is equidistant from the points P(6, 5) and Q(0, -3). Find the value of y. (2011D)
Solution:
PA = QA …[Given
PA2 = QA2 … [Squaring both sides
(3 – 6)2 + (y – 5)2 = (3 – 0)2 + (y + 3)2
9 + (y – 5)2 = 9 + (y + 3)2
(y – 5)2 = (y + 3)2
y – 5 = ±(y + 3) … [Taking sq. root of both sides
y – 5 = y + 3 y – 5 = -y – 3
0 = 8 … which is not possible ∴ y = 1
Question 23.
If a point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), then find the value of p. (2012D)
Solution:
Similar to Question 24, Page 103.
Question 24.
Find the value of k, if the point P(2, 4) is equidistant from the points A(5, k) and B(k, 7). (2012OD)
Solution:
Let P(2, 4), A(5, k) and B(k, 7).
![]()
PA = PB …[Given
PA2 = PB2 … [Squaring both sides
(5 – 2)2 + (k – 4)2 = (k – 2)2 + (7 – 4)2
9 + (k – 4)2 – (k – 2)2 = 9
(k – 4 + k – 2) (k – 4 – k + 2) = 0
(2k – 6)(-2) = 0
2k – 6 = 0
2k = 6 ∴ k = \(\frac{6}{2}\) = 3
Question 25.
If the point P(k – 1, 2) is equidistant from the points A(3, k) and B(k, 5), find the values of k. (2014OD)
Solution:
PA = PB …Given
PA2 = PB2 … [Squaring both sides
⇒ (k – 1 – 3)2 + (2 – k)2 = (k – 1 – k)2 + (2 – 5)2
⇒ (k – 4)2 + (2 – k)2 = (-1)2 + (-3)2
k2 – 8k + 16 + 4 + k2 – 4k = 1 + 9
2k2 – 12k + 20 – 10 = 0
2k2 – 12k + 10 = 0
⇒ k2 – 6k + 5 = 0 …[Dividing by
⇒ k2 – 5k – k + 5 = 0
⇒ k(k – 5) – 1(k – 5) = 0
⇒ (k – 5) (k – 1) = 0
⇒ k – 5 = 0 or k – 1 = 0
∴ k = 5 or k = 1
Question 26.
Find a point P on the y-axis which is equidistant from the points A(4, 8) and B(-6, 6). Also find the distance AP. (2014OD)
Solution:
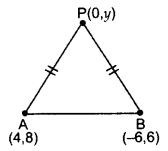
Let P(0, y) be any point on y-axis.
PA = PB … [Given
PA2 = PB2 … [Squaring both sides
⇒ (4 – 0)2 + (8 – y)2 = (-6 – 0)2 + (6 – y)2
16 + 64 – 16y + y2 = 36 + 36 + y2 – 12y
80 – 72 = -12y + 16y
8 = 4y ⇒ y = 2
∴ Point P (0, 2).
Now, AP = \(\sqrt{(4-0)^{2}+(8-2)^{2}}\)
∴ Distance, AP = \(\sqrt{16+36}=\sqrt{52}\)
Question 27.
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b), prove that bx = ay. (2016OD)
Solution:
PA = PB … [Given
PA2 = PB2 … [Squaring both sides
⇒ [(a + b) – x]2 + [(b a) – y)2 = [(a – b) – x]2 + [(a + b) – y]2
⇒ (a + b)2 + x2 – 2(a + b)x + (b – a)2 + y2 – 2(b – a)y = (a – b)2 + x2 – 2(a – b)x + (a + b)2 + y2 – 2(a + b)y …[∵ (a – b) 2 = (b – a)2
⇒ -2(a + b)x + 2(a – b)x = -2(a + b)y + 2(b – a)y
⇒ 2x(-a – b + a – b) = 2y(-a – b + b – a)
⇒ -2bx = – 2ay
⇒ bx = ay (Hence proved)
Question 28.
If the point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also find the length of AB. (2014D)
Solution:
AB = AC … [Given
∴ AB2 = AC2 …[Squaring both sides
⇒ (3 – 0)2 + (p – 2)2= (p – 0)2 + (5 – 2)2
⇒ 9+ (p – 2)2 = p2 + 9
⇒ p2 – 4p + 4 – p2 = 0
⇒ -4p + 4 = 0
⇒ -4p = -4 ⇒ p = 1
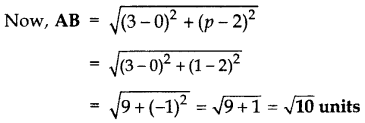
Question 29.
If the point P(2, 2) is equidistant from the points A(-2, k) and B(-2k, -3), find k. Also find the length of AP. (2014D)
Solution:
PA = PB … [Given
PA2 = PB2 … [Squaring both sides
⇒ (2 + 2)2 + (2 – k)2 = (2 + 2k)2 + (2 + 3)2
16 + 4 + k2 – 4k = 4 + 4k2 + 8k + 25
4k2 + 8k + 25 – k2 + 4k – 16 = 0
3k2 + 12k + 9 = 0
⇒ k2 + 4k + 3 = 0 …[Dividing by 3
k2 + 3k + k + 3 = 0
k(k + 3) + 10k + 3) = 0
(k + 1) (k + 3) = 0
k + 1 = 0 ork + 3 = 0
i k = -1 or k = -3
AP = \(\sqrt{(2+2)^{2}+(2-k)^{2}}\)
When k = -1
AP =\(\sqrt{16+(2+1)^{2}}=\sqrt{16+9}\) = 5 units
When k = -3
AP = \(\sqrt{16+(2+3)^{2}}=\sqrt{16+25}\) units
Question 30.
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right angled isosceles triangle. (2016OD)
Solution:
Similar to Question 19, Page 102.
Question 31.
Prove that the points A(0, -1), B(-2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD. (2013D)
Solution:

Opposite sides BC = AD = \(4 \sqrt{5}\)
Diag. AC = BD = 10
∴ ABCD is a rectangle.
… [∵ Opp. sides are equal & diagonals are also equal
Question 32.
Show that the points (-2, 3), (8, 3) and (6, 7) are the vertices of a right triangle. (2013D)
Solution:
Let A (-2, 3), B(8,3), C(6, 7).
(AB)2 = (8 + 2)2 + (3 – 3)2 = 102 + 02 = 100
(BC)2 = (6 – 8)2 + (7 – 3)2 = (-2)2 + 42 = 20
(AC)2 = (6 + 2)2 + (7 – 3)2 = 82 + 42 = 80
Now, (BC)2 + (AC)2= 20 + 80 = 100 = (AB)2
…[By converse of Pythagoras’ theorem
Therefore, Points A, B, C are the vertices of a right triangle.
Question 33.
Prove that the points A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1) are the vertices of a square ABCD. (2013OD)
Solution:
Given: A(2, 3), B(-2, 2), C(-1, -2), D(3, -1)
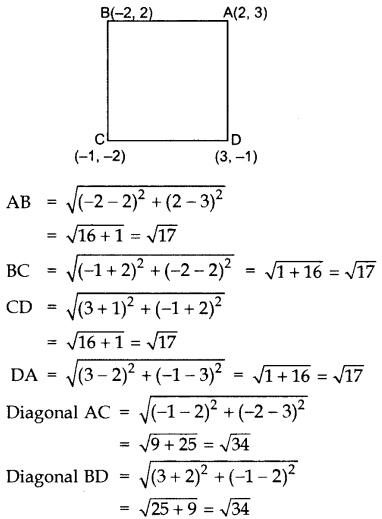
AB = BC = CD = DA …[All four sides are equal
AC = BD …[Also diagonals are equal
∴ ABCD is a Square.
Question 34.
Prove that the points A(2, -1), B(3, 4), C(-2, 3) and D(-3, -2) are the vertices of a rhombus ABCD. Is ABCD a square? (2013OD)
Solution:
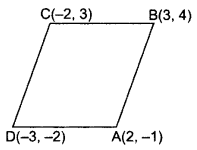
Given: A(2, -1), B(3, 4), C(-2,3), D(-3, -2)

Question 35.
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) & D(2,6), are equal and bisect each other. (2014OD)
Solution:
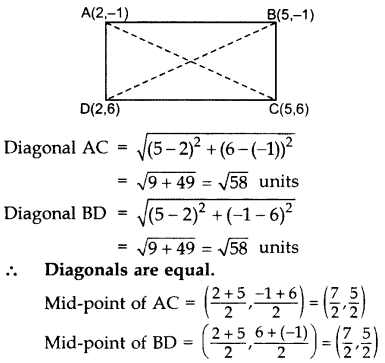
∴ Diagonals also bisect each other.
Question 36.
Find that value of k for which point (0, 2), is equidistant from two points (3, k) and (k, 5). (2013OD)
Solution:
Similar to Question 29, Page 104.
Question 37.
If the points A(-2, 1), B(a, b) and C(4, -1) are collinear and a – b = 1, find the values of a and (2014D)
Solution:
Since A(-2, 1), B(a, b) and C(4, -1) are collinear.
∴ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) = 0
⇒ -2[b – (-1)] + a(-1 – 1) + 4(1 – b) = 0
⇒ -2b – 2 – 2a + 4 – 4b = 0
⇒ -2a – 6b = -2
⇒ a + 3b = 1 … [Dividing by (-2)
⇒ a = 1 – 3
We have, a – b = 1 …[Given
(1 – 3b) – b = 1 …[From (i)
1 – 3b – b = 1
-4b = 1 – 1 = 0 ∴ b = \(\frac{0}{-4}\) = 0
From (i), a = 1 – 3(0) = 1 – 0 = 1
∴ a = 1, b = 0
Question 38.
If the points A(-1, -4), B(b, c) and C(5, -1) are collinear and 2b + c = 4, find the values of b and c. (2014D)
Solution:
A(-1, -4), B(b, c), C(5, -1) are collinear.
∴ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) = 0
⇒ -1(c + 1) + b(-1 + 4) + 5(-4 – c) = 0
⇒ -c – 1 – b + 4b – 20 – 5c = 0
⇒ 3b – 6c = 21
⇒ – b – 2c = 7 …[Dividing by 3
⇒ b = 7 + 2c
We have, 2b + c = 4 … [Given
2(7 + 2c) + c = 4 … [From (i)
⇒ 14 + 4c + c = 4
⇒ 5c = 4 – 14 = -10 ⇒ c = -2
⇒ b = 7 + 2(-2) = 3 … [From (i)
∴ b = 3, c = -2
Question 39.
Find the area of the triangle ABC with A(1, 4) and mid-points of sides through A being (2, -1) and (0, -1). (2015D)
Solution:

Question 40.
Find the area of the triangle PQR with Q(3, 2) and the mid-points of the sides through Q being (2, -1) and (1, 2). (2015D)
Solution:
Let P(x, y), R(z, t).

Question 41.
Find the ratio in which the y-axis divides the line segment joining the points (-4, -6) and (10, 12). Also find the coordinates of the point of division. (2013D)
Solution:

Question 42.
Find the ratio in which point P(-1, y) lying on the line segment joining points A(-3, 10) and B(6, -8) divides it. Also find the value of y. (20130D)
Solution:

Question 43.
In what ratio does the point (14.4) divide the line segment joining the points P(2, -2) and Q(3, 7)? Also find the value of y. (2017OD)
Solution:

Question 44.
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) such that AP = AB. (2015OD)
Solution:

Question 45.
Points A(-1, y) and B(5, 7) lie on a circle with centre 0(2, -3y). Find the values of y. Hence find the radius of the circle. (2014D)
Solution:
Join OA and OB. …[radii of a circle
∴ OA = OB OA2 = OB2 …[Squaring both sides
⇒ (2 + 1)2 + (-3y – y)2 = (5 – 2)2 + (7 + 3y)2
⇒ 9+ (-4y)2 = 9 + (7 + 3y)2
⇒ 16y2 = 49 + 42y + 9y2
⇒ 16y2 – 9y2 – 42y – 49 = 0
⇒ 7y2 – 42y – 49 = 0
⇒ y2 – 6y – 7 = 0 …[Dividing both sides by 7
⇒ y2 – 7y + y – 7 = 0
⇒ y(y – 7) + 1(y – 7) = 0
⇒ (y – 7) (y + 1) = 0
y – 7 = 0 or y + 1 = 0
y = 7 or y = -1
(i) Taking y = 7

Question 46.
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a + b = 1, find the values of a and b. (2014D)
Solution:
Similar to Question 37, Page 105.
Question 47.
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3,-2). If the third vertex is \(\left(\frac{7}{2}, y\right)\), find the value of y. (2017D)
Solution:
Given: Area of ∆ = 5 sq. units
Vertices: (2, 1), (3, -2) and \(\left(\frac{7}{2}, y\right)\)
Area of ∆
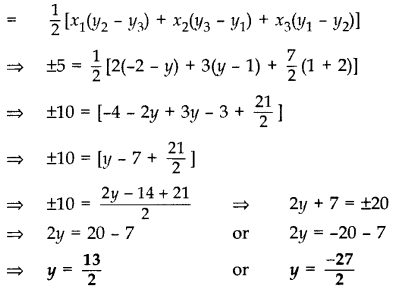
Question 48.
Find the ratio in which the line segment joining the points A(3, -3) and B(-2, 7) is divided by x-axis. Also find the coordinates of the point of division. (2014OD)
Solution:
Similar to Question 41, Page 106.
Question 49.
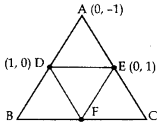
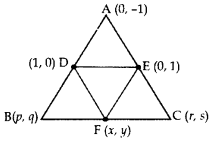
In the Figure, ABC is a triangle coordinates of whose vertex A are (0, -1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the midpoint of BC, find the areas of ∆ABC and ∆DEF. (2016D)
Solution:
Let B (p, q), C (r, s)
and F(x, y)
Mid-point of AB = Coordinates of D

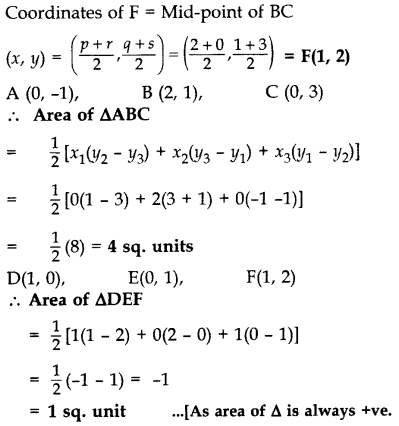
Coordinate Geometry Class 10 Important Questions Long Answer (4 Marks)
Question 50.
If the points A(x, y), B(3, 6) and C(-3, 4) are collinear, show that x – 3y + 15 = 0. (2012OD)
Solution:
Pts. A(x, y), B(3, 6), C(-3, 4) are collinear.
∴ Area of ∆ = 0
As area of ∆
= \(\frac{1}{2}\)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
∴Area of ∆ABC
= x(6 – 4) + 3(4 – y) + (-3) (y – 6) = 0
= 2x + 12 – 3y – 3y + 18 = 0
= 2x – 6y + 30 = 0
∴ x – 3y + 15 = 0 … [Dividing both sides by 2
Question 51.
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear. (2015OD)
Solution:
A (k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k).
When points are collinear, area of ∆ is 0.
∴ Area of triangle = 0
⇒ [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
⇒ [(k + 1) (2k + 3 – 5k) + 3k (5k – 2k) + (5k – 1) (2k – 2k – 3)] = 0
⇒ [(k + 1) (3 – 3k) + 3k(3k) + (5k – 1)(-3)] = 0
⇒ [3k – 3k2 + 3 – 3k + 9k2 – 15k + 3) = 0
⇒ 6k2 – 15k + 6 = 0
⇒ 2k2 – 5k + 2 = 0
⇒ 2k2 – 4k – 1k + 2 = 0
⇒ 2k(k – 2) – 1(k – 2) = 0
⇒ (k – 2)(2k – 1) = 0
⇒ k – 2 = 0 or 2k – 1 = 0
⇒ k = 2 or k = \(\frac{1}{2}\)
We get, k = 2, \(\frac{1}{2}\)
Question 52.
If two vertices of an equilateral triangle are (3, 0) and (6, 0), find the third vertex. (2011D)
Solution:
Let A (3,0), B (6, 0), C (x, y).
∴ ∆ABC is an equilateral
∴ AB = BC = AC
AB2 = BC2 = AC2 …[Squaring throughout
(6 – 3)2 + (0 – 0)2 = (x – 6)2 + (1 – 0)2 = (x – 3)2 + (y – 0)2
9 = x2 – 12x + 36 + y2 = x2 – 6x + 9 + y2

Question 53.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5). (2011D)
Solution:
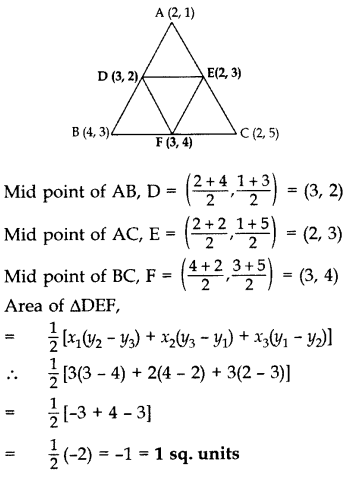
Question 54.
If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value(s) of p. (2012D)
Solution:
Area of ∆ = 15 sq. units
\(\frac{1}{2}\) [1(p – 7) + 4(7 + 3)) + (-9)(-3 – p)] = ±15
p – 7 + 40 + 27 + 9p = ±30
10p + 60 = ± 30
10p = -60 ± 30
p = \(\frac{-60 \pm 30}{10}\)
∴ Taking +ve sign, p = \(\frac{-60+30}{10}=\frac{-30}{10}\) = -3
Taking -ve sign, p = \(\frac{-60-30}{10}=\frac{-90}{10}\) = -9
Question 55.
For the triangle ABC formed by the points A(4, -6), B(3,-2) and C(5, 2), verify that median divides the triangle into two triangles of equal area. (2013OD)
Solution:
Let A(4, -6), B(3, -2) and C(5, 2) be the vertices of ∆ABC.
Since AD is the median
∴ D is the mid-point of BC.
⇒ D\(\left(\frac{3+5}{2}, \frac{-2+2}{2}\right)\) ⇒ D(4,0)
Area of ∆ABD
= \(\frac{1}{2}\) [4(-2 – 0) + 3(0 + 6) + 4(-6 + 2)]
= \(\frac{1}{2}\) [-8 + 18 – 16) = \(\frac{1}{2}\) [-6] = -3
But area of A cannot be negative.
∴ ar(∆ABD) = 3 sq.units …(i)
Area of ∆ADC
= \(\frac{1}{2}\) [4(0 – 2) + 4(2 + 6) + 5(-6 – 0)]
= \(\frac{1}{2}\)(-8 + 32 – 30] = \(\frac{1}{2}\) [-6] = -3
But area of ∆ cannot be negative.
∴ ar(∆ADC) = 3 sq.units
From (i) and (ii),
∴ Median AD of AABC divides it into two ∆s of equal area.
Question 56.
If A(4, 2), B(7,6) and C(1, 4) are the vertices of a AABC and AD is its median, prove that the median AD divides AABC into two triangles of equal areas. (2014OD)
Solution:
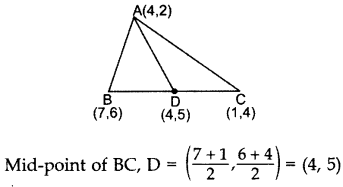
Area of ∆ABD
= \(\frac{1}{2}\) (x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\)[4(6 – 5) + 7(5 – 2) + 4(2 – 6))
= \(\frac{1}{2}\)(4 + 21 – 16) = \(\frac{9}{2}\) sq.units …(i)
Area of ∆ADC
= \(\frac{1}{2}\) [4(5 – 4) + 4(4 – 2) + 162 – 5)]
= \(\frac{1}{2}\)(4 + 8 – 3) = \(\frac{9}{2}\)sq.units
From (i) and (ii),
Area of ∆ABD = Area of ∆ADC
∴ Median AD divides ∆ABC into two triangles of equal area.
Question 57.
Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units. (2015OD)
Solution:
Let A(k + 1, 1), B(4, -3) and C(7, -k).
We have, Area of ∆ABC = 6 … [Given
6 = \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
6 = \(\frac{1}{2}\)[(k + 1)(-3 + k) + 4(-k – 1) + 7(1 + 3)]
12 = (-3k + k2 – 3 + k – 4k – 4 + 28]
12 = [k2 – 6k + 21]
⇒ k2 – 6k + 21 – 12 = 0
⇒ k2 – 6k + 9 = 0
⇒ k2 – 3k – 3k + 9 = 0
⇒ k(k – 3) – 3(k – 3) = 0 =
⇒ (k – 3) (k – 3) = 0
⇒ k – 3 = 0 or k – 3 = 0
⇒ k = 3 or k = 3
Solving to get k = 3.
Question 58.
Prove that the area of a triangle with vertices (t, t – 2), (t + 2, t + 2) and (t + 3, t) is independent of t. (2016D)
Solution:
Let A(t, t – 2), B(t + 2, + + 2), C(t + 3, t).
Area of ∆ABC
= \(\frac{1}{2}\)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\) [t(t + 2 – t) + (t + 2)(t – (t – 2)) +(t + 3)((t – 2) – (t + 2))]
= \(\frac{1}{2}\) [t(2) + (t + 2)(2) + (t + 3)(-4)]
= \(\frac{1}{2}\) (2+ + 2+ + 4 – 46 – 12] = \(\frac{1}{2}\) [-8] = -4
Area of ∆ is always positive.
∴ Area of ∆ = 4 sq. units, which is independent of t.
Question 59.
If the centroid of ∆ABC, in which A(a, b), B(b, c), C(c, a) is at the origin, then calculate the value of (a3 + b3 + c). (2012OD)
Solution:
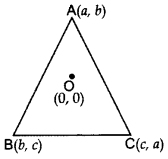
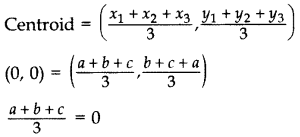
a + b + c = 0
If a + b + c = 0
then, as we know
a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ac) ∴ a3 + b3 + c3 – 3abc = 0 … [Since a + b + c = 0
∴ a3 + b3 + c3 = 3abc …(Hence proved)
Question 60.
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 or x + y = -9. (2013D)
Solution:
Let A(x, y), B(1, 2), C(2, 1).
Area of ∆ABC = 6 sq. units …[Given
As \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 6
∴ x(2 – 1) + 1(1 – y) + 2(y – 2) = ±12
x + 1 – y + 2y – 4 = ±12
Taking +ve sign
x + y = 12 + 4 – 1
∴ x + y = 15
Taking -ve sign
x + y = -12 + 4 – 1
∴ x + y = -9
Question 61.
In the given figure, the vertices of ∆ABC are A(4, 6), B(1, 5) and C(7, 2). A line segment DE is drawn to intersect the sides AB and AC at D and E respectively such that \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{3}\). Calculate the area of ∆ADE and compare it with area of ∆ABC. (2016OD)
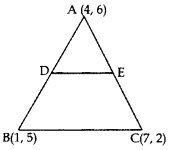
Solution:
AD : AB = 1 : 3; AE : AC = 1 : 3
∴AD : DB = 1 : 2; AE : EC = 1 : 2

Question 62.
Point P(x, 4) lies on the line segment joining the points A(-5, 8) and B(4, -10). Find the ratio in which point P divides the line segment AB. Also find the value of x. (2011OD)
Solution:

Question 63.
A point P divides the line segment joining the points A(3, -5) and B(-4, 8) such that \(\frac{\mathbf{A P}}{\mathbf{P B}}=\frac{\mathbf{K}}{\mathbf{1}}\). If P lies on the line x + y = 0, then find the value of K. (2012D)
Solution:
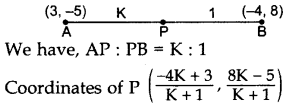
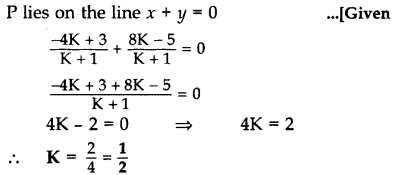
Question 64.
Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, -3). Also, find the value of x. (2014D)
Solution:

Question 65.
If (3, 3), (6, y), (x, 7) and (5, 6) are the vertices of a parallelogram taken in order, find the values of x and y. (2011D)
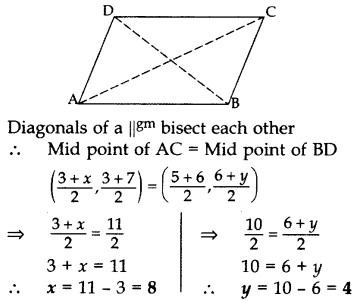
Solution:
Let A (3, 3), B (6, y), C (x, 7) and D (5, 6).
Question 66.
Find the area of the quadrilateral ABCD whose vertices are A(-3, -1), B(-2, -4), C(4, -1) and D(3, 4). (2011D, 2012OD)
Solution:
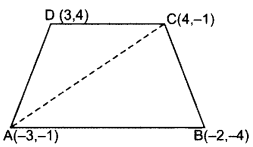
Area of ∆ = \(\frac{1}{2}\)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
∴ Area of ∆ABC
= \(\frac{1}{2}\)[(-3)(4 + 1) + (-2){-1 – (-1)} +4{-1 – (- 4}}]
= \(\frac{1}{2}\)[9+ 0 + 12] = 21 sq. units …(i)
∴ Area of ∆ACD
= \(\frac{1}{2}\)[-3(-1 – 4) + 4{(4 – (-1)} + 34{-1 – (-1)}]
= \(\frac{1}{2}\) [15 + 20 + 0]
= \(\frac{1}{2}\)[15 + 20] = \(\frac{35}{2}\) sq. units
∴ ar(quad. ABCD) = ar (∆ABC) + ar(∆ACD)
= \(\frac{21}{2}+\frac{35}{2}\) …[From (i) & (ii)
= \(\frac{56}{2}\) = 28 sq. units
Question 67.
The three vertices of a parallelogram ABCD are A(3, 4), B(-1, -3) and C(-6, 2). Find the coordinates of vertex D and find the area of ABCD. (2013D)
Solution:
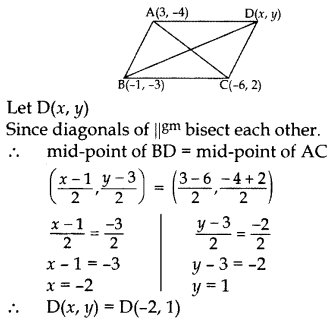
Area of ∆ = \(\frac{1}{2}\)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
∴ Area of ∆ABC
= \(\frac{1}{2}\) [3(-3 – 2) + (-1)(2 + 4) + (-6)(+4+3)]
= \(\frac{1}{2}\) [-15 – 6 +6] = \(\frac{-15}{2}\)
= \(\frac{15}{2}\) sq. units …[∵ ar of A cannot be -ve.
Since diagram of a parallelogram divides it into 2 equal areas.
∴ ar(||gm ABCD) = 2(area of ∆ABC) = 2\(\left(\frac{15}{2}\right)\)
= 15 sq. units
Question 68.
If the points A(1, -2), B(2, 3), C(-3, 2) and D(-4, -3) are the vertices of parallelogram ABCD, then taking AB as the base, find the height of this parallelogram. (2013OD)
Solution:
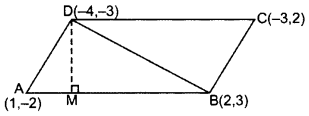
1st method. A(1, -2), B(2, 3), D(-4, -3)
.. Area of ∆ABD
= \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\) [1(3 + 3) + 2(-3 + 2) + (-4)(-2 – 3)]
= \(\frac{1}{2}\) [6 – 2 + 20) = \(\frac{24}{2}\) sq.units
ar(∆ABD) = 12 sq.units
= \(\frac{1}{2}\) × AB × DM = 12 sq.units …[Area of ∆ = 1/2 × Base × Altitude
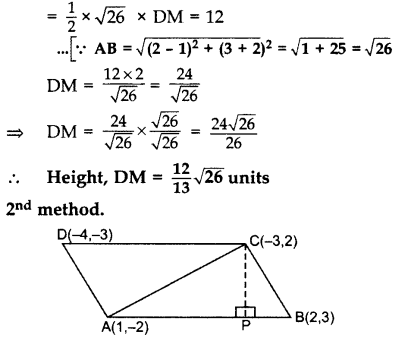
Area of ∆ABC
= \(\frac{1}{2}\) [x2(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\)[1(3 – 2) + 2(2 + 2) + (-3)(-2 – 3)]
= \(\frac{1}{2}\)[1 + 8 + 15] = 12 sq. unit
Area of ∆ABC = 12
⇒ \(\frac{1}{2}\) × AB × CP = 12 …[Area of ∆ = 1/2 × Base × Height
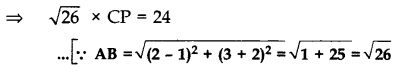
Question 69.
Find the value of k, if the points P(5, 4), Q(7, k) and R(9, – 2) are collinear. (2011D)
Solution:
Given points are P(5, 4), Q(7, k) and R(9, -2).
x1 (y2 – y3) + x2(y3 – y1) + x3(y1 – y2) = 0 …[∵ Points are collinear
∴ 5 (k + 2) + 7 (- 2 – 4) + 9 (4 – k) = 0
5k + 10 – 14 – 28 + 36 – 9k = 0
4 = 4k ∴ k=1
Question 70.
If P(2, 4) is equidistant from Q(7, 0) and R(x, 9), find the values of x. Also find the distance PQuestion (2011D)
Solution:
![]()
PQ = PR …[Given
PQ2 = PR2 … [Squaring both sides
∴ (7 – 2)2 + (0 – 4)2 = (x – 2)2 + (9 – 4)2
⇒ 25 + 16 = (x – 2)2 + 25
⇒ 16 = (x – 2)2
⇒ ±4 = x – 2 …[Taking sq. root of both sides
⇒ 2 ± 4 = x
⇒ x = 2 + 4 = 6 or x = 2 – 4 = -2
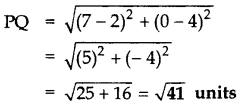
Question 71.
Find the point of y-axis which is equidistant from the points (-5, -2) and (3, 2). (2011D)
Solution:
Similar to Question 26, Page 103.
Question 72.
Point M(11, y) lies on the line segment joining the points P(15, 5) and Q(9, 20). Find the ratio in which point M divides the line segment PQuestion Also find the value of y. (2011OD)
Solution:
Similar to Question 62, Page 110.
Question 73.
Find the coordinates of a point P, which lies on the line segment joining the points A(-2, -2) and B(2, -4) such that AP = \(\frac{3}{7}\)AB. (2012OD)
Solution:
![]()
AP = \(\frac{3}{7}\)AB …(Given)
\(\frac{\mathrm{AP}}{\mathrm{AB}}=\frac{3}{7}\)
Let AP = 3K, AB = 7K
BP = AB – AP = 7K – 3K = 4K
∴ \(\frac{A P}{A B}=\frac{3 K}{4 K}=\frac{3}{4}\)
Using Section formula, we have
\(P\left(\frac{6-8}{3+4}, \frac{-12-8}{3+4}\right) \Rightarrow\left(\frac{-2}{7}, \frac{-20}{7}\right)\)
Question 74.
Find the value of k, for which the points A(6,-1), B(k, -6) and C(0, -7) are collinear. (2012OD)
Solution:
Similar to Question 69, Page 112.
Question 75. Find the value of p, if the points A(1, 2), B(3, p) and C(5, -4) are collinear. (2012OD)
Solution:
Similar to Question 69, Page 112.
Question 76. Find the value of x for which the points (x, -1), (2, 1) and (4, 5) are collinear. (2013D)
Solution:
Similar to Question 69, Page 112.
Question 77.
Find the area of a parallelogram ABCD if three of its vertices are A(2, 4), B(2 + \(\sqrt{3}\), 5) and C(2,6). (2013OD)
Solution:
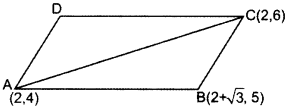
Area of ∆ABD
= \(\frac{1}{2}\) (x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\) [2(5 – 6) + (2 + \(\sqrt{3}\))(6 – 4) + 2(4 – 5))
= \(\frac{1}{2}\) (-2 + 4 + 2\(\sqrt{3}\) – 2)
= \(\frac{1}{2}\) (2\(\sqrt{3}\)) = \(\sqrt{3}\)
Since diagonal of a ||gm divides it into two equal areas.
Area of ABCD (||gm) = 2(Area of ∆ABC)
= 2\(\sqrt{3}\)3 sq. units
Question 78.
If A(-3,5), B(-2, -7), C(1, -8) and D(6, 3) are the vertices of a quadrilateral ABCD, find its area. (2014OD0
Solution:
Similar to Question 66, Page 111.
Question 79.
A(4, -6), B(3, -2) and C(5, 2) are the vertices of a ∆ABC and AD is its median. Prove that the median AD divides AABC into two triangles of equal areas. (2014OD)
Solution:
Similar to Question 56, Page 109.
Question 80.
If A(-, 8), B(-3,-4), C(0, -5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area. (2015D)
Solution:
Similar to Question 66, Page 111.
Question 81.
If P(-5, -3), Q(-4, -6), R(2, -3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area. (2015D)
Solution:
Similar to Question 66, Page 111.
Question 82.
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units. (2015OD)
Solution:
Similar to Question 57, Page 109.
Question 83.
The x-coordinate of a point P is twice its y coordinate. If P is equidistant from Q (2, -5) and R(-3, 6), find the coordinates of P. (2016D)
Solution:
Let the point P be (2k, k), Q(2,-5), R(-3, 6)
![]()
PQ = PR …Given
PQ2 = PR2 …[Squaring both sides
(2k – 2)2 + (k + 5)2 = (2k + 3)2 + (k – 6)2 …Given
4k2 + 4 – 8k + k2 + 10k + 25 = 4k2 + 9 + 12k + k2 – 12k + 36
⇒ 2k + 29 = 45
⇒ 2k = 45 – 29
⇒ 2k = 16
⇒ k = 8
Hence coordinates of point P are (16, 8).