Important Questions for Class 10 Maths Chapter 12 Areas Related to Circles

Important Questions for Class 10 Maths Chapter 12 Areas Related to Circles

Areas Related to Circles Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, calculate the diameter of the larger circle (in cm). (2012D)
Solution:
πR² = πr²₁ + πr²₂
πR² = π(r²₁ + πr²₂) [ r₁ = \(\frac{10}{2}\) = 5cm, r₂ = \(\frac{24}{2}\) = 12 cm]
R² = 5² + 12² = 25 + 144
R² = 169 = 13 cm
∴ Diameter = 2(13) = 26 cm

Question 2.
The circumference of a circle is 22 cm. Calculate the area of its quadrant (in cm²). (2012OD)
Solution:
Circumference of a circle = 22 cm 2πr = 22 cm

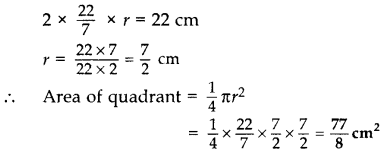
Question 3.
If the difference between the circumference and the radius of a circle is 37 cm, then using π = \(\frac{22}{7}\), calculate the circumference (in cm) of the circle. (2013D)
Solution:
2πr – r = 37 ⇒ r(2π – 1) = 37

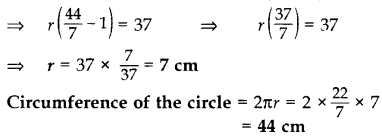
Question 4.
If he is taken as \(\frac{22}{7}\), calculate the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution. (2013OD)
Solution:
Radius (r) = \(\frac{35}{2}\)
Required distance = Perimeter = 2πr
= 2 × \(\frac{22}{7}\) × \(\frac{35}{7}\) cm = 110 cm or 1.1 m

Question 5.
In Figure , find the area of the shaded region. (2011OD)

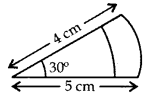
Solution:
Area of shaded region

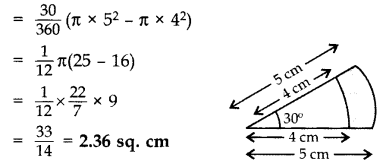
Areas Related to Circles Class 10 Important Questions Short Answer-I (2 Marks)

Question 6.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. (2013OD)
Solution:

Question 7.
PQRS is a diameter of a circle of radius 6 cm. The equal lengths PQ, QR and RS are drawn on PQ and QS as PToo RT diameters, as shown in Figure. Find the perimeter of the shaded region. (2011OD)

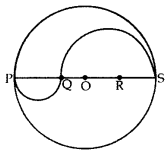
Solution:
Radius OS = 6 cm
∴ Diameter PS = 12 cm
∵ PQ, QR and RS, three parts of the diameter are equal.
∴ PQ = QR = RS = 4 cm
and QS = 2 × 4 = 8 cm
∴ Required perimeter

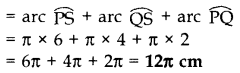
Question 8.
In Figure, a square OABC is inscribed in a quadrant OPBQ of a cirlce. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14) (2014D)

Solution:
Diagonal of the square (OB) = Side \(\sqrt{2}\)
∴ r = 20\(\sqrt{2}\) cm …[Side of square, OA = 20 cm
∴ θ = 90°
ar(Shaded region) = ar(Quad. Sector) – ar(Square)

Question 9.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. [Use π = \(\frac{22}{7}\)] (2013D)
Solution:

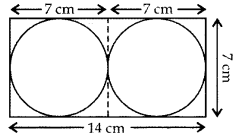
Here r = \(\frac{7}{2}\) cm, L = 14 cm, B = 7 cm
Area of the remaining card board
= ar(rectangle) – 2(area of circle)
= L x B – 2πr²)
= 14 × 7 – 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\)
= 98 – 77 = 21 cm²

Areas Related to Circles Class 10 Important Questions Short Answer-II (3 Marks)

Question 10.
Find the area of a quadrant of a circle, where the circumference of circle is 44 cm. (Use π = \(\frac{22}{7}\)] (2011OD)
Solution:
Circumference of a circle = 44 cm
⇒ 2πr = 44 cm

Question 11.
Area of a sector of a circle of radius 14 cm is 154 cm². Find the length of the corresponding arc of the sector. [Use π = \(\frac{22}{7}\)] (2011OD)
Solution:
Area of sector = 154 cm²

Question 12.
In the Figure, PQ and AB are respectively the arcs of two concentric circles of a radii 7 cm and 3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [Use π = \(\frac{22}{7}\)] (2012D)

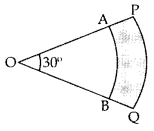
Solution:
Area of sector with radius 7 cm

Question 13.
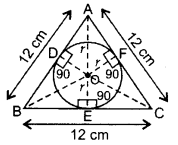
In Figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. (Use π = 3.14 and \(\sqrt{3}\) = 1.73) (2014D)

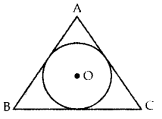
Solution:
Area of an Equilateral ∆ = \(\frac{\sqrt{3}}{4}\) (side)²
Construction: Draw OD ⊥ AB, OE ⊥ BC and OF ⊥ AC. Join OA, OB and OC.
Proof: Area of ∆ABC
= ar(∆AOB) + ar(∆BOC) + ar(∆AOC)

Question 14.
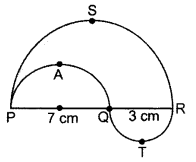
In the figure, PSR, RTQ and PAQ are three semicircles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of the shaded region. [Use π = 3.14] (2014D)

Solution:
Radius of circle QTR = r₁ = \(\frac{3}{2}\) = 1.5 cm
Radius of circle PAQ = r₂ = \(\frac{7}{2}\) = 3.5 cm
Radius of circle PSR = r₃ = \(\frac{7+3}{2}\) = 5 cm

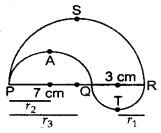
Perimeter of the shaded region
= πr₁ + πr₂ + πr₃
= π(r₁ + r₂ + r₃)
= 3.14(1.5 + 3.5 + 5)
= 3.14(10) = 31.4 cm

Question 15.
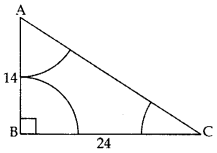
In Figure, ABC is a triangle rightangled at B, with AB = 14 cm and BC = 24 cm. With the vertices A, B and C as centres, arcs are drawn, each of radius 7 cm. Find the area of the shaded region. (Use π = \(\frac{22}{7}\)) (2011OD)

Solution:
Let ∠BAC = θ₁, ∠ABC = θ₂ and ∠ACB = θ₃
Area of the shaded region
= ar(∆ABC) – [ar(sector A) + ar(sector B) + ar(sector C)]

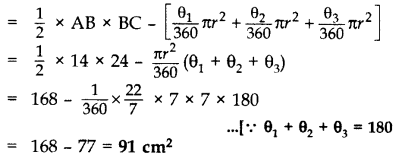
Question 16.
Find the area of the major segment APB, in the figure of a circle of radius 35 cm and ∠AOB = 90°. (Use π = \(\frac{22}{7}\)) (2011D)

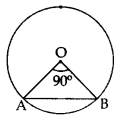
Solution:
Here θ = 90°, p = OA = OB = 35 cm
Area of minor segment = ar(minor sector) – ar(∆AOB)

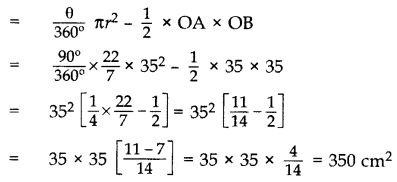
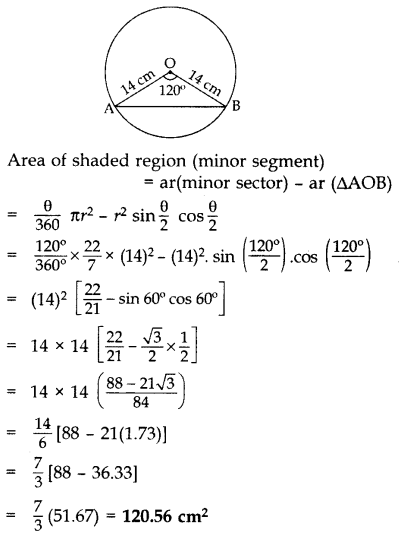
Question 17.
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. (Use π = \(\frac{22}{7}\) and \(\sqrt{3}\) = 1.73] (2011OD)
Solution:
Here θ = 120°, r = 14 cm

Question 18.
In Figure, a semi-circle is drawn with O as centre and AB as diameter. Semi-circles are drawn with AO and A OB as diameters. If AB = 28 m, find the perimeter of the shaded region. [Use π = \(\frac{22}{7}\) (2011OD)

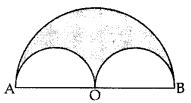
Solution:

Question 19.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) the length of the arc
(ii) area of the sector formed by the arc. [Use π = \(\frac{22}{7}\)] (2013D)
Solution:
(i) Length of the arc: r = 21 cm, θ = 60°
Length of the arc

Question 20.
In Figure, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region. (Use π = \(\frac{22}{7}\)] (2014OD, 2016OD)

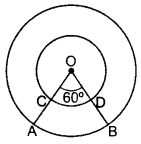
Solution:
1^st Method: Here θ = 60°
∴ Area of the shaded region = ar (major sector of large circle) – ar (major sector of small circle)

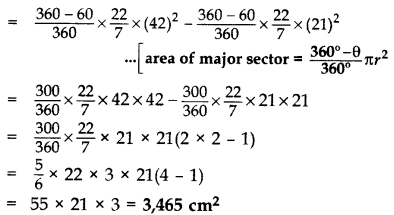
2^nd Method: Required area
= ar (large circle) – ar (small circle) – ar (ABCD)
= ar (large circle) – ar (small circle) – ar (minor sector of large circle) – ar (minor sector of small circle)

3^rd Method:
Shaded region = ar (large circle)
– ar (minor sector of large circle) – ar (major sector of small circle)

Question 21.
In Figure, APB and AQO are semi-circles, and AO = OB. If the peri-meter of al the figure is 40 cm, find the area of the shaded region. [Use π = \(\frac{22}{7}\)] (2015D)

Solution:
OA = OB …[Given
Let OA = OB = r
AO is the diameter of small semicircle
∴ Radius of small semicircle, R = \(\frac{AO}{2}\) = \(\frac{r}{2}\)
BO is the radius of big semicircle, r
Total perimeter = Perimeter of small semi-circle + Perimeter of big semi-circle + OB

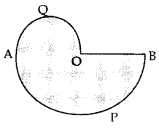
Question 22.
In Figure, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14) (2016OD)

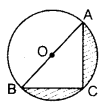
Solution:
∠ACB = 90° …[Angle in a semi-circle
∴ AC² + BC² = AB² …[Pythagoras’ theorem
(12)² + BC² = (13)²
144 + BC² = 169
BC² = 169 – 144 = 25
BC = + 5 cm

Question 23.
In Figure, are shown two arcs PAQ and 0 PBQuestion Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with centre M. If OP = PQ = 10 cm, show that area of shaded region is 25(\(\sqrt{3}=\frac{\pi}{6}\))cm². (2016D)

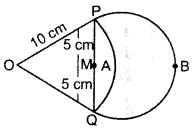
Solution:
OP = OQ = 10 cm (Tangents drawn from an external point are equal
PQ = 5 + 5 = 10 cm
OP = OQ = PQ = 10 cm … [sides are equal
∴ ∆POQ is an equilatral ∆.
⇒ ∠POQ = 60° …[Angles of an equilateral ∆
Side = 70 cm, r = 5 cm, θ = 60°, R = 10 cm
Area of the shaded region = Area of ∆OPQ + Area of Semi-circle(PBQM) – Area of sector (OPAQ)

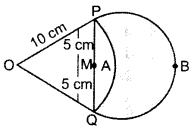
Question 24.
In Figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. (Use π = 3.14) (2012OD)

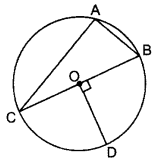
Solution:
∠BAC = 90° …[Angle in a semi-circle
Int rt. ∆BAC,
BC² = AC² + AB² …(Pythagoras’ theorem
= 242 + 72
= 576 + 49 = 625
BC = \(\sqrt{625}\) = 25 cm

Question 25.
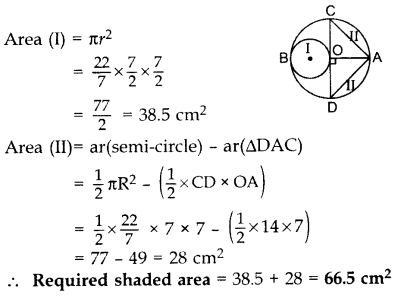
In Fig., AB and CD are two diameters of a circle with centre 0, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. (Use π = \(\frac{22}{7}\)) (2013D)

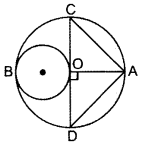
Solution:
Here, r = 7/2 cm, R = 7 cm

Question 26.
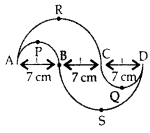
In Figure, APB and CCD are semi-circles of diameter 7 cm each, while ARC and a BSD are semi-circles of diameter 14 cm each. Find the perimeter of the shaded region. [Use π = \(\frac{22}{7}\)] (2011D)

Solution:
BC = R = 7 cm
AB = r = \(\frac{7}{2}\)cm
The perimeter of the shaded region

Question 27.
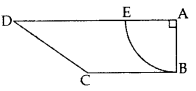
In Figure, ABCD is a trapezium of area 24.5 sq. cm. In it, AD || BC, ∠DAB = 90°, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π = \(\frac{22}{7}\)] (2014OD)

Solution:
ar (trapezium) = 24.5 cm² … [Given
= \(\frac{1}{2}\)(AD + BC) × AB = 24.5 …(i)
= (10 + 4) × AB = 24.5 × 2
= 14.(AB) = 49
AB = \(\frac{49}{14}\) = \(\frac{7}{2}\) cm = r

Question 28.
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60°. Also find the area of the corresponding major segment. [Use π = \(\frac{22}{7}\)] (2015OD)
Solution:
Here, r = 14 cm, θ = 60°

Area of major segment = Area of circle – Area of minor segment
= 616 – 17.9 = 598.10 cm² (Approx.)

Question 29.
Find the perimeter of the D shaded region in Figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles. [Use π = \(\frac{22}{7}\)] (2011OD)

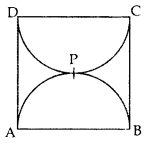
Solution: Perimeter of the shaded region
= Circumference of circle + AD + BC
= 2πr + 14 + 14
= 2 × \(\frac{22}{7}\) × 7 + 28 ….[. r = \(\frac{14}{2}\) = 7 cm
= 44 + 28 = 72 cm

Question 30.
In Figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the sha- o ded region. [Use π = \(\frac{22}{7}\)] (2012D)

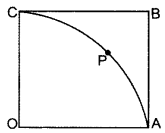
Solution:
Area of shaded region = Area of Square – Area of Quadrant

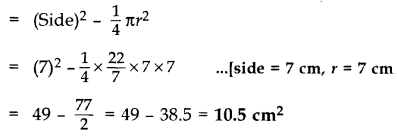
Question 31.
In Figure ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. (Use π = 3.14) (2012OD)

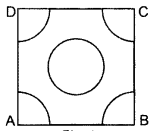
Solution:
Area of 4 quadrants (a circle)
= 4 × \(\frac{1}{4}\)π(1)²
= π sq.cm
Area of the square = (4)² sq.cm = 16 sq.cm
Area of the circle at the centre = π(r)² = π(1)²
= π sq.cm
∴ Area of shaded portion
= Area of square – 2 (Area of circle)
= 16 – (11 + r) sq.cm

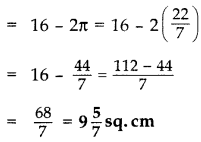
Question 32.
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semi-circular portion with BC as diameter is cut off. Find the area of the remaining paper. (Use π = \(\frac{22}{7}\)) (2012OD)

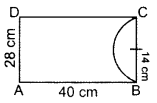
Solution:
Length of paper,
AB, l = 40 cm
Width of paper,
AD, b = 28 cm
Area of paper = l × h
= 40 × 28 = 1120 sq. cm
Diameter of semi-circle = 28 cm …(i)
Radius of semi-circle, r = 14 cm
Area of semi-cirice = \(\frac{1}{2} \pi r^{2}=\frac{1}{2} \times \frac{22}{7} \times 14 \times 14\)
= 308 sq.cm …(ii)
∴ Area of remaining paper = 1120 – 308
= 812 sq.cm

Question 33.
In Figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semi-circles. (2012OD)

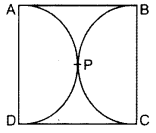
Solution:
Side (diameter) = 14 cm
∴ radius, r = 7 cm
Area of shaded region
= ar(Square) – 2ar(semi-circle)

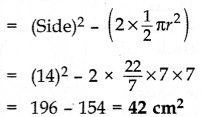
Question 34.
In Figure, find the area of the shaded region. [Use π = 3.14] (2015D)

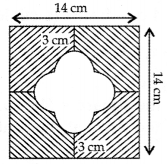
Solution:
Let the side of big square = A = 14 cm
Let the radius of circle,

∴ Required area = (Area of big square – Area of small square – Ar. of 4 semicircles)
= (196 – 16 – 25.12) cm²
= 154.88 cm²

Question 35.
All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if the area of the circle is 1256 cm². [Use π = 3.14] (2015OD)
Solution:
Let r be the radius of circle
In rhombus, AB = BC = CD = AD
⇒ AC = BD = 2r

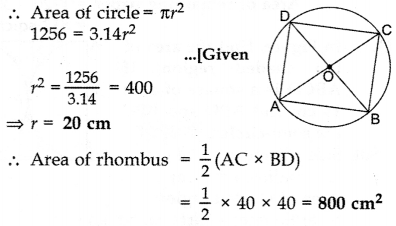
Question 36.
In Figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region. [Use π = \(\frac{22}{7}\)] (2016D)

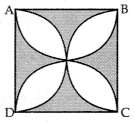
Solution:

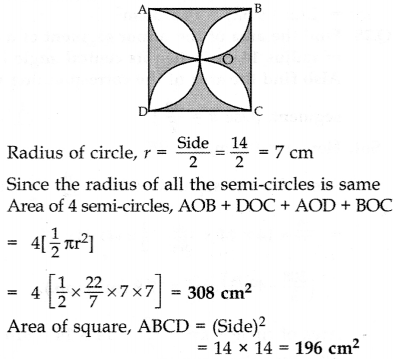
Area of shaded region
= 2(Area of square) – 4(Area of semicircle)
= 2 × 196 – 308 = 392 – 308 = 84 cm²

Areas Related to Circles Class 10 Important Questions Long Answer (4 Marks)

Question 37.
In Figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle ABC of side 14 cm as centres to intersect the sides BC, CA and AB at BZ their respective mid-points D, E and F. Find the area of the shaded region. [Use π = \(\frac{22}{7}\) and \( \sqrt{{3}} \) = 1.73] (2011D)

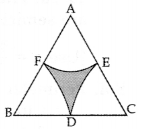
Solution:
∠ABC = ∠BAC = ∠ACB = 60° … [equilateral ∆

Question 38.
Find the area of the shaded region in Figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD, where the length of each side of square is 14 cm. (Use π = \(\frac{22}{7}\)) (2011D)

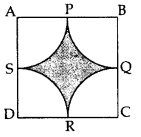
Solution:
Side = 14 cm, radius, r = \(\frac{14}{2}\) = 7 cm
Area of the shaded region
= ar (square) – 4 (ar of quadrant)

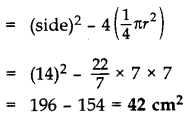
Question 39.
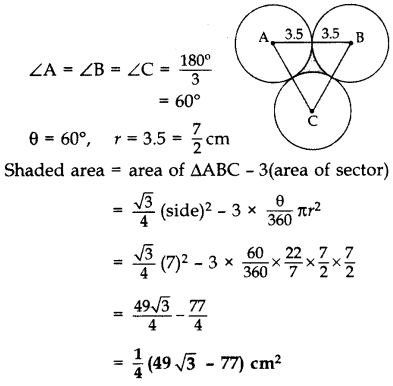
In Figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). [Use π = \(\frac{22}{7}\)] (2011OD)

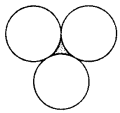
Solution:
AB = BC = CA
= 2(3.5) = 7 cm
∴ ∆ABC is an equilateral ∆

Question 40.
Find the area of the shaded region in Figure, where ABCD is a square of side 28 cm. (2011OD)

Solution:
Here r = \(\frac{28}{4}\) = 7 cm
Area of the shaded region
= ar(square) – 4(circle)
= (side)² – 4 (πr²)
= (28)² – 4 × \(\frac{22}{7}\) × 7 × 7 = 784 – 616 = 168 cm²

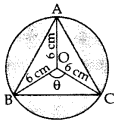
Question 41.
In Figure, an equilateral triangle has been inscribed in a circle of radius 6 cm. Find the area of the shaded region. [Use π = 3.14] (2011OD)

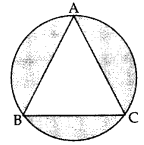
Solution:
Here θ = \(\frac{360}{3}\) = 120°, r = 6 cm
Area of shaded region
= 3(ar of minor segment) = 3[ar(minor sector) – ar(∆ABC)]

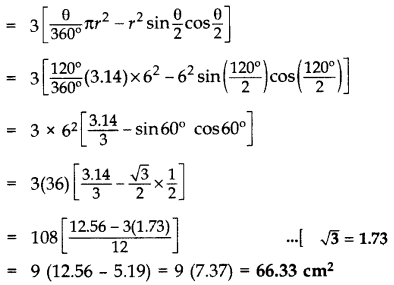
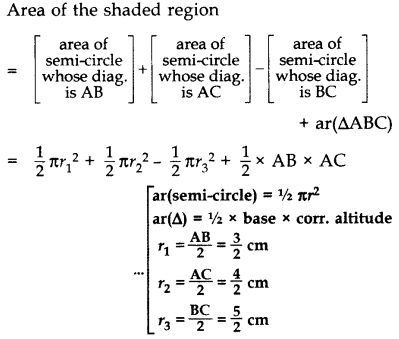
Question 42.
In Figure, ABC is a right-angled triangle right angled at A. Semicircles are drawn on AB, AC and BC as diametres. Find the area of the shaded region. (2013D)

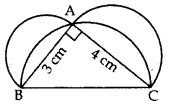
Solution:
In rt. ∆BAC,

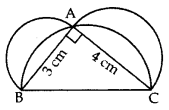
∴ BC² = AB² + AC² …[Pythagoras’ theorem
= (3)² + (4)
= 9 + 16 = 25 cm²
∴ BC = +5 cm … [Side of ∆ can’t be -ve

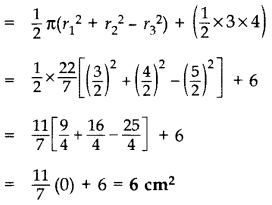
Question 43.
In Figure, PQRS is a square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the inter- section of its diagonals. Find the total area of the two flower beds (shaded parts). (2015OD)

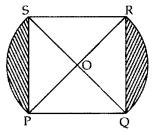
Solution:
PO = 42 m …[Given
PS = QR …[∵ side of square
OR = OP …[Radius of circle
Let OR be the radius of circle = x
So, PR = OR + OP = 2x
Using Pythagoras’ theorem,
⇒(PR)² = (RQ)² + (PQ)²
⇒(2x)² = (42)² + (42)²

Question 44.
An elastic belt is placed around the rim of a pulley of radius 5 cm. (given figure) From one point C on the belt, the elastic belt is pulled directly away from the centre o of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also find the shaded area. (Use π = 3.14 and \(\sqrt{3}\) = 1.73) (2016D)

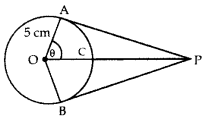
Solution:
∠OAP = 90° ….[Tangent is ⊥ to the center through the point of contact
In rt. ∆OAP,
Cos θ = \(\frac{\mathrm{OA}}{\mathrm{OP}}=\frac{5}{10}=\frac{1}{2}\) = cos 60°
∴ θ = 60°
∠AOB = 60° + 60° = 120° …(i)
Reflex ∠AOB = 360° – ∠AOB
= 360° – 120° = 240°
α = 240° …[Let Reflex ∆AOB = α
The length of the belt that is still in contact with the pulley = ADB = lenght of major arc

Question 45.
In Figure, is shown a sector OAP of a circle with centre 0, containing ∠θ. AB is a perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r [tan θ + sec θ + \(\frac{\pi \theta}{180^{\circ}}\) – 1] (2016OD)

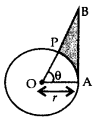
Solution:

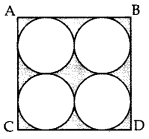
Question 46.
In the Figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where 0 and Oare centres of the circles. Find the area of shaded region. (2017D)

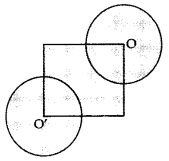
Solution:
Side = 28 cm, Radius = \(\frac{28}{2}\) cm = 14 cm
The area of the shade = Area of square + \(\frac{3}{4}\) (Area of circle) + \(\frac{3}{4}\) (Area of circle)
= Area of square + \(\frac{3}{2}\) (Area of circle) …[Area of square = (Side)²; Area of circle = πr²
= (28)² + \(\frac{3}{2}\) × \(\frac{22}{7}\) × 14 × 14
= 784 + 924 = 1708 cm²

Important Questions for Class 10 Maths