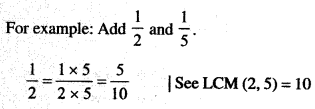Class 6 Maths Chapter 7 Notes Fractions
Class 6 Maths Notes Chapter 7 – Class 6 Fractions Notes
→ Fraction as equal share: A fraction results when a whole number of units is divided into equal parts and shared equally.
→ Fractional Units: When one basic unit is divided into equal parts, each part is called a fractional unit.
→ Reading Fractions: In a fraction such as \(\frac {5}{6}\), 5 is called the numerator and 6 is called the denominator.
![]()
→ Mixed fractions contain a whole number part and a fractional part.
→ Number line: Fractions can be shown on a number line. Every fraction has a point associated with it on the number line.
→ Equivalent Fractions: When two or more fractions represent the same share/number, they are called equivalent fractions.
→ Lowest terms: A fraction whose numerator and denominator have no common factor other than 1 is said to be in lowest terms or its simplest form.
→ Brahmagupta’s method for adding fractions: When adding fractions, convert them into equivalent fractions with the same fractional unit (i.e., the same denominator), and then add the number of fractional units in each fraction to obtain the sum. This is accomplished by adding the numerators while keeping the same denominator.
→ Brahmagupta’s method for subtracting fractions: When subtracting fractions, convert them into equivalent fractions with the same fractional unit (i.e., the same denominator), and then subtract the number of fractional units. This is accomplished by subtracting the numerators while keeping the same denominator.
Recall that when a whole number of things are shared equally among some people, fractions tell us how much each share is.
Shabnam: Do you remember, if one roti is divided equally between two children, how much roti will each child get?
Mukta: Each child will get half a roti.

Shabnam:The fraction ‘one half’ is written as \(\frac{1}{2}\). We also sometimes read this as ‘one upon two.’
Mukta:If one roti is equally shared among 4 children, how much roti will one child get?
Shabnam: Each child’s share is \(\frac{1}{4}\) roti.

Mukta: And which is more \(\frac{1}{2}\) roti or \(\frac{1}{4}\) roti?
![]()
Shabnam: When 2 children share 1 roti equally, each child gets \(\frac{1}{2}\) roti. When 4 children share 1 roti equally, each child gets \(\frac{1}{4}\) roti. Since more children in the second group share the same roti, each child gets a smaller share. So, \(\frac{1}{2}\) roti is more than \(\frac{1}{4}\) roti.
\(\frac{1}{2}\) > \(\frac{1}{4}\)
Fraction
→ A fraction means a part of a group or of a region. A fraction is of the form \(\frac{\text { Numerator }}{\text { Denominator }}\).
→ Denominator represents the number of equal parts into which the whole has been divided.
→ The numerator represents the number of equal parts that have been taken out.
→ For example: \(\frac{3}{4}\) is a fraction. We read it as “three-fourths”.
→ Here, 3 is the numerator and 4 is the denominator.
→ It shows that the whole has been divided into 4 equal parts out of which 3 parts have been taken out.
→ An example of a fraction from daily life can be taken as the division of a pizza into 4 equal parts. Each part (slice) of pizza represents \(\frac{1}{4}\) of the pizza.
→ The fraction \(\frac{1}{4}\) is read as ‘one-fourth’ or ‘one-quarter’.

→ In the adjoining figure, the shaded part represents the fraction \(\frac{1}{4}\).
→ Similarly, in the following figure, the shaded part represents the fraction \(\frac{1}{6}\).

→ and the shaded part in the following figure represents the fraction \(\frac{1}{8}\).

Example 1.
Write the fraction representing the shaded portion.

Solution:
(i) Here number of equal parts = 4
and number of equal parts which have been shaded = 2
∴ Fraction representing the shaded portion = \(\frac{2}{4}=\frac{1}{2}\)
(ii) Here number of equal parts = 9
and number of equal parts which have been shaded = 8
∴ Fraction representing the shaded portion = \(\frac{8}{9}\)
(iii) Here number of equal parts = 4
and dumber of equal parts which have been shaded = 1
∴ Fraction representing the shaded portion = \(\frac{1}{4}\)
(iv) Here number of equal parts = 8
and number of equal parts which have been shaded = 4
∴ Hence fraction representing the shaded portion = \(\frac{4}{8}=\frac{1}{2}\)
Fractional Units and Equal Shares Class 6 Notes
Fractional Units:
In math, a unit fraction can be defined as a fraction whose numerator is 1. It represents 1 shaded part of all the equal parts of the whole. The term “unit” means one. For instance, if a pizza is divided into 4 equal portions and one person is eating one portion of it, it can be numerically represented as \(\frac{1}{4}\).

Equal Shares
If a shape is divided into parts of the same size, we get equal shares. We can divide shapes like triangles, squares, rectangles, and circles partitioning shapes into equal shares.
Beni: Which fraction is greater? \(\frac{1}{5}\) or \(\frac{1}{9}\)?
Arvin: 9 is bigger than 5. So I would guess that \(\frac{1}{9}\) is greater than \(\frac{1}{5}\). Am I right?
Beni: No! That is a common mistake. Think of these fractions as shares.
Arvin: If one roti is shared among 5 children, each one gets a share of \(\frac{1}{5}\) roti. If one roti is shared among 9 children,
each one gets a share of \(\frac{1}{9}\) roti?
Beni: Exactly! Now think again – which share is higher?
Arvin: If I share with more people, I will get less. So \(\frac{1}{9}\) < \(\frac{1}{5}\).
Beni: You got it!
Oh, so \(\frac{1}{100}\) is bigger than \(\frac{1}{200}\)!
When one unit is divided into several equal parts, each part is called a fractional unit. These are all fractional units:
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \ldots, \frac{1}{10}, \ldots, \frac{1}{50}, \ldots, \frac{1}{100}\), etc.
We also sometimes refer to fractional units as ‘unit fractions.’
Fractions have been used and named in India since ancient times. In the Rig Veda, the fraction \(\frac{3}{4}\) is referred to as tripada. This has the same meaning as the words for \(\frac{3}{4}\) in many Indian languages today, e.g., ʻteen paavʼ in colloquial Hindi and ‘mukkaal’ in Tamil. Indeed, words for fractions used today in many Indian languages go back to ancient times.
Fractional Units as Parts of a Whole Class 6 Notes
The picture shows a whole chikki.

Below is a picture of the chikki broken into pieces. A whole chikki is shown in 2 pieces. How much of the original chikki is each piece?

We can see that the bigger piece has 3 pieces of \(\frac{1}{4}\) chikki in it. So, we can measure the bigger piece using the fractional unit \(\frac{1}{4}\). We see that the bigger piece is \(\frac{3}{4}\) chikki.

What is the fractional unit of chikki shown below?

Measuring Using Fractional Units Class 6 Notes
Take a strip of paper. We consider this paper strip to be one unit long.

Fold the strip into two equal parts and then open up the strip again. Taking the strip to be one unit in length, what are the lengths of the two new parts of the strip created by the crease?

What will you get if you fold the previously-folded strip again into two equal parts? You will now get four equal parts.

Fractional quantities can be measured using fractional units.
Let us look at another example,

We can describe how much the quantity is by collecting together the fractional units.
Reading Fractions
We usually read the fraction 34 as ‘three quarters’ or ‘three upon four’, but reading it as ‘3 times \(\frac{1}{4}\)’ helps us to understand the size of the fraction because it clearly shows what the fractional unit is (\(\frac{1}{4}\)) and how many such fractional units (3) there are. Recall what we call the top number and the bottom number of fractions. In the fraction \(\frac{5}{6}\), 5 is the numerator and 6 is the denominator.
![]()
Marking Fraction Lengths on the Number Line Class 6 Notes
We have marked lengths equal to 1, 2, 3, … units on the number line. Now, let us try to mark lengths equal to fractions on the number line. What is the length of the blue line? Write the fraction that gives the length of the blue line in the box.

The distance between 0 and 1 is one unit long. It is divided into two equal parts. So, the length of each part is \(\frac{1}{2}\) unit. So, this blue line is \(\frac{1}{2}\) unit long.
Mixed Fractions Class 6 Notes
Fractions greater than one
You marked some fractions on the number line earlier. Did you notice that the lengths of all the blue lines were less than one and the lengths of all the black lines were more than 1? Write down all the fractions you marked on the number line earlier. Now, let us classify these into two groups:

Did you notice something common between the fractions that are greater than 1?
In all the fractions that are less than 1 unit, the numerator is smaller than the denominator, while in the fractions that are more than 1 unit, the numerator is larger than the denominator.
We know that \(\frac{3}{2}\), \(\frac{5}{2}\) and \(\frac{7}{2}\) are all greater than 1 unit. But can we
see how many whole units they contain?

Writing fractions greater than one as mixed numbers
We saw that: \(\frac{3}{2}\) = 1 + \(\frac{1}{2}\)
We can similarly write other fractions. For example,

A mixed number/mixed fraction contains a whole number (called the whole part) and a fraction that is less than 1 (called the fractional part).

Mixed Fractions Class 6 Notes
A combination of a whole number and a proper fraction is called a mixed fraction.
For example: \(1 \frac{1}{2}, 2 \frac{3}{4}, 3 \frac{4}{5}\), etc. all are mixed functions.
Conversion of a Mixed Fraction into an Improper Fraction
Multiply the whole number by the denominator of the proper fraction and add the numerator of the proper fraction to it. This gives the numerator of the improper fraction. The denominator of the improper fraction is the same as the denominator of the proper fraction.
For example: \(3 \frac{1}{4}=\frac{3 \times 4+1}{4}=\frac{12+1}{4}=\frac{13}{4}\)
Note: Improper Fraction = \(\frac{(\text { Whole number } \times \text { Denominator })+\text { Numerator }}{\text { Denominator }}\)
Conversion of an Improper Fraction into a Mixed Fraction
To convert an improper fraction into a mixed fraction, we divide the numerator by the denominator to obtain the quotient and the remainder. Then the mixed fraction can be written as
Mixed fraction = Quotient \(\frac{\text { Remainder }}{\text { Divisor }}\)
For Example: \(\frac{9}{2}=4 \frac{1}{2}\) as 
Example 1.
Write \(\frac{5}{2}\) in mixed fraction.
Solution:

Example 2.
Write \(\frac{7}{3}\) in mixed fraction.
Solution:

Example 3.
Write 4\(\frac{3}{4}\) in improper fraction.
Solution:

Example 4.
Write 2\(\frac{1}{5}\) in improper fraction.
Solution:

Equivalent Fractions Class 6 Notes
→ Observe the shaded portion in each of the following figure.

→ We note that length of shaded part in each of the above strips is same. This means, \(\frac{1}{2}=\frac{2}{4}=\frac{4}{8}\)
→ We conclude \(\frac{1}{2}, \frac{2}{4}, \frac{4}{8}\) are equivalent fractions. They all represent the same value part of a whole.
→ Fractions having the same value are called equivalent fractions.
→ To find equivalent fractions we multiply or divide both the numerator and denominator by the same number.
→ There are two ways of obtaining an equivalent fraction of a given fraction:
→ By multiplying the numerator and the denominator of the given fraction by the same non-zero number.
For example: The equivalent fraction of \(\frac{1}{2}\) are \(\frac{2}{4}, \frac{3}{6}, \frac{4}{8}\), etc. as \(\frac{1 \times 2}{2 \times 2}=\frac{2}{4}, \quad \frac{1 \times 3}{2 \times 3}=\frac{3}{6}, \quad \frac{1 \times 4}{2 \times 4}=\frac{4}{8}\), etc.
→ By dividing the numerator and the denominator of the given fraction by the same non-zero number other than 1.
For example:
- The equivalent fraction of \(\frac{12}{10}\) is \(\frac{6}{5}\) as \(\frac{12 \div 2}{10 \div 2}=\frac{6}{5}\)
- The equivalent fraction of \(\frac{9}{21}\) is \(\frac{3}{7}\) as \(\frac{9 \div 3}{21 \div 3}=\frac{3}{7}\)
- The equivalent fraction of \(\frac{15}{40}\) is \(\frac{3}{8}\) as \(\frac{15 \div 5}{40 \div 5}=\frac{3}{8}\)
Note: Every proper or improper fraction has infinitely many equivalent fractions.
Using a fraction wall to find equal fractional lengths!
In the previous section, you used paper folding to represent various fractions using fractional units. Let us do some more activities with the same paper strips.

These are ‘equivalent fractions’ that denote the same length, but they are expressed in terms of different fractional units. Now, check whether \(\frac{1}{3}\) and \(\frac{2}{6}\) are equivalent fractions or not, using paper strips.
Make your fraction wall using such strips as given in the picture below!

We can extend this idea to make a fraction wall up to the fractional unit \(\frac{1}{10}\).

Understanding Equivalent Fractions Using Equal Shares
One roti was shared equally by four children. What fraction of the whole did each child get?
The adjoining picture shows the division of a roti among four children. The fraction of roti each child got is \(\frac{1}{4}\).

You can also express this event through division facts, addition facts, and multiplication facts.
The division fact is 1 ÷ 4 = \(\frac{1}{4}\)
The addition fact is 1 = \(\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}\)
The multiplication fact is 1 = 4 × \(\frac{1}{4}\)

So, the share of each child is the same in both these situations!
Let us examine the shares of each child in the following situations.
- 1 roti is divided equally between 2 children.
- 2 rotis are divided equally among 4 children.
- 3 rotis are divided equally among 6 children.
![]()
Let us draw and share!
Did you notice that in each situation the share of every child is the same?
So, we can say that \(\frac{1}{2}=\frac{2}{4}=\frac{3}{6}\).

Fractions, where the shares are equal, are called ‘equivalent fractions’.
So, \(\frac{1}{2}\), \(\frac{2}{4}\), and \(\frac{3}{6}\) are all equivalent fractions.
In which group will each child get more chikki?
1 chikki divided between 2 children or 5 chikkis divided among 8 children.
Mukta: So, we must compare \(\frac{1}{2}\) and \(\frac{5}{8}\). Which is more?
Shabnam: Well, we have seen that \(\frac{1}{2}\) = \(\frac{4}{8}\); and clearly \(\frac{4}{8}\) < \(\frac{5}{8}\). So, the children for whom 5 chikkis are divided equally among 8 will get more than those children for whom 1 chikki is divided equally among 2. The children of the second group will get more chikki each.
What about the following groups? In which group will each child get more?
1 chikki divided between 2 children or 4 chikkis divided among 7 children.
Shabnam: The children of which group will get more chikki this time?
Mukta: We must compare \(\frac{1}{7}\) and \(\frac{4}{7}\).
Now \(\frac{1 \times 4}{2 \times 4}=\frac{4}{8}\) so, \(\frac{1}{2}=\frac{4}{8}\).
Shabnam: But why did you multiply the numerator and denominator by 4 again?
Mukta: You will see!


Now, decide in which of the two groups will each child get a larger share:
- Group 1: 3 glasses of sugarcane juice divided equally among 4 children.
- Group 2: 7 glasses of sugarcane juice divided equally among 10 children.
- Group 1: 4 glasses of sugarcane juice divided equally among 7 children.
- Group 2: 5 glasses of sugarcane juice divided equally among 7 children.
Which groups were easier to compare? Why?

Shabnam: To compare the first two groups, we have to find fractions equivalent to the fractions \(\frac{3}{4}\) and \(\frac{7}{10}\).
Mukta: How about \(\frac{6}{8}=\frac{3}{4}\) and \(\frac{21}{30}=\frac{7}{10}\)?
Shabnam: There is a condition. The fractional unit used for the two fractions has to be the same! Like \(\frac{2}{6}\) and \(\frac{3}{6}\) both use the same fractional unit \(\frac{1}{6}\) (i.e., the denominators are the same).
But \(\frac{6}{8}\) and \(\frac{21}{30}\) do not use the same fractional units (they have different denominators).
Mukta: Okay, so let us start making equivalent fractions then:
\(\frac{3}{4}=\frac{6}{8}=\frac{9}{12}=\frac{12}{16}=\frac{15}{20}\)… But when do I stop?
Shabnam: Got it! How about we go on till 4 × 10 = 40.
Mukta: You mean the product of the two denominators?
Sounds good! We have \(\frac{3}{4}\) and \(\frac{7}{10}\). The product of the two denominators (4 and 10) is 40.

Shabnam: So, fractions equivalent to \(\frac{3}{4}\) and \(\frac{7}{10}\) with the same fractional unit (same denominators) are \(\frac{30}{40}\) and \(\frac{28}{40}\), or \(\frac{15}{20}\) and \(\frac{14}{20}\).
Since clearly \(\frac{30}{40}\) > \(\frac{28}{40}\), we conclude that \(\frac{3}{4}\) > \(\frac{7}{10}\).
![]()
Expressing a Fraction in the Lowest Terms (or in its Simplest Form)
In any fraction, if its numerator and denominator have no common factor except 1, then the fraction is said to be in the lowest terms or its simplest form. In other words, a fraction is said to be in the lowest terms if its numerator and denominator are as small as possible. Any fraction can be expressed in the lowest terms by finding an equivalent fraction whose numerator and denominator are as small as possible. Let’s see how to express fractions in the lowest terms.
Example: Is the fraction \(\frac{16}{20}\) in lowest terms?
No, 4 is a common factor of 16 and 20. Let us reduce \(\frac{16}{20}\) to lowest terms.
We know that both 16 (numerator) and 20 (denominator) are divisible by 4. So, \(\frac{16 \div 4}{20 \div 4}=\frac{4}{5}\).
Now, there is no common factor between 4 and 5. Hence, \(\frac{16}{20}\) expressed in lowest terms is \(\frac{4}{5}\). So, \(\frac{4}{5}\) is called the simplest form of \(\frac{16}{20}\), since 4 and 5 have no common factor other than 1.

Expressing a fraction in the lowest terms can also be done in steps.
Suppose we want to express \(\frac{36}{60}\) in lowest terms.
First, we notice that both the numerator and denominator are even. So, we divide both by 2, and see that \(\frac{36}{60}=\frac{18}{30}\).
Both the numerator and denominator are even again, so we can divide them each by 2 again; we get \(\frac{18}{30}=\frac{9}{15}\)
We now notice that 9 and 15 are both multiples of 3, so we divide both by 3 to get \(\frac{9}{15}=\frac{3}{5}\)
Now, 3 and 5 have no common factor other than 1, so, \(\frac{36}{60}\) in lowest terms is \(\frac{3}{5}\).
Alternatively, we could have noticed that in \(\frac{36}{60}\), both the numerator and denominator are multiples of 12: we see that 36 = 3 × 12 and 60 = 5 × 12. Therefore, we could have concluded that \(\frac{36}{60}=\frac{3}{5}\) straight away.
Either method works and will give the same answer! But sometimes it can be easier to go in steps.
Simplest form of a Fraction Class 6 Notes
A fraction is said to be in its simplest (lowest or standard) form if its numerator and denominator have no common factor except 1, i.e., when the HCF of its numerator and denominator is 1 or in other words when its numerator and denominator are co-prime. (Co-prime numbers have no common factor except 1)
Example 1.
Write 3 equivalent fractions of
(i) \(\frac{2}{5}\)
(ii) \(\frac{16}{24}\)
Solution:


are equivalent fractions.
Example 2.
Express \(\frac{16}{24}\) in simplest form.
Solution:
Here factors of 16 are 1, 2, 4, 8, 16 and factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24
∴ HCF of 16 and 24 = Common factors of 16 and 24 = 8
∴ \(\frac{16 \div 8}{24 \div 8}=\frac{2}{3}\)
Hence Simplest form of \(\frac{16}{24}=\frac{2}{3}\)
Comparing Fractions Class 6 Notes
Which is greater, \(\frac{4}{5}\) or \(\frac{7}{9}\)?
It can be difficult to compare two such fractions directly. However, we know how to find fractions equivalent to two fractions with the same denominator.

Let us see how we can use it:
\(\frac{4}{5}=\frac{4 \times 9}{5 \times 9}=\frac{36}{45}\)
\(\frac{7}{9}=\frac{7 \times 5}{8 \times 5}=\frac{35}{45}\)
Clearly, \(\frac{36}{45}>\frac{35}{45}\)
So, \(\frac{4}{5}>\frac{7}{9}\)!
Let us try this for another pair: \(\frac{7}{9}\) and \(\frac{17}{21}\).
63 is a common multiple of 9 and 21. We can then write:
\(\frac{7}{9}=\frac{7 \times 7}{9 \times 7}=\frac{49}{63}, \frac{17}{21}=\frac{17 \times 3}{21 \times 3}=\frac{51}{63}\)
Clearly, \(\frac{49}{63}<\frac{51}{63}\). So, \(\frac{7}{9}<\frac{17}{21}\)!
Let’s Summarise!
Steps to compare the sizes of two or more given fractions:
- Step 1: Change the given fractions to equivalent fractions so that they all are expressed with the same denominator/same fractional unit.
- Step 2: Now, compare the equivalent fractions by simply comparing the numerators, i.e., the number of fractional units each has.
Addition and Subtraction of Fractions Class 6 Notes
Meena’s father made some chikki. Meena ate \(\frac{1}{2}\) of it and her younger brother ate \(\frac{1}{4}\) of it. How
much of the total chikki did Meena and her brother eat together?


We can arrive at the answer by visualising it. Let us take a piece of chikki and divide it into two halves first like this. Meena ate \(\frac{1}{2}\) of it as shown in the picture.

Let us now divide the remaining half into two further halves as shown. Each of these pieces is \(\frac{1}{4}\) of the whole chikki.

Meena’s brother ate \(\frac{1}{4}\) of the whole chikki, as is shown in the picture.

The total chikki eaten is \(\frac{1}{2}\) (by Meena) and \(\frac{1}{4}\) (by her brother)
The total chikki eaten is = \(\frac{1}{2}+\frac{1}{4}\)
= \(\frac{1}{4}+\frac{1}{4}+\frac{1}{4}\)
= 3 × \(\frac{1}{4}\)
= \(\frac{3}{4}\)
How much of the total chikki is remaining?
![]()
Adding Fractions with the Same Fractional Unit or Denominator
Example: Find the sum of \(\frac{2}{5}\) and \(\frac{1}{5}\).
Let us represent both using the rectangular strips. In both fractions, the fractional unit is the same \(\frac{1}{5}\), so, each strip will be divided into 5 equal parts. So \(\frac{2}{5}\) will be represented as—

And \(\frac{1}{5}\) will be represented as—

Adding the two given fractions is the same as finding out the total number of shaded parts, each of which represents the same fractional unit \(\frac{1}{5}\).
In this case, the total number of shaded parts is 3. Since each shaded part represents the fractional unit \(\frac{1}{5}\), we see that the 3 shaded parts together represent the fraction \(\frac{3}{5}\).

Therefore, \(\frac{2}{5}+\frac{1}{5}=\frac{3}{5}\)!
Example: Find the sum of \(\frac{4}{7}\) and \(\frac{6}{7}\).
Let us represent both again using the rectangular strip model. Here in both fractions, the fractional unit is the same, i.e., \(\frac{1}{7}\), so each strip will be divided into 7 equal parts. Then \(\frac{4}{7}\) will be represented as—

and \(\frac{6}{7}\) will be represented as—

In this case, the total number of shaded parts is 10, and each shaded part represents the fractional unit \(\frac{1}{7}\), so, the 10 shaded parts together represent the fraction \(\frac{10}{7}\) as seen here.

Adding Fractions with different fractional Units or Denominators
Example: Find the sum of \(\frac{1}{4}\) and \(\frac{1}{3}\).
To add fractions with different fractional units, first convert the fractions into equivalent fractions with the same denominator/fractional unit. In this case, the common denominator can be made 3 × 4 = 12, i.e., we can find equivalent fractions with fractional unit \(\frac{1}{12}\).
Let us write the equivalent fraction for each given fraction.
\(\frac{1}{4}=\frac{1 \times 3}{4 \times 3}=\frac{3}{12}, \quad \frac{1}{3}=\frac{1 \times 4}{3 \times 4}=\frac{4}{12}\)
Now, \(\frac{3}{12}\) and \(\frac{4}{12}\) have the same fractional unit, i.e., \(\frac{1}{12}\).
Therefore, \(\frac{1}{4}+\frac{1}{3}=\frac{3}{12}+\frac{4}{12}=\frac{7}{12}\).
This method of addition, which works for adding any number of fractions, was first explicitly described in general by Brahmagupta in the year 628 CE! We will describe the history of the development of fractions in more detail later in the chapter. For now, we simply summarise the steps in Brahmagupta’s method for addition of fractions.
Brahmagupta’s method for adding fractions
- Find equivalent fractions so that the fractional unit is common for all fractions. This can be done by finding a common multiple of the denominators (e.g., the product of the denominators, or the smallest common multiple of the denominators).
- Add these equivalent fractions with the same fractional units. This can be done by adding the numerators and keeping the same denominator.
- Express the result in the lowest terms if needed.
Let us carry out another example of Brahmagupta’s method.
Example 1: Find the sum of \(\frac{2}{3}\) and \(\frac{1}{5}\).
The denominators of the given fractions are 3 and 5. The lowest common multiple of 3 and 5 is 15. Then we see that \(\frac{2}{3}=\frac{2 \times 5}{3 \times 5}=\frac{10}{15}, \frac{1}{5}=\frac{1 \times 3}{5 \times 3}=\frac{3}{15}\)
Therefore, \(\frac{2}{3}+\frac{1}{5}=\frac{10}{15}+\frac{3}{15}=\frac{13}{15}\).
Example 2: Find the sum of \(\frac{1}{6}\) and \(\frac{1}{3}\).
The smallest common multiple of 6 and 3 is 6.
\(\frac{1}{6}\) will remain \(\frac{1}{6}\).
\(\frac{1}{3}=\frac{1 \times 2}{3 \times 2}=\frac{2}{6}\)
Therefore, \(\frac{1}{6}+\frac{1}{3}=\frac{1}{6}+\frac{2}{6}=\frac{3}{6}\).
The fraction \(\frac{3}{6}\) can now be re-expressed in lowest terms, if desired. This can be done by dividing both the numerator and denominator by 3 (the biggest common factor of 3 and 6):
\(\frac{3}{6}=\frac{3 \div 3}{6 \div 3}=\frac{1}{2}\)
Therefore, \(\frac{1}{6}+\frac{1}{3}=\frac{1}{2}\).
![]()
Subtraction of Fractions with the same Fractional Unit or Denominator
Brahmagupta’s method also applies when subtracting fractions!
Let us start with the problem of subtracting \(\frac{4}{7}\) from \(\frac{6}{7}\), i.e., what is \(\frac{6}{7}\) – \(\frac{4}{7}\)?
To solve this problem, we can again use the rectangular strips. In both fractions, the fractional unit is the same i.e. \(\frac{1}{7}\). Let us first represent the bigger fraction using a rectangular strip model as shown:

Each shaded part represents \(\frac{1}{7}\). Now, we need to subtract \(\frac{4}{7}\). To do this let us remove 4 of the shaded parts:

So, we are left with 2 shaded parts, i.e., \(\frac{6}{7}-\frac{4}{7}=\frac{2}{7}\).
Try doing this same exercise using the number line.
Subtraction of Fractions with Different Fractional Units or Denominators
Example: What is \(\frac{3}{4}\) – \(\frac{2}{3}\)?
As we already know the procedure for subtraction of fractions with the same fractional units, let us convert each of the given fractions into equivalent fractions with the same fractional units.

Brahmagupta’s method for subtracting two fractions:
- Convert the given fractions into equivalent fractions with the same fractional unit, i.e., the same denominator.
- Carry out the subtraction of fractions having the same fractional units. This can be done by subtracting the numerators and keeping the same denominator.
- Simplify the result into the lowest terms if needed.
A Pinch of History Class 6 Notes
Do you know what a fraction was called in ancient India? It was called binna in Sanskrit, which means ‘broken’. It was also called bhaga or ansha meaning ‘part’ or ‘piece’. The way we write fractions today, globally, originated in India. In ancient Indian mathematical texts, such as the Bakshali manuscript (from around the year 300 CE), when they wanted to write \(\frac{1}{2}\), they wrote it as \(\frac{1}{2}\) which is indeed very similar to the way we write it today! This method of writing and working with fractions continued to be used in India for the next several centuries, including by Aryabhata (499 CE), Brahmagupta (628 CE), Sridharacharya (c. 750 CE), and Mahaviracharya (c. 850 CE), among others. The line segment between the numerator and denominator in ‘\(\frac{1}{2}\)’ and in other fractions was later introduced by the Moroccan mathematician Al-Hassar (in the 12th century). Over the next few centuries, the notation then spread to Europe and around the world.
Fractions had also been used in other cultures such as the ancient Egyptian and Babylonian civilizations, but they primarily used only fractional units, that is, fractions with a 1 in the numerator. More general fractions were expressed as sums of fractional units, now called ‘Egyptian fractions’. Writing numbers as the sum of fractional units, e.g., \(\frac{19}{24}=\frac{1}{2}+\frac{1}{6}+\frac{1}{8}\), can be quite an art and leads to beautiful puzzles. We will consider one such puzzle below.
General fractions (where the numerator is not necessarily 1) were first introduced in India, along with their rules of arithmetic operations like addition, subtraction, multiplication, and even division of fractions. The ancient Indian treatises called the ‘Sulbasutras’ show that even during Vedic times, Indians had discovered the rules for operations with fractions. General rules and procedures for working with and computing with fractions were first codified formally and in a modern form by Brahmagupta.
Brahmagupta’s methods for working with and computing with fractions are still what we use today. For example, Brahmagupta described how to add and subtract fractions as follows:
“By the multiplication of the numerator and the denominator of each of the fractions by the other denominators, the fractions are reduced to a common denominator. Then, in case of addition, the numerators (obtained after the above reduction) are added. In case of subtraction, their difference is taken.’’ (Brahmagupta, Brahmasphutasiddhanta, Verse 12.2, 628 CE)
![]()
The Indian concepts and methods involving fractions were transmitted to Europe via the Arabs over the next few centuries and they came into general use in Europe around the 17th century and then spread worldwide.
It is easy to add up fractional units to obtain the sum 1, if one uses the same fractional unit,
e.g., \(\frac{1}{2}+\frac{1}{2}=1, \frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1, \frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=1\), etc.
However, can you think of a way to add fractional units that are all different to get 1?
It is not possible to add two different fractional units to get 1.
The reason is that \(\frac{1}{2}\) is the largest fractional unit, and \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1.
To get different fractional units, we would have to replace at least one of the \(\frac{1}{2}\)’s with some smaller fractional unit – but then the sum would be less than 1! Therefore, two different fractional units can’t add up to 1. We can try to look instead for a way to write 1 as the sum of three different fractional units.
Can you find three different fractional units that add up to 1?
It turns out there is only one solution to this problem (up to changing the order of the 3 fractions)! Can you find it? Try to find it before reading further.
Here is a systematic way to find the solution. We know that \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\) = 1. To get the fractional units to be different, we will have to increase at least one of the \(\frac{1}{3}\)’s and decrease at least one of the other \(\frac{1}{3}\)’s to compensate for that increase. The only way to increase \(\frac{1}{3}\) to another fractional unit is to replace it with \(\frac{1}{2}\). So \(\frac{1}{2}\) must be one of the fractional units.
![]()
Now \(\frac{1}{2}+\frac{1}{4}+\frac{1}{4}\) = 1. To get the fractional units to be different, we will have to increase one of the \(\frac{1}{2}\)’s and decrease the other \(\frac{1}{4}\) to compensate for that increase. Now the only way to increase \(\frac{1}{4}\) to another fractional unit, that is different from \(\frac{1}{2}\), is to replace it with \(\frac{1}{3}\). So two of the fractions must be \(\frac{1}{2}\) and \(\frac{1}{3}\)! What must be the third fraction then, so that the three fractions add up to 1? This explains why there is only one solution to the above problem.

What if we look for four different fractional units that add up to 1?
Relation to Number Sequences Class 6 Notes
Subtraction of fractions with the same fraction (Unit or Denominator)
\(\frac{3}{5}-\frac{2}{5}\)
As the fractional unit is the same i.e. \(\frac{1}{5}\)
Represent \(\frac{3}{5}\) diagrammatically

If we remove \(\frac{2}{5}\) from \(\frac{3}{5}\) the figure will look like

The fraction remaining will be \(\frac{1}{5}\).
On a number line
\(\frac{3}{5}-\frac{2}{5}\)
Divide 1 unit on the number line in 5 parts.

Subtracting when a fractional unit of fractions is different
Steps to be followed:
- Find the LCM of the denominator.
- Make LCM the fractional units, for the fractions to be subtracted.
- Subtract the numerators while keeping the common fractional unit for the denominator.
- Simplify the answer to the lowest fraction.
Example:
\(\frac{2}{3}-\frac{2}{5}\)
Solution:
Here LCM of 3 and 5 is 15.
Fractional units for both fractions should be \(\frac{1}{15}\).

————————————————————————————-
A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects. The other way around, we can say that a fraction is an operation on a number.
A Fraction
A fraction means a part of a group or of a region. \(\frac { 3 }{ 4 }\) is a fraction. We read it as “Three-fourths”.
Here, 4 stands for the number of equal parts into which the whole has been divided and 3 stands for the number of equal parts which have been taken out. It is to be noted that while expressing a situation of counting parts to write a fraction, all parts must be equal. Here, 3 is called the numerator and 4 is called the denominator. The numerator and denominator can be identified for any fraction.
Fractions can be represented on a number line. Any fraction has a point associated with it on the number line.
We know that a fraction essentially has a numerator and a denominator which can be identified for any fraction under consideration. If the numerator is less than the denominator, then the fraction is called a proper fraction.
For example:
\(\frac { 1 }{ 2 }\), \(\frac { 3 }{ 4 }\), \(\frac { 5 }{ 8 }\), \(\frac { 0 }{ 2 }\), etc.
A fraction, whose numerator is bigger than the denominator, is called an improper fraction.
For example: \(\frac { 5 }{ 4 }\), \(\frac { 7 }{ 2 }\), \(\frac { 11 }{ 3 }\), etc.
Improper fractions can be written as a combination of a whole and a part, and are then called mixed fractions.
For example: \(\frac { 5 }{ 4 }\) when written as 1\(\frac { 1 }{ 4 }\) is called a mixed fraction.
To express an improper fraction as a mixed fraction, we divide the numerator by denominator to get the quotient and the remainder. Then the mixed fraction can be written as
Quotient \(\frac { Remainder }{ Divisor }\)
To express a mixed fraction as an improper fraction, we multiply the whole with the denominator and add the numerator to it. Then the mixed fraction can be written as
\(\frac { (Whole\quad \times \quad Denominator)+Numerator }{ Denominator }\)
Two fractions are said to be equivalent if they represent the same quantity. Each proper or improper fraction has infinitely many equivalent fractions. To find an equivalent fraction of a given fraction, we multiply or divide both the numerator and the denominator of the given fraction by the same nonzero number. If two fractions are equivalent, then the product of the numerator of the first and the denominator of the second is equal to the product of the denominator of the first and the numerator of the second. This rule proves to be useful to find equivalent fractions.
The simplest form of a Fraction
A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1, i.e., they are coprime natural numbers. Thus, to find the equivalent fraction in the simplest form, we find the HCF of the numerator and the denominator. Then, we divide both of them by their HCF and get the equivalent fraction in the simplest form.
Like Fractions
Fractions, whose denominators are the same, are called like fractions.
For example: \(\frac { 1 }{ 9 }\), \(\frac { 4 }{ 9 }\), \(\frac { 7 }{ 9 }\) are all like fractions whereas \(\frac { 1 }{ 19 }\) and \(\frac { 1 }{ 20 }\) are not like fractions. The latter are called unlike fractions as their denominators are different.
Comparing Fractions
For fractions with the same numerators, the smaller the denominator, the greater the fraction.
For fractions with the same denominators, the greater the numerator, the greater the fraction.
Comparing like fractions
Since the like fractions are fractions with the same denominator, therefore, to compare two like fractions, it is just sufficient to compare their numerators. Greater the numerator, greater the fraction.
We know that in two fractions with the same denominator, one fraction with a bigger numerator is larger. Since in such cases the denominators are the same, i.e., these are like fractions, therefore only numerators are to be compared, so these comparisons are easy to make.
Comparing unlike fractions
We know that unlike fractions are fractions with different denominators. Now if their numerators are the same, then smaller the denominator, greater the fraction. However, if the two fractions have different numerators, then we find equivalent fractions of both and choose one from each such that their denominators are the same.
Then for comparison, greater the numerator, greater the fraction. Thus, we can find the greater of the two given fractions with different numerators and different denominators.
In daily life situations, sometimes we have to add two fractions and sometimes we have to subtract one from the other. This is respectively known as addition and subtraction of fractions.
An example of the addition of fractions is as follows:
Manish bought 2\(\frac { 1 }{ 2 }\) kg sugar whereas Preeti bought 1\(\frac { 1 }{ 2 }\) kg sugar. Find the total amount of sugar bought by them.
An example of subtraction of fractions is as follows:
The teacher taught \(\frac { 2 }{ 5 }\) of the book. Yash revised \(\frac { 2 }{ 5 }\) more on his own. How much does he still have to revise?
Adding or Subtracting like fractions
Addition of two or more like fractions can be carried out as follows:
Step 1. Add the numerators.
Step 2. Retain the denominator (common).
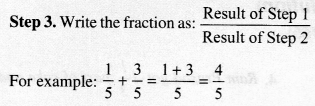
Subtraction of two fractions can be carried out as follows:
Step 1. Subtract the smaller numerator from the bigger numerator.
Step 2. Retain the denominator (common).
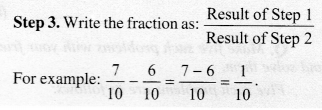
Adding and Subtracting Fractions
To add and subtract fractions that do not have the same denominator, we convert them into equivalent fractions with the same denominators and then proceed as above.