Force and Laws of Motion Class 9 Extra Questions Science Chapter 9
Extra Questions for Class 9 Science Chapter 9 Force and Laws of Motion
Force and Laws of Motion Class 9 Extra Questions Very Short Answer Questions
Question 1.
Name the scientist who proved for the first time that objects move with constant speed when no force acts on them.
Answer:
Galileo.
Question 2.
Why do bicycles begin to slow down when we stop pedalling?
Answer:
This is because of the frictional forces acting opposite to the direction of motion.
Question 3.
Which law of motion gives the measure of force?
Answer:
Newton’s second law of motion.
Question 4.
Write the C.G.S unit of force.
Answer:
Dyne.
Question 5.
Can every force produce motion in every object?
Answer:
No.
Question 6.
When a force is applied to a body, what are the two essential effects it can produce?
Answer:
- It can bring about the change in the state of motion of a body or
- It can deform a body, i.e., it can change its shape.
Question 7.
Define 1 newton force.
Answer:
1 newton is the magnitude of force which produces an acceleration of 1 m/s2 in a body of mass 1 kg.
Question 8.
What do you mean by an impact force?
Answer:
The force produced by the impact of a fast moving object on another is called impact force.
Question 9.
Define force of friction.
Answer:
The force acting between any two surfaces in contact and tending to oppose motion is called force of friction.
Question 10.
Define electrostatic force.
Answer:
The force exerted by an electrically charged body is called electrostatic force.
Question 11.
If the body is found to be accelerated, is the force acting on it balanced or unbalanced?
Answer:
Unbalanced.
Question 12.
What do balanced forces usually do to a body?
Answer:
Balanced forces usually produce a change in the shape of the body.
Question 13.
When a body moves on flat surface, will its speed change?
Answer:
No.
Question 14.
What did Galileo conclude on the basis of his experiments on the motion of objects?
Answer:
A body continues to move with the same velocity if no unbalanced force acts on it.
Question 15.
What do you mean by a resultant force?
Answer:
When two or more forces act on a body simultaneously, then the single force which produces the same effect as produced by all the forces acting together is known as the resultant force.
Question 16.
Do action and reaction act on the same body?
Answer:
No, action and reaction act on different bodies.
Question 17.
Plot a graph between force applied on a body and the acceleration produced in the given mass, assuming that the magnitude of force is constantly changing.
Answer:
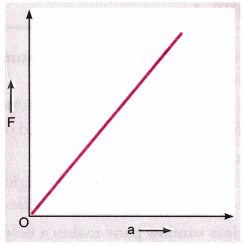
Question 18.
Write the SI unit of impulse.
Answer:
Ns.
Question 19.
What is the total momentum of a bullet and a gun before firing?
Answer:
Zero.
Question 20.
Name the principle on which a rocket works.
Answer:
Newton’s third law of motion
Question 21.
Body A is heavier than body Question Which has more inertia?
Answer:
A has more inertia.
Question 22.
A body is moving with uniform acceleration. Is its momentum constant?
Answer:
No.
Question 23.
Name the physical quantity that corresponds to the rate of change of momentum.
Answer:
Force.
Question 24.
Which principle is involved in the working of a jet plane?
Answer:
Newton’s third law of motion.
Question 25.
Why mass is sometimes called coefficient of linear inertia?
Answer:
It is easier to pull a lighter body than a heavier body. Therefore, more the mass more will be the inertia. That is why mass is sometimes termed as coefficient of linear inertia.
Question 26.
When a force acting on a body has equal and opposite reaction, then why should the body move at all?
Answer:
The action and reaction act on different bodies. Therefore, the body moves under the action of the acting force.
Question 27.
Does Newton’s third law apply to a system where bodies do not actually touch each other?
Answer:
Yes, whenever the bodies are in actual contact or even if there is an interaction between the bodies (e.g., attraction or repulsion between two magnets charges, etc.), Newton’s third law is applicable.
Question 28.
Suppose a ball of mass m is thrown vertically upwards with an initial speed v, its speed decreases continuously till it becomes zero. Therefore, the ball begins to fall downward and attains the speed v again before striking the ground. It implies that the magnitude of initial and final momenta of the ball are same. Yet, it is not an example of conservation of momentum. Explain why.
Answer:
Law of conservation of momentum is applicable to isolated system (no external force is applied). In this case, the change in velocity is due to the gravitational force of earth.
Force and Laws of Motion Class 9 Extra Questions Short Answer Questions-I
Question 1.
What is the ratio of SI units to CGS units of momentum? How do you measure the effect of an impulsive force on the body?
Answer:
A ratio of SI units to CGS units of momentum is (kg m/s)/(g cm/s) i.e., 10s.
The effect of an impulse force on the body is measured only in terms of impulse.
Question 2.
On which factors does friction depend?
Answer:
The force of friction is directly proportional to the weight of the body sliding over the surface. The force of friction also depends on the nature of the surfaces in contact.
Question 3.
A bullet fired against a glass window pane makes a hole in it, and the glass pane is not cracked. But on the other hand, when a stone strikes the same glass pane, it gets smashed. Why is it so?
Answer:
When the bullet strikes the glass pane, the part of the glass pane which comes in contact with the bullet immediately shares the large velocity of bullet and makes a hole, while the remaining part of the glass remains at rest and is therefore not smashed due to inertia of rest.
But when a slow moving stone strikes the same glass pane, the various parts of the glass pane gets enough time to share the velocity of the stone, and the glass is smashed.
Question 4.
Why can a small mass such as a bullet kill a person when fired from a gun?
Answer:
It is so because even if the mass of the bullet is small, it moves out of the gun with a very high velocity, due to which the momentum produced is high (p = mv). This high momentum of the bullet kills a person.
Question 5.
Why does a boat tend to leave the shore, when passengers are alighting from it?
Answer:
When the passengers alight from the boat, they push the boat in backward direction. As a result, the boat has a tendency to slip back into water. This difficulty is usually overcome by the boatman by tying the boat to some rigid support.
Question 6.
Describe our walking in terms of Newton’s third law of motion.
Answer:
When we walk on the ground or road, our foot pushes the ground backward (action) and the ground pushes our foot forward (reaction). Thus, the forward reaction exerted by the ground on our foot makes us walk forward.
Question 7.
There are three solids made up of aluminium, steel and wood, of the same shape and same volume. Which of them would have highest inertia? [NCERT Exemplar]
Answer:
Steel has the highest inertia. As the mass is a measure of inertia, the ball of same shape and size, having more mass than other balls will have highest inertia. Since steel has greatest density and greatest mass, therefore, it has highest inertia.
Question 8.
Why does a cricket player moves his hand backward while catching the ball?
Answer:
A fast moving cricket ball has a large momentum. In stopping or catching this ball, its momentum has reduced to be zero. Now, when a cricket player moves back his hands on catching the fast ball, then the time taken to reduce the momentum of ball to zero is increased. Due to more time taken to stop the ball, the rate of change of momentum of ball is decreased and hence a small force is exerted on the hands of player. So, the hands of player do not get hurt.
Question 9.
Two identical bullets are fired one by a light rifle and the other by a heavy rifle with the same force. Which rifle will hurt the shoulder more and why? [NCERT Exemplar]
Answer:
According to conservation of momentum, the rifle recoils with same momentum as that of bullet. As momentum = mass X velocity; so light rifle will recoil with larger velocity and hence, will hurt the shoulder more.
Question 10.
Water sprinkler used for grass lawns begins to rotate as soon as as the water is supplied. Explain the principle on which it works. [NCERT Exemplar]
Answer:
The working of the rotation of sprinkler is based on third law of motion. As the water comes out of the nozzle of the sprinkler, an equal and opposite reaction force comes into play. So the sprinkler starts rotating.
Force and Laws of Motion Class 9 Extra Questions Short Answer Questions—II
Question 1.
Deduce Newton’s first law from the second law.
Answer:
According to second law, F = ma
If F = 0, a =0 since m ≠ 0,
But a = \(\frac{v-u}{t}\)
or, v – u =0 so, v = u for whatever time t is taken.
This means that the object will continue moving with uniform velocity, u throughout the time, t. If u is zero then v will also be zero. That is, the object will remain at rest.
Question 2.
When small boy is trying to push a heavy stone, mention various forces acting on the stone.
Answer:
The various forces acting on the stone are:
- The gravitational force exerted by the earth which pulls the stone downwards.
- The force of reaction exerted by the ground on the stone vertically upwards.
- The force of pushing exerted by the boy.
- The force of friction exerted by the stone.
When a small boy tries to push a heavy stone, then all these forces are balanced, and therefore the stone does not move.
Question 3.
Describe in brief an activity to illustrate the property of inertia of rest.
Answer:

- Make a pile of similar carom coins on a table, as shown in figure.
- Attempt a sharp horizontal hit at the bottom of the pile using another carom coin or the striker. If the hit is strong enough, the bottom coin moves out quickly. Once the lowest coin is removed, the inertia of the other coins makes them ‘fall’ vertically on the table.
- The inertia of coins tries to maintain its state of rest even when one of the coin moves out.
Question 4.
Give few examples of Newton’s third law of motion.
Answer:
- Jet aeroplanes and rockets work on the principle of third law of motion.
In this case, the hot gases come out of a nozzle with great force, i.e., action and the rocket moves ‘ with high speed upwards as a reaction. - If we fill a balloon with air and hold it with its mouth downwards, then when release the balloon, the air rushes out vertically downwards (action). The balloon moves vertically upwards (reaction).
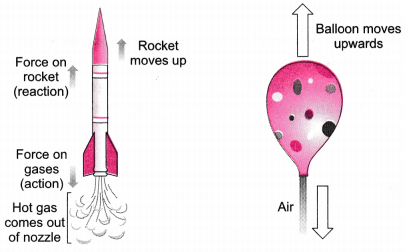
Question 5.
Two friends on roller-skates are standing 5 m apart facing each other. One of them throws a ball of 2 kg towards the other, who catches it. How will this activity affect the position of the two? Explain your answer. [NCERT Exemplar]
Answer:
Separation between them will increase. Initially the momentum of both of them are zero as they are at rest. In order to conserve the momentum the one who throws the ball would move backward. The second will experience a net force after catching the ball and therefore will move backwards that is in the direction of the force.
Question 6.
Why does an athlete puts some sands or cushion on the ground while high jumping?
Answer:
When a high jumper falls on a soft landing site(such as cushion or a heap of sand), then the jumper takes a longer time to come to stop. The rate of change of momentum of athlete is less due to which a smaller stopping force acts on the athlete. And the athlete does not get hurt. Thus, the cushion or sand, being soft, reduces the athlete’s momentum more gently. If however, a high jumping athlete falls from a height on to hard ground, then his momentum will be reduced to zero in a very short time. The rate of change of momentum will be large due to which a large opposing force will act on the athlete. This can cause serious injuries to the athlete.
Question 7.
Describe balanced forces with the help of two examples.
Answer:
If the resultant of various forces acting on a body is zero, the forces are said to be ‘balanced forces’. These forces do not change the speed but usually change the shape of an object.
Examples:
(a) Consider a wooden block lying on a table, the strings tied to its two opposite faces, as shown in the figure.
If we pull at point P, it begins to move towards left. If we pull at point Q, it begins to move . towards right. But if we pull from both the sides with equal force, the block does not move. The two forces have now balanced each other.
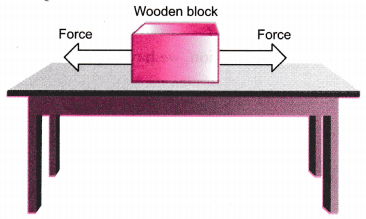
(b) In a tug-of-war, the two teams pull the rope with equal effort; the rope is not moved in any direction. This is clearly because the forces exerted by the two teams are equal and opposite and thus get balanced.
Question 8.
Why do the driver and the person seated in front seat need a seat belt?
Answer:
In a car accident, a fast running car stops suddenly. Due to this the car’s large momentum is reduced to zero in a very short time. The stretchable seat belts tightened by the passengers of the car increases time taken by the passengers to fall forward. Due to longer time, the rate change of momentum of passengers is reduced and hence less stopping force acts on them. So, the passengers may either not get injured at all or may get less injuries. It is obvious that seat belts reduce the passengers’ momentum more gently and hence prevent injuries.
Force and Laws of Motion Class 9 Extra Questions Long Answer Questions
Question 1.
Describe Newton’s first law of motion in detail, giving examples.
Answer:
According to Newton’s first law of motion, a body at rest or in uniform motion will remain at rest or in uniform motion unless an unbalanced force acts upon it. This law consists of three parts:
- The first part says that a body at rest continues in its state of rest. For instance, a boy standing in a train falls backward when the train suddenly starts moving forward. This is because when the bus moves, the lower part of his body begins to move along with the train while the upper part of his body continues to remain at rest due to inertia.
- The second part says that a body in uniform motion continues to move in straight line path with a uniform speed, e.g., when a moving train stops suddenly a person sitting in it falls forward. This is because as the train stops, the lower part of the person’s body comes to rest along with the bus while upper part of his body continues to remain in ^notion due to inertia of motion and thus he falls forward.
- Third part says that a body moving with a uniform speed in a straight line cannot change its direction of motion by itself. For example, when a bus takes a sharp turn, a person sitting in the bus gets force acting away from the centre of the curved path due to his tendency to move in the original direction.
Question 2.
Derive the mathematical relation of Newton’s second law of motion.
Answer:
Consider an object of mass m moving along a straight line with an initial velocity u (say). It is uniformly accelerated to velocity u in time t by the application of a constant force F in time t.
Then, initial momentum of the object = mu
p1 =mu
Final momentum of the object = mv
p2 = mv
∴ Change in momentum = mv – mu = m(v – u)
The rate of change in momentum = \(\frac{m \times(v-u)}{t}\)
According to Newton’s second law of motion, we have
F ∝ \(\frac{m(v-u)}{t}\)
F = km\(\frac{(v-u)}{t}\)
F = kma ……….(1)
Here, a = \(\frac{v-u}{t}\) = the rate of change of velocity.
= acceleration
k = a constant of proportionality
Putting m = 1kg, a = 1 ms-2
F becomes 1 N.
So, 1 N = 4 × 1kg × 1 ms-2
∴ k = 1
From equation (1), we have
F = ma
This represents the second law of motion.
Thus, the second law of motion gives a method to measure the force acting on an object as a product of its mass and acceleration.
Question 3.
Derive the mathematical formula of conservation of momentum.
Answer:
To explain conservation of momentum, let us take the following example. Consider two balls A and B having masses ml andm, respectively. Let the initial velocity of ball A be u1, and that of ball B be u2 (u1 > u2). Their collision takes place for a very short interval of time t and after that A and B start moving with velocities v1 and v2 (now v1 < v2) respectively as shown in Figure.
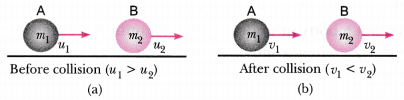
The momentum of ball A before and after the collision is miul and mlvl respectively. If there are no external forces acting on the body, then the rate of change of momentum of ball A, during the collision will be
= \(\frac{m_{1}\left(v_{1}-u_{1}\right)}{t}\)
and, similarly the rate of change in momentum of ball B
= \(\frac{m_{2}\left(v_{2}-u_{2}\right)}{t}\)
Let F12 be the force exerted by hall A on B F21 be the force exerted by hall B on A. Then, according to Newton’s second law of motion
F12 = \(\frac{m_{1}\left(v_{1}-u_{1}\right)}{t}\) and F21 = \(\frac{m_{2}\left(v_{2}-u_{2}\right)}{t}\)
According to Newton’s third law of motion, we have
F12 = -F21
or \(\frac{m_{1}\left(v_{1}-u_{1}\right)}{t}=-\frac{m_{2}\left(v_{2}-u_{2}\right)}{t}\)
or m1v1 – m1u1 = -m2v2 + m2u2 or m1u1 + m2u2 =m1v1 + m2v2
i.e..Total momentum before collision = Total momentum after collision
Thus, we find that in a collision between the two balls the total momentum before and after the collision remains unchanged or conserved provided no net force acts on the system. This result is law of conservation of momentum.
Question 4.
What is the relationship between mass and inertia? Explain with the help of examples.
Answer:
The mass of a body is a measure of its inertia. It means larger the mass of a body, larger will be the inertia offered by the body to change its state of motion. The following examples will clarify the concept:
- When we kick a football, it flies a long way but at the same time if we kick a stone of the same size, it hardly moves, as the stone resists a change in its motion better than the football because of its more mass.
- We can increase the velocity of our bicycle by pedaling harder, i.e., on applying more force. But the same force will produce a negligible change in the motion of a bus, because in comparison to the bicycle, a bus has more tendency to oppose any change in its state of motion because of its larger mass i.e., the bus has more inertia than the bicycle.
The SI unit of mass and inertia is kilogram (kg).
Question 5.
Describe Newton’s third law of motion.
Answer:
According to this law, to every action, there is an equal and opposite reaction.
When an object, say A, exert a force (action) on another object, say B, then B also exerts a force (reaction) on the A. These two forces are always equal in magnitude but opposite in direction.
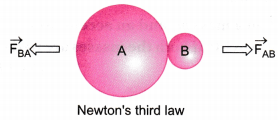
As shown in the above figure, if \(\overrightarrow{\mathbf{F}}_{\mathrm{AB}}\) be the force exerted by body A on B and \(\overrightarrow{\mathbf{F}}_{\mathrm{BA}}\) is the force exerted by B on A, then according to Newton’s third law,
\(\overrightarrow{\mathbf{F}}_{\mathrm{BA}}\) = – \(\overrightarrow{\mathbf{F}}_{\mathrm{AB}}\)
or Force on A by B = – Force on B by A
or Reaction = – Action
This law clarifies that a single force can never exist and that the forces always exist in pairs. The two opposing forces are known as action and reaction. The forces of action and reaction always act on two different bodies.
Numericals
Question 1.
A bullet of 10 g strikes a sand bag at a speed of 103 ms-1 and gets embedded after travelling 5 cm. Calculate
(i) the resistive force exerted by the sand on the bullet.
(ii) the time taken by the bullet to come to rest. [NCERT Exemplar]
Answer:
(i) m = 10 g = \(\frac{10}{100}\) kg, u = 103 m / s, v = 0, s = \(\frac{5}{100}\) m
v2 – u2 = 2as
0 – (103)2 = 2.a.\(\frac{5}{100}\)
a = \(\frac{-1000 \times 1000}{2 \times 5}\) × 100
= -107 ms-2
F = m . a = -105 N
(ii) v = u + at
0 = 103 – 107t
107t = 103
t = \(\frac{10^{3}}{10^{7}}\) = 10-4 s
Question 2.
A body of mass 300 g kept at rest breaks into two parts due to internal forces. One part of mass 200 g is found to move at a speed of 12 m/s towards the east. What will be the velocity of the other part?
Answer:
Initially the body was at rest. The linear momentum of the body is thus p = mu = 0. The body breaks due to internal forces. As the external force acting on it is zero, its linear momentum will remain constant, that is, zero.
p1 = m1v1 = (200 g) × (12 m/s), towards the east.
The linear momentum of the other part must have the same magnitude and should be opposite in direction. It therefore moves towards the west. If its speed is v2, its linear momentum is
p2 = m2v2 = (100 g) × v2.
Now, m1v1 = m2v2.
Thus, (200 g) × (12 m/s) = (100 g) × v2 or, v2 = 24m/s.
The velocity of the other part is 24 m/s towards the west.
Question 3.
A force of 5 N produces an acceleration of 8 ms-2 on a mass m1 and an acceleration of 24 ms-2 on a mass m2. What acceleration would the same force provide if both the masses are tied together? [NCERT Exemplar]
Answer:
We know, T=m a = 5 N or 5kg ms-2

Question 4.
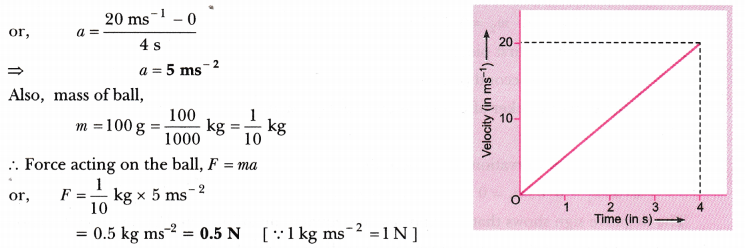
The velocity-time graph of a ball moving on the surface of floor is shown in the figure. Calculate the force acting on the ball, if mass of the ball is 100 g.
Answer:
The velocity-time graph shows that the velocity of the ball at t = 0 is zero. Initial velocity of ball, u = 0
Velocity of ball at t = 4 s is 20 ms-1
That is, final velocity, v = 20 ms-1
Time, t = 4 s
∴ Acceleration of the ball, a = \(\frac{v-u}{t}\)
Question 5.
A bullet of mass 4 g when fired with a velocity of 50 ms-1, can enter a wall up to a depth of 10 cm. How much will be the average resistances offered by the wall?
Answer:
The hindrance offered by the wall to the motion of bullet is called the resistance offered by wall.
Mass of the bullet, m = 4 × 1-3 kg
Initial velocity, Depth, u = 50 ms-1
Depth, s = 10cm = \(\frac{1}{10}\) m
Final velocity, v = 0,
Force, F = ?
We know
v2 = u2 + 2as
v2 – u2 = 2as
0 – (50)2 = 2a × \(\frac{1}{10}\)
or, -2500 = \(\frac{a}{5}\)
⇒ a = -12500ms-1
Force, F = ma = 4 × 10-3 × (-12500)
= -50N
Thus, the average resistance offered = 50 N
Negative sign indicates that the force is acting opposite to the motion.
Question 6.
What is the acceleration produced by a force of 12 newton exerted on an object of mass 3 kg?
Answer:
In this problem, force, F = 12 N
Mass, m = 3 kg
We know that F = m × a,
Putting the given values, we have
12 = 3 × a
a = \(\frac{12}{3}\) m/ s2
or, Acceleration, a = 4 m/s2.
Question 7.
A cracker of mass 100 g explodes into two pieces of equal mass. Show that these two pieces of the cracker fly in opposite direction.
Answer:
Mass of a cracker, m = 100 g = \(\frac{100}{1000}\) kg = 0·1 kg.
Initially, cracker is at rest, i.e. ,u = 0
Therefore, initial momentum of the cracker = mu = 0
After explosion, mass of each piece = \(\frac{0 \cdot 1}{2}\) kg = 0·05 kg
∴ m1 = 0·05 kg and m2 = 0·05 kg
Let, v1 = velocity of first piece
v2 = velocity of second piece Momentum of cracker after explosion = m1v1 + m2v2
= 0·05 v1 + 0·05 v2
Applying law of conservation of momentum
0·05 v1 + 0·05 v2 = 0 or v1 = -v2
The negative sign shows that v1 and v2 are equal in magnitude and opposite in direction.
Thus, two pieces of the cracker fly in opposite directions with same speed.
Question 8.
An iron sphere of mass 1 kg is dropped from a height of 10 m. If the acceleration of sphere is 9.8 ms-2, calculate the momentum transferred to the ground by the ball.
Answer:
Here, initial velocity of sphere, u = 0
Distance travelled, s = 10 m
Acceleration of sphere, a = 9.8 ms-2
Final velocity of sphere when it just reaches the ground can be calculated using
v2 – u2 = 2as
or, v2 – 0 = 2 × 9·8 ms-2 × 10 m = 196 m2s-2
or, v = \(\sqrt{196 \mathrm{m}^{2} \mathrm{s}^{-2}}\) = 14 ms-1
Momentum of the sphere just before it touches the ground = mv
= 1 kg × 14 ms– 1 = 14 kg ms-1
On reaching the ground, the iron sphere comes to rest, so its final momentum is equal to zero according to the law of conservation of momentum.
Momentum transferred to the ground = Momentum of the sphere just before it comes to rest = 14 kg ms-1
Question 9.
A bullet of mass 0.02 kg is fired from a gun weighing 7.5 kg. If the initial velocity of the bullet is 200 m/s, calculate the speed with which the gun recoils.
Answer:
Here, the mass of the bullet, m1 = 0.02 kg
Mass of gun, m2 = 7.5 kg
Velocity of bullet, v1 = 200 m / s
and the speed of gun, v2 = ?
According to law of conservation of momentum, we have
Total momentum of system after firing = Total momentum of system before firing
i.e., m1v1 + m2v2 = 0
(since initial velocities of gun and bullet before firing is zero.)
or, 0.02 × 200 + 7.5 × v2 = 0
or,7.5 × v2 =- 0.02 × 200
or, v2 = \(-\frac{4}{7 \cdot 5}\) = – 0.533
or v2 = – 0.53 m/s
Question 10.
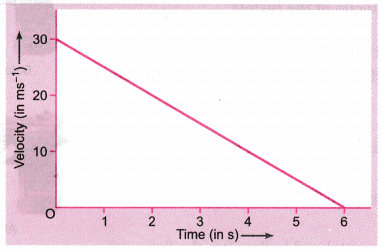
The velocity-time graph of a ball moving on the surface of a floor is shown in the figure. Find the force acting on the ball if the mass of the ball is 50 g.
Answer:
The velocity-time graph shows that velocity of the ball at t = 0 is 30 ms-1. That is, initial velocity of the ball, w = 30 ms-1
The velocity of the ball at t = 6 s is zero.
That is, final velocity of the ball, v = 0
Time, t = 6 s
Acceleration of the ball,
a = \(\frac{v-u}{t}=\frac{0-30 \mathrm{ms}^{-1}}{6 \mathrm{s}}\)
= – 5 ms -2
Negative sign shows that the ball is retarded or decelerated.
Also, mass of ball, m = 50 g = \(\frac{50}{1000}=\frac{1}{20}\) kg
∴ Force acting on the ball, F =ma
= \(\left(\frac{1}{20} \mathrm{kg}\right)\left(-5 \mathrm{ms}^{-2}\right)\)
= – 0.25 kg ms-2
= – 0.25 N [∵ 1 kg ms-2 = 1 N]
Here -ve sign indicates that the force is retarding or stopping force.
Question 11.
A man throws a ball of mass 0.4 kg vertically upwards with a velocity of 10 m/s. What will be its initial momentum? What would be its momentum at the highest point of its reach?
Answer:
Here, m = 0.4 kg, u = 10 m/s
Initial momentum of the ball = mu = 0.4 × 10 = 4 kg m/s At the highest point, velocity of ball is zero,
So momentum of the ball = 0 × 4 × 0 = 0
Question 12.
Which would require a greater force—accelerating a 2 kg mass at 5 ms-2 or a 4 kg mass at 2 ms-2 ?
Answer:
Here, m1 = 2 kg , a1 = 5 ms-2, m2 = 4 kg, a2 = 2 ms-2
F1 = m1a1 = 2 × 5 = 10N
F2 = m2a2 = 4 × 2 = 8 N
F1 > F2
Thus, accelerating a 2 kg mass at 5 ms-2 acceleration would require a greater force.
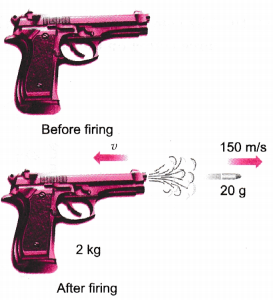
Question 13.
A bullet of mass 20 g is horizontally fired with a horizontal velocity 150 ms-1 from a pistol of mass 2 kg. What is the recoil velocity of the pistol?
Answer:
For bullet: m1 = 20g = 0.02 kg,
u1 = 0 ms-1, v1 = + 150 ms-1
[By convention, the direction of bullet is taken from left to right (positive)]
For pistol: m2 = 2kg, u2 = 0 ms-1,
Total momenta of the pistol and bullet before the fire
= m1u1 + m2u2
= 0.02 kg × 0 ms-1 + 2kg × 0 ms-1
= 0 kg ms-1
Total momenta of the pistol and bullet after the fire
= m1v1 + m2v2
= 0.02 kg × (+ 150 ms-1) + 2kg + v2 ms-1
= (3+ 2v2) kg ms-1
According to the law of conservation of momentum,
Total momenta after the fire = Total momenta before the fire
3 + 2v2 = 0
⇒ 2v2 = – 3
⇒ v2 = —1.5 ms-1
Negative sign indicates that the direction in which the pistol would recoil is opposite to that of bullet (right to left).
Total momenta of the pistol and bullet before the fire
= m1u1 + m2u2
= 0.02 kg × 0 ms-1 + 2 kg × 0 ms-1
= 0 kg ms-1
Total momenta of the pistol and bullet after the fire = m1v1 + m2v2
= 0.02kg × (+150ms-1) + 2kg + v2 ms-1
= (3 + 2v2)kg ms-1
According to the law of conservation of momentum, we have
Total momenta after the fire = Total momenta before the fire
3 + 2v2 = 0
⇒ 2v2 = – 3
⇒ v2 = – 1.5 ms-1
Negative sign indicates that the direction in which the pistol would recoil is opposite to that of bullet (right to left).
Question 14.
A boy of mass 40 kg jumps with a horizontal velocity of 5 ms-1 onto a stationary cart with frictionless wheels. The mass of the cart is 3 kg. What is his velocity as the cart starts moving? Assume that there is no external unbalanced force working in horizontal direction.
Answer:
Suppose the velocity of the boy on the cart, as the cart starts moving is v.
∴ The total momenta of the boy and cart before the interaction
= 40 kg × 5 ms-1 + 3 kg × 0 ms-1
= 200 kg ms-1
Also, the total momenta after the interaction
= (40 + 3) kg × v ms-1
= 43v kg ms-1
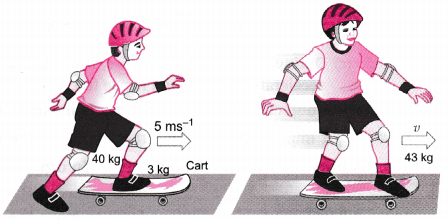
As per the law of conservation of momentum, the total momentum is conserved during the interaction.
In other words,
43 v = 200
or, v = \(\frac{200}{43}\) = 4.65 ms-1
Thus, the boy on cart would move with a velocity of 4.65 ms-1 in the direction in which the boy jumped onto the cart.
Force and Laws of Motion Class 9 Extra Questions HOTS (Higher Order Thinking Skills)
Question 1.
Why does an athlete run a certain distance before taking a leap?
Answer:
An athlete runs a certain distance before taking a leap so that the inertia of motion of his body at the time of leaping may help him in his muscular efforts.
Question 2.
Two balls of the same size of different materials, rubber and iron are kept on the smooth floor of a moving train. The brakes are applied suddenly to stop the train. Will the balls start rolling? If so, in which direction? Will they move with the same speed? Give reasons for your answer. [NCERT Exemplar]
Answer:
Yes, the balls will start rolling in the direction in which the train was moving. Due to the application of the brakes, the train comes to rest but due to inertia the balls try to remain in motion, therefore, they begin to roll. Since the masses of the balls are not the same, therefore, the inertial forces are not same on both the balls. Thus, the balls will move with different speeds.
Question 3.
The velocity-time graph of an object of mass m = 50 g is shown in figure. Observe the graph carefully and answer the following questions.
(a) Calculate the force on the object in time interval 0 to 3 s.
(b) Calculate the force on the object in the time interval 6 to 10 s.
(c) Is there any time interval in which no force acts on the object? Justify your answer.
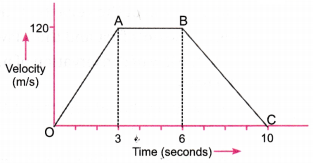
Answer:
(a) Acceleration during interval 0 to 3 s

Force, F2 = ma2 = \(\frac{50^{\circ}}{1000} \times(-30)\) = – 1.5 N
(c) During time interval 3 to 6 s, the velocity of object is constant, so in this time interval, acceleration is zero and hence force, F (= ma) is zero.]
Question 4.
If an object is not moving, does it mean that no force is acting on it?
Answer:
No, it implies that all the forces acting on the body are balanced.
Question 5.
A horse continues to apply a force in order to move a cart with a constant speed. Explain why? [NCERT Exemplar]
Answer:
A horse exerts a continuous force to move the cart with a constant velocity to overcome the force of friction between ground and cart.