We have given these Important Questions for Class 10 Science Chapter 12 Electricity to solve different types of questions in the exam. Previous Year Questions & Important Questions of Electricity Class 10 Science Chapter 12 will help the students to score good marks in the board examination.
Important Questions of Electricity Class 10 Science Chapter 12
Question 1.
A current of 10 A flows through a conductor for two minutes.
(i) Calculate the amount of charge passed through any area of cross section of the conductor.
(ii) If the charge of an electron is 1.6 × 10-19 C, then calculate the total number of electrons flowing. (Board Term I, 2013)
Answer:
Given that: I = 10 A, t = 2 min = 2 × 60 s = 120 s
(i) Amount of charge Q passed through any area of cross-section is given by I = \(\frac { Q }{ t }\)
or Q = I × t ∴ Q = (10 × 120) A s = 1200 C
(ii) Since, Q = ne
where n is the total number of electrons flowing and e is the charge on one electron
∴ 1200 = n × 1.6 × 10-19
or n = \(\frac { 1200 }{ 1.6×10^{-19} }\) = 7.5 × 1021
Question 2.
Define electric current. (1/5, Board Term 1,2017)
Answer:
Electric current is the amount of charge flowing through a particular area in unit time.
Question 3.
Define one ampere. (1/5, Board Term 1,2015)
Answer:
One ampere is constituted by the flow of one coulomb of charge per second.
1 A = 1 C s-1
Question 4.
Name a device that you can use to maintain a potential difference between the ends of a conductor. Explain the process by which this device does so. (Board Term I, 2013)
Answer:
A cell or a battery can be used to maintain a potential difference between the ends of a conductor. The chemical reaction within a cell generates the potential difference across the terminals of the cell, even when no current is drawn from it. When it is connected to a conductor, it produces electric current and, maintain the potential difference across the ends of the conductor.
Question 5.
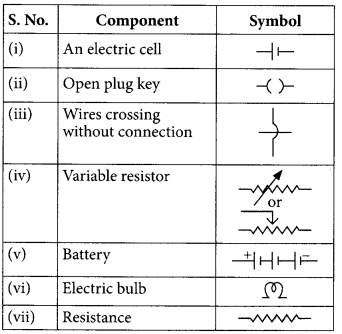
Draw the symbols of commonly used components in electric circuit diagrams for
(i) An electric cell
(ii) Open plug key
(iii) Wires crossing without connection
(iv) Variable resistor
(v) Battery
(vi) Electric bulb
(vii) Resistance (4/5, Board Term 1,2017)
Answer:
Question 6.
A student plots V-I graphs for three samples of nichrome wire with resistances R1, R2 and R3. Choose from the following the statements that holds true for this graph. (2020)
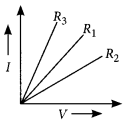
(a) R1 = R2 = R3
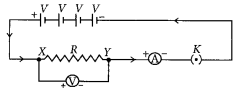
(b) R1 > R2 > R3
(c) R3 > R2 > R1
(d) R2 > R1 > R3
Answer:
(d) : The inverse of the slope of I-V graph gives the resistance of the material. Here the slope of -Rj is highest. Thus, R2 > R1 > R3
Question 7.
State Ohms law. (AI 2019)
Answer:
It states that the potential difference V, across the ends of a given metallic wire in an electric circuit is directly proportional to the current flowing through it, provided its temperature remains the same. Mathematically,
V ∝ I
V = RI
where R is resistance of the conductor.
Question 8.
A V-I graph for a nichrome wire is given below. What do you infer from this graph? Draw a labelled circuit diagram to obtain such a graph. (2020)
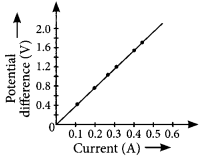
Answer:
As graph is a straight line, so it is clear from the graph that V ∝ I.
The shape of the graph obtained by plotting potential difference applied across conductor against the current flowing v. llmuigh il will be a straight line.
According to ohms law,
V = IR or R = \(\frac { V }{ I }\)
So, the slope of V’-/ graph at any point represents the resistance of the given conductor.
Question 9.
Study the V-I graph for a resistor as shown in the figure and prepare a table showing the values of I (in amperes) corresponding to four different values V (in volts). Find the value of current for V = 10 volts. How can we determine the resistance of the resistor from this graph? (Board Term I, 2016)
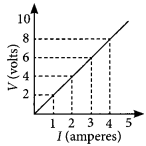
Answer:
Since, the graph is straight line so we can either extrapolate the data or simply mark the value from graph as shown in figure.
| Current, I(A) | Voltage, V(V) |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
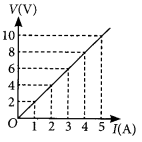
Hence, the value of current for V = 10 volts is 5 amperes (or 5 A).
From Ohm’s law, V = IR,
We can write, R = \(\frac { V }{ I }\)
At any point on the graph, resistance is the ratio of values of V and I. Since, the given graph is straight line (ohmic conductor) so, the slope of graph will also give the resistance of the resistor
R = \(\frac { 10 V }{ 5A }\) = 2Ω
Alternately, R = \(\frac { (8-2)V }{ (4-1)A }\) = \(\frac { 6 V }{ 3A }\) = 2 Ω
Question 10.
V-I graph for a conductor is as shown in the figure
(i) What do you infer from this graph?
(ii) State the law expressed here. (Board Term I, 2014)
Answer:
(i) Refer to answer 8.
(ii) Refer to answer 7.
Question 11.
State Ohm’s law. Draw a labelled circuit diagram to verify this law in the laboratory. If you draw a graph between the potential difference and current flowing through a metallic conductor, what kind of curve will you get? Explain how would you use this graph to determine the resistance of the conductor. (Board Term I, 2016)
Answer:
Refer to answer 7 and 8.
Question 12.
State and explain Ohm’s law. Define resistance and give its SI unit. What is meant by 1 ohm resistance? Draw V-I graph for an ohmic conductor and list its two important features. (Board Term I, 2014)
Answer:
Ohm’s law: Refer to answer 7.
Resistance : It is ihe properly of a conductor lo resist the How of charges through it.
Its SI unit is ohm (Ω). If the potential difference across the two ends of a conductor is 1 V and the current through it is 1 A, then the resistance R, of the conductor is 1 ohm (1 Ω). lvolt
1 ohm = \(\frac { 1 volt }{ 1 ampere }\)
V-I graph for an ohmic conductor can be drawn as given in figure.
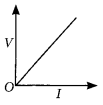
Important feature of V-I graph are:
(i) It is a straight line passing through origin.
(ii) Slope of V-I graph gives the value of resistance of conductor slope = R = \(\frac { V }{ I }\)
Question 13.
Assertion (A) : The metals and alloys are good conductors of electricity.
Reason (R) : Bronze is an alloy of copper and tin and it is not a good conductor of electricity.
(a) Both (A) and (R) are true and (R) is the correct explanation of the assertion (A).
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion (A).
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true. (2020)
Answer:
(c) : Metals and alloys are good conductors of electricity. Bronze is an alloy of copper and tin which are metals and thus is a good conductor of electricity.
Question 14.
A cylindrical conductor of length ‘l’ and uniform area of cross section ‘A’ has resistance ‘R’. The area of cross section of another conductor of same material and same resistance but of length ‘2l’ is (2020)
(a) \(\frac { A }{ 2 }\)
(b) \(\frac { 3A }{ 2 }\)
(c) 2A
(d) 3A
Answer:
(c) : The resistance of a conductor of length!, and area of cross section, A is
R = ρ\(\frac { l }{ A }\)
where ρ is the resistivity of the material.
Now for the conductor of length 21, area of cross-section A’ and resistivity ρ.
R’ = ρ\(\frac { l’ }{ A’ }\) = ρ\(\frac { 2l }{ A’ }\)
But given, R = R’ ⇒ ρ\(\frac { l }{ A }\) = ρ\(\frac { 2l }{ A }\) or A’ = 2A
Question 15.
Assertion (A) : Alloys are commonly used in electrical heating devices like electric iron and heater.
Reason (R): Resistivity of an alloy is generally higher than that of its constituent metals but the alloys have low melting points then their constituent metals.
(a) Both (A) and (R) are true and (R) is the correct explanation of the assertion (A).
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion (A).
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true. (2020)
Answer:
(a)
Question 16.
How is the resistivity of alloys compared with those of pure metals from which they may have been formed? (Board Term I, 2017)
Answer:
The resistivity of an alloy is generally higher than that of its constituent metals.
Question 17.
(i) List three factors on which the resistance of a conductor depends.
(ii) Write the SI unit of resistivity. (Board Term 1, 2015)
Answer:
(i) Resistance of a conductor depends upon the following factors:
(1) Length of the conductor : (Treater the length (I) of the conductor more will be the resistance (R).
R ∝ I
(2) Area ol cross section of the conductor: (Ireater the cross-sectional area of the conductor, less will be the resistance.
R ∝ \(\frac { 1 }{ A }\)
(3) Nature of conductor.
(ii) SI unit of resistivity is Ω m.
Question 18.
Calculate the resistance of a metal wire of length 2m and area of cross section 1.55 × 106 m², if the resistivity of the metal be 2.8 × 10-8 Ωm. (Board Term I, 2013)
Answer:
For the given metal wire,
length, l = 2 m
area of cross-section, A = 1.55 × 10-6 m²
resistivity of the metal, p = 2.8 × 10-8 Ω m
Since, resistance, R = ρ\(\frac { l }{ A }\)
So R = (\(\frac { 2.8×10^{-8}×2 }{ 1.55×10^{-6} }\))Ω
= \(\frac { 5.6 }{ 1.55 }\) × 10-2 Ω = 3.6 × 10-2Ω or R = 0.036Ω
Question 19.
(a) List the factors on which the resistance of a conductor in the shape of a wire depends.
(b) Why are metals good conductors of electricity whereas glass is a bad conductor of electricity ? Give reason.
(c) Why are alloys commonly used in electrical heating devices ? Give reason. (2018)
Answer:
(a) Refer to answer 17 (i).
(b) Metal have very low resistivity and hence they are good conductors of electricity.
Whereas glass has very high resistivity so glass is a bad conductor of electricity.
(c) Alloys are commonly used in electrical heating devices due to the following reasons
(i) Alloys have higher resistivity than metals
(ii) Alloys do not get oxidised or burn readily.
Question 20.
Calculate the resistivity of the material of a wire of length 1 m, radius 0.01 cm and resistance 20 ohms. (Board Term I, 2017)
Answer:
We are given, the length of wire, l = 1 m, radius of wire, r = 0.01 cm = 1 × 10-4 m and resistance, R = 20Ω As we know,
R = ρ\(\frac { l }{ A }\), where ρ is resistivity of the material of the wire.
∴ 20Ω.= ρ\(\frac{l}{\pi r^{2}}\) = ρ\(\frac{1 \mathrm{~m}}{3.14 \times\left(10^{-4}\right)^{2} \mathrm{~m}^{2}}\)
∴ ρ = 6.28 × 10-7 Ω m
Question 21.
A copper wire has diameter 0.5 mm and resistivity 1.6 × 10-8 Ω m. Calculate the length of this wire to make it resistance 100 Ω. How much does the resistance change if the diameter is doubled without changing its length? (Board Term I, 2015)
Answer:
Given; resistivity of copper = 1.6 × 10-8 Ω m, diameter of wire, d = 0.5 mm and resistance of wire, R = 100 Ω
Radius of wire, r = \(\frac {d }{ 2}\) = \(\frac {0.5 }{ 2 }\) mm
= 0.25 mm = 2.5 × 10-4 m
Area of cross-section of wire, A = nr²
∴ A = 3.14 × (2.5 × 10-4)²
= 1.9625 × 10-7 m²
= 1.9 × 10-7 m²
As, R = ρ\(\frac { l }{ A }\)
∴ 100 Ω = \(\frac{1.6 \times 10^{-8} \Omega \mathrm{m} \times l}{1.9 \times 10^{-7} \mathrm{~m}^{2}}\)
l = 1200 m
If diameter is doubled (d’ = 2d), then the area of cross-section of wire will become
A’ = πr² = π(\(\frac { d’ }{ 2 }\))² = π(\(\frac { 2d }{ 2 }\))² = 4A
Now R ∝ \(\frac { 1 }{ A }\), so the resistance will decrease by four times or new resistance will be
R’ = \(\frac { R }{ 4 }\) = \(\frac { 100 }{ 4 }\) = 25Ω
Question 22.
The resistance of a wire of 0.01 cm radius is 10 Ω. If the resistivity of the material of the wire is 50 × 10-8 ohm meter, find the length of the wire. (Board Term I, 2014)
Answer:
Here, r = 0.01 cm = 10-4 m, ρ = 50 × 10-8 Ω m and R = 10 Ω
As, R = ρ\(\frac { l }{ A }\)
or l = \(\frac{R A}{\rho}=\frac{R}{\rho}\left(\pi r^{2}\right)\)
so l = \(\frac{10}{50 \times 10^{-8}} 3.14 \times\left(10^{-4}\right)^{2}\)
= 0.628 m = 62.8 cm
Question 23.
A wire has a resistance of 16 Ω. It is melted and drawn into a wire of half its original length. Calculate the resistance of the new wire. What is the percentage change in its resistance? (Board Term I, 2013)
Answer:
When wire is melted, its volume remains same, so,
V’ = V or A’l’ = Al
Here, l’ = \(\frac { l }{ 2 }\)
Therefore, A’ = 2 A
Resistance, R = ρ\(\frac { l }{ A }\) = 16 Ω
Now, R’ = \(\rho \frac{l^{\prime}}{A^{\prime}}=\rho \frac{(l / 2)}{2 A}=\frac{1}{4} \rho \frac{l}{A}\)
So, R’ = \(\frac { R }{ 4 }\) = \(\frac { 16 }{ 4 }\) = 4 Ω
Percentage change in resistance,
= \(\left(\frac{R-R^{\prime}}{R}\right) \times 100=\left(\frac{16-4}{16}\right)\) × 100 = 75%
Question 24.
If the radius of a current carrying conductor is halved, how does current through it change? (2/5 Board Term I, 2014)
Answer:
If the radius of conductor is halved, the area of cross-section reduced to (\(\frac { 1 }{ 4 }\)) of its previous value.
Since, R ∝ \(\frac { 1 }{ A }\), resistance will become four times
From Ohm’s law, V = IR
For given V, I ∝ \(\frac { 1 }{ R }\)
So, current will reduce to one-fourth of its previous value.
Question 25.
Define resistance of a conductor. State the factors on which resistance of a conductor depends. Name the device which is often used to change the resistance without changing the voltage source in an electric circuit. Calculate the resistance of 50 cm length of wire of cross sectional area 0.01 square mm and of resistivity 5 × 10-8 Ω m. (Board Term I, 2014)
Answer:
Resistance is the property of a conductor to resist the flow of charges through it.
Factors affecting resistance of a conductor:
Refer to answer 17(i)
Rheostat is the device which is often used to change the resistance without changing the voltage source in an electric circuit.
We are given, length of wire, l = 50 cm = 50 × 10-2 m cross-sectional area, A = 0.01 mm²
= 0.01 × 10-6 m²
and resistivity, ρ = 5 x 10-8 Ω m.
As, resistance, R = ρ\(\frac { l }{ A }\)
∴ R = \(\left(\frac{5 \times 10^{-8} \times 50 \times 10^{-2}}{0.01 \times 10^{-6}}\right)\) Ω
= 2.5 Ω
Question 26.
If a person has five resistors each of value \(\frac { 1 }{ 5 }\) Ω, then the maximum resistance he can obtain by connecting them is
(a) 1 Ω
(b) 5 Ω
(c) 10 Ω
(d) 25 Ω (2020)
Answer:
(a) The maximum resistance can be obtained from a group of resistors by connecting them in series. Thus,
Rs = \(\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\) 1 Ω
Question 27.
The maximum resistance which can be made using four resistors each of 2 Ω is
(a) 2 Ω
(b) 4 Ω
(c) 8 Ω
(d) 16 Ω (2020)
Answer:
(c) : A group of resistors can produce maximum resistance when they all are connected in series.
∴ Rs = 2 Ω + 2 Ω + 2 Ω + 2 Ω = 8 Ω
Question 28.
The maximum resistance which can be made using four resistors each of resistance \(\frac { 1 }{ 2 }\) Ω is
(a) 2 Ω
(b) 1 Ω
(c) 2.5 Ω
(d) 8 Ω (2020)
Answer:
(a) The maximum resistance can be produced from a group of resistors by connecting them in series.
Thus, Rs = \(\frac { 1 }{ 2 }\) Ω + H \(\frac { 1 }{ 2 }\) Ω + \(\frac { 1 }{ 2 }\) Ω + \(\frac { 1 }{ 2 }\) Ω = 2 Ω
Question 29.
Three resistors of 10 Ω, 15 Ω and 5 Ω are connected in parallel. Find their equivalent resistance. (Board Term I, 2014)
Answer:
Here, R1 = 10 Ω, R2 =15 Ω, R3 = 5 Ω.
In parallel combination, equivalent resistance, (Req) is given by
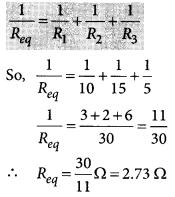
Question 30.
List the advantages of connecting electrical devices in parallel with an electrical source instead of connecting them is series. (Board Term I, 2013)
Answer:
(a) When a number of electrical devices are connected in parallel, each device gets the same potential difference as provided by the battery and it keeps on working even if other devices fail. This is not so in case the devices are connected in series because when one device fails, the circuit is broken and all devices stop working.
(b) Parallel circuit is helpful when each device has different resistance and requires different current for its operation as in this case the current divides itself through different devices. This is not so in series circuit where same current flows through all the devices, irrespective of their resistances.
Question 31.
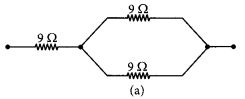
Show how would you join three resistors, each of resistance 9 Ω so that the equivalent resistance of the combination is (i) 13.5 Ω, (ii) 6 Ω (2018)
Answer:
(i) The resistance of the series combination is higher than each of the resistances. A parallel combination of two 9 Ω resistors is equivalent to 4.5 Ω. We can obtain 13.5 Ω by coupling 4.5 Ω and 9 Ω in series. So, to obtain 13.5 Ω, the combination is as shown in figure (a).
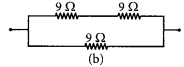
(ii) To obtain a equivalent resistance of 6 Ω, we have to connect two 9 Ω resistors in series and then connect the third 9 Ω resistor in parallel to the series combination as shown in the figure (b).
Question 32.
Three resistors of 3 Ω each are connected to a battery of 3 V as shown. Calculate the current drawn from the battery. (Board Term I, 2017)
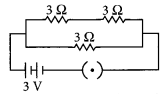
Answer:
As given in circuit diagram, two 3 Ω resistors are connected in series to form R1; so R1 = 3 Ω + 3 Ω = 6 Ω
And, R1 and R2 are in parallel combination, Hence, equivalent resistance of circuit (Req) given by
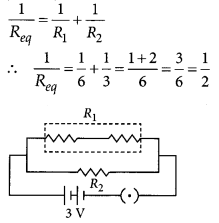
Req = 2 Ω
Using Ohm’s law, V = IR
We get,
3 V = I × 2 Ω
or I = \(\frac { 3 }{ 2 }\) A = 1.5 A
Current drawn from the battery is 1.5 A.
Question 33.
Two identical resistors are first connected in series and then in parallel. Find the ratio of equivalent resistance in two cases. (Board Term I, 2013)
Answer:
Let resistance of each resistor be R.
For series combination,
Rs = R1 + R2
So, Rs = R + R = 2R
For parallel combination,
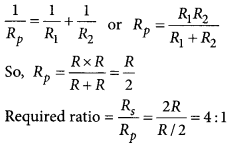
Question 34.
(a) A 6 Ω resistance wire is doubled on itself. Calculate the new resistance of the wire.
(b) Three 2 Ω resistors A, B and C are connected in such a way that the total resistance of the combination is 3 Ω. Show the arrangement of the three resistors and justify your answer. (2020)
Answer:
(a) Given resistance of wire, R = 6 Ω
Let l be the length of the wire and A be its area of
cross-section. Then
R = \(\frac { ρl }{ A }\) = 6 Ω
Now when the length is doubled, l’ = 2l and A’ = \(\frac { A }{ 2 }\)
∴ R’ = \(\frac{\rho(2 l)}{A / 2}=\frac{4 \rho l}{A}\) = 4 × 6 Ω = 24 Ω
(b) Given the total resistance of the combination = 3 Ω
In order to get a total resistance of 3 Ω, the three resistors has to be connected as shown.
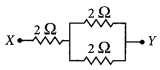
Such that, \(\frac{1}{R_{P}}=\frac{1}{2}+\frac{1}{2}\) = 1
⇒ Rp = 1 Ω
and Rs = 2 Ω + 1 Ω = 3 Ω
Question 35.
Draw a schematic diagram of a circuit consisting of a battery of 3 cells of 2 V each, a combination of three resistors of 10 Ω, 20 Ω and 30 Ω connected in parallel, a plug key and an ammeter, all connected in series. Use this circuit to find the value of the following :
(a) Current through each resistor
(b) Total current in the circuit
(c) Total effective resistance of the circuit. (2020)
Answer:
The circuit diagram is as shown below.
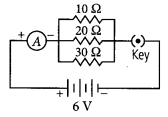
(a) Given, voltage of the battery = 2V + 2V + 2V = 6 V
Current through 10 Ω resistance,
I10 = \(\frac{V}{R}=\frac{6}{10}\) = 0.6 A
Current through 20 Ω resistance,
I20 = \(\frac{V}{R}=\frac{6}{20}\) = 0.3 A
Current through 30 Ω resistance,
I30 = \(\frac{V}{R}=\frac{6}{30}\) = 0.2 A
(b) Total current in the circuit, 1= I10 + I20 + I30
= 0.6 + 0.3 + 0.2 = 1.1 A
(c) Total resistance of the circuit,
\(\frac{1}{R_{P}}=\frac{1}{10}+\frac{1}{20}+\frac{1}{30}=\frac{11}{60}\)
Question 36.
(a) With the help of a suitable circuit diagram prove that the reciprocal of the equivalent resistance of a group of resistances joined in parallel is equal to the sum of the reciprocals of the individual resistances.
(b) In an electric circuit two resistors of 12 Ω each are joined in parallel to a 6 V battery. Find the current drawn from the battery. (Delhi 2019)
Answer:
(a) Resistors in parallel : When resistors are connected in parallel.
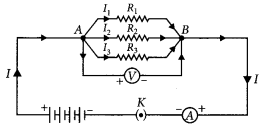
(i) The potential difference across their ends is the same.
(ii) The sum of current through them is the current drawn from the source of energy or cell.
I = I1 + I1 + I3 or \(\frac{V}{R_{P}}=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}}\)
(iii) The equivalent resistance is given by,
\(\frac{1}{R_{P}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\)
Hence equivalent resistance in parallel combination is equal to the sum of reciprocals of the individual resistances.
Question 37.
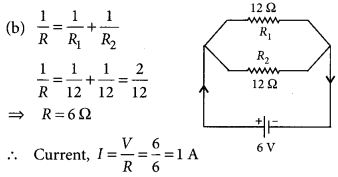
For the series combination of three resistors current in each resistor, establish the relation R = R1 + R2 + R3 where the symbols have their usual meanings. Calculate the equivalent resistance of the combination of three resistors of 6 Ω, 9 Ω and 18 Ω joined in parallel. (Board Term I, 2016)
Answer:
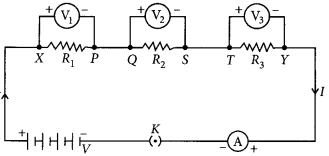
Given figure shows the series combination of three resistors R1, R2 and R3 connected across a voltage source of potential difference V.
Let current I is flowing through the circuit.
V1, V2 and V3 are the potential differences across resistors R1, R2 and R3 respectively.
Since, the total potential difference across a combination of resistors in series is equal to the sum of potential difference across the individual resistors.
∴ v = v1 + v2 + v3 …(i)
In series current through each resistor is same. Applying the Ohms law,
V1 = IR1, V2 = IR2 and V3 = IR1 ……..(ii)
If Rs is the equivalent resistance of the circuit, then
V = IRs …(iii)
From eqns. (i), (ii) and (iii),
we can write IRs = IR1 + IR2 + IR3
or Rs = R1 + R2 + R3
We can conclude that when several resistors are joined in series, the resistance of the combination Rs equals the sum of their individual resistances,
R1, R2 and R3
Given : R1 = 6 Ω, R2 = 9 Ω,
R3 = 18 Ω are connected in parallel.
Equivalent resistance, Req, is given by
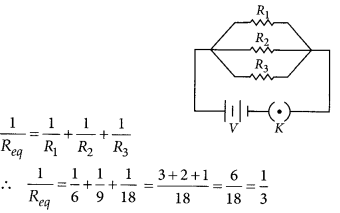
or Req = 3 Ω
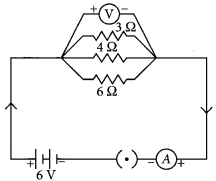
Question 38.
State ohms law. Represent it graphically. In the given circuit diagram calculate
(i) the total effective resistance of the circuit.
(ii) the current through each resistor.
Answer:
Ohm’s law: Refer to answer 7.
Graphical representation of Ohm’s law
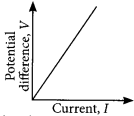
For the given circuit
R1 = 3 Ω, R2 = 4 Ω., R3 = 6 Ω and V = 6V.
(i) Total effective resistance of the circuit, Req is given by
\(\frac{1}{R_{\mathrm{eq}}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}=\frac{1}{3}+\frac{1}{4}+\frac{1}{6}=\frac{9}{12}\)
or Req = \(\frac { 12 }{ 9 }\) Ω = \(\frac { 4 }{ 3 }\) Ω = 1.33 Ω
(ii) Since, potential difference across each resistor connected in parallel is same.
So, V1 = V2 = V3 = 6 V
Applying Ohm’s law,
V1 = I1R1 or I1 = \(\frac { V_1 }{ R_1 }\) or I3 = \(\frac { 6 }{ 3 }\) A = 2A
Similarly, I2 = \(\frac { 6A }{ 4 }\) = 1.5 A and I3 = \(\frac { 6 }{ 6 }\) A = 1 A
Question 39.
(a) Prove that the equivalent resistance of three resistors R1, R2 and R3 in series is R1 + R2 + R3
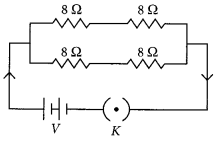
(b) You have four resistors of 8 Ω each. Show how would you connect these resistors to have effective resistance of 8 Ω? (4/5, Board Term I, 2015)
Answer:
(a) Refer to answer 37.
(b) If you have four 8 Ω resistors and the effective resistance is also 8 Ω then the two 8 Ω resistors are connected in series. Now you have pair of two 16 Ω resistors (8 Ω + 8 Ω). If you connect these resistors in parallel, you will have net resistance 8 Ω.
Question 40.
Draw a labelled circuit diagram showing three resistors R1, R2 and R3 connected in series with a battery (E), a rheostat (Rh), a plug key (K) and an ammeter (A) using standard circuit symbols. Use this circuit to show that the same current flows through every part of the circuit. List two precautions you would observe while performing the experiment. (Board Term I, 2014)
Answer:
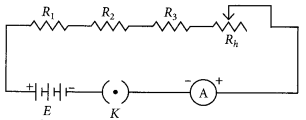
Change the positions of ammeter and note the reading of ammeter each time. You will find that all the reading obtained are same.
So, the value of the current in the ammeter is the same, independent of its position in the electric circuit. It means that in this circuit (series combination) the current is the same in every part of the circuit.
Precautions:
(i) All the connections are neat and tight.
(ii) Ammeter is connected with the proper polarity, i.e., positive terminal of the ammeter should go to positive terminal and negative terminal of ammeter to the negative terminal of the battery or cell used.
Question 41.
Two wires A and B are of equal length and have equal resistances. If the resistivity of A is more than that of B, which wire is thicker and why ? For the electric circuit given below calculate:
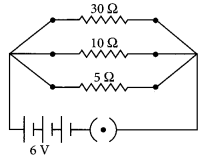
(i) current in each resistor
(ii) total current drawn from the battery, and
(iii) equivalent resistance of the circuit. (Board Term I, 2014)
Answer:
Let lA, aA and RA be the length, area of cross-section and resistance of wire A and lB, aB and RB are that of wire B.
Here, lA = lB and RA = RB
If ρA and ρB are the resistivities of wire A and B respectively then
RA = ρA \(\frac{l_{A}}{a_{A}}\) and RB = ρB \(\frac{l_{B}}{a_{B}}\), As RA = RB
∴ ρA \(\frac{l_{A}}{a_{A}}\), ρB \(\frac{l_{B}}{a_{B}}\)
or \(\frac{ρ_{A}}{ρ_{B}}\) = \(\frac{a_{A}}{a_{B}}\)
Since ρA > ρB therefore aA > aB Hence, wire A is thicker than wire B.
For parallel combination,
V1 = V2 = V3 = 6V
(i) Using Ohm’s law
I1 = V1/R1 = 6/30 = 0.2 A
I2 = V2/R2 = 6/10 = 0.6 A
I3 = V3/R3 = 6/5 = 1.2 A
(ii) Total current drawn from battery,
I = I1 + I2 + I3 = 0.2 + 0.6 + 1.2 = 2 A
(iii) Equivalent resistance of the circuit, Req can be obtained by Ohm’s law
V= I Req
So, 6 V = 2 A × Req or, Req = \(\frac { 6 }{ 2 }\) = 3 Ω
Aliter, \(\frac{1}{R_{e q}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\)
\(\frac{1}{30}+\frac{1}{10}+\frac{1}{5}=\frac{1+3+6}{30}=\frac{10}{30}=\frac{1}{3}\)
or Req = 3 Ω
Question 42.
(a) Derive an expression to find the equivalent resistance of three resistors connected in series. Also draw the schematic diagram of the circuit.
(b) Find the equivalent resistance of the following circuit.
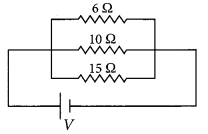
Answer:
(a) Refer to answer 37.
(b) For the given circuit,
R1 = 6 Ω, R2 = 10 Ω, R3 = 15 Ω.
As \(\frac{1}{R_{e q}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\)
\(\frac{1}{R_{e q}}=\frac{1}{6}+\frac{1}{10}+\frac{1}{15}\)
= \(\frac{5+3+2}{30}=\frac{10}{30}=\frac{1}{3}\)
Req = 3 Ω
Question 43.
Draw a circuit diagram for a circuit consisting of a battery of five cells of 2 volts each, a 5 Ω resistor, a 10 Ω resistor and a 15 Ω resistor, an ammeter and a plug key, all connected in series. Also connect a voltmeter to record the potential difference across the 15 Ω resistor and calculate
(i) the electric current passing through the above circuit and
(ii) potential difference across 5 Ω resistor when the key is closed. (Board Term 1, 2013)
Answer:
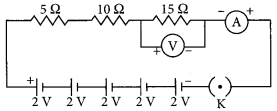
Potential of the battery, V = (2 × 5) V = 10 V
Equivalent resistance,
Req = R1 + R2 + R3
= (5 + 10 + 15)Ω = 30 Ω
(i) Current through circuit, I = \(\frac{V}{R}=\frac{10}{30} \mathrm{~A}=\frac{1}{3} \mathrm{~A}\)
(ii) Potential across 5 Ω resistor, V1 = IR1
= \(\frac { 1 }{ 3 }\) × 5 = \(\frac { 5 }{ 3 }\) V = 1.67 V
Question 44.
The resistance of a resistor is reduced to half of its initial value. In doing so, if other parameters of the circuit remain unchanged, the heating effects in the resistor will become
(a) two times
(b) half
(c) one-fourth
(d) four times (2020)
Answer:
(a) : We know, H = I²Rt = \(\frac { V^2 }{ 4 }\). t
Now when, R’ = \(\frac { R }{ 24 }\), V’ = V and t’ = t
H’ = \(\frac{V^{\prime 2} t^{\prime}}{R^{\prime}}=\frac{V^{2} t}{R / 2}=\frac{2 V^{2} t}{R}\) = 2H
Question 45.
(a) Write the mathematical expression for Joules law of heating.
(b) Compute the heat generated while transferring 96000 coulomb of charge in two hours through a potential difference of 40 V. (2020)
Answer:
(a) The Joule’s law of healing implies that heat produced in a resistor is
(i) directly proportional to the square of current lor a given resistance,
(ii) directly proportional to resistance for a given current, and
(iii) directly proportional to the time for which the current flows through the resistor.
i.e., H = I² Rt
(b) Given, charge q = 96000 C, time t = 2 h = 7200 s and potential difference V = 40 V
We know, H = I²Rt = \(\frac{Q^{2}}{t^{2}} \times \frac{V}{Q}\) × t × t = VQ
= 40 × 96000 = 3.84 × 106 J = 3.84 MJ
Question 46.
Write Joules law of heating. (1/3, 2018)
Answer:
Refer to answer 45(a).
Question 47.
Explain the use of an electric fuse. What type of material is used for fuse wire and why? (Board Term I, 2016)
Answer:
Electric fuse protects circuits and appliances by stopping the flow of any unduly high electric current. It consists of a piece of wire made of a metal or an alloy of appropriate melting point, for example aluminium, copper, iron, lead etc. If a current larger than the specified value flows through the circuit, the temperature of the fuse wire increases. This melts the fuse wire and breaks the circuit.
Question 48.
(a) Why is tungsten used for making bulb filaments of incandescent lamps?
(b) Name any two electric devices based on heating effect of electric current. (2/5, Board Term I, 2015)
Answer:
(a) (i) Tungsten is a strong metal and has high melting point (3380°C).
(ii) It emits light at high temperatures (about 2500°C).
(b) Electric laundry iron and electric heater are based on heating effect of electric current.
Question 49.
A fuse wire melts at 5 A. If it is desired that the fuse wire of same material melt at 10 A, then whether the new fuse wire should be of smaller or larger radius than the earlier one? Give reasons for your answer. (3/5, Board Term I, 2014)
Answer:
Let the resistance of the wire be R, heat produced in the fuse at 5 A in Is is
H=(5)²R ( H – I²Rt)
50. fuse melts at (5)²R joules of heat.
Let, the resistance of new wire is R’
So, heat produced in 1 second = (10)²R’
To prevent it from melting
(5)²R = (10)²R’ or R’ = \(\frac { R }{ 4 }\)
As R ∝ \(\frac { 1 }{ A }\)
∴ cross-sectional area of new fuse wire is four times the first fuse.
Now, A = πr², so new radius is twice the previous one. So, at 10 A, the new fuse wire of same material and length has larger radius than the earlier one.
Question 50.
What is heating effect of current? List two electrical appliances which work on this effect. (2/5, Board Term I, 2013)
Answer:
If only resislors are connected to the battery, the source energy continually gets dissipated entirely in the form of heal. This is known as healing effect of current, ’file amount of heat (77) produced in time t is given by Joule’s law of heating.
H = I²Rt
Where, 7 is current flowing through resistor R.
The electric laundry iron, electric toaster, electric oven, electric kettle and electric heater are some common devices based on heating effect of current.
Question 51.
Two bulbs of 100 W and 40 W are connected in series. The current through the 100 W bulb is 1 A. The current through the 40 W bulb will be
(a) 0.4 A
(b) 0.6 A
(c) 0.8 A
(d) 1A (2020)
Answer:
(d) : Given power of first bulb, P1 = 100 W and second bulb P2 = 40 W
Current through 100 W bulb, I1 = 1 A
Current through 40 W bulb, I2 = ?
Since both the bulbs are connected in series, the electric current passing through both the bulbs are same i.e., I2 = 1 A.
Question 52.
Write the relation between resistance (R) of filament of a bulb, its power (P) and a constant voltage V applied across it. (Board Term I, 2017)
Answer:
P = \(\frac { V^2}{ R }\)
Question 53.
Power of a lamp is 60 W. Find the energy in joules consumed by it in Is. (Board Term I, 2016)
Answer:
Here, power of lamp, P = 60 W time,
t = 1 s
So, energy consumed = Power × time = (60 × 1)J = 60 J
Question 54.
Two lamps, one rated 100 W; 220 V, and the other 60 W; 220 V, are connected in parallel to electric mains supply. Find the current drawn by two bulbs from the line, if the supply voltage is 220 V. (2/3, 2018, Board Term I, 2014)
Answer:
Since both the bulbs are connected in parallel and to a 220 V supply, the voltage across each bulb is 220 V. Then
Current drawn by 100 W bulb,
I1 = \(\frac { power rating}{ voltage applied }\) = \(\frac { 100 W}{ 220 V }\) = 0.454 A
Current drawn by 60 W bulb,
I2 = \(\frac { 60 W}{ 220 V }\) = 0.273 A
Total current drawn from the supply line,
I = I1 + I2 = 0.454 A + 0.273 A = 0.727 A = 0.73 A
Question 55.
How much current will an electric iron draw from a 220 V source if the resistance of its element when hot is 55 ohms? Calculate the wattage of the electric iron when it operates on 220 volts. (Board Term I, 2016)
Answer:
Here, V = 220 V, R = 55 Ω
By Ohm’s law V = IR
∴ 220 = 7 × 55 or I = 4A
Wattage of electric iron = Power
= \(\frac{V^{2}}{R}=\frac{(220)^{2}}{55}\) = 880 W
Question 56.
An electric iron has a rating of 750 W; 200 V. Calculate:
(i) the current required.
(ii) the resistance of its heating element.
(iii) energy consumed by the iron in 2 hours. [Board Term 1, 2015]
Answer:
Here, P = 750 W, V = 200 V
(i) As P = V7
I = P/V= (750/200) A = 3.75A
(ii) By Ohm’s law V = IR or R = V/I
∴ R = \(\frac { 200}{ 3.75 }\) Ω = 53.3 Ω
(iii) Energy consumed by the iron in 2 hours
= P × t = 750 W × 2h = 1.5 kWh
or E = (750 × 2 × 3600) J = 5.4 × 106 J
Question 57.
An electric bulb is connected to a 220 V generator. The current is 2.5 A. Calculate the power of the bulb. (1/3, Board Term I, 2015)
Answer:
Here, V= 220 V,/= 2.5 A
Power of the bulb P = VI = 220 × 2.5 W = 550 W
Question 58.
(a) Define power and state its SI unit.
(b) A torch bulb is rated 5 V and 500 mA. Calculate its
(i) power
(ii) resistance
(iii) energy consumed when it is lighted for 2 \(\frac { 1 }{ 2 }\) hours.
Answer:
(a) Power is defined as the rate at which electric energy is dissipated or consumed in an electric circuit.
P = VI = I²R = V²/R
The SI unit of electric power is watt (W). It is the power consumed by a device that carries 1 A of current when operated at a potential difference of IV.
1 W = 1 volt × 1 ampere = 1 V A
(b) Given, V = 5 V and I = 500 mA = 0.5 A
(i) Power, P = V × 7 = 5 × 0.5 = 2.5 W
(ii) As, P = \(\frac{V^{2}}{R} \Rightarrow R=\frac{V^{2}}{P}=\frac{25}{2.5}\) = 10 Ω
(iii) Given, time t = 2.5 hrs = 9000 s
∴ The energy consumed, E = P × t
= 2.5 × 9000 = 2.25 × 104 J
= 6.25 Watt hour
Question 59.
Two identical resistors, each of resistance 15 Ω, are connected in (i) series, and (ii) parallel, in turn to a battery of 6 V. Calculate the ratio of the power consumed in the combination of resistors in each case. (2020)
Answer:
Given, R1 = R1 = 15 Ω, V = 6 V
(i) When connected in series,
Rs = R1 + R2 = 15 Ω + 15 Ω = 30 Ω
Power, PS = \(\frac{V^{2}}{R_{S}}=\frac{36}{30}\) W
(ii) When connected in parallel,
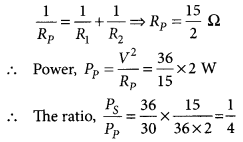
Question 60.
An electric lamp of resistance 20 Ω and a conductor of resistance 4 Ω. are connected to a 6 V battery as shown in the circuit. Calculate.
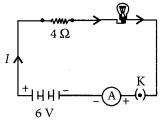
(a) the total resistance of the circuit
(b) the current through the circuit,
(c) the potential difference across the (i) electric lamp and (ii) conductor, and
(d) power of the lamp. (Delhi 2019)
Answer:
Resistance of the lamp = 20 Ω
External resistance = 4 Ω
(a) As both the lamp and external resistance are connected in series, therefore the total resistance,
R = 20 + 4 = 24 Ω
(b) Current, I = \(\frac { V}{ R }\) = \(\frac { 6 }{ 24 }\) = 0.25 A
(c) (i) Potential difference across the electric lamp
\(\frac { Total voltage }{ Total resistance }\) × resistance of lamp
= \(\frac { 6}{ 24 }\) × 20 = 5 V
(ii) Potential difference across conductor
\(\frac { Total voltage }{ Total resistance }\) × resistance of conductor
= \(\frac { 6}{ 24 }\) × 4 = 1 V
(d) Power of the lamp
= (current)² × resistance of lamp
= (0.25)² × 20 = 1.25 W
Question 61.
Compare the power used in 2 Ω. resistor in each of the following circuits. (AI 2019)
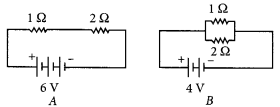
Answer:
In circuit A,
Total resistance, R = l + 2 = 3Ω
Voltage across 2 Ω = \(\frac { V_{Total}}{ R_{Total} }\) × 2 Ω = \(\frac { 6}{ 3 }\) × 2 = 4 V
∴ Power used in 2 Ω resistor,
p = \(\frac { V^2}{ R }\) = \(\frac { (4)^2}{2 }\) = 8 w
In circuit B, Voltage across both the resistance is same i.e. 4 V and both are connected in parallel combination.
∴ Power used in 2 Ω resistor = \(\frac { V^2}{ R }\) = \(\frac { (4)^2}{2 }\) = 8 w
∴ Power used in 2 Ω resistor in each case is same i.e. 8 W.
Question 62.
A bulb is rated 40 W; 220 V. Find the current drawn by it, when it is connected to a 220 V supply. Also find its resistance. If the given bulb is replaced by a bulb of rating 25 W; 220 V, will there be any change in the value of current and resistance? Justify your answer and determine the change. (AI 2019)
Answer:
In first case, P = 40 W, V = 220 V
Current drawn l = \(\frac { P}{ V }\) = \(\frac { 40}{ 220 }\) = 0.18 A
Also, resistance of bulb,
R = \(\frac{V^{2}}{P}=\frac{(220)^{2}}{40}\) = 1210 Ω
In second case, P = 25 W, V = 220 V
Current drawn, I = \(\frac { P}{ V }\) = \(\frac { 25}{ 220 }\) = 0.11 A
Also, resistance of the bulb,
R = \(\frac { V^2}{ P }\) = \(\frac { (220)^2}{ 25 }\) = 1936 Ω
Hence, by replacing 40 W bulb to 25 W bulb, having same source of voltage the amount of current flows decreases while resistance increases.
Question 63.
(a) How two resistors, with resistances R1 Ω and R1 Ω respectively are to be connected to a battery of emf V volts so that the electrical power consumed is minimum?
(b) In a house 3 bulbs of 100 watt each lighted for 5 hours daily, 2 fans of 50 watt each used for 10 hours daily and an electric heater of 1.00 kW is used for half an hour daily. Calculate the total energy consumed in a month of 31 days and its cost at the rate of Rs 3.60 per kWh. (Board Term I, 2017)
Answer:
(a) Power consumed is minimum when current through the circuit is minimum, so the two resistors are connected in series.
(b) Power of each bulb P1 = 100 watt
Total power of 3 bulbs, P1 = 3 × 100 = 300 watt
Energy consumed by bulbs in 1 day
E1 = P1 × t = 300 watt × 5 hours.
= 1500 Wh = 1.5 kWh
Power of each fan = 50 watt
Total power of 2 fans = 2 × 50 watt
P2 = 100 watt
Energy consumed by fans in 1 day
E2 = P2 × t = 100 watt × 10 hours
= 1000 watt hour = 1 kWh
Energy consumed by heater,
E3 = 1 kW × 1/2 h = 0.5 kWh
Total energy consumed in one day
E = E1 + E2 + E3 = (1.5 + 1 + 0.5) kWh = 3 kWh
Total energy consumed in a month of 31 days
= E × 31 = (3 × 31) kWh = 93 kWh
Cost of energy consumed = Rs (93 × 3.60) = Rs 334.80
Question 64.
(a) An electric bulb is connected to a 220 V generator. If the current drawn by the bulb is 0.50 A, find its power.
(b) An electric refrigerator rated 400 W operates 8 hours a day. Calculate the energy per day in kWh.
(c) State the difference between kilowatt and kilowatt hour. (3/5, Board Term I, 2013)
Answer:
(a) Here, V = 220 V, I = 0.50 A
Power of the bulb, P = VI = (220 × 0.5)W = 110 W
(b) Energy consumed by electric refrigerator in a day = Power x time
= 400 W × 8 h = 3200 Wh = 3.2 kWh
(c) Kilowatt is unit of power and kilowatt hour is a unit of energy.
Question 65.
(i) State one difference between kilowatt and kilowatt hour. Express 1 kWh in joules.
(ii) A bulb is rated 5V; 500 mA. Calculate the rated power and resistance of the bulb when it glows. (Board Term I, 2013)
Answer:
(i) Refer to answer 64(c).
1 kWh = 1000 W × 1 h
= 1000 W × 3600 s = 3600000 J = 3.6 × 106 J
(ii) Here, V = 5 V, I = 500 mA = 0.5 A
Power rating of bulb is
P = VI = ( 5 × 0.5)W = 2.5W
Resistance of the bulb is R = V/I = (5/0.5) Ω = 10 Ω