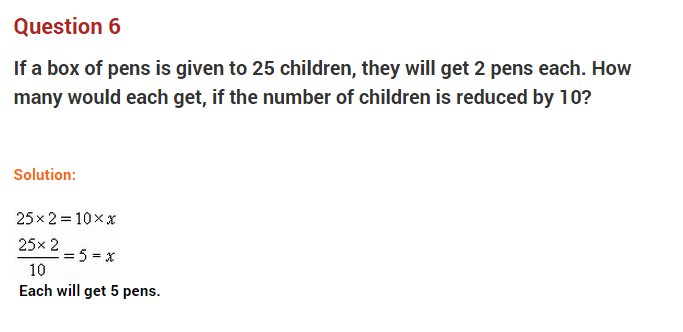Direct and Inverse Proportions Class 8 Extra Questions Maths Chapter 13
Extra Questions for Class 8 Maths Chapter 13 Direct and Inverse Proportions
Direct and Inverse Proportions Class 8 Extra Questions Very Short Answer Type
Question 1.
A train is moving at a uniform speed of 100 km/h. How far will it travel in 20 minutes?
Solution:
Let the distance travelled by train in 20 minutes be x km.

Since the speed is uniform, the distance travelled will be directly proportional to time.

Hence, the required distance is 33\(\frac { 1 }{ 3 }\) km.
Question 2.
Complete the table if x and y vary directly.

Solution:
Let the blank spaces be filled with a, b and c.


Hence, the required values are a = 7, b = 15 and c = 7.5.
Question 3.
If the cost of 20 books is ₹ 180, how much will 15 books cost?
Solution:
Let the required cost be ₹ x.
Here, the two quantities vary directly.

Question 4.
If x1 = 5, y1 = 7.5, x2 = 7.5 then find y2 if x and y vary directly.
Solution:
Since x and y vary directly.

Hence, the required value is 11.25.
Question 5.
If 3 kg of sugar contains 9 × 108 crystals. How many sugar crystals are there in 4 kg of sugar?
Solution:
Let the required number of crystals be x.

Hence, the required number of crystals = 1.2 × 109.
Question 6.
If 15 men can do a work in 12 days, how many men will do the same work in 6 days?
Solution:
Let the required number of men be x.
Less days → more men.
Thus the two quantities are inversely proportional to each other.

Hence, the required number of days = 30.
Question 7.
A train travels 112 km in 1 hour 30 minutes with a certain speed. How many kilometres it will travel in 4 hours 45 minutes with the same speed?
Solution:
Let the required distance be x km.
More distance → more time
Thus, the two quantities are directly proportional.


Hence, the required distance = 354.6 km.
Question 8.
The scale of a map is given as 1 : 50,000. Two villages are 5 cm apart on the map. Find the actual distance between them.
Solution:
Let the map distance be x cm and actual distance be y.
1 : 50,000 = x : y

Hence, the required distance = 250 km.
Question 9.
8 pipes are required to fill a tank in 1 hr 20 min. How long will it take if only 6 pipes of the same type are used?
Solution:
Let the required time be ‘t’ hours.

Question 10.
15 men can build a wall in 42 hours, how many workers will be required for the same work in 30 hours?
Solution:
Let the required number of workers be x.
The number of workers, faster will they do the work.
So, the two quantities are inversely proportional.

x1y1 = x2y2
⇒ 42 × 15 = 30 × x
⇒ x = 21
Hence, the required number of men = 21
Direct and Inverse Proportions Class 8 Extra Questions Short Answer Type
Question 11.
The volume of a gas V varies inversely as the pressure P for a given mass of the gas. Fill in the blank spaces in the following table:

Solution:
Since volume and pressure are inversely proportional.
PV = K



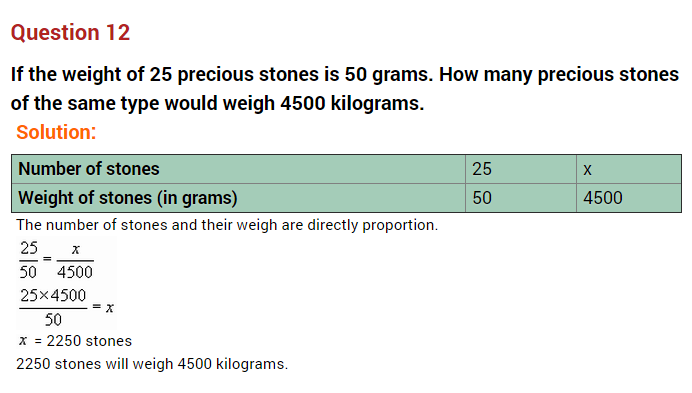
Question 12.
The cost of 5 metres of cloth is ₹ 210. Tabulate the cost of 2, 4, 10 and 13 metres of cloth of the same type.
Solution:
Let the length of the cloth be x m and its cost be ₹ y. We have the following table.



Question 13.
Six pumps working together empty a tank in 28 minutes. How long will it take to empty the tank if 4 such pumps are working together?
Solution:
Let the required time be t minutes.

Less pump → More time
Since there is an inverse variation.
x1y1 = x2y2
6 × 28 = 4 × x
x = 42
Hence, the required time = 42 minutes.
Question 14.
Mohit deposited a sum of ₹ 12000 in a Bank at a certain rate of interest for 2 years and earns an interest of ₹ 900. How much interest would be earned for a deposit of ₹ 15000 for the same period and at the same rate of interest?
Solution:
Let the required amount of interest be ₹ x.


Hence, the required amount of interest = ₹ 1125.
Question 15.
A garrison of 120 men has provisions for 30 days. At the end of 5 days, 5 more men joined them. How many days can they sustain on the remaining provision?
Solution:
Let the number of days be x.

[∵ Remaining days = 30 – 5 = 25]
[Total men = 120 + 5 = 125]
Since there is an inverse variation.
x1y1 = x2y2
120 × 25 = 125 × x
x = 24
Hence, the required number of days be 24.
Question 16.
In a scout camp, there is food provision for 300 cadets for 42 days. If 50 more persons join the camp, for how many days will the provision last? (NCERT Exemplar)
Solution:
More the persons, the sooner would be the provision exhausted. So, this is a case of inverse proportion.
Let the required number of days be x.
Hence, 300 × 42 = (300 + 50) × x
300 × 42 = 350 × x
x = 36
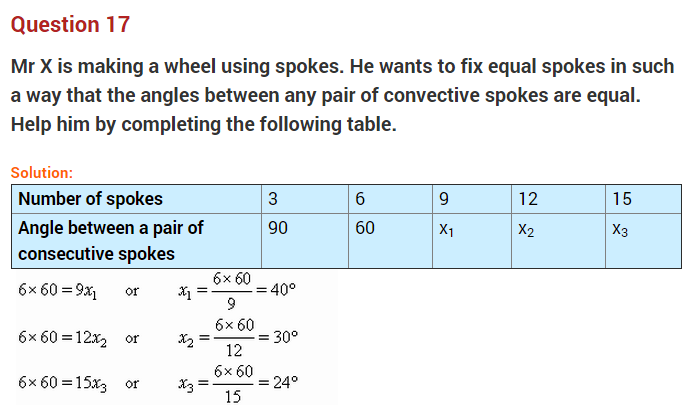
Question 17.
If two cardboard boxes occupy 500 cubic centimetres space, then how much space is required to keep 200 such boxes? (NCERT Exemplar)
Solution:
As the number of boxes increases, the space required to keep them also increases.
So, this is a case of direct proportion.

Thus, the required space is 50,000 cubic centimetres.
Question 18.
Under the condition that the temperature remains constant, the volume of gas is inversely proportional to its pressure. If the volume of gas is 630 cubic centimetres at a pressure of 360 mm of mercury, then what will be the pressure of the gas if its volume is 720 cubic centimetres at the same temperature? (NCERT Exemplar)
Solution:
Given that, at constant temperature pressure and volume of a gas are inversely proportional.
Let the required pressure be x.

Therefore, the required pressure is 315 mm of mercury.