Inverse Trigonometric Functions Class 12 Maths Important Questions Chapter 2

Get access to Class 12 Maths Important Questions Chapter 2 Inverse Trigonometric Functions, Inverse Trigonometric Functions Class 12 Important Questions with Solutions Previous Year Questions will help the students to score good marks in the board examination.

Inverse Trigonometric Functions Class 12 Important Questions with Solutions Previous Year Questions

Question 1.
Write the value of
tan^-1 (√3) – cot^-1 (- √3). (All India 2019,13)
Answer:
We have, tan^-1 (√3) – cot^-1 (-√3)
= tan^-1 (√3) – {π – cot^-1 (√3)} [∵ cot^-1 (- x) = π – cot^-1 x; x ∈ R]
= tan^-1 √3 – π + cot^-1 √3
= (tan^-1 √3 + cot^-1 √3) – π
= \(\frac{\pi}{2}\) – π = – \(\frac{\pi}{2}\) [∵ tan^-1x + cot^-1x = \(\frac{\pi}{2}\); x ∈ R]
Which is the required principal value.

Question 2.
Find the principal value of
tan^-1√3 – sec^-1 (- 2). (CBSE 2018 C; All India 2012)
Answer:
We have, tan^-1√3 – sec^-1 (- 2)

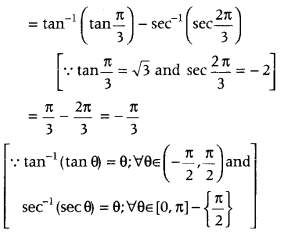
Which is the required principal value.

Question 3.
If sin (sin^-1\(\frac{1}{5}\) + cos^-1x) = 1, then find the value of x. (Delhi 2014)
Answer:

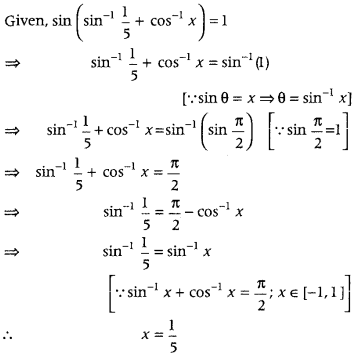
Question 4.
If tan^-1x + tan^-1 y = \(\frac{\pi}{4}\); xy < 1, then write the value of x + y + xy. (All India 2014)
Answer:

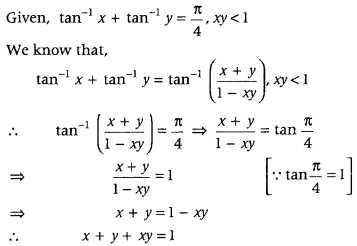
Question 5.
Write the value of cos^-1\(\left(-\frac{1}{2}\right)\) + 2 sin^-1\(\left(\frac{1}{2}\right)\). (Foreign 2014)
Answer:

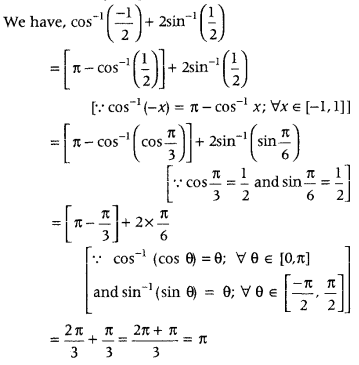
Question 6.
Write the principal value of cos^-1 [cos(680)°]. (Delhi 2014C)
Answer:
First we check the given angle lies in the principal value branch. If it is so, then use the property cos¹ (cos θ) = θ, ∀θ ∈ [0, 180°]. Otherwise reduce the angle such that, it lies in principal value branch.

We know that, principal value branch of cos^-1 x is [0, 180°].
Since, 680° ∉ [0, 180°], so write 680° as 2 × 360° – 40°
Now, cos^-1 [cos(680)°] = cos^-1 [cos(2 × 360° – 40°)]
= cos^-1 (cos 4o°) [∵ cos(4π – θ) = cos θ]
Since, 40° ∈ [0, 180°]
∴ cos^-1[cos(680°)] = 40° [∵ cos^-1 (cos θ) = θ; ∀ θ ∈ [0, 1 80°]]
which is the required principal value.

Question 7.
Write the principal value of tan^-1[sin\(\left(\frac{-\pi}{2}\right)\)]. (All India 2014C)
Answer:

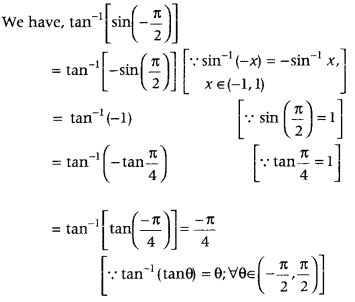
which is the required principal value.

Question 8.
Find the value of the following.
cot (\(\frac{\pi}{2}\) – 2 cot^-1√3) (All India 2014C)
Answer:
First, use cot\(\left(\frac{\pi}{2}-\theta\right)\) = tan θ, then put
cot^-1 √3 = \(\frac{\pi}{6}\) and simplify it .

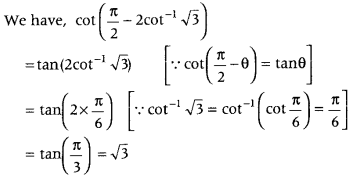
Question 9.
Write the principal value of the following.
\(\left[\cos ^{-1} \frac{\sqrt{3}}{2}+\cos ^{-1}\left(-\frac{1}{2}\right)\right]\) (Delhi 2013C)
Answer:

Question 10.
Write the principal value of
tan^-1 (1) + cos^-1\(\left(-\frac{1}{2}\right)\). (Delhi 2013)
Answer:

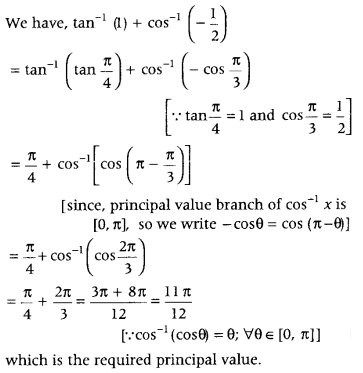
Alternate Method:
We have

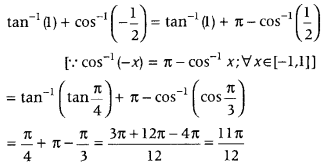
which is the required principal value.

Question 11.
Write the value of tan (2 tan^-1\(\frac{1}{5}\)). (Delhi 2013)
Answer:
We have,

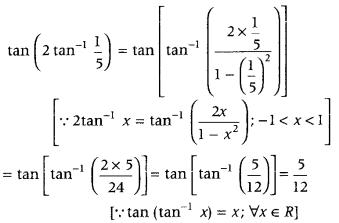
Question 12.
Write the value of
tan^-1\(\left[2 \sin \left(2 \cos ^{-1} \frac{\sqrt{3}}{2}\right)\right]\). (All India 2013)
Answer:

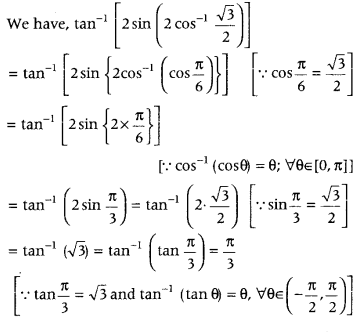
Question 13.
Write the value of cos^-1 \(\left(\frac{1}{2}\right)\) – 2 sin^-1 \(\left(\frac{1}{2}\right)\). (DeIh 2012)
Answer:
\(\frac{2 \pi}{3}\)

Question 14.
Using the principal values, write the value of cos^-1\(\left(\frac{1}{2}\right)\) + 2 sin^-1\(\left(\frac{1}{2}\right)\).
Answer:
\(\frac{2 \pi}{3}\)

Question 15.
Write the value of sin \(\left[\frac{\pi}{3}-\sin ^{-1}\left(-\frac{1}{2}\right)\right]\) (Delhi 2011).
Answer:
We have,

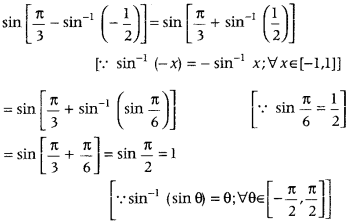
Question 16.
Write the value of tan^-1(tan \(\frac{3 \pi}{4}\)). (Delhi 2011)
Answer:
First, we check the given angle lies in the principal value branch. If it is so, then use the property tan^-1 (tan θ) = θ, ∀ θ ∈ \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\), Otherwise reduce the angle such that it lies in principal value branch.

We know that, principal value branch of tan^-1 x is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\).

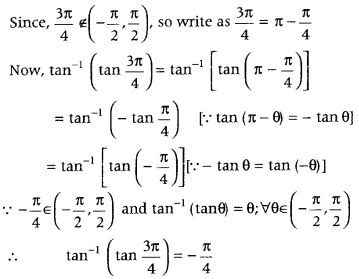
Question 17.
Write the value of cos^-1 (cos \(\frac{7 \pi}{6}\)). (Delhi 2011, 2009; All India 2009)
Answer:
We know that, the principal value branch of cos^-1x is [0, π].

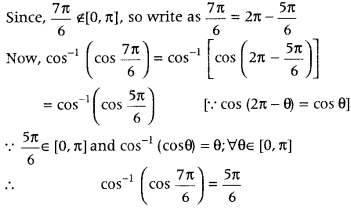
Question 18.
What is the principal value of
cos^-1\(\left(\cos \frac{2 \pi}{3}\right)\) + sin^-1\(\left(\sin \frac{2 \pi}{3}\right)\)? (All India 2011, 2009C. 2008)
Answer:
We know that, the principal value branch of cos^-1 x is [0, π] and for sin^-1 x is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\).

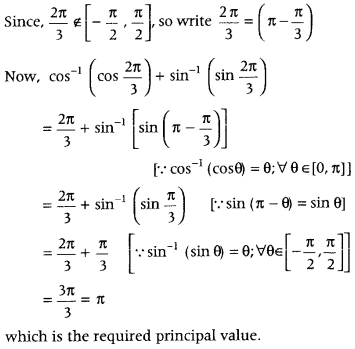
Question 19.
What is the principal value of tan^-1 (- 1)? (Foreign 2011, 2o08c)
Answer:
We have,

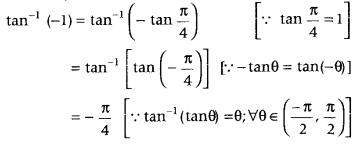
Which is the required principal value.

Alternate Method:
We have,
tan^-1 (-1) = – tan^-1 (1) [∵ tan^-1 x; x ∈ R]
= – tan^-1(tan \(\frac{\pi}{4}\)) [∵ tan \(\frac{\pi}{4}\) = 1]
= \(\frac{-\pi}{4}\) [∵ tan^-1 (tan θ) = θ; ∀ θ ∈ \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)]
which is the required principal value.

Question 20.
Using the principal values, write the value of sin^-1\(\left(-\frac{\sqrt{3}}{2}\right)\). (All India 2011C, Delhi 2010)
Answer:
We have

Question 21.
Write the principal value of sin^-1\(\left(-\frac{1}{2}\right)\). (Delhi 2010)
Answer:
– \(\frac{\pi}{6}\)

Question 22.
What is the principal value of sin^-1 (- 2)? (All India 2010)
Answer:
We have, sec^-1 (-2) = π – sec^-1 (2)
[∵ sec^-1 (- x) = π – sec^-1 (x); |x| ≥ 1
= π – sec^-1(sec \(\frac{\pi}{3}\)) = π – \(\frac{\pi}{3}\)
[∵ sec \(\frac{\pi}{3}\) = 2 and sec^-1 (sec θ) = θ; ∀ θ ∈ [0, π] – \(\left\{\frac{\pi}{2}\right\}\)]
= \(\frac{2 \pi}{3}\)
which is the required principal value.

Question 23.
What is the domain of the function sin^-1 x? (Foregin 2010)
Answer:
The domain of the function sin^-1 x is [-1, 1].

Question 24.
Using the principal values, find the value of cos^-1\(\left(\cos \frac{13 \pi}{6}\right)\). (All India 2010C ).
Answer:
\(\frac{\pi}{6}\)

Question 25.
If tan^-1 (√3) + cot^-1 x = \(\frac{\pi}{2}\)‚ then find the value of x. (All India 2010C)
Answer:
Given, tan^-1 √3 + cot^-1 x = \(\frac{\pi}{2}\)
⇒ tan^-1 √3 = \(\frac{\pi}{2}\) – cot^-1 x
⇒ tan^-1 √3 = tan^-1 x
[∵ tan^-1 x + cot^-1 x = \(\frac{\pi}{2}\); x ∈ R]
∴ x = √3

Question 26.
Prove that
3 sin^-1x = sin^-1(3x – 4x³), x ∈ \(\left[-\frac{1}{2}, \frac{1}{2}\right]\). (CBSE 2018)
Answer:
Consider, RHS = sin^-1 (3x – 4x³) ……(i)
Let x = sin θ,
then θ = sin^-1 x
Now, from Eq. (i), we get
RHS = sin^-1 (3 sin θ – 4 sin³ θ)
= sin^-1 (sin 3 θ) [∵ sin 3A = 3sin A – 4sin³ A]
= 3θ

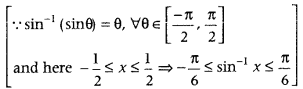
= 3 sin^-1 x [∵ θ = sin^-1 x]
= LHS
Hence Proved.

Question 27.
Prove that
3 cos^-1x = cos^-1(4x³ – 3x), x ∈\(\left[\frac{1}{2}, 1\right]\).
Answer:
Consider, RHS = cos^-1 (4x³ – 3x)
Let x = cos θ ⇒ θ = cos^-1 x
Now, from Eq. (1), we get
RHS = cos^-1 (4 cos³ θ – 3 cos θ)
= cos^-1 (cos 3θ) [∵ cos 3A = 4 cos³ A – 3 cos A]

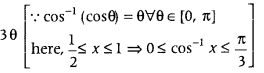
= 3 cos^-1 x
= LHS
Hence proved.

Question 28.
Solve for X,
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1\(\frac{8}{31}\). (All India 2019,15)
Answer:
First, use the formula tan^-1 x + tan^-1 y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\); xy < 1, then simplify it and get the values of x. Further, verify the given equation by obtained values of x.

Given, tan^-1(x + 1) + tan^-1(x – 1) = tan^-1 \(\frac{8}{31}\) …… (i)

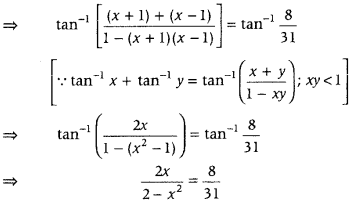
⇒ 62x = 16 – 8x²
⇒ 8x² + 62x – 16 = 0
⇒ 4x² + 31x – 8 = 0
⇒ 4x² + 32x – x – 8 = 0
⇒ 4x(x + 8) – 1 (x + 8) = 0
⇒ (x + 8) (4x – 1) = 0
∴ x = -8 or x = \(\frac{1}{4}\)
But x = – 8 gives LHS = tan^-1 (- 7) + tan^-1 (- 9)
= – tan^-1 (7) – tan^-1 (9),
which is negative, while RHS is positive.
So, x = – 8 is not possible.
Hence, x = \(\frac{1}{4}\) is the only solution of the given equation.

Question 29.
Find the value of sin (cos^-1 + tan^-1\(\frac{2}{3}\)). (All India 2019)
Answer:

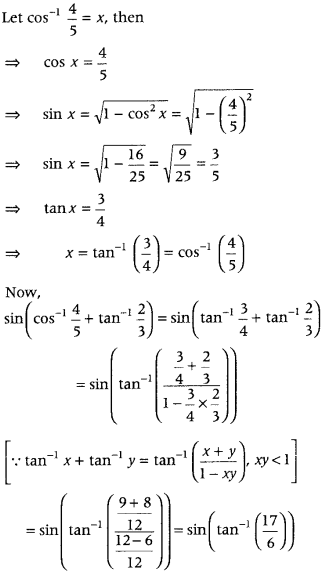
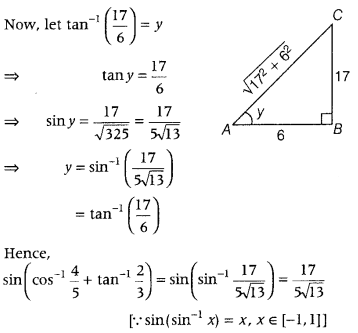
Question 30.
Solve for x, tan^-1 3x + tan^-1 2x = \(\frac{\pi}{4}\). (Delhi 2019. 2015, 2013C)
Answer:
Given, tan^-1 3x + tan^-1 2x = \(\frac{\pi}{4}\) …………. (i)

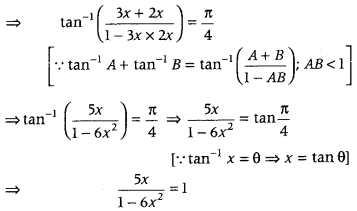
⇒ 5x = 1 – 6x²
⇒ 6x² + 5x – 1 = 0
⇒ 6x² + 6x – x – 1 = 0
⇒ 6x(x + 1) – 1(x + 1) = 0
⇒ (6x – 1) (x + 1) = 0
⇒ 6x – 1 = 0 or x + 1 = 0
∴ x = \(\frac{1}{6}\) or x = – 1
But x = – 1 does not satisfy the Eq. (1). as LHS becomes negative. So, x = \(\frac{1}{6}\) is the only solution of the given equation.

Question 31.
Solve tan^-1 4x + tan^-1 6x = \(\frac{\pi}{4}\) (Delhi 2019)
Answer:

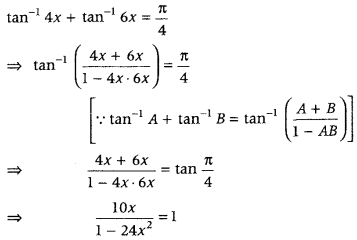
⇒ 10x = 1 – 24x²
⇒ 24x² + 10x – 1 = 0
⇒ 24x² + 12x – 2x – 1 = 0
⇒ 12x(2x + 1) – 1 (2x + 1) = 0
⇒ (2x + 1) (12x – 1) = 0
⇒ 2x + 1 = 0
x = – \(\frac{1}{2}\)
or 12x – 1 = 0
x = \(\frac{1}{12}\)
But x = – \(\frac{1}{2}\) does not satisfy the given equation.
Hence, the required solution is x = \(\frac{1}{12}\)

Question 32.
If tan^-1\(\frac{x-3}{x-4}\) + tan \(\frac{x+3}{x+4}=\frac{\pi}{4}\), then find the value of x. (All India 2017)
Answer:
Given

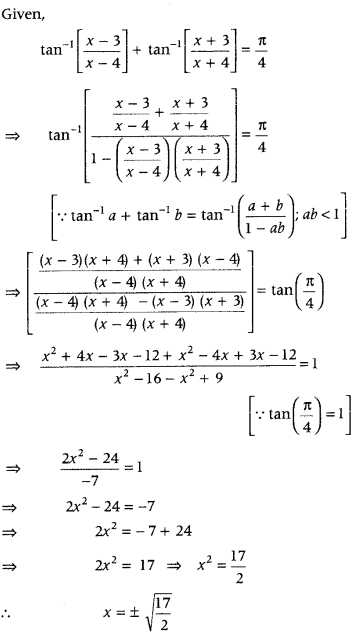
Question 33.
Prove that tan\(\left\{\frac{\pi}{4}+\frac{1}{2} \cos ^{-1} \frac{a}{b}\right\}\) + tan\(\left\{\frac{\pi}{4}-\frac{1}{2} \cos ^{-1}\left(\frac{a}{b}\right)\right\}\) = \(\frac{2 b}{a}\).
Answer:

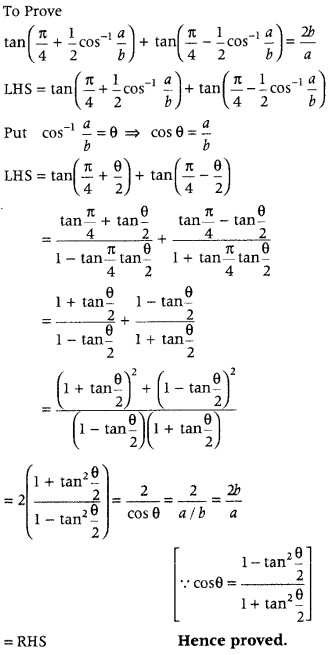
Question 34.
Solve the following equation for x.
cos(tan^-1 x) = sin(cot^-1\(\frac{3}{4}\)) (Delhi 2017, Foregin 2014; All India 2013)
Answer:
We have, cos(tan^-1 x) = sin(cot^{– 1} \(\frac{3}{4}\)) …….. (i)
Let tan^-1 x = θ and cot^-1\(\frac{3}{4}\) = Φ ∀θ ∈ \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
and Φ ∈ (0, π)
⇒ tan θ = x and cot Φ = \(\frac{3}{4}\)
⇒ sec θ = \(\sqrt{1+\tan ^{2} \theta}\) and cosec Φ = \(\sqrt{1+\cot ^{2} \phi}\)
[taking positive square root as θ ∈ \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) and Φ ∈ (θ, π)]

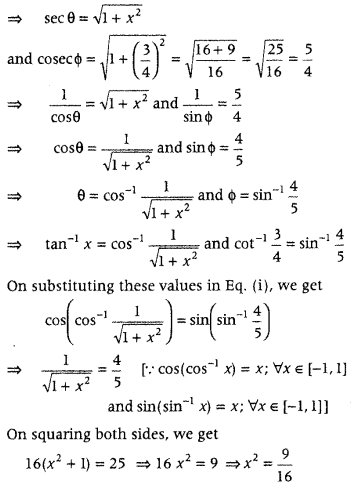
⇒ x = ± \(\frac{3}{4}\) [taking square root both sides]
But x = \(\frac{-3}{4}\) does not satisfy the given equation. Hence, the required solution is x = \(\frac{3}{4}\).

Question 35.
Prove that
\(\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}\) (DelhI 2018; Foreign 2015; Delhi 2008; 2008C)
Answer:

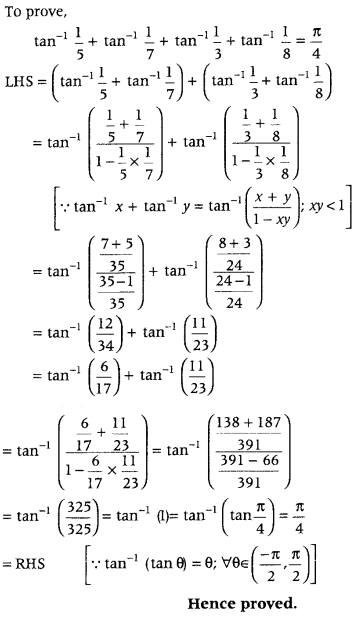
Question 36.
Solve for x,
2 tan^-1x (cos x) = tan^-1 (2 cosecx). (Delhi 2016; Foreign 2015, Delhi 2014C; All India 2009)
Answer:
Given equation is
2 tan^-1 (cos x) = tan^-1 (2 cosec x)

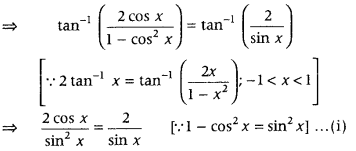
⇒ sin x cos x – sin² x = 0
⇒ sin x (cos x – sin x) = 0
⇒ sin x = 0 or cos x = sin x
⇒ sin x = sin 0
or cot x = 1 = cot \(\frac{\pi}{4}\)
∴ x = 0 or \(\frac{\pi}{4}\)
But here at x = 0, the given equation does not exist.
Hence, x = \(\frac{\pi}{4}\) is the only solution.

Question 37.
Solve for x,
tan^-1(x – 1) + tan^-1 x + tan^-1(x + 1) = tan^-1 3x (All India 2016)
Answer:
Given,
tan^-1 (x – 1) + tan^-1 x + tan^-1 (x + 1) = tan^-1 3x
⇒ tan^-1 (x – 1) + tan^-1 (x + 1) = tan^-1 3x – tan^-1 x

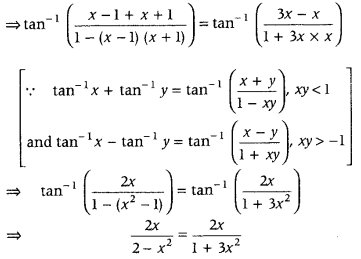
⇒ 2x(1 + 3x²) = 2x(2 – x²)
⇒ 2x[1 + 3x² – (2 – x²)] = 0
⇒ x(4x² – 1) = 0 ⇒ x = 0 or 4x² – 1 = 0
∴ x = 0 or x = ± \(\frac{1}{2}\)

Question 38.
Prove that
tan^-1\(\left(\frac{6 x-8 x^{3}}{1-12 x^{2}}\right)\) – tan^-1\(\left(\frac{4 x}{1-4 x^{2}}\right)\) = tan^-1 2x; |2x| < \(\frac{1}{\sqrt{3}}\). (All India 2016)
Answer:

Question 39.
Prove that
cot^-1\(\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)\) = \(\frac{x}{2}\), 0 < x < \(\frac{\pi}{2}\), or x ∈ \(\frac{\pi}{4}\)
(Foreign 2016; Delhi 2014, 2011; All India 2009)
Answer:

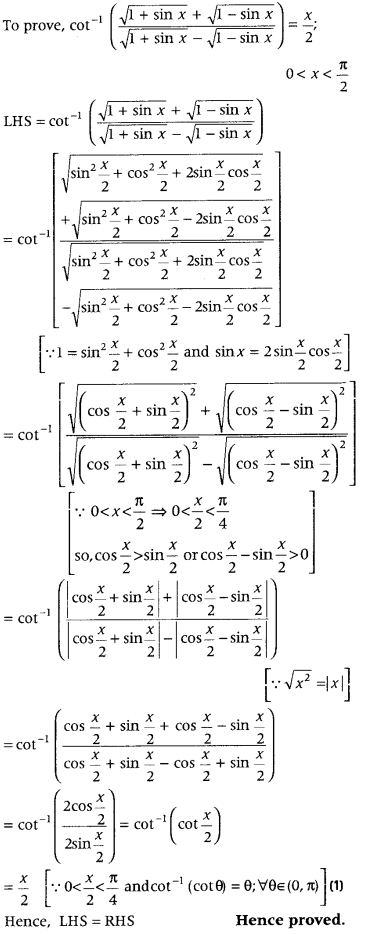
Alternate Method:

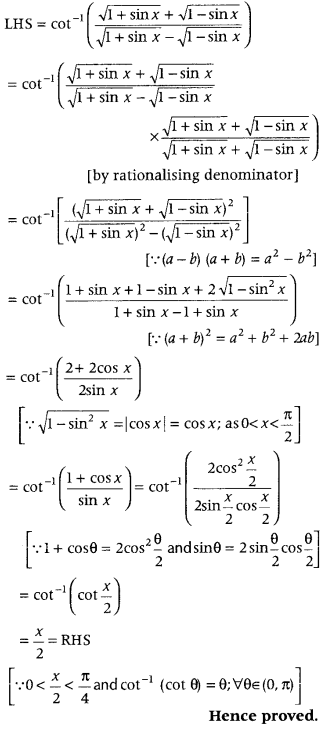
Question 40.
Solve for x,
tan^-1\(\left(\frac{x-2}{x-1}\right)\) – tan^-1\(\left(\frac{x+2}{x+1}\right)\) = \(\frac{\pi}{4}\) (Foreign 2016)
Answer:
\(\sqrt{\frac{7}{2}},-\sqrt{\frac{7}{2}}\)

Question 41.
If sin [cot^-1 (x + 1)] = cos (tan^-1 x), then find x. (Delhi 2015)
Answer:
– \(\frac{1}{2}\)

Question 42.
If(tan^-1 x)² + (cot^-1 x)² = \(\frac{5 \pi^{2}}{8}\), then find x. (Delhi 2015)
Answer:

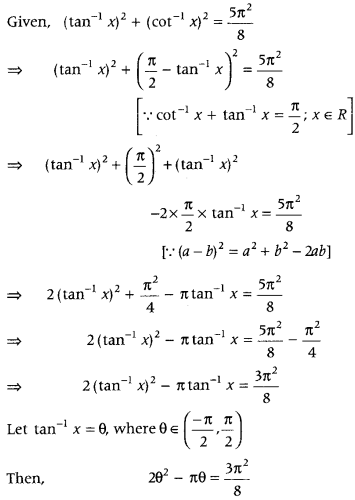
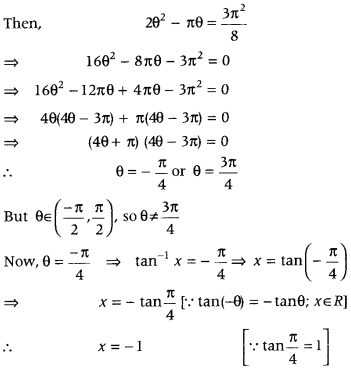
Question 43.
Prove the following.

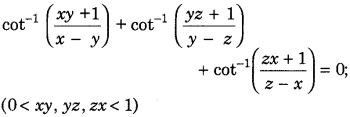
(All India 2015)
Answer:

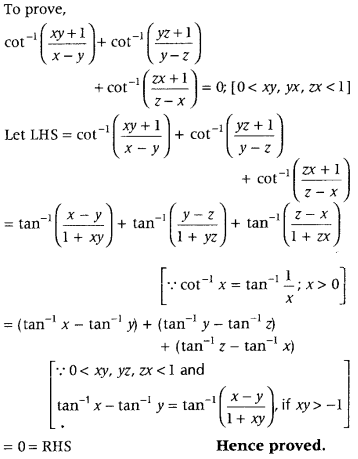
Question 44.

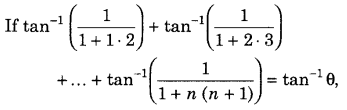
then find the value of θ. (Foregin 2015)
Answer:
First, convert each inverse trigonometric function in the form, of tan^-1\(\left(\frac{x-y}{1+x y}\right)\)1 and then use the formula tan^-1 \(\left(\frac{x-y}{1+x y}\right)\) = tan^-1x – tan^-1 y; xy > – 1 Further, simplify it and again use the above formula.

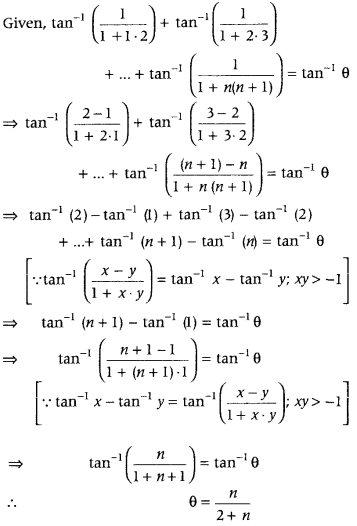
Question 45.
Prove that
2 tan^-1\(\left(\frac{1}{2}\right)\) + tan^-1\(\left(\frac{1}{7}\right)\) = sin^-1\(\left(\frac{31}{25 \sqrt{2}}\right)\) (All India 2015C)
Answer:
First, use the relation,
2 tan^-1 x = tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\); – 1 < x < 1 and then use tan^-1 x + tan^-1y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\); xy < 1

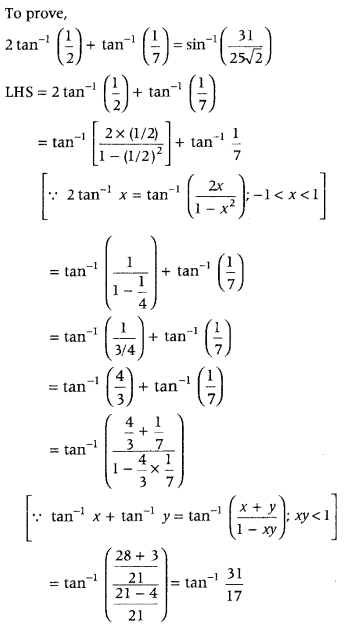
Question 46.
Solve the following equation for x.
tan^-1\(\left(\frac{1-x}{1+x}\right)\) = \(\frac{1}{2}\)tan^-1x, x > 0
(All India 2015C, 2O14C, 2010, 2009C; Foreign 2011C, 2008C)
Answer:

⇒ 3x² = 1 ⇒ x² = \(\frac{1}{3}\)
⇒ x = ± \(\frac{1}{\sqrt{3}}\)
[∵ x > 0 given, so we do not take x = – \(\frac{1}{\sqrt{3}}\)]
[∴ x = \(\frac{1}{\sqrt{3}}\) is the only solution of the given equation.]

Question 47.
Solve for x, tan^-1x + 2 cot^-1 x = \(\frac{2 \pi}{3}\). (All India 2014C; Delhi 2009C)
Answer:
Given equation is tan^-1 x + 2 cot^-1 x = \(\frac{2 \pi}{3}\)
Then, the given equation can be written as

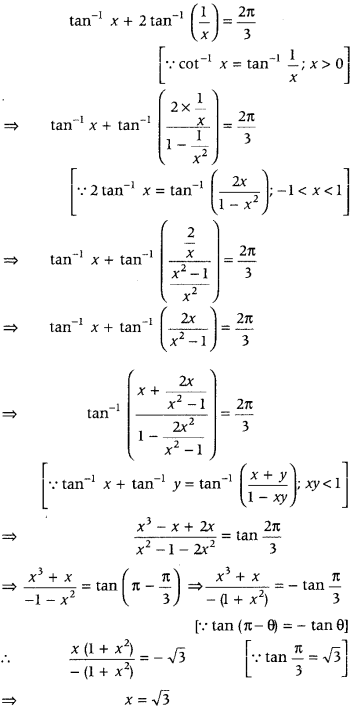
Question 48.
Prove that
2 tan^-1\(\left(\frac{1}{5}\right)\) + sec^-1\(\left(\frac{5 \sqrt{2}}{7}\right)\) + 2 tan^-1\(\left(\frac{1}{8}\right)=\frac{\pi}{4}\). (Delhi 2014)
Answer:

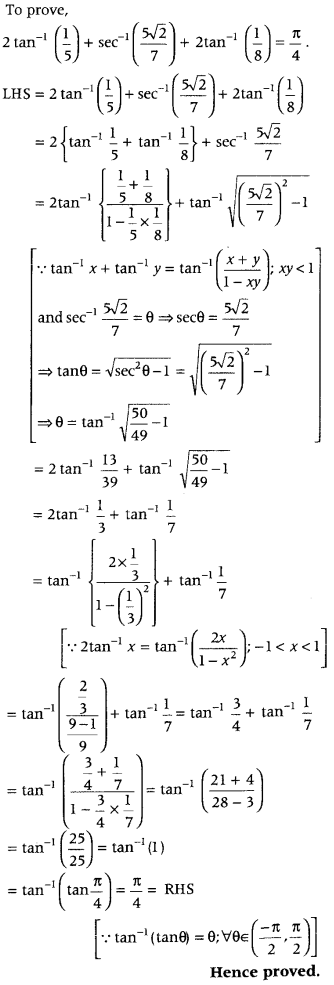
Question 49.
Prove that tan^-1\(\left[\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right]\) = \(\frac{\pi}{4}-\frac{1}{2}\) cos^-1x, – \(\frac{1}{\sqrt{2}}\) ≤ x ≤ 1. (All India 2014, 2014C, 2011)
Answer:
To prove,

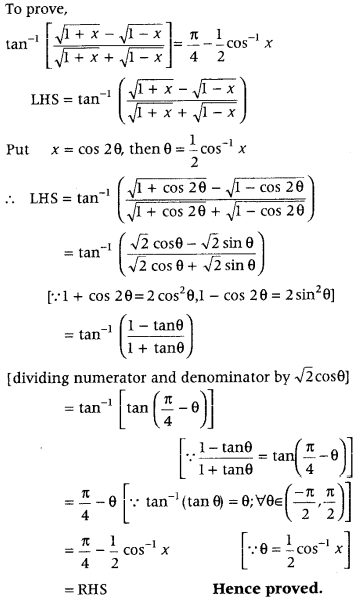
Question 50.
If tan^-1 \(\left(\frac{x-2}{x-4}\right)\) + tan^-1 \(\left(\frac{x+2}{x+4}\right)\) then find the value of x. (All India 2014)
Answer:
x = ± √2

Question 51.
Prove that
cos^-1 (x) + cos^-1\(\left\{\frac{x}{2}+\frac{\sqrt{3-3 x^{2}}}{2}\right\}\) = \(\frac{\pi}{3}\). (All India 2014C)
Answer:

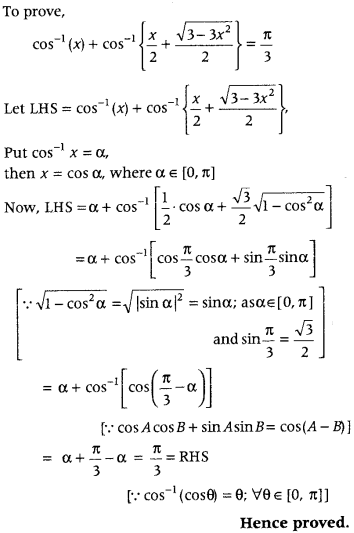
Question 52.
Prove that
cot^-1 7 + cot^-1 8 + cot^-1 18 = cot^-1 3. (Forei9n 2014)
Answer:
To prove. cot^-1 7 + cot^-1 8 + cot^-1 18 = cot^-1 3
LHS = cot^-1 7 + cot^-1 8 + cot^-1 18

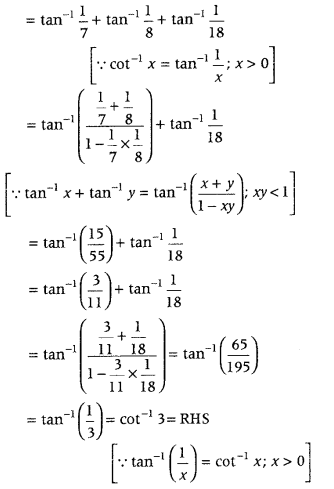
Hence proved.

Question 53.
Prove that
sin^-1\(\left(\frac{8}{17}\right)\) + sin^-1\(\left(\frac{3}{5}\right)\) = cos^-1\(\left(\frac{36}{85}\right)\). (All India 2014C; Delhi 2012, 2010C)
Answer:

Question 54.
Show that tan\(\left(\frac{1}{2} \sin ^{-1} \frac{3}{4}\right)=\frac{4-\sqrt{7}}{3}\). (All India 2013).
Answer:

Question 55.
Solve for x, sin^-1 (1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\). (All India 2013C)
Answer:

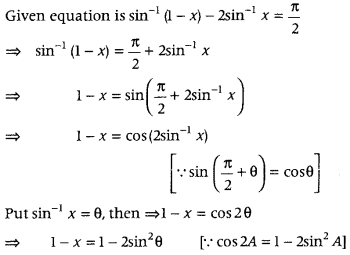
⇒ 1 – x = 1 – 2x² [∵ sin^-1 x = θ ⇒ x = sin θ]
⇒ 2x² – x = 0
⇒ x(2x – 1) = 0
∴ x = 0 or x = \(\frac{1}{2}\)
For x = \(\frac{1}{2}\) , LHS = sin^-1\(\left(\frac{1}{2}\right)\) – 2 sin^-1\(\left(\frac{1}{2}\right)\)
= \(\frac{\pi}{6}-\frac{2 \pi}{6}=\frac{-\pi}{6} \neq \frac{\pi}{2}\)
∴ x = \(\frac{1}{2}\) is not a solution of given equation.
Hence, x = 0 is the only solution. (1)

Question 56.
Prove that sin^-1\(\frac{8}{17}\) + sin^-1\(\frac{3}{5}\) = tan^-1\(\frac{77}{36}\). (Delhi 2013C)
Answer:

Question 57.
Find the value of the following. (Delhi 2013)

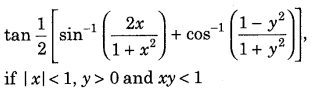
Answer:

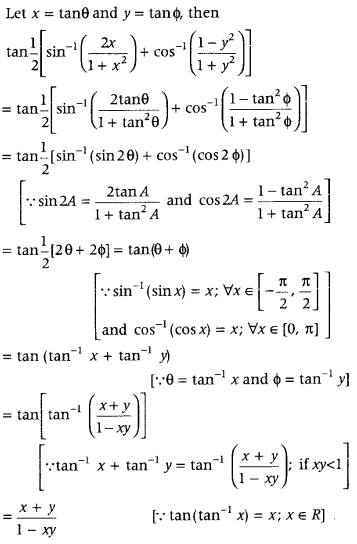
Question 58.
Prove that (Delhi 2013; All India 2011, 2008C)

Answer:

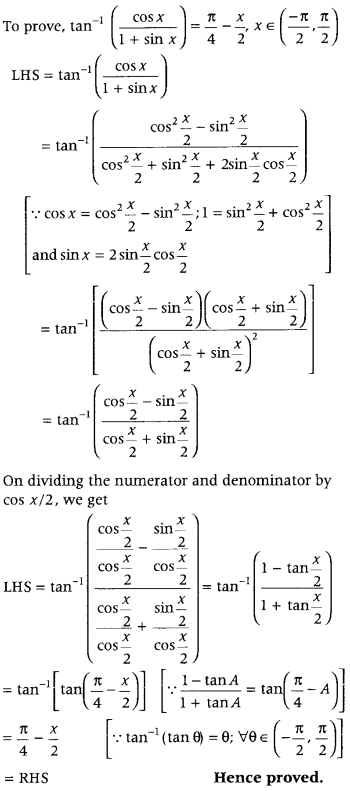
Question 59.
Prove that (Delhi 2012)

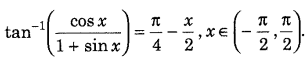
Answer:

Question 60.
Prove that (All India 2012; Delhi 2010C, 2009)

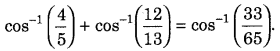
Answer:

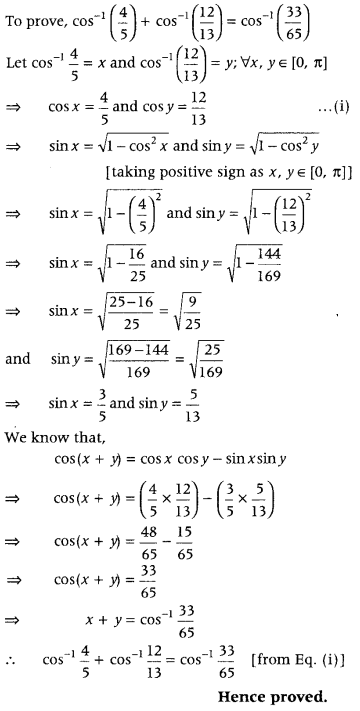
Question 61.
Prove the following. (All India 2012)

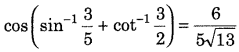
Answer:

Question 62.
Prove that
sin^-1\(\left(\frac{63}{65}\right)\) = sin^-1\(\left(\frac{5}{13}\right)\) + cos^-1\(\left(\frac{3}{5}\right)\). (Foregin 2012).
Answer:

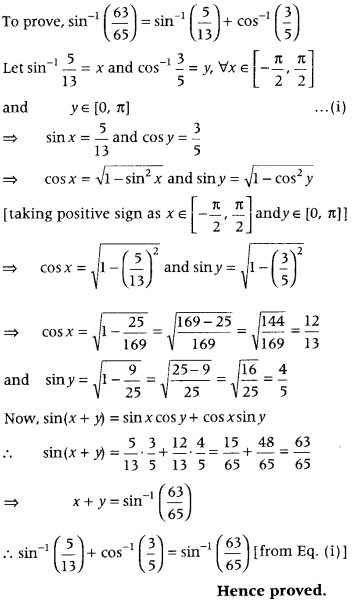
Question 63.
Solve for x ,
2 tan^-1(sin x) = tan^-1(2 sec x), x ≠ \(\frac{\pi}{2}\). (Foregin 2012)
Answer:
\(\frac{\pi}{4}\)

Question 64.
Find the value of
tan^-1\(\left(\frac{x}{y}\right)\) – tan^-1\(\left(\frac{x-y}{x+y}\right)\) (Delhi 2011)
Answer:

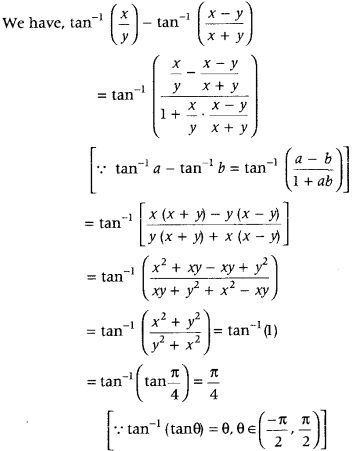
Question 65.
Prove that (All India 2011; Delhi 2009C, 2008C)
2 tan^-1\(\left(\frac{1}{2}\right)\) + tan^-1\(\left(\frac{1}{7}\right)\) = tan^-1\(\left(\frac{31}{17}\right)\).
Answer:
First, use the relation,
2 tan^-1 x = tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\); – 1 < x < 1 and then use tan^-1 x + tan^-1y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\); xy < 1

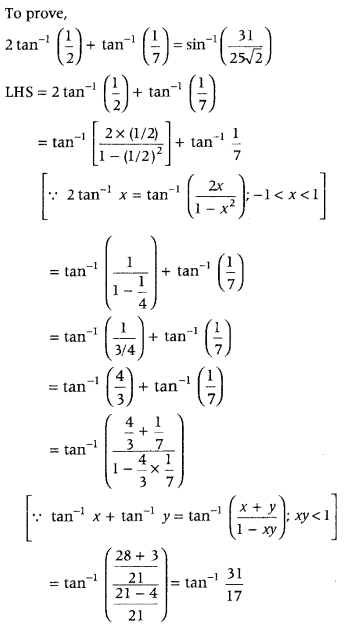
Question 66.
Prove that (Foregin 2011)

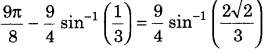
Answer:

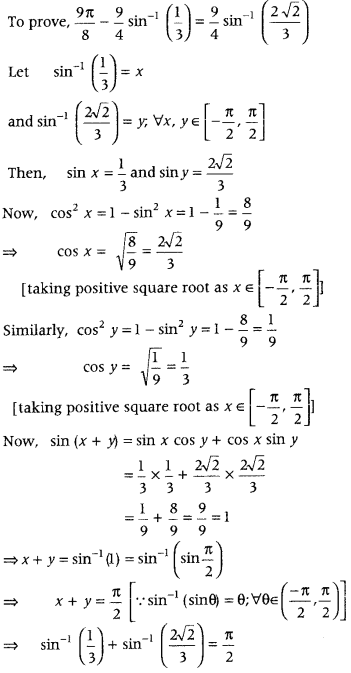
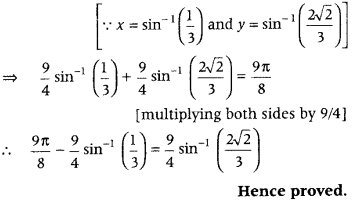
Alternate Method:

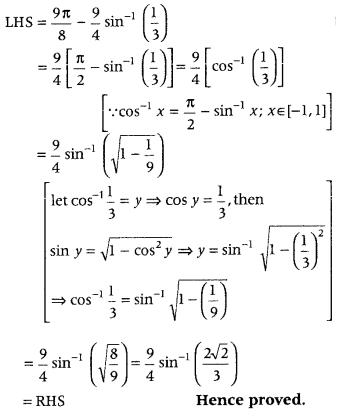
Question 67.
Prove that tan^-1 \(\frac{1}{4}\) + tan^-1 \(\frac{2}{9}\) = \(\frac{1}{2}\) tan^-1 \(\frac{4}{3}\). (All India 2011C)
Answer:

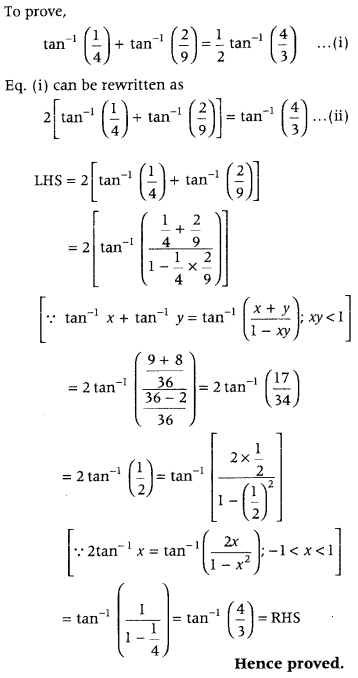
Question 68.
Solve for x, cos (2 sin^-1 x) = \(\frac{1}{9}\); x > 0. (All India 2011C)
Answer:
Given equation is
cos (2 sin^-1 x) = \(\frac{1}{9}\) , x > 0 ……. (i)
Put sin^-1x = y
⇒ x = sin y
Then, Eq. (1) becomes, cos 2y = \(\frac{1}{9}\)
⇒ 1 – 2 sin² y = \(\frac{1}{9}\) [∵ cos 2θ = 1 — 2s1n2 01(1)
⇒ 2 sin² y = 1 – \(\frac{1}{9}\) = \(\frac{8}{9}\)
⇒ sin² y = \(\frac{4}{9}\)
⇒ x² = \(\frac{4}{9}\) [∵ sin y = x]
∴ x = ± \(\frac{2}{3}\) [taking square root]
But it is given that, x > 0.
∴ x = \(\frac{2}{3}\)

Question 69.
Prove that 2 tan^-1 \(\frac{3}{4}\) – tan^-1 \(\frac{17}{31}=\frac{\pi}{4}\). (Delhi 2011C)
Answer:
First, use the relation
2 tan^-1 x = tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\) – 1 < x < 1 and then use the relation tan^-1 x – tan^-1 y = tan^-1 \(\left(\frac{x-y}{1+x y}\right)\), xy > – 1 and get the required result.

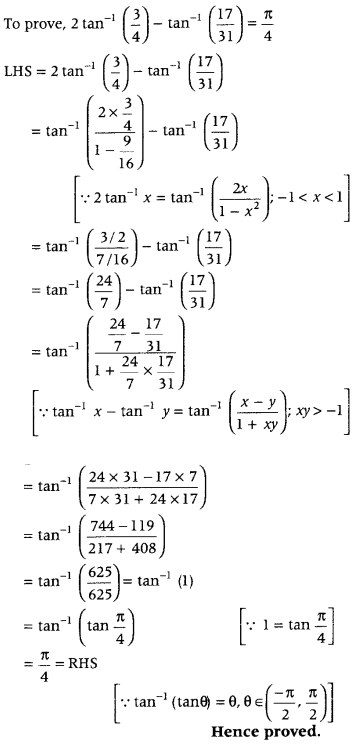
Question 70.
Solve for x,
tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\) + cot^-1\(\left(\frac{1-x^{2}}{2 x}\right)\) = \(\frac{\pi}{3}\), – 1 < x < 1. (Delhi 2011C)
Answer:

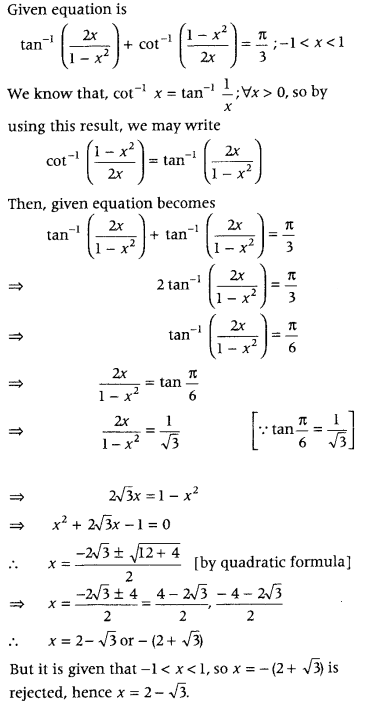
Question 71.
Prove that
tan^-1 √x = \(\frac{1}{2}\) cos^-1\(\left(\frac{1-x}{1+x}\right)\) , x ∈ (0, 1). (Delhi 2010)
Answer:
First, put √x = tan θ ⇒ θ = tan^-1 √x and then use cos 2θ = \(\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}\)

Question 72.
Prove that (Delhi 2010)
cos^-1\(\left(\frac{12}{13}\right)\) + sin^-1\(\left(\frac{3}{5}\right)\) = sin^-1\(\left(\frac{56}{65}\right)\)
Answer:

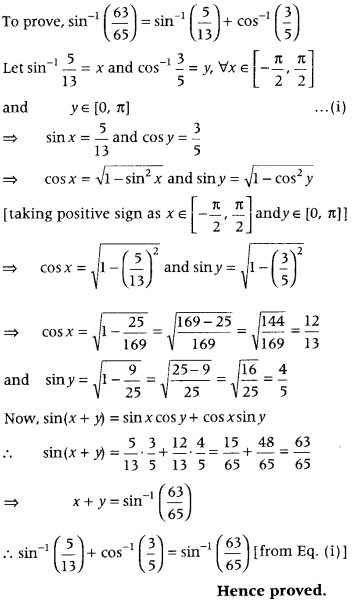
Question 73.
Prove that
tan^-1(1) + tan^-1(2) + tan^-1(3) = π. (Delhi 2010)
Answer:
To prove,
tan^-1(1) + tan^-1(2) + tan^-1(3) = π
LHS = tan^-1(1) + tan^-1(2) + tan^-1(3)

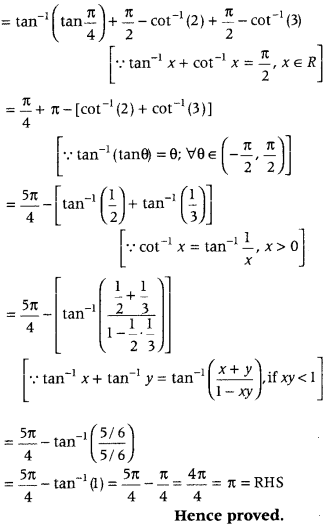
Question 74.
Prove that
tan^-1x + tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\) = tan^-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\). (All India 2010).
Answer:

Question 75.
Prove that
cos [tan^-1{sin(cot^-1 x)}] = \(\sqrt{\frac{1+x^{2}}{2+x^{2}}}\). (All India 2010).
Answer:
To prove, cos [tan^-1 {sin (cot^-1x}] = \(\sqrt{\frac{1+x^{2}}{2+x^{2}}}\)
LHS = cos (tan^-1 {sin(cot^-1 x)}]
Put cot^-1 x = θ ⇒ x = cot θ
Then, LHS = cos (tan^-1 (sin θ)]

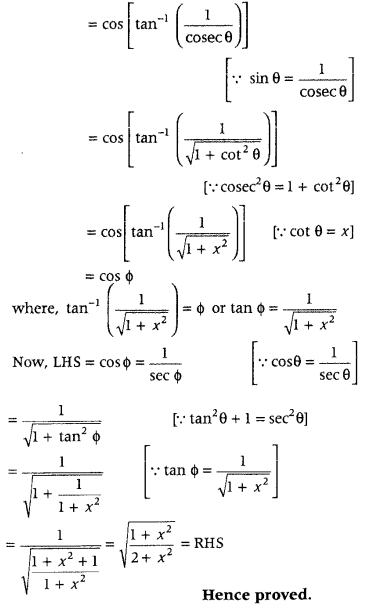
Question 76.
Solve for x, cos^-1x + sin^-1\(\left(\frac{x}{2}\right)\) = \(\frac{\pi}{6}\). (All India 2010C)
Answer:

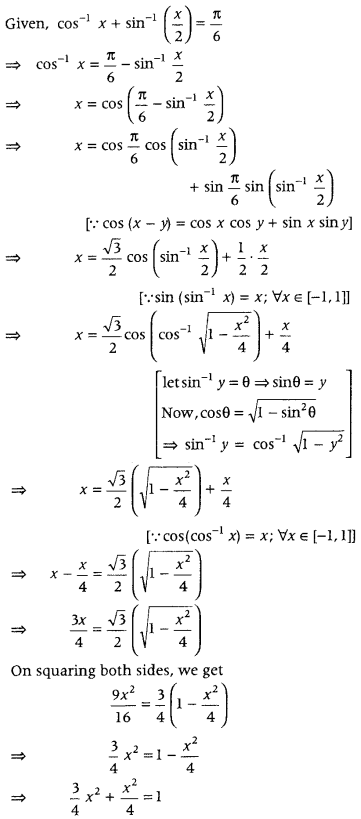
⇒ \(\frac{4 x^{2}}{4}\) = 1
∴ x² = 1 ⇒ x = ± 1
But x = -1, does not satisfy the given equation.
Hence, x = 1 satisfy the given equation.

Question 77.
Prove that
2 tan^-1 \(\frac{1}{3}\) + tan^-1 \(\frac{1}{7}=\frac{\pi}{4}\). (All India 2010C)
Answer:
First, use the relation
2 tan^-1 x = tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\) – 1 < x < 1 and then use the relation tan^-1 x – tan^-1 y = tan^-1 \(\left(\frac{x-y}{1+x y}\right)\), xy > – 1 and get the required result.

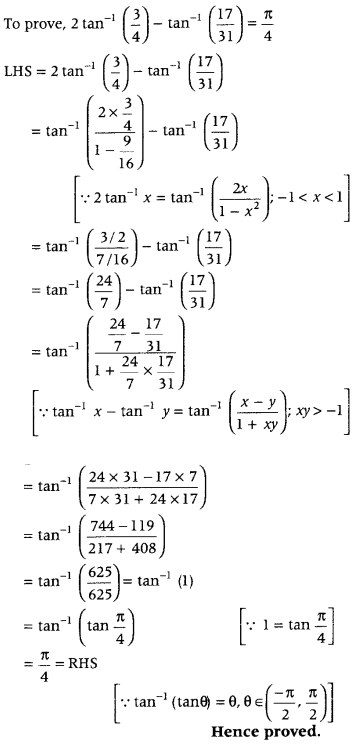
Question 78.
Solve for x, tan^-1\(\frac{x}{2}\) + tan^-1\(\frac{x}{3}=\frac{\pi}{4}\), (√6 > x > 0. (Delhi 210C)
Answer:

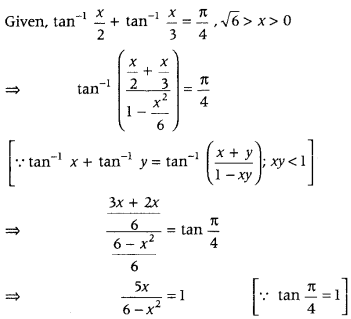
⇒ 5x = 6 – x²
⇒ x² + 5x – 6 = 0
⇒ x² + 6x – x – 6 = 0
⇒ x(x + 6) – 1(x + 6) = 0
⇒ (x – 1) (x + 6) = 0
∴ x = 1 or – 6
But it is given that. √6 > x > 0 ⇒ x > 0
∴ x = – 6 is rejected.
Hence. x =1 is the only solution of the given equation.

Question 79.
Solve for x, tan^-1(x + 2) + tan^-1(x – 2) = tan^-1\(\left(\frac{8}{79}\right)\), x > 0 (Delhi 2010C)
Answer:
First, use the formula tan^-1 x + tan^-1 y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\); xy < 1, then simplify it and get the values of x. Further, verify the given equation by obtained values of x.

Given, tan^-1(x + 1) + tan^-1(x – 1) = tan^-1 \(\frac{8}{31}\) …… (i)

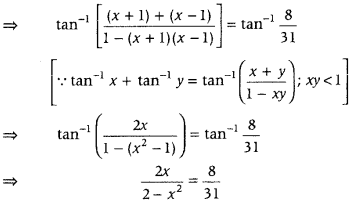
⇒ 62x = 16 – 8x²
⇒ 8x² + 62x – 16 = 0
⇒ 4x² + 31x – 8 = 0
⇒ 4x² + 32x – x – 8 = 0
⇒ 4x(x + 8) – 1 (x + 8) = 0
⇒ (x + 8) (4x – 1) = 0
∴ x = -8 or x = \(\frac{1}{4}\)
But x = – 8 gives LHS = tan^-1 (- 7) + tan^-1 (- 9)
= – tan^-1 (7) – tan^-1 (9),
which is negative, while RHS is positive.
So, x = – 8 is not possible.
Hence, x = \(\frac{1}{4}\) is the only solution of the given equation.