Get access to Class 12 Maths Important Questions Chapter 10 Vector Algebra, Vector Algebra Class 12 Important Questions with Solutions Previous Year Questions will help the students to score good marks in the board examination.
Vector Algebra Class 12 Important Questions with Solutions Previous Year Questions
Algebra of Vectors
Question 1.
Find the position vector of a point which divides the join of points with position vectors \(\vec{a}-2 \vec{b}\) and 2\(2 \vec{a}+\vec{b}\) externally in the ratio 2:1. (Delhi 2016)
Answer:
Let given position vectors are \(\overrightarrow{O A}=\vec{a}-2 \vec{b}\) and \(\overrightarrow{O B}=2 \vec{a}+\vec{b}\).
Let \(\overrightarrow{O A}\) be the position vector of a point C which divides the join of points, with position vectors
\(\overrightarrow{O A}\) and \(\overrightarrow{O B}\), externally in the ratio 2:1.
∴ \(\overrightarrow{O A}\) = \(\frac{2 \overrightarrow{O B}-1 \overrightarrow{O A}}{2-1}=\frac{2(2 \vec{a}+\vec{b})-1(\vec{a}-2 \vec{b})}{1}\) [by external section formula]
= 4\(\vec{a}\) + 2\(\vec{b}\) – \(\vec{a}\) + 2\(\vec{b}\) = 3\(\vec{a}\) + 4\(\vec{b}\)
Question 2.
If \(\vec{a}\) = 4î – ĵ + k̂ and \(\vec{b}\) = 2î – 2ĵ + k̂, then find a unit vector parallel to the vector \(\vec{a}+\vec{b}\). (All India 2016)
Answer:
Given vectors are
\(\vec{a}\) = 4î – ĵ + k̂, \(\vec{b}\) = 2î – 2ĵ + k̂.
Now, \(\vec{a}+\vec{b}\) == (4î – ĵ + k̂) + (2î – 2ĵ + k̂)
= 6î – 3ĵ + 2k̂
and \(|\vec{a}+\vec{b}|=\sqrt{(6)^{2}+(-3)^{2}+(2)^{2}}\)
= \(\sqrt{36+9+4}=\sqrt{49}\) = 7units
∴ The unit vector parallelto the vector \(\vec{a}+\vec{b}\) is
\(\frac{\vec{a}+\vec{b}}{|\vec{a}+\vec{b}|}=\frac{6 \hat{i}-3 \hat{j}+2 \hat{k}}{7}\)
Question 3.
The two vectors ĵ + k̂ and 3î – ĵ + 4k̂ represent the two sides \(\overrightarrow{A B}\) and \(\overrightarrow{A C}\) respectively of triangle ABC. Find the length of the median through A. (Delhi 2016; Foreign 2015)
Answer:
Given, \(\overrightarrow{A B}\) = ĵ + k̂ and \(\overrightarrow{A C}\) = 3î – ĵ + 4k̂


Alternate Method:
Given \(\overrightarrow{A B}\) = ĵ + k̂ and \(\overrightarrow{A C}\) = 3î – ĵ + 4k̂
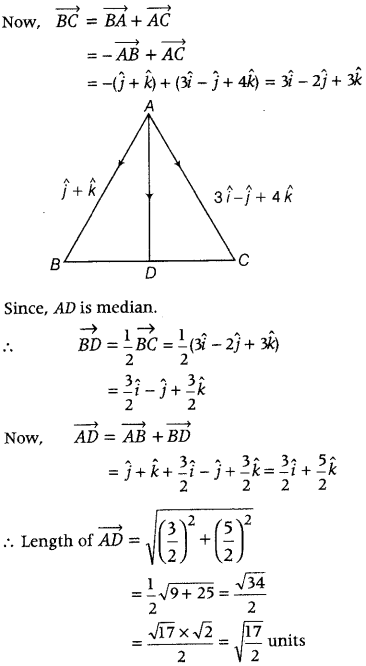
Question 4.
Write the direction ratios of the vector 3\(\vec{a}\) + 2\(\vec{b}\), where \(\vec{a}\) = î + ĵ – 2k̂ and \(\vec{b}\) = 2î – 4ĵ + 5k̂ (All India 2015C)
Answer:
Clearly, 3\(\vec{a}\) + 2\(\vec{b}\) = 3 (î + ĵ – 2k̂) + 2 (2î – 4ĵ + 5k̂)
= (3î + 3ĵ – 6k̂) + (4î – 8ĵ + 10k̂)
= 7î – 5ĵ + 4k̂
Hence, direction ratios of vectors 3\(\vec{a}\) + 2\(\vec{b}\) are 7, – 5 and 4.
Question 5.
Find the unit vector in the direction of the sum of the vectors 2î + 3ĵ – k̂ and 4î – 3ĵ + 2k̂. (Foreign 2015)
Answer:
Let \(\vec{a}\) = 2î + 3ĵ – k̂ and \(\vec{b}\) = 4î – 3ĵ + 2k̂
Now, sum of two vectors,
\(\vec{a}+\vec{b}\) = (2î + 3ĵ – k̂) + (4î – 3ĵ + 2k̂) = 6î + k̂
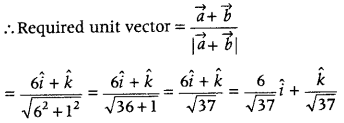
Question 6.
Find a vector in the direction of vector 2î – 3ĵ + 6k̂ which has magnitude 21 units. (Foreign 2014)
Answer:
To find a vector in the direction of given vector, first of all we find unit vector in the direction of given vector and then multiply it with given magnitude.
Let \(\vec{a}\) = 2î – 3ĵ + 6k̂
Then, |\(\vec{a}\)| = \(\sqrt{(2)^{2}+(-3)^{2}+(6)^{2}}\)
= \(\sqrt{4+9+36}=\sqrt{49}\) = 7 units
The unit vector in the direction of the given vector \(\vec{a}\) is
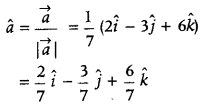
Now, the vector of magnitude equal to 21 units
and in the direction of a is given by
21â = 21\(\left(\frac{2}{7} \hat{i}-\frac{3}{7} \hat{j}+\frac{6}{7} \hat{k}\right)\) = 6î – 9ĵ + 18k̂
Question 7.
Find a vector a of magnitude 5√2, making an angle of \(\frac{\pi}{4}\) with X-axis, \(\frac{\pi}{2}\) with Y-axis and an acute angle 0 with Z-axis. (All India 2014)
Answer:
Here, we have l = cos \(\frac{\pi}{4}\), m = cos \(\frac{\pi}{2}\) and n = cosθ
⇒ l = \(\frac{1}{\sqrt{2}}\), m = 0 and n = cosθ

Question 8.
Write a unit vector in the direction of the sum of the vectors \(\vec{a}\) = 2î + 2ĵ – 5k̂ and \(\vec{b}\) = -2î + ĵ – 7k̂. (Delhi2014C)
Answer:
\(\frac{1}{13}\)(4î + 3ĵ – 12k̂)
Question 9.
Find the value of p for which the vectors 3î + 2ĵ + 9k̂ and î – 2pĵ + 3k̂ are parallel. (All India 2014)
Answer:
Given, 3î + 2ĵ + 9k̂ and î – 2pĵ + 3k̂ are two parallel vectors, so their direction ratios will be proportional.
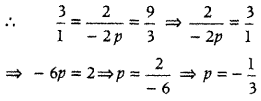
Question 10.
Write the value of cosine of the angle which the vector \(\vec{a}\) = î + ĵ + k̂ makes with Y-axis. (Delhi 2014C)
Answer:
Given, \(\vec{a}\) = î + ĵ + k̂
Now, unit vector in the direction of \(\vec{a}\) is
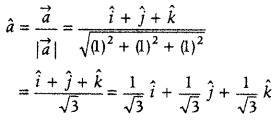
∴ Cosine of the angle which given vector makes with Z-axis is \(\frac{1}{\sqrt{3}}\)
Question 11.
Find the angle between X-axis and the vector î + ĵ + k̂. (All India 2014C)
Answer:
Let \(\vec{a}\) = î + ĵ + k̂
Now, unit vector in the direction of \(\vec{a}\) is

So, angle between X-axis and the vector
î + ĵ + k̂ is cos α = \(\frac{1}{\sqrt{3}}\) ⇒ α = cos-1 (\(\frac{1}{\sqrt{3}}\))
[∵ â = lî + mĵ + nk̂ and cos α = l ⇒ α = cos-1l]
Question 12.
Write a vector in the direction of the vector î – 2ĵ + 2k̂ that has magnitude 9 units. (Delhi 2014C)
Answer:
3î – 6ĵ + 6k̂
Question 13.
Write a unit vector in the direction of vector \(\vec{P Q}\), where P and Q are the points (1, 3, 0) and (4, 5, 6), respectively. (Foreign 2014)
Answer:
First, find the vector \(\overrightarrow{P Q}\) by using the formula (x2 – x1)î + (y2 – y1)ĵ + (z2 – z1)k̂, then required unit vector is given by \(\frac{\overrightarrow{P Q}}{|\overrightarrow{P Q}|}\)
Given points are P (1, 3, 0) and Q (4, 5, 6).
Here, x1 = 1, y1 = 3, z1 = 0
and x2 = 4, y2 = 5, z2 = 6
So, vector PQ = (x2 – x1)k̂ + (y2 – y1)ĵ + (z2 – z1)k̂
= (4 – 1)î + (5 – 3)ĵ + (6 – 0)k̂
= 3î + 2ĵ + 6k̂
∴ Magnitude of given vector
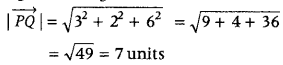
Hence, the unit vector in the direction of \(\vec{P Q}\) is
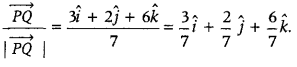
Question 14.
If a unit vector \(\vec{a}\) makes angle \(\frac{\pi}{3}\) with î, \(\frac{\pi}{4}\) with ĵ and an acute angle θ with k̂, then find the value of θ. (Delhi 2013)
Answer:
Here, we have
l = cos\(\frac{\pi}{3}\), m = cos \(\frac{\pi}{4}\) and n = cos θ
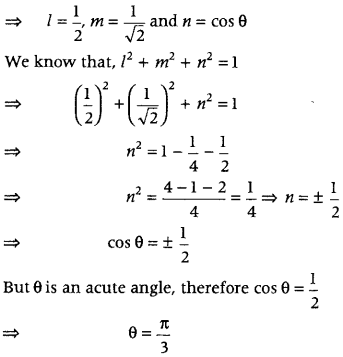
Question 15.
Write a unit vector in the direction of the sum of vectors \(\vec{a}\) = 2î – ĵ + 2k̂ and \(\vec{b}\) = – î + ĵ + 3k̂. (Delhi 2013)
Answer:
\(\frac{1}{\sqrt{26}} \hat{i}+\frac{5}{\sqrt{26}} \hat{k}\)
Question 16.
If \(\vec{a}\) = xî +2ĵ – zk̂ and \(\vec{b}\) = 3î – yĵ + k̂ are two equal vectors, then write the value of x + y + z. (Delhi 2013)
Answer:
Two vectors are equal, if coefficients of their components are equal.
Given, \(\vec{a}=\vec{b}\) ⇒ xî + 2ĵ – zk̂ = î – yĵ + k̂
On comparing the coefficient of components, we get
x = 3, y = -2, z = -1
Now, x + y + z = 3 – 2 – 1 = 0
Question 17.
P and Q are two points with position vectors 3\(\vec{a}\) – 2\(\vec{b}\) and \(\vec{a}\) + \(\vec{b}\), respectively. Write the position vector of a point R which divides the line segment PQ in the ratio 2 : 1 externally. (All India 2013)
Answer:
\(-\vec{a}+4 \vec{b}\)
Question 18.
L and M are two points with position vectors 2\(\vec{a}\) – \(\vec{b}\) and \(\vec{a}\) + 2\(\vec{b}\), respectively. Write the position vector of a point N which divides the line segment LM in the ratio 2 : 1 externally. (All India 2013)
Answer:
5\(\vec{b}\)
Question 19.
A and B are two points with position vectors 2\(\vec{a}\) – 3\(\vec{b}\) and 6\(\vec{b}\) – \(\vec{a}\), respectively. Write the position vector of a point P which divides the line segment AB internally in the ratio 1:2. (All India 2013)
Answer:
Given, A and B are two points with position vectors 2\(\vec{a}\) – 3\(\vec{b}\) and 6\(\vec{b}\) – \(\vec{a}\), respectively. Also, point P divides the line segment AB in the ratio 1 : 2 internally.

Question 20.
Find the sum of the vectors \(\vec{a}\) = î – 2ĵ + k̂ \(\vec{b}\) = – 2î + 4ĵ + 5k̂ and \(\vec{c}\) = î – 6ĵ – 7k̂. (Delhi 2012)
Answer:
Given vectors are \(\vec{a}\) = î – 2ĵ + k̂ \(\vec{b}\) = – 2î + 4ĵ + 5k̂ and \(\vec{c}\) = î – 6ĵ – 7k̂.
Sum of the vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) is
\(\vec{a}+\vec{b}+\vec{c}\) = (î – 2ĵ + k̂) + (- 2î + 4ĵ + 5k̂) + (î – 6ĵ – 7 k̂)
= – 4ĵ – k̂
Question 21.
Find the sum of the following vectors. \(\vec{a}\) = î – 3k̂, \(\vec{b}\) = 2ĵ – k̂, \(\vec{c}\) = 2î – 3ĵ + 2k̂. (Delhi 2012)
Answer:
3î – ĵ – 2k̂
Question 22.
Find the sum of the following vectors. \(\vec{a}\) = î – 2ĵ, \(\vec{b}\) = 2î – 3 ĵ, \(\vec{c}\) = 2î + 3k̂. (Deihi 2012)
Answer:
5î – 5ĵ + 3k̂
Question 23.
Find the scalar components of \(\vec{AB}\) with initial point A (2,1) and terminal point B(- 5, 7). (All India 2012)
Answer:
Given initial point is A (2,1) and terminal point is B (- 5, 7), then scalar component of \(\overrightarrow{A B}\) are
x2 – x1 = – 5 – 2 = – 7and y2 – y1 = 7 – 1 = 6.
Question 24.
For what values of \(\vec{a}\), the vectors 2î – 3ĵ + 4k̂ and aî + 6ĵ – 8k̂ are collinear? (Delhi 2011)
Answer:
If \(\vec{a}\) and \(\vec{b}\) are collinear, then use the condition \(\vec{a}\) = λ\(\vec{b}\), where λ is some scalar.
Let given vectors are \(\vec{a}\) = 2î – 3ĵ + 4k̂ and \(\vec{a}\) = aî + 6ĵ – 8k̂
We know that, vectors \(\vec{a}\) and \(\vec{b}\) are said to be collinear, if
\(\vec{a}\) = k. \(\vec{b}\), where k is a scalar.
∴ 2î – 3ĵ + 4k̂ = k(aî + 6ĵ – 8k̂)
On comparing the coefficients of î and ĵ, we get
2 = ka and -3 = 6k ⇒ k = –\(\frac{1}{2}\)
∴ 2 = –\(\frac{1}{2}\)a ⇒ a = -4
Question 25.
Write the direction cosines of vector -2î + ĵ – 5k̂. (Delhi 2011)
Answer:
Direction cosines of the vector aî + bĵ + ck̂ are
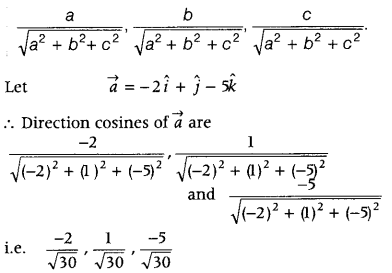
Question 26.
Write the position vector of mid-point of the vector joining points P(2, 3, 4) and Q (4, 1, – 2). (Foreign 2011)
Answer:
Mid-point of the position vectors
\(\vec{a}\) = a1î + a2ĵ + a3k̂ and
\(\vec{b}\) = b1î + b2ĵ + b3k̂ is \(\frac{\vec{a}+\vec{b}}{2}\) or \(\frac{\left(a_{1}+b_{1}\right) \hat{i}+\left(a_{2}+b_{2}\right) \hat{j}+\left(a_{3}+b_{3}\right) \hat{k}}{2}\)
Given points are P(2, 3, 4) and Q(4,1,-2) whose position vectors are \(\overrightarrow{O P}\) = 2 î + 5ĵ + 4k̂ and \(\overrightarrow{O Q}\) =4î + ĵ – 2k̂.
Now, position vector of mid-point of vector joining points P(2, 3, 4) and Q(4, 1, – 2) is
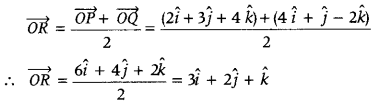
Question 27.
Write a unit vector in the direction of vector \(\vec{a}\) = 2î + ĵ + 2k̂. (All India 2011; Delhi 2009)
Answer:
We know that, unit vector in the direction of â is â = \(\frac{\vec{a}}{|\vec{a}|}\)
Required unit vector in the direction of vector
\(\vec{a}\) = 2î + ĵ + 2k̂
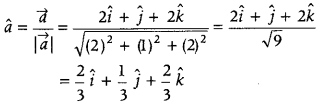
Question 28.
Find the magnitude of the vector \(\vec{a}\) = 3î – 2ĵ + 6k̂. (All India 2011C: Delhi 2008)
Answer:
Magnitude of a vector r = xî + yĵ + zk̂ is |\(\vec{r}\)| = \(\sqrt{x^{2}+y^{2}+z^{2}}\)
Given vector is a = 3i – 2/ + 6fc.
∴ Magnitude of \(\vec{a}\) = \(|\vec{a}|=\sqrt{(3)^{2}+(-2)^{2}+(6)^{2}}\)
= \(\sqrt{9+4+36}=\sqrt{49}\) = 7 units
Question 29.
Find a unit vector in the direction of vector \(\vec{a}\) = 2î + 3ĵ + 6k̂. (All India 2011C)
Answer:
\(\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{6}{7} \hat{k}\)
Question 30.
If A, B and C are the vertices of a ΔABC, then what is the value of \(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}\) ? (Delhi 2011C)
Answer:
Let ΔABC be the given triangle.
Now, by triangle law of vector addition,
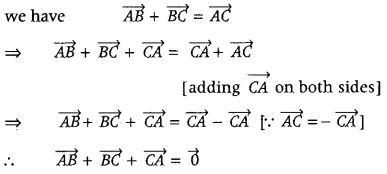
Question 31.
Find a unit vector in the direction of \(\vec{a}\) = 2î – 3ĵ + 6k̂. (Delhi 2011c)
Answer:
\(\frac{2}{7} \hat{i}-\frac{3}{7} \hat{j}+\frac{6}{7} \hat{k}\)
Question 32.
Find a vector in the direction of \(\vec{a}\) = 2î – ĵ + 2k̂, which has magnitude 6 units. (Delhi 2010C)
Answer:
4î – 2ĵ + 4k̂
Question 33.
Find the position vector of mid-point of the line segment AB, where A is point (3, 4, -2) and Bis point (1, 2, 4). (Delhi 2010)
Answer:
2î + 3ĵ + k̂
Question 34.
Write a vector of magnitude 9 units in the direction of vector -2î + ĵ + 2k̂. (All India 2010)
Answer:
-6î + 3ĵ + 6k̂
Question 35.
Write a vector of magnitude 15 units in the direction of vector î – 2ĵ + 2k̂. (Delhi 2010)
Answer:
5î – 10ĵ + 10k̂
Question 36.
What is the cosine of angle which the vector √2î + ĵ + k̂ makes with Y-axis? (Delhi 2010)
Answer:
\(\frac{1}{2}\)
Question 37.
Find a vector of magnitude 5 units and parallel to the resultant of \(\vec{a}\) = 2î + 3ĵ – k̂ and \(\vec{b}\) = î – 2ĵ + k̂. (Delhi 2011)
Answer:
First, find resultant of the vectors a and o, which is \(\vec{a}\) + \(\vec{b}\). Then, find a unit vector in the direction of \(\vec{a}\) + \(\vec{b}\). After this, the unit vector is multiplying by 5.
Given, \(\vec{a}\) = 2î + 3ĵ – k̂ and \(\vec{b}\) = î – 2ĵ + k̂.
Now, resultant of above vectors = \(\vec{a}\) + \(\vec{b}\)
= (2î + 3ĵ – k̂) + (î – 2ĵ + k̂) = 3î + ĵ

Question 38.
Let \(\vec{a}\) = î + ĵ + k̂, \(\vec{b}\) = 4î – 2ĵ + 8k̂ and \(\vec{c}\) = î – 2ĵ + k̂. Find a vector of magnitude 6 units, which is parallel to the vector 2\(\vec{a}\) – \(\vec{b}\) + 8 \(\vec{c}\). (All India 2010)
Answer:
First, find the vector 2 a – b + 3c, then find a unit vector in the direction of 2a-b + 3c.
After this, the unit vector is multiplying by 6.
Given, \(\vec{a}\) = î + ĵ + k̂, \(\vec{b}\) = 4î – 2ĵ + 8k̂ and \(\vec{c}\) = î – 2ĵ + k̂
∴ \(2 \vec{a}-\vec{b}+3 \vec{c}\)
= 2 (î + ĵ + k̂) – (4î – 2ĵ + 3k̂) + 3 (î – 2ĵ + k̂)
= 2î + 2ĵ + 2k̂ – 4î + 2ĵ – 3k̂ + 3î – 6ĵ + 3k̂
⇒ \(2 \vec{a}-\vec{b}+3 \vec{c}\) = î – 2ĵ + 2k̂
Now, a unit vector in the direction of vector
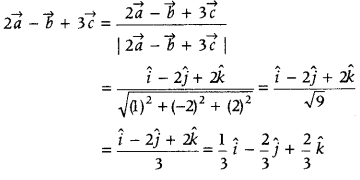
Hence, vector of magnitude 6 units parallel to the Vector \(2 \vec{a}-\vec{b}+3 \vec{c}\) = 6\(\left(\frac{1}{3} \hat{i}-\frac{2}{3} \hat{j}+\frac{2}{3} \hat{k}\right)\)
= 2î – 4ĵ + 4k̂
Question 39.
Find the position vector of a point R, which divides the line joining two points P and Q whose position vectors are 2\(\vec{a}\) + \(\vec{b}\) and \(\vec{a}\) – 8\(\vec{b}\) respectively, externally in the ratio 1 : 2. Also, show that P is the mid-point of line segment RO. (Delhi 2010)
Answer:
Given, \(\overrightarrow{O P}\) = Position vector of P = 2\(\vec{a}\) + \(\vec{b}\)
and \(\overrightarrow{O Q}\) = Position vector of Q = \(\vec{a}\) – 3\(\vec{b}\)
Let OR be the position vector of point R, which divides PQ in the ratio 1 : 2 externally
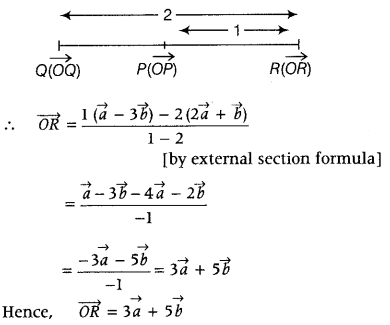
Now, we have to show that P is the mid-point of RQ,
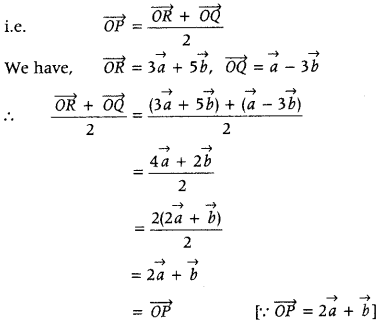
Hence, P is the mid-point of line segment RQ.
Product of Two Vectors and Scalar Triple Product
Question 1.
Find the magnitude of each of the two vectors \(\vec{a}\) and \(\vec{b}\), having the same magnitude such that the angle between them is 60° and their scalar product is \(\frac{9}{2}\). (CBSE 2018)
Answer:

Question 2.
Find the value of [î, k̂, ĵ], (CBSE 2018C)
Answer:
[î, k̂, ĵ] = î ∙ (k̂× ĵ)
= -[[î, k̂, ĵ] = –\(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\) = – 1
Question 3.
Find λ and μ, if (î + 3ĵ + 9k̂) × (3î – λĵ + μk̂) = 0. (All India 2016)
Answer:
Given, (î + 3ĵ + 9k̂) × (3î – λĵ + μk̂)
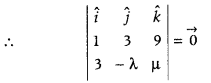
= î(3μ + 9λ) ĵ k̂
On comparing the coefficients of î, ĵ and k̂ , we get
3μ + 9λ = 0, – μ + 27 = 0 and – λ – 9 = 0
⇒ μ = 27 and – λ = 9
⇒ μ = 27 and λ = – 9
Also, the values of μ and λ satisfy the equation
3μ + 9λ = 0.
Hence, μ = 27 and λ = – 9.
Question 4.
Write the number of vectors of unit length perpendicular to both the vectors \(\vec{a}\) = 2î + ĵ + 2k̂ and \(\vec{b}\) = ĵ + k̂. (All India 2016)
Answer:
We know that, unit vectors perpendicular to \(\vec{a}\)
and \(\vec{b}\) are ±\(\left(\frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}\right)\)
So, there arc two unit vectors perpendicular to the given vectors.
Question 5.
If \(\vec{a}, \vec{b}, \vec{c}\) are unit vectors such that \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) = 0, then write the value of \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\). (Foreign 2016)
Answer:
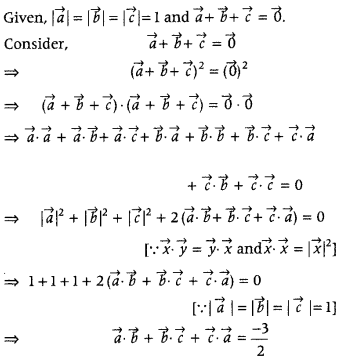
Question 6.
If \(|\vec{a} \times \vec{b}|^{2}+|\vec{a} \cdot \vec{b}|^{2}\) = 400 and \(|\vec{a}|\) = 5, then write the value of \(|\vec{b}|\). (Foreign 2016)
Answer:
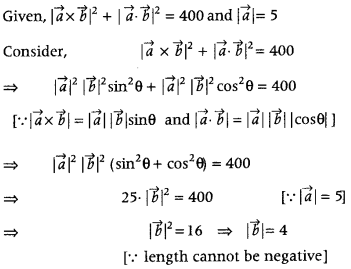
Question 7.
Find λ, if the vectors \(\vec{a}\) = î + 3ĵ + k̂, \(\vec{b}\) = 2 î – ĵ – k̂ and \(\vec{c}\) = λĵ + 3 k̂ are coplanar. (Delhi 2015)
Answer:
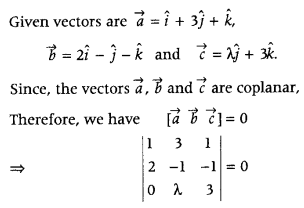
⇒ 1(- 3 + λ) – 3(6) + 1(2λ) = 0
[expanding along R1]
⇒ – 3 + λ – 18 + 2λ = 0
⇒ 3λ = 21
∴ λ = 7
Question 8.
If \(\vec{a}\) = 7î + ĵ – 4k̂ and \(\vec{b}\) = 2î + 6ĵ + 3k̂, then find the projection of \(\vec{a}\) on \(\vec{b}\). (Delhi 2015)
Answer:
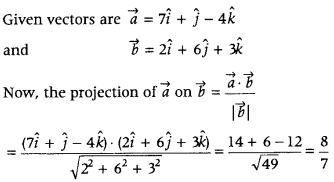
Question 9.
If â, b̂ and ĉ are mutually perpendicular unit vectors, then find the value of |2â + b̂ + ĉ |. (All India 2015)
Answer:
Given â, b̂ and ĉ are mutually perpendicular unit vectors, i.e.
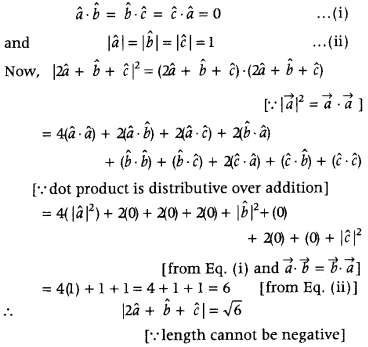
Question 10.
Write a unit vector perpendicular to both the vectors \(\vec{a}\) = î + ĵ + k̂ and \(\vec{b}\) = î + ĵ. (All India 2015)
Answer:
First, determine perpendicular vectors of \(\vec{a}\) and \(\vec{b}\), i.e., \(\vec{a} \times \vec{b}\). Further , determine perpendicular unit vector by using formula \(\frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}\).
Given vector are \(\vec{a}\) = î + ĵ + k̂ and \(\vec{b}\) = î + ĵ
As we know the, vectors \(\vec{a} \times \vec{b}\) is perpendicular to both the vectors, so let us first evaluate \(\vec{a} \times \vec{b}\).
Then, \(\vec{a} \times \vec{b}\) = \(\left|\begin{array}{lll}
\hat{i} & \hat{j} & \hat{k} \\
1 & 1 & 1 \\
1 & 1 & 0
\end{array}\right|\)
= î(0 -1) – ĵ(0 – 1) + k̂(1 – 1)
= – î + ĵ
Then , the unit vector perpendicular to both \(\vec{a}\) and \(\vec{b}\) is given by
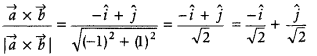
Question 11.
Find the area of a parallelogram whose adjacent sides are represented by the vectors 2 î – 3 k̂ and 4 ĵ + 2 k̂. (Foreign 2015)
Answer:
Let adjacent sides of a parallelogram bc
\(\vec{a}\) = 2 î – 3 k̂ and \(\vec{b}\) = 4 ĵ + 2 k̂.
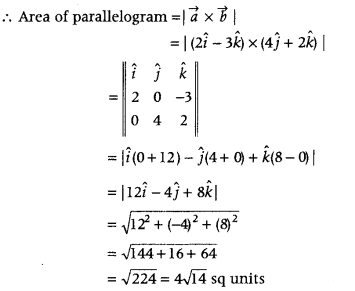
Question 12.
If \(\vec{a}\) and \(\vec{b}\) are perpendicular vectors, |\(\vec{a}\) + \(\vec{b}\)| = 13 and |\(\vec{a}\)| = 5, then find the value of |\(\vec{b}\)|. (All India 2014)
Answer:
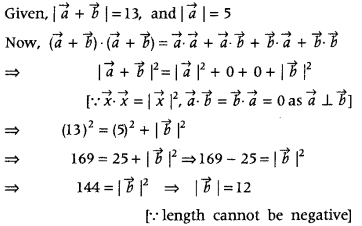
Question 13.
If \(\vec{a}\) and \(\vec{b}\) are two unit vectors such that \(\vec{a}\) + \(\vec{b}\) is also a unit vector, then find the angle between \(\vec{a}\) and \(\vec{b}\). (Delhi 2014)
Answer:
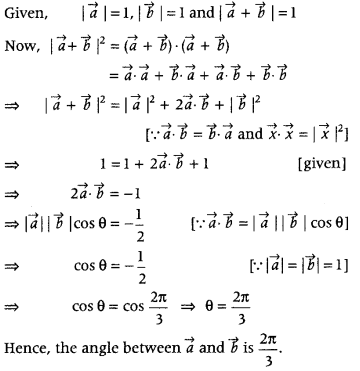
Question 14.
Find the projection of the vector î + 3ĵ + 7k̂ on the vector 2î – 3 ĵ + 6k̂. (Delhi 2014)
Answer:
let \(\vec{a}\) = î + 3ĵ + 7k̂ and \(\vec{a}\) = 2î – 3 ĵ + 6k̂
Question 15.
Write the projection of vector î + ĵ + k̂ along the vector ĵ. (Foreign 2014)
Answer:
1
Question 16.
Write the value of the following. î × (ĵ + k̂) + ĵ × (k̂ + î) + k̂ × (î + ĵ). (Foreign 2014)
Answer:
we have, î × (ĵ + k̂) + ĵ × (k̂ + î) + k̂ × (î + ĵ)
= î × ĵ + î × k̂ × ĵ × k̂ + ĵ × î + k̂ × î + k̂ × ĵ
[∵ cross product is distributive over addition]
= k̂ – ĵ + î – k̂ + ĵ – î = \(\vec{0}\)
[∵ î × ĵ = k̂, î × k̂ = – ĵ, ĵ × k̂ = î, ĵ × î = – k̂, k̂ × î = ĵ, k̂ × ĵ = – î ]
Question 17.
If vectors \(\vec{a}\) and \(\vec{b}\) are such that |\(\vec{a}\)| = 3, |\(\vec{b}\)| = 2/3 and \(\vec{a}\) × \(\vec{b}\) is a unit vector, then write the angle between \(\vec{a}\) and \(\vec{b}\). (Delhi 2014: All India 2010)
Answer:
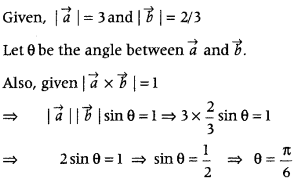
Question 18.
Find \(\vec{a} \cdot(\vec{b} \times \vec{c})\), if \(\vec{a}\) = 2î + ĵ + 3k̂, \(\vec{b}\) = -î + 2ĵ + k̂, and \(\vec{c}\) = 3î + ĵ + 2k̂. (All India 2014)
Answer:
Given, \(\vec{a}\) = 2î + ĵ + 3k̂, \(\vec{b}\) = -î + 2ĵ + k̂, and \(\vec{c}\) = 3î + ĵ + 2k̂.
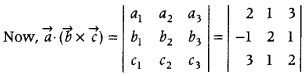
= 2(4 – 1) – 1 (- 2 – 3) + 3( – 1 – 6)
= 2 × 3 – 1 × (-5) + 3 × (- 7)
= 6 + 5 – 21 = 11 – 21 = – 10
Question 19.
If \(\vec{a}\) and \(\vec{b}\) are unit vectors, then find the angle between \(\vec{a}\) and \(\vec{b}\), given that (√3\(\vec{a}\) – \(\vec{b}\)) is a unit vector. (Delhi 2014C)
Answer:
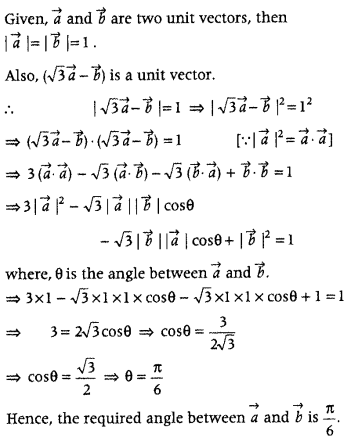
Question 20.
If |\(\vec{a}\)| = 8, |\(\vec{b}\)| = 3 and|\(|\vec{a} \times \vec{b}|\)| = 12, find the angle between \(\vec{a}\) and \(\vec{b}\). (All India 2014C)
Answer:
let θ be the angle between latex]\vec{a}[/latex] and \(\vec{b}\).
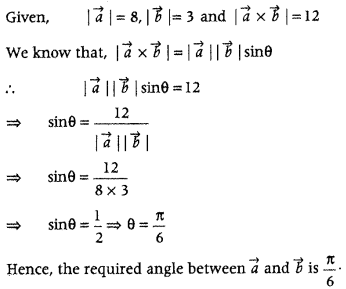
Question 21.
Write the projection of the vector \(\vec{a}\) = 2 î – ĵ + k̂ on the vector \(\vec{b}\) = î + 2ĵ + 2k̂. (Delhi 2014 C)
Answer:
\(\frac{2}{3}\)
Question 22.
Write the value of λ, so that the vectors a = 2î + λĵ + k̂ and b = î – 2ĵ + 3k̂ are perpendicular to each other. (Delhi 2013C, 2008)
Answer:
Given vectors are \(\vec{a}\) = 2î + λĵ + k̂
and \(\vec{b}\) = î – 2ĵ + 3k̂
Since, vectors are perpendicular.
∴ \(\vec{a} \cdot \vec{b}\) = 0
⇒ (2î + λĵ + k̂) ∙ (î – 2ĵ + 3k̂)
⇒ 2 – 2λ + 3 = 0
∴ λ = 5/2
Question 23.
Write the projection of (\(\vec{b}\) + \(\vec{c}\)) on \(\vec{a}\), where \(\vec{a}\) = 2î – 2ĵ + k̂, \(\vec{b}\) = î + 2ĵ – 2k̂ and \(\vec{c}\) = 2î – ĵ + 4k̂. (All India 2013 C)
Answer:
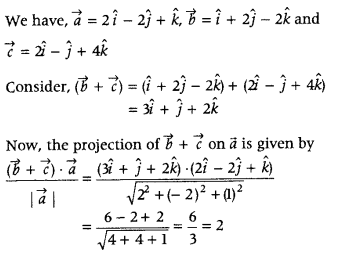
Question 24.
Write the projection of the vector 7î + ĵ – 4k̂ on the vector 2î + 6 ĵ + 3k̂. (Delhi 2013C)
Answer:
\(\frac{8}{7}\)
Question 25.
If \(\vec{a}\) and \(\vec{b}\) are two vectors such that |\(\vec{a}\) + \(\vec{b}\)| = |\(\vec{a}\)|, then prove that vector 2\(\vec{a}\) + \(\vec{b}\) is perpendicular to vector b. (Delhi 2013)
Answer:
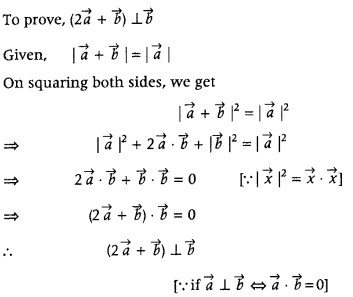
Question 26.
Find |\(\vec{x}\)|, if for â unit vector a, \((\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})\) = 15. (All India 2013)
Answer:
Given, \(\vec{a}\) is a unit vector. Then, |\(\vec{a}\)| = 1.
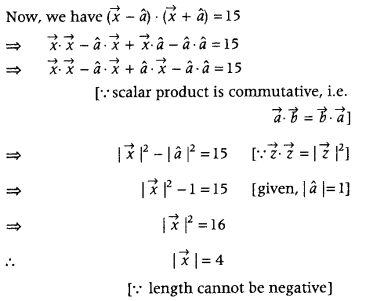
Question 27.
Find λ, when projection of \(\vec{a}\) = λî + ĵ + 4k̂ on \(\vec{b}\) = 2 î + 6 ĵ + 3k̂ is 4 units. (Delhi 2012)
Answer:
Given, \(\vec{a}\) = λî + ĵ + 4k̂ on \(\vec{b}\) = 2 î + 6 ĵ + 3k̂ and projection of \(\vec{a}\) and \(\vec{b}\) = 4.
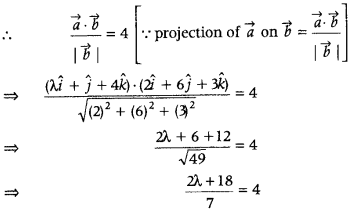
⇒ 2λ + 18 = 28
⇒ 2λ = 10
∴ λ = 5
Question 28.
Write the value of (k̂ × ĵ) . î + ĵ . k̂. (All India 2012)
Answer:
Use the results k̂ × ĵ = – î
ĵ ∙ k̂ and î ∙ î = 1 and simplify it.
Given, (k̂ × î) ∙ î + ĵ ∙ k̂ = (- î) ∙ î + ĵ ∙ k̂
= – (î ∙ î) + 0 = – 1 [∵ (î ∙ î) = 1]
Question 29.
If \(\vec{a} \cdot \vec{a}\) = 0 and \(\vec{a} \cdot \vec{b}\) = 0, then what can be concluded about the vector \(\vec{b}\)? (Foreign 2011)
Answer:
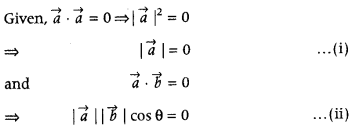
From Eqs. (i) and (ii). it may be concluded that \(\vec{b}\) is either zero or non-zero perpendicular vector.
Question 30.
Write the projection of vector î – ĵ on the vector î + ĵ. (All India 2011)
Answer:
0
Question 31.
Write the angle between vectors \(\vec{a}\) and \(\vec{b}\) with magnitudes √3 and 2 respectively, having \(\vec{a}\). \(\vec{b}\) = √6. (All India 2011)
Answer:
let θ be the angle between \(\vec{a}\) and \(\vec{b}\), then use the following formula
cos θ = \(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\).
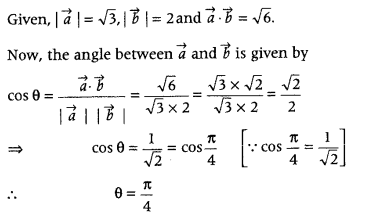
Question 32.
For what value of λ are the vectors î + 2λĵ + k̂ and 2î + ĵ – 3k̂ perpendicular? (All India 2011C)
Answer:
\(\frac{1}{2}\)
Question 33.
If |\(\vec{a}\)| = √3, |\(\vec{b}\)| = 2 and angle between \(\vec{a}\) and \(\vec{b}\) is 60°, then find \(\vec{a}\).\(\vec{b}\). (Delhi 2011C)
Answer:
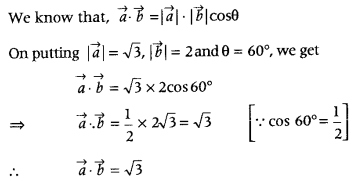
Question 34.
Find the value of λ, if the vectors 2î + λĵ + 3k and 3î + 2ĵ – 4k̂ are perpendicular to each other. (All India 2010c)
Answer:
3
Question 35.
If |\(\vec{a}\)| = 2, |\(\vec{b}\)| = 3 and \(\vec{a}\).\(\vec{b}\) = 3, then find the projection of \(\vec{b}\) on \(\vec{a}\). (All India 2010C)
Answer:
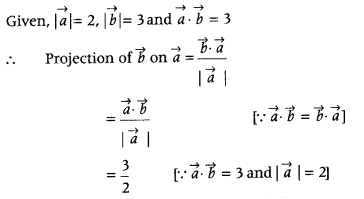
Question 36.
If \(\vec{a}\) and \(\vec{b}\) are two vectors, such that \(|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|\), then find the angle between \(\vec{a}\) and \(\vec{b}\). (All India 2010)
Answer:
Use the following formulae:
\(\vec{a} \cdot \vec{b}\) = \(|\vec{a}||\vec{b}|\) cos θ
and \(|\vec{a} \times \vec{b}|\) = \(|\vec{a}||\vec{b}|\) sin θ
where, θ is the angle between \(\vec{a}\) and \(\vec{b}\).
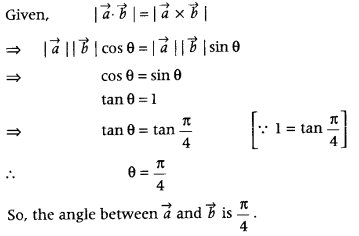
Question 37.
Find λ, if (2î + 6ĵ + 14k̂) × (î – λĵ + Ik̂) = 0. (All India 2010)
Answer:
– 3
Question 38.
If the sum of two unit vectors a and b is a unit vector, show that the magnitude of their difference is √3. (Delhi 2019, 2012c)
Answer:
let \(\vec{c}\) = \(\vec{a}\) + \(\vec{b}\). Then, according to given condition \(\vec{c}\) is a unit vector, i.e. |\(\vec{c}\)| = 1.

[taking positive square root, as magnitude cannot be negative]
Question 39.
If \(\vec{a}\) = 2î + 5ĵ + k̂, \(\vec{b}\) = î – 2 ĵ + k̂ and \(\vec{c}\) = – 3î + ĵ + 2k̂, find \([\vec{a} \vec{b} \vec{c}]\). (Delhi 2019)
Answer:
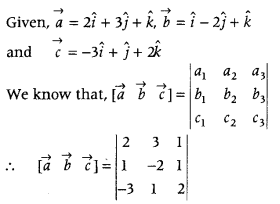
= 2(- 4 – 1) – 3(2 + 3) + 1(1 – 6)
= – 10 – 15 – 5 = – 30
Question 40.
If |\(\vec{a}\)| = 2, |\(\vec{b}\)| = 7 and \(\vec{a} \times \vec{b}\) = 3î + 2ĵ + 6k̂, find the angle between \(\vec{a}\) and \(\vec{b}\). (All India 2019)
Answer:
let θ be the angle between \(\vec{a}\) and \(\vec{b}\).
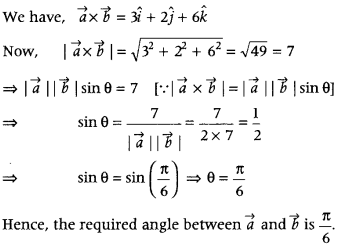
Question 41.
Find the volume of cuboid whose edges are given by -5î + 7ĵ + 5k̂, -5î + 7ĵ – 5k̂ and 7î – 5 ĵ – 5k̂. (All India 2019)
Answer:
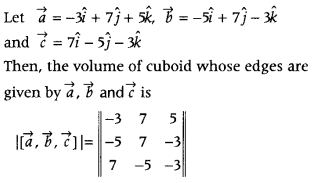
= |- 3 (- 21 – 15) – 7 (15 + 21) + 5(25 – 49)|
= |1108 – 252 – 120|
= 264 cubic units
Question 42.
Show that the points A(-2î + 5ĵ + 5k̂), B(î + 2 ĵ + 5k̂) and C(7î – k̂) are collinear. (All India 2019)
Answer:
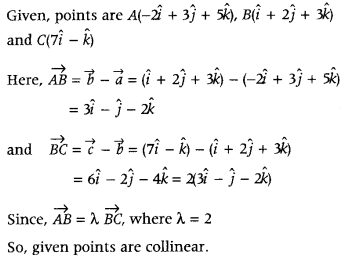
Question 43.
Find \(|\vec{a} \times \vec{b}|\), if \(\vec{a}\) = 2î + ĵ + 5k̂ and \(\vec{b}\) = 3î + 5ĵ – 2k̂. (All India 2019)
Answer:
We have, \(\vec{a}\) = 2î + ĵ + 3k̂ and \(\vec{b}\) = 3î + 5ĵ – 2k̂
∴ \(\vec{a} \times \vec{b}\) = \(\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
2 & 1 & 3 \\
3 & 5 & -2
\end{array}\right|\)
= î ( – 2 – 15) – ĵ (- 4 – 9) + k̂(10 – 3)
= – 17î + 13ĵ + 7k̂
Question 44.
If θ is the angle between two vectors î – 2 ĵ + 3k̂ and 3î – 2 ĵ + k̂, find sin θ. (CBSE 2018)
Answer:
let \(\vec{a}\) = î – 2 ĵ + 3k̂ and \(\vec{b}\) 3î – 2 ĵ + k̂
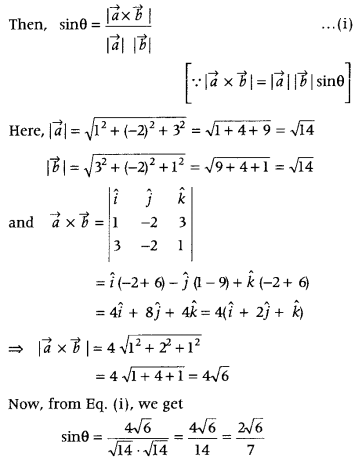
Question 45.
If \(\vec{a}+\vec{b}+\vec{c}\) = 0 and |\(\vec{a}\)| = 5, |\(\vec{b}\)| = 6 and |\(\vec{c}\)| = 9, then find the angle between \(\vec{a}\) and \(\vec{b}\). (CBSE 2018C)
Answer:
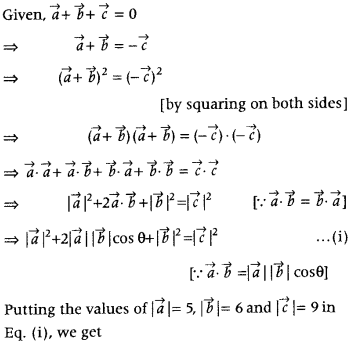
(5)2 + 2 × 5 × 6 × cos θ + (6)2 = (9)2
⇒ 25 + 60 cos θ + 36 = 81
⇒ cos θ = \(\frac{20}{60}=\frac{1}{3}\)
⇒ θ = cos-1\(\left(\frac{1}{3}\right)\)
Question 46.
If î + ĵ + k̂, 2î + 5ĵ, 5î + 2ĵ – 5k̂ and î – 6ĵ – k̂ respectively, are the position vectors of points A, B, C and D, then find the angle between the straight lines AB and CD. Find whether \(\overrightarrow{A B}\) and \(\overrightarrow{C D}\) are collinear or not. (Delhi 2019)
Answer:
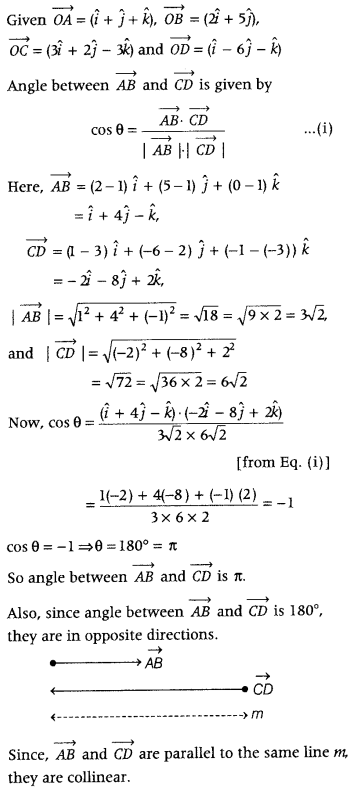
Question 47.
The scalar product of the vector \(\vec{a}\) = î + ĵ + k̂ with a unit vector along the sum of the vectors \(\vec{b}\) = 2î + 4ĵ – 5k̂ and \(\vec{c}\) = λî + 2ĵ + 5k̂ is equal to 1. Find the value of λ and hence find the unit vector along \(\vec{b}\) + \(\vec{c}\). (All India 2019)
Answer:
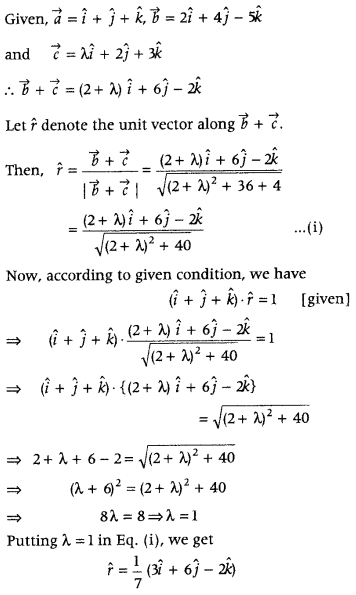
Question 48.
Let \(\vec{a}\) = 4 î + 5ĵ – k̂, \(\vec{b}\) = î – 4ĵ + 5k̂ and \(\vec{c}\) = 3î + ĵ – k̂. Find a vector which is perpendicular to both \(\vec{c}\) and \(\vec{b}\) and \(\vec{d} \cdot \vec{a}\) = 21. (CBSE 2018)
Answer:
We have, \(\vec{a}\) = 4 î + 5ĵ – k̂, \(\vec{b}\) = î – 4ĵ + 5k̂ and \(\vec{c}\) = 3î + ĵ – k̂.
Since, \(\vec{d}\) is perpendicular to both \(\vec{c}\) and \(\vec{b}\).
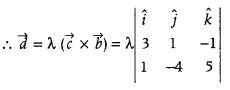
= λ[î(5 – 4) – ĵ(15 + 1) + k̂(- 12 – 1)]
= λ(î – 16ĵ – 13k̂)
Also, it is given that \(\vec{a} \cdot \vec{a}\) = 21
∴ λ(î – 16ĵ – 13k̂) ∙ (4î + 5ĵ – k̂) = 21
⇒ λ(4 – 80 + 13) = 21
⇒ λ(- 63) = 21
⇒ λ = \(\frac{-1}{3}\)
Now from Eq. (j), we get
\(\vec{d}\) = –\(\frac{-1}{3}\)(î – 16ĵ – 13k̂)
Question 49.
Find x such that the four points A(4, 4, 4), B(5, x, 8), C(5, 4, 1) and D (7, 7, 2) are coplanar. (CBSE 2018C)
Answer:
Given points are A(4, 4, 4), B (5, x, 8), C(5, 4, 1) and D(7, 7, 2), then position vectors of A, B, C and D respectively, are
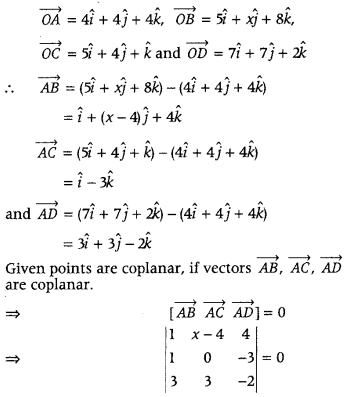
⇒ 1(0 + 9) – (x – 4) (- 2 + 9) + 4(3 – 0) = 0
⇒ 9 – (x – 4) (7) + 12 = 0
⇒ 9 – 7x + 28 + 12 = 0
⇒ 49 – 7x = 0
⇒ 7x = 49
⇒ x = 7
Question 50.
Find the value of x such that the points A(3, 2, 1), B(4, x, 5), C(4, 2,- 2) and D (6, 5, -1) are coplanar. (All India 2017)
Answer:
5
Question 51.
If \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are three mutually perpendicular vectors of the same magnitude, then prove that \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined with the vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\). (Delhi 2017, 2013C, 2011)
Answer:
If three vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are mutually perpendicular to each other, then \(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}\) = \(\vec{c} \cdot \vec{a}\) = 0 and if all three vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are equally inclined with the vector \((\vec{a}+\vec{b}+\vec{c})\) that means each vector \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) makes equal angle with \((\vec{a}+\vec{b}+\vec{c})\) by using formula
cos θ = \(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\).
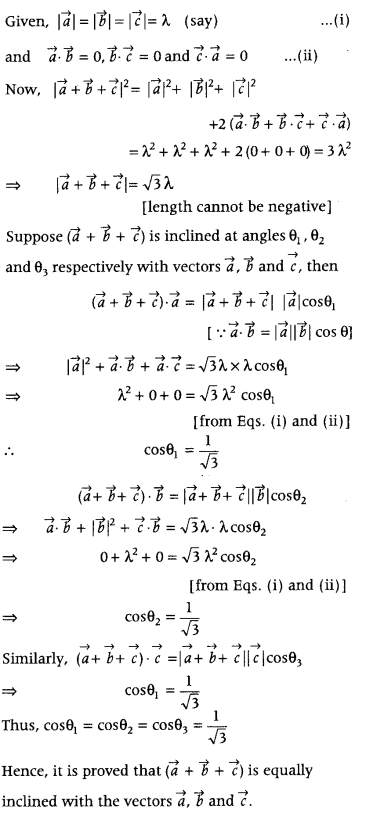
Question 52.
Using vectors, find the area of the ΔABC, whose vertices are A(1, 2, 5), 5(2, -1, 4) and C(4, 5, -1). (Delhi 2017; All India 2013)
Answer:
Let the position vectors of the verices A, B and C of ΔABC be
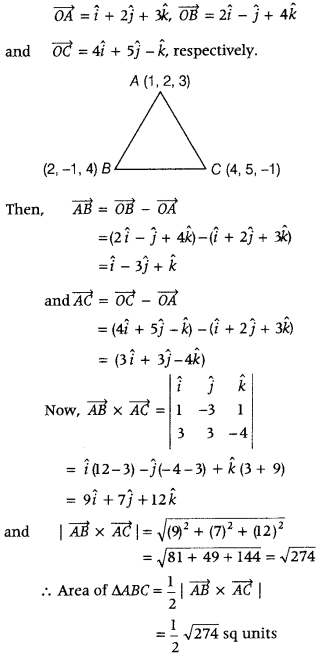
Question 53.
Let \(\vec{a}\) = î + ĵ + k̂, \(\vec{b}\) = î + 0 ∙ ĵ + 0 ∙ k̂ and \(\vec{c}\) = c1î + c2ĵ + c3k̂, then
(a) Let c1 = 1 and c2 = 2, find c3 which makes \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) coplanar.
(b) If c2 = – 1 and c3 = 1, show that no value of c1 can make \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) coplanar. (Delhi 2017)
Answer:
Given, \(\vec{a}\) = î + ĵ + k̂, \(\vec{b}\) = î + 0 ∙ ĵ + 0 ∙ k̂ and \(\vec{c}\) = c1î + c2ĵ + c3k̂
The given vectors are coplanar iff \([\vec{a} \vec{b} \vec{c}]\) = 0
(a) If c1 = 1 and c2 = 2,
Then, from Eq.(i), we get
\(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & 0 & 0 \\
1 & 2 & c_{3}
\end{array}\right|\) = 0
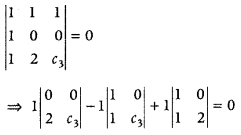
⇒ – 1(c3 – 0) + 1(2 – 0) = 0
⇒ – c3 + 2 = 0
⇒ – c3 = – 2
⇒ c3 = 2
(b) If c2 = – 1 and c3 = 1, then from Eq. (i), we get
\(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & 0 & 0 \\
c_{1} & -1 & 1
\end{array}\right|\) = 0
⇒ 1(0) – 1(1 – 0) + 1(- 1 – 0) = 0
⇒ 0 – 1 – 1 = 0
⇒ – 2 ≠ 0
∴ No value of c1 can make 1’ and coplanar.
Hence proved
Question 54.
Show that the points A, B, C with position vectors 2î – ĵ + k̂, î – 5ĵ – 5k̂ and 5î – 4ĵ – 4k̂ respectively, are the vertices of a right-angled triangle. Hence find the area of the triangle. (All India 2017)
Answer:

Question 55.
Show that the vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are coplanar, if a + b, 6+ c and c+ a are coplanar. (Delhi 2016, Foreign 2014)
Or
Prove that, for any three vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c},[\vec{a}+\vec{b} \vec{b}+\vec{c} \vec{c}+\vec{a}]=2[\vec{a} \vec{b} \vec{c}]\). (Delhi 2014)
Answer:
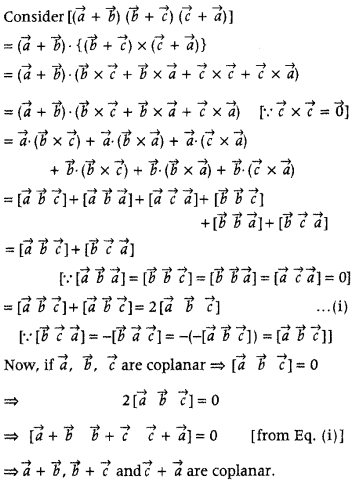
Question 56.
Show that the four points A (4, 5, 1), B(0, -1, -1), C(3, 9, 4) and D (-4, 4, 4) are coplanar. (All India 2016)
Or
Show that the four points A, B, C and D with position vectors 4î + 5ĵ + k̂, – ĵ – k̂, 3î + 9ĵ + 4k̂ and 4(- î + ĵ + k̂), respectively are coplanar. (All India 2014)
Answer:
Let the position vector of points A, B, C and D are
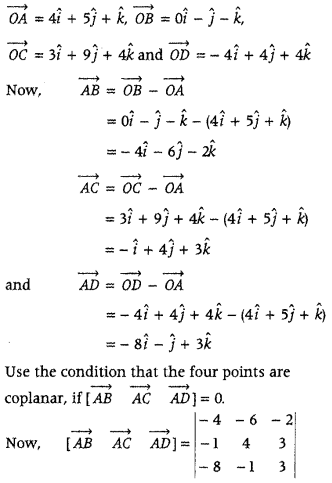
= – 4(12 + 3) + 6 (- 3 + 24) – 2(1 + 32)
= – 60 + 126 – 66 = 0
Hence, the four points A, B, C and D are coplanar.
Question 57.
The two adjacent sides of a parallelogram are 2î – 4ĵ – 5k̂ and 2î + 2 ĵ + 3k̂. Find the two unit vectors parallel to its diagonals. Using the diagonal vectors, find the area of the parallelogram. (All India 2016)
Answer:
Let ABCD be the given parallelogram with
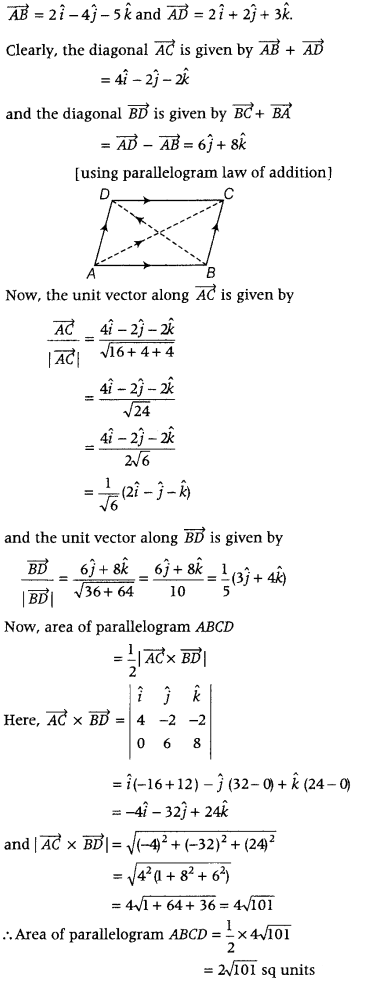
Question 58.
If \(\vec{a} \times \vec{b}=\vec{c} \times \vec{d}\) and \(\vec{a} \times \vec{c}=\vec{b} \times \vec{d}\), then show that \(\vec{a}-\vec{d}\) is parallel to \(\vec{b}-\vec{c}\), where \(\vec{a} \neq \vec{d}\) and \(\vec{b} \neq \vec{c}\). (Foreign 2016; Delhi 2009)
Answer:
Use the result, if two vectors are parallel, then their cross-product will be a zero vector.

Question 59.
If \(\vec{r}\) = xî + yĵ + zk̂, find \((\vec{r} \times \hat{i}) \cdot(\vec{r} \times \hat{j})\) + xy. (Delhi 2015)
Answer:

Question 60.
If \(\vec{a}\) = î + 2ĵ + k̂, \(\vec{b}\) = 2î + ĵ and \(\vec{c}\) = 3î – 4 ĵ – 5k̂, then find a unit vector perpendicular to both of the vectors \((\vec{a}-\vec{b})\) and \((\vec{c}-\vec{b})\). (All India 2015)
Answer:
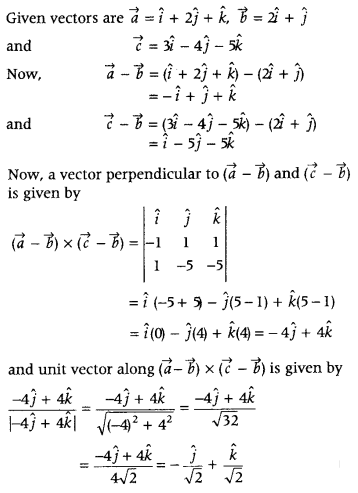
Question 61.
Find the value of λ so that the four points A, B,C and D with position vectors 4 î + 5ĵ + k̂, -ĵ – k̂,3i + Xj+4k and – 4 î + 4ĵ + 4 k̂, respectively are coplanar. (Delhi 2015C)
Answer:
Use the condition that four points with position vectors \(\vec{A}, \vec{B}, \vec{C}\) and \(\vec{D}\) are coplanar, if
\([\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D}]=\overrightarrow{0}\) = 0.
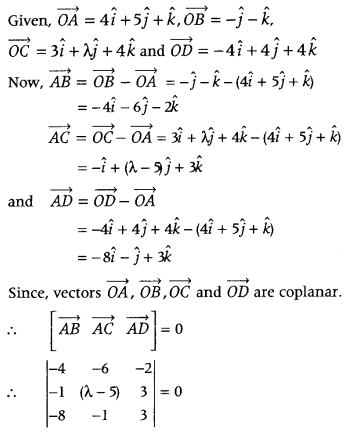
On expanding along R1, we get
⇒ – 4(3λ – 15 + 3) + 6(- 3 + 24) – 2(1 + 8λ – 40) = 0
⇒ – 4(3λ – 12) + 6(21) – 2(8λ – 39) = 0
⇒ – 12λ + 48 + 126 – 16λ + 78 = 0
⇒ – 28λ + 252 = 0
λ = 9
Question 62.
Prove that \(\left[\begin{array}{lll}
\vec{a} & \vec{b}+\vec{c} & \vec{d}
\end{array}\right]=\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{d}
\end{array}\right]+\left[\begin{array}{lll}
\vec{a} & \vec{c} & \vec{d}
\end{array}\right]\). (All India 2015C)
Answer:

Question 63.
If \(\vec{a}\) = 2î – 3ĵ + k̂, \(\vec{b}\) = – î + k̂, \(\vec{c}\) = 2 ĵ – k̂ are three vectors, find the area of the parallelogram having diagonals \(\) and \(\). (Delhi 2014C)
Answer:

Question 64.
Vectors \(\vec{a}, \vec{b}\) and \(\vec{c}\) are such that \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) and |\(\vec{a}\)| = 3, |\(\vec{b}\)| = 5 and |\(\vec{c}\)| = 7. Find the angle between \(\vec{a}\) and \(\vec{b}\). (Delhi 2014,2008; All India 2008)
Answer:
\(\frac{\pi}{3}\)
Question 65.
The scalar product of the vector \(\vec{a}\) = î + ĵ + k̂ with a unit vector along the sum of vectors \(\vec{b}\) = 2î + 4ĵ – 5k̂ and \(\vec{c}\) = λî + 2ĵ + 3k̂ is equal to one. Find the value of λ and hence, find the unit vector along \(\vec{b}\) + \(\vec{c}\). (All India 2014)
Or
The scalar product of vector i + j + k with the unit vector along the sum of vectors 2î + 4ĵ – 5k̂ and λî + 2ĵ + 3k̂ is equal to one. Find the value of λ. (All India 2009,2008C)
Answer:
First, determine the unit vector of \(\vec{b}+\vec{c}\), i.e. \(\frac{\vec{b}+\vec{c}}{|\vec{b}+\vec{c}|}\). Further put \(\vec{a} \cdot \frac{(\vec{b}+\vec{c})}{|\vec{b}+\vec{c}|}\) = 1 and then determine the value of λ.

⇒ (λ + 6)2 = λ2 + 4λ + 44 [squaring both sides]
⇒ λ2 + 36 + 12λ + 4λ + 44
⇒ 8λ = 8
⇒ λ = 1
Hence, the value of λ is 1.
On substituting the value of λ in Eq. (1), we get Unit vector along \(\vec{b}+\vec{c}\)
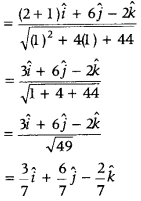
Question 66.
Find the vector \(\vec{p}\) which is perpendicular to both \(\vec{α}\) = 4î + 5ĵ – k̂ and \(\vec{β}\) = î – 4ĵ + 5k̂ and \(\vec{p}\). \(\vec{q}\) = 21, where \(\vec{q}\) = 3i + j – k. (All India 2014C)
Answer:
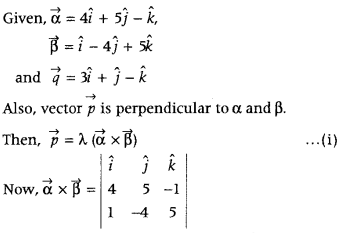
= î (25 – 4) – ĵ (20 + 1) + k̂(- 16 – 5)
= î(21) – ĵ(21) + k̂(- 21)
= 21î – 21ĵ – 21k̂
So, \(\vec{p}\) = 21λk̂—21λ?—21λk [fromEq.(i)] ….. (ii)
Also, given that \(\vec{p} \cdot \vec{q}\) = 21
∴ (21λî – 21λĵ – 21λk̂) . (3î + ĵ – k̂) = 21
⇒ 63λ – 21λ + 21λ = 21
⇒ 63λ = 21
⇒ λ = \(\frac{1}{3}\)
On putting λ = \(\frac{1}{3}\) in Eq. (ii), we get
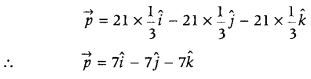
which is the required vector.
Question 67.
Find the unit vector perpendicular to both of the vectors \(\vec{a}+\vec{b}\) and \(\vec{a}-\vec{b}\) where, \(\vec{a}\) = î + ĵ + k̂ and \(\vec{b}\) = î + 2ĵ + 3k̂. (Foreign 2014)
Answer:

⇒ 2x + 3y + 4z = 0 …… (ii)
and (xî + yĵ + zk̂) . (- ĵ – 2k̂) = 0
⇒ – y – 2z = 0
⇒ y = – 2z
On putting the value of yin Eq. (ii), we get
2x + 3 (- 2z) + 4z = 0
⇒ x = z
On substituting the value of x and y in Eq. (1),
we get
⇒ z2 + 4z2 + z2 = 1
⇒ 6z2 = 1
⇒ z = ± \(\frac{1}{\sqrt{6}}\)
then, x = ± \(\frac{1}{\sqrt{6}}\)
and y = ± \(\frac{2}{\sqrt{6}}\)
Hence, the required vectors are
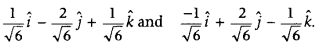
Question 68.
Find the unit vector perpendicular to the plane ABC where the position vectors of A, B and C are 2î – ĵ + k̂, î + ĵ + 2k̂ and 2î + 3k̂, respectively. (All India 2014C)
Answer:
A unit vector perpendicular to plane ABC is
\(\frac{\overrightarrow{A B} \times \overrightarrow{A C}}{|\overrightarrow{A B} \times \overrightarrow{A C}|}\)
Let O be the origin of reference.

Question 69.
Dot product of a vector with vectors î – ĵ + k̂, 2î + ĵ – 3k̂ and î + ĵ + k̂ are respectively 4, 0 and 2. Find the vector. (Delhi 2013C)
Answer:

⇒ a1 + a2 + a3 = 2
On subtracting Eq. (iii) from Eq. (i), we get
– 2a2 = 2
⇒ a2 = – 1
On substituting a2 = – 1 in Eq. (ii) and (iii),
we get
2a2 – 3a3 = 1 …… (iv)
⇒ a1 + a3 = 3
On multiplying Eq. (v) by 3 and then adding with Eq. (iv), we get
5a1 = 1 + 9 = 10
⇒ a1 = 2
On substituting a1 = 2 in Eq. (v), we get
a3 = 1
Hence, the vector is \(\vec{a}\) = 2î – ĵ + k̂
Question 70.
Find the values of λ for which the angle between the vectors \(\vec{a}\) = 2λ2î + 4λĵ + k̂ and \(\vec{b}\) = 7î – 2ĵ + λk̂ is obtuse. (All India 2013C)
Answer:
let θ be the obtuse angle between the vectors
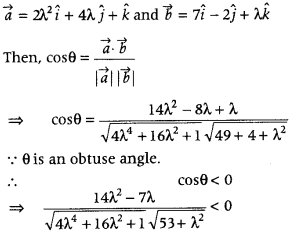
14λ2 – 7λ < 0
= 2λ2 – λ < 0
Either λ < 0, 2λ – 1 > 0 or λ > 0, 2λ – 1 < 0
= Either λ < 0, λ > \(\frac{1}{2}\) or λ > 0, λ < \(\frac{1}{2}\) Clearly, first option is impossible. ∴ λ > 0, λ < \(\frac{1}{2}\)
0 < λ < \(\frac{1}{2}\)
λ ∈ \(\left(0, \frac{1}{2}\right)\)
Question 71.
If a, b and c are three vectors such that each one is perpendicular to the vector obtained by sum of the other two and |\(\vec{a}\)| = 3, |\(\vec{b}\)| = 4 and |\(\vec{c}\)| = 5, then prove that |\(\vec{a}+\vec{b}+\vec{c}\)| = 5√2. (All India 2013C, 2010C)
Or
If \(\vec{a}, \vec{b}\) and \(\vec{c}\) are three vectors, such that |\(\vec{a}\)| = 3, |\(\vec{b}\)| = 4 and |\(\vec{c}\)| = 5 and each one of these is perpendicular to the sum of other two, then find |\(\vec{a}+\vec{b}+\vec{c}\)|. (All India 2011C, 2010C)
Answer:

Question 72.
If \(\vec{a}\) = 3î – ĵ and \(\vec{b}\) = 2î + ĵ – 3k̂, then express \(\vec{b}\) in the form \(\vec{b}=\vec{b}_{1}+\vec{b}_{2}\), where \(\vec{b}_{1} \| \vec{a}\) and \(\vec{b}_{2} \perp \vec{a}\). (All India 2013C)
Answer:
Given \(\vec{a}\) = 3î – ĵ and \(\vec{b}\) = 2î + ĵ – 3k̂
Let \(\overrightarrow{b_{1}}\) = x1î + y1ĵ + z1k̂ are two vectors such that \(\overrightarrow{b_{1}}+\overrightarrow{b_{2}}=\vec{b}, \overrightarrow{b_{1}} \| \vec{a}\) and \(\overrightarrow{b_{2}} \perp \vec{a}\)
Consider, \(\vec{b}_{1}+\vec{b}_{2}=\vec{b}\)
⇒ (x1 + x2)î + (y1 + y2)ĵ + (z1 + z2)k̂ = 2î + ĵ – 3k̂
On comparing the coefficient of î ĵ and k̂ both sides, we get
x1 + x2 = 2
y1 + y2 = 1
z1 + z2 = -3
Now, consider \(\overrightarrow{b_{1}} \| \vec{a}\)
⇒ \(\frac{x_{1}}{3}=\frac{y_{1}}{-1}=\frac{z_{1}}{0}\)
⇒ x1 = 3λ, y1 = -λ,and z1 = 0 …(iv)
On substituting the values of x, y and z, from Eq. (iv) to Eq. (i), (ii) and (iii), respectively, we get
x2 = 2- 3λ, y2 = -1 + λ and z2 = -3 …(v)
Since, b2 ± a , therefore b2 a = 0
⇒ 3x2 – y2 = 0
⇒ 3 (2 – 3λ) – (1 + λ) = 0
⇒ 6 – 9λ – 1 – λ = 0
⇒ 5 – 10λ = 0
⇒ λ = \(\frac{1}{2}\)
On substituting λ = \(\frac{1}{2}\) in Eqs. (iv) and (v), we get
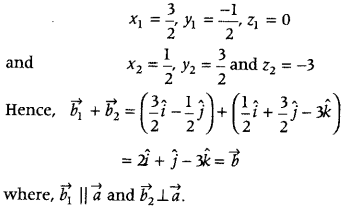
Question 73.
If \(\vec{a}\) = î + ĵ + k̂ and \(\vec{b}\) = ĵ – k̂, then find a vector \(\vec{c}\), such that \(\vec{a} \times \vec{c}=\vec{b}\) and \(\vec{a} \cdot \vec{c}\) = 3. (Delhi 2013, 2008)
Answer:
Given \(\vec{a}\) = î + ĵ + k̂ and \(\vec{b}\) = ĵ – k̂
Let \(\vec{c}\) = xî + yĵ + zk̂

= î (z – y) – ĵ(z – x) + k̂(y – x)
Now, \(\vec{a} \times \vec{c}=\vec{b}\) [given]
= î(z – y) + ĵ(x – z) + k̂(y – x)
= 0î + 1ĵ + (-1)k̂ [∵ \(\vec{b}\) = ĵ – k̂]
On comparing the coefficients from both sides, we get
z – y = 0,x – z = 1, y – x = -1
⇒ y = z and x – y = 1…(i)
Also given, \(\vec{a} \cdot \vec{c}\) = 3
⇒ (î + ĵ + k̂) . (xî + yĵ + zk̂) = 3
⇒ x + y + z = 3 (1)
⇒ x + 2y = 3 [∵ y = z] …(ii)
On subtracting Eq. (i) from Eq. (ii), we get
3y = 2
⇒ y = \(\frac{2}{3}\) = z [∵ y = z]
From Eq. (i),
x = 1 + y + 1 = 1 + \(\frac{2}{3}=\frac{5}{3}\)
Hence, \(\vec{c}=\frac{5}{3} \hat{i}+\frac{2}{3} \hat{j}+\frac{2}{3} \hat{k}\)
Question 74.
If \(\vec{a}\) = î – ĵ + 7k̂ and \(\vec{b}\) = 5î – ĵ + λk̂, then find the value of λ, so that \(\) and \(\) are perpendicular vectors. (All India 2013)
Answer:
Use the result that if \(\vec{a}\) and \(\vec{b}\) are perpendicular, then their dot product should be zero and simplify it.
Given, \(\vec{a}\) = î – ĵ + 7k̂ and \(\vec{b}\) = 5î – ĵ + λk̂
Then, \(\vec{a}+\vec{b}\) = (î – ĵ + 7k̂) + (5î – ĵ + λk̂)
= 6î – 2ĵ + (7 + λ) k̂
and a – = (î – ĵ + 7k̂) – (5î – j ̂+ λk̂)
= -4î + (7 – λ)k̂
Since, \((\vec{a}+\vec{b})\) and \((\vec{a}-\vec{b})\) are perpendicular
vectors, then \((\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})\) = 0
⇒ [6î – 2ĵ + (7 + λ)k̂]- [-4î + (7 – λ)k̂] = 0 (1)
⇒ -24 + (7+ X)(7 – X) =0
⇒ 49 – λ2 = 24
⇒ λ2 = 25
∴ λ = ± 5
Question 75.
If p = 5î + λĵ – 3k̂ and q = î + 3ĵ – 5k̂, then find the value of λ, so that \(\vec{p}+\vec{q}\) and \(\vec{p}-\vec{q}\) are perpendicular vectors. (All India 2013)
Answer:
λ = ± 1
Question 76.
If \(\vec{a}, \vec{b}\) and \(\vec{c}\) are three vectors, such that |\(\vec{a}\)| = 5, |\(\vec{b}\)| = 12, |\(\vec{c}\)| = 13 and \(\vec{a}+\vec{b}+\vec{c}\) = 0, then find the value of \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\). (Delhi 2012)
Answer:
-169
Question 77.
Let \(\vec{a}\) = î + 4ĵ + 2k̂, \(\vec{b}\) = 3î – 2ĵ + 7k̂ and \(\vec{c}\) = 2î – ĵ + 4k̂. Find a vector \(\vec{p}\), which is perpendicular to both \(\vec{a}\) and \(\vec{b}\) and \(\vec{p}.\vec{c}\) = 18. (All India 2012,2010)
Answer:
Given vectors are \(\vec{a}\) = î + 4ĵ + 2k̂,
\(\vec{b}\) = 3î – 2ĵ + 7k̂
and \(\vec{c}\) = 2î – ĵ + 4k̂
Let \(\vec{p}\) = xî + yĵ + zk̂
We have, \(\vec{p}\) is perpendicular to both \(\vec{a}\) and \(\vec{b}\).
\(\vec{p} \cdot \vec{a}\) = 0
⇒ (xî + yĵ + zk̂) – (î + 4ĵ + 7k̂) = 0
⇒ x + 4y + 2z = 0 ………….(i)
and \(\vec{p} \cdot \vec{b}\) = 0
⇒ (xî + yĵ + zk̂) . (3î – 2ĵ + 7k̂) = 0
⇒ 3x – 2y + 7z = 0 …(ii)
Also, given ~p-~c =18 (1)
⇒ (xî + yĵ + zk̂) . (2î – ĵ + 4k̂) = 0
⇒ 2x – y + 4z = 18 …(iii)
On multiplying Eq. (i) by 3 and subtracting it from Eq. (ii), we get
– 14y + z = 0 ..(iv)
Now, multiplying Eq. (i) by 2 and subtracting it from Eq. (iii), we get
– 9y = 18
⇒ y = -2
On putting y = -2 in Eq. (iv), we get
-14 (-2) + z = 0
⇒ 28 + z = 0
⇒ z = -28
On putting y = -2 and z = -28 in Eq. (i), we get
x + 4 (-2) + 2 (-28) = 0
⇒ x – 8 – 56 = 0
⇒ x = 64
Hence, the required vector is
\(\vec{p}\) = xî + yĵ + zk̂
i.e. \(\vec{p}\) = 64î – 2ĵ – 28k̂
Question 78.
Find a unit vector perpendicular to each of the vectors \(\vec{a}+\vec{b}\) and \(\vec{a}-\vec{b}\), where a = 3î + 2 ĵ + 2k̂ and b = î + 2ĵ – 2k̂. (Delhi 2011)
Answer:
\(\frac{2}{3} \hat{i}-\frac{2}{3} \hat{j}-\frac{1}{3} \hat{k}\)
Question 79.
If a and 6 are two vectors, such that |\(\vec{a}\)| = 2, |\(\vec{b}\)| = 1 and \(\vec{a}\).\(\vec{b}\) = 1, then find \((3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b})\). (Delhi 2011)
Answer:
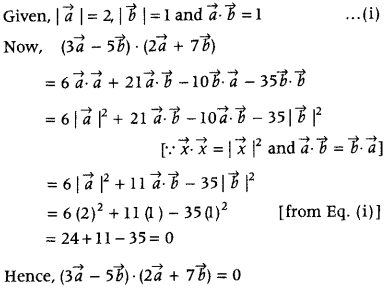
Question 80.
If vectors \(\vec{a}\) = 2î + 2ĵ + 3k̂, \(\vec{b}\) = -î + 2ĵ + k̂ and \(\vec{c}\) = 3î + ĵ are such that \(\vec{a}+\lambda \vec{b}\) is perpendicular to \(\vec{c}\), then find the value λ. (Foreign 2011; All India 2009C)
Answer:
Given, \(\vec{a}\) = 2î + 2ĵ + 3k̂,
\(\vec{b}\) = -î + 2ĵ + k̂
and \(\vec{c}\) = 3î + ĵ
Also, \(\vec{a}\) + λ\(\vec{b}\) is perpendicular to \(\vec{c}\).
∴ (\(\vec{a}\) + λ\(\vec{b}\)).\(\vec{c}\) = 0 …(i) [∵ when \([latex]\)[/latex], then \(\vec{a} \cdot \vec{b}\) = 0]
Now, \(\vec{a}\) + λ\(\vec{b}\) = (2î + 2ĵ + 3k̂) + λ (-î + 2ĵ + k̂)
⇒ \(\vec{a}\) + λ\(\vec{b}\) = î(2 – λ) + ĵ(2 + 2λ) + k̂(3 + λ)
Then, from Bq. (i), we get
[î (2 – λ) + ĵ (2 + 2λ) + k̂(3 + λ)].[3î + ĵ] = 0
⇒ 3(2 – λ) + 1(2+ 2k) = 0
⇒ 8 – λ = 0
∴ λ = 8
Question 81.
Using vectors, find the area of triangle with vertices A (1, 1, 2), 5(2, 3, 5) and C (1, 5, 5). (All India 2011)
Answer:
\(\frac{1}{2}\)\(\sqrt{61}\) sq.units
Question 82.
Using vectors, find the area of triangle with vertices A (2, 3, 5), B (3, 5, 8) and C(2, 7, 8). (Delhi 2010C)
Answer:
\(\frac{1}{2}\)\(\sqrt{61}\) sq.units