CBSE Sample Papers for Class 11 Maths Set 4 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 11 Maths with Solutions Set 4 are designed as per the revised syllabus.

CBSE Sample Papers for Class 11 Maths Set 4 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D, and E. Each section is compulsory. However, there are internal choices in some questions.
• Section A has 18 MCQs and 2 Assertion-Reason-based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
• Section C has 6 Short Answer (SA)-type questions of 3 marks each.
• Section D has 4 Long Answer (LA)-type questions of 5 marks each.
• Section E has 3 source-based/case-based/passage-based/integrated units of assessment of 4 marks each with sub-parts.

Section – A

(Multiple Choice Questions) Each Question Carries 1 Mark.

Question 1.
Which of the following is an empty set?
(A) {x | x is a prime number less than 5}
(B) {x | x is an even number greater than 10}
(C) {x | x is a multiple of 7}
(D) {x | x is a number in the word “set”}
Answer:
(D) {x | x is a number in the word “set”}
Explanation:
An empty set is a set that has no elements.
Option A is not an empty set as there are two prime numbers less than 5 (namely 2 and 3).
Option B is also not an empty set as there are many even numbers greater than 10.
Option C is not an empty set as there are many multiples of 7.
Option D is an empty set as there are no numbers in the word “set”.

Question 2.
The domain of the function f defined by f(x) = \(\sqrt{4-x}+\frac{1}{\sqrt{x^2-1}}\) is equal to
(A) (-∞, -1) ∪ (1, 4]
(B) (-∞, -1] ∪ (1, 4]
(C) (-∞, -1) ∪ [1, 4]
(D) (-∞, -1] ∪ [1, 4)
Answer:
(A) (-∞, -1) ∪ (1, 4]
Explanation:
For domain of f(x), f(x) ≥ 0
i.e., \(\sqrt{4-x}+\frac{1}{\sqrt{x^2-1}}\) ≥ 0
⇒ \(\sqrt{4-x}\) ≥ 0 or \(\sqrt{x^2-1}\) ≥ 0
⇒ 4 – x ≥ 0 or x² – 1 ≥ 0
⇒ -x ≥ -4 or (x – 1)(x + 1) ≥ 0
⇒ x ≥ 4 or x < -1 and x > 1
Thus, Domain of f(x) = (-∞, -1) ∪ (1, 4]

Question 3.
\(\lim _{x \rightarrow 0} \frac{|\sin x|}{x}\) is equal to
(A) 1
(B) -1
(C) 0
(D) does not exist
Answer:
(D) does not exist
Explanation:
Right hand side limit = \(\lim _{x \rightarrow 0^{+}} \frac{|\sin x|}{x}\)
= \(\lim _{x \rightarrow 0^{+}} \frac{\sin x}{x}\)
= 1
Left hand side limit = \(\lim _{x \rightarrow 0^{-}} \frac{|\sin x|}{x}\)
= \(\lim _{x \rightarrow 0^{-}} \frac{-\sin x}{x}\)
= -1
RHS ≠ LHS
Therefore, the solution does not exist.

Question 4.
What is the mean deviation from the mean for the following data?
117, 156, 206, 198, 223
(A) 0
(B) 3
(C) 1
(D) 12
Answer:
(A) 0
Explanation:

Question 5.
Let S = set of points inside the square, T = set of points inside the triangle, and C = set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then
(A) S ∩ T ∩ C = φ
(B) S ∪ T ∪ C = C
(C) S ∪ T ∪ C = S
(D) S ∪ T = S ∩ C
Answer:
(C) S ∪ T ∪ C = S
Explanation:
The question may represented by the following diagram.

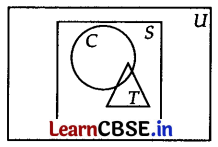
S = S ∪ T ∪ C

Question 6.
The real value of θ for which the expression \(\frac{1+i \cos \theta}{1-2 i \cos \theta}\) is a real number is
(A) \(n \pi+\frac{\pi}{4}\)
(B) \(n \pi+(-1)^n \frac{\pi}{4}\)
(C) \(2 n \pi \pm \frac{\pi}{2}\)
(D) none of these
Answer:
(C) \(2 n \pi \pm \frac{\pi}{2}\)
Explanation:

Question 7.
The coefficient of y in the expansion of \(\left(y^2+\frac{c}{y}\right)^5\) is
(A) 10c
(B) 10c²
(C) 10c³
(D) none of these
Answer:
(C) 10c³
Explanation:
Given binomial expression is \(\left(y^2+\frac{c}{y}\right)^5\)
Here, \(T_{r+1}={ }^5 C_r \times\left(y^2\right)^{5-r} \times\left(\frac{c}{y}\right)^r\) = \({ }^5 C_r \times y^{10-3 r} \times c^r\)
Now, 10 – 3r =1
⇒ 3r = 9
⇒ r = 3
So, coefficient of y = ⁵C₃ × c³ = 10c³

Question 8.
If x is a real number and |x| < 3, then
(A) x ≥ 3
(B) -3 < x < 3
(C) x ≤ -3
(D) -3 ≤ x ≤ 3
Answer:
(B) -3 < x < 3
Explanation:
We have, |x| < 3
∴ -3 < x < 3
[Since, |x| < a then -a < x < a]

Question 9.
Let R be the relation in the set N given by R = {(a, b): a = b – 2, b > 6}. Choose the correct answer.
(A) (2, 4) ∈ R
(B) (3, 8) ∈ R
(C) (6, 8) ∈ R
(D) (8, 7) ∈ R
Answer:
(C) (6, 8) ∈ R
Explanation:
R = {(a, b): a = b – 2, b > 6}
⇒ (a, b) ∈ R
⇒ a = b – 2 where b > 6
⇒ (6, 8) ∈ R as 6 = 8 – 2 where b = 8 > 6

Question 10.
The sum of A.P. 2, 5, 8,… upto 50 terms is
(A) 3775
(B) 3557
(C) 3757
(D) 3575
Answer:
(A) 3775
Explanation:
S_n = \(\frac{n}{2}\) (2a + (n – 1)d)
S₅₀ = \(\frac{50}{2}\) (2 × 2 + (50 – 1)3)
= 25(4 + 49 × 3)
= 25(4 + 147)
= 25 × 151
= 3775

Question 11.
School A has eight players. A five-member team will be selected out of these eight players. How many different selections can be made?
(A) 66
(B) 56
(C) 46
(D) 36
Answer:
(B) 56
Explanation:
In this case, n = 8 and r = 5,
Thus ⁿC_r = ⁸C₅
= \(\frac{8 !}{3 ! \times 5 !}\)
= \(\frac{8 \times 7 \times 6 \times 5 \times 4}{5 \times 4 \times 3 \times 2 \times 1}\)
= 56

Question 12.
The value of i^-999 is
(A) 1
(B) -1
(C) i
(D) -i
Answer:
(C) i
Explanation:

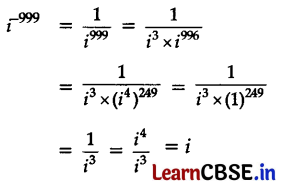
Question 13.
If a, b, c, d, and e are the observations of the mean m and standard deviation s, then find the standard deviation of the observations a + k, b + k, c + k, d + k, and e + k is
(A) s
(B) ks
(C) s + k
(D) \(\frac{s}{k}\)
Answer:
(A) s
Explanation:
On adding a constant to each observation, the mean, median, and quartiles will be changed, but the range, interquartile range, standard deviation, and variance will remain the same.

Question 14.
What is the distance of (5, 12) from the origin?
(A) 5 units
(B) 8 units
(C) 12 units
(D) 13 units
Answer:
(D) 13 units
Explanation:
Let the points be A(0, 0) and B(5, 12).
A(0, 0) = (x₁, y₁)
B(5, 12) = (x₂, y₂)
The distance between two points,

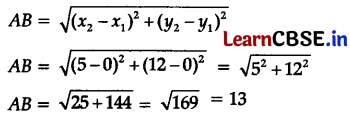
Hence, the distance of (5, 12) from the origin is 13 units.

Question 15.
The length of a rectangle is three times the breadth. If the minimum perimeter of the rectangle is 160 cm, then
(A) breadth > 20 cm
(B) length < 20 cm
(C) breadth ≥ 20 cm
(D) length ≤ 20 cm
Answer:
(C) breadth ≥ 20 cm
Explanation:
If x cm is the breadth.
⇒ Length = 3x
Given, the perimeter is greater than equal to 160,
i.e., 2(3x + x) ≥ 160
⇒ 2(4x) ≥ 160
⇒ x ≥ 20
⇒ breadth ≥ 20 cm

Question 16.
The perpendicular distance of the point P(6, 7, 8) from the XY-plane is
(A) 8
(B) 7
(C) 6
(D) None of these
Answer:
(A) 8
Explanation:
Let Q be the foot of the perpendicular drawn from the point P (6, 7, 8) to the XY plane. Thus, the distance of this foot Q from P is the z-coordinate of P, i.e., 8 units.

Question 17.
If 3 tan (x – 15°) = tan (x + 15°), then the value of x is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Answer:
(B) 45°
Explanation:

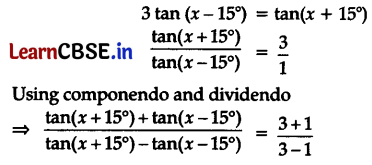
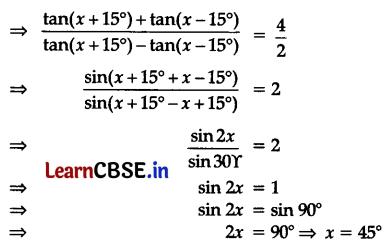
Question 18.
The minimum value of \(4^x+4^{1-x}\), x ∈ R, is
(A) 2
(B) 4
(C) 1
(D) 0
Answer:
(B) 4
Explanation:
Since, AM ≥ GM

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A): A five-digit number divisible by 3 is to be formed using the digits 0, 1, 2, 3, 4, and 5 with repetition. The total number formed is 216.
Reason (R): If the sum of digits of any number is divisible by 3 then the number must be divisible by 3.
Answer:
(D) (A) is false but (R) is true.
Explanation:
Since a five-digit number is formed by using digits 0, 1, 2, 3, 4, and 5, divisible by 3
i.e., only possible when the sum of digits is multiple of three which gives two cases.
Case I: Using digits 0, 1, 2, 4, 5
the number of ways = 4 × 4 × 3 × 2 × 1 = 96
Case II: Using digits 1, 2, 3, 4, 5
the number of ways = 5 × 4 × 3 × 2 × 1 = 120
Therefore, total numbers formed = 120 + 96 = 216 (taking numbers without repetition)

Question 20.
Assertion (A): The measure of rotation of a given ray about its initial point is called an angle.
Reason (R): The point of rotation is called a vertex.
Answer:
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).

Section-B

[This section comprises very short answer-type questions (VSA) of 2 marks each]

Question 21.
Solve \(\frac{x+3}{x-1}\) > o, x ∈ R.
OR
The coefficient of x in the equation x² + px + q = 0 was taken as 17 in place of 13 and thus its roots were found to be -2 and -15. Find the roots of the original equation.
Answer:
We have, \(\frac{x+3}{x-1}\) > 0 …….(i)
Equating x – 1 and x + 3 to zero, we obtain x = 1, -3 as critical points. Plot these points on a real line as shown in the figure. The real line is divided into three regions. In the rightmost region the expression on L.H.S. of (i) is positive and in the remaining two regions it is alternatively negative and positive.

Since the expression in (i) is positive, the solution set is given by
\(\frac{x+3}{x-1}\) > 0
⇒ (-∞, -3) ∪ (1, ∞)
OR
By given conditions, -2 and -15 are roots of the equation x² + 17x + q = 0.
The product of roots = (-2) (-15) = \(\frac{q}{1}\)
⇒ q = 30
Therefore, the original equation is x² + 13x + 30 = 0
⇒ x² + 10x + 3x + 30 = 0
⇒ x(x + 10) + 3(x + 10) = 0
⇒ (x + 10)(x + 3) = 0
⇒ (x + 10)(x + 3) = 0
⇒ x = -3, -10
Hence, the roots of the original equation are -3, -10.

Question 22.
The reporting time of an employee is given below:

Day	Mon	Tue	Wed	Thu	Fri	Sat
Time (a.m)	10:35	10:20	10:22	10:27	10:25	10:40

If the reporting time is 10:30 a.m., then find the probability of his coming late.
Answer:
Let ‘S’ be the sample space and ‘E’ be the event that the employee is coming late.
∴ n(S) = 6
E = {10 : 35, 10 : 40}
∴ n(E) = 2
∴ P(E) = \(\frac{n(F)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)
Thus, the probability of the employee coming late is \(\frac{1}{3}\).

Question 23.
Evaluate the left-hand and right-hand limits of the following function at x = 2. Does \(\lim _{x \rightarrow 2} f(x)\) exist?
f(x) = \(\left\{\begin{array}{c}
2 x+3, \text { if } x \leq 2 \\
x+5, \text { if } x>2
\end{array}\right.\)
OR
Evaluate: \(\lim _{x \rightarrow 0} \frac{\tan 2 x-\sin 2 x}{x^3}\)
Answer:

Question 24.
In how many ways can the letters of the word “ABACUS” be arranged such that the vowels always appear together?
Answer:
In the word ABACUS, there are 3 vowels – 2A’s and U.
Number of letters in ABACUS are 6.
Let us take the vowels as one, so the number of letters now = 4
∴ The Number of ways in which vowels occur together = 4!
But the 3 vowels can rearrange amongst themselves in \(\frac{3 !}{2 !}\) ways as ‘A’ appears twice.
Hence, the total number of ways in which vowels occur together = 4! × \(\frac{3 !}{2 !}\) = 72

Question 25.
Are sets A = {1, 2, 3, 4}, B = {x : x ∈ N and 5 ≤ x ≤ 7} disjoint? Why?
Answer:
Yes, sets A and B are disjoint, because A ∩ B = φ.
∵ A = {1, 2, 3, 4} and B = {5, 6, 7}
∴ A ∩ B = {1, 2, 3, 4} ∩ {5, 6, 7} = φ

Section-C

[This section comprises short answer type questions (5A) of 3 marks each]

Question 26.
Prove that the line lx + my + n = 0 will touch the parabola y² = 4ax if ln = am².
Answer:
Given equation of the parabola is y² = 4ax …….(i)
and equation of the line is lx + my + n = 0
⇒ y = \(\frac{-n-l x}{m}\) …….(ii)
From (ii) and (i),
\(\left(-\frac{(n+l x)}{m}\right)^2\) = 4ax
⇒ n² + 2lnx + l²x² = 4am²x
⇒ l²x² + (2ln – 4am²)x + n² = 0 ……(iii)
Since, line (ii) touches the parabola (i), so roots of (i) must be equal.
i.e., (2ln – 4am²)² – 4l²n² = 0
⇒ 4l²n² – 16lnam² + 16a²m⁴ – 4l²n² = 0
⇒ a²m⁴ = lnam²
⇒ am² = ln
Hence proved.

Question 27.
Prove that: cos A cos 2A cos 4A cos 8A = \(\frac{\sin 16 A}{16 \sin A}\)
Answer:

Hence proved.

Question 28.
Find the coefficient of x¹⁵ in the expansion of (x – x²)¹⁰.
OR
If the continued product of three numbers in G.P. is 216 and the sum of their products in pair is 156, find numbers.
Answer:
Given expansion is (x – x²)¹⁰
Let the term T_r+1 be the general term
∴ \(T_{r+1}={ }^{10} C_r x^{10-r}\left(-x^2\right)^r\)
= \((-1)^r \cdot{ }^{10} C_r \cdot x^{10-r} \cdot x^{2 r}\)
= \((-1)^r{ }^{10} C_r x^{10+r}\)
For the coefficient of x¹⁵,
10 + r = 15
⇒ r = 5
\(T_{5+1}=(-1)^5{ }^{10} C_5 x^{15}\)
∴ coefficient of x¹⁵ = \(-1 \times \frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 !}{5 \times 4 \times 3 \times 2 \times 1 \times 5 !}\)
= -3 × 2 × 7 × 6
= -252
OR
Let three numbers in G.P. be \(\frac{a}{r}\), a, ar.
Given, \(\frac{1}{2}\) . a . ar = 216
⇒ a³ = 216 = 6³
⇒ a = 6
Therefore sum of their product in pairs are:
\(\frac{a}{r}\) × a + a × ar + ar × \(\frac{a}{r}\) = 156
⇒ \(\frac{36}{r}\) + 36r + 36 = 156 (∵ a = 6)
⇒ \(\frac{36}{r}\) + 36r = 120
⇒ \(\frac{3}{r}\) + 3r = 10
⇒ 3r2 – 10r + 3 = 0
⇒ (3r – 1)(r – 3) = 0
⇒ r = \(\frac{1}{3}\), 3
Substituting the value of a and r in equation (i), we get
18, 6, 2 when r = \(\frac{1}{3}\) and 2, 6, 18 when r = 3

Question 29.
Show that the points A(1, 3, 0), B(-5, 5, 2), C(-9, -1, 2), and D(-3, -3, 0), are the vertices of a parallelogram ABCD, but it is not a rectangle.
OR
Find the coordinates of focus, the axis of the parabola, the equation of directrix, coordinate of the vertex of the parabola x² – 6x – 4y – 11 = 0.
Answer:

Since, AB = CD, BC = DA and AC ≠ BD
∴ The opposite sides are equal and diagonals are unequal, so the given points are the vertices of a parallelogram, not a rectangle.
OR
Given equation of the parabola is x² – 6x – 4y – 11 = 0
⇒ (x² – 6x + 9) – 9 – 4y – 11 = 0
⇒ (x – 3)² = 4y + 20
⇒ (x – 3)² = 4(y + 5) = 4 . 1 . (y + 5)
For vertex, x – 3 = 0 ⇒ x = 3
and y + 5 = 0 ⇒ y = -5
Vertex = (3, -5)
Axis of parabola x – 3 = 0 ⇒ x = 3
For directrix, y + 5 = -1
⇒ y + 6 = 0
And for focus, y + 5 = 1 and x – 3 = 0
⇒ y = -4 and x = 3
∴ Focus = (3, -4), axis of parabola is x = 3, equation of directrix is y + 6 = 0 and co-ordinates of vertex are (3, -5).

Question 30.
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that
(i) All the three balls are white.
(ii) all the three balls are red.
(iii) one ball is red and two balls are white.
OR
A die is loaded in such a way that each odd number is twice as likely to occur as each even number. Find P(G), where G is the event that a number greater than 3 occurs on a single roll of the die.
Answer:
Given the number of red balls = 8
and number of white balls = 5
(i) P(all the three balls are white)

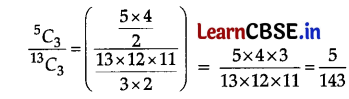
(ii) P(all the three balls are red)

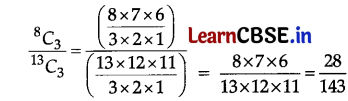
(iii) P(one ball is red and two balls are white)

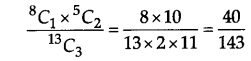
OR
It is given that, 2 × Probability of even number = Probability of odd number
⇒ P = 2P
Let (A odd number, B even number)
⇒ P(A) : P(B) = 2 : 1
∴ Probability of occurring odd number,
P(A) = \(\frac{2}{2+1}=\frac{2}{3}\)
and Probability of occurring even number,
P(B) = \(\frac{1}{2+1}=\frac{1}{3}\)
Now, G is the event that a number greater than 3 occurs in a single roll of die.
So, the possible outcomes are 4,5 and 6 out of which two are even and one odd.
∴ Required probability P(G) = 2 × P(A) × P(B)
= \(2 \times \frac{1}{3} \times \frac{2}{3}\)
= \(\frac{4}{9}\)

Question 31.
Prove that: \(\sqrt{2+\sqrt{2+2 \cos 4 \theta}}\) = 2 cos θ
Answer:

Section-D

[This section comprises long answer type questions (LA) of 5 marks each]

Question 32.
Determine the mean and standard deviation of the first n terms of an A.P. whose first term is a and whose common difference is d.
Answer:

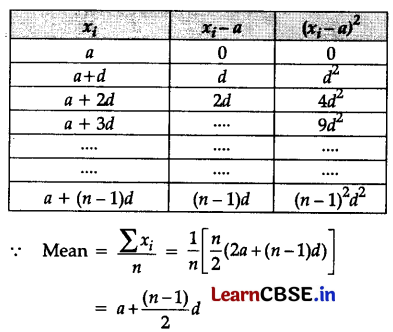
Question 33.
For any two sets A and B, prove that A ∪ B = A ∩ B ⇔ A = B.
OR
Draw the graph of the function |x – 2|.
Answer:
Let A = B, then A ∪ B = A and A ∩ B = A
A ∪ B = A ∩ B
Thus, A = B …..(i)
Conversely, let A ∪ B = A ∩ B
Now, let x ∈ A
x ∈ (A ∪ B) [∴ A ∪ B = A ∩ B]
x ∈ (A ∩ B)
x ∈ A and x ∈ B, x ∈ B
∴ A ⊆ B …….(ii)
Now, let y ∈ A
y ∈ A ∪ B, y ∈ A ∩ B [∴ A ∪ B = A ∩ B]
y ∈ A and y ∈ B
y ∈ A
∴ B ⊆ A …..(iii)
From equations (ii) and (iii), we get A = B
Thus, (A ∪ B) = (A ∩ B)
∴ A = B
From equations (iii) and (iv), we get
A ∪ B = A ∩ B ⇔ A = B
Hence proved.
OR
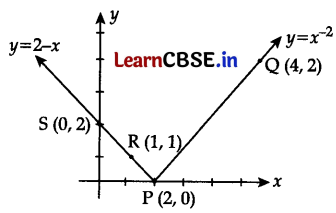
Clearly,

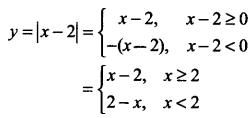
We know that a linear equation in r and y represents a line for drawing a line, we need only two points for y = x – 2

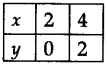
So, plot the points P(2, 0), Q(4, 2) and join PQ to get the graph of y = x – 2
For y = 2 – x

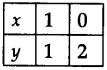
Plot the points R(1, 1), S(0, 2) and join RS to get the graph of y = 2 – x

Question 34.
Find the derivative of the following function: \(\frac{4 x+5 \sin x}{3 x+7 \cos x}\)
Answer:

Question 35.
There are 15 points in a plane out of which only 6 are in a straight line, then
(a) how many different straight lines can be made?
(b) how many triangles can be made?
OR
If a, b, c are positive and not all equal, then prove that: (a + b + c) (bc + ca + ab) > 9abc.
Answer:
(a) A straight line can be formed by joining 2 points, so several ways in which we select 2 points from 15 points is ¹⁵C₂.
But it also includes that in which 6 points are in a straight line. From those 6 points, only one line can be formed.
So, we have to subtract ⁶C₂ – 1 from the above result.
So, Total lines are ¹⁵C₂ – ⁶C₂ + 1
= \(\frac{15 !}{2 ! 13 !}-\frac{6 !}{2 ! 4 !}+1\)
= \(\frac{15 \times 14}{2 \times 1}-\frac{6 \times 5}{2 \times 1}+1\)
= 105 – 15 + 1
= 91
(b) Non-collinear point 9 and collinear point 6
Case I: We choose 1 non-collinear and 2 collinear points to make a triangle.
⁹C₁ × ⁶C₂ = \(\frac{9 !}{8 ! \cdot 1 !} \times \frac{6 !}{4 ! \cdot 2 !}\)
= \(\frac{9 \times 6 \times 5}{2}\)
= 135
Case II: We choose 2 non-collinear points and 1 collinear point to make a triangle.
⁹C₂ × ⁶C₁ = \(\frac{9 !}{2 ! \cdot 7 !} \times \frac{6 !}{1 ! \cdot 5 !}\)
= \(\frac{9 \times 8 \times 6}{2}\)
= 216
Case III: We choose 3 non-collinear points to make a triangle.
⁹C₃ = \(\frac{9 !}{3 ! 6 !}\)
= \(\frac{9 \cdot 8 \cdot 7}{3 \cdot 2}\)
= 84
Total number of triangles = 135 + 216 + 84 = 435
OR
We have, (a + b + c) (bc + ca + ab) – 9abc
= abc + a²c + a²b + b²c + abc + b²a + c²b + c²a + abc – 9abc
= a(b² + c²) + b(c² + a²) + c(a² + b²) – 6abc
= a(b² + c² – 2bc) + b(c² + a² – 2ca) + c(a² + b² – 2ab)
= a(b – c)² + b(c – a)² + c(a – b)²
which is positive because each term of R.H.S. is positive.
Thus, (a + b + c) (bc + ca + ab) – 9abc > 0
(a + b + c) (bc + ca + ab) > 9abc

Section-E

[This section comprises three case-study/passage-based questions of 4 marks each with sub-parts.]

The first two case study questions have three sub-parts (i), (ii), and (iii) of marks 1, 1, and 2 respectively. The third case study question has two sub-parts of 2 marks each.

Question 36.
Read the following passage and answer the questions given below:
Ordered Pairs: The ordered pair of two elements a and b is denoted by (a, b): a is the first element (or first component) and b is the second element (or second component).
Two ordered pairs are equal if their corresponding elements are equal, i.e., (a, b) = (c, d)
⇒ a = c and b = d
Ordered Pair (x, y)
x = first coordinate
y = second coordinate
Cartesian Product of Two Sets
For two non-empty sets A and B, the cartesian product A × B is the set of all ordered pairs of elements from sets A and B.
In symbolic form, it can be written as A × B = {(a, b) : a ∈ A, b ∈ B}
(i) If (a – 3, b + 7) = (3, 7), find the value of a and b.
(ii) Let A and B be two sets such that Ax B consists of 6 elements. If three elements of A × B are (1, 4), (2, 6), and (3, 6), then show that (A × B) ≠ (B × A).
(iii) If (x + 2, 4) = (5, 2x + y), find the value of x and y.
OR
If (x + 6, y – 2x) = (0, 6), then find the value of x and y.
Answer:
(i) We know that two ordered pairs are equal if their corresponding elements are equal.
(a – 3, b + 7) = (3, 7)
⇒ a – 3 = 3 and b + 7 = 7 [equating corresponding elements]
⇒ a = 3 + 3 and b = 7 – 7
⇒ a = 6 and b = 0

(ii) Since, (1, 4), (2, 6), and (3, 6) are elements of A × B, it follows that 1, 2, 3 are elements of A and 4, 6 are elements of B. It is given that A × B has 6 elements.
So, A = {1, 2, 3} and B = {4, 6}
Hence, A × B = {1, 2, 3} × {4, 6} = {(1, 4), (1, 6), (2, 4), (2, 6), (3, 4), (3, 6)}
and B × A = {4, 6} × {1, 2, 3} = {(4, 1), (4, 2), (4, 3), (6, 1), (6, 2), (6, 3)}
Thus A × B ≠ B × A

(iii) (x + 2, 4) = (5, 2x + y)
⇒ x + 2 = 5
⇒ x = 5 – 2 = 3
Also 4 = 2x + y
⇒ 4 = 2 × 3 + y
⇒ y = 4 – 6 = -2
OR
(x + 6, y – 2x) = (0, 6)
x + 6 = 0
⇒ x = -6
y – 2x = 6
⇒ y = 6 + 2(-6) = -6

Question 37.
Read the following passage and answer the questions given below:
Consider two complex numbers z₁ = 1 + i and z₂ = 2 – i.

(i) Find the value of \(z_1^6+\bar{z}_1^3\).
(ii) Find the value of \(z_1^{-1}\).
(iii) Find the conjugate of \(\frac{z_2}{z_1}\)
OR
Find the value of \(z_1 \cdot \bar{z}_2\).
Answer:

Question 38.
Read the following passage and answer the questions given below:
Indian track and field athlete Neeraj Chopra, who competes in the Javelin throw, won a gold medal at the Tokyo Olympics. He is the first track and field athlete to win a gold medal for India at the Olympics.

(i) If the equation of such a curve is given by x2 = -16y, then find the coordinates of the foci.
(ii) Write the equation of the directrix.
Answer:
(i) x² = -4ay
On comparing, -16y = -4ay
⇒ 4a = 16
⇒ a = 4
Focus = (0, -a) = (0, -4)

(ii) x² = -4ay
Equation of directrix is y = a
⇒ y = 4
⇒ y – 4 = 0