Students must start practicing the questions from CBSE Sample Papers for Class 11 Maths with Solutions Set 3 are designed as per the revised syllabus.
CBSE Sample Papers for Class 11 Maths Set 3 with Solutions
Time Allowed: 3 Hours
Maximum Marks: 80
General Instructions:
- This Question paper contains five sections A, B, C, D, and E. Each section is compulsory. However, there are internal choices in some questions.
- Section A has 18 MCQs and 2 Assertion-Reason-based questions of 1 mark each.
- Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
- Section C has 6 Short Answer (SA)-type questions of 3 marks each.
- Section D has 4 Long Answer (LA)-type questions of 5 marks each.
- Section E has 3 source-based/case-based/passage-based/integrated units of assessment of 4 marks each with sub-parts.
Section – A
(Multiple Choice Questions) Each Question Carries 1 Mark.
Question 1.
If X = {8n – 7n – 1| n ∈ N} and Y = {49n – 49| n ∈ N}. Then
(A) X ⊂ Y
(B) Y ⊂ X
(C) X = Y
(D) X ∩ Y = φ
Answer:
(A) X ⊂ Y
Explanation:
X = {8n – 7n -1 | n ∈ N} = {0, 49, 490, …..}; n = 1, 2, 3
Y = {49n – 49 | n ∈ N} = {0, 49, 98, …..}; n = 1, 2, 3
Every element of X belonging to Y
∴ X ⊂ Y
Question 2.
If nC12 = nC8, then n is equal to
(A) 20
(B) 12
(C) 6
(D) 30
Answer:
(A) 20
Explanation:
Given, nC12 = nC8
⇒ nC12 = nCn-8 [∵ nCr = nCn-r]
⇒ n – 8 = 12
⇒ n = 20
![]()
Question 3.
The value of tan 20° × tan 40° × tan 80° is
(A) tan 30°
(B) tan 60°
(C) 2 tan 30°
(D) 2 tan 60°
Answer:
(B) tan 60°
Explanation:

So, tan 20° × tan 40° × tan 80° = tan 60°
Question 4.
x and b are real numbers. If b > 0 and |x| > b, then
(A) x ∈ (-b, ∞)
(B) x ∈ (-∞, b)
(C) x ∈ (-b, b)
(D) x ∈ (-∞, -b) ∪ (b, ∞)
Answer:
(D) x ∈ (-∞, -b) ∪ (b, ∞)
Explanation:
We have, |x| > b and b > 0
∴ x < -b or x > b
Thus, x ∈ (-∞, -b) ∪ (b, ∞)
Question 5.
\(\lim _{x \rightarrow 0} x \sin \left(\frac{1}{x}\right)\) is equal to
(A) 0
(B) 1
(C) \(\frac{1}{2}\)
(D) Does not exist
Answer:
(A) 0
Explanation:
We know that, \(\lim _{x \rightarrow 0} x=0\)
and -1 ≤ \(\sin \frac{1}{x}\) ≤ 1
By the sandwich theorem,
\(\lim _{x \rightarrow 0} x \sin \left(\frac{1}{x}\right)=0\)
Question 6.
Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively
(A) 4, 7
(B) 7, 4
(C) 4, 4
(D) 7, 7
Answer:
(B) 7, 4
Explanation:
Number of subsets of a given set having m element = 2m
Number of subsets of a given set having n element = 2n
As per given condition,
⇒ 2m – 2n = 112
⇒ 2n (2m-n – 1) = 112
⇒ 2n (2m-n – 1) = 24 × 7
⇒ n = 4, 2m-n – 1 = 7
⇒ n = 4, m – n = 3
⇒ n = 4, m = 7
![]()
Question 7.
If x, 2y, 3z are in A.P., where the distinct numbers x, y, z are in G.P. then the common ratio of the G.P. is
(A) 3
(B) \(\frac{1}{3}\)
(C) 2
(D) \(\frac{1}{2}\)
Answer:
(B) \(\frac{1}{3}\)
Explanation:
Given, x, 2y, 3z are in A.P.
∴ 2(2y) = x + 3z
4y = x + 3z ……..(i)
Also, given x, y and z are in G.P.
∴ y2 = xz ……(ii)
From equationss (i) and (ii), we get
y2 = (4y – 3z)z
⇒ y2 = 4yz – 3z2
⇒ 3z2 – 4yz + y2 = 0
⇒ 3z2 – 3yz – yz + y2 = 0
⇒ 3z(z – y) – y(z – y) = 0
⇒ (z – y)(3z – y) = 0
⇒ z – y = 0 or 3z – y = 0
⇒ z = y or 3z – y = 0
⇒ z = y or z = \(\frac{y}{3}\)
⇒ z = \(\frac{y}{3}\) [∵ z and y are distinct]
\(\frac{z}{y}=\frac{1}{3}\) or r = \(\frac{1}{3}\) (∵ Common ratio in G.P. (r) = \(\frac{z}{y}\))
Question 8.
The domain of the function f given by f(x) = \(\frac{x^2+2 x+1}{x^2-x-6}\)
(A) R – {-2, 3}
(B) R – {-3, 2}
(C) R – [3, -2]
(D) R – (3, -2)
Answer:
(A) R – {-2, 3}
Explanation:
Given, f(x) = \(\frac{x^2+2 x+1}{x^2-x-6}\)
f(x) is defined if x2 – x – 6 ≠ 0
⇒ x2 – 3x + 2x – 6 ≠ 0
⇒ (x – 3)(x + 2) ≠ 0
⇒ x ≠ 3 and x ≠ -2
So, Domain of f(x) = R – {-2, 3}
Question 9.
Let the sets be A, B, C, D then (A × B) × (C × D) is equivalent to
(A) (A × C) × (B × D)
(B) (A × D) × (B × C)
(C) (A × C) × (B × D)
(D) None of these
Answer:
(A) (A × C) × (B × D)
Explanation:
(A × B) × (C × D) = (A × C) × (B × D)
Question 10.
In how many ways can the letters of the word BIHAR be re-arranged?
(A) 99
(B) 129
(C) 119
(D) 125
Answer:
(C) 119
Explanation:
The number of ways in which the word BIHAR can be rearranged = 5!
= 5 × 4 × 3 × 2 × 1
= 120
Since one arranged i.e., BIHAR is given, the number of ways in which the word BIHAR can be re-arranged = 120 – 1 = 119
![]()
Question 11.
The total number of words formed by 2 vowels and 3 consonants taken from 4 vowels and 5 consonants is equal to
(A) 60
(B) 120
(C) 7200
(D) 720
Answer:
(C) 7200
Explanation:
Total no. of required ways = 4C2 × 5C3 × 5!
= \(\frac{4 !}{2 ! 2 !} \times \frac{5 !}{3 ! 2 !} \times 5 !\)
= 6 × 10 × 120
= 7200
Question 12.
The value of sin (45° + θ) – cos (45° – θ) is
(A) 2 cos θ
(B) 2 sin θ
(C) 1
(D) 0
Answer:
(D) 0
Explanation:
sin (45° + θ) – cos (45° – θ)
= (sin 45° cos θ + cos 45° sin θ) – (cos 45° cos θ + sin 45° sin θ)
[∵ sin (A + B) = sin A cos B + cos A sin B, cos (A – B) = cos A cos B + sin A sin B]
= \(\left(\frac{1}{\sqrt{2}} \cos \theta+\frac{1}{\sqrt{2}} \sin \theta\right)-\left(\frac{1}{\sqrt{2}} \cos \theta+\frac{1}{\sqrt{2}} \sin \theta\right)\)
= 0
Question 13.
Range of data 4, 7, 8, 9, 10, 12, 13 and 17 is
(A) 4
(B) 17
(C) 13
(D) 21
Answer:
(C) 13
Explanation:
Range = Max. Value – Min. value
Range = 17 – 4 = 13
Question 14.
The first three term of a G.P. are m – 1, m + 1, m + 7. Find the value of m.
(A) 7
(B) 5
(C) 6
(D) 3
Answer:
(B) 5
Explanation:
The first three terms of a geometric progression are m – 2, m + 1 and m + 7.
Common ratio = \(\frac{a_2}{a_1}\) = \(\frac{a_3}{a_2}\)
⇒ \(\frac{m+1}{m-2}=\frac{m+7}{m+1}\)
⇒ (m + 1)2 = (m + 7)(m – 2)
⇒ m2 + 2m + 1 = m2 + 5m – 14
⇒ 3m = 15
⇒ m = 5
![]()
Question 15.
A plane is parallel to YZ plane, so it is perpendicular to
(A) X-axis
(B) Y-axis
(C) Z-axis
(D) None of these
Answer:
(A) X-axis
Explanation:
If a plane is parallel to the YZ plane, it is perpendicular to the X-axis.
Question 16.
If the coefficients of the 2nd, 3rd, and 4th terms in the expansion of (1 + x)n are in A.P., then the value of n is
(A) 2
(B) 7
(C) 11
(D) 14
Answer:
(B) 7
Explanation:
We know that,
\((1+x)^n={ }^n C_0+{ }^n C_1 x+{ }^n C_2 x^2+{ }^n C_3 x^3+\ldots+{ }^n C_n x^n\)
Now, nC1, nC2, and nC3 are coefficients of the second, third, and fourth terms in A.P.
∴ 2 . nC2 = nC1 + nC3
⇒ \(\text { 2. } \frac{n !}{2 !(n-2) !}=\frac{n !}{1 !(n-1) !}+\frac{n !}{3 !(n-3) !}\)
⇒ n(n – 1) = n + \(\frac{n(n-1)(n-2)}{6}\)
⇒ 6n(n – 1) = 6n + n(n – 1)(n – 2)
⇒ 6(n – 1) = 6 + (n – 1)(n – 2)
⇒ 6n – 6 = 6 + n2 – 3n + 2
⇒ n2 – 9n + 14 = 0
⇒ n – 7n – 2n + 14 = 0
⇒ n(n – 7) – 2(n – 2) = 0
⇒ (n – 7)(n – 2) = 0
Thus, n = 2 or n = 7
Question 17.
The area of the circle centered at (1, 2) and passing through the point (4, 6) is
(A) 5π sq. units
(B) 10π sq. units
(C) 25π sq. units
(D) None of these
Answer:
(C) 25π sq. units
Explanation:
Radius of circle (r) = \(\sqrt{(4-1)^2+(6-2)^2}\)
= \(\sqrt{(3)^2+(4)^2}\)
= √25
= 5 units
Thus, the area of the circle = πr2
= π(5)2
= 25π sq. units
![]()
Question 18.
The coefficient of x6 in the expansion of (1 + x2 + x)-3 is
(A) 9
(B) 3
(C) 1
(D) 0
Answer:
(B) 3
Explanation:

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Question 19.
Assertion (A): If 3x + 8 > 2, then x ∈ {-1, 0, 1, 2,…}, when x is an integer.
Reason (R): The solution set of the inequality 4x + 3 < 5x + 7 ∀ x ∈ R is [4, ∞).
Answer:
(C) (A) is true but (R) is false.
Explanation:
The assertion is correct. 3x + 8 > 2
3x > -6
x > -2
x ∈ {-1, 0, 1, 2,…}
The reason is incorrect.
4x + 3 < 5x + 7
-x < 4
x > -4
x ∈ (-4, ∞)
Question 20.
Assertion (A): The probability of getting a head in a toss of an unbiased coin is \(\frac{1}{2}\).
Reason (R): In a simultaneous toss of two coins, the probability of getting ‘no tails’ is \(\frac{1}{4}\).
Answer:
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
Explanation:
The assertion is correct.
The sample space for tossing a coin is given by S = {H, T}
n(S) = 2
The event for getting a head is only one (H).
n(E) = 1
So, required probability = \(\frac{1}{2}\)
The reason is correct.
The sample space for tossing two coins is given by S = {HH, HT, TH, TT}
n(S) = 4
The event for getting no tail is only one (HH).
n(E) = 1
So, required probability = \(\frac{1}{4}\)
Section-B
[This section comprises very short answer-type questions (VSA) of 2 marks each]
Question 21.
The coefficient of variation of the two distributions are 60 and 70, and their standard deviations are 21 and 16 respectively. What are their arithmetic mean?
OR
Find the standard deviation of the first ‘ten’ natural numbers.
Answer:
Given, CV1 = 60, CV2 = 70
σ1 = 21, σ2 = 16
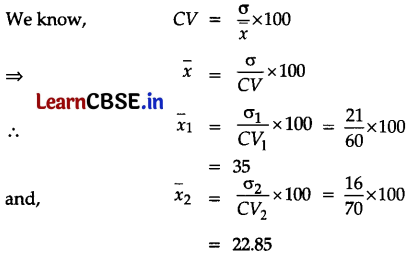
∴ Their arithmetic mean is 35 and 22.85.
OR
Here, the variables are 1, 2, 3,…, 9, 10
N = 10
∴ Standard deviation,
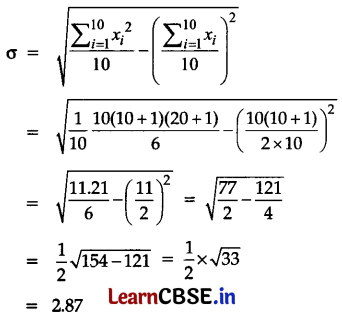
Question 22.
Differentiate \(\frac{x}{\sin x}\) with respect to x.
Answer:
Let f(x) = \(\frac{x}{\sin x}\)
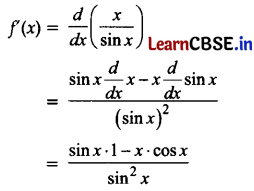
= cosec x – x cot x cosec x
= (1 – x cot x) . cosec x
![]()
Question 23.
Write the last two digits of the number 3400.
OR
In a G.P., the 3rd term is 24, and the 6th term is 192. Find the 10th term.
Answer:

We observe that all terms except the first one are divisible by 100, so the remainder when 3400 ÷ 100 is the same as the \(\left[{ }^{400} C_0(1)^{400}(2)^0\right]\) ÷ 100 = 1 ÷ 100
Therefore, the remainder when 3400 ÷ 100 is the same as when 1 ÷ 100, which is 0.01.
The last two digits are 0.01.
OR
Let the first term of G.P.be a and the common ratio be r.
Given, T3 = 24
⇒ ar2 = 24 ……(i)
and T6 = 192
⇒ ar5 = 192 …….(ii)
Dividing eq. (i) by (ii), we get
\(\frac{a r^5}{a r^2}=\frac{192}{24}\)
⇒ r3 = 8
⇒ r = 2
Putting the value of r in eq. (i), we get
a(2)2 = 24
⇒ a = 6
∴ T10 = ar9
= 6(2)9
= 3072
Question 24.
If the arcs of the same lengths in two circles subtend angles 75°and 120° at the center, find the ratio of their radii.
Answer:
Let r1 and r2 be the radii of the two circles.
Given, θ1 = 75°
= \(\frac{\pi}{180} \times 75\) radians
= \(\frac{5}{12} \pi\) radians
and θ2 = 120°
= \(\frac{\pi}{180} \times 120\) radians
= \(\frac{4}{6} \pi\) radians
Let l be the length of each of the arc.
Then l = r1θ1 = r2θ2, which gives
\(\frac{5}{12} \pi \times r_1=\frac{4}{6} \pi \times r_2\)
⇒ \(\frac{r_1}{r_2}=\frac{\frac{4}{6}}{\frac{5}{12}}=\frac{8}{5}\)
Hence r1 : r2 = 8 : 5.
Question 25.
If the letters of the word ‘RACHIT’ are arranged in all possible ways as listed in the dictionary. Then, what is the rank of the word ‘RACHIT’?
Answer:
The letters of the word ‘RACHTT in alphabetical order are A, C, H, I, R, and T.
Now, words beginning with A = 5!
words beginning with C = 5!
words beginning with H = 5!
words beginning with I = 5!
Word beginning with R i.e., RACHIT = 1
The rank of the word ‘RACHIT’ in the dictionary = 4 × 5! + 1
= 4 × 120 + 1
= 480 + 1
= 481
Section-C
[This section comprises short answer type questions (SA) of 3 marks each]
Question 26.
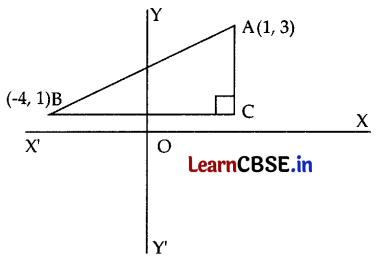
The hypotenuse of a right-angled triangle has its ends at the points (1, 3) and (-4, 1). Find the equation of the perpendicular sides of the triangle.
Answer:
Let us plot the points A(1, 3) and B(-4, 1) in the XY-plane.
From A(1, 3), we draw a line parallel to the Y-axis, and from B(-4, 1), we draw a line parallel to the X-axis.
These two lines meet at C, which is the right angle of ∆ABC.
The coordinates of C are (1, 1).
Now, equation of the line passing through B(-4, 1) and C(1, 1) is given by
y – 1 = \(\frac{1-1}{1+4}(x+4)\)
⇒ y = 1
and equation of the line passing through A(1, 3) and B(1, 1) is given by
y – 1 = \(\frac{1-3}{1-1}(x-1)\)
⇒ x = 1
∴ The equation of the two perpendicular lines is x = 1 and y = 1.
![]()
Question 27.
Evaluate: \(\left(1+\cos \frac{\pi}{8}\right)\left(1+\cos \frac{3 \pi}{8}\right)\left(1+\cos \frac{5 \pi}{8}\right)\left(1+\cos \frac{7 \pi}{8}\right)\)
Answer:
We have,

Question 28.
Find real θ such that \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) is purely real.
OR
Prove that 33! is divisible by 215. What is the largest integer n such that 33! is divisible by 2n?
Answer:

For z to be purely real
\(\frac{8 \sin \theta}{1+4 \sin ^2 \theta}\) = 0
⇒ sin θ = 0
⇒ θ = 0, π, 2π
Hence θ = nπ
OR
33! = 33 × 32 × 31 × 30 × 29….. × 16…… × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 33 × (2)5 × 31 × 30 × 29 ×….. × (2)4….. × (2)3 × 7 × 6 × 5 × (2)2 × 3 × (2)1 × 1
Now take all 2’s out we get
33! = (2)5 . (2)4 . (2)3 . (2)2 . (2)1 [33 × 31 × 30 × 29 ×….. × 1]
[33 × 31 × 30 × 29 × …… × 1] contains numbers 6, 10, 12, 14, 18, 20, 22, 24, 26, 28, and 30, which have 2 as one of their factors.
So, the product of 2 present in these numbers = 2 × 2 × 22 × 2 × 2 × 22 × 2 × 23 × 2 × 22 × 2 = 216
Therefore, we have 215 × 216 = 231
Thus, 31 is the largest integer such that 33! is divisible by 2n.
Question 29.
An arc is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the center. Find the height of the arc at a point 1.5 m from one end.
OR
Find the coordinates of the point P which is five-sixth of the way from A(-2, 0, 6) to B(10, -6, -12).
Answer:
Let ABA’ be the given arc such that AA’ = 8 m and OB = 2 m.
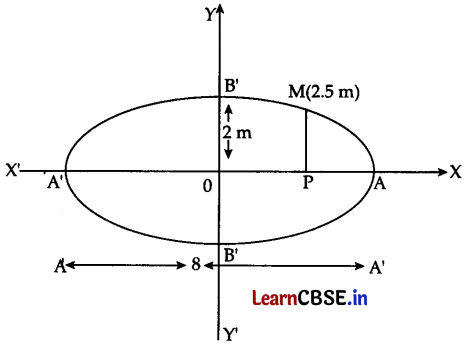
The arc is a part of the ellipse.
AA’ = 8 m
⇒ 2a = 8
⇒ a = 4
and OB = 2 m
⇒ b = 2
∴ The equation of the ellipse is \(\frac{x^2}{16}+\frac{y^2}{4}=1\) ……(i)
To find PM.
Putting x = 2.5 = \(\frac{5}{2}\) and y = PM

∴ The height of the arc at a point 1.5 from one end is \(\frac{\sqrt{39}}{4}\) m
OR
Let P(x, y, z) be the required point which is \(\frac{5}{6}\) of AB.

Question 30.
A box contains 10 red marbles, 20 blue marbles, and 30 green marbles. 5 marbles are drawn from the box. What is the probability that
(i) All will be blue?
(ii) At least one will be green.
OR
A committee of two persons is selected from two men and two women. What is the probability that the committee will have
(i) no man?
(ii) one man?
(iii) two man?
Answer:
Total number of marbles = 10 + 20 + 30 = 60
Number of ways of drawing 5 marbles from 60 marbles = 60C5.
(i) All the drawn marbles will be blue if we draw 5 marbles out of 20 blue marbles.
5 blue marbles can be drawn from 20 blue marbles in 20C5 ways.
∴ Probability that all marbles will be blue = \(\frac{{ }^{20} C_5}{{ }^{60} C_5}\)
(ii) Number of ways in which the drawn marbles are not green = \({ }^{(20+10)} C_5={ }^{30} C_5\)
∴ Probability that no marble is green = \(\frac{{ }^{30} C_5}{{ }^{60} C_5}\)
∴ Probability that at least one marble is green = 1 – \(\frac{{ }^{30} C_5}{{ }^{60} C_5}\)
OR
Let w1, w2 be the two women, and M1, M2 be the two men. Then, sample space,
S = {w1w2, w1M1, w1M2, w2w1, w2M1, w2M2, M1w1, w1w2, M1M2, M2w1, M2w2, M2w1}
⇒ n(S) = 12
(i) Let ‘A’ be the event of selecting no man.
∴ A = {w1w2, w2w1}
⇒ n(A) = 2
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{2}{12}=\frac{1}{6}\)
Thus, the probability of selecting no man is \(\frac{1}{6}\).
(ii) Let ‘B’ be the event of selecting one man.
∴ B = {w1M1, w1M2, w2M1, w2M2, M1w1, M1w2, M2w1, M2w2}
⇒ n(B) = 8
⇒ P(B) = \(\frac{n(B)}{n(S)}=\frac{8}{12}=\frac{2}{3}\)
Thus, the probability of selecting one man is \(\frac{2}{3}\).
(iii) Let ‘C’ be the event of selecting 2 men.
∴ C = {M1M2, M2M1}
⇒ n(C) = 2
∴ P(C) = \(\frac{n(C)}{n(S)}=\frac{2}{12}=\frac{1}{6}\)
Thus, the probability of selecting 2 men is \(\frac{1}{6}\).
![]()
Question 31.
If A = {1, 3, 5, 7, 9, 11, 13, 15, 17}, B = {2, 4, 6, 8, 10, 12, 14, 16, 18}, U = {1, 2, 3,……….} and U is universal set then find A’ ∪ {(A ∪ B) ∩ B’}.
Answer:
Given, A = {1, 3, 5, 7, 9, 11, 13, 15, 17}
i.e., A = {x : x is an odd number; 1 ≤ x ≤ 18}
and B = {2, 4, 6, 8, 10, 12, 14, 16, 18}
i.e., B = {x : x is an even number; 1 ≤ x ≤ 18}
Now, A’ = {x : x is an even number; 1 ≤ x ≤ 18}
= {2, 4, 6, 8, 10, 12, 14, 16, 18}
= B
and B’ = {x : x is an odd number; 1 ≤ x ≤ 18}
= {1, 3, 5, 7, 9, 11, 13, 15, 17}
= A
(A ∪ B) = {1, 3, 5, 7, 9, 11, 13, 15, 17} ∪ {2, 4, 6, 8, 10, 12, 14, 16, 18} = {1, 2, 3, 4, ……., 18}
(A ∪ B) ∩ B’ = {1, 2, 3, 4, ….., 18} ∩ {1, 3, 5, 7, 9, 11, 13, 15, 17} = {1, 3, 5, 7, 9, 11, 13, 15, 17}
A’ ∪ {(A ∪ B) ∩ B’} = {2, 4, 6, 8, 10, 12, 14, 16, 18} ∪ {1, 3, 5, 5, 7, 9, 11, 13, 15, 17} = {1, 2, 3, ……, 18}
Section-D
[This section comprises long answer type questions (LA) of 5 marks each]
Question 32.
Evaluate: \(\lim _{x \rightarrow 0} \frac{\sin (\alpha+\beta) x+\sin (\alpha-\beta) x+\sin 2 \alpha x}{\cos 2 \beta x-\cos 2 \alpha x} \cdot x\)
Answer:

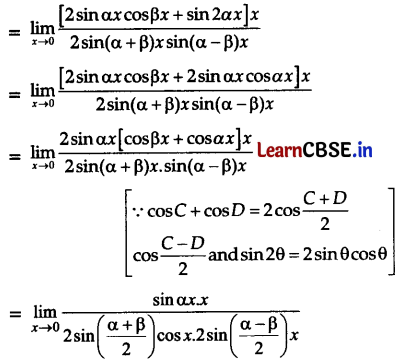
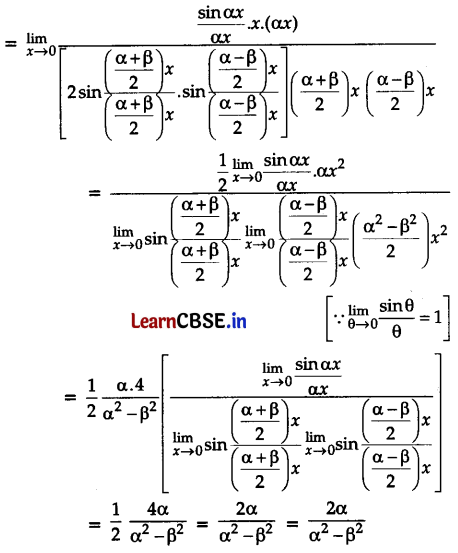
Question 33.
Three positive numbers form an increasing G.P. If the middle term in the G.P. is doubled, the new numbers are in A.P., then the common ratio of the G.P.
OR
In the expansion of (x + a)n, if O and the sum of the even term by E denote the sum of odd terms. Then, prove that:
(i) O2 – E2 =(x2 – a2)n
(ii) 4OE = (x + a)2n – (x – a)2n
Answer:
The three numbers in G.P. be \(\frac{a}{r}\), a, ar
The double of the middle term is 2a.
Now, \(\frac{a}{r}\), 2a, ar becomes in A.P.
∴ t2 – t1 = t3 – t2
⇒ 2a – \(\frac{a}{r}\) = ar – 2a
⇒ \(\frac{2 a r-a}{r}\) = ar – 2a
⇒ 2ar – a = ar2 – 2ar
⇒ ar2 – 4ar + a = 0
⇒ r2 – 4r + 1 = 0
solving the quadratic equation, we get r = 2 ± √3
OR
(i) Given expansion is (x + a)n
∴ (x + a)n = \({ }^n C_0 x^n a^0+{ }^n C_1 x^{n-1} a^1+{ }^n C_2 x^{n-2} a^2\) + \({ }^n C_3 x^{n-3} a^3+\ldots+{ }^n C_n a^n\)
Now, the sum of odd terms
i.e., O = \({ }^n C_0 x^n+{ }^n C_2 x^{n-2} a^2+\ldots\)
and the sum of even terms
i.e., E = \({ }^n C_1 x^{n-1} a+{ }^n C_3 x^{n-3} a^3+\ldots\)
∴ (x + a)n = O + E ……(i)
Similarly, (x – a)n = O – E …..(ii)
∴ (O + E)(O – E) = (x + a)n (x – a)n
[on multiplying equations (i) and (ii)]
⇒ O2 – E2 = (x2 – a2)n
(ii) 4OE = (O + E)2 – (O – E)2
= [(x + a)n]2 – [(x – a)n]2 [from equations (i) and (ii)]
= (x + a)2n – (x – a)2n
Hence Proved.
![]()
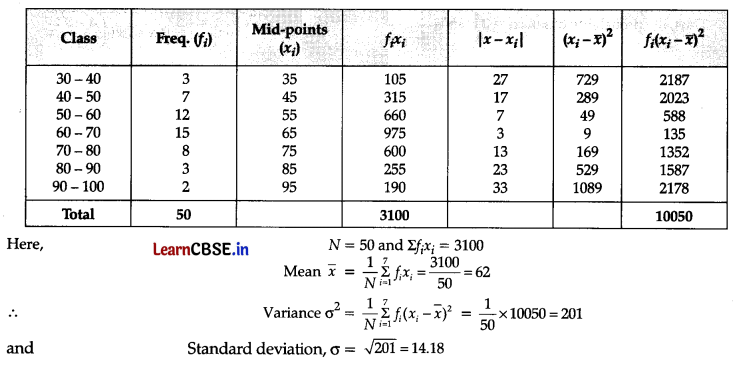
Question 34.
Calculate the variance and standard deviation for the following data:
| Class | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| Frequency | 3 | 7 | 12 | 15 | 8 | 3 | 2 |
Answer:
Question 35.
If sin(θ + α) = a and sin(θ + β) = b, then prove that cos2(α – β) – 4ab cos(α – β) = 1 – 2a2 – 2b2.
OR
Using the properties of sets and their complements prove that (A ∪ B) – C = (A – C) ∪ (B – C)
Answer:
Given, sin(θ + α) = a and sin(θ + β) = b
cos(α – β) = cos[θ + α – θ – β]
= cos[(θ + α) – (θ + β)]
= cos (θ + α) cos (θ + β) + sin (θ + α) sin (θ + β)
= \(\sqrt{1-\sin ^2(\theta+\alpha)} \sqrt{1-\sin ^2(\theta+\beta)}+a \cdot b\)
= \(\sqrt{\left(1-a^2\right)\left(1-b^2\right)}\) + ab
= ab + \(\sqrt{1-a^2-b^2+a^2 b^2}\)
Now, cos2(α – β) – 4ab cos(α – β) = 2cos2(α – β) – 1 – 4ab cos(α – β) [∵ cos 2θ = 2cos2θ – 1]

Hence, cos2(α – β) – 4ab cos (α – β) = 1 – 2a2 – 2b2
Hence proved.
OR
(A ∪ B) – C = (A – C) ∪ (B – C)
Let x ∈ [(A∪ B) – C]
x ∈ (A ∪ B) and x ∉ C
(x ∉ A or x ∉ B) and x ∉ C
(x ∉ A and x ∉ C) or (x ∉ B and x ∉ C)
x ∉ {(A – C) or x ∉ (B – C)}
x ∉ {(A – C) ∪ (B – C)}
(A ∪ B) – C ⊆ (A – C) ∪ (B – C) ……(i)
Again, Let y ∉ [(A – C) ∪ (B – C)]
y ∈ (A – C) or y ∈ (B – C)
(y ∈ A and y ∉ C) or (y ∈ B and y ∉ C)
(y ∈ A or y ∈ B) and y ∉ C
y ∈ {(A ∪ B) and y ∉ C}
y ∈ {(A ∪ B) – C}
(A – C) ∪ (B – C) ⊆ (A ∪ B) – C …..(ii)
From eqs. (i) and (ii),
(A ∪ B) – C = (A – C) ∪ (B – C)
Hence proved.
Section-E
[This section comprises 3 case-study/passage-based questions of 4 marks each with sub-parts.]
The first two case study questions have three sub-parts (i), (ii), and (iii) of marks 1, 1, and 2 respectively. The third case study question has two sub-parts of 2 marks each.
Question 36.
Read the following passage and answer the questions given below:
A submarine is moving in such a way that at a particular moment of time, its angle of elevation for two ships, situated at different positions on the surface of water is α and β respectively.
If cosec α = √3 and sec β = 2, then:
(i) What will be the value of sec α?
(ii) What will be the measure of angle β?
(iii) What will be the value of tan α?
OR
What will be the value of tan β?
Answer:

![]()
Question 37.
Read the following passage and answer the questions given below:
Consider the expansion of \(\left(x^2-\frac{1}{x}\right)^{18}\)
The general term of Binomial expansion of (x + y)n is as follows:
\(T_{r+1}={ }^n C_r \cdot x^{n-r} \cdot y^r\)
(i) Find the middle term.
(ii) What is the constant term?
(iii) Find the fourth term from the end.
OR
Find the coefficient of x12.
Answer:

Question 38.
Read the following passage and answer the questions given below:
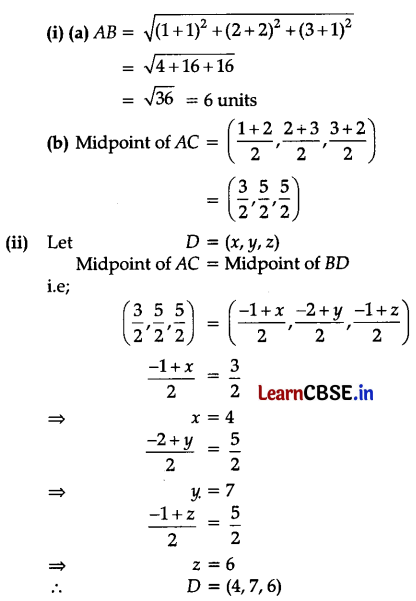
ABCD is a parallelogram as shown in the figure. Three of its vertices are A(1, 2, 3), B(-1, -2, -1) and C(2, 3, 2).

(i) Find (a) the length of AB and (b) the midpoint of AC.
(ii) Find the fourth vertex D.
Answer: