CBSE Sample Papers for Class 11 Maths Set 2 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 11 Maths with Solutions Set 2 are designed as per the revised syllabus.

CBSE Sample Papers for Class 11 Maths Set 2 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D, and E. Each section is compulsory. However, there are internal choices in some questions.
• Section A has 18 MCQs and 2 Assertion-Reason-based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
• Section C has 6 Short Answer (SA)-type questions of 3 marks each.
• Section D has 4 Long Answer (LA)-type questions of 5 marks each.
• Section E has 3 source-based/case-based/passage-based/integrated units of assessment of 4 marks each with sub-parts.

Section – A

(Multiple Choice Questions) Each Question Carries 1 Mark

Question 1.
The value of cos 5π is
(A) 0
(B) 1
(C) -1
(D) None of these
Answer:
(C) -1
Explanation:
cos 5π
= cos(π + 4π)
= cos π
= -1

Question 2.
If f(x) = ax + b, where a and b are integers, f(-1) = -5 and f(3) = 3, then a and b are equal to
(A) a = -3, b = -1
(B) a = 2, b = -3
(C) a = 0, b = 2
(D) a = 2, b = 3
Answer:
(B) a = 2, b = -3
Explanation:
Given, f(x) = ax + b …….(i)
f(-1) = -5 and f(3) = 3
Also, from (i)
f(-1) = -a + b and f(3) = 3a + b
⇒ -5 = -a + b ……(ii)
and 3 = 3a + b ……(iii)
On solving equations (ii) and (iii),
we get a = 2, b = -2

Question 3.
If |x – 3| < 2x + 9, then x lies in the interval
(A) (-∞, -2)
(B) (-2, 0)
(C) (-2, ∞)
(D) (2, ∞)
Answer:
(C) (-2, ∞)
Explanation:
Given, |x – 3| < 2x + 9
⇒ -(2x + 9) < x – 3 < 2x + 9
⇒ -2x – 9 < x – 3 and x – 3 < 2x + 9
⇒ -3x < 6 and -x < 12
⇒ x > -2 and x > -12
⇒ x > -2
Therefore, x ∈ (-2, ∞)

Question 4.
If sets A and B have 3 and 4 elements respectively then the number of subsets of a set (A × B) is
(A) 1024
(B) 2048
(C) 512
(D) 4096
Answer:
(D) 4096
Explanation:
Number of elements in (A × B) = 3 × 4 = 12
Number of subsets of (A × B) = 2¹² = 4096

Question 5.
If the 5th term of a G.P. is 2, then the product of the first 9 terms is
(A) 64
(B) 512
(C) 128
(D) 256
Answer:
(B) 512
Explanation:
Let a and r be the first term and common ratio of the required G.P.
Given, 5th term = 2
⇒ ar⁴ = 2
To find: Product of find 9 terms = a . ar . ar² . ar³ …..ar⁸
⇒ \(a^9 r^{1+2+3+\ldots+8}=a^9 r \frac{8 \times 9}{2}\) = a⁹r³⁶
⇒ (ar⁴)⁹ = 2⁹ = 512

Question 6.
The equation of a straight line that passes through the point (3, 4) and perpendicular to the line 3x + 2y + 5 = 0 is
(A) 2x – 3y + 6 = 0
(B) 2x + 3y + 6 = 0
(C) 2x – 3y – 6 = 0
(D) 2x + 3y – 6 = 0
Answer:
(A) 2x – 3y + 6 = 0
Explanation:
The equation of a straight line perpendicular to 3x + 2y + 5 = 0 is 2x – 3y + λ = 0 ……(i)
This passes through the point (3, 4).
Now, substitute in equation (i), we get
2(2) – 3(4) + λ = 0
⇒ 4 – 12 + λ = 0
⇒ -6 + λ = 0
⇒ λ = 6
Substituting λ = 6 in (i), we get
2x – 3y + 6 = 0, which is the required equation.

Question 7.
The sum of the digits in unit place of all the numbers formed with the help of 3, 4, 5, and 6 taken all at a time is
(A) 432
(B) 108
(C) 36
(D) 18
Answer:
(B) 108
Explanation:
Required no. of unit digits of all such numbers can be formed with the digits 3, 4, 5, and 6 taken all at a time = 3! × 3 + 3! × 4 + 3! × 5 + 3! × 6
[∵ If we fix one digit at the unit place, the remaining places can be filled in 3! ways]
= 3! (3 + 4 + 5 + 6)
= 3! × 18
= 6 × 18
= 108

Question 8.
If -3x + 17 < -13, then
(A) x ∈ (10, ∞)
(B) x ∈ [10, ∞)
(C) x ∈ (-∞, 10]
(D) x ∈ [-10, 10)
Answer:
(A) x ∈ (10, ∞)
Explanation:
We have, -3x + 17 < -13
⇒ -3x + 17 – 17 < -13 – 17 (Adding -17 on both sides)
⇒ -3x < -30
⇒ x > 10 (On dividing by -3 on both sides)
⇒ x ∈ (10, ∞)

Question 9.
The lengths of three unequal edges of a rectangular solid block are in G.P. The volume of the block is 216 cm3 and the total surface is 252 cm2. The length of the longest edge is
(A) 12 cm
(B) 6 cm
(C) 18 cm
(D) 3 cm
Answer:
(A) 12 cm
Explanation:
Let the length, breadth, and height of a rectangular block be \(\frac{a}{r}\), a, and ar.
[Since, given length, breadth, and height are in G.P]
∵ Volume = length × breath × height
⇒ 216 = \(\frac{a}{r}\) × a × ar
⇒ a³ = 216
⇒ a = 6 ……(i)
Now, Total surface area = 2[length × breath + breath × height + length × height]

⇒ 2 + 2r + 2r² = 7r
⇒ 2r² – 5r + 2 = 0
⇒ (r – 2)(2r – 1) = 0
⇒ r = 2 or r = \(\frac{1}{2}\)
Therefore, edges are 3, 6, 12 when r = 2 and edges are 12, 6, 3 when r = \(\frac{1}{2}\).

Question 10.
The equation with roots 3 and 4 will be
(A) x² + 7x + 12 = 0
(B) x² – 7x + 12 = 0
(C) x² – x + 12 = 0
(D) x² + 7x – 12 = 0
Answer:
(B) x2 – 7x + 12 = 0
Explanation:
The quadratic equation is given by x – Sx + P = 0
⇒ x² – (3 + 4)x + (3 × 4) = 0
⇒ x² – 7x + 12 = 0

Question 11.
The derivative of x² cos x is
(A) 2x sin x – x² sin x
(B) 2x cos x – x² sin x
(C) 2x sin x – x² cos x
(D) cos x – x² sin x cos x
Answer:
(B) 2x cos x – x² sin x
Explanation:

Question 12.
Coordinate planes divide the space into _________ octants.
(A) 8
(B) 4
(C) 6
(D) 10
Answer:
(A) 8
Explanation:
The coordinate planes divide the 3D space into eight octants.

Question 13.
Variance is independent of the change of
(A) origin only
(B) scale only
(C) origin and scale both
(D) None of these
Answer:
(A) origin only
Explanation:
Changing origin is the same as adding some constant to values and if we add a constant to values, the dispersion of the values from the mean is not changed, so the variance is not affected and remains the same. But if we multiply our values by a constant, then the variance is to be multiplied by (constant)2. Therefore, it is independent of origin but not of scaling.

Question 14.
In a town of 840 persons, 450 persons read Hindi, 300 read English, and 200 read both. Then the number of persons who read neither Hindi nor English newspapers are
(A) 210
(B) 290
(C) 180
(D) 260
Answer:
(B) 290
Explanation:
Total number of people in town = 840
Number of people who read Hindi n(H) = 450
Number of people who read English n(E) = 300
Number of people who read both n(H ∩ E) = 200
∴ n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
= 450 + 300 – 200
= 550
n(H’ ∩ E’) = n(U) – n(H ∪ E)
= 840 – 550
= 290

Question 15.
The value of tan 3A – tan 2A – tan A is equal to
(A) tan 3A tan 2A tan A
(B) -tan 3A tan 2A tan A
(C) tan A tan 2A – tan 2A tan 3A – tan 3A tan A
(D) None of the above
Answer:
(A) tan 3A tan 2A tan A
Explanation:
tan 3A = tan(2A + A)
⇒ tan 3A = \(\frac{\tan A+\tan 2 A}{1-\tan A \tan 2 A}\)
⇒ tan 3A – tan A . tan 2A tan 3A = tan A + tan 2A
⇒ tan 3A – tan 2A – tan A = tan A tan 2A tan 3A

Question 16.
What is the probability of selecting a vowel in the word “PROBABILITY”?
(A) \(\frac{2}{11}\)
(B) \(\frac{3}{11}\)
(C) \(\frac{4}{11}\)
(D) \(\frac{5}{11}\)
Answer:
(B) \(\frac{3}{11}\)
Explanation:
In the word ‘PROBABILITY’,
Vowels = 3
Total letters = 11
Probability of choosing a vowel = \(\frac{3}{11}\)

Question 17.
In the expansion of (a + bn, if n is even, then the middle term is
(A) \(\left(\frac{n}{2}+1\right)^{\text {th }}\) term
(B) \(\left(\frac{n}{2}\right)^{\mathrm{th}}\) term
(C) nth term
(D) \(\left(\frac{n}{2}-1\right)^{\text {th }}\) term
Answer:
(A) \(\left(\frac{n}{2}+1\right)^{\text {th }}\) term
Explanation:
In the expansion of (a + b)ⁿ, if n is even, the middle term is \(\left(\frac{n}{2}+1\right)^{\text {th }}\) term.

Question 18.
In a chess tournament, each of the six players will play with every other player exactly once. What is the number of matches that will be played during the tournament?
(A) 10
(B) 15
(C) 20
(D) 25
Answer:
(B) 15
Explanation:
Since each player will play every other player once.
So, to play a game 2 players are to be chosen out of 6 players.
n = 6 and r = 2
⁶C₂ = \(\frac{6 !}{2 ! \times 4 !}\)
= \(\frac{6 \times 5 \times 4 !}{2 ! \times 4 !}\)
= 15

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A): Let A = {a, b, c} and B = {a, b, c, d}. Then, A ⊂ B.
Reason (R): If every element of A is also an element of B, then A is a subset of B.
Answer:
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).

Question 20.
Assertion (A): The reason ix² – 3ix + 2i = 0 has no real roots.
Reason (R): If a, b, c are real and b² – 4ac ≥ 0, then the roots of the equation ax² + bx + c = 0 are real and if b² – 4ac < 0, then roots of ax² + bx + c = 0 are non-real.
Answer:
(D) (A) is false but (R) is true.
Explanation:
We have ix² – 3ix + 2i = 0
⇒ i(x² – 3x + 2) = 0
⇒ x² – 3x + 2 = 0
⇒ x = 1, 2, which are real.

Section – B

[This section comprises very short answer-type questions (VSA) of 2 marks each]

Question 21.
If A and B are mutually exclusive events of an experiment. If P(not A) = 0.65, P(A ∪ B) = 0.65 and P(B) = P, then find the value of P.
OR
Find the mean deviation about the mean of the distribution.

Size	20	21	22	23	24
Frequency	6	4	5	1	4

Answer:
Given, P(not A) = 0.65
⇒ 1 – P(A) = 0.65
⇒ P(A) = 0.35
P(A ∪ B) = 0.65, P(B) = P
Since, A and B are mutually exclusive,
so P(A ∪B) = P(A) + P(B)
⇒ 0.65 = 0.35 + P
⇒ P = 0.30
OR

Question 22.
Find the derivative of f(x) = x cos x.
Answer:
Given, f(x) = x cos x
f'(x) = \(\frac{d}{d x}\)(x cos x)
= cos x \(\frac{d}{d x}\) x + x \(\frac{d}{d x}\) cos x
= cos x . 1 + x . (-sin x)
= cos x – x sin x

Question 23.
Let A = {All prime numbers less than 10} and B = {all odd numbers less than 10}. Find (A – (A ∩ B)).
OR
Find the domain of the real function f(x) = \(\sqrt{x^2-4}\)
Answer:
Here, A = {2, 3, 5, 7} and B = {1, 3, 5, 7, 9}
A ∩ B = {2, 3, 5, 7} ∩ {1, 3, 5, 7, 9} = {3, 5, 7}
A – {A ∩ B) = {2, 3, 5, 7} – {3, 5, 7} = {2}
OR
Given, f(x) = \(\sqrt{x^2-4}\)
f is real only when x – 4 ≥ 0,
i.e., (x – 2)(x + 2) ≥ 0
∴ Domain of f = (-∞, -2] ∪ [2, ∞)

Question 24.
If z = x + iy and the amplitude of (z – 2 – 3i) is \(\frac{\pi}{4}\). Find the relation between x and y.
Answer:
Let z₁ = z – 2 – 3i
= x + iy – 2 – 3i [∵ given z = x + iy]
= (x – 2) + i(y – 3)
Now, amplitude of z₁ = \(\frac{\pi}{4}\) (given)
∴ \(\tan \left(\frac{\pi}{4}\right)=\frac{y-3}{x-2}\)
⇒ 1 = \(\frac{y-3}{x-2}\)
⇒ x – 2 = y – 3
⇒ x – y + 1 = 0
Hence, the locus of z is a straight line.

Question 25.
What is the maximum number of chords that can be drawn across 21 points on a circle?
Answer:
Any two points on a circle can be joined to form a chord. As a result, the total number of chords drawn via 21 points equals the number of ways to choose two points from 21 points. This can be accomplished in ²¹C₂. As a result, the total number of chords = ²¹C₂
= \(\frac{21 !}{19 ! \times 2 !}\)
= 21 × 10
= 210

Section – C

[This section comprises short answer type questions (SA) of 3 marks each]

Question 26.
The function ‘t’ which maps temperature in degrees Celsius into temperature in degrees Fahrenheit is defined by t(C) = \(\frac{9 C}{5}\) + 32. Find:
(i) t(0)
(ii) t(28)
(iii) t(-10)
(iv) The value of C, when t(C) = 212.
Answer:

Question 27.
Find the equation of the circle passing through the vertices of a triangle whose sides are represented by the equations x + y = 2, 3x – 4y = 6, and x – y = 0.
Answer:
Let AB, BC, and CA represent the three sides of the triangle given by x + y = 2, 3x – 4y = 6, and x – y = 0, respectively.
On solving AB and BC, we get the coordinates of vertex B(2, 0).
On solving BC and CA, we get C(-6, -6).
On solving AB and CA, we get A(1, 1).
Let the equation of the circle be
x² + y² + 2gx + 2fy + c = 0 ……(i)
Since, the circle (i) passes through A(1, 1), B(2, 0) and C(-6, -6), so, equation (i) implies
12 + 12 + 2g . 1 + 2f . 1 + c = 0
⇒ 2g + 2f + c = -2 ……(ii)
2² + 0² + 2g . 2 + 2f . 0 + c = 0
⇒ 4g + c + 4 = 0 …….(iii)
and, (-6)² + (-6)² + 2g . (-6) + 2f . (-6) + c = 0
⇒ 12g + 12f – c = 72 …..(iv)
Solving equations (ii), (iii), and (iv), we get
g = 2, f = 3, c = -12
Now putting the value of g, f, c in equation (i),
x² + y² + 4x + 6y – 12 = 0, is the required equation of the circle.

Question 28.
Let A = (1, 2, 4, 5}, B = {2, 3, 5, 6}, C = {4, 5, 6, 7}, verify the following identity A ∪ (B ∩ C) = [(A ∪ B) ∩ (A ∪ C)]
OR
If f(x) = \(\frac{\cot x}{1+\cot x}\) and α + β = \(\frac{5 \pi}{4}\), then find f(α).f(β).
Answer:
L.H.S = A ∪ (B ∩ C)
= {1, 2, 4, 5} ∪ [{2, 3, 5, 6} ∩ {4, 5, 6, 7}]
= {1, 2, 4, 5} ∪ (5, 6}
= {1, 2, 4, 5, 6}
R.H.S = {A ∪ B) ∩ (A ∪ C)
= [{1, 2, 4, 5} ∪ {2, 3, 5, 6}] ∩ [{1, 2, 4, 5} ∪ {4, 5, 6, 7}]
= {1, 2, 3, 4, 5, 6} ∩ {1, 2, 4, 5, 6, 7}
= {1, 2, 4, 5, 6}
∴ L.H.S = R.H.S
Hence verified.
OR

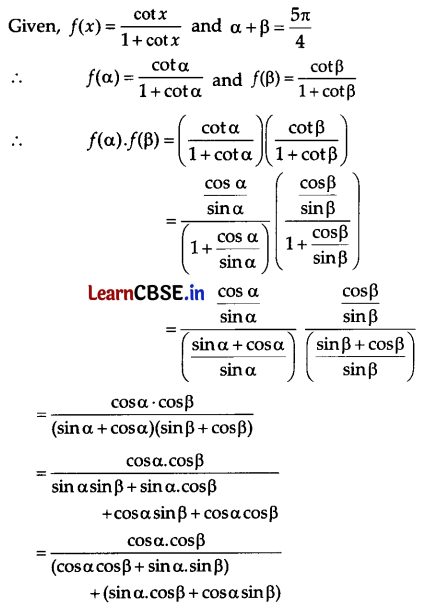
Question 29.
Find number of solutions of z² + |z|² = 0
OR
A polygon has 35 diagonals. Find the number of its sides.
Answer:
Given, z² + |z|² = 0
Let z = x + iy
∴ (x + iy)² + |(x + iy)|² = 0
⇒ x² – y² + 2xyi + x² + y² = 0
⇒ 2x² + i2xy = 0
⇒ 2x(x + iy) = 0
x = 0 or x + iy = 0 (not possible)
Therefore, x = 0 and z ≠ 0
So, y can have any real value. Hence, infinitely many solutions.
OR
Let n be the number of sides of a polygon and D be the number of diagonals of that polygon.
We know that, D = ⁿC₂ – n = \(\frac{n(n-3)}{2}\)
∴ 35 = \(\frac{n^2-3 n}{2}\)
⇒ n² – 3n – 70 = 0
⇒ (n – 10)(n + 7) = 0
⇒ n = 10, -7
Since sides cannot be negative, therefore n = 10.
Hence, the polygon is a decagon.

Question 30.
Find the mean deviation about the mean for the following data:

Income per day	0-100	100-200	200-300	300-400	400-500	500-600	600-700	700-800
Number of Persons	4	8	9	10	7	5	4	3

OR
Two dice are thrown and the sum of the numbers which come up on the dice is noted. Let us consider the following events associated with this experiment.
A: the sum is even
B: the sum is less than 4
C: the sum is greater than 11
Which pair of these events are mutually exclusive?
Answer:
Let us calculate the Mean Deviation.

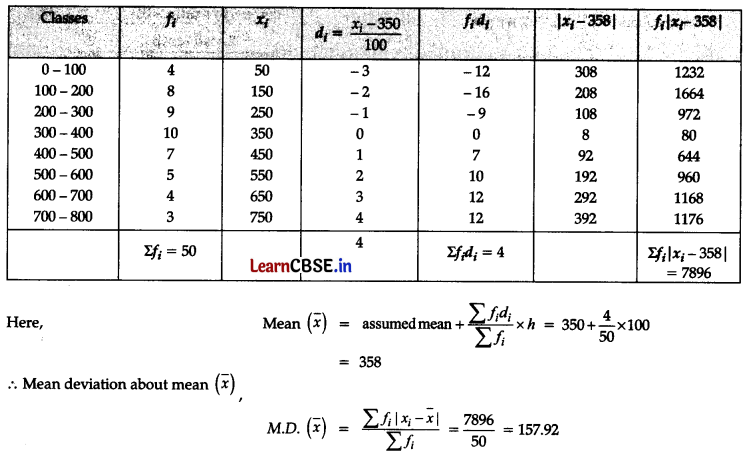
OR
When dice are thrown, sample space is
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
A = {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 1), (3, 5), (4, 2), (4, 4), (4, 6), (5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6), (3, 3)}
B = {(1, 1), (1, 2), (2, 1)}
C = {(6, 6)}
Since, A ∩ B ≠ φ, B ∩ C ≠ φ, A ∩ C ≠ φ.
So, B and C are mutually exclusive.

Question 31.
Show that the points (\(a t_1^2\), 2at1), (\(a t_2^2\), 2at2) and (a, 0) are collinear if t₁t₂ = -1.
Answer:
Let the given points be A(x₁, y₁) = (\(a t_1^2\), 2at₁), B(x₂, y₂) = (\(a t_2^2\), 2at₂) and C(x₃, y₃) = (a, 0)
∴ Area of ∆ABC

If t₁t₂ = -1, then t₁t₂ + 1 = 0
∴ Area of ∆ABC = 0
Hence, the given points are collinear.

Section – D

[This section comprises long answer type questions (LA) of 5 marks each]

Question 32.
If cos x = cos α cos β, then prove that: \(\tan \left(\frac{x+a}{2}\right) \times \tan \left(\frac{x-a}{2}\right)=\tan ^2 \frac{\beta}{2}\)
Answer:
Given, cos x = cos α cos β

Question 33.
Find the derivative of the following functions using the first principle (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): sin (x + a)
OR
Evaluate: \(\lim _{x \rightarrow 1 / 2}\left(\frac{8 x-3}{2 x-1}-\frac{4 x^2+1}{4 x^2-1}\right)\)
Answer:
Let, f(x) = sin (x + a)
f'(x + h) = sin f(x + h + a)
By first principle,

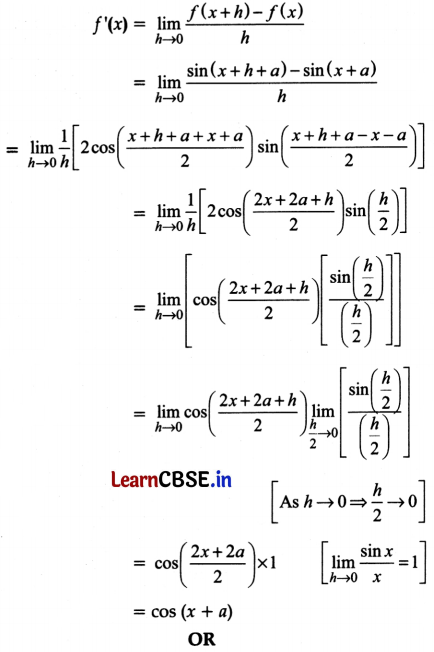
Question 34.
Following are the marks obtained out of 100, by two students Reeta and Seeta in 10 tests.

Reeta	25	50	45	30	70	42	36	48	35	60
Seeta	10	70	50	20	95	55	42	60	48	80

Who is more intelligent and who is more consistent?
Answer:
For Reeta:

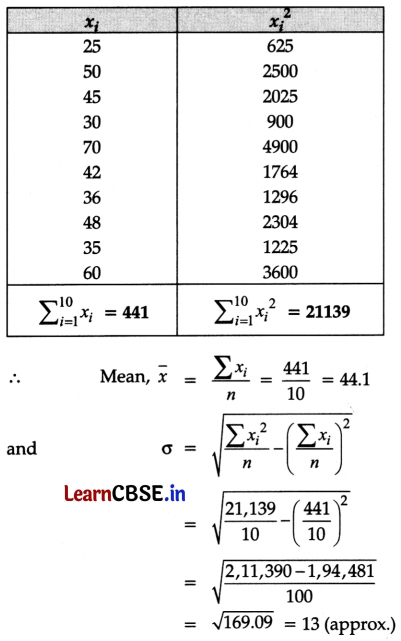
For Seeta:


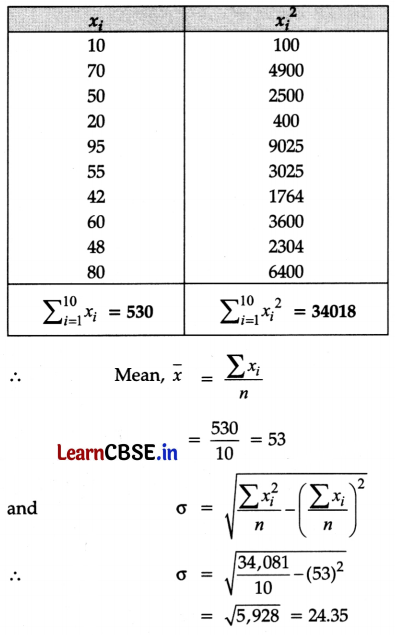
Since the coefficient of variation for Seeta is more than that of Reeta, so Seeta is more variable, and hence Reeta is more consistent. Thus, Seeta is more intelligent.

Question 35.
The sum of an infinite G.P. is 57 and the sum of the cubes of its term is 9747, find the G.P.
OR
The 3rd, 4th, and 5th terms in the expansion of (x + a)ⁿ are 84, 280, and 560 respectively. Find the value of x, a, n.
Answer:
Let the first term of G.P. be ‘a’ and the common ratio be ‘r’ where -1 < r < 1
The G.P. is a, ar, ar²…..
Therefore the sum of the infinite terms of the G.P. is
\(\frac{a}{1-r}\) …..(i)
If taking the cube of each term the new G.P. is a³, a³r³, a³r⁶,…
Therefore the sum of their cube is
\(\frac{a^3}{1-r^3}\) = 9747 ……(ii)
Taking the cube of the (i)
\(\frac{a^3}{(1-r)^3}\) = (57)3
⇒ a³ = (57)³(1 – r)³ ……(iii)
Substituting the value of ‘a’ in terms of r in (ii)

⇒ 19(1 + r² – 2r) = 1 + r² + r
⇒ 18r² – 39r + 18 = 0
⇒ 6r² – 13r + 6 = 0
⇒ 6r² – 9r – 4r + 6 = 0
⇒ (2r – 3)(3r – 2) = 0
Therefore, r = \(\frac{3}{2}\) or r = \(\frac{2}{3}\) since, r < 1.
∴ r = \(\frac{2}{3}\)
Substitute in eq. (i),
\(\frac{a}{1-\frac{2}{3}}\) = 57
⇒ 3a = 57
⇒ a = 19
Thus, the first term of the G.P. is 19 and the common ratio is \(\frac{2}{3}\).
The G.P. is 19, \(\frac{38}{3}\), \(\frac{76}{9}\) and so on.
OR
The 3rd, 4th and 5th terms in the expansion of (x + a)ⁿ are

⇒ 5n – 15 = 4n – 8
⇒ n = 7 …..(vi)
On putting n = 7 in equation (iv)
5a = 10x
⇒ a = 2x ……(vii)
Now, from (i)
⇒ \({ }^n C_2 x^{n-2} \cdot a^2\) = 84
⇒ \({ }^7 C_2 \cdot(x)^5(2 x)^2\) = 84
⇒ 21 × 4 × x⁷ = 84
⇒ x = 1
and a = 2x
= 2 × 1
= 2
∴ n = 7, x = 1 and a = 2.

Section – E

[This section comprises three case-study/passage-based questions of 4 marks each with sub-parts.]

The first two case study questions have three sub-parts (i), (ii), and (iii) of marks 1, 1, and 2 respectively. The third case study question has two sub-parts of 2 marks each.

Question 36.
Read the following passage and answer the questions given below:
In a class test of class XI, a teacher asked the students to consider A + B = \(\frac{\pi}{4}\), where A and B are acute angles.

(i) Find the value of (1 + tan A)(1 + tan B)?
(ii) Find the value of (cot A – 1)(cot B – 1).
(iii) Find the value of sin(A + B) – cos(A + B) + tan(A + B).
OR
Find the value of cosec(A + B) – sec(A + B) – cot(A + B).
Answer:
(i) A + B = \(\frac{\pi}{4}\)
tan (A + B) = tan \(\frac{\pi}{4}\)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = 1
⇒ tan A + tan B = 1 – tan A tan B
⇒ tan A + tan B + tan A tan B = 1
⇒ 1 + tan A + tan B + tan A tan B = 1 + 1
⇒ 1(1 + tan A) + tan B(1 + tan A) = 2
⇒ (1 + tan A)(1 + tan B) = 2

(ii) cot (A + B) = cot \(\frac{\pi}{4}\)
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}\) = 1
⇒ cot A cot B – 1 = cot B + cot A
⇒ cot A cot B – cot A – cot B = 1
⇒ cot A (cot B – 1) – cot B + 1 = 1 + 1
⇒ cot A (cot B – 1) – 1(cot B – 1) = 2
⇒ (cot B – 1)(cot A – 1) = 2

(iii) \(\sin \frac{\pi}{4}-\cos \frac{\pi}{4}+\tan \frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}\) + 1
= 1
OR
\({cosec} \frac{\pi}{4}-\sec \frac{\pi}{4}-\cot \frac{\pi}{4}\)
= √2 – √2 – 1
= -1

Question 37.
Read the following passage and answer the questions given below:
Rahul is playing with a long string, he hangs the ends of the string at two points on the wall. Now, it is in the form of a parabola with its vertical axis and is 10 m high and 5 m wide at its base as shown in the following figure:

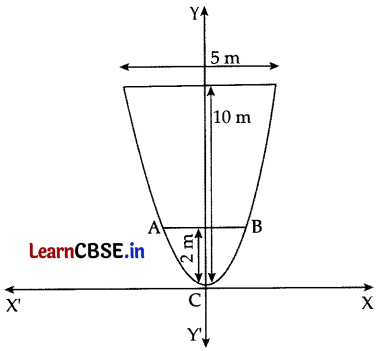
(i) What is the standard equation of parabola in this case?
(ii) Write the point through which the parabola passes.
(iii) What is the particular equation of a parabola?
OR
How wide is it 2 m from the vertex of the parabola?
Answer:
(i) The equation of the parabola is of the form x² = 4ay (as it opens upwards).
(ii) It can be seen from the given figure that the parabola passes through point (\(\frac{5}{2}\), 10).
(iii) The equation of parabola is x² = 4ay
x² = 4(\(\frac{5}{32}\))y
x² = \(\frac{5}{8}\)y
OR
Since the equation of a parabola is x² = \(\frac{5}{8}\)y

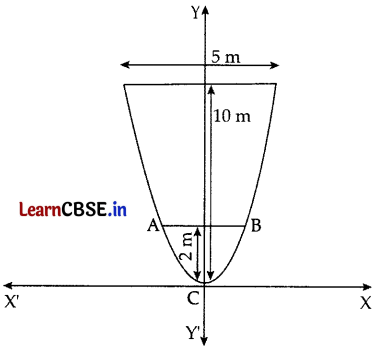
AB = 2 × \(\sqrt{\frac{5}{4}}\)
= √5 m (approx.)
= 2.23 m (approx.)

Question 38.
Read the following passage and answer the questions given below:
A school administration decides to send some of its students of class XI to an educational tour. From a class of 25 students, 10 are to be chosen for the tour. There are 3 friends – Rajesh, Shreya, and Deepa who decide that either all of them will join or none of them will join the tour.
(i) In how many ways can the students be chosen for this educational tour, if these three friends will not join?
(ii) In how many ways can the students be chosen for this educational tour?
Answer:
(i) As three friends won’t join the tour so, we need to select 10 students out of 22 students only.

(ii) In part (ii), either these three friends will not join or all the three friends will join. So, we either need to select 10 students out of 22 students or we need to select just 7 students from 22 students.
= ²²C₁₀ + ³C₃ . ²²C₇
= ²²C₁₀ + ²²C₇
= 646646 + ²²C₇
= 646646 + \(\frac{22 !}{7 !(22-7) !}\)
= 646646 + \(\frac{22 !}{7 ! 15 !}\)
= 646646 + 170544
= 817190