CBSE Sample Papers for Class 11 Maths Set 1 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 11 Maths with Solutions Set 1 are designed as per the revised syllabus.

CBSE Sample Papers for Class 11 Maths Set 1 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D, and E. Each section is compulsory. However, there are internal choices in some questions.
• Section A has 18 MCQs and 2 Assertion-Reason-based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
• Section C has 6 Short Answer (SA)-type questions of 3 marks each.
• Section D has 4 Long Answer (LA)-type questions of 5 marks each.
• Section E has 3 source-based/case-based/passage-based/integrated units of assessment of 4 marks each with sub-parts.

Section – A

(Multiple Choice Questions) Each Question Carries 1 Mark

Question 1.
The set {1, 2, 3} is a subset of which of the following sets?
(A) {1, 2, 3, 4}
(B) {2, 4, 6}
(C) {1, 2, 4}
(D) {1, 3, 5}
Answer:
(A) {1, 2, 3, 4}
Explanation:
A set A is a subset of a set B if every element of A is also an element of B.
The set {1, 2, 3} is a subset of the set {1, 2, 3, 4} because every element of {1, 2, 3} (namely 1, 2 and 3) is also an element of {1, 2, 3, 4}.

Question 2.
Which of the following is true for the complement of a set A?
(A) A ∪ A’ = φ
(B) A ∩ A’ = A
(C) A ∪ A’= U
(D) A ∩ A’ = A’
Answer:
(C) A ∪ A’= U
Explanation:
The complement of a set A, denoted by A’, is the set of all elements in the universal set U that are not in A.
Option A is incorrect because the union of a set and its complement gives the universal set, not the empty set.
Option B is incorrect because the intersection of a set and its complement gives the empty set, not the set itself.
Option C is correct because the union of a set and its complement gives the universal set.
Option D is incorrect because the intersection of a set and its complement gives the empty set, not the complement.

Question 3.
Express the function f: A → R, f(x) = x² – 1, where A = {-4, 0, 1, 4) as a set of ordered pairs.
(A) {(-4, 15), (0, -1), (1, 0), (4, 15)}
(B) {(-4, -15), (0, -1), (1, 0), (4, 15)}
(C) {(4, 15), (0, -1), (1, 0), (4, 15)}
(D) {(-4, 15), (0, -1), (1, 0)}
Answer:
(A) {(-4, 15), (0, -1), (1, 0), (4, 15)}
Explanation:
Given, A = {-4, 0, 1, 4} and f(x) = x² – 1
⇒ f(-4) = (-4)² – 1 = 16 – 1 = 15
⇒ f(0) = (0)² – 1 = -1
⇒ f(1) = (1)² – 1 = 0
⇒ f(4) = (4)² – 1 = 16 – 1 = 15
Therefore, the set of ordered pairs = {(-4, 15), (0, -1), (1, 0), (4, 15)}

Question 4.
If [x]² – 5[x] + 6 = 0, where [.] denote the greatest integer function, then
(A) x ∈ [3, 4]
(B) x ∈ (2, 3]
(C) x ∈ [2, 3]
(D) x ∈ [2, 4)
Answer:
(C) x ∈ [2, 3]
Explanation:
We have, [x]² – 5[x] + 6 = 0
⇒ [x]² – 3[x] – 2[x] + 6 = 0
⇒ [x] {[x] – 3} – 2{[x] – 3} = 0
⇒ ([x] – 3) {[x] – 2} = 0
⇒ [x] = 3, 2

Question 5.
The value of cos 1° cos 2° cos 3° ….cos 179° is
(A) \(\frac{1}{\sqrt{2}}\)
(B) 0
(C) 1
(D) -1
Answer:
(B) 0
Explanation:
cos 1° cos 2° cos 3°…..cos 179°
= cos 1° cos 2° cos 3° …cos 89° cos 90°cos 91° …cos 179°
= cos 1° cos 2° cos 3° …cos 89° (0) cos 91° …cos 179°
= 0 {since, the value of cos 90° = 0}

Question 6.
If sin θ + cosec θ = 2, then sin²θ + cosec²θ is equal to
(A) 1
(B) 4
(C) 2
(D) None of these
Answer:
(C) 2
Explanation:
Given, sin θ + cosec θ = 2
⇒ sin²θ + cosec²θ + 2 sin θ cosec θ = 4 (On squaring both sides)
⇒ sin²θ + cosec²θ + 2 = 4
⇒ sin²θ + cosec²θ = 2

Question 7.
The roots of the equation x² – 2√2x + 1 = 0 are
(A) Real and different
(B) Imaginary and different
(C) Real and equal
(D) Imaginary and equal
Answer:
(A) Real and different
Explanation:
The discriminant of the equation, D = b² – 4ac
⇒ D = (-2√2)² – 4(1)(1)
⇒ D = 8 – 4
⇒ D = 4
Since, D > 0, therefore, the roots are real and different.

Question 8.
If the roots of the equation x² + 2x + p = 0 are real, then the value of p is
(A) p ≤ 2
(B) p ≤ 1
(C) p ≤ 3
(D) None of these
Answer:
(B) p ≤ 1
Explanation:
Here, a = 1, b = 2, c = p
For real roots, b² – 4ac ≥ 0
⇒ (2)² – 4(1)(p) ≥ 0
⇒ 4 – 4p ≥ 0
⇒ 4 ≥ 4p
⇒ p ≤ 1

Question 9.
The interval in which f(x) = (x – 1)(x – 2)(x – 3) is negative as
(A) x > 2
(B) 2 < x and x < 1
(C) 2 < x < 1 and x < 3
(D) 2 < x < 3 and x < 1
Answer:
(D) 2 < x < 3 and x < 1
Explanation:
Given, f(x) = (x – 1)(x – 2)(x – 3).
It has all factors with odd powers. So, putting them equal to zero i.e.,
x – 1 = 0, x – 2 = 0, x – 3 = 0
⇒ x = 1, 2, 3
Now, f(x) < 0 when 2 < x < 3 and x < 1

Question 10.
If x < 5, then
(A) -x < -5
(B) -x ≤ -5
(C) -x > -5
(D) -x ≥ -5
Answer:
(C) -x > -5
Explanation:
According to the inequality rule, when inequality is multiplied by a negative number, then the sign of inequality is reversed. Thus, if x < 5, then -x > -5

Question 11.
In a group of 6 women and 4 men, 4 people are to be selected. In how many different ways they can be selected such that at least one woman should be there?
(A) 203
(B) 215
(C) 339
(D) 209
Answer:
(D) 209
Explanation:
The total number of ways to select a group of 4 people from 10 people is ¹⁰C₄ = 210.
Now we need to count the ways to select a group of 4 people with no women. There are 4 men to choose from and we need to choose all 4 of them.
Thus, the number of ways to select a group of 4 people with no women is ⁴C₄ = 1.
Therefore, the number of ways to select a group of 4 people with at least one woman is 210 – 1 = 209.

Question 12.
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is
(A) 6
(B) 18
(C) 12
(D) 9
Answer:
(B) 18
Explanation:
Required no. of parallelograms = ⁴C₂ × ³C₂
= \(\frac{4 !}{2 ! 2 !} \times \frac{3 !}{2 ! 1 !}\)
= 6 × 3
= 18

Question 13.
The greatest coefficient in the expansion of (1 + x)¹⁰ is
(A) \(\frac{10 !}{5 ! 6 !}\)
(B) \(\frac{10 !}{2 ! 8 !}\)
(C) \(\frac{10 !}{5 ! 5 !}\)
(D) \(\frac{10 !}{5 ! 4 !}\)
Answer:
(C) \(\frac{10 !}{5 ! 5 !}\)
Explanation:
Given term is (1 + x)¹⁰
Here, the total number of terms in the expansion of this value is, T = 10 + 1 = 11
Now, the greatest coefficient takes place in the middle.
The middle term of its expansion is \(\frac{11+1}{2}\)th term = 6th term
Now, 6th term of the expansion, T_r+1 = ¹⁰C_rx^r
⇒ T₅₊₁ = ¹⁰C₅x⁵
⇒ T₆ = ¹⁰C₅x⁵
Thus, ¹⁰C₅ is the greatest coefficient.
Since, \({ }^n C_r=\frac{n}{(n-r) ! r !}\)
∴ \({ }^{10} C_5=\frac{10 !}{5 ! 5 !}\)
So, the greatest coefficient in the expansion of (1 + x)¹⁰ is \(\frac{10 !}{5 ! 5 !}\)

Question 14.
If the nth term of a G.P. is 2ⁿ, then find the sum of its first 6 terms.
(A) 126
(B) 124
(C) 190
(D) 154
Answer:
(A) 126
Explanation:
Sum of n terms of a GP = \(\frac{a\left(r^n-1\right)}{(r-1)}\)
a_n = 2ⁿ
a₁ = 2
a₂ = 4
a₃ = 8
Common ratio (r) = 4 ÷ 2 = 8 ÷ 4 = 2
Sum of 6 terms, S6 = \(\frac{2\left(2^6-1\right)}{(2-1)}\)
= 2(64 – 1)
= 2 × 63
= 126

Question 15.
If the nth term of an AP is 3n – 4, find the 10th term of the AP.
(A) 10
(B) 12
(C) 22
(D) 26
Answer:
(D) 26
Explanation:
a_n = 3n – 4
⇒ a₁₀ = 3(10) – 4
⇒ a₁₀ = 30 – 4
⇒ a₁₀ = 26

Question 16.
The equation of a line that passes through the points (1, 5) and (2, 3) is
(A) 2x + y – 7 = 0
(B) 2x – y – 7 = 0
(C) x + 2y – 7 = 0
(D) 2x + y + 7 = 0
Answer:
(A) 2x + y – 7 = 0
Explanation:
We know that the equation of a line passes through two points (x₁, y₁) and (x₂, y₂) is \(\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}\)
(x₁, y₁) = (1, 5)
(x₂, y₂) = (2, 3)
Now, substitute the values in the formula, we get
\(\frac{y-5}{x-1}=\frac{3-5}{2-1}\)
⇒ \(\frac{y-5}{x-1}=\frac{-2}{1}\)
⇒ y – 5 = -2(x – 1)
⇒ y – 5 = -2x + 2
⇒ 2x + y – 5 – 2 = 0
⇒ 2x + y – 7 = 0
Therefore, the equation of a line that passes through the points (1, 5) and (2, 3) is 2x + y – 7 = 0.

Question 17.
The eccentricity of a hyperbola is
(A) e = 1
(B) e > 1
(C) e < 1
(D) 0 < e < 1
Answer:
(B) e > 1
Explanation:
The eccentricity of a hyperbola is greater than 1. (i.e.,) e > 1.

Question 18.
Which one is a measure of the dispersion method?
(A) Standard Deviation, Median, Range
(B) Standard Deviation, Mode, Range
(C) Standard Deviation, Variance, Range
(D) Mean, Mode, Median
Answer:
(C) Standard Deviation, Variance, Range
Explanation:
Standard Deviation, Variance, and Range are measures of dispersion but the Mean, Mode, and Median are the measures of central tendency.

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A): Derivative of f(x) = 2 is zero.
Reason (R): Differentiation of a constant function is zero.
Answer:
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
Explanation:
Both assertion and reason are true and reason is the correct explanation of assertion.

Question 20.
Assertion (A): In tossing a coin, the exhaustive number of cases is 2.
Reason (R): If a pair of dice is thrown, then the exhaustive number of cases is 6 × 6 = 36.
Answer:
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
Explanation:
Both assertion and reason are true but reason is not the correct explanation of assertion.

Section – B

[This section comprises very short answer-type questions (VSA) of 2 marks each]

Question 21.
Let A and B be two events such that P(A) = 0.3 and P(A ∪ B) = 0.8, find P(B) if P(A ∩ B) = P(A).P(B).
OR
The variance of 10 observations is 16 and their mean is 12. If each observation is multiplied by 4, what are the new mean and the new variance?
Answer:
Given, P(A) = 0.3, P(A ∪ B) = 0.8
We know P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ P(A ∪ B) = 0.3 + P(B) – P(A).P(B)
⇒ 0.8 = 0.3 + P(B) – 0.3 P(B)
⇒ 0.7 P(B) = 0.5
⇒ P(B) = \(\frac{5}{7}\)
OR
Given, N = 10, σ² = 16 and \(\bar{x}\) = 12
Let the new mean be \(\bar{x}\) and the new variance be \(\sigma_1^2\).
We know,


∴ New mean = 48 and new variance = 256.

Question 22.
Evaluate: \(\lim _{x \rightarrow 0} \frac{1-\cos 2 x}{x^2}\)
Answer:

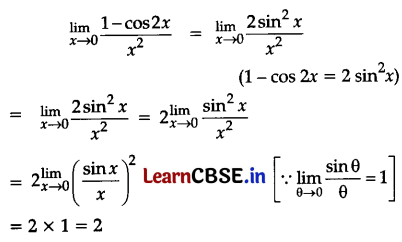
Question 23.
Find the number of terms in the A.P. 7, 10, 13, …. 31.
OR
If a, b, c are in G.P., then show that a² + b², ab + bc, b² + c² are also in G.P.
Answer:
Given A.P. is 7, 10, 13,…. 31
Here, a = 7, l = 31 and d = 3
Using formula, l = a + (n – 1)d
⇒ 31 = 7 + (n – 1)3
⇒ 31 – 7 = 3n – 3
⇒ 24 + 3 = 3n
⇒ n = 9
OR
Given that, a, b, c are in G.P.
⇒ b² = ac
⇒ b² – ac = 0
⇒ (b² – ac)2 = 0
⇒ b⁴ + a²c² – 2b²ac = 0
⇒ 2b²ac = b⁴ + a²c²
⇒ a²b² + b²c² + 2b²ac = a²b² + b²c² + a²c² + b⁴ (Adding a²b² + b²c² both sides)
⇒ (ab + bc)² = (a² + b²)(b² + c²)
⇒ a² + b², ab + bc, b² + c² are in G.P.
Hence Proved.

Question 24.
From a class of 40 students, in how many ways can five students be chosen for an excursion party?
Answer:
From a class of 40 students, five students can be chosen for an excursion party in ⁴⁰C₅ ways.

Question 25.
If A and B are finite sets such that n(A) = 5 and n(B) = 7, then find the number of functions from A to B.
Answer:
Given, n(A) = 5 and n(B) = 7
We know that, if n(A) = p and n(B) = q,
then number of functions from A to B = q^p
∴ Number of functions from A to B = 7⁵

Section – C

[This section comprises short answer type questions (SA) of 3 marks each]

Question 26.
On the real number line, if A = [0, 3] and B = [2, 6], then find the following:
(i) A’
(ii) A ∪ B
(iii) A ∩ B
(iv) A – B
Answer:
Given, A = [0, 3] and B = [2, 6]
(i) A’ = (-∞, 0) ∪ (3, ∞)
(ii) A ∪ B = [0, 3] ∪ [2, 6] = [0, 6]
(iii) A ∩ B = [0, 3] ∩ [2, 6] = [2, 3]
(iv) A – B = [0, 3] – [2, 6] = [0, 2)

Question 27.
Prove that: tan 13x = tan 4x + tan 9x + tan 4x . tan 9x . tan 13x
Answer:
tan 13x = tan(4x + 9x)
⇒ tan 13x = \(\frac{\tan 4 x+\tan 9 x}{1-\tan 4 x \cdot \tan 9 x}\) [∵ tan(A + B) = \(\frac{\tan A+\tan B}{1-\tan A \tan B}\)]
⇒ tan 13x (1 – tan 4x . tan 9x) = tan 4x + tan 9x
⇒ tan 13x – tan 13x . tan 4x . tan 9x = tan 4x + tan 9x
⇒ tan 13x = tan 4x + tan 9x + tan 4x . tan 9x . tan 13x

Question 28.
Show that 2⁴ⁿ⁺⁴ – 15n -16, where n ∈ N is divisible by 225.
OR
In the first four papers each of 100 marks, Rohit got 72, 83, 73, 95 marks. If he wants an average of greater than or equal to 75 marks and less than 80 marks, find the range of marks he should score in the fifth paper.
Answer:
We have


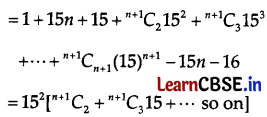
Thus, 2⁴ⁿ⁺⁴ – 15n – 16 is divisible by 225.
OR
Let the marks he scored in the fifth paper be x
Then average = (95 + 72 + 73 + 83 + x) ÷ 5
⇒ Average = \(\frac{323+x}{5}\)
As per question 75 ≤ \(\frac{323+x}{5}\) < 80
Solving 75 ≤ \(\frac{323+x}{5}\)
Multiplying both sides by 5, we get
⇒ 75 × 5 ≤ 323 + x
⇒ 375 ≤ 323 + x
⇒ 375 – 323 ≤ 323 + x – 323
⇒ 52 ≤ x
Solving, \(\frac{323+x}{5}\) < 80
Multiplying both sides by 5, we get
⇒ 323 + x < 80 × 5
⇒ 323 + x < 400
⇒ 323 + x – 323 < 400 – 323
⇒ x < 77
Thus, 52 ≤ x < 77.

Question 29.
The line 2x – 3y = 4 is the perpendicular bisector of the line segment AB. If the coordinates of A are (-3, 1), find the coordinates of B.
OR
Find the equation of the circle which passes through (2, -2) and (3, 4) and whose center lies on the line x + y = 2.
Answer:
Let the coordinates of B are (p, q).
Then, slope of line AB, m₁ = \(\frac{q-1}{p+3}\)
And, slope of line 2x – 3y = 4 is \(\frac{2}{3}\) = m₂
Since, the lines are perpendicular, so m₁m₂ = -1
⇒ \(\frac{q-1}{p+3} \times \frac{2}{3}=-1\)
⇒ 2q – 2 = -3p – 9
⇒ 3p + 2q + 7 = 0 ………(i)
The midpoint of AB is \(\left(\frac{p-3}{2}, \frac{q+1}{2}\right)\), which lies on the line 2x – 3y = 4.
∴ \(2\left(\frac{p-3}{2}\right)-3 \cdot\left(\frac{q+1}{2}\right)=4\)
⇒ 2p – 6 – 3q – 3 = 8
⇒ 2p – 3q – 17 = 0 ……(ii)
Solving (i) and (ii), we get p = 1, q = -5
OR
Let, the equation of the circle with centre (h, k) and radius ‘r’ be
(x – h)² + (y – k)² = r² ……(i)
Since, the circle passes through (2, -2) and (3, 4).
(2 – h)² + (-2 – k)² = r² ……(ii) and (3 – h)² + (4 – k)² = r² ……(iii)
(ii) and (iii) ⇒ (2 – h)² + (2 + k)² = (3 – h)² + (4 – k)²
⇒ 4 – 4h + h² + 4 + 4k + k² = 9 – 6h + h² + 16 – 8k + k²
⇒ -4h + 4k + 8 + 6h + 8k – 25 = 0
⇒ 2h + 12k – 17 = 0 …….(iv)
Also, the center (h, k) lies on x + y = 2
∴ h + k = 2 …..(v)
(iv) – 2 × (v) ⇒ 10k – 17 = -4
⇒ k = \(\frac{13}{10}\)
⇒ k = 1.3
(iv) ⇒ h = 0.7
(i) ⇒ (x – 0.7)² + (y – 1.3)² = r² …..(vi)
(ii) ⇒ (2 – 0.7)² + (-2 – 1.3)² = r²
⇒ r² = 12.58
∴ (vi) ⇒ (x – 0.7)² +(y – 1.3)² = 12.58 is the required equation of the circle.

Question 30.
Find the equation of the ellipse in which the length of the minor axis is equal to the distance between foci, given length of the latus rectum is 10 units and the major axis is along X-axis.
OR
Find the length of the medians of the triangle with vertices A(0, 0, 6), B(0, 4, 0) and C(6, 0, 0).
Answer:
Let the equation of the ellipse be
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) [a > b] …….(i)
Given, the length of the minor axis = distance between the foci
⇒ 2b = 2c
⇒ b = c
And the length of the latus rectum = 10
⇒ \(\frac{2 b^2}{a}\) = 10
⇒ b² = 5a
Also, c² = a² – b²
⇒ 2b² = a²
⇒ 10a = a²
⇒ a²– 10a = 0
⇒ a(a – 10) = 0
Since, a ≠ 0, so a = 10
⇒ b² = 50
From (i), \(\frac{x^2}{100}+\frac{y^2}{50}=1\)
⇒ x² + 2y² = 100, is the required equation of the ellipse.
OR
Let AD, BF, and CF be the medians from vertex A, B, and C to BC, CA, and AB respectively.

∴ The lengths of the medians are 7, √34, 7.

Question 31.
In a single throw of two dice, determine the probability of getting a total of 7 or 9.
Answer:
Let S be the sample space.
Then, n(S) = 6² = 36
Let ‘A’ and ‘B’ be the events of getting a total of 7 and 9 respectively.
∴ A = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
⇒ n(A) = 6
B = {(3, 6) (4, 5), (5, 4), (6, 3)}
⇒ n(B) = 4
A ∩ B = φ
⇒ n(A ∩ B) = 0
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}\)
P(B) = \(\frac{n(B)}{n(S)}=\frac{4}{36}\)
and P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}\) = 0
We know P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{6}{36}+\frac{4}{36}\) – 0
= \(\frac{10}{36}\)
= \(\frac{5}{18}\)
∴ The probability of getting a total of 7 or 9 is \(\frac{5}{18}\).

Section – D

[This section comprises long answer type questions (LA) of 5 marks each]

Question 32.
If each of the observations x₁, x₂, ….., x_n is increased by ‘a’, where ‘a’ is a negative or positive number, then show that the variance remains unchanged.
Answer:
Let \(\bar{a}\) be the mean of x₁, x₂, ……, x_n.
Then, the variance is given by
\(\sigma_1^2=\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2\) ……(i)
If ‘a’ is added to each observation, then the new observation will be y_i = x_i + a ……(ii)
Let the mean of the new observation be \(\bar{y}\). Then,

∴ Variance remains unchanged.

Question 33.
Evaluate: \(\lim _{y \rightarrow 0} \frac{(x+y) \sec (x+y)-x \sec x}{y}\)
OR
Find the derivative of the following functions using the first principle (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax + b)ⁿ
Answer:



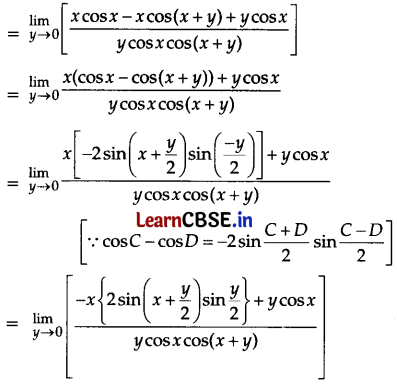
OR
Let f(x) = (ax + b)ⁿ
Accordingly, f(x + h) = {a(x + h) + b}ⁿ = (ax + ah + b)ⁿ
By first principle,

Question 34.
If A = {2, 4, 6, 9} B = {4, 6, 18, 27, 54} and a relation R from A to B is defined by R = {(a, b) : a ∈ A, b ∈ B, a is a factor of b and a < b}, then express it in Roster form. Also, find its domain, co-domain, and range.
Answer:
Given, A = {2, 4, 6, 9} and B = {4, 6, 18, 27, 54}
and R = {(a, b) : a ∈ A, b ∈ B, a is a factor of b and a < b}
Roster form:
R = {(2, 4), (2, 6), (2, 18), (2, 54), (6, 18), (6, 54), (9, 18), (9, 27), (9, 54)}
Domain of R = {2, 6, 9}
Co-domain of R = {4, 6, 18, 27, 54}
Range of R = {4, 6, 18, 27, 54}

Question 35.
Find the values of x and y for which complex numbers -3 + ix²y and x² + y + 4i are conjugate to each other.
OR
If the A.M. between pth and qth terms of an A.P. be equal to AM. between rth and sth terms of the A.P., then show that p + q = r + s.
Answer:
Since, -3 + ix²y and x² + y + 4i are complex conjugates.
∴ -3 + ix²y = x² + y + 4i
and -3 + ix²y = x² + y – 4i
⇒ -3 = x² + y …….(i)
and x²y = -4 …….(ii)
-3 = x² – \(\frac{4}{x^2}\)
⇒ x⁴ + 3x² – 4 = 0
⇒ (x⁴ + 4)(x² – 1) = 0
⇒ x² – 1 = 0
⇒ x = ±1
From (ii), y = -4, when x = ±1
Hence, x = 1, y = -4 or x = -1, y = -4
OR
Let a be the first term and d be the common difference of the given A.P. Then
a_p = pth term = a + (p – 1)d;
a_q = qth term = a + (q – 1)d;
a_r = rth term = a + (r – 1)d;
a_s = sth term = a + (s – 1)d
It is given that
A.M. between a_p and a_q = A.M. between a_r and a_s
⇒ \(\frac{1}{2}\left(a_p+a_q\right)=\frac{1}{2}\left(a_r+a_s\right)\)
⇒ a_p + a_q = a_r + a_s
⇒ a + (p – 1)d + a + (q – 1)d = a + (r – 1)d + a + (s – 1)d
⇒ (p + q – 2)d = (r + s – 2)d
⇒ p + q = r + s
Hence proved.

Section – E

[This section comprises three case-study/passage-based questions of 4 marks each with sub-parts.]

The first two case study questions have three sub-parts (i), (ii), and (iii) of marks 1, 1, and 2 respectively. The third case study question has two sub-parts of 2 marks each.

Question 36.
Read the following passage and answer the questions given below:
Soniya, Payal, Geeta, and Ramesh are on the school hockey team while Geeta, Manish, Pawan, and Ritu are on the school football team of a school. Let X be the set of students who are on the hockey team and Y be the set of students who are on a football team. Answer the following questions:

(i) Find X ∪ Y.
(ii) Find X – Y.
(iii) Are X and Y disjoint sets? Justify your answer.
OR
What is the number of proper subsets of X? Given the number of elements in set X, i.e., n(X) = 4
Answer:
(i) X = {Soniya, Payal, Geeta, Ramesh} and Y = {Geeta, Manish, Pawan and Ritu},
then X ∪ Y = {Soniya, Payal, Geeta, Ramesh, Manish, Pawan, Ritu}
(ii) X = {Soniya, Payal, Geeta, Ramesh} and Y = {Geeta, Manish, Pawan, Ritu},
then X – Y = {Soniya, Payal, Ramesh}
(iii) No, X and Y are not disjoint sets,
Since, X = {Soniya, Payal, Geeta, Ramesh} and Y = {Geeta, Manish, Pawan, Ritu},
then X ∩ Y = {Geeta} ≠ φ, So, X and Y are not disjoint sets.
OR
Number of elements in set X, n(X) = 4
Now, number of proper subset = 2^n(X)
= 2⁴
= 16

Question 37.
Read the following passage and answer the questions given below:
An Intelligence Quotient (IQ) is a total score derived from standardized tests or sub-tests designed to assess human intelligence. The abbreviation “IQ” was coined by the Psychologist William Stern for the German term Intelligence Quotient, his term for a scoring method for intelligence tests at the University of Breslau he advocated in a 1912 book.

Priya is a Psychology student and nowadays she is learning about Intelligence Quotient (IQ). She calculates the result as follows:
Intelligence Quotient = \(\frac{\text { Mental Age }}{\text { Chronological Age }} \times 100\)
(i) What could be the range of mental age if a group of children with the chronological age of 15 years have the IQ range as 90 ≤ IQ ≤ 150? (1)
(ii) What could be the range of IQ if a group of children the age of 12 years have the mental age range as 9 ≤ MA ≤ 15? (1)
(iii) What could be the range of IQ if a group of children with a mental age of 18 years have the mental age range as 12 < CA < 15? (2)
OR
Find the solution set for the inequality: 8x + 6 < 10x + 14
Answer:


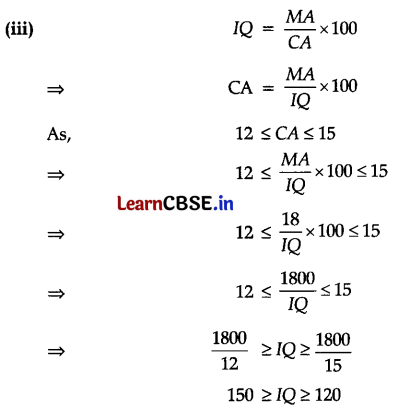
OR
Given, 8x + 6 < 10x + 14
⇒ 8x + 6 – 14 < 10x + 14 – 14 (On adding -14 both sides)
⇒ 8x – 8 < 10x
⇒ 8x – 8x – 8 < 10x – 8x (On adding -8x both sides)
⇒ -8 < 2x
⇒ -4 < x (On dividing by 2 on both sides)
⇒ x > -4
The solution set is (-4, ∞).

Question 38.
Read the following passage and answer the questions given below:
A parking lot in an IT company is triangular-shaped with two of its vertices at B(-2, 0) and C(1, 12). The third vertex A is at the midpoint of the line joining the points (1, 1) and (3, 11).

(i) Find the equation of the line that passes through the points B(-2, 0) and C(1, 12). (2)
(ii) Find the equation of the line perpendicular to the above line (line obtained in part (i)) and passing through the vertex A. (2)
Answer:
(i) Equation of line through B(-2, 0) and C(1, 12) is given by
\(\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}\)
⇒ \(\frac{y-0}{12-0}=\frac{x+2}{1+2}\)
⇒ \(\frac{y}{12}=\frac{x+2}{3}\)
⇒ 4x – y + 8 = 0

(ii) A is the midpoint of the line segment joining (1, 1) and (3, 11).
By midpoint formula, A = \(\left(\frac{1+3}{2}, \frac{1+11}{2}\right)\)
A = (2, 6)
The equation of line perpendicular to 4x – y + 8 = 0 and passing through A (2, 6) is
y – 6 = \(\frac{-1}{4}\)(x – 2)
⇒ 4y – 24 = -x + 2
⇒ x + 4y = 26