Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 8 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 8 for Practice
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions
SECTION – A
(12 Marks)
Question 1.
A ladder 30 m long, is placed against a 15 m high wall such that it just reaches the top of the wall. Find the angle of elevation of top of the wall from the foot of the ladder.
OR
A portion of 60 m long tree is broken by tornado and the top struck up the ground making an angle of 30° with the ground level. Find the height of the point from where the tree is broken. (2)
Question 2.
The arithmetic mean of the following frequency distribution is 53. Find the value of k. (2)
| Class | Frequency |
| 0-20 | 12 |
| 20-40 | 15 |
| 40-60 | 32 |
| 60-80 | k |
| 80-100 | 13 |
Question 3.
In a school project, Neha cut a sphere of maximum volume from a solid hemisphere of radius 6 cm. Find the volume of the cut-out sphere. [Use π = 3.14] (2)
Question 4.
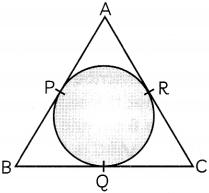
In the given figure, ΔABC is circumscribing a circle. If AP = 4 cm, PB = 3 cm and AC =11 cm, find the length of BC. (2)
Question 5.
An observer 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer. (2)
Question 6.
Given below is a cumulative frequency distribution table. Corresponding to it, make an ordinary frequency distribution table.
| Class | Cumulative Frequency |
| Less than or equal to 50 | 45 |
| Less than or equal to 40 | 40 |
| Less than or equal to 30 | 34 |
| Less than or equal to 20 | 18 |
| Less than or equal to 10 | 17 |
| Less than or equal to 0 | 0 |
OR
Determine the mode of the following distribution.
| Class Interval | Frequency |
| 40-50 | 5 |
| 50-60 | 8 |
| 60-70 | 15 |
| 70-80 | 12 |
SECTION – B
(12 Marks)
Question 7.
For what value of n are the nth terms of two A.Ps. 63, 65, 67, …. and 3, 10, 17, ….. equal? (3)
Question 8.
The pitot of an aircraft, flying horizontally at a speed of 1200 km/hr, observes the angle of depression of a point on the ground changes from 30° to 45° in 15 seconds. Find the height at which aircraft is flying. (3)
Question 9.
Draw a circle of radius 3.5 cm. From a point 6 cm from its centre, construct two tangents to the circle. (3)
Question 10.
Three-eighth of the students of a class opted for visiting an old age home. Sixteen students opted for visiting a nature walk. Square root of total number of students in the class opted for tree plantation in the school. If the number of students who opted to visit old age home is same as the number of students who opted for nature walk and tree plantation, then find the total number of students in the class.
OR
Solve for x:
\(\frac{x-1}{x-2}+\frac{x-3}{x-4}=3 \frac{1}{3}, x \neq 2,4\)
SECTION – C
(16 Marks)
Question 11.
In the given figure a, triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and CD are of lengths 6 cm and 9 cm, respectively. If the area of ΔABC is 54 cm2, find the length of sides AB and AC.
Question 12.
Water in a canal, 5.4 m wide and 1.8 m deep, is flowing with a speed of 25 km/hr. How much area can it irrigate in 30 minutes, if 10 cm of standing water is required for irrigation?
OR
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that density of the iron is 8 g/cm3. [Use π = 3.14] (3)
Question 13.
Case Study-1
A trader bought a number of articles for ₹ 900. Five articles were found damaged so he sold the each of the remaining article at ₹ 2 more than what he paid for. Fie got a profit of ₹ 80 on the whole transaction.

If x represent the total number of articles the trader bought, then answer the following:
(A) Find the number of articles bought by the trader. (2)
(B) If instead of a profit of ₹ 80, trader made a loss of ₹ 100 on the whole transaction, then find the number of articles sold by the trader. (2)
Question 14.
Case Study-2
The Tulip Public School organized a health check-up camp for their students of class X. After the check-up, a BMI report of each student was submitted to the Principal of the school. Principal of the school asked the Mathematics teacher to arrange the reports of all students in the form of a table. Thus, the following table is made which describes the weight (in Kilogram) of the students:
| Weight (in kg.) | Number of students |
| 34-38 | 4 |
| 38-42 | 6 |
| 42-46 | 10 |
| 46-50 | 14 |
| 50-54 | 10 |
| 54-58 | 8 |
| 58-62 | 6 |
| 62-66 | 2 |
(A) Find the mean weight of the students. (2)
(B) Find the median weight of the students. (2)