Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 7 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 7 for Practice
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions
SECTION – A
(12 Marks)
Question 1.
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.
OR
In the given figure, PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA. (2)
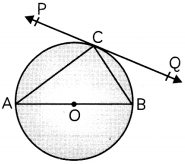
Question 2.
Find the median of the following data: (2)
| Class Interval | Frequency |
| 0-10 | 2 |
| 10-20 | 12 |
| 20-30 | 22 |
| 30-40 | 8 |
| 40-50 | 6 |
Question 3.
A solid spherical ball, of diameter 3 cm, is melted and recast into three spherical balls. If the diameters of two of the spherical balls are 2.5 cm and 2 cm, find the diameter of the third ball. (2)
Question 4.
Two towers of heights h1 and h2 subtend angles of elevation 60° and 30° respectively, at the mid-point of the line joining their feet. Find the ratio of their heights. (2)
Question 5.
To help in submission of school fees of one of their financially weak classmate, students saved pockets as shown in the following table.
| Money saved (in ?) | Number of Students |
| 20-23 | 6 |
| 23-26 | 3 |
| 26-29 | 9 |
| 29-32 | 5 |
| 32-35 | 7 |
Find the mode of this distribution. (2)
Question 6.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
OR
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. Find the distance of the car from the base of the tower. (2)
Question 7.
Draw a line segment PQ of length 4.7 cm and mark a point X on it such that
\(\mathrm{QX}=\frac{1}{3} \mathrm{PX}\). (3)
Question 8.
Solve the following quadratic equation:
9x2 – 9(a + b)x + (2a2 + 5ab + 2b2) = 0 (3)
Question 9.
The window of a house is h m above the ground. From the window, the angles of elevation and depression of the top and bottom of another house situated on the opposite side of the lane, are found to be α and β, respectively. Prove that the height of the other house is h(1 + tan α cot β). (3)
Question 10.
Find the sum of natural numbers between 101 and 999 which are divisible by both 2 and 5. (3)
OR
An A.P. consist of 21 terms. If the sum of its three terms in the middle is 129 and that of the last three terms is 237, then find its nth term.
SECTION – C
(16 Marks)
Question 11.
If mean of the following data is 14.7, find the values of p and q. (4)
| Class | Frequency |
| 0-6 | 10 |
| 6-12 | P |
| 12-18 | 4 |
| 18-24 | 7 |
| 24-30 | q |
| 30-36 | 4 |
| 36-42 | 1 |
| Total | 40 |
Question 12.
From an external point T, tangents TP and TQ are drawn to a circle with centre O. Prove that OT is the right bisector of chord PQ.
OR
In the given figure, PA and PB are tangents drawn from an external P to two concentric circles of radii 8 cm and 7 cm. If the length of tangent AP is 15 cm, find the perimeter of quadrilateral OAPB. [Use \(\sqrt{15}\) = 3.9] (4)
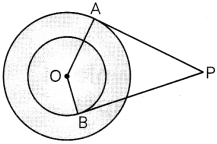
SECTION – C
(16 Marks)
Question 13.
Case Study-1
Reshu Loves writing her notes with pens of different colours. So to keep her pens in one place on her study table, she asked her dad to buy a pen stand. Her dad went to a carpenter and asked him to make a pen stand of wood in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid should be 15 cm x 10 cm x 3.5 cm and the radius of each depression should be 0.5 cm, and the depth be 1.2 cm.
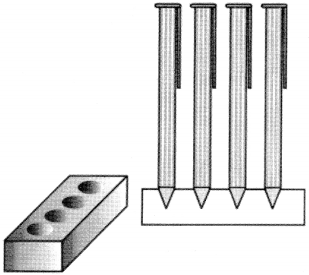
On the basis of above information, answer the following questions: [Use n = 3.14]
(A) Find the total surface area of the pen stand. (2)
(B) Find the amount of wood used in making the pen stand. (2)
Question 14.
Case Study-2
Make in India is an initiative of the Government of India which was launched in the year 2014 as a part of wider set of nation-building initiatives. The moto of this initiative is to make and encourage companies to develop, manufacture and assemble products in our own country and incentivize investments into start-ups. 16 January is now celebrated as National Startup Day.
A manufacturer of mobiles produced 6000 units in third year and 7000 units in the seventh year. Assuming that production increases uniformly by a fixed number every year, answer the following questions:

(A) Find the total production of mobiles in 15 years. (2)
(B) If the production of mobiles in k years is 43,750, then find the value of k. (2)