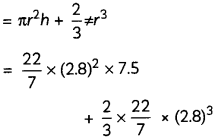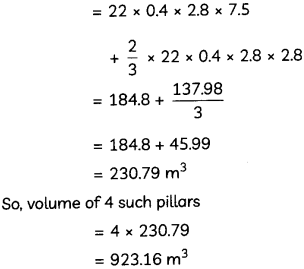Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 5 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 5 with Solutions
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
SECTION – A
(12 Marks)
Question 1.
Find the value(s) of k for which the roots are real and equal in the equation x2 – 2kx +7k – 12 = 0.
OR
If (1 – b) is a root of the equation x2 + bx + 1 – b = 0, then find the value of b. (2)
Answer:
Given equation is x2 – 2kx + 7k – 12 = 0
∴ a = 1, b = -2k, c = 7k – 12
For real and equal roots, Discriminant = 0
⇒ b2 – 4ac = 0
⇒ (-2k)2 – 4 x 1 x (7k – 12) = 0
⇒ 4k2 – 28k + 48 = 0
⇒ k2 – 7k + 12 = 0
⇒ (k – 4) (k – 3) = 0
⇒ k = 4, 3
Hence, the values of k are 3 and 4.
OR
Since, (1 – b) is a root of the equation x2 + bx + 1 – b = 0,
∴ (1 – b)2 + b(1 – b) + 1 – b = 0
⇒ (1 – b) [(1 – b) + b + 1] = 0
⇒ (1 – b) (2) = 0
⇒ b = 1
Hence, the value of b is 1.
Question 2.
Tangents PQ and PL are drawn to a circle from an external point P. Another tangent is drawn to the circle at point N such that it intersect the tangents PQ and PT at points L and M respectively. If PQ = 28 cm, then find the perimeter of ΔPLM. (2)
Answer:
We know, tangents drawn from an external point to a circle are equal in length.
∴ PQ = PT, LQ = LN, MN = MT
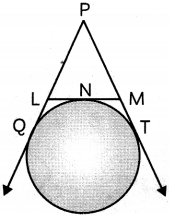
Now, perimeter of ΔPLM = PL + LM + PM
= PL + (LN + NM) + PM
= (PL+ LN) + (NM + PM)
= (PL + LQ) + (MT + PM)
[∵ LN = LQ, NM = MT]
= PQ + PT
= 2PQ [∵ PQ = PT]
= 2 x 28 [∵ PQ = 28 cm]
= 56
Hence, the perimeter of ΔPLM is 56 cm.
Question 3.
Convert the following equation into standard form of a quadratic equation.
\(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}, x \neq-4,7\) (2)
Answer:
We have,
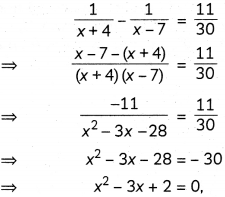
which is the required standard form of quadratic equation.
Question 4.
Reena calculated the mean of 20 observations to be 37. Later on, it was found that the data 12, 23 and 43 are wrongly entered as 21, 32 and 34 respectively. What is the correct mean? (2)
Answer:
Given: Mean of 20 observations = 37
∴ Sum of 20 observations = 37 x 20
= 740
Since, 12, 23 and 43 are wrongly entered as 21, 32, and 34 respectively
∴ Correct sum = 740 – (21 + 32 + 34) + (12 + 23 + 43)
= 731
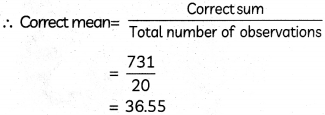
Question 5.
Write the next term of the A.P. \(\sqrt{2}, \sqrt{8}, \sqrt{18}, \sqrt{32}\) (2)
Answer:

Hence, next term of the A.P. is \(\sqrt{50}\).
Caution
Here, in the given A.P., common difference is not directly calculable so try to simplify the terms of the A.P. to find its common difference.
Question 6.
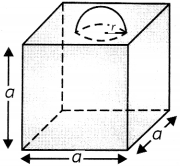
A copper sphere of radius 3 cm is beaten and drawn into a wire of length 36 m. Find the diameter of the wire.
OR
Find the total surface area of the solid, shown in the given figure. (2)
Answer:
Let the radius of the wire be r cm.
Then,
Volume of copper in the wire = Volume of copper sphere

∴ Diameter of wire = 2r
= 2 x 0.1
= 0.2 cm
OR
TSA of solid = Surface area of cube + CSA of hemisphere – Area of base of hemisphere
= 6a2 + 2πr2 – πr2
= 6a2 + πr2
SECTION – B
(12 Marks)
Question 7.
The lengths of 40 leaves of a plant are measured correct to nearest millimetre, and the data obtained is represented in the following table.
| Length (in mm) | Number of leaves |
| 118 – 126 | 3 |
| 127 – 135 | 5 |
| 136 – 144 | 9 |
| 145 – 153 | 12 |
| 154 – 162 | 5 |
| 163 – 171 | 4 |
| 172 – 180 | 2 |
Find the median length of the leaves. (3)
Answer:
Given frequency distribution is given in inclusive form. First we wilL convert this distribution into exclusive form by adding and subtracting \(\frac{h}{2}\) to upper limit and lower limit of a class, respectively, where h = upper limit of a class – lower limit of preceeding class.
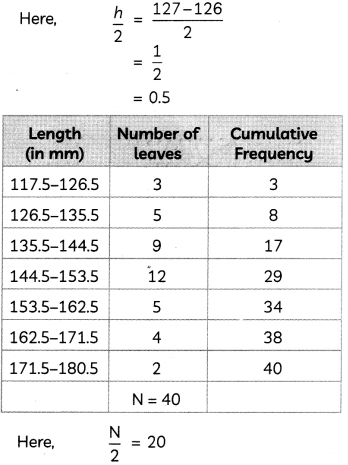
Cumulative frequency just greater than 20 is 29, which belongs to class 144.5-153.5.
∴ Median class = 144.5 – 153.5
We know,
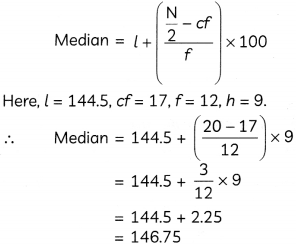
Hence, median legnth of the leaves is 146.75 mm.
Question 8.
Draw two concentric circles of radii 2 cm and 5 cm. Take a point P on the outer circle and construct a pair of tangents PA and PB to the smaller circle. (3)
Answer:
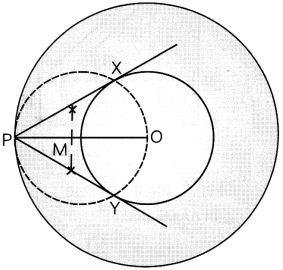
Steps of construction:
- Draw two concentric circles with centre O and radii 2 cm and 5 cm.
- Take a point P on the outer concentric circle and join OP.
- Draw perpendicular bisector of OP to get its mid-point M.
- Taking M as centre and MO = MP as radius, draw a cricle which intersects the smaller concentric circle, drawn in step (1) at points X and Y.
- Join PX and PY.
Thus, PX and PY are the required tangents to the smaller concentric circle.
Question 9.
Find the missing frequency fin the given data, if mode of the distribution is 55. (3)
| Class Interval | Frequency |
| 10-20 | 5 |
| 20-30 | 3 |
| 30-40 | 4 |
| 40-50 | 7 |
| 50-60 | 13 |
| 60-70 | f |
| 70-80 | 2 |
Answer:
Given: Mode = 55
∴ Modal class = 50 – 60
We know,
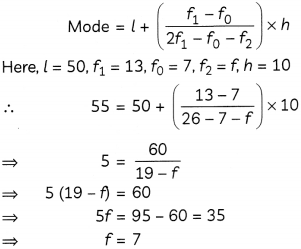
Hence, the value of f is 7.
Concept Applied
Mode always lie within the modal class.
Question 10.
The length of a string between a kite and a point on the roof of a building 10 m high, is 180 m. If the string makes an angle 0 with the horizontal level, such that tan \(\theta=\frac{4}{3}\), how high is the kite from the ground?
OR
From the top of a hill, the angles of depression of two consecutive kilometre stones due East are found to be 30° and 45°. Find the height of the hill.
[Use \(\sqrt{3}\) = 1.73] (3)
Answer:
Let AB be the building K be the position of kite ¡n the sky and KM be its vertical height.
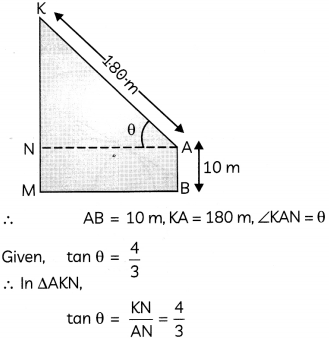
So, let KN = 4x and AN = 3x
Applying Pythagoras theorem in ΔAKN, we have
(AK)2 = (KN)2 + (AN)2
⇒ (180)2 = (4x)2 + (3x)2
⇒ 32400 = 25x2
⇒ \(x^{2}=\frac{32400}{25}\)
⇒ x = \(\sqrt{324 \times 4}\)
= \(\sqrt{(18)^{2} \times(2)^{2}}\)
= 18 x 2
= 36
So, KN = 4x = 4 x 36 = 144 m
∴ Vertical height of kite
= KM = KN + NM
= KN + AB [∵ NM = AB]
= 144 + 10
= 154 m
Concept Applied
In a right-angled triangle,
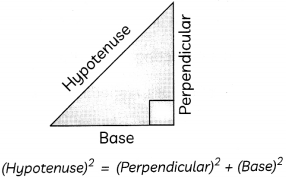
OR
Let AB be the hill and, C and D be the two consecutive kilometre stones.
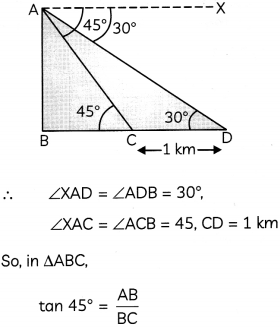
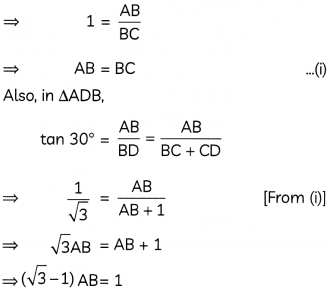
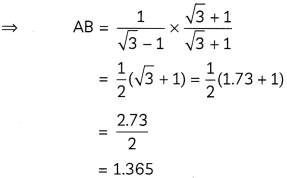
Hence, height of the hill is 1.365 km.
Caution
If the value of \(\sqrt{3}\) is specified in the question, then do not leave your final answer in term of \(\sqrt{3}\) In such a case, marks can be deducted.
SECTION – C
(16 Marks)
Question 11.
If the angle of elevation of a cloud from a point 10 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud from the surface of lake. (4)
Answer:
Let A be the point of observation, C be the position of cloud in the sky and C’ be its reflection in the lake BP.
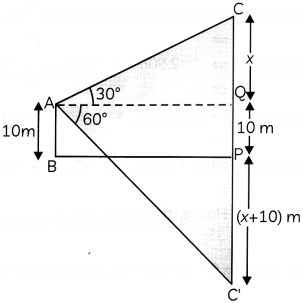
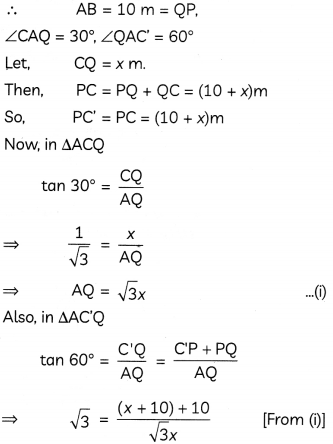
⇒ 3x = x + 20
⇒ 2x = 20
⇒ x = 10
So, height of cloud from the surface of Lake
= CP = CQ + PQ
= x + 10 = 10 + 10
= 20 m
Concept Applied
Here, surface of take acts as a mirror, and distance of an object from the mirror is equal to the distance of its image in the mirror.
So, PC = PC’
Question 12.
Prove that the parallelogram circumscribing a circle is a rhombus.
OR
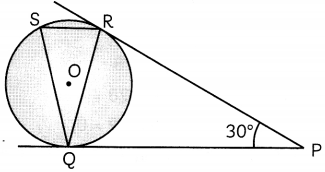
In the given figure, tangents PQ and PR are drawn to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS. (4)
Answer:
Given: A parallelogram ABCD, which is circumscribing a circle such that the sides AB, BC, CD and AD touches the circle at points P, Q, R and S respectively.
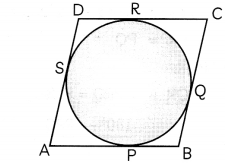
To prove: ABCD is a rhombus.
Proof: Tangents drawn from an external point to a circle are equal in Length.
∴ AP = AS
BP = BQ
CR = CQ and
DR = DS
Adding the above equations, we get
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
⇒ 2AB = 2AD
[∵ Opposite sides of parallelogram are equal]
⇒ AB = AD
i.e. adjacent sides of parallelogram ABCD are equal.
∴ ABCD is a rhombus.
Hence, proved.
OR
We have
∠RPQ = 30°
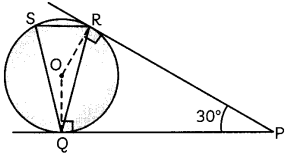
Join OR and OQ.
Then, in quadrilateral ORPQ
∠ORP = ∠OQP = 90°
[∵ Tangent ⊥ Radius]
and ∠RPQ = 30°
∴ ∠ROQ = 360° – ∠RPQ – ∠ORP – ∠OQP
= 360° – 30° – 90° – 90°
= 150°
Also, ∠ROQ = 2∠RSQ
⇒ ∠RSQ = \(\frac{1}{2}\) ∠ROQ = \(\frac{1}{2}\) x 150° = 75°
We know, tangents drawn from an external point to a circle are equal in length.

Question 13.
Case Study-1
Vikram gets pocket money from his father every day. Out of the pocket money, he saves money for poor people in his locality. On first day, he saves? 27.50, and on each succeeding day, he increases his savings by ₹ 2.50.

Based on the above information, answer the following questions:
(A) Check whether savings done by Vikram every day forms an A.P. or not. If yes, then find the 10th and nth terms of the A.P. (2)
(B) Suppose Vikram saved a total amount of? 2450. In how many days, will this amount be saved by him? (2)
Answer:
(A) Since, savings done by Vikram each successive day, increases uniformly by a fixed amount, so his savings form an A.P. with a = ₹ 27.50 and d = ₹ 2.50.
Now, 10th term = a10
= a + 9d
= 27.50 + 9 x 2.50
= 50
and, nth term = an
= a + (n – 1)d
= 27.50 + (n – 1) x 2.50
= 2.5 n + 25
(B) Let Vikram saved the amount of ₹ 2450 in n days.
∴ Sn = 2450
⇒ \(\frac{n}{2}\) [2a + (n – 1)d] = 2450
⇒ \(\frac{n}{2}\) [2 x 27.50 + (n- 1) x 2.50] = 2450
⇒ n (52.50 + 2.50n) = 4900
⇒ 2.50n2 + 52.50n – 4900 = 0
or, n2 + 21n – 1960 = 0
⇒ (n + 56) (n – 35) = 0
⇒ n =-56, 35
Since, number of days cannot be negative
∴ n = 35
Hence, the required number of days is 35.
Question 14.
Case Study-2
A school trip was organised for the students of class X to one of the seven wonders of the world, ‘Taj Mahal’. Teacher told them about the history of Taj Mahal. He also asked them to observe some solid figures in the monument. One student said, there are four pillars, that are cylindrical in shape. Other student said, there is a big dome in the centre and two smaller domes on both sides of the big dome. Also, the domes are hemispherical in shape. Teacher said there are domes on the top of pillars too.

On the basis of this information, answer the following questions: \(\left[\text { Use } \pi=\frac{22}{7}\right]\)
(A) Find the volume of the four pillars with hemispherical tops, if the height of cylindrical part is 7.5 m and radii of cylindrical base and hemispherical dome is 2.8 m each. (2)
(B) Find the volume of the four pilars with hemispherical tops, if the height of cylndrical part is 7.5 m and radii of cylindrical base and hemispherical dome is 2.8 m each. (2)
Answer:
(A) Radius of bigger dome (R) = \(\frac{7}{2}\)m
∴ CSA of bigger dome (A1) = 2πR2 ………………………………. (i)
Radius of each of smaller dome (r)
= \(\frac{3.5}{2}\)m
∴ CSA of two smaller domes (A2)
= 2πr2 + 2πr2
= 4πr2 ………………………………. (ii)
Now, ratio of CSAs of bigger dome and two smaller domes
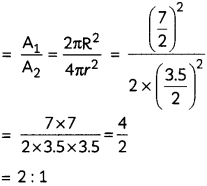
(B) Given:
Radius (r) = 2.8 m and height of cylindrical part (h) = 7.5 m
∴ Volume of each pillar = Volume of cylindrical part + Volume of hemispherical dome