CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 4 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.
2. All questions are compulsory.
3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
4. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
5. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

SECTION – A
(12 Marks)

Question 1.
Which term of the A.P. 3, 15, 27, 39, …. will be 132 more than its 54^th term?
OR
Find the 15^th term from the end of the A.P. 3, 8,13 253. (2)
Answer:
Given A.P. is 3,15, 27, 39…….
Here, a = 3, d = 15 – 3 = 12
Let n^th term be the required term of the A.P.
∴ a_n = 132 + 054
⇒ a + (n – 1)d = 132 + 0 +53d
⇒ (n – 1)12 = 132 + 53 x 12 = 768
⇒ \(n-1=\frac{768}{12}=64\)
⇒ n = 65
Hence, 65^th term is the required term of the A.P.
OR
Given A.P. is 3, 8,13, 253.
Now,
15^th term from the end of the A.P. 3,8,13,… 253 = 15^th term from the
beginning of the A.P. 253, 248 13, 8, 3.
For the A.P. 253, 248 13, 8,3
a = 253, d = 248-253 = -5
∴ 15th term, a₁₅ = a + 14d
= 253 + 14 x (-5)
= 253 – 70
= 183
Hence, the required term is 183.

Related Theory
Alternatively, n^th term from the end of an A.P. is given as a_n = 1 – (n – 1) d
where, 1 is the last term and d is the common difference of the A.P.

Question 2.
The volume of a right circular cylinder with its height equal to the radius, is 25\(\frac{1}{7}\)cm³. Find the height of the cylinder. (2)
Answer:
Given: Radius of cylinder (r)
= Height of cylinder (h)
Also,
Volume of cylinder = 25\(\frac{1}{7}\)cm³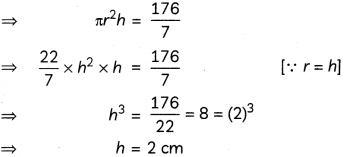
Hence, height of the cylinder is 2 cm.

Question 3.
Mrs. Bansal recorded the marks obtained by her students in the subject of mathematics, in the form of the following table. (3)

Marks obtained	0 – 20	20 – 40	40 – 60	60 – 80	80 – 100
Number of  students	3	10	25	7	5

Answer:

Class	Cumulative Frequency
Less than 20	3
Less than 40	3 + 10 = 13
Less than 60	3 + 10 + 25 = 38
Less than 80	3 + 10 + 25 + 7 = 45
Less than 100	3 + 10 + 25 + 7 + 5 = 50

Question 4.
Find the nature of roots of the quadratic equation 4x² – 12x + 9 = 0. (2)
Answer:
Given equation is 4x² – 12x + 9 = 0
∴ o = 4, b = -12, c = 9
We know,
Discriminant = b² – 4ac
= (-12)² – 4 x 4 x 9
= 144 – 144
= 0
Hence, the nature of roots is real and equal.

Question 5.
Draw a line segment AB of length 7.6 cm and divide it in the ratio 5:8. (2)
Answer:

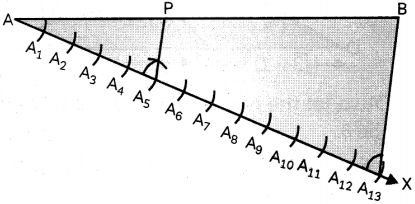
Steps of construction:

• Draw a Line segment AB of length 7.6 cm.
• From point A, draw a ray AX such that ∠BAX in acute.
• Mark (5 + 8) i.e. 13 points, namely, A₁, A₂, A₃ A₁₂, A₁₃ on AX at equaL distances.
• Join A₁₃B.
• From point A₅, draw a Line A₅P, parallel to A₁₃B, intersecting line segment AB at point P.

Thus, P is the required point which divides AB in the ratio 5:8.

Question 6.
Find the roots of the quadratic equation \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0.
OR
If α and β are the roots of the equation 2x² – 11x + 5 = 0, then find the value of (2α + 1) (3β + 4). (2)
Answer:
We have,
⇒ \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0
⇒ \(\sqrt{2}\)x² + 2x + 5x + 5\(\sqrt{2}\) = 0
⇒ \(\sqrt{2}\)x (x + \(\sqrt{2}\)) + 5 (x + \(\sqrt{2}\)) = 0
⇒ (\(\sqrt{2}\)x + 5) (x + \(\sqrt{2}\)) = 0
⇒ \(x=-\frac{5}{\sqrt{2}},-\sqrt{2}\)
Flence, the roots of the given quadratic equation are \(-\frac{5}{\sqrt{2}}\) and –\(\sqrt{2}\).
OR
We have,
2x² – 11x + 5 = 0
⇒ 2x² – 10x – x + 5 = 0
⇒ 2x(x – 5) – 1(x – 5) = 0
⇒ (2x – 1) (x – 5) = 0
⇒ x = \(\frac{1}{2}\), 5
α = \(\frac{1}{2}\), β = 5
Now, (2α + 1) (3β + 4) = (2 × \(\frac{1}{2}\) + 1) (3 × 5 + 4)
= 2 × 19
= 38

SECTION – B
(12 Marks)

Question 7.
Calculate the mode of the following data:

Marks obtained	0-20	20-40	40-60	60-80	80-100
Number of students	5	9	12	6	3

Answer:
Here, maximum frequency = 12
And, class with maximum frequency is 40 – 60.
∴ Modal class = 40 – 60

We know,

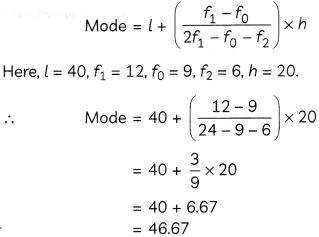
Hence, mode of the data is 46.67.

Question 8.
The length of shadow of a person is x m long when the angle of elevation of the Sun is 45°. If the length of the shadow increases by (\(\sqrt{3}\) – 1)m, then find the new angle of elevation of the Sun. (3)
Answer:
Let AB be the person, BC be its shadow when angle of elevation of Sun is 45° and BD be its longer shadow.

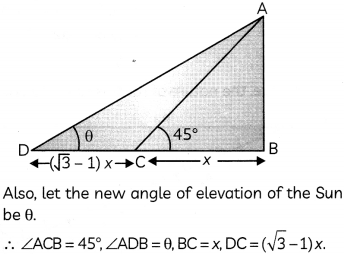
Now, in ΔABC

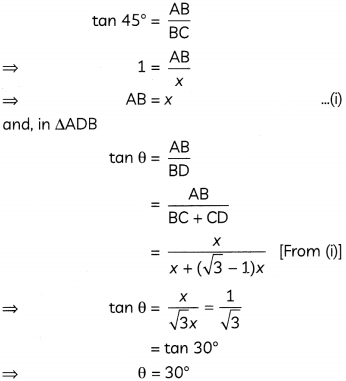
Hence, the new angLe of elevation of the Sun is 30°.

Question 9.
Prove that the lengths of tangents drawn from an external point to a circle are equal. (3)
Answer:
Given: A circle with centre O at which tangents TP and TQ are drawn from an external point T.

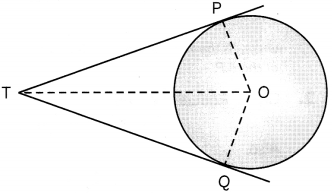
To prove: TP = TQ
Construction: Join OP, OQ and OT.
Proof: We know, tangent is perpendicular to radius at the point of contact.
TP ⊥ OP and TQ ⊥ OQ
⇒ ∠OPT = 90°, ∠OQT = 90°
Now, in ΔOPT and AOQT
∠OPT = ∠OQT = 90° [Proved above]
OT = OT [Common side]
OP = OQ [Radii]
∴ ΔOPT ≅ ΔOQT [RHS congrency rule]
∴ PT = QT [c.p.c.t.] Hence, proved.

Question 10.
The marks obtained by 110 students in examination are given below: (3)
Answer:

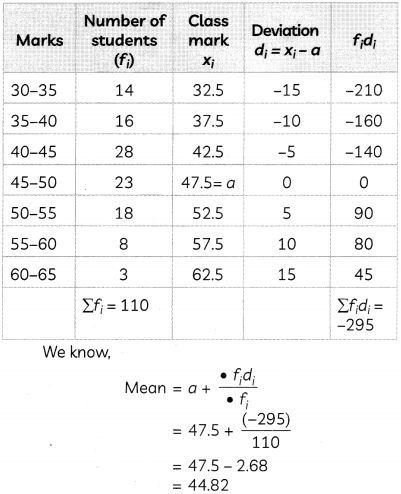
Hence, mean marks of the students is 44.82.

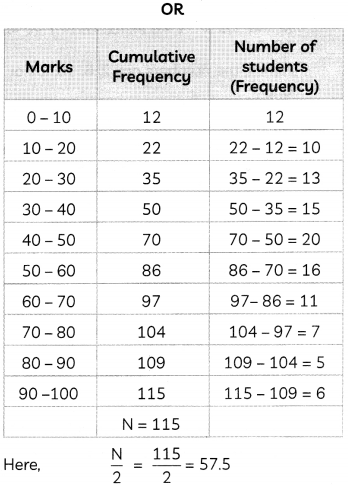
Cumulative frequency just greater than 57.5 is 70, which belongs to class 40-50.
∴ Median class = 40 – 50

We know,

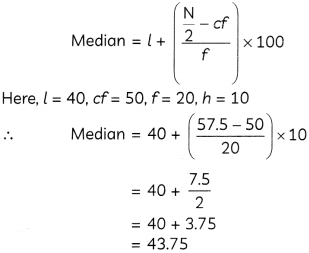
Hence, the median of given frequency distribution is 43.75.

SECTION – C
(16 Marks)

Question 11.

Marks	Number of students
30-35	14
35-40	16
40-45	28
45-50	23
50-55	18
55-60	8
60-65	3

Find the mean marks of the students.
OR
Find the median of the following frequency distribution.

Marks	Number of students
Below 10	12
Below 20	22
Below 30	35
Below 40	50
Below 50	70
Below 60	86
Below 70	97
Below 80	104
Below 90	109
Below 100	115

Answer:
Let the four consecutive terms in A.P. be (a – 3d), (a – d), (a +„d) and (a + 3d).
∴ (a – 3d) + (a – d) + (a + d) + (a + 3d) = 32
⇒ 4a = 32
⇒ a = 8
Also,


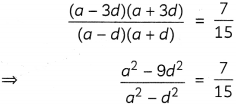
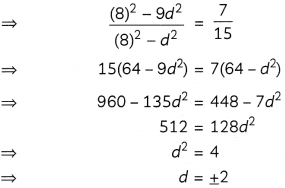
For a = 8 and d = 2, the numbers are [8 – 3(2)], (8 – 2), (8 + 2), [8 + 3(2)] i.e. 2, 6, 10, 14..

And, for a = 8 and d = -2, the numbers are [8 – 3(-2)], [8 – (-2)], [8 + (-2)], [8 + 3(-2)] i.e. 14, 10, 6, 2.

Hence, the numbers are 2, 6, 10, 14 or 14, 10, 6, 2.

Question 12.
The sum of four consecutive numbers in A.P. is 32 and the ratio of the product of the first and last terms to the product of two middle terms is 7:15. Find the numbers. (4)
Answer:
Let the radius of other sphere be r.

Since, the two given spheres are of same metaL, so their densities must be same.

Now, let the volume of new sphere be R.

Then, volume of new sphere = volume of two spheres

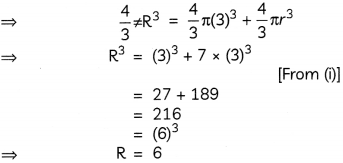
Hence, the radius of the new sphere is 6 cm.

Concept Applied

Density = \(\frac{\text { Mass }}{\text { Volume }}\) remains same in all shapes and sizes.
OR
Let the number of bricks used to construct the wall be n.

Since, \(\frac{1}{8}\)th of space of wall is covered by mortar.

∴ Remaining space, i.e. 1 – \(\frac{1}{8}\) = \(\frac{7^{\text {th }}}{8}\) of space of wall is occupied by the bricks.

So, n × volume of a brick = \(\frac{7}{8}\) × volume of the wall
⇒ n × 22.5 × 11.25 x 8.75 = \(\frac{7}{8}\) × (270 × 300 × 350)
⇒ \(n=\frac{7 \times 270 \times 300 \times 350}{8 \times 22.5 \times 11.25 \times 8.75}\)
= 11200
Hence, the required number of bricks is 11,200.

Question 13.
Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single bigger sphere. Find the radius of the new sphere.
OR
A mason construct a wall of dimensions 270 cm x 300 cm x 350 cm with bricks, each of size 22.5 cm x 11.25 cm x 8.75 cm. If it is assumed that one-eighth of the space is covered by mortar, then find the total number of bricks used to construct the wall. (4)
Answer:

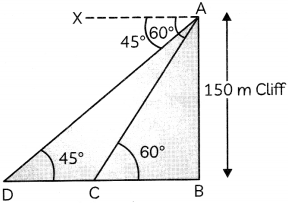
Here, AB is the cliff and, CandDarethe two positions of the boat, moving away from the cliff.

Now, in ΔABC,

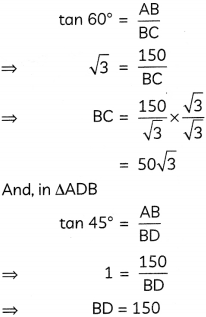
Now, distance travelled by the boat during the period of observation
= CD
= BD – BC
= 150 – 50\(\sqrt{3}\)
= 150 – 50 x 1.73
= 150 – 86.5
= 63.5 m

(B) We have, time taken by the boat to cover the distance CD i.e. 63.5 m is 1 min, or, 60 seconds.

Hence, speed of the boat is 1.06 m/sec.

Question 14.
Case study-1
In geology, a cliff is a part of huge rock, which is generally vertical. They are formed by the processes of weathering and erosion with the effect of gravity.

A moving boat is observed from the top of a 150 m high cliff, moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in one minute.

Based on this answer the following questions:

(A) Make a labelled figure on the basis of given information and find the distance travelled by the boat during the period of observation. [Use \(\sqrt{3}\) = 1.73]. (2)

(B) Find the speed of the boat. (2)
Answer:
(A) Given: ∠APB = 50°
We know, tangent is perpendicular to radius at the point of contact.
∴ AP ⊥ OA, BP ⊥ OB
∴ ∠OAP = 90°, ∠OBP = 90°
So, in quadrilateral OAPB,
∠AOB = 360° – ∠OAP
∠APB – ∠OBP
= 360° – 90° – 50° – 90°
= 130°

(B) In ΔOAP,

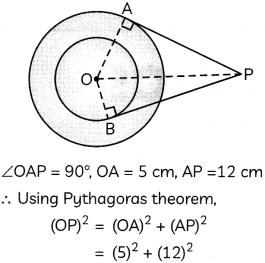
= 169
⇒ OP = 13 cm
Similarly, in ΔOBP,
∠OBP = 90°, OB = 3 cm, OP = 13 cm
∴ (PB)² = (OP)² – (OB)²
= (13)² – (3)² = 169 – 9
= 160
⇒ PB = 4\(\sqrt{10}\)cm

Now,
Area of quadrilateral OAPB
= ar(ΔPOA) + ar(ΔPOB)

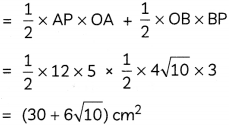
Question 15.
Case study-2
Reshma took one bangle of her mother and one of her size, and put the smaller one within the gap of the bigger one to form two concentric circles. She then took two straws and put them on the bangles as shown in the figure.

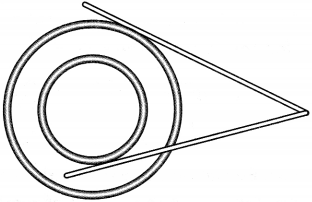
Let O be the centre of the two concentric circles, P be the point from where straws PA and PB are drawn to these circles.

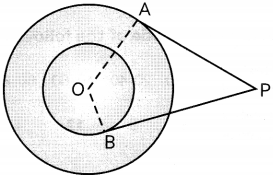
If OA = 5 cm, OB = 3 cm and AP = 12 cm, then answer the following questions,

(A) If the angle made between the two straws is 50°, find the angle made between the radii of the two bangles i.e. ∠AOB. (2)

(B) Find the area of the quadrilateral formed by the two straws and the radii of two bangle, Le. area of quadrilateral OAPB. (2)
Answer: