CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 3 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.
2. All questions are compulsory.
3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
4. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
5. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions

SECTION – A
(12 Marks)

Question 1.
Neil has a toy in the shape of a right circular cone whose height and radius are in the ratio 12 : 5. If its volume is 2512 cm³, find the radius of the cone. [ Use π = 3.14]
OR
Find the volume of a cube, whose surface area is 150 cm². (2)
Answer:
Given: Height: Radius =12:5
So, Let height and radius of the cone be 12x and 5x respectively.
Also,
Volume of cone = 2512 cm³ [Given]

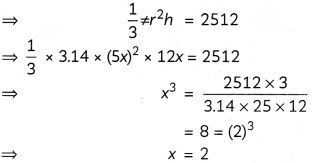
∴ Radius = 5x = 5 x 2 = 10
Hence, radius of the right circular cone is 10 cm.

Concept Applied

If two quantities are given in a particular ratio, then their actual values will be the multiple of values given in the ratio.
OR

Let edge of the cube be a cm.
Given:
Surface area of cube = 150 cm²
⇒ 6a² = 150
⇒ a³ = 25
⇒ a = 5
So,
Volume of cube = a³
= (5)³ = 125 cm³

Question 2.
If the mean of the following distribution is 6, then find the value of p.
Answer:

xi	fi	fixi
2	3	6
4	2	8
6	3	18
10	P	10p
12	2	24
	Σfi = 10 + p	Σfixi = 10p + 56

We know,

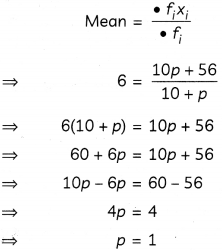
Hence, the value of p is 1.

Question 3.
A cone, hemisphere and a cylinder stand on equal bases and have the same height. Find the ratio of their volumes. (2)
Answer:
Let the equal radii of the cone, hemisphere and the cylinder be r and their equal heights be h.

Now,
Volume of cone : Volume ofhemisphere : Volume of cylinder

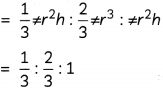
[For hemisphere, radius = height]
= 1 : 2 : 3
Hence, the ratio of volumes of cone, hemisphere and the cylinder is 1 : 2 : 3.

A Caution
The height of a hemisphere is equal to its radius, so in the given question, r = h.

Question 4.
In the given figure, find the radius of the circle.
Answer:
We know, tangent is perpendicular to radius at the point of contact.
∴ ∠OPT = 90°
∴ ΔPOT is a right-angled triangle.
∴ Applying Pythagoras theorem in ΔPOT, we have
(OT)² = (OP)² + (PT)²
⇒ (x + 2)² = (x – 6)² + (x + 1)²
⇒ x² + 4x + 4 = 2x² – 10x + 37
⇒ x² – 14x + 33 = 0
⇒ (x – 11) (x – 3) = 0
⇒ x = 11, 3

But x ≠ 3, as in this case, (x – 6) will be negative, which is not possible.
∴ x = 11
∴ Radius of circle = OP = x – 6
= 11 – 6
= 5 cm

Question 5.
If the diameter of a garden roller, 2 m long, is 1.4 m, then how much area will it cover in 7 revolutions? (2)
Answer:
Area covered by roller in one revolution
= CSA of roller
= πr²h
[∵ Garden roller is cylindrical in shape]
\(=\frac{22}{7} \times\left(\frac{1.4}{2}\right)^{2} \times 2\)
= 22 x 0.1 x 0.7 x 2
= 3.08 m²
∴ Area covered in 7 revolutions
= 7 x Area covered in one revolution
= 7 x 3.08
= 21.56 m²

Question 6.
The following table shows sale of shoes in a store during a month.
Find the modal size of the shoes sold.
OR
If mean and mode of a certain distribution are 10.5 and 7.8 respectively, find their median. (2)
Answer:
Here, maximum frequency = 25
And, observation with maximum frequency is 5.
∵ Mode is observation with maximum frequency,
∴ Modal size of the shoes sold is 5.

Concept Applied
In a given set of data, an observation which occurs maximum number of times, is its mode.
OR
Given: Mean = 10.5, Mode = 7.8
We know, Mode = 3 Median – 2 Mean
⇒ 7.8 = 3 Median – 2 x 10.5
⇒ Median \(\frac{7.8+21}{3}\)
\(=\frac{28.8}{3}\)
= 936
Hence, median of the distribution is 9.6.

SECTION – B
(12 Marks)

Question 7.
If S_n, the sum of first n terms of an A.P. is given by S_n = 5n² + 3n, then find the A.P. (3)
Answer:
We have, S_n = 5n² + 3n
For n = 1, S₁ = 5(1)² + 3(1) = 8
For n = 2, S₂ = 5 (2)² + 3(2) = 26
Now, a = S₁ = 8
and, S₂ = a₁ + a₂
⇒ 26 = 8 + a₂
⇒ a₂ = 18
⇒ a + d = 18
⇒ 8 + d = 18
⇒ d = 10
∴ a = 8 and d = 10
So, the A.P. is 8, 18, 28, 38, …..

Related Theory
Alternczriveiy a_n = S_n – S(n -1)
Using this formuLa, we cari find the terms of the AP.

Question 8.
Draw a line segment AB of length 7 cm. Talcing A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each other from the centre of other circle. (3)
Answer:

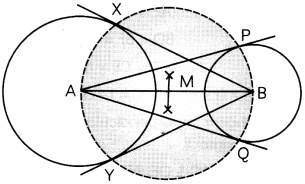
Steps of construction:

1. Draw a line segment AB of length 7 cm.
2. Taking A and B as centres, draw two circles of radii 3 cm and 2 cm respectively.
3. Draw perpendicular bisector of AB to get its mid-point M.
4. Taking M as centre and MA = MB as radius, draw a circle intersecting the circle with centre A at points X and Y, and the circle with centre B at points P and Q.
5. Join AP, A, BX and BY.
   Thus, AP and AQ are the required tangents to the circle with centre B and, BX and BY are the required tangents to the circle with centre A.

Question 9.
A window in the building is at a height of 10 m from the gound. The angle of depression of o point P on the ground from the window is 30°. If the angLe of eLevation of the top of the buiLding from the point P Is 60°, find the height of the buiLding. (3)
Answer:
Let AB be the building and W be the position of window in the building.

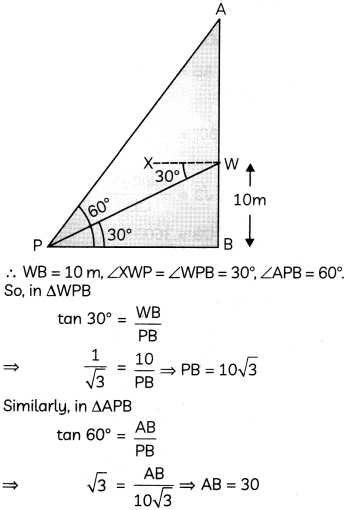
Hence, height of the building is 30 m.

Question 10.
If the equation (1 + m²) x² + 2mcx + c² – a² = 0 has equal roots, then show that c² = a²(1 + m²).
OR
The sum of a number and its positive square root is \(\frac{6}{25}\). Find the number. (3)
Answer:
Given equation is
(1 + m²) x² + 2mcx + c² – a² = 0
∴ A = 1 + m² B = 2mc, C = c² – a²
Since, the equation has equal roots
Discriminant = 0
⇒ B² – 4AC = 0
⇒ (2mc)² – 4 x (1 + m²) (c² – a²) = 0
⇒ 4m²c² – (4c² – 4a² + 4m²c² – 4m²a²) = 0
⇒ 4a² – 4c² + 4a²m² = 0
⇒ a² – c² + a²m² = 0
⇒ a² + a²m² = c^2
⇒ a²(l + m²) = c²
Hence, proved,
OR
Let the required number be x.
Then according to the question.

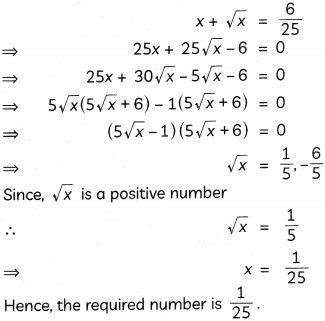
SECTION – C
(16 Marks)

Question 11.
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds, the angle of elevation changes to 30°. If the plane is flying at a constant height of 3600\(\sqrt{3}\)m, find the speed of the aeroplane. (4)
Answer:
Let 0 be the point of observation on the ground, A be the inital position of the aeroplane and A’ be its position after 30 seconds.

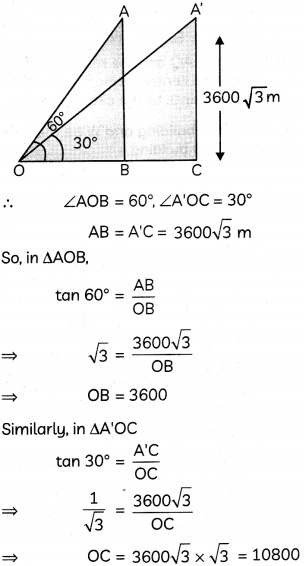
Now, horizontal distance covered by plane during the flight of 30 seconds
= AA’ = BC = OC – OB
= 10800 – 3600
= 7200

We know,
Speed = \(\frac{\text { Distance }}{\text { Time }}=\frac{7200}{30}=240\)
Hence, speed of the plane is 720 m/sec.

Question 12.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and CD, into which BC is divided by the point of contact D, are of lengths 8 cm and 6 cm, respectively. Find the length of sides AB and AC.
OR
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end-points of the arc. (4)
Answer:
Let O be the centre of incircle.
Join OC, OE, OA, OF and OB.
We know, tangents drawn from an external point to a circle are equal in length.

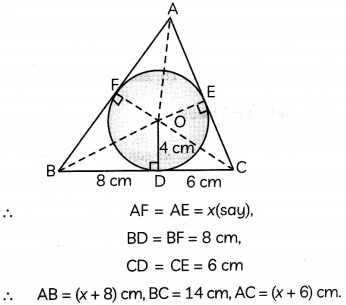
Also, tangent is perpendicular to radius at the point of contact.
∴ BC ⊥ OD, AC ⊥ OE, AB ⊥ OF.
So, in ΔABC,

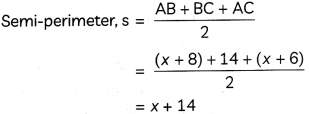
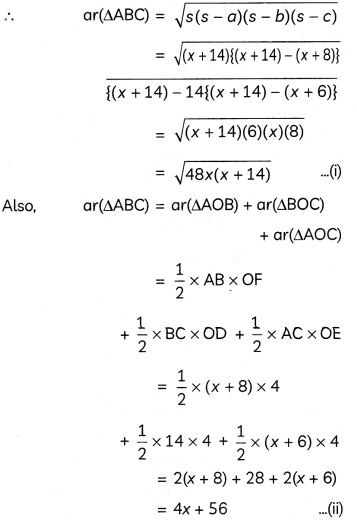
From (i) and (ii), we have,

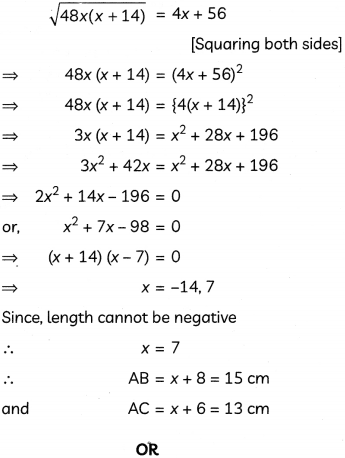
Given: A circle with centre O in which a tangent PQ is drawn at the mid-pointT of a minor arc ATB.

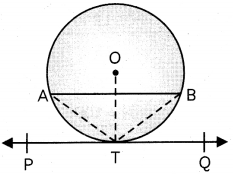
To prove: AB|| PQ
Construction: Join OT, AT and BT.
Proof: Since, T is the mid-point of arc ATB
∴ arc AT = arc BT
or AT = BT
[Equal arcs makes equal chords]
∴ ΔATB is isosceles.

So, perpendicular bisector of side AB of isosceles triangle ATB passes through point T. ALso, perpendicular bisector of chord AB passes through the centre O.

∴ Perpendicular bisector of AB passes through points O as well as T.

∴ AB ⊥ OT ….(i)

We know that, tangent is perpendicular to radius at the point of contact.

∴ PQ ⊥ OT ….(ii)

From (i) and (ii), chord AB and tangent PQ are perpendicular to the same line OT.

∴ AB || PQ

Hence, proved

Question 13.
Case Study-1
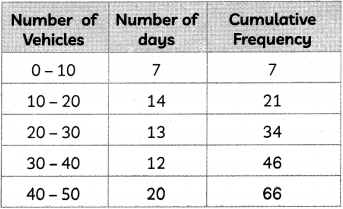
A data was recorded regarding the number of four wheeiers passing through a particular road in 5 minutes for 100 days. Recorded data is tabulated below:

Number of Vehicles	Number of Days
0-10	7
10-20	14
20-30	13
30-40	12
40-50	20
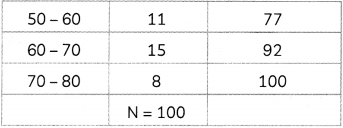
50-60	11
60-70	15
70-80	8

On the basis of above data, answer the following questions.

(A) Later on, it was found that the data for 20-30 vehicles and 60-80 vehicles was written on approximate basis. Find the class marks of 20-40 and 60-80.

(B) Find the median number of vehicles that passes through the road.
Answer:
Case Study-1

(A) We know,

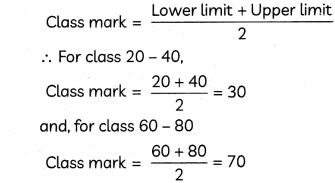
(B)


Cumulative frequency just greater than 50 is 66, which belongs to class 40 – 50.
Median class = 40-50

We know,

Hence, median number of vehicles that passes through the road is 42.

Question 14.
Case Study-2
A passenger while boarding a plane slipped from the stairs and got hurt. The pilot took the passenger to the emergency clinic at the airport for treatment. Due to this, plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/h than the usual speed.

On the basis of above information answer the following questions:

(A) It x represent the usual speed of the plane, then find the quadratic equation in x, formed in this case. (2)

(B) Find the increased speed of the plane. (2)
Answer:
Case Study-2

(A) We have,
Usual speed of plane = x km/hr
Since, speed of plane was increased by 250 km/hr,
So, increased speed of plane = (x + 250) km/hr

Now, we know,
\(\text { Time }=\frac{\text { Distance }}{\text { Speed }}\)

So, time taken to cover 1500 km with usual speed = \(\frac{1500}{x} \mathrm{hr}\) and, time taken to cover 1500 km with increased speed = \(\frac{1500}{x+250} \mathrm{hr}\)

According to the question,

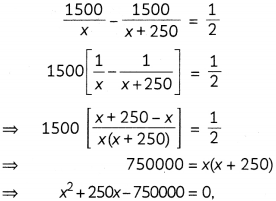
which is the required quadratic equation.

(B) Since, the quadratic equation is x² + 250x – 750000 = 0
⇒ (x + 1000) (x – 750) = 0
⇒ x = -1000,750
Since, speed cannot be negative
∴ x = 750
∴ x + 250 = 750 + 250
= 1000
So, the increased speed of the plane is 1000 km/h.