Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 1 with Solutions
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions
Section – A
Question 1.
Find the value of a25 – a15 for the AP: 6, 9, 12, 15, ………………………..
OR
If 7 times the seventh term of the AP is equal to 5 times the fifth term, then find the value of its 12th term. (2)
Answer:
a = 6, d = 3 ;
a25 = 6 + 24(3) = 78
a15 = 6 + 14(3) = 48 ;
a25 – a15 = 78 – 48 = 30
Given A.P. is 6, 9, 12, 15 …..
a = 6, d = 9 – 6 = 3
Now, a25 – a15 = (a + 24d) – (a + 14d)
= 10d
= 10 x 3 = 30
OR
7(a + 6d) = 5 (a + 4 d)
⇒ 2a+ 22=0
⇒ a + lid = 0
⇒ t12 = 0
Let a and d be the first term and the common difference of the A.P., respectively.
Now, 7 a7 = 5a5
7(a + 6d) = 5 (a + 4 d)
7a + 42d = 5a + 20d
2a = -22d
a = -11d ………………………………… (i)
a12 = o + 11d
= -11d + 11d [From (i)]
= 0
Hence, the 12th term of the A.P. is zero.
Question 2.
Find the value of m so that the quadratic equation mx (5x – 6) + 9 = 0 has two equal roots. (2)
Answer:
5mx2 – 6mx + 9=0
b2 – 4ac = 0
⇒ (-6m)2 – 4(5m)(9) = 0
⇒ 36m(m – 5) = 0
⇒ m = 0, 5 ;
Rejecting m = 0
we get m = 5
Given quadratic equation is:
mx (5x – 6) + 9 =0
⇒ 5 mx2 – 6 mx + 9 = 0
Since, the equation has equal roots,
∴ Discriminant = 0
⇒ b2 – 4ac = 0
Here, a = 5m, b = -6m, c = 9
∴ (- 6m)2 – 4 x 5m x 9 = 0
⇒ 36m2 – 180m = 0
⇒ 36m(m – 5) = 0
⇒ m = 0, 5
But, m ≠ 0, as it does not satisfy the given equation.
∴ m = 5
Hence, the value of m is 5.
► Caution
The standard form of a quadratic equation is ax2 + bx + c = 0, a ≠ 0.
Question 3.
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB? (2)
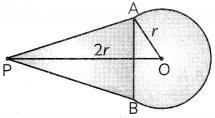
Answer:
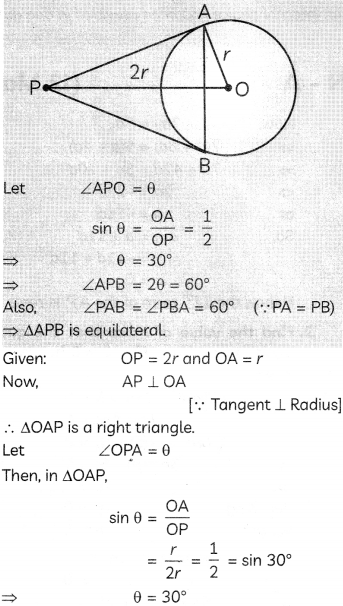
Since, tangents are equally inclined to the line, joining the centre of the circle to their common external point.

Also, in ΔAPB,
AP = PB [∵ Tangents drawn from an external point are equal]
⇒ ∠ABP = ∠PAB = x° (say)
[Equal angles opposite to equal sides]
∴ ΔAPB is an equilateral triangle.
Question 4.
The curved surface area of a right circular cone is 12320 cm2. If the radius of its base is 56 cm, then find its height. (2)
Answer:
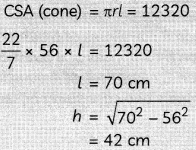
Given:
CSA of cone = 1232 cm2 and radius (r) = 56 cm Let height of the cone be h cm.
We know,

Hence, height of the cone is 42 cm.
Question 5.
Mrs. Garg recorded the marks obtained by her students in the following table. She calculated the modal marks of the students of the class as 45. While printing the data, a blank was left. Find the missing frequency in the table given below. (2)
| Marks Obtained | Number of Students |
| 0-20 | 5 |
| 20-40 | 10 |
| 40-60 | … |
| 60-80 | 6 |
| 80-100 | 3 |
Answer:
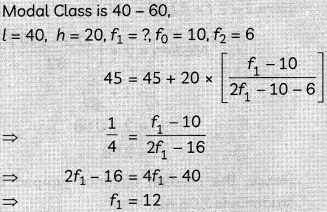
Given: Modal marks = 45
∴ Modal class = 40 – 60
Let the missing frequency be x.

Hence, the value of missing frequency is 12.
Question 6.
If Ritu were younger by 5 years than what she really is, then the square of her age would have been 11 more than five times her present age. What is her present age?
OR
Solve for x: 9x2 – 6px + (p2 – q2) = 0 (2)
Answer:
Let the present age of Ritu be x years.
(x – 5)2 = 5x + 11
x2 – 15x + 14 = 0
(x – 14) (x – 1) = 0
x = 1 or 14
x = 14 years
(rejecting x = 1 as in that case Ritu’s age 5 years ago will be – ve)
Let, the present age of Ritu be x years.
Then, according to the question
(x – 5)2 = 11 + 5x
⇒ x2– 10x+ 25 = 11 + 5x
⇒ x2 – 15x + 14 = 0
⇒ x2 – 14x – x + 14 = 0
⇒ x(x – 14) – 1 (x – 14) = 0
⇒ (x – 1) (x – 14) = 0
⇒ x = 1, 14
But x = 1 is not possible, as in this case, (x – 5) will be negative.
∴ x = 14
Hence, the present age of Ritu is 14 years.
OR
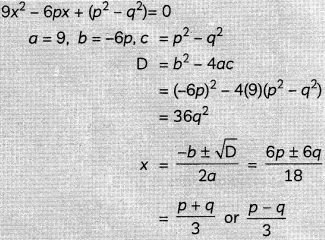
Given:
9x2 – 6px + (p2 – q2) = 0
Using quadratic formula, we have
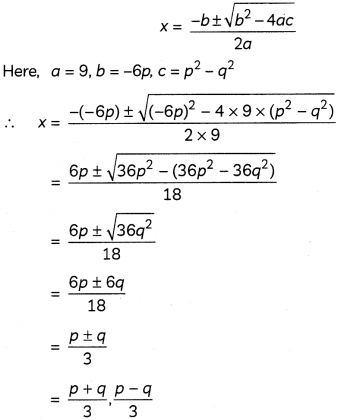
Section – B
Question 7.
Following is the distribution of the long jump competition in which 250 students participated. Find the median distance jumped by the students. Interpret the median. (3)
| Distance (in m) | Number of Students |
| 0 – 1 | 40 |
| 1 – 2 | 80 |
| 2 – 3 | 62 |
| 3 – 4 | 38 |
| 4 – 5 | 30 |
Answer:
| Distance (in m) | Number of Students | cf |
| 0 – 1 | 40 | 40 |
| 1 – 2 | 80 | 120 |
| 2 – 3 | 62 | 182 |
| 3 – 4 | 38 | 220 |
| 4 – 5 | 30 | 250 |
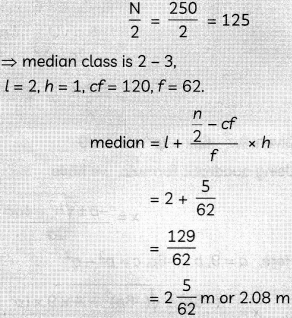
50% of students jumped below \(2 \frac{5}{62}\) m and 50% above it.
| Distance (in m) | Number of Students |
Cumulative Frequency |
| 0 – 1 | 40 | 40 |
| 1 – 2 | 80 | 120 |
| 2 – 3 | 62 | 182 |
| 3 – 4 | 38 | 220 |
| 4 – 5 | 30 | 250 |
| N = 250 |
Here, \(\frac{\mathrm{N}}{2}=125\)
And, cumulative frequency just greater than 125 is 182, which belongs to class 2 – 3.
∴ Median ctass = 2 – 3
We know,
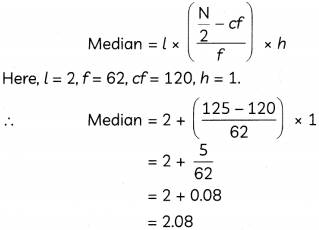
Hence, the median distance jumped by the students is 2.08 m.
Interpretation: HaLf of the students jumped above 2.08 m.
→ Caution
Remember cf is cumulative frequency of the class, preceding the median class and f is frequency of median class
Question 8.
Construct a pair of tangents to a circLe of radius 4 cm, which are inclined to each other at an angLe of 600. (3)
Answer:
Draw a circLe of radius 4 cm.
Draw OA and construct ∠AOB = 120°
Draw ∠OAP = ∠OBP = 90°
PA and PB ore required tangents
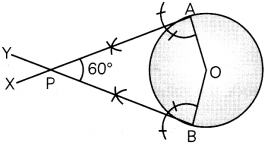
Steps of construction:
- Draw a circle with centre O and radius 4 cm.
- Take any point A on the circumference of the circLe and join CA.
- At point O, construct rAOB = 120e, such that the angle ray OB touches the circLe at point B.
- At points A and B, construct ∠OAX = 900 and ∠OBY = 900. Let rays AX and BY intersect each other at point P.
Thus, PA and PB are the required tangents to the circle which are inclined to each other at an angle of 60°.
→ Concept Applied
In quadrilateral OAPB,
∠OBP = ∠OAP = 90°
[∵ Tangent ⊥ Radius]
Also,
∠AOB + ∠OAP + ∠OBP + ∠APB = 360°
⇒ ∠AOB + 90°+ 90° + ∠APB =360°
⇒ ∠AOB + ∠APB = 1800
∵ ∠APB = 60° [Given]
∴ ∠AOB = 180° – 60°
= 120°
Hence, we constructed an angle of 120° at the centre of the circle.
Question 9.
The distribution given below shows the runs scored by batsmen in one-day cricket matches. Find the mean number of runs. (3)
| Runs scored | Number of batsmen |
| 0-40 | 12 |
| 40-80 | 20 |
| 80-120 | 35 |
| 120-160 | 30 |
| 160-200 | 23 |
Answer:
| Runs scored | Number of batsman f | xi | fi xi |
| 0-40 | 12 | 20 | 240 |
| 40-80 | 20 | 60 | 1200 |
| 80-120 | 35 | 100 | 3500 |
| 120-160 | 30 | 140 | 4200 |
| 160-200 | 23 | 180 | 4140 |
| Total | 120 | 13280 |
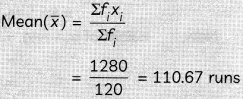
| Runs scored | Number of batsmen fi | Classmark xi | Deviation di = xi – a | fidi |
| 0-40 | 12 | 20 | – 80 | -960 |
| 40-80 | 20 | 60 | -40 | -800 |
| 80-120 | 35 | 100 = a | 0 | 0 |
| 120-160 | 30 | 140 | 40 | 1200 |
| 160-200 | 23 | 180 | 80 | 1840 |
| ∑fi = 120 | Σfidi = 1280 |
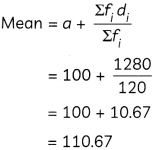
Hence, the mean number of runs is 110.67.
Question 10.
Two vertical poles of different heights are standing 20 m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take \(\sqrt{3}\) = 1-73)
OR
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take \(latex\) = 1-73) (3)
Answer:
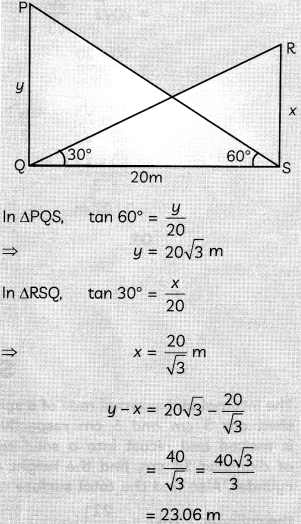
Let AB and CD be the two poles with AB > CD.
∴ ∠ADB 60°, ∠CBD = 30° and BD = 20 m

OR
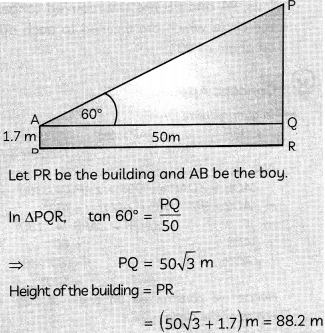
Let AB be the boy and PQ be the building.
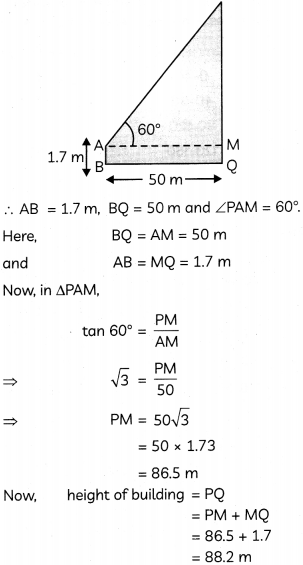
Section – C
Question 11.
The internet and externaL radii of a spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cyLinder. Also find the total surface area of the cylinder. (Take π = \(\frac{22}{7}\)) (4)
Answer:
Volume of shell = Volume of cylinder
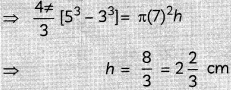
TSA of cylinder is:
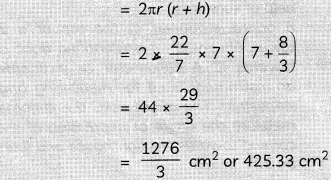
For a sphericaL shelL:
Internal radius (r1) = 3 cm
External radius (r2) = 5 cm
For a solig cyLinder:
Diameter = 14 cm
∴ Radius (R) = 14/2 cm = 7cm
Let height of the cylinder be H cm.
Since, spherical shell is recast into a solid cylinder
∴ Volume of shell = Volume of cylinder

→ Concept Applied
When a solid is converted from one shape to another its volume remain same.
Question 12.
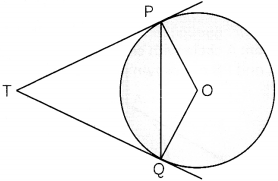
Prove that the angle between the two tangents drawn from an externat point to a circle is supplementary to the angLe subtended by the Line segment joining the points of contact to the centre.
OR
Two tangents W and TQ are drawn to a circLe with centre O from an externaL point T. Prove that ∠PTQ = 2∠OPQ. (4)
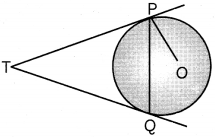
Answer:
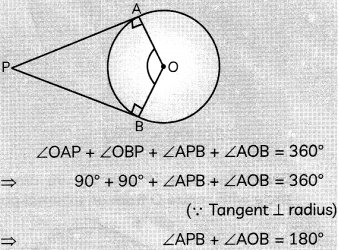
Given:
A circle with centre O at which tangents PA and PB are drawn from an externat point P.
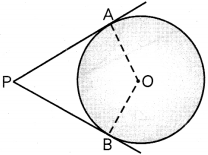
To prove: ∠APB = 180° – ∠AOB
or, ∠APB + ∠AOB = 180°
Proof: We know, tangent is perpendicular to radius at the point of contact.
∴ AP ⊥ OA, PB ⊥ OB
⇒ ∠OAP = 90°, ∠OBP = 90°
Now, in quadrilateral OAPB,
∠AOB + ∠OBP + ∠APB + ∠OAP = 360°
⇒ ∠AOB + 90° + ∠APB + 90° = 360°
⇒ ∠AOB + ∠APB = 360° – 180° = 180°
∴ ∠APB + ∠AOB = 180°
Hence, proved
OR
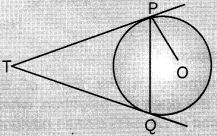
Given:
Tangents TP and TQ are drawn to a circle with centre O from an external point T.
To prove: ∠PTQ = 2∠OPQ
Proof: We have,
∠OPT = 90°
[∵ Tangent Z Radius]
⇒ ∠OPQ + ∠TPQ = 90°
⇒ ∠OPQ = 90° – ∠TPQ …………………………….(i)
Now, we know, tangents drawn from an external point to a circle are equal in length. So, in ΔTPQ,
TP =TQ
⇒ ∠TQP = ∠TPQ
[Equal angles opposite to equal sides]
∴ ∠PTQ = 180° – ∠TQP – ∠TPQ
= 180° – 2∠TPQ = 2(90° – ∠TPQ)
⇒ ∠PTQ = 2(∠OPQ) [From (i)]
Hence, proved.
Question 13.
Case Study-1
Trigonometry in the form of triangulation forms the basis of navigation, whether it is by land, sea or air. GPS a radio navigation system helps to locate our position on earth with the help of satellites.
A guard, stationed at the top of a 240 m tower, observed an unidentified boat coming towards it. A clinometer or inclinometer is an instrument used for measuring angles or slopes(tilt). The guard used the clinometer to measure the angle of depression of the boat coming towards the lighthouse and found it to be 30°.
(Lighthouse of Mumbai Harbour. Picture credits – Times of India Travel)
(A) Make a labeled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation tower. (2)
(B) After 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(\(\sqrt{3}\) – 1)m. He immediately raised the alarm. What was the new angle of depression of the boat from the top of the observation tower? (2)
Answer:
(A)
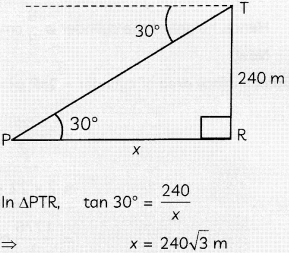
Let PQ be the 240 m high tower and B be the position of boat.
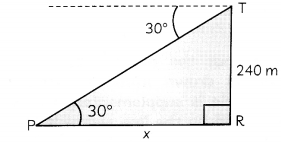
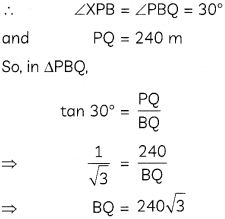
Hence, distance of the boat from the foot of observation tower is 240\(\sqrt{3}\)m.
(B) Distance of boat from tower
= 240\(\sqrt{3}\) – 240(\(\sqrt{3}\) – 1)
= 240 m
Let the angle of depression = θ
\(\begin{aligned}
\tan \theta &=\frac{240}{240}=1 \\
\Rightarrow \quad \theta &=45^{\circ}
\end{aligned}\)
Let B be the position of boat after 10 minutes.
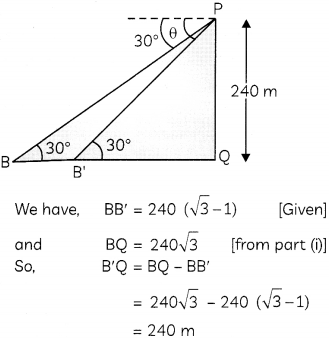
Let θ be the new angle of depression of boat from the top of tower PQ.
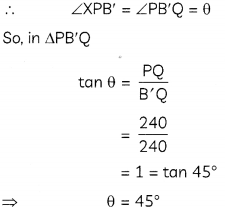
Hence, the new angLe of depression of boat from the top of the tower is 45°.
Question 14.
Case Study-2
Push-ups are a fast and effective exercise for building strength. These are helpful in almost all sports including athletics. While the push¬up primarily targets the muscles of the chest, arms, and shoulders, support required from other muscles helps in toning up the whole body.
Nitesh wants to participate in the push-up challenge. He can currently make 3000 push-ups in one hour. But he wants to achieve a target of3900 push-ups in 1 hour for which he practices regularly. With each day of practice, he is able to make 5 more push-ups in one hour as compared to the previous day. If on first day of practice he makes 3000 push-ups and continues to practice regularly till his target is achieved. Keeping the above situation in mind answer the following questions:
(A) Form an A.P representing the number of push-ups per day and hence find the minimum number of days he needs to practice before the day his goal is accomplished?
(B) Find the total number of push-ups performed by Nitesh up to the day his goal is achieved. (2)
Answer:
(A) 3000, 3005, 3010, …., 3900.
an = a + (n – 1 )d
3900 = 3900 + (n – 1)5
⇒ 900 = 5n – 5
⇒ 5 n = 905
⇒ n – 181
Minimum number of days of practice
= n – 1
= 180 days
Since, Nitesh makes 3000 push-ups on day one, and then increases 5 push-ups each successive day, so the A.P. is 3000, 3000 + 5, 3000 + 2(5), …i.e., 3000, 3005, 3010, 3015, ….
Now, we have
3000, 3005, 3010, 3015, ….. 3900
Here, a = 3000, d = 5, l = 3900
Let Nitesh took n days to make 3900 push-ups in one hour.
l = a + (n – 1)d
⇒ 3900 = 3000 + (n – 1) x 5
⇒ 900 = (n – 1) x 5
⇒ n – 1 = 180
⇒ n = 181
So, required minimum number of days
= n – 1 = 180
(B) \(S_{n}=\frac{n}{2}(a+l)\)
= \(\frac{181}{2}\) x (3000 + 3900)
= 624450 push-ups
From part (A), we have
a = 3000, l = 3900, n = 181
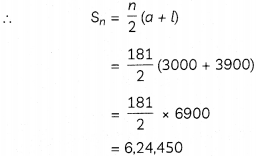
Hence, the total number of push-ups performed by Nitesh up to the day, his goaL is achieved, is 6,24,450.