CBSE Sample Papers for Class 10 Maths Standard Set 4 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Standard with Solutions Set 4 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 4 with Solutions

Time: 3 hrs
Max. Marks: 80

Instructions:
1. This question paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section A
(Section-A consists of 20 Questions of 1 mark each)

Question 1.
If two positive integers a and b are written as a = x³y² and b = xy³, where .r, y are prime numbers, then the result obtained by dividing the product of the positive integers by the LCM (a, b) is  [1]
(a) xy
(b) xy²
(c) x³y³
(d) x²y²
Answer:
(b) xy²

Given, a = x³y²
ana b = xy³
⇒ ab = (x³y²)(xy³)
= x⁴y⁵
and LCM (a, b) = x³y³
∴ \(\frac{a b}{{LCM}(a, b)}=\frac{x^4 y^5}{x^3 y^3}=x y^2\)

Question 2.
Given below is a pair of linear equations:
4x + y = 8
4x – 2y = 16
Is the given pair of equations:
(A) Consistent
(B) Inconsistent
(C) Consistent with unique solution
(D) Consistent with many solutions
Solution:
(C) Consistent with unique solution

∴ Equations have unique solution.
Hence they are consistent.

Question 3.
The given pair of linear equations is non-intersecting. Which of the following statements is true? [1]

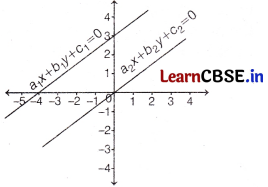
(a) \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
(b) \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
(c) \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}=\frac{c_1}{c_2}\)
(d) \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Answer:
(b) \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

Since the given pair of linear equations is non-intersecting i.e. parallel.
∴ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

Question 4.
If the zeroes of quadratic polynomial are 1, 1; then the polynomial can be.
(A) x² + x + 1
(B) x² – 2x + 1
(C) x² + 3x + 2
(D) x² + 2x + 2
Solution:
(B) x² – 2x + 1

Explanation: Given that
Two zeroes are 1 and 1
So the quadratic polynomial satisfying these roots is:
⇒ (x – 1)(x – 1)
⇒ x² – 2x + 1

Question 5.
Two APs have the same common difference. The first term of one of these is -1 and that of the other is -8. Then, the difference between their 4th terms is [1]
(a) 1
(b) 8
(c) 7
(d) 9
Answer:
(c) 7

Let the common difference of two APs be d.
Given, first term of one AP(a₁) = -1
and first term of second AP(b₁) = – 8
Fourth term of 1 st AP(a₄) = a₁ + (4 – 1)d
= -1 + 3d
and fourth term of 2nd AP(b₄) = b₁ + (4 – 1)d
= – 8 + 3d
∴ a₄ – b₄ = (-1 + 3d) – (- 8 + 3d)
= -1 + 3d + 8 – 3d = 7

Question 6.
Points A(-1, y) and B(5, 7) lie on a circle with centre O(2, -3y). The values of y are:
(A) 1, -7
(B) -1, 7
(C) 2, 7
(D) -2, -7
Solution:
(B) -1, 7

Explanation: As points A and B lie on the circle and O is the centre.
AO and BO will be the radii of the circle.

(3)² + (-4y)² = (-3)² + (-3y – 7)²
9 + 16y² = 9 + 9y² + 49 + 42y
16y² – 9y² – 42y – 49 = 0
7y² – 42y – 49 = 0
7(y² – 6y – 7) = 0
y² – 7y + 1y – 7 = 0
y(y – 7) + 1(y – 7) = 0
(y – 7)(y + 1) = 0

Question 7.
(x, y) is 5 unit away from the origin. How many such points lie in the third quadrant? [1]
(a) 0
(b) 1
(c) 2
(d) infinitely many
Answer:
(d) infinitely many

Let the point (- x, -y) lie in the third quadrant and it is at a distance of 5 units from the origin.

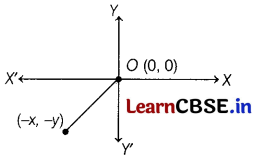
By distance formula, distance of (- x, -y)from origin is
\(\sqrt{(-x-0)^2+(-y-0)^2}=\sqrt{x^2+y^2}\)
⇒ \(\sqrt{x^2+y^2}\) = 5
On squaring both the sides, we get x² + y² = 25
Since, infinitely many values of (x, y) satisfy this equation, infinitely many points lie in the third quadrant.

Question 8.
In the figure below, DE || AC and DF || AE. Which of these is equal to \(\frac{B F}{F E}\)?

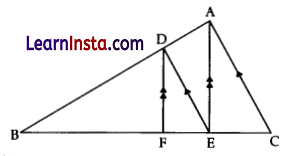
(A) \(\frac{D F}{A E}\)
(B) \(\frac{B E}{E C}\)
(C) \(\frac{B A}{A C}\)
(D) \(\frac{E E}{E C}\)
Solution:
(B) \(\frac{B E}{E C}\)

Explanation: In ΔABC,
DE || AC (Given)
∴ \(\frac{B D}{D A}\) = \(\frac{B E}{E C}\) (From BPT) …(i)
In ΔABE,
DF || AE (Given)
∴ \(\frac{B D}{D A}\) = \(\frac{F B}{F E}\) (From BPT) …(ii)
From eqs. (i) and (ii), we get
\(\frac{B F}{F E}\) = \(\frac{B E}{E C}\)

Question 9.
If O is centre of a circle and chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle made by the chord at the centre is [1]

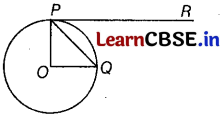
(a) 130°
(b) 100°
(c) 50°
(d) 30°
Answer:
(b) 100°

In the given figure,

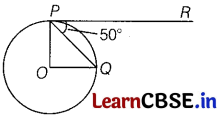
OP ⊥ PR [tangent to a circle is perpendicular to the radius through the point of contact]
⇒ ∠OPR = 90°
∠QPO = 90° – 50°= 40° ……(i)
Also, OQ = OP [radii of a circle]
⇒ ∠OQP = ∠OPQ [angles opposite to equal sides of a triangle]
⇒ ∠OQP = 40°
In ∆OPQ,
∠OQP + ∠OPQ + ∠POQ =180°
⇒ ∠POQ = 180° – 2(40°) = 100°

Question 10.
The area of the circle that can be inscribed in a square of 6 cm is
(A) 36π cm²
(B) 18π cm²
(C) 22π cm²
(D) 9π cm²
Solution:
(D) 9π cm²

Explanation:

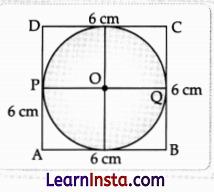
ABCD is a square of side 6 cm. PQ is a diameter of given circle such that
PQ = AB = 6 cm
∴ Radius (r) = \(\frac{\text { Diameter }}{2}\)
= 6/2 = 3 cm
Area of the circle = πr²
= π(3)² = 9πr cm²

Question 11.
Given that sin θ = \(\frac{a}{b}\), then cos θ is [1]
(a) \(\frac{b}{\sqrt{b^2-a^2}}\)
(b) \(\frac{b}{a}\)
(c) \(\frac{\sqrt{b^2-a^2}}{b}\)
(d) \(\frac{a}{\sqrt{b^2-a^2}}\)
Answer:
(c) \(\frac{\sqrt{b^2-a^2}}{b}\)

Given, sin θ = \(\frac{a}{b}\)
We know that sin²θ + cos²θ = 1
⇒ cos²θ = 1 – \(\frac{a^2}{b^2}\)
⇒ cosθ = \(\frac{\sqrt{b^2-a^2}}{b}\)

Question 12.
If cot θ = \(\frac{1}{\sqrt{3}}\), the value of sec² θ + cosec² θ is a
(A) 1
(B) \(\frac{40}{9}\)
(C) \(\frac{38}{9}\)
(D) 5\(\frac{1}{3}\)
Solution:
(D) 5\(\frac{1}{3}\)

Explanation: It is given that

Question 13.
A pole 6 m high casts a shadow 2√3 m long on the ground, then the Sun’s elevation is [1]
(a) 60°
(b) 45°
(c) 30°
(d) 90°
Answer:
(a) 60°

Let AS = 6 m be the height of the pole and the length of the shadow SC = 2√3 m.

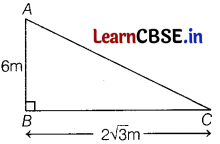
In right-angled ∆ABC
tan C = \(\frac{A B}{B C}\) = \(\frac{6}{2√3}\) = √3
∠C = 60°

Question 14.
In the given figure, if PQR is the tangent to a circle at Q, whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to

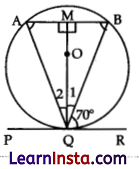
(A) 20°
(B) 40°
(C) 35°
(D) 45°
Solution:
(B) 40°

Explanation: Given that AB || PQR
∠B = ∠BQR = 70° [Alternate interior angles]
∠OQR = ∠AMQ [Alternate interior angles]
As PQR and OQ are tangent and radius at contact point Q
∴ ∠OQR = 90°
⇒ ∠1 + ∠70° = 90°
⇒ ∠1 = 90° – 70° = 20°
∴ ∠AMO = 90°
∵ Perpendicular from centre to chord bisect the chord
MA = MB
∠QMA = ∠QMB = 90°
MQ = MQ [Common]
ΔQMA = ΔQMB [SAS congruence]
⇒ ∠A = ∠B
⇒ ∠A = 70° [∵ ∠B = 70°]
∴ ∠A + ∠AMQ + ∠2 = 180° [Angle sum property of a triangle]
⇒ 70° + 90° + ∠2 = 180°
⇒ ∠2 = 180° – 160°
⇒ ∠2 = 20°
∴ ∠AQB = ∠1 + ∠2
= 20° + 20° = 40°

Question 15.
It is proposed to build a single circular park equal in area to the stun of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park is [1]
(a) 10 m
(b) 15 m
(c) 20 m
(d) 24 m
Answer:
(a) 10 m

Let the radius of new park be r m.
Let radius of two circular parks be r₁ and r₁, respectively.
∴ πr₁² + πr₂² = πr²
⇒ r₁² + r₂² = r²
⇒ \(\left(\frac{16}{2}\right)^2+\left(\frac{12}{2}\right)^2=r^2\) = r²
⇒ 64+ 36 = r²
⇒ r² = 100 ⇒ r = 10 m

Question 16.
The probability that the drawn card from a pack of 52 cards is neither an ace nor a spade is
(A) \(\frac{9}{13}\)
(B) \(\frac{35}{52}\)
(C) \(\frac{10}{13}\)
(D) \(\frac{19}{26}\)
Solution:
(A) \(\frac{9}{13}\)

Explanation: Total ace cards = 4 and total spade cards
= 13 – 1 = 12 (One card among aces is also a spade)
Cards which are neither ace or spade = 52 – 16 = 36
Required probability = \(\frac{36}{52}\) = \(\frac{9}{13}\)

Question 17.
2 cards of heart and 4 cards of spade are missing from a pack of 52 cards. What is the probability of getting a black card from the remaining pack? [1]
(a) \(\frac{22}{52}\)
(b) \(\frac{22}{46}\)
(c) \(\frac{24}{52}\)
(d) \(\frac{24}{46}\)
Answer:
(a) \(\frac{22}{52}\)

Total cards left in the pack = 52 – 6 = 46
Black cards left in the pack = 26 – 4 = 22
[∵ total black cards in a complete pack = 26]
∴ P(getting a black card from the remaining pack) = \(\frac{22}{46}\)

Question 18.
Arti owns a manufacturing company. She hires 5 supervisors and 20 operators for a 6-month project. The table given below shows their salary breakup.

Position	Salary for the two months	Salary for the remaining four months
Supervisor	Between ₹18,000 to ₹20,000	Between ₹22,000 to ₹25,000
Operator	Between ₹8,000 to ₹10,000	Between ₹13,000 to ₹15,000

Arti agrees to pay the maximum decided amount as salary to the operators.
What would be the total amount (in Rs) that Arti will have to pay the operators for the first two months?
(A) ₹10,000
(B) ₹200,000
(C) ₹300,000
(D) ₹500,000
Solution:
(B) ₹200,000

Explanation: Maximum decided amount for first two months paid by Arti as salary to operators = ₹10,000
Number of operators = 20
Total amount = 20 × 10,000 = ₹200,000

Directions In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Direction In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option. [1]

Assertion (A) : The total surface area of the top is the sum of the curved surface area of the hemisphere and the curved surface area of the cone.
Reason (R) : Top is obtained by fixing the plane surfaces of the hemisphere and cone together.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true and Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

Given,

Total surface area (TSA) of top
= Curved surface area of hemisphere + Curved surface area of cone
This is because the top is obtained by joining the plane surfaces of the hemisphere and cone.

Question 20.
Assertion (A): a, b, c are in A.P. if and only if 2b = a + c.
Reason (R): The sum of first n odd natural numbers is n².
Solution:
(B) Both (A) and (R) are true but (R) is not the correct explanation of the (A).

Explanation: Assertion is true because
b – a = c – b (a, b, c are in A.P.)
⇒ 2b = a + c
Reason: Let 1 + 3 + 5 + 7 + 9 + … + n, are sum of n odd natural numbers.
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S_n = \(\frac{n}{2}\)[2(1) + (n – 1)2]
S_n = \(\frac{n}{2}\)(2n)
S_n = n²
Hence, the sum of the first n natural number is n².

Section B
(Section B consists of 5 questions of 2 marks each)

Question 21.
Prove that √2 is an irrational number. [2]
Solution:
Let us assume that √2 is rational.
The √2 can be expressed as \(\frac{p}{q}\), where p and q are
co-primes and q 0.
∴ √2 = \(\frac{p}{q}\)
On squaring both sides, we get
2 = \(\frac{p^2}{q^2}\) ⇒ \(p^2=2 q^2\) ………(i) (1/2)
⇒ p² is a multiple of 2
=> 2 divides p²
∴ 2 divides p.
∴ p = 2a for some integer a.
Substituting p = 2a in Eq. (i), we get
(2a)² = 2q²
⇒ 4a² = 2q²
⇒ q² = 2a²
⇒ q² is a multiple of 2
⇒ 2 divides q²
∴ 2 divides q (1/2)
⇒ p and q have atleast 2 as a common factor.
But this contradicts the statement that p and q are co-primes.
This contradiction has arisen because of our incorrect assumption that √2 is rational.
∴ √2 is irrational. (1)

Question 22.
In the figure below, OPQ is a triangle with OP = OQ. RS is an arc of a circle with centre O.

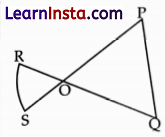
(Note: The figure is not to scale.)
Triangle OSR is similar to triangle OPQ.
Is the above statement true or false? Justify your reason.
Solution:
Let ∠ROS = ∠POQ = x
(vertically opposite angles are equal)
In ΔORS, OR =OS (radii of circle)
∴ ∠ORS = ∠OSR
(Angles opposite to equal sides)
Now, ∠ORS + ∠OSR + ∠ROS = 180°
∠ORS + ∠ORS + x = 180°
2∠ORS = (180° – x)
∠ORS = \(\frac{\left(180^{\circ}-x\right)}{2}\)
Similarly, In ΔOPQ
OPQ = \(\frac{\left(180^{\circ}-x\right)}{2}\)
Thus, ∠ORS = ∠OSR = ∠OPQ
= ∠OQP = \(\frac{\left(180^{\circ}-x\right)}{2}\)
In ΔORS and ΔOPQ
∠ROS = ∠POQ (proved above)
∠ORS = ∠OQP (proved above)
∠OSR = ∠OPQ (proved above)
∴ ΔORS ∼ ΔOPQ (AAA Similarity)
Thus, It is true.

Question 23.
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. [2]

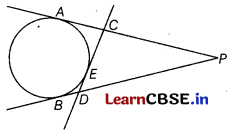
At point E on the circle, a tangent is drawn to intersect PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of APCD.
Solution:
Given, PA = 10 cm
PB = PA = 10 cm
[∵ tangents from an external point to a circle are equal]
Similarly, DE = BD
and CE = AC
⇒ DE + CE = BD + AC
⇒ CD=BD + AC ..(i) (1)
∴ Perimeter of APCD = PC + PD + CD
= (PA – AC) + (PB – BD) + CD
= PA – AC + PB – BD + BD + AC [Using Eq. (i)]
= PA + PB = 10+ 10 =20 cm (1)

Question 24.
(A) If √3 sin θ – cos θ = 0 and 0° < θ < 90°, find the value of θ.
Solution:
Here √3 sin θ – cos θ = 0 and 0° < θ < 90°
or, √3 sin θ = cos θ

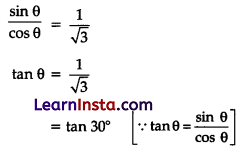
θ = 30°

OR

(B) Find an acute angle θ when \(\frac{\cos \theta-\sin \theta}{\cos \theta+\sin \theta}=\frac{1-\sqrt{3}}{1+\sqrt{3}}\).
Solution:

⇒ tan θ = √3
θ = 60°

Question 25.
With vertices A, B and C of ∆ABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle, so obtained are removed. Find the total area removed from the triangle. [2]
Or
Find the area of the unshaded region shown in the given figure.

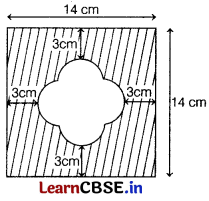
Solution:
According to the given information, the figure is given below.

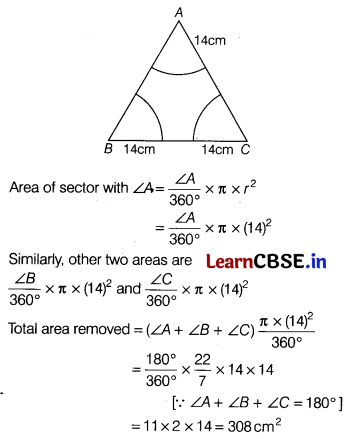
Or

The given figure is

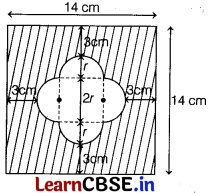
Let the radius of each semi-circle = r
∴ From figure,
3 + r + 2r + r + 3 = 14
4r + 6 = 14
r = \(\frac{8}{4}\) = 2 cm (1)
Area of unshaded region
= 4 × Area of each semi-circle + Area of square with the length of each side, 2r
= 4 × \(\frac{\pi r^2}{2}\) + (2r)²
= 2πr² + 4r² = 2r²(π + 2) cm² (1)

Section C
(Section C consists of 6 questions of 3 marks each)

Question 26.
The LCM of 6⁴, 8² and k is 12⁴ where k is a positive integer. Find the smallest value of k. Show your steps.
Solution:
Prime factorization of 6⁴ = 2⁴ × 3⁴
Prime factorization of 8² = 2⁶
∴ LCM of 6⁴, 8² and k = 2⁶ × 3⁴ × k … (i)
As, LCM of 6⁴, 8² and k = 12⁴ (given) …(ii)
From (i) and (ii) we get
2⁶ × 3⁴ × k = 12⁴
k = 4
Thus smallest value of k = 4.

Question 27.
If α, ß are zeroes of quadratic polynomial x² +5x + 1, find the value of [3]
(i) α² + ß²
(ii) α^-1 + ß^-1
Solution:
Given, a and p are the roots of the quadratic polynomial x² + 5x + 1.
Sum of roots = α + ß = \(\frac{-5}{1}\) = -5 (1)
Product of roots = αß = 1
(i) α² + ß² = (α + ß)² – 2αß = 25 – 2 = 23 (1)
(ii) α^-1 + ß^-1 = \(\frac{1}{α}\) + \(\frac{1}{ß}\)
= \(\frac{α + ß}{αß}\) = \(\frac{-5}{1}\) = -5 (1)

Question 28.
(A) Represent the following pair of linear equations graphically and hence comment on the condition of consistency of this pair.
x – 5y = 6, 2x – 10y = 12.
Solution:
Given, x – 5y = 6
⇒ y = \(\frac{x-6}{5}\)

x	6	1	-4
y	0	-1	-2

and 2x – 10y = 12 ⇒ y = \(\frac{x-6}{5}\)

x	6	1	-4
y	0	-1	-2

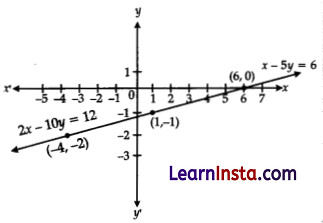
Since, the lines are coincident, so the system of linear equations is consistent with infinitely many solutions.

OR

(B) A fraction becomes \(\frac{1}{3}\) when 2 is subtracted from the numerator and it becomes \(\frac{1}{2}\) when 1 is subtracted from the denominator. Find the fraction.
Solution:
Let the fraction bc\(\frac{1}{3}\)
∴ \(\frac{x-2}{y}\) = \(\frac{1}{3}\)   … (i)
and \(\frac{x}{y-1}\) \(\frac{1}{2}\)   … (i)
Solving Eqs. (i) and (ii), we get
x = 7 and y = 15
∴ Required fraction is \(\frac{7}{15}\).

Question 29.
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact.
If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.

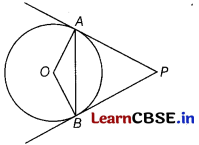
Or
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ. [3]
Solution:
The given figure is

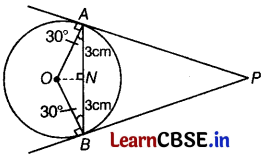
In ∆OAB
∠OAB + ∠OBA + ∠AOB = 180°
⇒ ∠AOB + 2 × 30° = 180°
∠AOB = 120°
Draw ON ⊥ AB.
⇒ AN = \(\frac{6}{2}\) = 3cm
[∵ perpendicular from centre to a chord bisects the chord]
In right angled ∆ONA,
cos 30° = \(\frac{A N}{A O}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{3}{A O}\)
⇒ AO = 2√3 cm
Now, OB ⊥ BP [tangent to a circle is perpendicular to the radius through the point of contact]
⇒ ∠OBP = 90°
⇒ ∠ABP = 90° – ∠OBA
= 90° – 30°
= 60°
Similarly,
∠BAP = 60°
∴ In ∆ABP
∠APB = 60°
∆ABP is an equilateral triangle
∴ AB = BP = PA = 6cm

Or

Given, two tangents TP and TQ drawn to a circle, as shown in the figure.

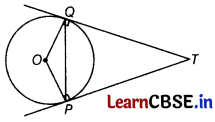
OP ⊥ PT
[tangent to a circle is perpendicular to the radius through the point of contact]
⇒ ∠OPT = 90°
⇒ ∠TPQ =90° -∠OPQ …(i)
In ATPQ,
TP = TQ
[tangents to a circle from an external point]
⇒ ∠TPQ = ∠TQP
[angles opposite to equal sides are equal]
and ∠TPQ + ∠TQP + ∠PTQ =180°
⇒ ∠PTQ = 180° – 2 ∠TPQ
⇒ ∠PTQ = 180° – 2(90° – ∠OPQ) [using Eq. (i)]
⇒ ∠PTQ = 2∠OPQ

Question 30.
Prove that: \(\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + tan θ + cos θ
Solution:

= tan θ + 1 + cot θ
= RHS

Question 31.
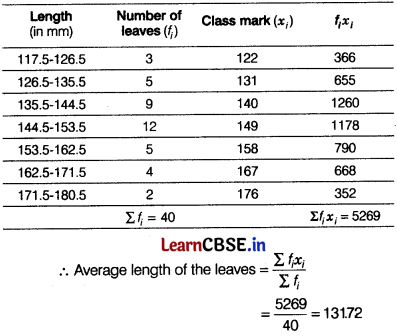
The length of 40 leaves of a plant are measured correct to nearest millimetre and the data obtained is represented in the following table. [3]

Length [in mm]	Number of leaves
118-126	3
127-135	5
136-144	9
145-153	12
154-162	5
163-171	4
172-180	2

Find the average length of the leaves.
Solution:
Let us make the table for given data.

Section D
(Section D consists of 4 questions of 5 marks each.)

Question 32.
(A) The difference of the squares of two numbers is 180. The square of the smaller number is 8 times the greater number. Find the two numbers.
Solution:
Let the greater number be x.
The square of the smaller number is 8 times the greater number = 8x
Given, the difference of squares of two numbers is 180.
∴ x² – 8x = 180
⇒ x² – 8x – 180 = 0
⇒ x² – 18x + 10x – 180 = 0
⇒ x(x – 18) + 10(x – 18) = 0
⇒ (x – 18)(x + 10) =0
Either (x – 18) = 0 or (x + 10) = 0
Either x = 18 or x = -10
Since, number cannot be negative. So, x = 18
Now, square of smaller number = 8x
= 8 × 18
= 144
∴ Smaller number = √144 = 12
Hence, smaller number is 12 and greater number is 18.

OR

(B) A shopkeeper buy certain number of books in ₹80. If he buy 4 more books then new cost price of each book is reduced by ₹1. Find the number of books initially he buy.
Solution:
Let the number of books bought be x. Then,
Cost of x books = ₹80
⇒ Cost of one book = ₹\(\frac{80}{x}\)
If the number of books bought is x + 4, then
Cost of one book = ₹\(\frac{80}{x+4}\)
It is given that the cost of one book is reduced by one rupee.
\(\frac{80}{x}\) – \(\frac{80}{x+4}\) = 1
80(\(\frac{1}{x}\) – \(\frac{1}{x+4}\)) = 1
80(\(\frac{x+4-x}{x(x+4)}\)) = 1
\(\frac{320}{x^2+4 x}\) = 1
⇒ x² + 4x = 320
⇒ x² + 4x – 320 = 0
⇒ x² + 20x – 16x – 320 = 0
⇒ x(x + 20) – 16(x + 20) = 0
⇒ (x + 20)(x – 16) = 0
⇒ x = -20 or, x = 16
⇒ x = 16 [∵ x cannot be negative]
Hence, the number of books is 16.

Question 33.
(a) State and prove Basic Proportionality theorem.
(b) In the given figure ∠CEF = ∠CFE. F is the mid-point of DC.
Prove that \(\frac{A B}{B D}=\frac{A E}{F D}\). [5]

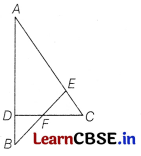
Solution:
(a) Statement If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Proof

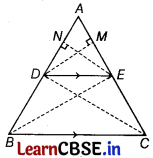
Let ABC be a triangle in which a line parallel to side SC intersects the other two sides AB and AC at D and E, respectively.
To prove: \(\frac{A D}{D B}=\frac{A E}{E C}\)
Construction: Join CD, BE and draw DM ⊥ AC and EN ⊥ AB.

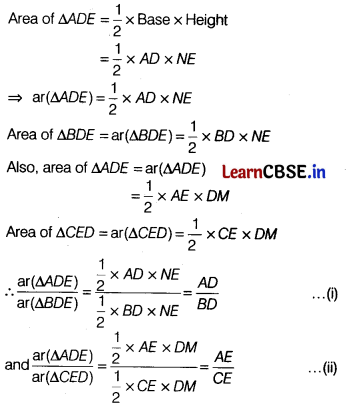
Since, ∆BDE and ∆CED are on the same base DE and between the same parallel lines DE and SC.
∴ ar(∆BDE) = ar(∆CED) ………(iii)
From Eqs. (i), (ii) and (iii), we get
\(\frac{A D}{B D}=\frac{A E}{C E}\)

(b) The given figure is

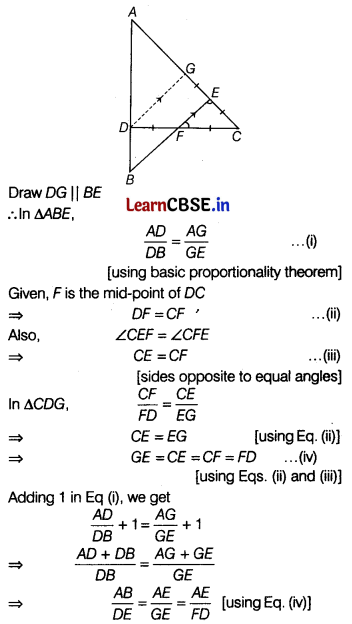
Question 34.
(A) In a rain water harvesting system, the rain water from a roof 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3.5 m. If the tank is full, find the rainfall in cm. Write your views on water conservation.
Solution:
Volume of rain water on the roof = volume of cylindrical tank
i.e., 22 × 20 × h = \(\frac{22}{7}\) × 1 × 3.5
⇒ h =  \(\frac{1}{40}\)m
⇒ h = 2.5 cm
Water conservation must be encouraged.

Detailed Answer
Let length of roof, l = 22 m
breadth of roof, b = 22 m
and height of roof = h m
Also, given, height of cylinder = 3.5 m

Views on water conservation:
Water conservation reduces energy use and can even save household money. Water conservation must be encouraged.

OR

(B) Rohan wants to renovate his room. He calls an architect for this work to measure the room. The length, breadth and height of a room are 8 m 50 cm; 6m 25 cm and 4 m 75 cm respectively. He wants to put the longest rod that can measure the dimensions of the room exactly.
Solution:
Given Length = 8 m 50 cm = 850 cm
breadth = 6 m 25 cm = 625 cm
height = 4 m 75 cm = 475 cm
Since, the length of the longest rod is equal to
HCF of 850, 625 and 475.
Prime factor of 850 = 2 × 5² × 17
Prime factor of 625 = 54
Prime factor of 475 = 5² × 19
Hence, HCF (625, 850, 475) = 5² = 25
Thus, the longest rod that can measure the dimensions of the room exactly = 25 cm

Question 35.
The median of the following data is 50. Find the values of ‘p’ and ‘q’ , if the sum of all frequencies is 90. Also, find the mode. [5]

Marks obtained	Number of students
20-30	p
30-40	15
40-50	25
50-60	20
60-70	q
70-80	8
80-90	10

Solution:
Table for cumulative frequency is given below

Marks obtained	Number of students (f)	Cumulative frequency
20-30	p	P
30-40	15	p+ 15
40-50	25	p+ 40
50-60	20	p+ 60
60-70	q	p+ q + 60
70-80	8	p+ q + 68
80-90	10	p + q + 78
	M = Σf = p + q + 78 = 90	Cumulative frequency

⇒ p + q = 12 …(i)
Since, median = 50, therefore median class is 50-60.
∴ Median = \(I+\left(\frac{\frac{n}{2}-c f}{f}\right) \times h\)
Where, l = lower limit of median class,
n = number of observations,
cf = cumulative frequency of class preceding the median class,
f = frequency of median class
h = class size
Here, \(\frac{n}{2}\) = \(\frac{90}{2}\) = 45
l = 50, cf = p + 40, f = 20 and h = 10
∴ 50 = 50 + \(\left(\frac{45-(p+40)}{20}\right)\) × 10
⇒ 45 – (p + 40) = 0
⇒ p + 40 = 45
⇒ p = 5
From Eq. (i),
q = 12 – p = 12 – 5 = 7
Now, modal class = 40-50
∴ Mode = l + \(\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right)\) × h
Where, l = lower limit of modal class,
f₁ = frequency of modal class,
f₀ = frequency of class preceeding the modal class,
f₂ = frequency of class succeeding the modal class,
h = size of the class interval.
Here, l = 40, f₁ = 25, f₀ = 15, f₂ = 20 and h = 10
∴ Mode = 40 + \(\left(\frac{25-15}{2(25)-15-20}\right)\) × 10
= 40 + \(\frac{10}{15}\) × 10
= 40 + \(\frac{20}{3}\)
= 46.66

Section E
(Case study based questions are compulsory)

Question 36.
Read the following text and answer the following questions:

Your elder brother wants to buy a car and plans to take loan from a bank for his car. He repays his total loan of ₹1,18,000 by paying every month starting with the first instalment of & 1000. If he increases the instalment by ₹100 every month, answer the following:
(i) Find the amount paid by him in 30th instalment.
(ii) If total instalments are 40 then amount paid in the last instalment?
(iii) How much the amount will he pay in 30 instalments?
Solution:
(i) Here, a = 1000
d = 100
a₃₀ = a + (n – 1)d
= 1000 + (30 – 1)100
= 1000 + 2900 = 3900

(ii) Amount paid in 40^th instalment,
a₄₀ = a + (n – 1)d
= 1000 + (40 – 1)100
= 1000 + 3900
= 4900

(iii) Sum of 30 instalments
= \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{30}{2}\)[2 × 1000 + (30 – 1)100]
= 15[2000 × 4900 + 2900]
= 15 × 4900
= 73500
Total Amount paid in 30 instalments = ₹73500

OR

Find the ratio of the 1st instalment to the last instalment.
Solution:
Amount paid in last instalment = ₹4900 [From Part (ii)]
Principal for 1^st instalment = ₹1000
Hence, Ratio of 1^st instalment to the last instalment = \(\frac{1000}{4900}\) = 10 : 49.

Question 37.
Tharunya was thrilled to know that the football tournament is fixed with a monthly time frame from 20th July to 20th August 2023 and for the first time in the FIFA Women’s World Cup’s history, two nations host in 10 venues. Her father felt that the game can be better understood if the position of players is represented as points on a coordinate plane.

(i) At one instance, the midfielders and
forward formed a parallelogram. Find the position of the central midfielder (D), if the position of other players who formed the parallelogram are A(1, 2), 5(4, 3), and C (6, 6). [1]
(ii) Check if the Goal keeper G(-3, 5), Sweeper H(3, 1) and Wing-back K(0, 3) fall on a same straight line. [2]
Or
Check if the full-back J(5, – 3) and center-back I(- 4, 6) are equidistant from forward C(0, 1) and if C is the mid-point of IJ. [2]
(iii) If Defensive Midfielder A(1, 4), Attacking Midfielder B(2, -3) and Striker E(a, b) lie on the same straight line and B is equidistant from A and E, find the position of E. [1]
Solution:
(i) Let the coordinates of point D be (x, y).

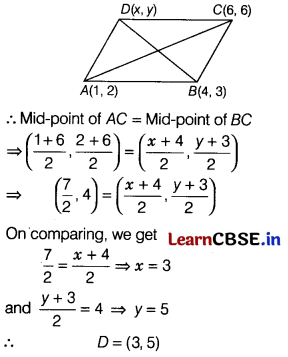
(ii) Distance between G and H,

Or

(iii) ∵ 6(2, – 3) is equidistant from A(1,4) and E(a,b)

∴ B is the mid-point of AE.
⇒ a + 1 = 4 and b + 4 = – 6
⇒ a = 3 and b = – 10

Question 38.
Read the following and answer the following questions:
An electrician has to repair an electric fault on a pole of height 5 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work (see figure).

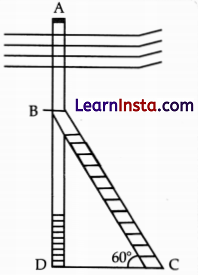
(i) What is the length of BD?
(ii) What should be the length of ladder, when inclined at an angle of 60° to the horizontal?
(iii) How far from the foot of the pole should he place the foot of the ladder?
OR
If the horizontal angle is changed to 30°, then what should be the length of the ladder?
Solution:
(i) From figure, the electrician is required to reach at the point B on the pole AD.
So, BD = AD – AB
= (5 – 1.3) m = 3.7 m