CBSE Sample Papers for Class 10 Maths Standard Set 3 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Standard with Solutions Set 3 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 3 with Solutions

Time: 3 hrs
Max. Marks: 80

Instructions:
1. This question paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2-mark questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section A
(Section-A consists of 20 Questions of 1 mark each)

Question 1.
Prime factorisation of 120 is
(a) 2⁴ × 3 × 5
(b) 2³ × 3² × 4
(c) 2³ × 3 × 5
(d) 2² × 3 × 5
Answer:
(c) 2³ × 3 × 5

We have, 120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3 × 5

Question 2.
Amit designs a flower vase using a graph of polynomial equations. Equation of the curve is given in the graph.
The curve m is a mirror image of p(y) on the y-axis. Which polynomial represents curve m?

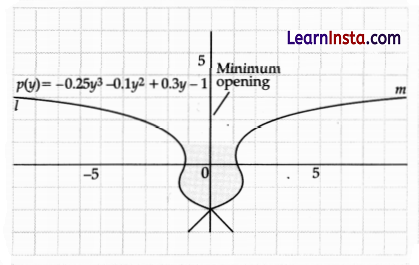
(A) p(y) = -0.25y³ – 0.1y² + 0.3y – 1
(B) p(y) = -0.25y³ – 0.1y² – 0.3y – 1
(C) p(y) = 0.25y³ + 0.1y² – 0.3y + 1
(D) p(y) = 0.25y³ + 0.1y² – 0.3y
Solution:
(C) p(y) = 0.25y³ + 0.1y² – 0.3y + 1

Explanation: Since, the curve m is a mirror image of the curve l, so all the signs are reversed i.e, polynomial represents the curve m as
p(y) = 0.25y³ + 0.1y² – 0.3y + 1

Question 3.
The ratio in which the points P(\(\frac{3}{4}\), \(\frac{5}{12}\)) divides the line segments joining the points A(\(\frac{1}{2}\), \(\frac{3}{2}\)) and B (2, – 5) is
(a) 5 : 1
(b) 1 : 6
(c) 1 : 5
(d) 6 : 1
Answer:
(c) 1 : 5

Let the point P divides the line joining the points AB in the ratio k : 1.

On comparing the x and y-coordinates, we get
\(\frac{3}{4}\) = \(\frac{4 k+1}{2 k+2}\) and \(\frac{5}{12}\) = \(\frac{-10 k+3}{2 k+2}\)
⇒ 6k + 6 = 16k + 4
⇒ 10k = 2 ⇒ k = \(\frac{1}{5}\)
Hence, point P divides the Pine segment AB in the ratio 1 : 5.

Question 4.
Digital images consist of pixels. A pixel can be considered as the smallest unit on a display screen in a mobile or a computer. The number of pixels, their size and colours depend on the display screen and its graphic card. Display screens are rectangular in shape and their size is defined as the length of the diagonal.

Anmol is designing a web page for a display on a screen whose size is 1000 pixels. The width of the screen is 800 pixels.
Which of the following equation can be used to calculate the height (h) of the screen?
(A) h² + 200 × 1800 = 0
(B) h² – 200 × 1800 = 0
(C) h² – 200 = 0
(D) h² – 1800 = 0
Solution:
(B) h² – 200 × 1800 = 0

Explanation: In right angled ΔABC,
Size, AC is the diagonal.
∴ AC = 1000 pixels
and AB is the width, so
AB = 800 pixels.

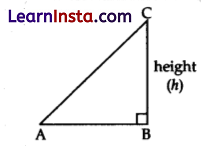
Using Pythagoras theorem,
h² = (AC)² – (AB)²
⇒ h² = (1000)² – (800)²
⇒ h² = (1000 + 800) (1000 – 800)
[Using a² – b² = (a + b) (a – b)]
⇒ h² = 1800 × 200
⇒ h² – 1800 × 200 = 0

Question 5.
The value of p in which the system of linear equations -x + py = 1 and px – y = 1 represent parallel lines is
(a) 0
(b) 1
(c) -1
(d) 2
Answer:
(b) 1

Given, pair of Linear equation is
-x + py – 1 = 0 and px – y – 1 = 0
On comparing the given equations with standard form, i.e. a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = -1, b₁ = p, c₁ = -1
and a₂ = p, b₂ = -1, c₂ = -1
Condition for parallel lines,
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
⇒ \(\frac{-1}{p}\) = \(\frac{p}{-1}\) ⇒ p² = 1 ⇒ p = ±1
But p = -1 does not satisfy the condition \(\frac{p}{-1}\) ≠ \(\frac{-1}{-1}\), so we neglect it.
Hence, for p = 1, the given system of equations will represent parallel lines.

Question 6.
Δ ABC is a triangle such that AB : BC = 1 : 2. Point A lies on the Y-axis and the coordinates of B and C are known. Which of the following formula can DEFINITELY be used to find the coordinates of A?
(i) Section formula
(ii) Distance formula
(A) only (i)
(B) only (ii)
(C) both (i) and (ii)
(D) neither (i) or (ii)
Solution:
(B) only (ii)

Explanation: As A lies on the Y-axis therefore co-ordinates of A will be (0, y).
So, we can find the value of y-co-ordinate by using the distance formula.

Question 7.
The H.C.F and L.C.M of two numbers are 12 and 5040 respectively. If one of the numbers is 144 find the other number
(a) 420
(b) 202
(c) 101
(d) 111
Answer:
(a) 420

Given, HCF =12, LCM = 5040
and also one number is 144.
Let the other number be x.
As we know that
HCF × LCM = 144 × x
12 × 5040 = 144 × x
⇒ x = \(\frac{12 \times 5040}{144}\)
⇒ x = 420

Question 8.
Leela has a triangular cabinet that fits under his staircase. There are four parallel shelves as shown below.

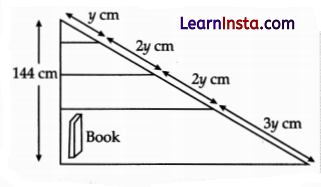
(Note: The figure is not to scale)
The total height of the cabinet is 144 cm. Whatis the maximum height of a book that can stand upright on the bottom-most shelf?
(A) 18 cm
(B) 36 cm
(C) 54 cm
(D) 86.4 cm
Solution:
(C) 54 cm

Explanation:

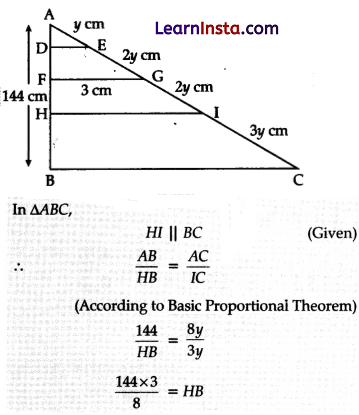
HB = 54 cm
Thus, the maximum height of a book is 54 cm.

Question 9.

is equal to
(a) \(\frac{3}{2 \sqrt{2}}\)
(b) 0
(c) \(\frac{1}{2 \sqrt{2}}\)
(d) \(\frac{1}{2}\)
Answer:
(d) \(\frac{1}{2}\)

We have,

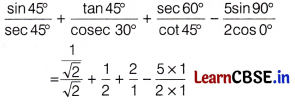
Question 10.
Here is a circle with centre O.

Manu wants to draw a tangent RS to the circle.
What is the number of points at which the line RS will meet the circle?
(A) 0
(B) 1
(C) 2
(D) 3
Solution:
(B) 1

Explanation: There is one and only one tangent to a circle passing through a point lying on the circle.

Question 11.
In the given figure, if TP and TQ are the two tangents to a circle with centre O, so .that ∠POQ = 120°. The value of ∠PTQ is

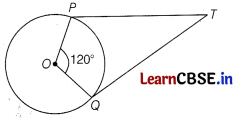
(a) 30°
(b) 120°
(c) 60°
(d) None of these
Answer:
(a) 30°

Given, TP and TQ are two tangents to a circle and ∠POQ = 120°. Join PQ.

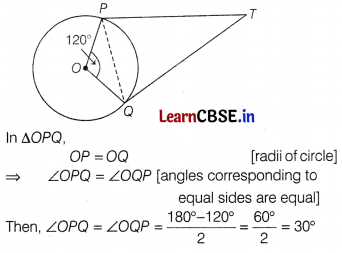
Question 12.
ABC is an isosceles right triangle, right-angled at B. What is the value of 2 sin A × cos A?
(A) \(\frac{1}{2}\)
(B) 1
(C) \(\frac{3}{2}\)
(D) 2
Solution:
(B) 1

Explanation: Since ABC is an isosceles triangle.
Let AB = BC = x.

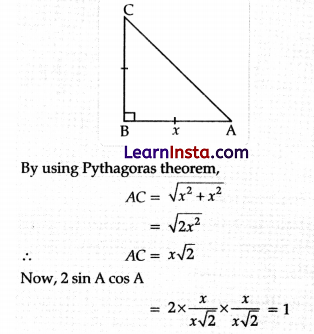
Question 13.
The exponent of 2 factorization of 1440 is
(a) 5
(b) 6
(c) 3
(d) 4
Answer:
(a) 5

The prime factorization of 1440 is
1440 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5
= 2⁵ × 3² × 5¹
Hence, the exponent of 2 in the prime factorisation of given number is 5.

Question 14.
Shown below is a circle with centre O. The shaded sector has an angle of 280° and area A cm².

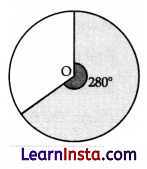
(Note: The figure is not to scale.)
Which of these is the area of the unshaded sector?
(A) \(\frac{2}{7}\) A cm²
(B) \(\frac{1}{3}\) A cm²
(C) \(\frac{2}{3}\) A cm²
(D) \(\frac{7}{9}\) A cm²
Solution:
(A) \(\frac{2}{7}\) A cm²

Explanation: Angle of shaded sector = 280°
Area of shaded sector = A cm²

Question 15.
The value of cos²θ + \(\frac{1}{1+\cot ^2 \theta}\) is
(a) 0
(b) 1
(c) -1
(d) None of these
Answer:
(b) 1

[∵ cosec²A – cot²A = 1]
= cosec²θ + sin²θ = 1

Question 16.
Romy is blind folded and asked to pick one ball from each of the jars.

The chance of Romy picking a red ball is same in
(A) jars 2 and 3
(B) jars 1 and 3
(C) jars 1 and 2
(D) all the three jars
Solution:
(C) jars 1 and 2

Thus chance of Romy picking a red ball is same in jars 1 and 2.

Question 17.
The median of the first 10 prime numbers is
(a) 12
(b) 10
(c) 24
(d) None of these
Answer:
(a) 12

First 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Here, n = 10 which is even, therefore

Question 18.
In statistics, an outlier is a data point that differs significantly from other observations of a data set.
If an outlier is included in the following data set, which measure (s) of central tendency would change?
12, 15, 22, 44, 44, 48, 50, 51
(A) only mean
(B) only the mean and median
(C) all-mean, median, mode
(D) cannot be said without knowing the outlier
Solution:
(A) only mean

Explanation:
Mean = \(\frac{\text { Sum of all observations }}{\text { Total number of values }}\)
∴ On including the outlier sum as well the total number of values both will change.
So, the mean would also change.

Directions In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) If the outer and inner diameter of a circular path is 10 m and 6 m, then area of the path is 16 π m².
Reason (R) If R and r be the radius of outer and inner circular path respectively, then area of path = π(R² – r²).
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

∴ Area of the path = π\(\left[\left(\frac{10}{2}\right)^2-\left(\frac{6}{2}\right)^2\right]\)
= π(25 – 9)
= 16π m²
Hence, both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).

Question 20.
Assertion (A): If nth term of an A.P. is (2n + 1), then the sum of its first three terms is 15.
Reason (R): The sum of first 16 terms of the A.P. 10, 6, 2, … is 420.
Solution:
(C) (A) is true but (R) is false.

Explanation: In case of assertion:
∵ a_n = (2n + 1)
∴ a₁ – 2 x 1 + 1 = 3
l = a₃ =2 x 3 + 1 = 7
Since, S_n = \(\frac{n}{2}\)[a + l]
Hence, S_n = \(\frac{3}{2}\)[3 + 7]
S_n = 15
∴ Assertion is true.
In case of reason:
Here, a = 10, d = 6 – 10 = -4 and n = 16
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S_n = \(\frac{16}{2}\)[2 × 10 + (16 – 1)(-4)]
= 8[20 + 15 × (-4)]
= 8[20 – 60]
= 8 × (-40)
= -320
∴ Reason is false.
Hence, assertion is true but reason is false.

Section B
(Section B consists of 5 questions of 2 marks each)

Question 21.
5 yr hence, the age of Shivangi is 3 times the age of Anshika while 5 yr earlier the age of Shivangi was 7 times the age of Anshika. Find the present age of Shivangi.
Answer:
Let the present age of Shivangi = x
and present age of Anshika = y
After 5 yr, age of Shivangi = (x + 5)
After 5 yr, age of Anshika = (y + 5)
According to the question
x + 5 = 3(y + 5)
⇒ x + 5 = 3y + 15
⇒ x – 3y = 10
⇒ x = 10 + 3y …….. (i)
and 5 yr earlier
Age of Shivangi = x – 5
and age of Anshika = y – 5
According to the question,
x – 5 = 7(y – 5)
⇒ x – 7y = – 30 …… (ii)
Subtracting Eq. (i) from Eq. (ii), we get
– 4y = – 40
⇒ y = 10
On substituting the value of y in Eq. (i), we get
10 + 3 × 10 = 40
‘Hence, present age of Shivangi = 40 yr.

Question 22.

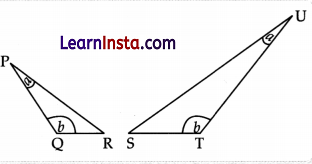
In the below figure, QR = 4 cm, RP = 8 cm and ST = 6 cm.
(Note: The figure is not to scale.)
If the perimeter of ΔSTU is 27 cm, find the length of PQ. Show your steps.
Solution:
In ΔPQR and ΔSTU
∠P = ∠U = a (Given)
∠Q = ∠T = b (Given)
∴ ΔPQR – ΔSTU (By AA Similarity)
\(\frac{\text { Perimeter of } \triangle \mathrm{PQR}}{\text { Perimeter of } \triangle \mathrm{STU}}=\frac{Q R}{S T}\)
(∵ Ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides)
⇒ \(\frac{\text { Perimeter of } \triangle \mathrm{PQR}}{27}=\frac{4}{6}\)
= \(\frac{4 \times 27}{6}\)
= 18 cm
Now, In ΔPQR
Perimeter = PQ + QR + PR
18 = PQ + 4 + 8
PQ = 18 – 12
PQ = 6 cm

Question 23.
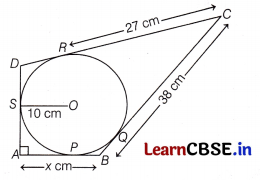
In the figure, quadrilateral ABCD is circumscribing a circle with centre O and AD ⊥ AB. If radius of incirclte is 10 cm, then find the value of x.

Or
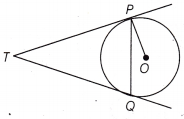
In the figure, two tangents TP and TQ are drawn to a circle with centre O from an external point T.
Prove that ∠PTQ = 2∠OPQ.

Answer:
Given, in radius of circle, r = 10 cm.
Draw a line perpendicular from centre to the tangent line AB.
∠A = ∠OPA = ∠OSA = 90°
[∵ all lines in quadrilateral APOS are perpendicular]
∠SOP = 90°

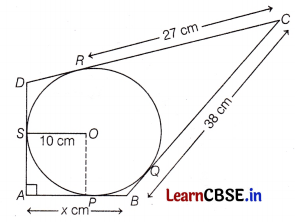
Also, AP = AS
[∵ pair of tangents drawn from outside point of a circle are equal in lengths]
Hence, OSAP is i i square.
AP = OS = 10 cm
CR = CQ = 27 cm
Now, BQ = BC – CQ
= 38 – 27 = 11 cm
Here, BP = BQ = 11 cm
∴ x = AB = AP + BP = 10 + 11 = 21 cm

Or

Given, TP and TO are two tangents of a circle with centre O and P and Q point of contact, let ∠PTQ = 0 As we know that the length of tangents drawn from an external point to a circle are equal.
So, ∆TPQ is an isosceles triangle

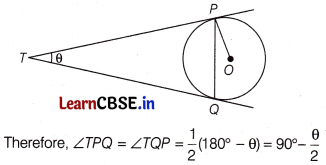
As we know the tangents at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠OPT = 90°
Now, ∠OPQ = ∠OPT – ∠TPQ
= 90° – (90° – \(\frac{\theta}{2}\)) = \(\frac{\theta}{2}\) = \(\frac{\angle P T Q}{2}\)
⇒ ∠PTQ = 2∠OPQ
Hence proved.

Question 24.
(A) Show that sin θ = cos (90° – θ) is true using the definition of trigonometric ratios.

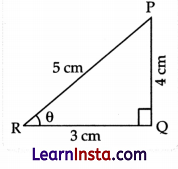
Solution:
In ΔPQR
∠P + ∠Q + ∠R = 180° (Angle sum property)
∠P = 180° – (90° + θ)
∠P = 90° – θ

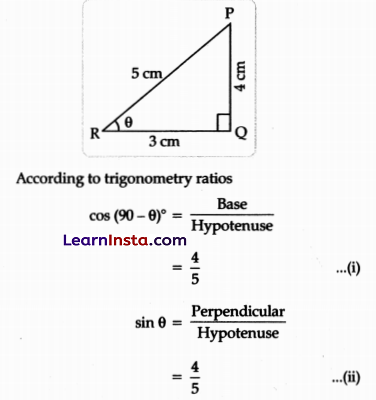
From (i) and (ii)
sin θ = cos (90° – θ) Hence Proved

OR

(B) In the triangles shown below, ∠Q = ∠T.

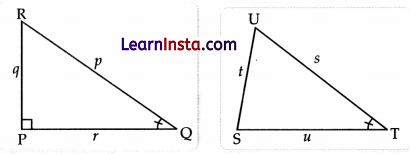
Write an expression each for cos Q and sin T.
Solution:
In right ΔPQR

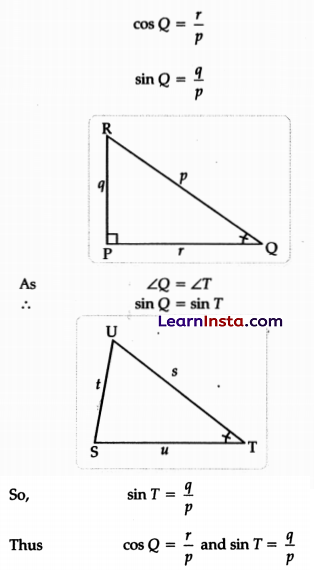
Question 25.
If tan θ = \(\frac{7}{13}\), then find the value of \(\frac{(2+2 \sin \theta)(1-\sin \theta)}{(1+\cos \theta)(2-2 \cos \theta)}\).

Or

If cos θ = \(\frac{b}{\sqrt{a^2+b^2}}\), 0 < θ < 90°, find the value of sin θ and tan θ.
Answer:

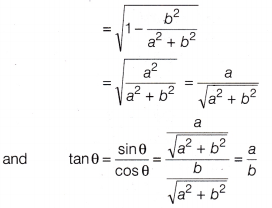
Section C
(Section C consists of 6 questions of 3 marks each)

Question 26.
Find all pairs of positive integers whose sum is 91 and HCF is 13. Show your work.
Solution:
Let pair of numbers be and ‘b’
HCF (a, b) = 13 (Given)
So, a and b be will be of the form.
a = 13x
b = 13y
(where x and y are co-primes)
Now a + b = 91 (Given)
So, 13x + 13y = 91
x + y = 7
Now all possible values of x and y are:
1 and 6
2 and 5
3 and 4
So, all values of a and b are
13 and 78
26 and 65
39 and 52

Question 27.
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) a queen of red colour.
(ii) a face card.
(iii) a black face card.
Answer:
Total number of cards in one deck of cards is 52.
∴ Total number of possible outcomes = 52
(i) Let E₁ = Event of getting a queen of red colour
∴ Number of outcomes favourable to E₁ = 2
[∵ there are four queen in a deck of playing cards out of which two are red and two are black]
Hence, probability of getting a queen of red colour,
P(E₁) = \(\frac{2}{52}\) = \(\frac{1}{26}\)

(ii) Let E₂ = Event of getting a face card
∴ Number of outcomes favourable to E₂ = 12
[∵ in a deck of cards, there are 12 face cards, namely 4 kings, 4 jacks, 4 queens]
Hence, probability of getting a face card,
P(E₂) = \(\frac{12}{52}\) = \(\frac{3}{13}\)

(iii) Let E₃ = Event of getting a black face card
∴ Number of outcomes favourable to E₃ = 6
[∵ in a deck of cards, there are 12 face cards out of which 6 are red and 6 are black]
Hence, probability of getting a black face card,
P(E₃) = \(\frac{6}{52}\) = \(\frac{3}{26}\)

Question 28.
(A) The two circles represent the ordered pairs, (a, b), which are solutions of the respective equations. The circles are are divided into 3 regions P, Q and R as shown.
Write one ordered pair each belonging to P, Q and R. Show your work.

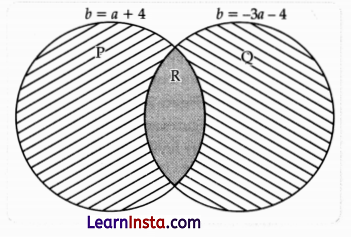
Solution:
From Figure given
P ⇒ (b = a + 4)
If a = 0, then b = 4
∴ Ordered pair of P (0, 4).
Q ⇒ (b = -3a – 4)
If a – 0, then b = -4
∴ Ordered pair of Q (0, -4).
R ⇒ Equate both P and Q equation as L.H.S. is equal
b = a + 4
b = -3a – 4
a + 4 = -3o – 4
a + 3a = -4 – 4
4a = -8
Now, If a = -2
b = -2 + 4 = 2
Thus Ordered pair of R = (-2, 2)

OR

(B) Shown below is a pair of linear equations.
x + 0.999 y = 2.999
0.999x + y = 2.998
(i) Without finding the values of x and y, prove that x – y = 1.
(ii) Find the values of x and y. Show your work.
Solution:

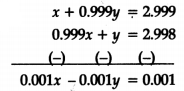
0.001 (x – y) = 0.001
Thus x – y = 1 … (i)

(ii) Add both the equation

x = 2
Equating value of x, we get
2 – y = 1
-y = 1 – 2
-y = -1
y = 1
Thus x = 2 and y = 1

Question 29.
In a class test, the sum of the marks obtained by Shyam in Mathematics and Science is 28. Had he got 3 more marks in Mathematics and 4 marks USS in Science, the product of marks obtained in two subjects would have been 180. Find the marks obtained by him in the two subjects separately.
Answer:
Suppose, Shyam gets x marks in Mathematics and y marks in Science. Then,
x + y = 28 ……… (i)
Again, (x + 3)(y – 4) = 180 ……… (ii)
On putting y = (28 – x) from Eq. (i) in Eq. (ii), we get
(x + 3)(28 – x – 4) = 180
⇒ (x + 3)(24 – x) = 180
⇒ -x² + 21x + 72 = 180
⇒ x² – 21x + 108 = 0
⇒ (x – 12) (x – 9) = 0
⇒ x -12 = 0 or x – 9 = 0
⇒ x = 12 or x = 9
Now, x = 12, then y = 28 -12 = 16
and when x = 9, then y = 28 – 9 = 19
∴ Either he got 12 marks in Mathematics and 16 marks in Science or he got 9 marks in Mathematics and 19 marks in Science.

Question 30.
Prove that:
\(\frac{{cosec}^2 x-\sin ^2 x \cot ^2 x-\cot ^2 x}{\sin ^2 x}\) = 1
Solution:

= cosec² x – cot² x
= 1
Thus, LHS = RHS Hence Proved

Question 31.
Prove that
\(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) = cosec A + cot A
Using the identity cosec² A – cot² A = 1.

Or

Evaluate \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}-2}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}+1}\)
Answer:

Or

Section D
(Section D consists of 4 questions of 5 marks each )

Question 32.
(A) In a flight of 600 km, an aircraft was slowed down due to bad weather. Its average speed for the trip was reduced by 200 km/h from its usual speed and time of flight increased by 30 minutes. Find the scheduled duration of flight.
Solution:
Let usual speed of flight be x km/h, then according to question

= 600, -400
Since, speed cannot be negative, therefore original speed = 600 km/h
and original distance = 600 km
∴ Time = \(\frac{\text { Original distance }}{\text { Original speed }}\)
= \(\frac{600 \mathrm{~km}}{600 \mathrm{~km} / \mathrm{h}}\)
= 1 h
Hence, the scheduled duration of flight is 1 h.

OR

(B) A boat goes 30 km upstream and 44 km downstream in 10 h. In 13 h, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
Solution:
Let the speed of the boat in still water be x km/h and speed of the stream be y km/h.
Given, \(\frac{30}{x-y}+\frac{44}{x+y}\) = 10 …(i)
and \(\frac{40}{x-y}+\frac{55}{x+y}\) = 13 …(ii)
Solving Eqs. (i) and (ii), we get
x + y = 11 …(iii)
and x – y = 5 …(iv)
Solving Eqs. (iii) and (iv), we get
x = 8 and y = 3
Hence, speed of boat = 8 km/h and speed of stream = 3 km/h.

Question 33.
Find the missing frequencies f₁ and f₂ in the following frequency distribution table, if N = 100 and the median is 32.

Or

The table below shows the salaries of 280 persons.

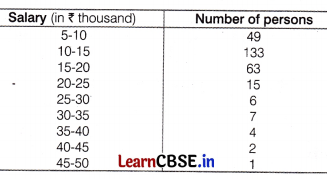
Calculate
(i) median of the data.
(ii) mode of the data.
Answer:
Given, median = 32 and N = Σf =100
Since, sum of frequencies =100
∴ 10 + f₁ + 25 + 30 + f₂ + 10 = 100
⇒ f₁ + f₂ = 100 – 75
⇒ f₁ + f₂ = 25
⇒ f₂ = 25 – f₁ ……. (i)
Now, the cumulative frequency table distribution is

Here, N = 100 ⇒ \(\frac{N}{2}\) = 50
Given, median = 32, which belongs to the class 30 – 40.
So, the median class is 30 – 40.
Then, l = 30, h = 10, f = 30 and cf = 35 + f₁

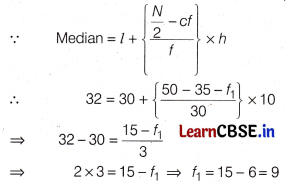
On putting the value of f₁ in Eq. (i), we get
f₂ = 25 – 9 = 16
Hence, the missing frequencies are
f₁ = 9 and f₂ = 16

Or

First, we construct a cumulative frequency table

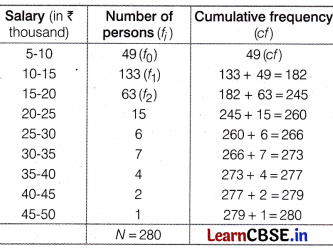
∴ \(\frac{N}{2}\) = \(\frac{280}{2}\) = 140

(i) Here, median class is 10-15, because 140 lies in it.
∴ l = 10, f = 133, cf = 49 and h = 5

(ii) Here, the highest frequency is 133, which lies in the interval 10-15, called modal class.
∴ l = 10, h = 5, f₁ = 133, f₀ = 49 and f₂ = 63

Hence, the median and modal salary are ₹ 13421 and ₹ 12727, respectively.

Question 34.
(A) A restaurant stores ice-cream in a box with a dispenser attached for filling ice-cream cones. The dimensions of the box and the ice-cream cones used by the restaurant are shown in Figure 1 below. To make each serving of dessert, the cone is first filled with ice-cream and then topped with a hemispherical scoop of ice-cream taken from the same box, as shown in Figure 2.

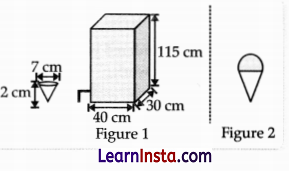
(Note: The figures are not to scale.)
Approximately how many desserts can be served out of a filled box of ice cream?
Show your steps.
(Note: Take π as \(\frac{22}{7}\))
Solution:
Shape of dispenser is cuboid.
So, volume of dispenser = lxbxh = 40 × 30 × 115
= 138000 cm³

OR

(B) A right-circular cylindrical water taker supplies water to colonies on the outskirts of a city and a nearby village. Each colony has a cuboidal water tank. In villages, people come with matkas (spherical clay pots) to fill water for their households.

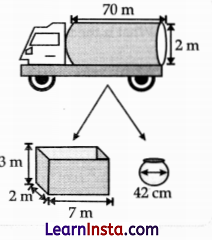
(Note: The figures are not to scale.)
(i) How many colonies in total would one full tanker be able to supply?
Solution:
Volume of right circular cylindrical water tanker = πr²h

As number of colonies cannot be in decimal,
∴ One full tanker will supply water to = 5 colonies.

(ii) If a tanker supplies water to 3 colonies and then goes to a village where 400 people fill their mistakes, roughly how much water is supplied by the tanker in all? Give your answer in m³.
Show your work.
(Note: Assume all the tanks/matkas are filled without any loss of water; Take π as \(\frac{22}{7}\); Use 1000000 cm³ = 1 m³.)
Solution:
Volume of one colony cuboidal tank = 42
Volume of 3 colonies cuboidal tank = 42 × 3
= 126 m³
Volume of one matka = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 21 × 21 × 21
= 38808 cm³
1000000 cm³ = 1 m³
38808 cm³ = 0.038808 m³
= 0.04 m³
Volume of 400 matkas = 400 × 0.04 = 16 m³
Total water supplied by tanker = 126 + 16
= 142 m³

Question 35.
The sum of n terms of three arithmetic progressions are S₁, S₂ and S₃. The first term of each is unity and the common difference are 1, 2, 3 respectively. Prove that S₁ + S₃ = 2 S₂

Or

The ratio of the sums of m and n terms of an AP is m² : n². Show that the ratio of the mth and nth terms is (2m – 1) : (2n – 1).
Answer:
Given, S₁ = Sum of n terms of an AP with first term 1 and common difference 1.

Or

Let a and d be the first term and common difference of an AP. Then, the sums of m and n terms are

Replacing on both sides m by 2m – 1 and n by 2n – 1, we get

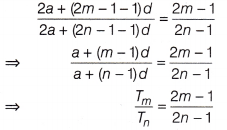
Section E
(Case study based questions are compulsory)

Question 36.

The school auditorium was to be constructed to accommodate at least 1500 people. The chairs are to be placed in concentric circular arrangement in such a way that the each succeeding circular row has 10 seats more than the previous one.
(i) If the first circular row has 30 seats, how many seats will be there in the 10^th row?
Solution:
Since each row is increasing by 10 seats, so it is an A.P. with first term a = 30, and common difference d = 10.
So, number of seats in 10^th row = = a₁₀
= a + 9d
= 30 + 9 × 10 = 120

(ii) For 1500 seats in the auditorium, how many rows need to be there?
Solution:
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
1500 = \(\frac{n}{2}\)[2 × 30 + (n – 1)(10)]
3000 = 50n + 10n²
n² + 5n – 300 = 0
n² + 20n – 15n – 300 =0
(n + 20)(n – 15) = 0
Rejecting the negative value, n = 15

OR

If 1500 seats are to be arranged in the auditorium, how many seats are still left to be put after 10^th row?
Solution:
No. of seats already put up to the 10^th row = S₁₀
S₁₀ = \(\frac{10}{2}\){2×30 + (10 – 1)10)}
= 5(60 + 90) = 750
So, the number of seats still required to be put are 1500 – 750 = 750

(iii) If there were 17 rows in the auditorium, how many seats will be there in the middle row?
Solution:
Given, no. of rows = 17
Then the middle row is the 9^th row.
a₉ = a + 8d
= 30 + 80
= 110 seats

Question 37.
School Trophy
A school decide to give a trophy of the best student in the class, which is the form of cylinder mounted on a solid hemisphere with the same radius and is made from some metal. This trophy is mounted on a wooden cuboid as shown in the figure.

Suppose the diameter of the hemisphere is 24 cm and total height of the trophy is 28 cm.

Based on above information, answer the following questions.
(i) Find the curve surface area of cylinder. (1)
(ii) Find the volume of cylinder. (1)
(iii) Find the curved surface area of the trophy. (2)

Or

Find the volume of the trophy. (2)
Answer:
Given, diameter of hemisphere,
d = 24 cm
Radius,
r = \(\frac{d}{2}\) = \(\frac{24}{2}\) = 12 cm
Now, height of cylinder,
h = 28 – 12
= 16 cm

(iii) Curved surface area of trophy = Curved surface area of cylinder + Curved surface area of hemisphere
= 2πrh + 2πr² = 2πr(h+ r)
= 2 × \(\frac{22}{7}\) × 12(16+ 12)
= \(\frac{528 \times 28}{7}\) = 2112 cm²

Or

Question 38.

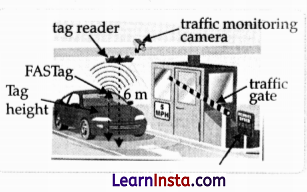
At a toll plaza, an electronic toll collection system has been installed. FASTag can be used to pay the fare. The tag can be pasted on the windscreen of a car.
At the toll plaza a tag scanner is placed at a height of 6 m from the ground. The scanner reads the information on the tag of the vehicle and debits the desired toll amount from a linked bank account.
For the tag scanner to function properly the speed of a car needs to be less than 30 km per hour. A car with a tag installed at a height of 1.5 m from the ground enters the scanner zone.

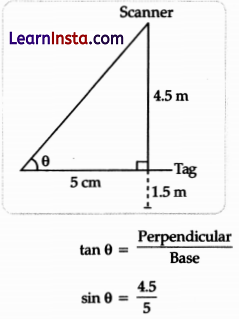
(i) The scanner gets activated when the car’s tag is at a distance of 5 m from it.
Give one trigonometric ratio for the angle between the horizontal and the line between the car tag and the scanner?
Solution:
One trigonometric ratio is

(ii) The scanner reads the complete information on the car’s tag while the angle between tag and scanner changes from 30° to 60° due to car movement. What is the distance moved by the car?
Solution:
Let the distance moved by the car

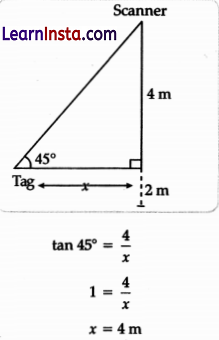
OR

A vehicle with a tag pasted at a height of 2 m from the ground stops in the scanner zone. The scanner reads the data at a angle of 45°. What is the distance between the tag and the scanner?
Solution:
Let the distance between the tag and the scanner be x m, then according to the figure

(iii) Which trigonometric ratio in a right triangle vary from 0 to 1?
Solution:
The values of sin and cos vary from 0 to 1.