Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 5 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths BasicTerm 2 Set 5 with Solutions
Time allowed: 2 hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one questions.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one questions. It contains two case study based questions.
Section – A (12 marks)
Question 1.
Check whether y(2y + 15) = 2(y2 + y + 8) is a quadratic equation or not.
OR
Find the value of b, for which the discriminant of the quadratic equation 6x2 + bx – 10 = 0 is 289. (2)
Answer:
We have,
y(2y + 15) = 2(y2 + y + 8)
⇒ 2y2 + 15y = 2y2 + 2y + 16
⇒ 2y2 – 2y2 + 15y – 2y – 16 = 0
⇒ 13y – 16 = 0
which is not a quadratic equation.
OR
Given, discriminant = 289
∴ b2 – 4ac= 289
⇒ b2 – 4 × 6 × (-10) = 289
⇒ b2 + 240 = 289
⇒ b2 = 49
⇒ b2 = ± 7
Question 2.
If the nth term of the A.P. 9, 7, 5 ………is same as the nth term of the A.P. 15, 12, 9, …………… then what is the volue of n? (2)
Answer:
Given A.P.s are 9, 7, 5 …….. and 15, 12, 9…………. consider a1 d1 and a2, d2 be the first terms and common difference of two A.P.s respectively.
So, a1 = 9,
d1 = 7 – 9 = – 2.
a2 = 15,
d2 = 12 – 15 = -3
A.T.Q.
a1 + (n – 1 )d1 = a2 +(n – 1)d2
⇒ 9 + (n – 1)(- 2) = 15 + (n – 1)(- 3)
⇒ 3(n – 1) – 2(n – 1) = 15 – 9
⇒ (n – 1) = 6
⇒ n = 7
Question 3.
A large IT company, assigns a job to a technician, to repair its 200 computer. The table below shows the time taken by him in repairing these computers.
| Time (t min) | Frequency |
| 20-30 | 24 |
| 30-40 | 56 |
| 40-50 | 40 |
| 50-60 | 35 |
| 60-70 | 27 |
| 70-80 | 18 |
Looking at the table answer the questions.
(A) How many computers took more than 50 minutes to get repaired?
(B) How many computers took less than 40 minutes to get repaired? (2)
Answer:
(A) Number of computers that took more than 50 min to get repaired = 35 + 27 + 18 = 80
(B) Number of computes that took Less than 40 min to get repaired = 24 + 56 = 80
Caution:
Read the table properly to get the relevant answer.
Question 4.
In which of the following situations, does the list of the numbers involved to make an A.P. If yes, give reason.
(A) The cost of digging a well after every meter of digging, where it cost ₹ 150 for the first metre and rises by ₹ 50 for each subsequent metre.
(B) The amount of money in the account every year when ₹ 10,000 is deposited at simple interest at 8% p.a. (2)
Answer:
(A) The numbers involved are :
150, 200, 250, 300, ……………
Here, 200 – 150 = 250 – 200
= 300- 250 = …………
∴ It forms an AP with
a = 150
and d = 50
(B) The numbers involved are 10,800, 11,600, 12,000 ………… which forms an A.P.
with a = 10,800
and d = 800.
Caution
First form the required A.P. to get the correct answers.
Question 5.
The table below shows the number of pages written by Vaishali for completing her own book in 30 days.
| No. of pages written/day | No. of days |
| 16-18 | 1 |
| 19-21 | 3 |
| 22-24 | 4 |
| 25-27 | 9 |
| 28-30 | 13 |
Find the average number of pages written each day. (2)
Answer:
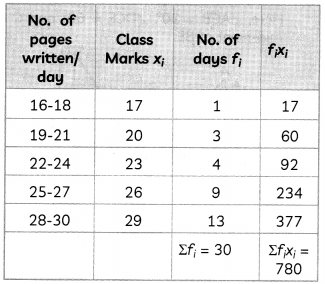
Mean x̄ = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
= \(\frac{780}{30}\)
= 26
Hence, the mean numbers of pages written per day is 26.
Question 6.
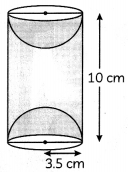
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If height of the cylinder is 10 cm and its base is of the radius 3.5 cm. What is the total surface area of the cylinder ?
OR
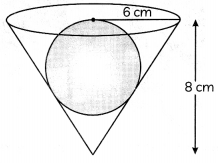
A conical vessel of radius 6 cm and height 8 cm is completely filled with water. A sphere is lowered into the water and its size is such that when it touches the sides, it is just immersed. What fraction of water overflows? (2)
Answer:
Given,
Height of cylinder, h = 10 cm
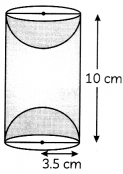
Radius of cylinder, r = 3.5 cm
T.S.A. of remaining figure = C.S.A of cylinder + C.SA of 2 hemispheres
= 2πrh + 2 × 2πr2
= 2 × \(\frac{22}{7}\) × 3.5 × 10 + 4 × \(\frac{22}{7}\) × 3.5 × 3.5
= 44 × 0.5 × 10 + 88 × 0.5 × 3.5
= 220 + 154
= 374 cm2
OR
Diameter of sphere = Radius of cone
6
Radius of sphere = \(\frac{6}{2}\) cm
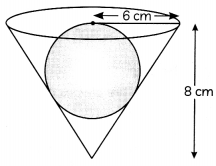

= \(\frac{3}{8}\)
Hence required ratio is 3:8
Caution
Here. radius of sphere with be equal to the diameter of the conical vessel
Section- B (12 marks)
Question 7.
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre. (3)
Answer:
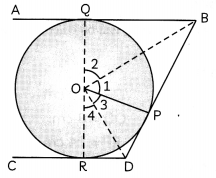
AB and CD are two tangents to a circle and AB ∥ CD.
Tangent BD intercepts an ∠BOD at the centre.
To Prove: ∠BOD = 90°
Construction: Join OQ, OB, OR.
Proof OP ⊥ BD
(Since, tangent at any point is perpendicular to the radius through the point of contact..)
In right angled triangles QQB and CPB
∠1 = ∠2
Similarly, in right angled triangles OPD and ORD
∠3 = ∠4
∴ ∠BOD = ∠ 1 + ∠3
= \(\frac{1}{2}\)(2∠1 + 2∠3)
= \(\frac{1}{2}\)(∠1 + ∠1 + ∠3 + ∠3)
= \(\frac{1}{2}\)(∠1 + ∠2 + ∠3 + ∠4)
= \(\frac{1}{2}\)(180°)
= 90°
Related Theory:
Parallel tangents are always drawn at the end of a diameter of a circle.
Question 8.
From the tap of building 60 m high, the angle of depression of the top and bottom of a vertical lamp post are observed to be 30° and 60° respectively. Find the height of the lamp post and the distance between the top of the building and top of lamp-post.
OR
The tops of two towers of height x and y standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x: y (3)
Answer:
Let h metres be the height of the lamp-post and d metres be the distance between feet of lamp-post and the building.
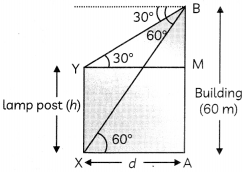
Then, from right ∆BMY.
\(\frac{\mathrm{BM}}{\mathrm{YM}}\) = tan30°
⇒ \(\frac{60-h}{d}=\frac{1}{\sqrt{3}}\)
⇒ d = √3(60 – h) …….(i)
From right ∆BAX, we hove
\(\frac{\mathrm{BA}}{\mathrm{XA}}\) = tan60°
⇒ \(\frac{60}{d}\) = √3
⇒ d = 20√3 ……………(ii)
From (i) and (ii), h = 40m and d= 20√3
Now, BY = \(\sqrt{Y M^{2}+B M^{2}}\)
= \(\sqrt{d^{2}+20^{2}}\)
= \(\sqrt{1200+400}\)
= \(\sqrt{1600}\)
= 40 m
Thus, the distance between the top of the building and top of the lamp post is 40 m.
OR
Here, AB and DE are two towers of height x and y respectively.
Here, ∠ACB = 30°, ∠DCE = 60° and C is the mid-point of BE.
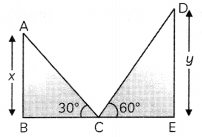
In ∆ABC,
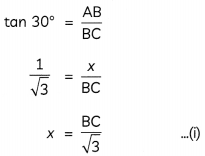
In ∆DCE

Caution
Here, ratio of x and y wilt be calculated by using the given values.
Question 9.
Two concentric circles are there of centre O. Their radii are 10 cm and 8 cm. RP and RQ are tangents to the two circles from R. If the length of RP is 24 cm, then what is the length of RQ? (3)
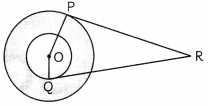
Answer:
Given that
OP = 10 cm
OQ = 8 cm
RP = 24 cm
Construction: Join OR
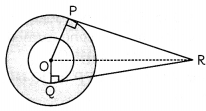
In ∆OPR, we have ∠OPR = 90°
As radius is perpendicular to the tangent at the point of contact.
OR= \(\sqrt{P R^{2}+O P^{2}}\)
(By Pythagoras theorem)
= \(\sqrt{24^{2}+10^{2}}\)
= \(\sqrt{576+100}\)
= \(\sqrt{676}\)
= 26 cm
In ∆OQR, OQ ⊥ QR
OR2 = RQ2 + OQ2
⇒ RQ2 = OR2 – OQ2
⇒ 262 – 82
⇒ 676 – 64
⇒ 612
RQ = \(\sqrt{612}\)
= 6\(\sqrt{17}\) cm
Related Theory:
Tangent drawn to the circle, is always perpendicular to the radius at the point contact to the circle.
Question 10.
Prove that a parallelogram circumscribing a circle is a rhombus. (3)
Answer:
Let ABCD be a parallelogram circumscribing a circle.
Let P, Q, R, S be the points where the circle touches the sides AB, BC, CD and DA respectively.
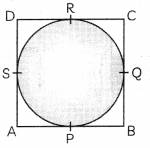
Now, AB = DC and AB ∥ CD
Also, AD = BC and AD ∥ BC
[∵ ABCD is a parallelogram]
From the figure, we have
AS = AP, BP = BQ, CR = CQ and DR = DS.
∵ AP + PB + CR + RD = AS + BQ + CQ + DS
⇒ AB + CD = AD + CB
⇒ 2AB = 2AD
(∵ ABCD is a parallelogram)
AB = AD
Using (i) we have
AB = BC = CD = DA
Thus, ABCD is a rhombus
Caution:
Use properties of parallelogram and rhombus to prove the desired result.
Section – C (16 marks)
Question 11.
The lower window of a house is at a height of 2m above the ground and its upper window is 4m above the lower window. At certain instant, the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon from the ground. (4)
Answer:
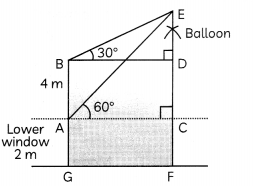
In the figure, A and B represent two windows and E is the position of the balloon. If balloon is h metres above the ground, then is AACE,
tan 60° = \(\frac{C E}{A C}\)
⇒ √3 = \(\frac{h-2}{\mathrm{AC}}\)
or AC = \(\frac{h-2}{\sqrt{3}}\) ……….. (i)
Also, in ∆BDE
tan 30° = \(\frac{D E}{B D}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{h-6}{\mathrm{AC}}\) (∵ BD = AC)
⇒ AC = √3 (h – 6)
\(\frac{h-2}{\sqrt{3}}\) = √3 (h – 6)
⇒ h – 2 = 3 (h – 6)
⇒ h – 2 = 3h – 18
⇒ – 2h = – 16
⇒ h = 8m
Hence, the height of the balloon above the ground is 8 m.
Related Theory:
Trigonometry has wide application in day to day life. For example, trigonometry is used in the construction of houses and cars. Trigonometry plays an important role in dealing with triangles, especially right-angled triangles.
Question 12.
The \(\frac{3}{4}\) th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
OR
A right triangle whose sides are 15 cm and 20 cm, is made to revolve about, its hypotenuse. Find the volume and the surface area of the double cone so formed. [use π = 3.14] (4)
Answer:
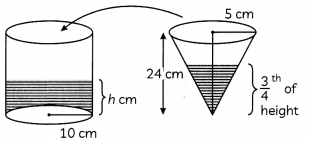
Let, the height of water in cylindrical vessel = h cm
Volume of water (in cylindrical vessel) = \(\frac{3}{4}\) volume of water (in cone)
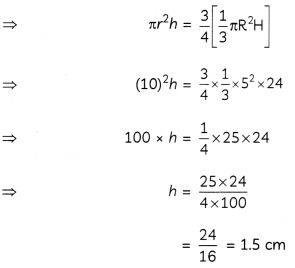
Hence, height of water in cylindrical vessel, h = 1.5 cm
Caution:
When water is transfered from one vessel to another, then volume of water remains constant.
OR
Let ∆PQR be the right triangle, right angled at P, whose sides PQ and PR measure 15 cm and 20 cm respectively.
Now, QR2 = PQ2 + PR2
QR = \(\sqrt{15^{2}+20^{2}}\)
= 25 cm
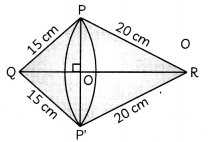
Here, PO (or P’O) is the radius of the common base of the double cone formed by revolving the right triangle about QR.
Height of the cone QPP’ is QO and slant height is 15 cm
Height of the cone RPP’ is RO and slant height is 20 cm
Now, in ∆sPOQ and RPQ
∠POQ = ∠RPQ = 90°
∠Q = ∠Q (common)
∴ ∆POQ ~ ∆RPQ
⇒ \(\frac{\mathrm{PO}}{20}\) = \(\frac{15}{25}\)
⇒ PO = 12 cm
Also \(\frac{\mathrm{QO}}{15}\) = \(\frac{15}{25}\)
⇒ QO = 9 cm
Now, volume of the double cone formed
= (\(\frac{1}{3}\) × 3.14 × 122 × 9 + \(\frac{1}{3}\) × 3.14 × 122 × 6) cm3
= \(\frac{3.14}{3}\) × 122 × (9 + 16) = 3768 cm3
Surface area of the double cone
= 3.14 × 12 × 15 + 3.14 × 12 × 20
= 3.14 × 12 × (15 + 20)
= 1318.8 cm2
Caution:
Double cone is the two cones formed on the either side of the revolving line.
Question 13.
Case Study-1
Play allows children to use their creativity while developing their imagination, dexterity and physical cognitive and emotional strength. Play-ing is also important for healthy brain development. It is through play that children at very early age engage and interact in the world around them. So, municipal corporation of the city want to put some playing equipments in the municipal parks. For this they hired an agency, to do the task. That agency had to install some playing equipment in the park area. For that they decided to study the age group of children playing in a park of a particular colony. The classification of children according to their age playing in a park are given in the table below:
| Age group of children (in years) | No. of children |
| 4 – 6 | 43 |
| 6- 8 | 58 |
| 8 – 10 | 70 |
| 10 – 12 | 42 |
| 12 – 24 | 27 |

Now, answer the following questions:
(A) What is the modal value of the given data? (2)
Answer:
In the given data modal class is 8 – 10
Here,
l = 8,
fo = 58,
f1 = 70,
f2 =40
h =2
Mode = l + \(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\) × h
= 8 + \(\frac{70-58}{140-58-40}\) × 2
= 8 + \(\frac{12 \times 2}{42}\)
= 8 + 0.57
= 8.57 (approx)
(B) What is the difference between lower limit of modal class and upper limit of median class? (2)
Answer:
Here, modal class is 8 – 10 and for median class:
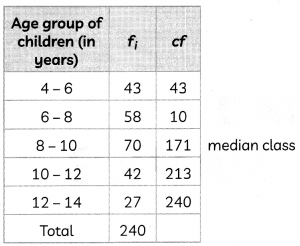
Here, N = 240
Then, \(\frac{N}{2}\) = \(\frac{240}{2}\) = 120
∴ Required difference = 10 – 8 = 2
Question 14.
Case Study-2
Rajesh was getting bored on a sunny afternoon. So he started playing a number card game. In the game, some number cards, in both + ve and – ve numbers are arranged in a row, such that they follows an arithmetic progression. In his first turn, he picked up 6th and 14th card, and find sum to be – 76. On the next pick, he picked 8th and 16th card and find their sum to be – 96. Now, answer the following questions.

(A) If the number on the cards form an A.P., then what is the common difference of the A.P.? (2)
Answer:
– 5
Explanation: Let, the numbers be a, a + d,
a + 2d …….
A.T.Q.,
a + 5d + a + 13 d = – 76
2a + 18d = – 76
or a + 9d = – 38 ………. (i)
And (a + 7d) + (a + 15d) = – 96
2a + 22d = – 96
or a + 11d = – 48 ……… (ii)
On solving (i) and (ii) we get
d = – 5
(B) Evaluate the average of 18th term and 9th term. (2)
Answer:
Here,
a18 = a + 17d
= 7 + 17 × (- 5)
= 7 – 85
= – 78
a9 = a + 8d
= 7 + 8 × (- 5)
= 7 – 40
= – 33
∴ a18 + a9 = – 78 – 33
= – 111
Then, \(\frac{a_{18}+a_{9}}{2}\) = \(\frac{-111}{2}\)
= – 55.5