CBSE Sample Papers for Class 10 Maths Basic Set 9 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 9 are designed as per the revised syllabus. BERGEPAINT Pivot Point Calculator

CBSE Sample Papers for Class 10 Maths Basic Set 9 with Solutions

Time : 3 hrs
Max. Marks : 80

General Instructions:

1. This question paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) Type Questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) Type Questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) Type Questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section – A
Section A consists of 20 questions of 1 mark each

Question 1.
Check the relation between the following triangles

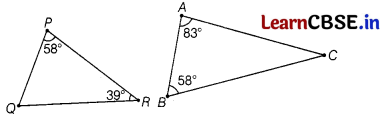
(a) similar by SAS
(b) similar by AAA
(c) similar by SSS
(d) similar by ASS
Answer:
(b) similar by AAA

In ∆ABC,
∠A + ∠B + ∠C = 180°
[sum of all angles of a triangle is 180°]
83° + 58° + ∠C = 180°
∠C = 180° – (83° + 58°)
∠C = 39°
Now, In ∆ABC and ∆QPR,
∠P + ∠Q + ∠R = 180°
⇒ 58° + ∠Q + 39° = 180°
⇒ ∠Q = 180° – (58° + 39°)
⇒ ∠Q = 83°
Now, In ∆ABC and ∆QPR,
∠A = ∠Q = 83°
∠B = ∠P = 58°
∠C = ∠R = 39°
∴ ∆ABC ~ ∆QPR [by AAA similarity criterion]

Question 2.
The value(s) of a, if the distance between the points (a, – 1) and (3, 2) is 5 units, is / are
(a) 7 only
(b) 1, – 7
(c) – 6, – 7
(d) 7, – 1
Answer:
(d) 7, – 1

Let A (a, – 1) and B (3, 2) be the given points,
then AB = 5
⇒ \(\sqrt{(a-3)^2+(-1-2)^2}\) = 5
⇒ (a – 3)² + (- 3)² = 25
⇒ a² + 9 – 6a + 9 = 25
⇒ a² – 6a + 18 – 25 = 0
⇒ a² – 6a – 7 = 0
⇒ (a – 7) (a + 1) = 0
⇒ a = 7 or a = – 1.

Question 3.
The distance between two parallel tangents to a circle of radius 7 cm is
(a) 7 cm
(b) 14 cm
(c) 3.5 cm
(d) 49 cm
Answer:
(b) 14 cm

The distance between two parallel tangents to a circle of radius 7 cm is
2 × 7 = 14 cm

Question 4.
In the given figure, if ∠PQR = 25°, then the value of ∠POR is

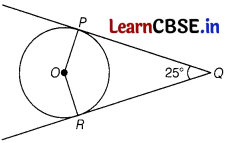
(a) 135°
(b) 155°
(c) 145°
(d) 165°
Answer:
(b) 155°

OP ⊥ QP and OR ⊥ QR
In quadrilateral OPQR,
∠OPQ + ∠PQR + ∠QRO + ∠MOP = 360°
⇒ 900+25e + 90° + IROP = 360°
⇒ ∠ROP = 360° – 180° – 25° = 155°

Question 5.
The minute hand of a clock is 12 cm long. The area of the face of the clock described by the minute hand in 35 min is
(a) 264 cm²
(b) 220 cm²
(c) 320 cm²
(d) 450 cm²
Answer:
(a) 264 cm²

(a) Angle subtended in 60 min = 360°
Angle subtended in 35 min = \(\left(\frac{360}{60} \times 35\right)^{\circ}\) = 210°
∴ θ = 210°
and r = 12 cm
Area swept by the minute hand in 35 min = \(\left(\frac{\pi r^2 \theta}{360^{\circ}}\right)\)
= \(\left(\frac{22}{7} \times 12 \times 12 \times \frac{210^{\circ}}{360^{\circ}}\right)\)
= 264 cm²

Question 6.
The value of cos 60° cos 30° – sin 60° sin 30° is
(a) 0
(b) 1
(c) 4
(d) 2
Answer:
(a) 0

We have,
cos 60° cos 30° – sin 6o° sin 30° = \(\left(\frac{1}{2} \times \frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2} \times \frac{1}{2}\right)\)
= \(\left(\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}\right)\) = 0

Question 7.
The nature of the roots of the equation 3x² + 6x + 1 = 0 is
(a) real, unequal and rational
(b) real and unequal
(c) real, unequal and irrational
(d) imaginary
Answer:
(c) real, unequal and irrational

Given, 3x² + 6x + 1 = 0
a = 3,
b = 6
and c =1
Discriminant, D = b² – 4ac
= (6)² – 4 × 3 × 1
= 36 – 12
= 24 > 0
We know that 24 is not a perfect square, so the roots will contain an irrational part.
Hence, the given equation has two distinct real and irrational roots.

Question 8.
The values of t, if (t + 4) x² + (t + 1) x + 1 = 0 has real and equal roots, are
(a) – 5, + 3
(b) – 3, – 5
(c) 5, 3
(d) – 3, 5
Answer:
(d) – 3, 5

Discriminant = b² – 4ac
= (t + 1)² – 4 (t + 4) × 1
= t² – 2t – 15
For equal roots, discriminant = 0
∴ t² – 2t – 15 = 0
t² – 5t + 3t – 15 = 0
t (t – 5) + 3 (t – 5) = 0
(t + 3) (t – 5) = 0
t = 5 or t = – 3
Hence, the values oft are 5 and – 3.

Question 9.
Find a quadratic polynomial whose zeroes are 1 and – 3. Verify relation between the coefficients and zeroes of the polynomial.
(a) x² + 4x + 3
(b) x² + 2x – 3
(c) x² + x – 3
(d) x² – 3x + 1
Answer:
(b) x² + 2x – 3

Let the zeroes of the quadratic polynomial be α = 1
and β = – 3
Sum of zeroes = (α + β)
= 1 + (- 3) = – 2
Product of zeroes = αβ
= 1 × (- 3) = – 3
So, the quadratic polynomial is
x² – (α + β) x+ αβ = x² – (- 2)x + (- 3)
= x² + 2x – 3

∴ Sum of zeroes = – 2
= \(\frac{-2}{1}\)
= \(\frac{- \text { Coefficient of } x}{\text { Coefficient of } x^2}\)

and product of zeroes = – 3
= \(\frac{-3}{1}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)

Question 10.
If the HCF of 35 and 45 is 5, LCM of 45 and 35 is 63 × a, then the value of a is
(a) 3
(b) 5
(c) 8
(d) 6
Answer:
(b) 5

We have,
HCF × LCM = Product of two numbers
5 × 63 × a = 35 × 45
⇒ a = \(\frac{35 \times 45}{63 \times 5}\)
⇒ a = 5

Question 11.
Two unbiased coins are tossed simultaneously. The probability of getting no head, is
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{3}{4}\)
Answer:
(c) \(\frac{1}{4}\)

Total number of elementary events = 4
(HT, TH, HH, TT)
No head is obtained i.e. TT.
∴ Favourable number of elementary elements = 1
∴ Required probability = \(\frac{1}{4}\)

Question 12.
In the given figure, MN || AB, BC = 7.5 cm, AM = 4 cm and MC = 2 cm. Then, the length of BN is

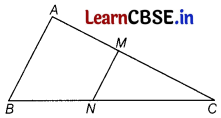
(a) 4 cm
(b) 2 cm
(c) 2√2 cm
(d) 5 cm
Answer:
(d) 5 cm

We know that
In ∆ABC, MN || AB
∴ \(\frac{M C}{A C}=\frac{N C}{B C}\) [by Thales theorem]
⇒ \(\frac{M C}{A M+M C}=\frac{N C}{B C}\)
⇒ \(\frac{2}{4+2}=\frac{y}{7.5}\) ,where NC = y cm
⇒ y = \(\frac{2 \times 7.5}{6}=\frac{15}{6}\) =2.5
⇒ NC = 2.5 cm
Hence, BN = BC – NC
= (7.5 – 2.5) cm = 5 cm

Question 13.
If 47x + 31y = 18 and 31x + 47y = 60, then the value of x + y is
(a) 1
(b) 2
(c) 36
(d) 78
Answer:
(a) 1

Given, 47x + 31y = 18 ………….(i)
and 31x + 47y =60 …………..(ii)
On adding Eqs. (i) and (ii), we get
78x + 78y =78
⇒ x + y = 1 [divide both sides by 78]

Question 14.
The value of \(\frac{\sin \theta}{1+\cos \theta}+\frac{1+\cos \theta}{\sin \theta}\) is
(a) sec θ
(b) 2 cosec θ
(c) cosec θ
(d) 2 cos θ
Answer:
(b) 2 cosec θ

Question 15.
In the given figure, DE || BC. If AD = 5 cm, BD = 8 cm and AE = 10 cm, then the value of EC is

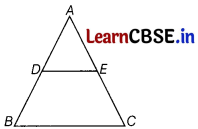
(a) 8 cm
(b) 16 cm
(c) 4 cm
(d) 5 cm
Answer:
(b) 16 cm

In ∆ABC, DE || BC
Let EC = x cm,
then \(\frac{A D}{D B}=\frac{A E}{E C}\)
[by Basic Proportionality theorem]
⇒ \(\frac{5}{8}=\frac{10}{x}\)
⇒ x = \(\frac{10 \times 8}{5}\) = 16
∴ EC = 16 cm

Question 16.
The value of \(\frac{2 \sin 30^{\circ}}{1-\cos ^2 60^{\circ}}\) is
(a) 4√3
(b) \(\frac{4}{3}\)
(c) 4
(d) \(\frac{4}{\sqrt{3}}\)
Answer:
(b) \(\frac{4}{3}\)

\(\frac{2 \sin 30^{\circ}}{1-\cos ^2 60^{\circ}}=\frac{2 \times \frac{1}{2}}{1-\left(\frac{1}{2}\right)^2}\)
= \(\frac{1}{1-\frac{1}{4}}\)
= \(\frac{1}{3 / 4}=\frac{4}{3}\)

Question 17.
Which of the following is not a polynomial?
(a) 2x^-3 – 5 + 3x^-1
(b) x³ + 2x – 9
(c)(x – 2)² + 3x
(d) \(\frac{(2 x+10)}{x+5} \times\left(x^2-25\right)\)
Answer:
(a) 2x^-3 – 5 + 3x^-1

A polynomial is an algebraic expression containing two or more terms.
Also, it requires the exponents of the variables in the each term should be positive integer.

(a) 2x³ – 5 + 3x^-1 it is not polynomial, because it has negative power in two terms.
(b) x³ + 2x – 9, it is a polynomial.
(c) (x – 2)² + 3x = x² + 4 – 4x + 3x
= x² – x + 4, it is a polynomial.
(d) \(\frac{2 x+10}{x+5}\) × (x² – 25)
= \(\frac{2(x+5)}{(x+5)}\) × (x² – 25)
= 2x² – 50, it is a polynomial.

Question 18.
The sum of the numerator and denominator of a fraction \(\frac{x}{y}\) is 8. If the denominator is increased by 1, the fraction becomes \(\frac{1}{2}\). The situation can be represented algebraically as
(a) x + y = 8 and \(\frac{x+1}{y}=\frac{1}{2}\)
(b) x + y = 8 and \(\frac{x}{y}+1=\frac{1}{2}\)
(c) \(\frac{x}{y\) = 8 and \(\frac{x}{y+1}=\frac{1}{2}\)
(d) x + y =8 and \(\frac{x}{y+1}=\frac{1}{2}\)
Answer:
(d) x + y =8 and \(\frac{x}{y+1}=\frac{1}{2}\)

We have, numerator and denominator of the fraction be x and y, respectively.
Sum of numerator and denominator = 8
i.e. x + y = 8
Since, denominator is increased by 1 i.e.
New denominator = y + 1
∴ New fraction is \(\frac{x}{y+1}=\frac{1}{2}\)
Hence, algebraically the situation can be represented as x + y = 8 and \(\frac{x}{y+1}=\frac{1}{2}\).

Directions : In the question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) : If length of a tangent from an external point to a circle is 18 cm, then length of the other tangent from the same point is 18 cm.
Reason (R) : Length of the tangents of drawn from an external point to a circle are equal.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

Both Assertion (A) and Reason (R) are true and Reason (R) is the correct exp!anation of Assertion (A).

Question 20.
Assertion (A) : ABCD is a trapezium with DC || AB. E and F are points on AD and BC respectively such that EF || AB. Then, \(\frac{A E}{E D}=\frac{B F}{F C}\).
Reason (R) : Any line parallel to parallel sides of a trapezium divides the non-parallel sides proportionally.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

Given, EF || AB
∴ OE || AB || CD
[∵ AB || CD]
In ∆ACD,
\(\frac{A E}{E D}=\frac{A O}{O C}\) [by BPT] …………(i)
Similarly in ∆ABC,
\(\frac{A O}{O C}=\frac{B F}{F C}\) …………. (ii)
From Eqs. (i) and (ii),
\(\frac{A E}{E D}=\frac{B F}{F C}\)

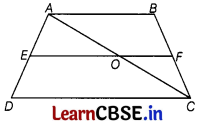
∴ Any line parallel to parallel sides of a trapezium divides the non-parallel sides proportionally.
Both Assertion (A) and Reason (R) are True and Reason (R) is the correct explanation of Assertion (A).

Section – B
Section B consists of 5 questions of 2 marks each

Question 21.
The following table shows the heights (in cm) of 50 girls of Class X of a school.

Find the mean of the above data.
Answer:
Let assumed mean, A = 145
Table for deviation is given below.

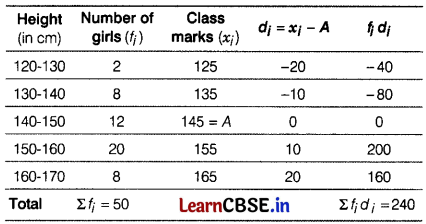
Here, Σf_i = 50
and Σf_id_i = 240
∴ Mean = A + \(\frac{\Sigma f_i d_i}{\Sigma f_i}\)
= 145 + \(\frac{240}{50}\)
= 145 + 48 = 149.8

Question 22.
Find the value of x in √3 tan 2 x = cos 60° + sin 45° cos 45°.
Answer:
Given, √3 tan 2x = cos 60° + sin 45° cos 45°
∴ √3 tan 2x = \(\frac{1}{2}+\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\)
⇒ tan 2x = \(\frac{1}{\sqrt{3}}\left(\frac{1}{2}+\frac{1}{2}\right)\)
⇒ tan 2x = \(\frac{1}{\sqrt{3}}\)
⇒ tan 2x = tan 30°
⇒ 2x = 30°
⇒ x = 15°

Or

If sin(A + B) = 1 and cos (A – B) = \(\frac{\sqrt{3}}{2}\); 0° < A + B ≤ 90°, A > B then find the values of A and B.
Answer:
We have, sin (A + B) = 1
⇒ sin (A + B) = sin 90°
[∵ sin 90° = 1]
⇒ A + B = 90° ………….(ii)
Now, cos (A – B) = \(\frac{\sqrt{3}}{2}\)
⇒ cos (A – B) = cos 30°
⇒ A – B = 30° ………..(ii)
On solving Eqs. (i) and (ii), we get
A = 60° and B = 30°.
Hence, A = 60° and B = 30°
[∵ cos 30° = \(\frac{\sqrt{3}}{2}\)]

Question 23.
Solve for x and y, using substitution method.
\(\frac{3 x}{2}-\frac{5 y}{3}\) = – 2, \(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\)
Answer:
Given pair of equation are
9x – 10y + 12 = 0 ……………(i)
2x + 3y – 13 = 0 …………….(ii)
From Eq. (ii), we get
y = \(\frac{13-2 x}{3}\)
On substituting y = \(\frac{13-2 x}{3}\) in Eq. (i), we get
9x – \(\frac{10(13-2 x)}{3}\) + 12 = 0
⇒ 27x – 10 (13 – 2x) + 36 = 0
⇒ 27x – 130 + 20x + 36 = 0
⇒ 47x – 94 = 0
⇒ 47x = 94
⇒ x = \(\frac{94}{47}\) = 2
Now, on substituting x = 2 in Eq. (i), we get
9 × 2 – 10y + 12 = 0
⇒ 10y = 30
⇒ y = \(\frac{30}{10}\) = 3
Hence, x = 2 and y = 3.

Question 24.
The difference between two numbers is 26 and one number is three times the other number. Find the numbers.
Answer:
Let the two numbers be x and y (x > y).
According to the question,
x – y = 26 ………….(i)
and x = 3y ………….(ii)
On substituting the value of x from Eq. (ii) in Eq. (i), we get
3y – y = 26
⇒ 2y = 26
⇒ y = 13
On substituting y = 13 in Eq. (ii), we get
x = 3 × 13
⇒ x = 39
Hence, the two numbers are 39 and 13.

Question 25.
If the 3rd and 9th terms of an AP are 4 and – 8 respectively, then which term of this AP is zero?
Answer:
Let a be the first term and d be the common difference of an AP
∵ The nth term of an AP is a_n = a + (n – 1) d
∴ a₃ = a + 2d = 4 [∵ a₃ = 4, given] …………..(i)
and a₉ = a + 8d = – 8 [: a₉ = – 8, given] …………(ii)
On subtracting Eq. (i) from Eq. (ii), we get
6d = – 12
⇒ d = \(\frac{-12}{6}\) = – 2
On putting the value of d in Eq. (i), we get
a + 2 × (- 2) = 4
⇒ a – 4 = 4
⇒ a = 4 + 4 = 8
Let the nth term of this AP be zero
i.e. a = 0
⇒ a+(n – 1) d = 0
⇒ 8 + (n – 1)(- 2) = 0 [∵ a = 8 and d = – 2]
⇒ (n – 1) (- 2) = – 8
⇒ n – 1 = \(\frac{-8}{-2}\) = 4
∴ n = 4 + 1 = 5
Hence, 5th term of this AP is zero.

Or

Find the common difference of an AP, whose first term is 1/2 and the 8th term is 17/6. Also, find the ratio of 4th term and 50th term.
Answer:
Let a be the first term and d be the common difference of an AP
Then, nth term,
T_n = a + (n – 1) d
Given, 8th term, T₈ = \(\frac{17}{6}\)
⇒ a + 7d = \(\frac{17}{6}\)
⇒ \(\frac{1}{2}\) + 7d = \(\frac{17}{6}\) [∵ a = \(\frac{1}{2}\)]
⇒ 7d = \(\frac{17}{6}-\frac{1}{2}\)
⇒ 7d = \(\frac{14}{6}\)
⇒ d = \(\frac{1}{3}\)
Now 4th term,
T₄ = a + 3d
= \(\frac{1}{2}\) + 3 (\(\frac{1}{3}\))
= \(\frac{1}{2}\) + 1
= \(\frac{3}{2}\)
and 50th term, T₅₀ = a + 49d
= \(\frac{1}{2}+49 \times \frac{1}{3}\)
= \(\frac{101}{6}\)
∴ Required ratio = \(\frac{3 / 2}{101 / 6}\)
= \(\frac{3}{2} \times \frac{6}{101}\)
= 9 : 101

Section – C
Section C consists of 6 questions of 3 marks each

Question 26.
If α and β are zeroes of the polynomial x² – 2x – 15, then form a quadratic polynomial whose zeroes are 2α and 2β.
Answer:
Let p(x) = x² – 2x – 15
On comparing with ax² + bx + c we get
a = 1, b = – 2 and c = – 15
Given, α and β are the zeroes of p(x).
∴ Sum of zeroes (α + β) = – \(\frac{b}{a}\)
⇒ α + β = – \(\frac{(-2)}{1}\)
⇒ α + β = 2 …………..(i)
and pcoduct of zeroes, (α.β) = \(\frac{c}{a}\)
⇒ αβ = \(\frac{-15}{1}\)
⇒ αβ = – 15 …………..(ii)
We have, to form a polynomial whose zeroes are 2α and 2β.
∴ Sum of zeroes = 2α + 2β = 2 (α + β)
= 2 × 2 = 4 [using Eq. (i)]
and product of zeroes = (2α) . (2β)
= 4αβ
= 4 × ( – 15)
= – 60 [using Eq. (ii)]
∴ Required polynomial = x² – (Sum of zeroes) x + (Product of zeroes)
= x² – 4x + (- 60)
= x² – 4x – 60.

Question 27.
A health officer took an initiative of organising a medical camp in a remote village. The medical checkup of 400 students of the age group of 10 yr and their heights were recorded as follows.

Height (in cm)	Frequency
160 – 162	15
163 – 165	117
166 – 168	136
169 – 171	118
172 – 174	14

Answer:
The given series is in inclusive form. Converting it to exclusive form and preparing the cumulative frequency table is given below

Class Interval	Frequency (fi)	Cumulative frequency
159.5 – 162.5	15	15
162.5 – 165.5	117	132
165.5 – 168.5	136	268
168.5 – 171.5	118	386
171.5 – 174.5	14	400
Total	N = Σfi = 400

Here, N = 400
Now \(\frac{N}{2}=\frac{400}{2}\) = 200
The cumulative frequency just greater than 200 is 268
and the corresponding class is 165.5 – 1685.
Thus, the median class is 165.5 – 168.5.
∴ l = 165.5, h = 3, f = 136 and C = 132
∴ Median = l + \(\left\{h \times \frac{\frac{N}{2}-C}{f}\right\}\)
= 165.5 + \(\left\{3 \times \frac{200-132}{136}\right\}\)
= 165.5 + \(\frac{3 \times 68}{136}\)
= 165.5 + 1.5
= 167
Hence, the median height is 167 cm.

Question 28.
Find the sum of first 22 terms of an AP in which 3rd term is 7 and 7th term is two more than thrice of its 3rd term.
Answer:
Let a be the first term and d be the common difference of an AP.
Then, a₃ = 7
and a₇ = 3a₃ + 2
⇒ a + (3 – 1) d = 7
and a + (7 – 1) d = 3 [a + (3 – 1) d] + 2
[∵ a_n = a (n – 1) d]
⇒ a + 2d = 7 and a + 6d =3 [a + 2d] + 2
⇒ a + 2d = 7 and 2a + 2 = 0
⇒ a + 2d = 7 and a = – 1
On putting the value of a in a + 2d = 7, we get
⇒ – 1 + 2d = 7
⇒ 2d = 8
⇒ d = 4.
∴ Sum of first 22 terms,
S₂₂ = \(\frac{22}{2}\) [2 × (- 1) + (22 – 1) × 4]
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1) d]]
= 11 [- 2 + 84]
= 11 × 82
= 902

Or

Anjali started work in 2001 at an annual salary of ₹ 5000 and received a ₹ 200 raise each year. In what year did his annual salary will reach ₹ 8000?
Answer:
Annual salary received by Anjali in 2001. 2002, 2003, ………… is ₹ 5000, ₹ 5200, ₹ 5400, ……………..
Clearly, it is an arithmetic progression with
first term a = 5000
and common difference, d = 200
Suppose Anjali annual salary reaches to 8000 in nth years.
Then, nth term of the above AP = ₹ 8000
a + (n – 1) d = 8000
⇒ 5000 + (n – 1) 200 = 8000
⇒ (n – 1) 200 = 3000
⇒ n – 1 = \(\frac{3000}{200}\)
⇒ n – 1 = 15
⇒ n = 16
Thus 16th annuat salary received by Anjah will be ₹ 8000.
This means that after 15 yr i.e. in the year 2016 his annual salary will reach to ₹ 8000.

Question 29.
In the given figure, AB is a diameter of the circle with centre O and AT is a tangent. Calculate the numerical value of x.

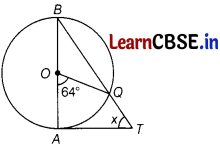
Answer:
Given, O is the centre of a circle AB is diameter and AT is tangent at A.
Also, ∠AOQ = 64°
∵ OA is radius and AT is tangent.
∴ ∠OAT = 90°

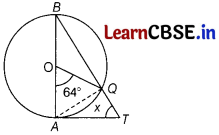
Also, ∠AOQ = 64° [given]
∴ ∠BOQ = 180° – ∠AOQ
= 180° – 64° = 116°
[linear pair axiom]
But OB = OQ [radii]
∠OQB = ∠OBQ
[∵ angles opposite to equal sides of a triangle are equal]
But ∠OBQ + ∠OQB + ∠BOQ = 180°
[by angle sum property of a triangle]
⇒ ∠OBQ + ∠OQB = 180° – 116° = 64° [using Eq. (i)]
⇒ ∠OBQ + ∠OBQ = 64°
⇒ ∠OBQ = 32°
∴ ∠OQB = 32° [∵ ∠OBQ = ∠OOB]
Now, in ∆BAT,
∠ABT + ∠BAT + ∠ATB = 180°
⇒ 32° + 90°+ x = 180°
[∵ ∠BAT = ∠OAT = 90°]
⇒ x = 180° – 32° – 90°
⇒ x = 58°.

Question 30.
A window of a house is h m above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be a and |3, respectively. Prove that the height of the other house is h (1 + tan α cot β) m.
Answer:
Let B be the position of the window

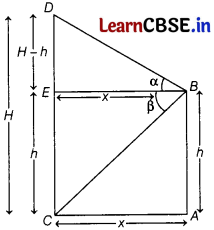
∴ AB = h m
Let CD = H m be the height of another house which is situated on the opposite side of the lane.
From the position of window B, the elevation and
depression are ∠EBD = α and ∠EBC = β
Draw a perpendicular line BE to the CD.
Let AC = BE = x
In right angled ∆EBD,
tan α = \(\frac{E D}{B E}\)
⇒ tan α = \(\frac{H-h}{x}\)
x = (H – h) cot α ………….(I)
In right angled ∆ABC,
tan β = \(\frac{A B}{C A}\)
⇒ tan = \(\frac{h}{x}\)
tan β = \(\frac{h}{(H-h) \cot \alpha}\) [from Eq. (i)]
(H – h) = h tan α cot β
∴ H = h (1 + tan α cot β).

Or

A balloon is connected to an electric pole. It is inclined at 60° to the horizontal by a cable of length 215 m. Determine the height of the balloon from the ground. Also, find the height of the balloon, if the angle of inclination is changed from 60° to 30°.
Answer:
Let D be the position of the balloon, when it is inclined at angle of 60°
and AB be the height of the pole.

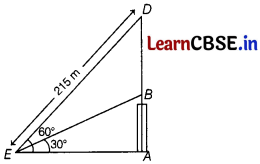
Given, length of cable,
DE = 215 m
In right angled ∆EAD,
sin 60° = \(\frac{A D}{E D}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{A D}{215}\) [∵ sin 60 = \(\frac{\sqrt{3}}{2}\)]
⇒ AD = \(\frac{215 \sqrt{3}}{2}\)
Hence, the initiai height of the balloon from the ground is \(\frac{215 \sqrt{3}}{2}\) m.
Again, in right angled ∆EAD,
cos 60° = \(\frac{A E}{D E}=\frac{A E}{215}\)
⇒ \(\frac{1}{2}=\frac{A E}{215}\)
⇒ AE = \(\frac{215}{2}\)
In right angled ∆EAB,
tan 30° = \(\frac{A B}{A E}\)
AB = \(\frac{215}{2 \sqrt{3}}\)
= \(\frac{215 \sqrt{3}}{6}\) m.

Question 31.
A chord AC of a circle of radius 10 cm makes a right angle at the centre. Find the areas of the minor segment and major sector of the circle, (π = 3.14)
Answer:
Given, radius of a circle AO = 10 cm
A perpendicular is drawn from centre of circle to the chord of the circle, which bisects the chord.

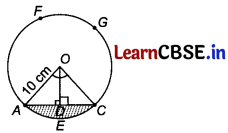
∴ AD = DC
Also, ∠AQD = ∠CQD = 45°
∠AOC = ∠AOD + ∠COD
= 45° + 45° = 90°
In right angled ∆AOD,
sin 45° = \(\frac{A D}{A O}\)
⇒ \(\frac{1}{\sqrt{2}}=\frac{A D}{10}\)
⇒ AD = 5√2 cm
and cos 45° = \(\frac{O D}{A O}\)
\(\frac{1}{\sqrt{2}}=\frac{O D}{10}\)
⇒ OD = 5√2 cm
Now, AC = 2 AD
= 2 × 5√2
= 10√2 cm
Now, area of ∆AOC = \(\frac{1}{2}\) AC × OD
= \(\frac{1}{2}\) × 10√2 × 5√2
= 50 cm²
Now, area of sector = \(\frac{\theta \pi r^2}{360^{\circ}}\)
= \(\frac{90^{\circ}}{360^{\circ}}\) × 3.14 × (10)²
= \(\frac{314}{4}\)
= 78.5 cm

(i) ∴ Area of minor segment AEC = Area of sector OAEC – Area of AOC
= 78.5 – 50
= 28.5 cm²

(ii) ∴ Area of major sector OAFGCO = Area of circle – Area of sector OAEC
= πr² – 78.5
= 3.14 × (10)² – 78.5
= 314 – 78.5
= 235.5 cm²

Section – D
Section D consists of 4 questions of 5 marks each

Question 32.
A sailor can row a boat 8 km downstream and return back to the starting point in 1 h 40 min. If the speed of the stream is 2 km/h, then find the speed of the boat in still water.
Answer:
Let the speed of the boat in still water be x km/h.
Speed of the stream = 2 km/h
:. Speed to travel downstream = (x + 2) km/h
Speed to travel upstream = (x – 2) km/h
Time taken to cover 8 km downstream and return back to the starting point = \(\frac{8}{(x+2)}+\frac{8}{(x-2)}\)
TotaL time = 1 h 40 min = \(\frac{5}{3}\) h
∴ \(\frac{8}{x+2}+\frac{8}{x-2}=\frac{5}{3}\)
⇒ \(\frac{1}{x+2}+\frac{1}{x-2}=\frac{5}{24}\)
⇒ \(\frac{(x-2)+(x+2)}{(x+2)(x-2)}=\frac{5}{24}\)
⇒ \(\frac{2 x}{\left(x^2-4\right)}=\frac{5}{24}\)
⇒ 5x² – 20 = 48x
⇒ 5x² – 48x – 20 = 0
⇒ 5x² – 50x + 2x – 20 = 0
⇒ 5x (x – 10) + 2 (x – 10) = 0
⇒ (x – 10) (5x + 2) = 0
⇒ x – 10 = 0 or 5x + 2 = 0
⇒ x = 10 or x = \(\frac{-2}{5}\)
⇒ x = 10 [∵ speed of the boat cannot be negative]
Hence, the speed of the boat in still water is 10 km/h.

Or

A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 m² more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m. Find its length and breadth.
Answer:
Let breadth of the rectangular park be x m.
So, its length = (x + 3) m
Therefore, the area of the rectangular park = Length × Breadth
= x × (x+ 3)
= (x² + 3x) m²

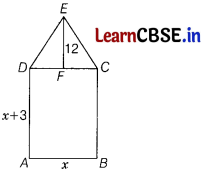
In the figure, AB = DC = x
Now, area of ∆DEC = \(\frac{1}{2}\) × DC × EF
= \(\frac{1}{2}\) × x × 12 = 6x m²
According to the given condition,
Area of rectangular park = Area of an isosceles triangle + 4
⇒ x² + 3x = 6x + 4
⇒ x² – 3x – 4= 0
By using quadratic formula,
x = \(\frac{-(-3) \pm \sqrt{(-3)^2-4 \times 1 \times(-4)}}{2(1)}\)
= \(\frac{3 \pm \sqrt{9+16}}{2}\)
= \(\frac{3 \pm 5}{2}\)
= \(\frac{8}{2} \text { or }-\frac{2}{2}\)
= 4 or – 1
But x ≠ – 1 [∵ x cannot be negative]
Therefore, x = 4,
So, the breadth of the park = 4 m
and its length will be = 4 + 3 = 7 m.

Question 33.
A container shape like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
Answer:
Let V₁ be the volume of the given ice-cream container.

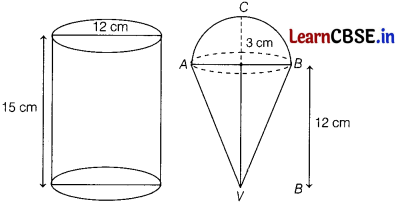
Let V₁ = \(\frac{2}{3}\) πr³ + \(\frac{1}{3}\) πr²h
= π [\(\frac{2}{3}\) × (3)³ + \(\frac{1}{3}\) × 3² × 12]
= π [18 + 36]
= 54π cm³
Let V₂ be the volume of ice-cream filled in the shape of circular cylinder having diameter 12 cm and height = 15 cm
V₂ = πr₁²h₁
= π (6)² (15)
= 540 π
Let the total number of cones that can be filled with ice-cream given in the container be n.
Then,
Volume of ice-cream in n cones = Volume of ice-cream in the container
⇒ nV₁ = V₂
⇒ n × 54π = 540π
⇒ n = 10.

Question 34.
A die is thrown once. Find the probability of getting

(i) a even prime number.
Answer:
On a die, there are six numbers 1, 2, 3, 4, 5 and 6.
∴ Total number of possible outcomes = 6

Let E₁ = Event of getting a even prime number
Then, E₁ would consist of one outcome namely 2.
∴ Number of outcome favourable to E₁ = 1
Probability of getting prime number, P(E₁) = \(\frac{1}{6}\)

(ii) a number lying between 2 and 6.
Answer:
Let E₂ = Event of getting a number lying between 2 and 6
Then, E₂ would consist of three outcomes, namely 3, 4 and 5.
∴ Number of outcomes favourable to E₂ = 3
Probability of getting a number lying between 2 and 6,
P(E₂) = \(\frac{3}{6}=\frac{1}{2}\)

(iii) an odd prime number.
Answer:
Let E₃ = Event of getting an odd prime number
Favourable outcomes = 3, 5
∴ Number of favourabLe outcomes = 2
Probability of getting an odd number P(E₃) = \(\frac{2}{6}=\frac{1}{3}\)

Or

One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting

(i) a king of red colour.
Answer:
Total number of cards in one deck of cards is 52.
Total number of outcomes = 52

Let E₁ = Event of getting a king of red colour
∴ Number of outcomes favourable to E₁ = 2
[∵ there are four kings ¡n a deck of playing cards out of which two are red and two are black]
Hence, probability of getting a king of red colour,
P(E₁) = \(\frac{2}{52}=\frac{1}{26}\)

(ii) a face card.
Answer:
Let E₂ = Event of getting a face card
∴ Number of outcomes favourable to E₂ = 12
[∵ in a deck of cards, there are 12 face cards, namely 4 kings, 4 jacks, 4 queens]
Hence, pobability of getting a face card,
P(E₂) = \(\frac{12}{52}=\frac{3}{13}\)

(iii) the jack of heart.
Answer:
Let E4 = Event of getting a jack of heart
∴ Number of outcomes favourable to E₄ = 1
[∵ there are four jack cards in a deck, namely 1 of heart, 1 of club.1 of spade and 1 of diamond]
Hence, probability of getting a jack of heart,
P(E₄) = \(\frac{1}{52}\)

(iv) a spade.
Answer:
Let E5 = Event of gõtting a spade
∴ Number of outcomes favourable to E₅ = 13
[∵ in a deck of cards, there are 13 spades, 13 clubs, 13 hearts and 13 diamonds]
Hence, probability of getting a spade.
P(E₅) = \(\frac{13}{52}=\frac{1}{4}\)

Question 35.
An army pilot is flying an aeroplane at an altitude of 1800 m observes some suspicious activity of two ships which are sailing towards it in the same directions and immediately report it to the navy chief. The angles of depression of the ships as observed from the aeroplane are 60° and 30°, respectively. Find the distance between two ships.
Answer:
Let the aeroplane is at B and Let the two ships are at point C and D such that their angles of depression from B are 60° and 30°, respectively.
We have, AB = 1800 m

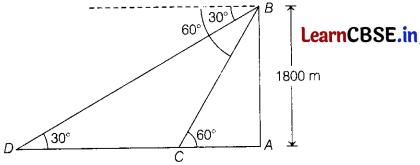
Now, in ∆BAC, we have
tan 60° = \(\frac{A B}{A C}\)
[∵ tan θ = \(\frac{\text { Perpendicular }}{\text { Base }}\)]
⇒ √3 = \(\frac{1800}{AC}\)
[∵ tan 60° = √3]
⇒ AC = \(\frac{1800}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
and in ∆BAD, we have
tan 30° = \(\frac{A B}{A D}\)
= \(\frac{1800}{A C+C D}\)
[∵ AD = AC = CD]
⇒ \(\frac{1}{\sqrt{3}}=\frac{1800}{600 \sqrt{3}+C D}\)
[∵ tan 30° = \(\frac{1}{\sqrt{3}}\)]
⇒ CD + 600√3 = 1800√3
⇒ CD = 1800√3 – 600√3
= 1200√3 m
Hence, the distance between the two ships is 1200√3 m.

Section – E
Case study based questions are compulsory

Question 36.
A student of Class X standard observing a girl of height 120 cm walking away from the base of lamp-post at a speed of 2.0 m/s. If the lamp is 5 m above and xbc the length of her shadow after 6 s.
The figure is shown below

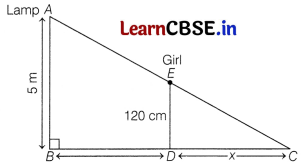
Give answer to his questions by looking at the figure.

(i) Find the distance of girl from lamp-post after 6s.
Answer:
Distance of the girl from lamp-post after 6 s.
BD = 2.0 × 6 = 12 m

(ii) Find the ratio of the squares of sides ED and AB.
Answer:
\(\left(\frac{E D}{A B}\right)^2=\left(\frac{1.2}{5}\right)^2\)
= \(\frac{1.44}{25} \times \frac{4}{4}\)
= \(\frac{5.76}{100}\)
= 0.00576

Or

Find the length of her shadow after 6 s.
Answer:
From part (ii), we have ∆ABC ~ ∆EDC
⇒ \(\frac{B C}{D C}=\frac{A B}{E D}\)
⇒ \(\frac{12+x}{x}=\frac{5}{1.2}\)
⇒ 14.4 + 1.2x = 5x
⇒ 3.8x = 14.4
⇒ x = \(\frac{14.4}{3.8}\) = 3.8 m [approx]

(iii) Which is the correct similarity criteria application for ∆ABC and ∆EDC?
Answer:
In ∆ABC and ∆EDC
∠B = ∠D = 90°
∠C = ∠C [common angle]
∴ By AA similarity criterion
∆ABC ~ ∆EDC

Question 37.
Class X students of a school in Gomtinagar have been alloted a rectangular plot of a land for gardening activity. Sapling of roses are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy fountain in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

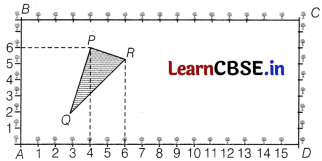
Considering A as origin answer the following questions

(i) What are the coordinates of R?
Answer:
The coordinates of R is (6, 5) as the point is 6 units on X-axis and 5 units on Y-axis.

(ii) What is the centroid of ∆PQR?
Answer:
The centroid of ∆PQR is \(\left(\frac{4+3+6}{3}, \frac{6+2+5}{3}\right)\) i.e., \(\left(\frac{13}{3}, \frac{13}{3}\right)\)

(iii) Find the distance between points Q and R.
Answer:
The coordinates of Q are (3, 2) and R are (6, 5).
∴ The distance between points Q and R is
QR = \(\sqrt{(6-3)^2+(5-2)^2}\)
= \(\sqrt{(3)^2+(3)^2latex]
= [latex]}\sqrt{9+9}[/\)
= 3√2 units

Or

What is ∆PQR?
Answer:
Since, coordinates of vertices of a ∆PQR are P (4, 6),Q (3, 2)and R (6, 5).
Now, PQ = \(\sqrt{(3-4)^2+(2-6)^2}\)
= \(\sqrt{(-1)^2+(-4)^2}\)
= \(\sqrt{1+16}\)
= \(\sqrt{17}\) units
PR = \(\sqrt{(6-4)^2+(5-6)^2}\)
= \(\sqrt{(2)^2+(-1)^2}\)
= \(\sqrt{5}\) units
and QR = 3 √2
Here, PQ ≠ QR ≠ PR
Hence, ∆PQR is a scalene triangle.

Question 38.
A vegetable seller has 420 potatoes and 130 tomatoes. He wants to stack them in such a way that each stack has same number and they take up the least area of the tray.

Based on the above information of a vegetable shop, answer the following questions

(i) Find the product of exponents of the prime factors of total number of vegetables.
Answer:
Since, total number of vegetables is 550
Prime factorisation of 550 = 2 × 5 × 5 × 11
= 2¹ × 5² × 11¹
The exponents are 1, 2 and 1
∴ Product of exponents = 1 × 2 × 1 = 2

(ii) What is the number of vegetables that can be placed in each stack for this purpose?
Answer:
Prime factors of 420 = 2² × 3 × 5 × 7
and 130 = 2 × 5 × 13
∴ HCF (420, 130) = 2 × 5 = 10
So, the number of vegetables that can be placed in each stack for this purpose is 10.

(iii) Find the sum of exponents of the prime factors of the number of vegetables that can be placed in each stack for this purpose.
Answer:
The number of vegetables that can be placed in each stack = 10
Prime factor of 10 = 2¹ × 5¹
The exponents are 1 and 1.
∴ Sum of exponents = 1 + 1 = 2

Or

What is the total number of rows in which they can be placed?
Answer:
Total number of vegetables = 550
Number of vegetables that can be placed in each stack = 10
∴ Number of rows of vegetables = 55.