Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 8 are designed as per the revised syllabus.
CBSE Sample Papers for Class 10 Maths Basic Set 8 with Solutions
Time : 3 hrs
Max. Marks : 80
General Instructions:
- This question paper has 5 Sections A, B, C, D and E.
- Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
- Section B has 5 Short Answer-I (SA-I) Type Questions carrying 2 marks each.
- Section C has 6 Short Answer-II (SA-II) Type Questions carrying 3 marks each.
- Section D has 4 Long Answer (LA) Type Questions carrying 5 marks each.
- 6. Section E has 3 Case Based integrated units of assessment (4 marks each).
- All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
- Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
Section A
Section A consists of 20 questions of 1 mark each
Question 1.
The mid-point of line segment joining origin and (- 4, – 2) is
(a) (2, 1)
(b) (1, 2)
(c) (- 4, – 2)
(d) (- 2, – 1)
Answer:
(d) (- 2, – 1)
The mid-point of line segment joining (0, 0) and (- 4, – 2) is \(\left(\frac{0-4}{2}, \frac{0-2}{2}\right)\) i.e. (- 2, – 1).
Question 2.
The mode of the following data is

(a) 16
(b) 14
(c) 12
(d) 10
Answer:
(b) 14
The mode is the most frequent observation.
Here, the mode is 14 with a frequency of 15.
![]()
Question 3.
The discriminant of the quadratic equation 2x2 – √5x + 1 = 0 is
(a) – 3
(b) \(\sqrt{-3}\)
(c) 1
(d) – 1
Answer:
(a) – 3
Given equation, 2x2 – √5x + 1 = 0
On comparing it with ax2 + bx + c = 0, we get
a = 2,
b = – √5
and c = 1
∴ D = b2 – 4ac
= (√5)2 – 4 (2)
= 5 – 8 = – 3
Question 4.
The formula for finding mean by direct method is \(\frac{\Sigma(A \times B)}{\Sigma A}\), where B and A are respectively,
(a) class mark, frequency of the class
(b) average frequency, class size
(c) class size, average frequency
(d) frequency of the class, class mark
Answer:
(a) class mark, frequency of the class
Class mark, frequency of the class
\(\bar{x}=\frac{\sum f x}{\sum f}=\frac{\sum(A \times B)}{\sum A}\),
where B is the class mark.
Class mark = \(\frac{1}{2}\) (upper limit + lower limit)
and A is the frequency of the class.
Question 5.
In ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then the value of DB is
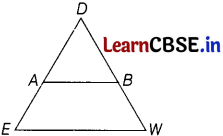
(a) 16 cm
(b) 4 cm
(c) 12 cm
(d) 8 cm
Answer:
(d) 8 cm
Given, AB || EW
![]()
Question 6.
The coordinates of the point which divides the line segment joining the point (4, – 3) and (8, 5) in the ratio 3 : 1 internally is
(a) (7, 3)
(b) (4, 5)
(c) (6, 8)
(d) (1, 1)
Answer:
(a) (7, 3)
Let P (x, y) be the required point using the section formula, we get
x = \(\frac{3(8)+1(4)}{3+1}\) = 7
and y = \(\frac{3(5)+1(-3)}{3+1}\) = 3
Therefore, (7, 3) is the required point.
Question 7.
A pendulum swings through an angle of 30° and describes an arc 4.4 cm in length, then the length of the pendulum is
(a) 8.4 cm
(b) 4.4 cm
(c) 10.2 cm
(d) 6.8 cm
Answer:
(a) 8.4 cm
∴ Length of the arc = \(\frac{\theta}{360^{\circ}}\) × 2πr
4.4 = \(\frac{30^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × r
⇒ 4.4 = \(\frac{1}{12} \times \frac{44}{7}\) × r
⇒ r = \(\frac{4.4 \times 12 \times 7}{44}\) = 8.4 cm
Question 8.
\(\frac{2 \tan 30^{\circ}}{1+\tan ^2 30^{\circ}}\) is equal to
(a) sin 60°
(b) cos 60°
(c) tan 60°
(d) sin 30°
Answer:
(a) sin 60°
We know that
sin 2A = \(\frac{2 \tan A}{1+\tan ^2 A}\)
∴ \(\) = sin 2 × 30°
= sin 60°
![]()
Question 9.
A card is drawn from a well-shuffled deck of 52 cards. The probability of getting a king of red colour is
(a) \(\frac{1}{52}\)
(b) \(\frac{1}{13}\)
(c) \(\frac{1}{26}\)
(d) \(\frac{1}{52}\)
Answer:
(c) \(\frac{1}{26}\)
Total number of cards = 52
Kings which are red in colour = 2
P(king of red colour) = \(\frac{2}{52}=\frac{1}{26}\)
Question 10.
In a right circular cone, the cross-section made by a plane parallel to the base is
(a) sphere
(b) hemisphere
(c) circle
(d) semi-circle
Answer:
(c) circle

Question 11.
For what value of k, is 3 a zero of the polynomial 2x2 + x + k?
(a) – 15
(b) – 9
(c) – 18
(d) – 21
Answer:
(d) – 21
Let f(x) = 2x2 + x + k ………….(i)
Given, 3 is a zero of the polynomial f(x).
Therefore, put x = 3 in Eq. (i) and consider 1(3) = 0
∴ f (3) = 2(3)2 + 3 + k = 0
⇒ 2 × 9 + 3 + k = 0
⇒ 18 + 3 + k = 0
⇒ k = – 21
![]()
Question 12.
The acute angle θ satisfying √3 sin θ = cos θ is
(a) 70°
(b) 30°
(c) 45°
(d) 60°
Answer:
(b) 30°
We have, √3 sin θ = cos θ
⇒ \(\frac{\sin \theta}{\cos \theta}=\frac{1}{\sqrt{3}}\)
⇒ tan θ = \(\frac{1}{\sqrt{3}}\)
⇒ tan θ = tan 30°
⇒ θ = 30°
Question 13.
The 17th term of an AP exceeds its 10th term by 7. Then, the common difference is
(a) 1
(b) \(\frac{7}{8}\)
(c) 2
(d) \(\frac{7}{6}\)
Answer:
(a) 1
Let d be the common difference of the AP.
According to the question,
a17 – a10 = 7
(a + 16d) – (a + 9d) = 7
⇒ 7d = 7
⇒ d = 1
Question 14.
The value of tan 45° cos 60° + sin 60° cot 60° is
(a) \(\frac{1}{2}\)
(b) 2
(c) 1
(d) \(\frac{1}{2}\) (√3 + 1)
Answer:
(c) 1
tan 45° cos 60° + sin 60° cot 60° = \(1 \times \frac{1}{2}+\frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{3}}\)
= \(\frac{1}{2}+\frac{1}{2}\) = 1
![]()
Question 15.
The coordinates of the mid-point of the line segment joining the point A (- 5, 4) and B (7, – 8) is
(a) (2, 3)
(b) (3, 1)
(c) (1, – 2)
(d) (5, 3)
Answer:
(c) (1, – 2)
![]()
x = \(\frac{(-5)+7}{2}\) = 1
and y = \(\frac{4+(-8)}{2}\) = – 2
Hence mid-point is M (1, – 2).
Question 16.
An unbiased die is thrown, the probability of getting an even number is
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{1}{3}\)
Answer:
(b) \(\frac{1}{2}\)
Let A be the event getting an even number.
Clearly, event A occurs, if we obtain any one of 2, 4, 6 as an outcome.
Number of outcomes favourable to A = 3
Hence, P(A) = \(\frac{3}{6}=\frac{1}{2}\)
Question 17.
A ladder 15 m long makes an angle of 60° with the wall. The height of the point, where the ladder touches the wall, is
(a) 15√3 m
(b) \(\frac{15 \sqrt{3}}{2}\) m
(c) \(\frac{15}{2}\) m
(d) 15 m
Answer:
(c) \(\frac{15}{2}\) m
Given, ∠ABC = 60°
In ∆ABC,
∠BAC + ∠ABC + ∠ACB = 180
⇒ ∠BAC = 180° – 90° – 60° = 30°
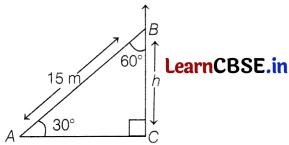
So, sin 30° = \(\frac{B C}{A B}=\frac{h}{15}\)
\(\frac{1}{2}=\frac{h}{15}\)
h = \(\frac{15}{2}\) m
![]()
Question 18.
If point P lies inside the circle, then the number of tangent(s) drawn from point P are
(a) 0
(b) 1
(c) 2
(d) ∞
Answer:
(a) 0
It point P lies inside the circle, then no tangent can be drawn.
Directions : In the question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.
Question 19.
Assertion (A) : The system of equations x + y – 8 = 0 and x – y – 2 = 0 has a unique solution.
Reason (R) : a1x + b1y + c1x = 0 and a2x + b2y + c2 = 0 unique solution, when \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(c) Assertion (A) is true but Reason (R) is false.
Assertion :
Given x + y – 8 = 0
and x – y – 2 = 0
Here, a1 = 1, b1 = 1, c1 = – 8
and a2 = 1, b2 = – 1, c2 = – 2
So, \(\frac{a_1}{a_2}=\frac{1}{1}\),
\(\frac{b_1}{b_2}=\frac{1}{-1}\)
and \(\frac{c_1}{c_2}=\frac{-8}{-2}\) = 4
∵ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
So, the system of equations has a unique solution
and therefore Assertion (A) is true.
Reason :
For equations to have a unique solution,
\(\frac{a_1}{a_2}\) should not be equal to \(\frac{b_1}{b_2}\).
∴ The given Reason (R) is false.
Question 20.
Assertion (A) : If the median and mode of a frequency distribution are 150 and 154 respectively, then its mean is 148.
Reason (R) : Mean, median and mode of a frequency distribution are related as Mode = 3 Median – 2 Mean
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Reason (R) is clearly true.
Using the relation given in reason, we have
2 Mean = 3 Median – Mode
= 3 × 150 – 154
= 296
Mean = \(\frac{296}{2}\) = 148 which is true.
Thus, both Assertion (A) and Reason (R) are true and Reason (R) is the corréct explanation of Assertion (A).
![]()
Section – B
Section B consists of 5 questions of 2 marks each
Question 21.
If α and β are the zeroes of the polynomial p(x) = 5x2 – 7x + 1, then find the value of \(\frac{1}{\alpha}+\frac{1}{\beta}\).
Answer:
We have, p(x) = 5x2 – 7x + 1, whose zeroes are α and β.
∴ Sum of zeroes = α + β
= – \(\frac{\text { Coefficent of } x}{\text { Coefficent of } x^2}\)
= – \(\frac{(-7)}{5}=\frac{7}{5}\) ……………(i)
amd product of zeroes = αβ
= \(\frac{\text { Constant term }}{\text { Coefficent of } x^2}\)
= \(\frac{1}{5}\) ……………(ii)
Now, \(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\beta+\alpha}{\alpha \beta}\)
= \(\frac{7 / 5}{1 / 5}\) = 7
[from Eqs. (i) and (ii)]
Question 22.
Show that \(\frac{2}{5 \sqrt{3}}\) is an irrational number.
Answer:
Let us assume that \(\frac{2}{5 \sqrt{3}}\) is a rational number.
\(\frac{2}{5 \sqrt{3}}\) = \(\frac{p}{q}\), where p, q (q ≠ 0) are integers and p, q are coprime.
Since, 2, 5, p and q are integers.
∴ \(\frac{2 q}{5 p}\) is rational, so √3 is rational.
But this contradicts the fact that √3 is irrational.
Hence, \(\frac{2}{5 \sqrt{3}}\) is an irrational number.
Hence proved.
Or
Show that 6 – 2√3 is irrational.
Answer:
Let us assume that 6 – 2√3 is rational number.
Then, it will be of the form \(\frac{a}{b}\), where a, b are coprime integers and b ≠ 0.
Now, 6 – 2√3 = \(\frac{a}{b}\)
On rearranging, we get
6 – \(\frac{a}{b}\) = 2√3
Since. 6and are rational. So, their difference will be rational
∴ 2√3 is rational.
But we know that, √3 is irrational.
So, this contradicts the fact that √3 is irrational.
Therefore, our assumption is wrong.
Hence, 6 – 2√3 is irrational.
Hence proved.
Question 23.
If x = a cos θ and y = b sin θ, then find b2x2 + a2y2.
Answer:
Given, x = a cos θ and y = b sin θ
∴ b2x2 + a2y2 = b2 (a cos θ)2 + a2 (b sin θ)2
= a2b2 cos2 θ + a2b2 sin2
= a2b2 (cos2 + sin2 8)
= a2b2 (1) [∵ cos2A + sin2A = 1]
= a2b2
![]()
Question 24.
Find the coordinates of the points of trisection of the line segment joining the points A (- 5, 6) and B (4, – 3).
Answer:
Let P and Q be the points of trisection of AB
Then, P divides AB in the ratio 1 : 2.
So, the coordinates of P are
![]()
⇒ P \(\left(\frac{1 \times 4+2 \times(-5)}{1+2}, \frac{1 \times(-3)+2 \times 6}{1+2}\right)\) = \(\left(\frac{4-10}{3}, \frac{-3+12}{3}\right)\)
∴ P (- 2, 3)
Also, Q divides AB in the ratio 2 : 1.
⇒ Q \(\left(\frac{2 \times 4+1 \times(-5)}{2+1}, \frac{2 \times(-3)+1 \times 6}{2+1}\right)\) = \(\left(\frac{8-5}{3}, \frac{-6+6}{3}\right)\)
∴ Q (1, 0)
Hence the points of trisection of AB are P(- 2, 3) and Q (1, 0).
Question 25.
In the given figure, if DEFG is a square and ∠BAC = 90°, then show that DE2 = BD × EC.
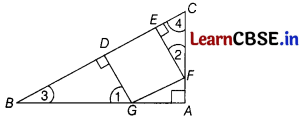
Answer:
∵ ∆AGF ~ ∆DBG …………… (i) [by AA similarity criterion]
Now, in ∆AGF and ∆EFC, we get
∠FAG = ∠CEF [each 90°]
and ∠AFG = ∠ECF
[corresponding angles because GF || BC and AC is the transversal]
∴ ∆AGF ~ ∆EFC ……………….(ii)
From Eqs. (i) and (ii), we get
∆ DBG ~ ∆ EFC
⇒ \(\frac{B D}{E F}=\frac{D G}{E C}\)
⇒ \(\frac{B D}{D E}=\frac{D E}{E C}/latex] [∵ DEFG is a square]
∴ DE2 = BD × EC
Hence proved.
Or
Prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Answer:
Given : A ∆ABC in which D is the mid-point of AB and DE || BC.
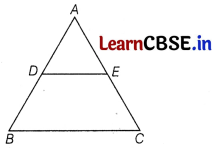
To prove : AE = EC
Proof : Since, DE || BC, by Thales theorem, we have
[latex]\frac{A E}{E C}=\frac{A D}{D B}\) = 1
[∵ AD = DB (given)]
⇒ \(\frac{A E}{E C}\) = 1
⇒ AE = EC.
Hence, E is the mid-point of AC.
![]()
Section – C
Section C consists of 6 questions of 3 marks each
Question 26.
Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector (use π = 3.14).
Answer:
Let the radius of circle, r = 4 cm
and angle, θ = 30°
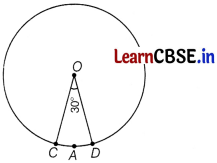
∴ Area of the sector (OCAD) = \(\frac{\theta}{360^{\circ}}\) × πr²
= \(\frac{30^{\circ}}{360^{\circ}}\) × 3.14 × 4 × 4
= \(\frac{12.56}{3}\) cm2
= 4.19 cm2 (approx.)
Area of the corresponding major sector = πr² – area of sector OCAD
= (3.14 × 16 – 4.19)
= 46.05 cm2
= 46.1 cm2 (approx.)
Question 27.
The following table shows the age distribution of cases of a certain disease admitted during a year in a particular hospital.

Find the average age for which maximum cases occurred.
Answer:
Here, class intervals are not in inclusive form.
So, we first convert them in inclusive form by subtracting h/2 from the lower limit and adding h/2 to the upper limit of each class, where h is the difference between the lower limit of a class and the upper limit of the preceding class.

We observe that the class 34.5 – 44.5 has the maximum frequency.
So, it is the modal class such that
l = 34.5,
h = 10,
f1 = 23,
f0 = 21
and f2 = 14
∴ Mode = l + \(\frac{f_1-f_0}{2 f_1-f_0-f_2}\) × h
⇒ Mode = 34.5 + \(\frac{23-21}{46-21-14}\) × 10
= 34.5 + \(\frac{2}{11}\) × 10
= 36.32
Question 28.
A die is thrown once. Find the probability of getting
(i) an even prime number.
Answer:
There are 6 possible outcomes (1 2, 3, 4, 5 and 6) in a single throw of a die.
We know that even prime number is only 2.
So, number of favourable outcomes = 1
∴ P (getting an even prime number) = \(\frac{1}{6}\)
(ii) a number divisible by 2.
Answer:
The numbers divisible by 2 are 2, 4 and 6.
So,number of favourable outcomes = 3
∴ P (getting a number divisible by 2) = \(=\frac{3}{6}=\frac{1}{2}\)
Or
A card is drawn at random from a well-shuffled pack of 52 cards. Find the probability that the card drawn is neither a red card nor a queen.
Answer:
Number of red cards = 26
Number of queens = 4
But, out of these 4 queens, 2 are red.
Number of queens which are not red = 2
Now, number of cards which are red or queen = 26 + 2 = 28
∴ p (getting either red card or queen) = Number of card which are red or queen / Total number of cards
= \(\frac{28}{52}=\frac{7}{13}\)
Now, P (not getting either red card or queen) = 1 – P (getting either red card or queen)
= 1 – \(\frac{7}{13}\)
= \(\frac{13-7}{13}\)
= \(\frac{6}{13}\)
![]()
Question 29.
In the given figure, if PQ = PR prove that QT = TR i.e. QR is bisected at T.
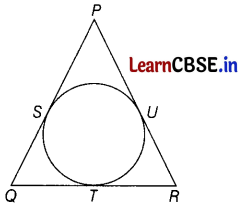
Answer:
Given : A circle inscribed in a ∆PQR such that PQ = PR
To prove : QT = TR
Proof : We know that the tangents from an external points to a circle are equal in length.
PS = PU [tangents from P] …………… (i)
QS =QT [tangentsfromQ] ………….(ii)
RT = RU [tangents from R] ………….(iii)
Now, PQ = PR [given] (1½)
⇒ PQ – PS = PR – PS [subtracting PS from both sides]
⇒ PO – PS = PR – PU [from Eq. (i]
⇒ QS = RU
⇒ QT = RU [from Eq. (ii)]
⇒ QT = RT [from Eq. (iii)]
Hence proved.
Question 30.
Solve for x and y using elimination method
10x + 3y = 75,
6x – 5y = 11
Answer:
The given equations are
10x + 3y = 75
6x – 5y = 11
On multiplying Eq (i) by 5 and Eq (ii) by 3, we get
50x + 15y = 375 ………….(iii)
18x – 15y = 33 ………….(iv)
On adding Eqs. (iii) and (iv), we get
68x = 408
⇒ x = \(\frac{408}{68}\)
⇒ x = 6
On putting x = 6 in Eq. (i), we get
(10 × 6) + 3y = 75
⇒ 60 + 3y = 75
⇒ 3y = 75 – 60
⇒ 3y = 15
⇒ y = 5
∴ x = 6 and y = 5.
Or
Solve for x and y using substitution method
11x + 15y + 23 = 0,
7x – 2y- 20 = 0
Answer:
The given equations are
11x – 15y + 23 = 0 …………..(i)
7x – 2y – 20 = 0 ……………(ii)
On multiplying Eq. (i) by 2 and Eq. (ii) by 15 and adding the results, we get
22x +1 05x = – 46 + 300
⇒ 127x = 254
⇒ x = \(\frac{254}{127}\) = 2
On putting x = 2 in Eq. (i), we get
22 + 15y = – 23
⇒ 15y = – 23 – 22
⇒ 15y = – 45
⇒ y = \(\frac{- 45}{15}\)
⇒ y = – 3
Hence, x = 2 and y = – 3.
Question 31.
Two pillars of equal height are on either sides of a road, which is 100 m wide. The angles of the top of the pillars are 60° and 30° at a point on the road between the pillars. Find the position of the point between the pillars. Also, find the height of each pillar.
Answer:
Let AB and CD be two pillars of equal height h and distance between them be BD = 100 m.
Let E be a point on the road such that BE x,
DE = (100 – x),
∠AEB = 60°
and ∠CED = 30°
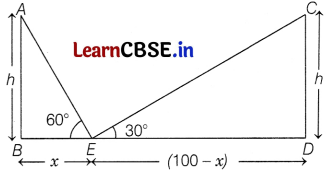
In right angled ∆ABE,
\(\frac{A B}{B E}\) = tan 60°
\(\frac{h}{x}\) = √3 [∵ tan 60° = √3]
∴ h = √3x ………….(i)
In right angled ∆CDE,
\(\frac{C D}{D E}\) = tan 30°
⇒ \(\frac{h}{100-x}=\frac{1}{\sqrt{3}}\) [∵ tan 30° = \(\frac{1}{\sqrt{3}}\)]
⇒ h = \(\frac{100-x}{\sqrt{3}}\) ………….(ii)
From Eqs. (i) and (Ii), we get
√3x = \(\frac{100-x}{\sqrt{3}}\)
3x = 100 – x
⇒ 4x = 100
∴ x = 25
On putting x = 25 in Eq. (i), we get
h = √3 × 25
= 25 × 1.732
= 43.3 m
Hence, height of each pillar is 43.3 m and position of the point from pillar making an angle of 60° is 25 m.
![]()
Section – D
Section D consists of 4 questions of 5 marks each
Question 32.
From a solid cylinder whose height is 2.8 cm and diameter is 1.8 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2.
Answer:
Let S be the total surface area of the remaining solid.
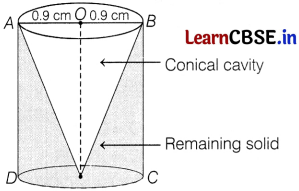
Then, S = Curved surface area of the cylinder + Area of the base of the cylinder + Curved surface area of the cone
= 2πrh + πr2 + πrl
= π [2rh + r2 + r \(\sqrt{r^2+h^2}\)]
[∵ l = \(\sqrt{h^2+r^2}\)]
= \(\frac{22}{7}\) [2 × 0.9 × 2.8 + (0.9)2 + 0.9 \(\sqrt{(0.9)^2+(2.8)^2}\)]
[∵ r = i-=0.9cmandh=2,8cm] (1)
= \(\frac{22}{7}\) [5.04 + 0.81 + 0.9 \(\sqrt{0.81+7.84}\)]
= \(\frac{22}{7}\) [5.85 + 0.9 \(\sqrt{8.65}\)]
= \(\frac{22}{7}\) [5.85 + 0.9 × 2.94]
= \(\frac{22}{7}\) [5.85 + 2.65]
= \(\frac{187}{7}\)
= 26.71 cm2
Or
Water in a canal, 6 m wide and 1.5 m deep is flowing with a speed of 10 km/h. How much area will it irrigate in 30 min, if 8 cm of standing water is needed?
Answer:
Given, speed of flow of water = 10 km/h
= 10 × 1000 m/h
[∵ 1 km = 1000 m]
⇒ Length of water flow in 1 h = 10 × 1000 m
⇒ Length of water flow in 30 min (i.e. in h)
= \(\frac{1}{2}\) × 10 × 1000 = 5000 m
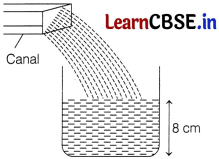
Now, volume of water flowing in 30 min = Volume of cuboid of length 5000 m, width 6 m and depth 1.5 m
= 5000 × 6 × 1.5 m3
= 45000 m3
Hence, the required area covered for irrigation with 8 cm or \(\frac{8}{100}\) m of standing water
= \(\frac{45000}{8}\) × 100
= 562500 m2
= \(\frac{562500}{10000}\) hec [∵ 1 hec = 10000 m2]
= 56.25 hec
Question 33.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O.
Using similarity criterion for two triangles, show that \(\frac{O A}{O C}=\frac{O B}{O D}\).
Answer:
Given : ABCD is a trapezium in which AB || DC.
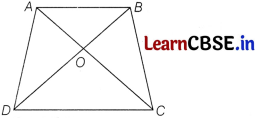
To prove : \(\frac{O A}{O C}=\frac{O B}{O D}\)
Proof : In ∆OAB and ∆ODC, we have AB || DC
Then, ∠OAB = ∠OCD [alternate interior angles]
∠AOB = ∠DOC [vertically opposite angles]
and ∠ABO = ∠CDO [alternate interior angles]
∴ ∆OAB ~ ∆OCD [by AAA similarity critenon]
Hence, \(\frac{O A}{O C}=\frac{O B}{O D}\)
[if two triangles are similar, then their corresponding sides are proportional]
Hence proved.
![]()
Question 34.
If the sum of the first n terms of an AP is 4n – n2, then what is the first term (i.e. S1)? What is the sum of first two terms? Find the nth term.
Answer:
Given, the sum of first n terms,
Sn = 4n – n2 …………..(i)
On putting n = 1 in Eq. (i), we get
S1 = 4 × 1 – 12
= 4 – 1 = 3
Thus, first term = 3
On putting n = 2 in Eq. (i), we get
S2 = 4 × 2 – 22
= 8 – 4 = 4
Thus, sum of first two terms = 4
Now, on replacing n by n – 1 in Eq. (i), we get
Sn – 1 = 4(n – 1) – (n – 1)2
= 4n – 4 – n2 + 2n – 1
= n2 + 6n – 5
∴ nth term = Sn – Sn – 1
= 4n – n2 – (- n2 + 6n – 5)
= 4n – n2 + n2 – 6n + 5
= 5 – 2n
Or
The first and the last term of an AP are 5 and 45, respectively. If the sum of all its terms is 400, find its common difference.
Answer:
Let a and d be the first term and common difference of an AP
Then, a = 5, Tn = 45
⇒ 45 = a + (n – 1) d
[∵ Tn = a + (n – 1) d]
⇒ 45 = 5 + (n – 1) d
⇒ 40 = (n – 1) d …………..(i)
We know that sum of n terms of an AP is
Sn = \(\frac{n}{2}\) [2a + (n – 1) d]
⇒ 400 = \(\frac{n}{2}\) [2 × 5 + 40] [from Eq (i)]
⇒ 800 = 50n
⇒ n = \(\frac{800}{50}\) = 16 ……………(ii)
Put n = 16 in Eq. (i) we get
(16 – 1) d = 40
⇒ 15d = 40
⇒ d = \(\frac{40}{15}=\frac{8}{3}\)
Question 35.
Find the value of k for which the given system of equations has infinitely many solutions.
kx + 3y = k – 3, 12 x + ky = k
Answer:
Given equation
kx + 3y + (3 – k) = 0
and 12x + ky – k = 0
These equations are of the form
a1x + b1y + c1 = 0
and a2x + b2y + c2 =0.
where a1 = k, b1 = 3, c1 = (3 – k)
and a2 = 12, b2 = k, c2 = – k
For infinitely many solution
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
⇒ \(\frac{k}{12}=\frac{3}{k}=\frac{(3-k)}{-k}\)
⇒ \(\frac{k}{12}=\frac{3}{k}=\frac{k-3}{k}\)
⇒ \(\frac{k}{12}=\frac{3}{k}\)
and \(\frac{3}{k}=\frac{k-3}{k}\)
⇒ k2 = 36
and k2 – 6k = 0
⇒ (k = 6 or k = – 6)
and k (k – 6) = 0
⇒ (k = 6 or k = – 6) and (k = 0 or k = 6)
∴ k = 6
![]()
Section – E
Case study based questions are compulsory
Question 36.
A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.
After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride. She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.
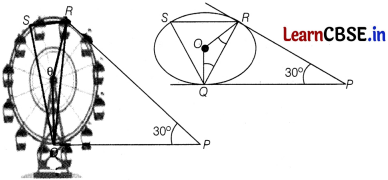
On the basis of above information, answer the following questions.
(i) In the given figure, find ∠ROQ.
Answer:
In quadrilateral PQOR, we have
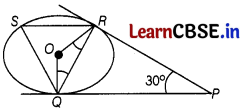
∠QPR + ∠PRO + ∠PQO + ∠ROQ = 360°
⇒ 30° + 90° + 90° + ∠ROQ = 360°
[∵ radius is always perpendicular to the tangent at point of contact]
⇒ ∠ROQ = 360° – 210° = 150°
(ii) In the given figure, find ∠RSQ.
Answer:
We know that angle subtended by an arc at centre is double the angle subtended by it at any other part of the circle.
2∠RSQ = ∠ROQ
∠RSQ = \(\frac{1}{2}\) × 150° = 75°
(iii) In the given figure, find ∠RQP.
Answer:
In, ∆QOR, OQ = OR [radii]
∴ ∠ORQ = ∠OQR
Now, ∠ROQ + ∠ORQ + ∠OQR = 180°
⇒ 2∠OQR= 180° – 150°
⇒ 2∠OQR = 30°
⇒ ∠OQR = 15°
Again, ∠OQP = 90°
⇒ ∠OQR + ∠RQP = 90°
⇒ ∠RQP = 90° – 15° = 75°
Or
In the given figure, two circles touch each other at C and AB is a tangent to both the circles. Find ∠ACB.
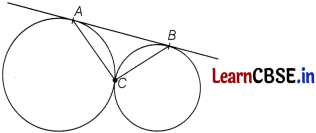
Answer:
Draw a tangent to the circles at point C.
Let it meets AB at P
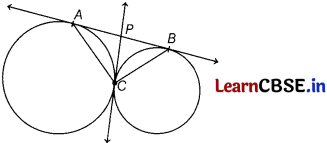
Then PA = PC
and PB = PC
[the tangents from an external points to a circle are equal in length]
PA = PC
⇒ ∠PAC = ∠PCA
PB = PC
⇒ ∠PBC = ∠PCB
∴ ∠PAC + ∠PBC = ∠PCA + ∠PCB = ∠ACB
⇒ ∠PAC + ∠PBC + ∠ACB = 2∠ACB
⇒ 180° = 2∠ACB
⇒ ∠ACB = 90°.
![]()
Question 37.
A group of students of class X visited India Gate on an educational trip. The teacher and students had interest in history as well. The teacher narrated that India Gate, official name Delhi Memorial, originally called All-India War Memorial, monumental sandstone arch in New Delhi, dedicated to the troops of British India who died in wars fought between 1914 and 1919.
The teacher also said that India Gate, which is located at the eastern end of the Rajpath (formerly called the Kingsway), is about 13 8 ft (42 m) in height.

On the basis of above information, answer the following questions.
(i) What is the angle of elevation, if they are standing at a distance of 42 m away from the monument?
Answer:
Let AB be the monument of height 42 m and C is the point where they are standing.
Such that, BC = 42 m.
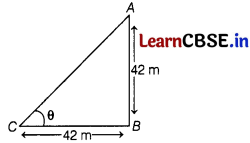
Now, in ∆ABC,
tan θ = \(\frac{A B}{B C}\)
[∵ tan θ = \(\frac{\text { Perpendicular }}{\text { Base }}\)]
⇒ tan θ = \(\frac{42}{42}\) = 1
⇒ tan θ = 1
⇒ θ = 45°
(ii) They want to see the gate at an angle of elevation 60°. So, they want to know the distance where they should stand and hence find the distance.
Answer:
In ∆ABC,
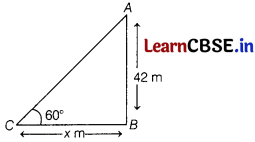
tan 60° = \(\frac{A B}{B C}\)
[∵ tan θ = \(\frac{\text { Perpendicular }}{\text { Base }}\)]
⇒ √3 = \(\frac{42}{B C}\)
⇒ BC = \(\frac{42}{\sqrt{3}}\)
= \(\frac{42 \sqrt{3}}{3}\)
= 14√3
(iii) The shadow of the gate when the Sun’s altitude is 30° is found to be 30 m longer than when it was 60°. Find the sum of length of its shadow.
Answer:
Let AB be the gate and let BC and BD be the lengths of its shadows wtien ∠ACB = 60° and ∠ADB = 30°.
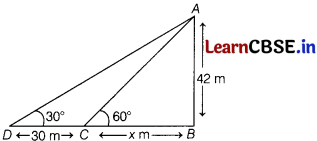
In right ∆CBA,
tan 60° = \(\frac{A B}{B C}=\frac{42}{x}\)
⇒ √3 = \(\frac{42}{x}\)
⇒ x = \(\frac{42 \sqrt{3}}{3}\) = 14√3 m
∴ Lengths of its shadows are 14√3 m and (30 + 14√3) m.
So, the sum of lengths of its shadows = (30 + 28√3) m
Or
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then find the height of the lamp-post.
Answer:
Let AB be the lamp-post and CD be the girl.
Let CE be the shadow of CD.
Then, CD = 1.5 m,
CE = 4.5 m
and AC = 3m
Let AB = h
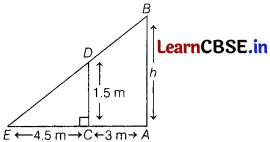
Now, ∆AEB and ∆CED are similar.
∴ \(\frac{A B}{C D}=\frac{A E}{C E}\)
⇒ \(\frac{A B}{A E}=\frac{C D}{C E}\)
⇒ \(\frac{h}{(3+4.5)}=\frac{1.5}{4.5}=\frac{1}{3}\)
⇒ h = \(\frac{1}{3}\) × 7.5 = 2.5
![]()
Question 38.
To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- Section A and Section B of grade X. There are 32 students in section A and 36 students in section B.

On the basis of above information, answer the following questions.
(i) What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?
Answer:
Given, number of students in Section A = 32
Number of students in Section B = 36
The minimum number of books to be acquired for the class library = LCM of (32, 36)
= 2 × 2 × 2 × 2 × 2 × 3 × 3
= 25 × 32
= 32 × 9
= 288
(ii) Express 36 as product of it primes.
Answer:
The prime factors of 36 are
36 = 2 × 2 × 3 × 3
= 22 × 32
(iii) Find the HCF of 96 and 404 by the prime factorisation method, hence find their LCM.
Answer:
The prime factorisation of 96 and 404 gives
96 = 25 × 3
and 404 = 2 × 101
Therefore, the HCF of there two integers is 2 = 4
Also, LCM (96, 404) = \(\frac{96 \times 404}{\ {HCF}(96,404)}\)
= \(\frac{96 \times 404}{4}\)
= 9696
Or
If LCM of 12 and 42 is 10m + 4, then find the value of m.
Answer:
Given, LCM (12, 42) = 10m + 4
Factors of 12 = 2 × 2 × 3
and factors of 42 = 2 × 3 × 7
Now, LCM (12, 42) = 2 × 2 × 3 × 7 = 84
∴ 84 = 10m + 4
⇒ 84 – 4 = 10m
∴ m = \(\frac{80}{10}\) = 8