CBSE Sample Papers for Class 10 Maths Basic Set 7 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 7 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Basic Set 7 with Solutions

Time : 3 hrs
Max. Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment questions (4 marks each).
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks question of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section – A
Section A consists of 20 questions of 1 mark each.

Question 1.
In ∆ABC, AD is the internal bisector of ∠A. If BD = 5 cm and BC = 7.5 cm, then the value of AB : AC is
(a) 2 : 1
(b) 2 : 4
(c) 1 : 4
(d) 3 : 2
Answer:
(a) 2 : 1

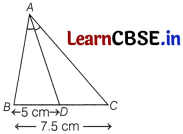
Given, AD is a internal bisector of ∠A.
Therefore,
\(\frac{A B}{A C}=\frac{B D}{D C}\)
= \(\frac{B D}{(B C-B D)}\)
= \(\frac{5}{(7.5-5)}\)
= \(\frac{5}{2.5}=\frac{2}{1}\)
= 2 : 1

Question 2.
The roots of the equation 2x² – 3x = 0 is
(a) 0, \(-\frac{2}{3}\)
(b) 0, \(\frac{3}{2}\)
(c) 0, 3
(d) 0, 2
Answer:
(b) 0, \(\frac{3}{2}\)

Given, 2x² – 3x = 0
⇒ x (2x – 3) = 0
⇒ x = 0 or 2x – 3 = 0
⇒ x = 0 or x = \(\frac{3}{2}\)
Hence, the roots are 0, \(\frac{3}{2}\).

Question 3.
The circumference of a circle of diameter 28 cm is
(a) 85 cm
(b) 88 cm
(c) 90 cm
(d) 75 cm
Answer:
(b) 88 cm

Diameter (d) = 28 cm
⇒ r = 14 cm
We know that, circumference of the circle = 2πr
= 2 × \(\frac{22}{7}\) × 14
= 88 cm

Question 4.
For which natural number (12)ⁿ can never end with the digit n?
(a) 0 or 5
(b) 2 or 4
(c) 2 or 3
(d) 4 or 3
Answer:
(a) 0 or 5

We have,
(12)ⁿ = (2² × 3)ⁿ
= (2²ⁿ × 3ⁿ)
Now, 2 and 3 are the only prime factors of (12)ⁿ.
∴ 5 is not a factor of (12)ⁿ.
Hence, (12)ⁿ cannot end with 5 or 0.

Question 5.
A circle is inscribed in a ∆ABC, touching BC, CA and AB at P, Q and R respectively. If AB = 10 cm, AQ – 7 cm and CQ = 5 cm, then the length of BC is
(a) 8 cm
(b) 5 cm
(c) 4 cm
(d) 10 cm
Answer:
(a) 8 cm

We have,
AR = AQ = 7 cm,
BR = (AB – AR)
= (10 – 7) cm
= 3 cm

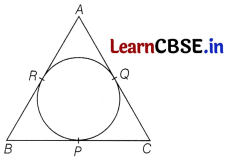
∴ BP = BR = 3 cm
CP = CQ = 5 cm
∴ BC = (BP + CP)
= (3 + 5) cm
= 8 cm

Question 6.
The value of tan 60° cot 30° + tan 30° cot 60° is
(a) 4
(b) 2
(c) \(\frac{10}{3}\)
(d) 5
Answer:
(c) \(\frac{10}{3}\)

tan 60° cot 30° + tan 30° cot 60° = √3 × √3 + \(\frac{1}{\sqrt{3}} \times \frac{1}{\sqrt{3}}\)
= 3 + \(\frac{1}{3}\)
= \(\frac{9+1}{3}\)
= \(\frac{10}{3}\)

Question 7.
The area of the sector of a circle having radius R making an angle of x, is
(a) \(\frac{x}{180^{\circ}} \times \pi R^2\)
(b) \(\frac{x}{360^{\circ}}\) × 2πR
(c) \(\frac{x}{180^{\circ}}\) × 2πR²
(d) \(\frac{x}{360^{\circ}}\) × πR²
Answer:
(d) \(\frac{x}{360^{\circ}}\) × πR²

Area = \(\frac{x}{360^{\circ}}\) × πR²

Question 8.
If ∆ABC ~ ∆DFE, ∠A = 30°, ∠C = 50°, then the value of ∠F is
(a) 80°
(b) 100°
(c) 30°
(d) 50°
Answer:
(b) 100°

In ∆ABC,
∠A + ∠B + ∠C = 180°
⇒ 30° + ∠B + 50° = 180°
⇒ ∠B = 100°
Since, ∆ABC ~ ∆DFE
∴ ∠F = ∠B = 100° [by CPCT]

Question 9.
The LCM of (2 × 3² × 5) and (2² × 3 × 5) is
(a) 4500
(b) 30
(c) 900
(d) 1500
Answer:
(a) 4500

LCM = Product of the greatest power of each
prime factor involved in the number = 2² × 3² × 5³
= 4 × 9 × 125
= 4500

Question 10.
The distance between the points (2, 3) and (4, 1), is
(a) √2 units
(b) 2 units
(c) 2√2 units
(d) 4 units
Answer:
(c) 2√2 units

Let A (2, 3) and 6 (4, 1) be the given points.
Here, x₁ = 2,
y₁ = 3
and x₂ = 4,
y₂ = 1
Now, AB = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\) [by distance formula]
= \(\sqrt{(4-2)^2+(1-3)^2}\)
= \(\sqrt{(2)^2+(-2)^2}\)
= \(\sqrt{4+4}=\sqrt{8}\)
= 2√2 units

Question 11.
The area of the sector of a circle with radius 4 cm and of angle 30° is
(a) 8.37 cm²
(b) 5.25 cm²
(c) 6.13 cm²
(d) 5.65 cm²
Answer:

Area of sector = \(\frac{\theta}{360^{\circ}}\) × πr²

= \(\frac{30^{\circ}}{360^{\circ}}\) × 3.14 × 4 × 4
= 8.37 cm² (approx)

Question 12.
The relation between x and y such that the point P(x, y) is equidistant from the points A (1, 4) and B (- 1, 2) is
(a) y = x + 4
(b) y = 3x + 2
(c) y = 3 – x
(d) y = 4x + 4
Answer:
(c) y = 3 – x

We have,
PA = PB
⇒ PA² = PB²
⇒ (x – 1)² + (y – 4)² = (x + 1)² + (y – 2)²
⇒ x² + y² – 2x – 8y + 17 = x² + y² + 2x – 4y + 5
⇒ x + y = 3
⇒ y = 3 – x
Hence, y = 3 – x is the required relation between x and y.

Question 13.
If the mean of the first n natural numbers is 18, then the value of n is
(a) 18
(b) 32
(c) 36
(d) 35
Answer:
(d) 35

We know that the sum of first n natural numbers is given by S_n = \(\frac{n(n+1)}{2}\)
∴ Mean of first n natural numbers = \(\frac{[n(n+1)] / 2}{n}\)
= \(\frac{n+1}{2}\)
Given, mean of first n natural numbers = 18
⇒ \(\frac{n+1}{2}\) = 18
⇒ n + 1 = 36
⇒ n = 35

Question 14.
The value of x for which 2x, x + 10 and 3x + 2 are in AP is
(a) 2
(b) 6
(c) 4
(d) 8
Answer:
(b) 6

Since, 2x. x + 10 and a + 2 are in AP
∴ (x + 10) – 2x = (3x + 2) – (x + 10)
[common difference must be same]
⇒ – x + 10 = 2x – 8
⇒ 3x = 18
⇒ x = 6

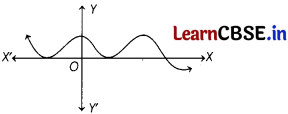
Question 15.
The graph of a polynomial f(x) is as shown in figure, the number of zeroes of f(x) is

(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(c) 3

The number of zeroes of f (x) is 3, as the graph of f(x) intersects the X-axis at three points.

Question 16.
If 2 is a root of the equation kx² – x – 2 = 0, then the value of k, is
(a) 2
(b) 0
(c) 1
(d) 4
Answer:
(c) 1

Since, x = 2 is a root of the equation.
∴ (k)² – 2 – 2 = 0
⇒ 4k – 2 – 2 = 0
⇒ 4k – 4= 0
⇒ k = 1

Question 17.
The pair of equations x + 2y – 5 = 0 and – 4x – 8 y + 20 = 0 has
(a) unique solution
(b) exactly two solutions
(c) infinitely many sulutions
(d) no solution
Answer:
(c) infinitely many sulutions

Here, \(\frac{a_1}{a_2}=\frac{1}{-4}\)
\(\frac{b_1}{b_2}=\frac{2}{-8}=\frac{1}{-4}\)
and \(\frac{C_1}{C_2}=\frac{-5}{20}=\frac{-1}{4}\)
This shows, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\).

Question 18.
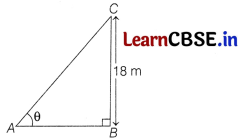
The length of the shadow on the ground of a pole of height 18m when the angle of elevation 0 of the sun is such that tan θ = \(\frac{6}{7}\), is
(a) 24 m
(b) 21 m
(c) 15.42 m
(d) None of these
Answer:
(b) 21 m

Let AB be the length of the shadow and height of the pole BC = 18 m
and elevation ∠BAC = θ
In right angled ∆ABC,
tan θ = \(\frac{B C}{A B}\)
[tan θ = \(\frac{\text { perpendicular }}{\text { base }}\)]
⇒ \(\frac{6}{7}=\frac{18}{A B}\)
[tan θ = \(\frac{6}{7}\), given]

⇒ 6 × AB = 18 × 7
⇒ AB = \(\frac{18 \times 7}{6}\) = 21
Hence, the length of the shadow is 21 m.

Directions : In the question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) : The point (- 1, 6) divides the line segment joining the points (- 3, 10) and (6, – 8) in the ratio 2 : 7 internally.
Reason (R) : Given, three points i.e. A, B, C from an equilateral triangle, then AB = BC = CA.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Assertion
Coordinates of the point which divides the line segment joining the points (- 3, 10) and (6, – 8) in the ratio 2 : 7, is
(x, y) = \(\left(\frac{2 \times 6+7 \times(-3)}{2+7}, \frac{2 \times(-8)+7 \times(10)}{2+7}\right)\)
= \(\left(\frac{12-21}{9}, \frac{-16+70}{9}\right)\)
= \(\left(-1, \frac{54}{9}\right)\)
= (- 1, 6)
So, the Assertion (A) is true.

Reason
Since, in equilateral ∆ABC, all sides are equal.
So, AB = BC = CA
So, the Reason (R) is true but it is not the correct explanation of Assertion (A).

Question 20.
Assertion (A) : If AABC and APQR are congruent triangles, then they are also similar triangles.
Reason (R) : All congruent triangles are similar but the similar triangles need not be congruent.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

Clearly, Assertion (A) is true.

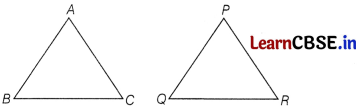
So, Reason (R) is also true and it is the correct explanation of Assertion (A).

Section – B
Section B consists of 5 questions of 2 marks each

Question 21.
Solve for x \(\frac{2 x}{x-3}+\frac{1}{2 x+3}+\frac{3 x+9}{(x-3)(2 x+3)}\) = 0, x ≠ 3, – \(\frac{3}{2}\)
Answer:
Given, \(\frac{2 x}{x-3}+\frac{1}{2 x+3}+\frac{3 x+9}{(x-3)(2 x+3)}\) = 0
⇒ \(\frac{2 x(2 x+3)+x-3+3 x+9}{(x-3)(2 x+3)}\) = 0
⇒ 4x² + 6x + x – 3 + 3x + 9 = 0
⇒ 4x² + 10x + 6 = 0
⇒ 2x²+ 5x + 3 = 0
⇒ 2x² + 2x + 3x + 3 = 0
⇒ (x + 1) (2x + 3) = 0
⇒ x = – 1 or x = – \(\frac{3}{2}\)
As, x ≠ – \(\frac{3}{2}\)
Hence, x = – 1.

Question 22.
Show that 2 (cos² 45° + tan² 60°) – 6 (sin² 45°- tan² 30°) = 6.
Answer:
We have,
LHS = 2 (cos² 45° + tan² 60°) – 6 (sin² 45°- tan² 30°)
= \(\)
= \(\)
= 1 + 6 – 3 + 2
= 6
= RHS

Or

Show that 2 (sin 45° + cos 45°) – tan² 45° + cosec 45° – sec 45° = 2√2 – 1
Answer:
LHS = 2 (sin 45° + cos 45°) – tan² 45° + cosec 45° – sec 45°
= 2 \(\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\right)\) – (1)² + √2 – √2
= \(2 \times \frac{2}{\sqrt{2}}\) – 1
= \(\frac{4-\sqrt{2}}{\sqrt{2}}\)
= \(\frac{4-\sqrt{2}}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}\)
[on multiplying and dividing by √2]
= \(\frac{4 \sqrt{2}-2}{\sqrt{2} \times \sqrt{2}}\)
= 2√2 – 1

Question 23.
Find the ratio in which the line segment joining A (1, – 5) and B (- 4, 5) is divided by the X-axis.
Answer:
For any point on X-axis, y = 0.
Let the ratio be k : 1, then by section formula, the coordinates of the point which divides AB in the ratio k : 1 are \(\left(\frac{-4 k+1}{k+1}, \frac{5 k-5}{k+1}\right)\)

Thus, point lies on the X-axis, and we know that on the X-axis, the ordinate is zero.
∴ \(\frac{5 k-5}{k+1}\) = 0
⇒ 5k – 5 = 0
⇒ k = 1
Therefore, the required ratio is 1 : 1.

Or

Find the coordinates of points on the X-axis which are at the distance of 17 units from the point (11, – 8).
Answer:
Let P (x, 0) be the point on X-axis.
Take other point (1 1, – 8) as Q.

∴ PQ = 17
⇒ \(\sqrt{(11-x)^2+(-8-0)^2}\) = 17
[∵ by using distance formula, distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)]
On squaring both sides, we get
(11 – x)² +(- 8)² = 289
⇒ 121 + x² – 22x + 64 – 289 = 0
⇒ x² – 22x – 104 = 0
⇒ x² – 26x + 4x – 104 = 0
[splitting middle term]
⇒ x (x – 26) + 4 (x – 26) = 0
⇒ (x – 26) (x + 4) = 0
⇒ x = 26 or x = – 4
When x =26, then P = (26, 0)
When x = – 4, then P = (- 4, 0)
So, points are (26, 0) and (- 4, 0).

Question 24.
In the given figure, O is the centre of the circle, PT is the tangent drawn from the point P to the circle and PAB passes through the centre O of the circle.

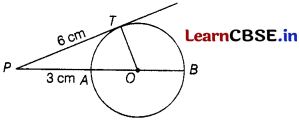
If PT = 6 cm and PA = 3 cm, then find the radius of the circle.
Answer:
Let the radius of circle be r cm.
Then, OA = OT = r cm …………..(i)
Since, PT is a tangent to circle at T and OTis a radius.
So, OT ⊥ PT
∴ ∠OTP = 90°
In right angled ∠OTP,
OP² = OT² + PT² [by Pythagoras theorem]
⇒ (PA + OA)² = OT² + 6²
⇒ (3 + r)² = r² + 36
[from Eq. (1) and PA = 3 cm, PT = 6cm, (given)]
⇒ r² + 6r + 9 – r² – 36 = 0
[∵ (a + b)² = a² + b² + 2ab]
⇒ 6r – 27 = 0
⇒ r = \(\frac{27}{6}\) = 4.5
Hence, the radius of the circle is 4.5 cm.

Question 25.
In the given figure, PQ || NO. If \(\frac{M P}{P N}=\frac{4}{13}\) and MO = 20.4 cm, then find MQ.

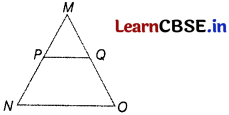
Answer:
In ∆MNO,
we have PQ || NO
⇒ \(\frac{M P}{P N}=\frac{M Q}{Q O}\)
[by basic proportionality theorem]
⇒ \(\frac{M P}{P N}=\frac{M Q}{M O-M Q}\)
[∵QO = MO – MQ]
⇒ \(\frac{4}{13}=\frac{M Q}{20.4-M Q}\)
[given, \(\frac{M P}{P N}=\frac{4}{13}\)
and MO = 20.4 cm]
⇒ 4 (20.4 – MQ) = 13 MQ
⇒ 81.6 – 4 MQ = 13 MQ
⇒ 81.6 = 17 MQ
⇒ MQ = 4.8 cm

Section – C
Section C consists of 6 questions of 3 marks each

Question 26.
A circle with diameter 20 cm is drawn somewhere on a rectangular piece of paper with length 40 cm and width 30 cm. This paper is kept horizontal on table top and a die, very small in size, is dropped on the rectangular paper without seeing 2. towards it. If the die falls and lands on the paper only, then find the probability that it will fall and land inside the circle.
Answer:
Area of rectangular paper = 40 × 30 = 1200 cm²

∴ Area of circle = πr²
∴ Number of possible outcomes = Area of rectangular paper
and number of favourable outcomes = Area of circle
∴ P (die will fall inside the circle) = Area of circle / Area of rectangular paper
= \(\frac{2200}{7 \times 1200}=\frac{11}{42}\)

Question 27.
In the following figure, CM and RN are respectively the medians of ∆ABC and ∆PQR. If ∆ABC ~ ∆PQR, prove that

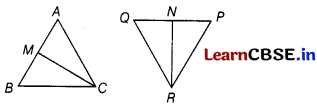
(i) ∆AMC ~ ∆PNR
(ii) \(\frac{C M}{R N}=\frac{A B}{P Q}\)
Answer:
Given ∆ABC and ∆PQR
CM is the median of ∆ABC and RN is the median of ∆PQR.
Also, ∆ABC ~ ∆PQR
To prove : (i) ∆AMC ~ ∆PNR
(ii) \(\frac{C M}{R N}=\frac{A B}{P Q}\)
Proof:
(i) Given, ∆ABC ~ ∆PQR
\(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\) ………….(i)
[∵ in similar triangles, corresponding sides are proportional]
and ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R …………..(ii)
[∵ in similar triangles, corresponding angles are equal]
We know that the median bisects the opposite side.
∴ AM = MB
⇒ AB = 2AM and PN= NQ
⇒ PQ = 2PN
From Eq. (i), we have
\(\frac{A B}{P Q}=\frac{A C}{P R}\)
⇒ \(\frac{A B}{P Q}=\frac{A C}{P R}\)
⇒ \(\frac{2 A M}{2 P N}=\frac{A C}{P R}\) ……………..(iii)
In ∆AMC and ∆PNR, we have ∠A = ∠P
and \(\frac{A M}{P N}=\frac{A C}{P R}\)
So, ∆AMC – ∆PNR [by SAS similarity criterion]

(ii) We have, ∆AMC ~ ∆PNR
⇒ \(\frac{A M}{P N}=\frac{A C}{P R}=\frac{C M}{R N}\)
[∵ triangles are similar, so corresponding sides will be proportional]
∴ \(\frac{C M}{R N}=\frac{A C}{P R}\)
⇒ \(\frac{C M}{R N}=\frac{A B}{P Q}\)
Hence proved.

Question 28.
Prove that cot² A \(\left(\frac{\sec A-1}{1+\sin A}\right)\) + sec² A \(\left(\frac{\sin A-1}{1+\sec A}\right)\) = 0.
Answer:
LHS = cot² A \(\left(\frac{\sec A-1}{1+\sin A}\right)\) + sec² A \(\left(\frac{\sin A-1}{1+\sec A}\right)\)

[∵ cot θ tan θ = 1
and sec θ cos θ = 1]
Hence Proved.

Or

Prove that \(\sqrt{\frac{\ {cosec} A-1}{\ {cosec} A+1}}+\sqrt{\frac{\ {cosec} A+1}{\ {cosec} A-1}}\) = 2 sec A.
Answer:

Question 29.
If the seventh term of an AP is \(\frac{1}{9}\) and its ninth term is \(\frac{1}{7}\), find its 63rd term.
Answer:
Let a be the first term and d be the common difference of the AP.
Then,
T₇ = \(\frac{1}{9}\)
⇒ a + 6d = \(\frac{1}{9}\) …………..(i)
T₉ = \(\frac{1}{7}\)
⇒ a + 8d = \(\frac{1}{7}\) ………….(ii)
On subtracting Eq (i) from Eq. (ii), we get
2d = \(\left(\frac{1}{7}-\frac{1}{9}\right)=\frac{2}{63}\)
⇒ d = \(\left(\frac{1}{2} \times \frac{2}{63}\right)=\frac{1}{63}\)
On putting d = \(\frac{1}{63}\) in Eq. (i), we get

Question 30.
Prove that √n is not a rational number, if n is not a perfect square.
Answer:
Let √n be a rational number.
Then, assume √n = \(\frac{p}{q}\)
[where p, q are co-prime and q ≠ 0]
⇒ n = \(\frac{p^2}{q^2}\) [squaring on both sides]
⇒ p² = nq²
⇒ n divides p²
⇒ n divides p [by using theorem] ………..(ii)
Let p = nm
⇒ p² = n²m² (squaring on both sides]
On putting the value of p² in Eq. (i), we get
n²m² = nq²
⇒ q² = nm²
⇒ n divides q²
⇒ n divides q
From Eq. (ii), n divides p and from Eq. (iii) n divides q.
It means n is a common factor of both p and q.
This contradicts the assumption that p and q are co-prime.
So, our supposition is wrong.
Hence, cannot be a rational number.

Or

The length, breadth and height of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm, respectively. Find the length of the longest rod that can measure the three dimensions of the room exactly.
Answer:
Given, length of the room = 8 m 25 cm
= 825 cm [‘∵ 1 m = 100 cm]
Breadth of the room = 6 m 75 cm = 675 cm
and height of the room = 4 m 50 cm = 450 cm
Clearly, the length of the longest rod (in cm) is the HCF of 825, 675 and 450.
Now,

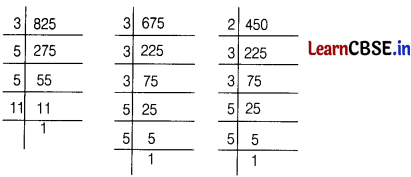
Thus, 825 = 3 × 5² × 11
675 = 33 × 5²
and 450 = 2 × 3² × 5²
Now, HCF (825 67 450) = Product of the smallest power of each common prime factor
= 3 × 5² = 75
Hence, the required length of the longest rod is 75 cm.

Question 31.
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 m towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
Answer:
Let the height of the tower PR be h m, the angle of elevation at point Q is 30°
i.e. ∠PQR = 30°
and S be the position of observer after moving 20 m towards the tower.

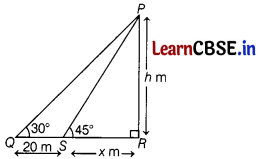
According to the question,
∠PSR = ∠PQR + 15°
⇒ ∠PSR = 30° + 15°
⇒ ∠PSR = 45°
Now, in right angled ∆PRS,
tan 45° = \(\frac{P R}{S R}=\frac{h}{x}\)
[∵ tan θ = \(\frac{\text { perpendicular }}{\text { base }}\)]
⇒ tan 45° = \(\frac{h}{x}\)
⇒ 1 = \(\frac{h}{x}\)
[∵ tan 45° = 1]
⇒ x = h
and in right angled ∆PRQ,
tan 30° = \(\frac{P R}{Q R}\)
= \(\frac{P R}{Q S+S R}\)
[∵ QR = QS + SR]
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{20+x}\) [∵ tan 30° = \(\frac{1}{\sqrt{3}}\)]
⇒ 20 + x = √3h
⇒ 20 + h = √3h [from Eq.i]
⇒ √3h – h = 20
⇒ h(√3 – 1) = 20
⇒ h = \(\frac{20}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}\) [by rationalising]
h = \(\frac{20(\sqrt{3}+1)}{3-1}\)
= \(\frac{20(\sqrt{3}+1)}{2}\)
= 10 (√3 + 1) m
Hence, the required height of the tower is 10(√3 + 1) m.

Section – D
Section D consists of 4 questions of 5 marks each

Question 32.
From a well-shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is

(i) a queen of black colour.
Answer:
Since, one card is drawn from 52 well-shuffled cards.
∴ Total number of possible outcomes = 52
Since, there are two queens of black colour.
∴ p (getting a queen of black colour) = \(\frac{2}{52}=\frac{1}{26}\)

(ii) a card with number 5 or 6.
Answer:
In each suit, there are two caids with number 5 and 6.
So, total such cards are 4 times 2 = 8
∴ p (getting a card with number 5 or 6) = \(\frac{8}{52}=\frac{2}{13}\)

(iii) a card with number less than 8.
Answer:
In each suit, there are six cards wh number less than 8, namely 2, 3, 4, 5, 6 and 7
∴ P (getting a card with number less than 8) = \(\frac{4 \times 6}{52}\)
= \(\frac{24}{52}=\frac{6}{13}\)

(iv) a card with number between 2 and 9.
Answer:
In each suit, there are six cards with number between 2 and 9, namely 3, 4, 5, 6, 7, 8.
∴ p (getting a card with number between 2 and 9) = \(\frac{4 \times 6}{52}\)
= \(\frac{24}{52}=\frac{6}{13}\)

(v) a face card.
Answer:
In a pack of cards, there are 12 face cards.
∴ p (getting a face card) = \(\frac{12}{52}=\frac{3}{13}\)

Or

Cards numbered 1, 2, 3, 4, 5, ………….., 17 are put ;in a box and mixed thoroughly. One person draws a card from the box.
Find the probability that the number on the card is

(i) an odd number.
Answer:
There are 17 cards numbered 1, 2, 3, 4, 5,…,17 ¡n a box.
Out of 17 cards, one card can be drawn in 17 ways.
∴ Total number of outcomes = 17 (1)

There are nine odd numbered cards, namely 1, 3, 5, 7, 9, 11, 13, 15 and 17.
∴ Number of favourable outcomes = 9
Hence, P (getting an odd number) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}\)
= \(\frac{9}{17}\)

(ii) a prime number.
Answer:
There are seven prime numbered cards, namely 2, 3, 5, 7, 11, 13 and 17.
Number of favourable outcomes = 7
Hence, P (getting a prime number) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}=\frac{7}{17}\)

(iii) divisible by 2 and 3 both.
Answer:
If a number is divisible by 2 and 3 both, then it must be a multiple of 6. In cards bearing number 1, 2, 3, 4, …. 17, there are only 2 cards which bear a number divisible by 2 and 3 both, i.e. by 6.
These cards bearing numbers 6 and 12.
∴ Number of favourable outcomes = 2
Hence, P (getting a card bearing number divisible by 2 and 3 both)
= \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}=\frac{2}{17}\)

(iv) a multiple of 3 or 5.
Answer:
There are 7 numbered cards, which are multiple of 3 or 5 namely, 3, 5, 6, 9, 10, 12 and 15.
Number of favourable outcomes = 7
Hence, P (getting a card bearing a number multiple of 3 or 5)
= \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}=\frac{7}{17}\)

Question 33.
If 2 is a root of the quadratic equation 3×2+px-8=0 and the quadratic equation 4×2 -2px+k=0 has equal roots, find the value of k.
Answer:
Given, 2 is a root of the quadratic equation 3x² + px – 8 = 0.
So, it satisfies the given equation.
3(2)² + p(2) – 8 = 0
⇒ 12 + 2p – 8 = 0
⇒ 2p = – 4
⇒ p = – 2
Put p = – 2 in the second given equation 4x² – 2px + k = 0, we get
4x² – 2(- 2) x + k = 0
⇒ 4x² + 4x + k = 0
It is given that, this equation has equal roots.
∴ b² – 4ac = 0 …………(i)
On comparing with ax² + bx + c = 0, we get
a = 4, b = 4 and c = k.
∴ (4)² – 4 × 4 × k = 0
⇒ 16 – 16k = 0
⇒ 16k = 16
⇒ k = 1.

Question 34.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure.

If the height of the cylinder is 20 cm and its base is of radius 5 cm, find the total surface area of the article.
Answer:
Given, base radius of cylinder, r = 5 cm
and its height, h = 20 cm
Also, radius of hemisphere, r = 5 cm
Now, total surface area of the article = Curved surface area of the cylinder + 2 (Surface area of a hemisphere)
= 2πrh + 2 (2πr²)
= 2 (h + 2r)
= 2 × \(\frac{22}{7}\) × 5(20 + 2 × 5)
= \(\frac{220}{7}\) × (20 + 10)
= \(\frac{220 \times 30}{7}\)
= \(\frac{6600}{7}\)
= 942.86 cm²

Or

The volume of two spheres are in the ratio 64 : 27. Find their radii, if the sum of their radii is 21 cm.
Answer:
Let the volume of two spheres are V₁ and V₂,
respectively and corresponding radii are r₁ and r₂.
Given, \(\frac{V_1}{V_2}=\frac{64}{27}\)
\(\frac{\frac{4}{3} \pi r_1^3}{\frac{4}{3} \pi r_2^3}=\left(\frac{4}{3}\right)^3\)
[∵ volume of the sphere (V) = \(\frac{4}{3}\) πr³
⇒ \(\frac{r_1^3}{r_2^3}=\left(\frac{4}{3}\right)^3\)
⇒ \(\left(\frac{r_1}{r_2}\right)^3=\left(\frac{4}{3}\right)^3\)
⇒ \(\frac{r_1}{r_2}=\frac{4}{3}\) [taking cube root]
⇒ r₁ = \(\frac{\frac{4}{3}\) r₂ ……………(i)
Also given, sum of their radii = 21 cm
∴ r₁ + r₂ = 21 ……………..(ii)
From Eqs. (i) and (ii), we get
\(\frac{\frac{4}{3}\) r₂ + r₂ = 21
⇒ \(\frac{4 r_2+3 r_2}{3}\) = 21
⇒ 7r₂ = 21 × 3
⇒ r₂ = 3 × 3
⇒ r₂ = 9 cm
On putting r₂ = 9 cm in Eq. (i), we get
r₁ = \(\frac{\frac{4}{3}\) × 9
= 12 cm
Hence, the radii of the two spheres are 12 cm and 9 cm.

Question 35.
Find the mean of the following frequency distribution using step-deviation method.

Marks obtained	Number of students
Less than 10	14
Less than 20	22
Less than 30	37
Less than 40	58
Less than 50	67
Less than 60	75

Answer:
The given data may be written as

Class	Frequency
0 – 10	14
10 – 20	22 – 14 = 8
20 – 30	37 – 22 = 15
30 – 40	58 – 37 = 21
40 – 50	67 – 58 = 9
50 – 60	75 – 67 = 8

Here, h = 10
Let assumed mean (A) = Mid – value of (30 – 40) = 35
Table for deviation and their product with corresponding frequency is given below.

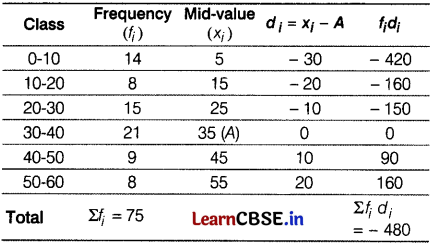
Here, h = 10, = 75,
Σf_i = 75,
Σ f_id_i = – 480
and A = 35
∴ Mean, \(\bar{x}=\left\{A+\frac{\Sigma f_i d_i}{\Sigma f_i}\right\}\)
= 35 + (- 6.4)
= 35 – 6.4
= 28.6

Section – E
Case study based questions are compulsory

Question 36.
Pankaj’s father gave him some money to buy avocado from the market at the rate of p(x) = x² – 24x + 128.

Let α, β are the zeroes of p(x).
On the basis of above information, answer the following questions.

(i) Find the value of α and β, where α < β.
Answer:
Wehave, p(x) = x² – 24x + 128
⇒ p(x) = x ² – 16x – 8x + 128
⇒ p(x) = x (x – 16) – 8 (x – 16)
⇒ p(x) = (x – 16) (x – 8)
So, the zeroes of p(x) are given by p(x) = 0
⇒ (x – 16) (x – 8) = 0
⇒ (x – 16) = 0 and (x – 8) = 0
⇒ x = 16 and x = 8
So, the values of aand pare 8 and 16, respectively. [∵ 8 ⇒ 16]

(ii) If α and β are zeroes of x² + 88x + 125, then find the value of \(\frac{1}{\alpha}+\frac{1}{\beta}\).
Answer:
Let q (x) = x² + 88x +125
Sum of roots = α + β = – 88
and product of roots = αβ = 125
∴ \(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\beta+\alpha}{\alpha \beta}=\frac{-88}{125}\)

Or

If sum of zeroes of q(x) = kx² + 2x + 3k is equal to their product, then find the value of k.
Answer:
Given, q (x) = kx² + 2x + 3k – 2
Sum of zeroes of q(x) = – \(\frac{2}{k}\)
Product of zeroes of q (x) = \(\frac{3 k}{k}\) = 3
According to the question,
– \(\frac{2}{k}\) = 3
k = – \(\frac{2}{3}\)

(iii) Find the value of p(2).
Answer:
p(2) = (2)² – 24 (2) + 128
= 4 – 48 + 128
= 132 – 48
= 84

Question 37.
A test consists of ‘True’ or ‘False’ questions. One mark is awarded for every correct answer while \(\frac{1}{4}\) mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing. He answered 120 questions and got 90 marks.

Type of question	Marks given for correct answer	Marks deducted for wrong answer
True/False	1	0.25

On the basis of above information, answer the following questions.

(i) If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly?
Answer:
Let the number of questions whose answer is known to the student be x and questions attempted by guessing be y.
Then, x + y = 120
and x – y = 90 ………..(i)
4x – y = 36O …………(ii)
On adding Eqs. (i) and (ii), we get
5x = 480
x = \(\frac{480}{5}\) = 96
Put x = 96 in Eq. (i), we get
96 + y = 120
⇒ y = 120 – 96 = 24

He answered 96 questions correctly.

(ii) How many questions did he guess?
Answer:
He guesses only 24 questions.

(iii) If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?
Answer:
In out of 120 questions attempted 80 answered are correct and 40 guessing answered are wrong.
Then, he got the marks = 80 – \(\frac{1}{4}\) of 40
= 80 – \(\frac{1}{4}\) × 40
= 80 – 10 = 70

Or

If answer to all questions he attempted by guessing were wrong, then how many questions answered correctly to score 95 marks?
Answer:
According to the given condition,
x – \(\frac{1}{4}\) 0f (120 – x) = 95
⇒ x – \(\frac{1}{4}\) × (120 – x) = 95
⇒ 4x – 120 + x = 380
⇒ 5x = 500
⇒ x = 100
Hence, he answered correctly 100 questions to score 95 marks.

Question 38.
Varun has been selected by his School to design logo for Sports Day T-shirts for students and staff. The logo design is as given in the figure and he is working on the fonts and different colours according to the theme.

In given figure, a circle with centre O is inscribed in a ∆ABC, such that it touches the sides AB, BC and CA at points D, E and F, respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm, respectively.

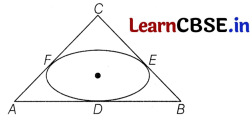
On the basis of above information, answer the following questions.

(i) Find the length of AD.
Answer:
Let AD = x = AF
[∵ lengths of tangents drawn from an external point to a circle are equal]

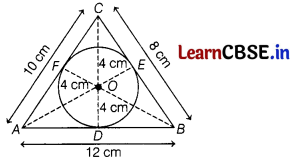
Then, BD = BE
= AB – AD
= 12 – x

and CF = CE
= AC – AF
= 10 – x

Now, BC = BE + CE
8 = 12 – x + 10 – x
⇒ 2x = 14
⇒ x = 7

AD = x = 7 cm

(ii) Find the length of BE.
Answer:
BE = 12 – x
= 12 – 7 = 5 cm

(iii) If radius of the circle is 4 cm, Find the area of ∆ABC.
Answer:
ar(∆ OAB) = \(\frac{1}{2}\) × AB × OD
= \(\frac{1}{2}\) × 10 × 4
= 24 cm²

ar(∆ OAC) = \(\frac{1}{2}\) × AC × OF
= \(\frac{1}{2}\) × 10 × 4
= 20 cm²

ar(∆ OBC) = \(\frac{1}{2}\) × BC × OE
= \(\frac{1}{2}\) × 8 × 4
= 16 cm²

ar(∆ ABC) = ar(∆ OAB) + ar(∆ OAC) + ar(∆ OBC)
= 24 + 20 + 16
= 60 cm²

Or

If radius of the circle is 4 cm, Find the area of ∆OFC.
Answer:
CF = 10 – x
= 10 – 7 = 3 cm
Area of ∆OCF = \(\frac{1}{2}\) × CF × OF
= \(\frac{1}{2}\) × 3 × 4= 6 cm²