CBSE Sample Papers for Class 10 Maths Basic Set 6 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 6 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Basic Set 6 with Solutions

Time : 3 hrs
Max. Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment questions (4 marks each).
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks question of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section – A
Section A consists of 20 questions of 1 mark each.

Question 1.
If the product of the zeroes of the polynomial mx² – 6x – 6 is – 3, then the value of m is
(a) 6
(b) 2
(c) – 2
(d) – 3
Answer:
(b) 2

Let α and β be the zeroes of mx² – 6x – 6.
Here, a = m,
b = – 6
and c = – 6
Given, αβ = – 3
∴ \(\frac{c}{a}\) = – 3
⇒ \(\frac{-6}{m}\) = – 3
⇒ m = 2.

Question 2.
If p(x) = x² + 5x + 6, then p(-2) is: 1
(a) 20
(b) 0
(c) -8
(d) 8
Answer:
(b) 0
Explanation: Given,
p(x) = x² + 5x + 6
Then, p(-2) = (-2)² + 5 × (-2) + 6
= 4 – 10 + 6 = 0

Question 3.
The value of cos² θ + \(\frac{1}{1+\cot ^2 \theta}\)
(a) 2 sin² θ
(b) 1
(c) 0
(d) cos² θ
Answer:
(b) 1

We have,
cos² θ +\(\frac{1}{1+\cot ^2 \theta}\)
[∵ 1 + cot² A = cosec² A]
= cos² θ + sin² θ
[∵ sin² A + cos² A = 1]
= 1

Question 4.
How many tangents can be drawn to a circle from a point on it? 1
(a) One
(b) Two
(c) Infinite
(d) Zero
Answer:
(a) One
Explanation: Only 1 tangent can be drawn to a circle from a point on it.

Question 5.
If a cylinder is covered by two hemispherical lids of equal shape, then the total curved surface area of the new object will be (where r is the radius and h is the height of the cylinder)
(a) 4πrh + 2πr²
(b) 4πrh – 2πr²
(c) 2πrh + 4πr²
(d) 2πrh + 4πr
Answer:
(c) 2πrh + 4πr²

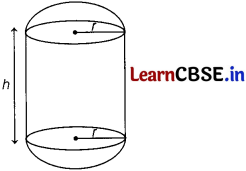
Total curved surface area = Curved surface area of cylinder + 2 × Curved surface area of hemispheres
= 2πrh + 2 × (2πr²)
= 2πrh + 4πr²

Question 6.
Which of the following is not a quadratic equation? 1
(a) 2(x – 1) = 4x² – 2x + 1
(b) 2x – x² = x² + 5
(c) (√2x + √3 )² + x² = 3x² – 5x
(d) (x² + 2x)² = x⁴ + 3 + 4x³
Answer:
(c) (√2x + √3)² + x² = 3x² – 5x
Explanation: (√2x + √3)² + x² = 3x² – 5x
⇒ 2x² + 3 + 2√6x + x² =3x² – 5x
⇒ 3x² + 3 + 2√6x = 3x² – 5x
⇒ (2√6 + 5)x + 3 = 0,
∴ This is not a quadratic equation

Question 7.
Suppose mean of 10 observations is 12.5 and each observation is multiplied by 5, then what is the new mean?
(a) 50
(b) 62.5
(c) 60
(d) 48.2
Answer:
(b) 62.5

Let 10 observations be x₁, x₂, x₃, …………, x₁₀.
Given, \(\frac{x_1+x_2+x_3+\ldots+x_{10}}{10}\) = 12.5 ………(i)
Now, if each observation multiplied by 5, then new
mean = \(\frac{5 x_1+5 x_2+\ldots+5 x_{10}}{10}\)
= \(\frac{5\left(x_1+x_2+\ldots+x_{10}\right)}{10}\) [using Eq. (1)]
= 5 × 12.5
= 62.5

Question 8.
(HCF × LCM) for the numbers 30 and 70 is: 1
(a) 2100
(b) 21
(c) 210
(d) 70
Answer:
(a) 2100
Explanation: Product of two numbers
= (LCM × HCF) of the numbers
So, (HCF × LCM) of 30 and 70 = 30 × 70 = 2100

Question 9.
The value of 3 sin 30° – 4 sin³ 60° is
(a) 3 – √3
(b) \(\frac{3(1-\sqrt{3})}{2}\)
(c) \(\frac{3 \sqrt{3}-1}{2}\)
(d) – \(\frac{3}{2}\)
Answer:
(b) \(\frac{3(1-\sqrt{3})}{2}\)

3 sin 30° – 4 sin³ 60°
= 3 × \(\frac{1}{2}\) – 4 \(\left(\frac{\sqrt{3}}{2}\right)^3\)
= \(\frac{3}{2}-4 \times \frac{3 \sqrt{3}}{8}\)
= \(\frac{3}{2}-\frac{3 \sqrt{3}}{2}\)
= \(\frac{3-3 \sqrt{3}}{2}\)
= \(\frac{3(1-\sqrt{3})}{2}\)

Question 10.
If the radius of a semi-circular protractor is 7 cm, then its perimeter is: 1
(a) 11 cm
(b) 14 cm
(c) 22 cm
(d) 36 cm
Answer:
(d) 36 cm
Explanation:

Perimeter of the semi-circular protractor
Length of arc AB + Length of AB
Given, radius = 7 cm,
So, AB = 7 cm + 7 cm
= 14 cm
Now, the circumference of the circle = 2πr
= 2 × \(\frac{22}{7}\) × 7
= 44 cm
Length of arc
AB = \(\frac{44}{2}\) = 22 cm.
Hence, the perimeter of the semi-circular protractor
= 22 cm + 14 cm
= 36 cm

Question 11.
If the lines given by 4x + ky = 1 and 6x – 10y = 14 have unique solutions, then the value of k is
(a) \(\frac{20}{3}\)
(b) – \(\frac{5}{7}\)
(c) – 15
(d) all real values except – \(\frac{20}{3}\)
Answer:
(d) all real values except – \(\frac{20}{3}\)

The given equations can be re-written as
4x + ky – 1= 0
and 6x – 10y – 14 = 0
On comparing with a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂ = 0, we get
a₁ = 4,
b₁ = k,
c₁ = – 1
and a₂ = 6,
b₂ = – 10,
c₂ = – 14
For unique solution,
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{4}{6} \neq \frac{k}{-10}\)
⇒ k ≠ \(-\frac{20}{3}\)
Thus, given lines have a unique solution for all real values of k, except \(-\frac{20}{3}\).

Question 12.
(\(\frac{2}{3}\)sin0°- \(\frac{4}{5}\)cos0°) is equal to: 1
(a) \(\frac{2}{3}\)
(b) \(\frac{-4}{5}\)
(c) 0
(d) \(\frac{-2}{15}\)
Answer:
(b) \(\frac{-4}{5}\)
Explanation:
(\(\frac{2}{3}\)sin0° – \(\frac{4}{5}\)cos0°) = \(\frac{2}{3}\) × 0 – \(\frac{4}{5}\) × 1) = \(\frac{-4}{5}\) [∵ sin0° = 0, cos0° = 1]

Question 13.
The distance between the points A (7, 13) and B (10, 9) is
(a) 5 units
(b) 6 units
(c) 9 units
(d) 10 units
Answer:
(a) 5 units

The given points are A (7, 13) and B (10, 9)
Then, x₁= 7,
y₁ = 13
and x₂ = 10,
y₂ = 9
∴ AB = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
= \(\sqrt{(10-7)^2+(9-13)^2}\)
= \(\sqrt{3^2+(-4)^2}\)
= \(\sqrt{9+16}\)
= \( \sqrt{25}\)
= 5 units

Question 14.
The number (5 – 3 √5 + √5 ) is: 1
(a) an integer
(b) a rational number
(c) an irrational number
(d) a whole number
Answer:
(c) an irrational number
Explanation: (5 – 3√5 + √5) = (5 – 2√5)
∴ √5 is an irrational number so, 2√5 is an irrational number.
Also, (5 – 2√5) or (5 – 3√5 + √5) is an irrational number.

Question 15.
The product of the HCF and LCM of two prime numbers a and b is
(a) \(\frac{a}{b}\)
(b) a – b
(c) a + b
(d) a × b
Answer:
(d) a × b

HCF (a, b) = 1
LCM (a, b) = ab
∴ HCF (a,b) × LCM(a, b) = 1 × ab = ab

Question 16.
If ΔABC ~ ΔDEF and ΔA = 47°, ΔE = 83°, then ΔC is equal: 1
(a) 47°
(b) 50°
(c) 83°
(d) 130°
Answer:
(b) 50°
Explanation: Given,
ΔABC ~ ΔDEF
So, corresponding angles are equal, that is,
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
Given, ∠A = ∠D = 47°
and ∠B = ∠E = 83°
In ΔABC,
∠A + ∠B + ∠C, = 180 [Property and triangle]
⇒ 47° + 83° + ∠C = 180°
⇒ 130° + ∠C = 180°
⇒ ∠C = 180° – 130° = 50°

Question 17.
If median = 143 and mean = 143.06, then the mode is
(a) 143.18
(b) 142.94
(c) 142.88
(d) 143
Answer:
(c) 142.88

We know that
Mode = 3 Median – 2 Mean
= 3 (143) – 2(143.06)
= 429 – 286.12
= 142.88.

Question 18.
The pair of linear equations x + 2y + 5 = 0 and – 3x – 6y + 1 = 0 has: 1
(a) a unique solution
(b) exactly two solutions
(c) infinitely many solutions
(d) no solution
Answer:
(d) no solution
Explanation: Given equations are
x + 2y + 5 = 0
and – 3x – 6y + 1 = 0
Here, a₁ = 1, b₁ = 2, c₁ = 5
and a₂ = -3, b₂ = -6, c₂ = 1
Now, \(\frac{a_1}{a_2}=\frac{1}{-3}=-\frac{1}{3}\);
\(\frac{b_1}{b_2}=\frac{2}{-6}=-\frac{1}{3}\);
\(\frac{c_1}{c_2}=\frac{5}{1}\) = 5
Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\), so equations have no solution.

Directions: In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) : The value of sin 60° cos 30° + sin30° cos60° is 1.
Reason (R) : sin 90° = 1 and cos 90° = 0
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Assertion
sin 60° cos 30° + sin 30° cos 60°
= \(\frac{\sqrt{3}}{2}\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\)
= \(\frac{3}{4}+\frac{1}{4}\)
= \(\frac{4}{4}\)
So, Assertion (A) is true.
Reason
We know, sin 90° = 1
and cos 90° = 0
So, Reason (R) is true.
But Reason (R) is not the correct explanation of Assertion (A).

Question 20.
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal. 1
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Explanation: We know that a tangent to a circle is perpendicular to the radius through the point of contact and the lengths of tangents drawn from an external point to a circle are equal. Hence both statements are true.

Section – B
Section B consists of 5 questions of 2 marks each

Question 21.
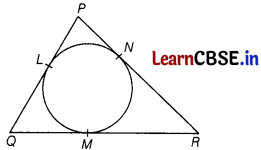
In the given figure, a circle is inscribed in a ∆PQR. If PQ = 10 cm, QR = 8 cm and PR = 12 cm, then find the lengths of QM,RN and PL.

Answer:
We know that the lengths of the tangents drawn from an external point to a circle are equal.
Let PL = PN = x;
QL = QM = y
and RM = RN = z
Now, PL + QL = PQ
⇒ x + y = 10 ………….. (i)
QM + RM = QR
⇒ y + z = 8 …………….(ii)
RN + PN = PR
⇒ z + x = 12 …………..(iii)
On subtracting Eq. (ii) from Eq. (iii), we get
x – y = 4 …………. (iv)
On solving Eqs. (i) and (iv), we get
x =7, y = 3
On substituting y = 3m Eq. (ii), we get
z = 5
∴ QM = y = 3 cm
RN = z = 5 cm
and PL = x = 7 cm.

Question 22.
In the adjoining figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR. 2

Answer:

Question 23.
Find the sum of first 15 even natural numbers.
Answer:
The sequence goes like this 2, 4, 6, 8, ……………..
Here, 4 – 2 = 6 – 4
= 8 – 6 = 2
So, it is an AP with first term, a = 2,
common difference, d = 4 – 2 = 2
and total number of terms, n = 15
∴ Sum of first 15 even natural numbers
S₁₅ = \(\frac{n}{2}\) [2a + (n – 1) d]
= \(\frac{15}{2}\) [2 × 2 + (15 – 1) 2]
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
= \(\frac{15}{2}\) [4 + 28]
= \(\frac{15}{2}\) × 32 = 240

Question 24.
Find the coordinates of the point that divides the join of A (-1, 7) and B (4, -3) in the ratio 2 : 3.
OR
If the points A (2, 3), B (-5, 6), C (6, 7), and D (p, 4) are the vertices of a parallelogram ABCD, find the value of p. 2
Answer:
Let C (x, y) divides the Line segment joining the points A (-1, 7) and B (4, – 3) in the ratio 2 : 3. Thus, the point C is,
[latex]\frac{2 \times 4+3 \times(-1)}{2+3}, \frac{2 \times(-3)+3 \times 7}{2+3}[/latex]
C[latex]\frac{8-3}{5}, \frac{-6+21}{5}[/latex] = C(1, 3)
So, the coordinates of the point are (1, 3).
OR

Given that ABCD is a parallelogram.
AB and CD are parallel, and AB = CD.
Since, diagonals of a parallelogram, bisect each other.
∴ Mid-point of diagonal BD = Mid-point of diagonal.
∴ (\(\frac{-5+p}{2}, \frac{6+4}{2}\)) = (\(\frac{2+6}{2}, \frac{3+7}{2}\))
\(\frac{-5+p}{2}\) = \(\frac{2+6}{2}\)
⇒ p = 3

Question 25.
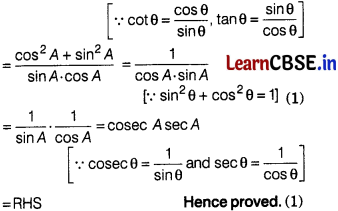
Prove that cot A + tan A = sec A cosec A.
Answer:
LHS = cot A + tan A

Or

Prove that \(\frac{\cot A-\cos A}{\cot A+\cos A}=\frac{\ {cosec} A-1}{\ {cosec} A+1}\).
Answer:
LHS = \(\frac{\cot A-\cos A}{\cot A+\cos A}\)
= \(\frac{\frac{\cos A}{\sin A}-\cos A}{\frac{\cos A}{\sin A}+\cos A}\)
= \(\frac{\cos A(1-\sin A)}{\cos A(1+\sin A)}\)
= \(\frac{\sin A(\ {cosec} A-1)}{\sin A(\ {cosec} A+1)}\)
= \(\frac{\ {cosec} A-1}{\ {cosec} A+1}\)
Hence proved.

Section – C
Section C consists of 6 questions of 3 marks each

Question 26.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of a corresponding major sector. 3
Answer:

Radius of circle, OB = OA = 7 cm, and ∠AOB = 90°
AOB is a quadrant of circle.
So, area of sector AOB
= \(\frac{90^{\circ}}{360^{\circ}}\) × πr²
= \(\frac{1}{4}\)πr²
= \(\frac{1}{4}\) × \(\frac{22}{7}\) × 7²
= \(\frac{77}{2}\) = 38.5 cm²
Area of major sector AOB = Area of circle – Area of quadrant
Area of circle = πr² = \(\frac{22}{7}\) × 7²
= 154 cm²
Now, area of major sector
= 154 cm² – 38.5 cm²
= 115.5 cm²

Question 27.
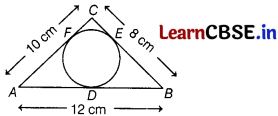
A coircle is inscribed in a ∆ABC having sides 8 cm, 10 cm and 12 cm as shown in figure. Find AD, BE and CF.

Answer:
Given, a circle is inscribed in the triangle, wtose sides are
BC = 8 cm,
AC = 10 cm
and AB = 12 cm.
Let AD = AF = x,
BD = BE = y
and CE = CF = z
[∵ the length of two tangents drawn from an external point to a circle are equal)
We have, AB = 12
⇒ AD + DB = 12
⇒ x + y = 12 …………(i)
AC = 10
⇒ AF + FC = 10
⇒ x + z = 10
and BC = 8
⇒ CE + EB = 8
⇒ z + y = 8 ………….(iii)
On adding Eqs. (i), (ii) and (iii), we get
2 (x + y + z) = 12 + 10 + 8
⇒ x + y + z = \(\frac{30}{2}\) = 15 ………….(iv)
On putting x + y = 12 from Eq. (i) in Eq. (iv), we get
12 + z = 15
⇒ z = 3
On putting z + y = 8 from Eq. (iii) in Eq. (iv), we get
x + 8 = 15
⇒ x = 7
On putting x + z =10 from Eq. (ii) in Eq. (iv). we get
10 + y = 15
⇒ y = 5
Hence, AD = 7 cm, BE = 5 cm and CF = 3 cm.

Question 28.
A die is rolled once. Find the probability of getting:
(A) an even prime number.
(B) a number greater than 4.
(C) an odd number. 3
Answer:
Numbers on a die: 1, 2, 3, 4, 5, 6
(A) Probability of getting an even prime number, that is, 2 = \(\frac{1}{6}\).

(B) Probability of getting a number greater than 4, that is, 5 and 6 = \(\frac{2}{6}\) = \(\frac{1}{3}\).

(C) Probability of getting an odd number, that is, 1, 3, 5= \(\frac{3}{6}\) = \(\frac{1}{2}\).

Question 29.
The tower is 50 m high. Its shadow is x m shorter when the Sun’s altitude is 45°, then when it is 30°. Find the value of x.
Answer:
Let AB = x m

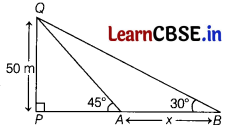
From right angted ∆APQ, we have
\(\frac{A P}{P Q}\) = cot 45°
⇒ \(\frac{A P}{50}\) = 1
⇒ AP = 50
From right angled ∆BPQ, we have
\(\frac{b P}{P Q}\) = cot 30°
\(\frac{x+50}{50}\) = √3
[∵ BP = AP + AB]
⇒ x = 50 (√3 – 1)
⇒ x = 50 (1.732 – 1)
∴ x = 36.6

Question 30.
Prove that the lengths of tangents drawn from an external point to a circle are equal.
OR
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P. 3

Answer:
Let PQ and PR be two tangents, drawn from an external point P to a circle C (0, r).

To prove: PQ = PR.
Construction: Join OP, OQ and OR.
Proof: Since, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠OQP = ∠ORP = 90°.
Now in right triangles OQP and ORP, we have
OQ = OR [Radii of the same circle]
∠OQP = ∠ORP [Each 90°]
OP = OP [Common]
ΔOQP ≅ ΔORP
[By RHS theorem of congruence]
⇒ PQ = PR
OR

In the figure, O is the common centre, of the given concentric circles.
AB is a chord of the bigger circle such that it is tangent to the smaller circle at P. Since, OP is the radius of the smaller circle through P, the point of contact
∴ OP ⊥ AB
⇒ ∠APO = 90°
Also, a radius perpendicular to a chord bisects the chord.
∴ OP bisects AB
⇒ AP = \(\frac{1}{2}\) AB
Now, in right ΔAPO, OA² = AP² + OP²
⇒ 5² = AP² + 3²
⇒ AP² = 5² – 3²
⇒ AP² = (5 – 3) (5 + 3) = 2 × 8
⇒ AP² = 16 = (4)²
⇒ AP = 4 cm
⇒ \(\frac{1}{2}\)AB = 4
⇒ AB = 2 × 4 = 8 cm
Thus, the required length of the chord AB is 8 cm.

Question 31.
In the given figure, two chords AB and CD intersect each other at the point P. Prove that

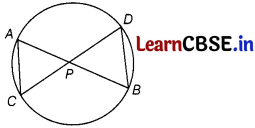
(i) ∆APC ~ ∆DPB
(ii) AP . PB = CP . DP
Answer:
Given, In figure, two chords AB and CD intersect each other at point P.
To prove :
(i) ∆APC ~ ∆DPB
(ii) AP . PB = CP DP
Proof:
(i) In ∆APC and ∆DPB,
∠APC = ∠DPB [vertically opposite angles]
and ∠CAP = ∠BDP [angles in the same segment]
∴ ∆APC ~ ∆DPB [by AA similarity criterion]

(ii) We have,
∆APC ~ ∆DPB [proved in part (i)]
∴ \(\frac{A P}{D P}=\frac{C P}{B P}\)
[∵ if two triangles are similar, then the ratio of their corresponding sides are equal]
∴ AP . BP = CP . DP
or AP . PB = CP . OP
Hence proved.

Section – D
Section D consists of 4 questions of 5 marks each

Question 32.
Find the sum of first 51 terms of an A.P. whose second and third terms are 14 and 18, respectively.
OR
The first term of an A.P. is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference. 5
Answer:
Given, the second and third terms of the A.P. are 14 and 18.
Let a be the first term and d be the common difference.
So, a + d = 14 …….. (i)
and a + 2d = 18 …….. (ii)
respectively subtracting equation (i) from (ii),
d = 4
Putting value of d in (i), we get
a + 4 = 14
⇒ a = 14 – 4
= 10
Sum of first n terms of an AP having first term a and common difference d, is:
S_n = \(\frac{n}{2}\)[2o + (n – 1)d]
Here, n = 51, a = 10 and d = 4
Putting values, S_n = \(\frac{51}{2}\)[2 × 10 + (51 – 1) × 4]
= \(\frac{51}{2}\)[20 + 200]
= \(\frac{51}{2}\) × 220
= 51 × 110
= 5610
OR
Given, a = 5 l = 45, and S_n = 400
We have. S_n = \(\frac{n}{2}\)(a + l)
Putting vaLues, 400 = \(\frac{n}{2}\)(5 + 45)
⇒ 400 = \(\frac{n}{2}\) × 50 = 25n
⇒ n = \(\frac{400}{25}\) = 16
Now, l = a + (n – 1)d
Putting values. 45 = 5 + (16 – 1)d
⇒ d = \(\frac{40}{15}\) = \(\frac{8}{3}\)
So, common difference = \(\frac{8}{3}\) and number of terms = 16.

Question 33.
The median of the distribution given below is 14.4. Find the values of x and y, if the total frequency is 20.

Answer:
Table for cumulative frequency is given below

Class interval	Frequency	Cumulative frequency
0 – 6	4	4 + 0 = 4
6 – 12	x	4 + x = (4 + x) (cf)
12 – 18	5(f)	5 +(4 + x) = 9 + x
18 – 24	y	y + (9 + x) = 9 + x + y
24 – 30	1	1 + (9 + x + y) = 10 + x + y

Since, N = 20
∴ 10 + x + y = 20
x + y = 20 – 10
x + y = 10
Also, we have, median = 14.4 …………..(i)
which lies in the class interval 12 – 18.
∴ The median class is 12 – 18, such that
l = 12,
f = cf = 4 + x
and h = 6
∴ Median = l + \(\left(\frac{\frac{N}{2}-c f}{f}\right)\) × h
⇒ 14.4 = 12 + \(\left[\frac{10-(4+x)}{5}\right]\) × 6
⇒ 144 – 12 = \(\frac{6-x}{5}\) × 6
⇒ 2.4 = \(\frac{36-6 x}{5}\)
⇒ 12 = 36 – 6x
⇒ 6x = 24
⇒ x = 4
Now, on putting the value of x in Eq. (i), we get
4 + y = 10
⇒ y = 10 – 4 = 6
Thus, x = 4 and y = 6.

Question 34.
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in the middle and two hemispherical parts at both ends.
The length of the cylindrical part is 7 m and the radius of the cylindrical part is \(\frac{1}{2}\) m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of the cylindrical part to the volume of one hemispherical part. 5

Answer:

Given: Radius of hemispherical ends, r = \(\frac{7}{2}\) m
We know that, surface area of each hemispherical end
= 2πr²
= 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) = 77 m²
∴ Surface area of both hemispherical ends
= 2 × 77 m²
= 154 m²
Length of cylindrical part = 7 m
Curved surface area of the cylindrical portion
= 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × 7
= 154 m²
Total surface area of the boiler
= 154 m² + 154 m²
= 308 m²
Thus, the required surface area is 308 m².
Volume of boiler = Volume of cylinder + Volume of 2 hemisphere

Question 35.
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
Answer:
Given, diameter of hemispherical bowl = 36 cm
Radius (r) = 18 cm
Volume of liquid in the bowl = \(\frac{2}{3}\) πr³
= \(\frac{2}{3}\) × π × 18 × 18 × 18
= 3888π cm³
Amount of the liquid wasted = 3888π × \(\frac{10}{100}\)
= \(\frac{3888 \pi}{10}\) cm³
Liquid transferred into the bottles = 3888π – \(\frac{3888 \pi}{10}\) cm³
= \(\frac{34992 \pi}{10}\) cm³ ………………(i)
Also, given diameter of bottle = 6 cm
⇒ Radius(r) = 3 cm
Let h be the height of the bottle,
Volume of bottle = πr²h
= π × 3 × 3 × h
= 9πh cm³
Volume of 72 such bottles = 72 × 9πh cm³
= 648πh cm³
Now, volume of 72 bottles = Volume of liquid transferred into the bottles
⇒ 648πh = \(\frac{34992 \pi}{10}\) [using Eq. (i)]
⇒ h = 5.4 cm
∴ Height of each bottle is 5.4 cm.

Section – E
Case study based questions are compulsory

Question 36.
Observe the figures given below carefully and answer the questions:


(A) Name the figure(s) wherein two figures are similar. 1
(B) Name the figure(s) where in the figures are congruent. 1
(C) Prove that congruent triangles are
also similar but not the converse.
OR
What more is least needed for two similar triangles to be congruent? 2
Answer:
(A) In Figure A both quadrilaterals are similar, and in Figure C both triangles are similar.

(B) In Figure C, both triangles are congruent.

(C) Congruent triangles are similar because, for each side in one triangle, there is a corresponding equal side in another. So, sides are in proportion, therefore congruent triangles are also similar.
But the converse is not true. In similar triangles, sides are in the same proportion but not equal in length.
OR
Two pairs of corresponding angles are equal.
Three pairs of corresponding sides are proportional.
Two pairs of corresponding sides are equal and the corresponding angles between them are equal.

Question 37.
Ritu is studying in X standard. She observes two poles AB and DC and the heights of these poles are a m and b m respectively, shown as figure below

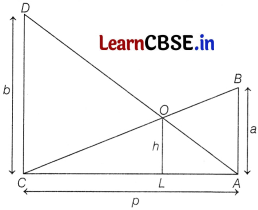
These poles are p m apart and O is the point of intersection of the lines joining the top of each pole to the foot of the opposite pole and the distance between points O and L is h m. Few questions came to his mind while observing the poles. Give answers to his questions by looking at the figure.

(i) If CL = x, then find x in terms of a, b and h.
Answer:
In ∆ABC and ∆LOC, we have
∠CAB = ∠CLO = 90° [common]
∴ ∆CAB ~ ∆CLO
∴ \(\frac{C A}{C L}=\frac{A B}{L O}\) [by AA similarity criterion]
⇒ \(\frac{p}{x}=\frac{a}{h}\)
⇒ x = \(\frac{p h}{a}\) ………….(i)

(ii) If AL = y, then find y in terms of a, b and h.3
Answer:
In ∆ALO and ∆ACD, we have
∠ALO = ∠ACD = 90°
∴ ∠A = ∠A [common]
∠ ∆ALO ~ ∆ACD [by AA similarity criterion]
⇒ \(\frac{A L}{A C}=\frac{O L}{D C}\)
⇒ \(\frac{y}{p}=\frac{h}{b}\)
⇒ y = \(\frac{p h}{b}\) ………..(ii)

(iii) Find h in terms of a and b.
Answer:
From Eqs. (i) and (ii), we get
x + y = \(\frac{p h}{a}\) + \(\frac{p h}{b}\)
= ph \(\left(\frac{1}{a}+\frac{1}{b}\right)\)
⇒ p = ph \(\left(\frac{a+b}{a b}\right)\)
[∵ x + y = CL + LA = p]
⇒ h = \(\frac{a b}{a+b}\) m

Or

If a = 5 m and b = 10 m, then find h.
Answer:
If a = 5 m
and b = 10 m then
h = \(\frac{a b}{a+b}\)
= \(\frac{5 \times 10}{5+10}\)
= \(\frac{50}{15}=\frac{10}{3}\) m.

Question 38.
Khushi wants to organise her birthday party. Being health conscious, she decided to serve only fruits in her birthday party. She bought 36 apples and 60 bananas and decided to distribute fruits equally among all.
Based on the above information, answer the following questions:
(A) How many guests Khushi can invite at the most? 1
(B) How many apples and bananas will each guest get? 1
(C) If Khushi decides to add 42 mangoes, how many guests Khushi can invite at the most?
OR
If the cost of 1 dozen of bananas is ₹ 60, the cost of 1 apple is ₹ 15 and cost of 1 mango is ₹ 20, find the total amount spent on 60 bananas, 36 apples and 42 mangoes. 2
Answer:
Khushi bought 36 apples and 60 bananas and she decided to distribute fruits equally among all guests.

(A) We need to find HCF of 36 and 60.
36 = 2 × 2 × 3 × 3;
60 = 2 × 2 × 3 × 5
HCF of 36 and 60 = 2 × 2 × 3 = 12
Therefore, Khushi can invite at most 12 guests.

(B) Each guest will get \(\frac{36}{12}\) = 3 apples and \(\frac{60}{12}\) = 5 bananas.

(C) If khusi add 42 mangoes, then maximum number guests she can invite = HCF of (36, 60 and 42)
36 = 2 × 2 × 3 × 3;
60 = 2 × 2 × 3 × 5;
42 = 2 × 3 × 7
HCF of (36, 60 and 42) = 2 × 3 = 6
Therefore, Khushi can invite at most 6 guests.
OR
Cost of 1 dozen banana is ₹ 60, then cost of 5 dozen bananas = 60 × 5 = ₹ 300
Cost of 1 apple is ₹ 15, then cost of 36 apples
= 15 × 36 = ₹ 540
Cost of 1 mango is ₹ 20, then cost of 42 mangoes = 20 × 42 = ₹ 840
Hence, total amount spent
= 300 + 540 + 840
= ₹ 1680