Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 5 are designed as per the revised syllabus.
CBSE Sample Papers for Class 10 Maths Basic Set 5 with Solutions
Time : 3 hrs
Max. Marks : 80
General Instructions:
- This Question Paper has 5 Sections A, B, C, D and E.
- Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
- Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
- Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
- Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
- Section E has 3 Case Based integrated units of assessment questions (4 marks each).
All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks question of Section E. - Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
Section – A
Section A consists of 20 questions of 1 mark each
Question 1.
The HCF of 85 and 152 is
(a) 1
(b) 17
(c) 13
(d) 19
Answer:
(a) 1
Let a = 85
and b = 152
∴ a = 1 × 5 × 17
and b = 1 × 23 × 19
HCF (85, 152) = 1
Question 2.
If given A.P. is 11, 8, 5, 2, …………… then the sum of 10th term is: 1
(a) -23
(b) 28
(c) 24
(d) -25
Answer:
(d) -25
Explanation: Given AP is 11, 8, 5, 2, …
a = 11
d = 8 – 11 = -3
n = 10
S10 = \(\frac{10}{2}\)[2 × 11 + (10 – 1) × -3]
= 5(22 – 27)
= 5 × -5
= -25
Question 3.
If the point (x, y) is equidistant from the points (2, 1) and (1, – 2), then
(a) x + 3y = 0
(b) 3x + y = 0
(c) x + 2y = 0
(d) 3x + 2y = 0
Answer:
(a) x + 3y = 0
Let the points be P(x, y), 4(2, 1) and B(1, – 2).
Since, P is equidistant from A and B.
∴ AP = BP
⇒ AP2 = BP2
⇒ (x – 2)2 + (y – 1)2 = (x – 1)2 + (y + 2)2
[by distance formula]
⇒ x2 – 4x + 4 + y2 – 2y + 1 = x2 – 2x + 1 + y2 + 4y + 4
⇒ 2x + 6y = 0
⇒ x + 3y = 0 [dividing by 2]
![]()
Question 4.
The solution of the pair of equations 2x + 3y = 9; 3x + 4y = 5 is: 1
(a) 21, -17
(b) 20, 14
(c) -21, 17
(d) 20, 3
Answer:
(c) -21, 17
Explanation: We have
2x + 3y = 9 ……….. (i)
3x + 4y = 5 …………. (ii)
Multiplying eq. (i) and (ii) by 3 and 2, respectively, and then subtracting them, we get

From eq. (i),
2x + 51 =9
⇒ 2x = -42
⇒ x = -21
Thus, x = -21, y = 17 is the required solution.
Question 5.
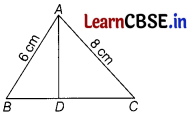
In an ∆ABC, it is given that AB = 6 cm, AC = 8 cm and AD is the bisector of A. Then, BD : DC is
(a) 3 : 4
(b) 9 : 16
(c) 4 : 3
(d) √3 : 2
Answer:
(a) 3 : 4
Given, AD is the bisector of ∠A.
By angle bisector theorem, bisector of an angle divides the opposite side in the same ratio as of two remaining sides.
∴ \(\frac{B D}{D C}=\frac{A B}{A C}\)
⇒ \(\frac{B D}{D C}=\frac{6}{8}\)
⇒ \(\frac{B D}{D C}=\frac{3}{4}\)
Question 6.
In the adjoining figure, if PA = 10 cm, then the perimeter of ΔPCD is: 1

(a) 16 cm
(b) 21 cm
(c) 18 cm
(d) 20 cm
Answer:
(d) 20 cm
Explanation: We know the lengths of tangents drawn from an external point to a circle are equal.
∴ From the figure, we have
PA = PB, CA = CE and DE = DB.
Now,
Perimeter of ΔPCD = PC + CE + ED + DP
= (PC + CE) + (ED + DP)
= (PC + CA) + (BD + DP)
= PA + PB
= 2 PA = 2 × 10 cm
= 20 cm
![]()
Question 7.
The ratio in which Y-axis divides the line segment joining the points P (- 2, 5) and Q (2, – 7) is
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{3}{2}\)
(d) \(\frac{4}{3}\)
Answer:
(a) 1
Suppose Y-axis divides PQ in the ratio λ : 1 at point R,
then the coordinates of R are \(\left(\frac{2 \lambda-2}{\lambda+1}, \frac{-7 \lambda+5}{\lambda+1}\right)\)
Since, R lies on Y-axis
∴ \(\frac{2 \lambda-2}{\lambda+1}\) = 0
⇒ 2λ – 2 = 0
⇒ λ = 1
Question 8.
If x sec 45° = 2, then what is the value of x? 1
(a) \(\frac{\sqrt{3}}{2}\)
(b) 2√2
(c) √2
(d) \(\frac{1}{\sqrt{2}}\)
Answer:
(c) √2
Explanation: Given,
x sec 45° = 2
⇒ x(√2) = 2
⇒ x = √2
Question 9.
In ∆DEW, AB || EW. If AD = 2 cm, DE = 6 cm and DW = 15 cm, then the value of DB is
(a) 2 cm
(b) 5 cm
(c) 9 cm
(d) 13 cm
Answer:
(b) 5 cm
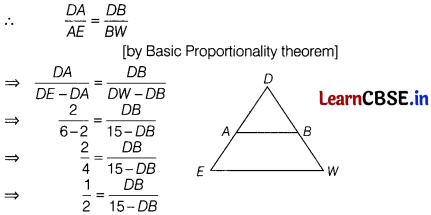
⇒ 15 – DB = 2 DB
⇒ 3 DB = 15
⇒ DB = \(\frac{15}{3}\) = 5 cm
![]()
Question 10.
AB is a chord of the circle and AOC is its diameter such that ∠BAC = 60°. If CP is the tangent to the circle at the point C, then ∠BCP is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Answer:
(b) 60°
∠ABC = 60°
[∵ angle in a semi-circle is right angle]
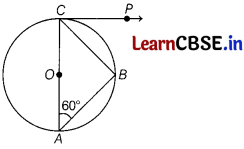
∠A + ∠B + ∠C = 180°
⇒ 60° + 90° + ∠C = 180°
⇒ ∠C = 180° – 150° = 30°
Now, ∠OCP = 90°
[∵ radius is perpendicular to the tangent at the point of contact]
∴ ∠BCP = 90° – ∠OCB
= 90° – 30° = 60°
Question 11.
If sec θ – tan θ = x, then the value of sec θ + tan θ in term of x is
(a) \(\frac{1}{x}\)
(b) x2
(c) \(\frac{x-1}{x}\)
(d) x
Answer:
(a) \(\frac{1}{x}\)
We know that
sec2 θ – tan θ = 1
⇒ (sec θ – tan θ) (sec θ + tan θ) = 1
⇒ x (sec θ + tan θ) = 1
⇒ sec θ + tan θ = \(\frac{1}{x}\)
Question 12.
A 6 faced cube has letters A, B, C, D, A and C on its six faces. This cube is rolled once. What is the probability of getting B or C?
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{4}\)
Answer:
(a) \(\frac{1}{2}\)
Explanation: Total number of outcomes = 6
∴ Number of favourable outcomes = 3
P (B or C) = \(\frac{3}{6}\) i.e. \(\frac{1}{2}\).
![]()
Question 13.
The value of \(\frac{4}{\cot ^2 30^{\circ}}+\frac{1}{\sin ^2 60^{\circ}}\) – cos2 45° is
(a) \(\frac{29}{6}\)
(b) \(\frac{77}{6}\)
(c) \(\frac{13}{6}\)
(d) \(\frac{29}{12}\)
Answer:
(c) \(\frac{13}{6}\)
\(\frac{4}{\cot ^2 30^{\circ}}+\frac{1}{\sin ^2 60^{\circ}}\) – cos2 45° = \(\)
= \(\frac{4}{(\sqrt{3})^2}+\frac{1}{\left(\frac{\sqrt{3}}{2}\right)^2}-\left(\frac{1}{\sqrt{2}}\right)^2\)
= \(\frac{4}{3}+\frac{4}{3}-\frac{1}{2}\)
= \(\frac{8}{3}-\frac{1}{2}\)
= \(\frac{16-3}{6}=\frac{13}{6}\)
Question 14.
In the following distribution, the class mark of the modal class is: 1
| Class interval | Frequency |
| 40 – 50 | 10 |
| 50 – 60 | 25 |
| 60 – 70 | 28 |
| 70 – 80 | 12 |
| 80 – 90 | 10 |
| 90 – 100 | 15 |
(a) 45
(b) 55
(c) 65
(d) 63
Answer:
(c) 65
Explanation: The class 60 – 70 is a modal class as it has the highest frequency.
∴ class mark = \(\frac{60+70}{2}\)
= 65
Question 15.
The zeroes of the polynomial x2 – √2x – 12 are
(a) √2, – √2
(b) 3√2, – 2√2
(c) – 3√2, 2√2
(d) 3√2, 2√2
Answer:
(b) 3√2, – 2√2
x2 – √2x – 12 = 0
⇒ x2 – 3√2 x + 2√2x – 12 = 0
⇒ x (x – 3√2) + 2√2 (x – 3√2) = 0
⇒ (x + 2√2) (x – 3√2) = 0
∴ x = – 2√2
or x = 3√2.
![]()
Question 16.
Which term of the A.P.: -2, -7, -12,… will be -77? 1
(a) 16th
(b) 10th
(c) 15th
(d) 12th
Answer:
(a) 16th
Explanation: Let, the nth term of the A.P. be -77.
Then, a + (n – 1 )d = -77
For the given A.P., a = -2 and d = -5.
So, a + (n – 1)d = (-2) + (n – 1)(-5) = -77
-5(n – 1) = -75
or n – 1 = 15 or n = 16
So, the 16th term of the A.P. is (-77).
Question 17.
If a = 2 cosec2 θ – 1 and b = cot2 θ – 3, then a – 2 b is equal to
(a) 6
(b) 7
(c) – 7
(d) 5
Answer:
(b) 7
We have,
a = 2cosec2 – 1
and b = cot2 – 3
∴ a – 2b = (2 cosec2 θ – 1) – 2 (cot2 θ – 3)
= 2(cosec2 θ – cot2 θ) – 1 + 6
= 2(1) – 1 + 6
[∵ cosec2 A – cot2A = 1]
= 2 – 1 + 6 = 7
Question 18.
A bridge across a river makes an angle of 45° with the river bank. If the length of the bridge across the river is 50 m, then what is the width of the river the river? 1

(a) 20√2 m
(b) 50√2 m
(c) 25√2 m
(d) 10√2 m
Answer:
(c) 25√2 m
Explanation: In right ΔABC, we have
sin 45° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
⇒ \(\frac{1}{\sqrt{2}}=\frac{B C}{50}\)
⇒ BC = \(\frac{50}{\sqrt{2}}\)
= 25√2 m
Hence, the width of the river is 25√2 m
![]()
Directions: In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.
Question 19.
Assertion (A) : If x = 3 sin2 θ and y = 3 cos2 θ + 1 then the value of x + y = 4.
Reason (R) : For any value of θ, sin2 θ + cos2 θ = 1
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Given, x = 3 sin2 θ
and y = 3 cos2 θ + 1
∴ x + y = 3 sin2 θ + 3 cos2 θ + 1
= 3(sin2 θ + cos2 θ) + 1
= 3 + 1 = 4
[∵ sin2 A + cos2 A = 1]
So, the given Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Question 20.
Assertion (A): If the circumference of two circles are equal, then their areas are also equal.
Reason (R): Two circles are congruent if their radii are equal. 1
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Answer:
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A)
Explanation: Let’s consider two circles of radii r1 and r2.
Then, 2πr1 = 2πr2
r1 = r2 = r
A1 = πr12 = πr2
Then, A2 = πr22 = πr2
∴ A1 = A2
![]()
Section – B
Section B consists of 5 questions of 2 marks each
Question 21.
A wheel has diameter 84 cm. Find how many complete revolutions must it take to cover 792 m.
Answer:
Let r be the radius of the wheel.
Then, diameter 84 cm
⇒ 2r = 84 cm
⇒ r = 42 cm
∴ Circumference of the wheel = 2πr
= 2 × \(\frac{22}{7}\) × 42
= 264 cm
= 2.64 m [∵ 1 m = 100 cm]
So, the wheel covers 264 m in one complete revolution.
∴ Total number of revolutions ¡n covering 792 m = \(\frac{792}{2.64}\) = 300.
Question 22.
Find the greatest number that divides 45 and 210 completely. 2
Answer:
The greatest number that divides 45 and 210 completely is the HCF of 45 and 210.
Now, 45 = 3 × 3 × 5, or 32 × 51
210 = 2 × 3 × 5 × 7,
So, HCF (45, 210) = 31 × 51, i.e. 15
Hence, the required number is 15.
![]()
Question 23.
The mid-point P of the line segment joining the points A (- 10, 4) and B (- 2, 0) lies on the line segment joining the points C (- 9, – 4) and D (- 4, y). Find the ratio in which P divides CD. Also, find the value of y.
Answer:
Given the mid-point P of the line segment joining the points A (- 10, 4) and B (- 2, 0).
The mid-point of P = \(\left(\frac{-10-2}{2}, \frac{4+0}{2}\right)\) = (-6, 2)
Let P (- 6 2) divide CD in the ratio k : 1.
Thus, \(\frac{-4 k-9}{k+1}\) = – 6
and \(\frac{k y-4}{k+1}\) = 2
⇒ – 4k – 9 = – 6k – 6
and ky – 4 = 2k + 2
⇒ 2k = 3
and k (y – 2) = 6
⇒ k = \(\frac{3}{2}\)
and (y – 2) = \(\frac{6}{k}\)
= 6 × \(\frac{2}{3}\) = 4
k = \(\frac{3}{2}\)
and y = 4 + 2 = 6
Hence, the ratio is 3 : 2 and y = 6.
Question 24.
Mayank made a bird bath for his garden in the shape of a cylinder with a hemispherical depression at one end (see figure). The height of the cylinder is 1.45m and its radius is 30 cm. Find the total surface area of the bird-bath.

OR
A toy is in the form of a cylinder with two hemispheres at two ends. If the height of the cylinder is 12 cm, and its base is of diameter 7 cm, find the total surface area of the toy. 2

Answer:
Let h be height of the cylinder, and r be the common radius of the cylinder and hemisphere. So, h = 1.45 m = 1.45 × 100 cm = 145 cm Then, the total surface area of the bird-bath = curved surface area of cylinder + curved surface area of the hemisphere
= 2πrh + 2πr2
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × 30(145 + 30)
= \(\frac{44}{7}\) × 30 × 175
= 33000 cm2
= \(\frac{33000}{10000}\)m2
= 3.3 m2
OR
Height of the cylinder = 12 cm
Diameter of the cylinder = 7 cm
∴ Radius of the cylinder = \(\frac{7}{2}\)cm
Curved surface area of cylinder
= 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × 12
= 264 cm2
Curved surface area of two hemispheres
= 4πr2
= 4 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\)
= 154 cm2
∴ Total surface area of toy = Curved surface area of the cylinder + Curved surface area of two hemispheres
= (264 + 154) cm2
= 418 cm2
Question 25.
Find the solution of the equation \(\frac{2 x}{x-4}+\frac{2 x-5}{x-3}=\frac{25}{3}\), x ≠ 3, 4.
Answer:
Given, equation is \(\frac{2 x}{x-4}+\frac{2 x-5}{x-3}=\frac{25}{3}\), x ≠ 3, 4
⇒ \(\frac{2 x(x-3)+(x-4)(2 x-5)}{(x-4)(x-3)}=\frac{25}{3}\)
⇒ \(\frac{2 x^2-6 x+\left(2 x^2-13 x+20\right)}{(x-4)(x-3)}=\frac{25}{3}\)
⇒ 3(4x2 – 19x + 20) = 25 (x2 – 7x + 12)
⇒ 25x2 – 12x2 – 175x + 57x + 300 – 60 = 0
⇒ 13x2 – 118x + 240 = 0
⇒ 13x2 – 78x – 40x + 240 = 0 [by factorisation method]
⇒ 13x (x – 6) – 40 (x – 6) = 0
⇒ (13x – 40) (x – 6) = 0
⇒ 13x – 40 = 0 or x – 6 = 0
⇒ x = \(\frac{40}{13}\) or x = 6
Or
If \(\frac{1}{2}\) is a root of the equation x2 + kx – \(\frac{5}{4}\) = 0, then find the value of k.
Answer:
Since, \(\frac{1}{2}\) is a root of the quadratic equation.
x2 + kx – \(\frac{5}{4}\) = 0
∴ \(\left(\frac{1}{2}\right)^2+k\left(\frac{1}{2}\right)-\frac{5}{4}\) = 0
\(\frac{1}{4}+\frac{k}{2}-\frac{5}{4}\) = 0
⇒ \(\frac{1+2 k-5}{4}\) = 0
⇒ 2k – 4 = 0
⇒ 2k = 4
∴ k = 2.
![]()
Section – C
Section C consists of 6 questions of 3 marks each
Question 26.
If α and β are the zeroes of the quadratic polynomial f(x) = kx2 + 4x + 4 such that 2 α2 + β2 = 24, then find the values of k.
Answer:
Since, α and β is a root of the quadratic equation.
polynomial f(x) = kx2 + 4x + 4
∴ α + β = – \(\frac{4}{k}\)
and αβ = \(\frac{4}{k}\)
Now, given
α2 + β2 = 24
⇒ (α + β)2 – 2αβ = 24
⇒ \(\left(-\frac{4}{k}\right)^2-2 \times \frac{4}{k}\) = 24
⇒ \(\frac{16}{k^2}-\frac{8}{k}\) = 24
⇒ 16 – 8k = 24k2
⇒ 3k2 + k – 2 = 0
⇒ 3k2 + 3k – k – 2 = 0
⇒ 3k (k + 1) – 2 (k + 1) = 0
⇒ (k + 1) (3k – 2) = 0
⇒ k + 1 = 0 or 3k – 2 = 0
⇒ k = – 1 or k = \(\frac{2}{3}\)
Hence, k = – 1 or k = \(\frac{2}{3}\).
Question 27.
Prove that √2 + √5 is irrational, given that √2 is irrational.
Answer:
Let us assume on the contrary that √2 + √5 be a rational number.
Then, there exist coprime positive integers a and b such that
√2 + √5 = \(\frac{a}{b}\)
⇒ \(\frac{a}{b}\) – √2 = √5
⇒ \(\left(\frac{a}{b}-\sqrt{2}\right)^2\) = (√5)2 [squaring both sides]
⇒ \(\frac{a^2}{b^2}-\frac{2 a}{b}\) √2 + 2 = 5
⇒ \(\frac{a^2}{b^2}-3=\frac{2 a}{b} \sqrt{2}\)
⇒ \(\frac{a^2-3 b^2}{2 a b}\) = √2
√2 is a rational number.
[∵ a, b are integers
∵\(\frac{a^2-3 b^2}{2 a b}\) is rational]
This contradicts the fact that √2 is irrational.
So, our assumption is wrong.
Hence, √2 + √5 is irrational.
Hence proved.
Question 28.
Prove that the lengths of tangents drawn from an external point to a circle are equal. 3
Answer:
Let AP and AQ be the two tangents drawn to the circle from an external point A.
We need to show that AP = AQ.
Join OA, OP.and OQ.
We know that tangent is perpendicular to radius at the point of contact.
∴ OP ⊥ AP and OQ ⊥ QA.

Consider ΔOPA and ΔOQA.
Here, OQ = OP [radii of the circle]
OA = OA [common]
∠OPA = ∠OQA
So, ΔOPA ≅ ΔOQA [By SAS Criterion]
⇒ PA = QA or AP = AQ [By cpct]
![]()
Question 29.
One number of two digits is such that the product of digits is 12. If 36 is added to the number, then the places of the digits are interchanged. Find the number.
Answer:
Let the units place digit be y and tens place digit be x.
Then, number of two digits = 10x + y
∵ Product of digits. xy = 12 [given] …………….(i)
Interchanging the position of digits, new number = 10y + x
According to the question,
10x + y + 36 = 10y + x
⇒ 10x – x + y- 10y + 36 = 0 [on transposition]
⇒ 9x – 9y + 36 = 0
⇒ x – y + 4 = 0 [on dividing by 9]
⇒ y = x + 4 …………….(ii)
On putting the value of y from Eq (ii) in Eq. (i), we get
x (x + 4) = 12
⇒ x2 + 4x = 12
⇒ x2 + 4x – 12 = 0 [on transposition]
By using factorisation method,
⇒ x2 + (6 – 2) x – 12 = 0
⇒ x2 + 6x – 2x – 12 = 0
⇒ x (x + 6) – 2 (x + 6) = 0
⇒ (x + 6) (x – 2) = 0
⇒ x + 6 = 0 or x – 2 = 0
⇒ x = – 6 or x = 2
∴ x = 2
[∵ x ≠ – 6]
On putting the value of x in Eq. (ii), we get
y = x + 4
= 2 + 4 = 6
Hence, the required number of two digits = 10x + y
= 10 × 2 + 6
= 20 + 6 = 26
Question 30.
Prove that:
\(\frac{5 \sin ^2 30^{\circ}+\cos ^2 45^{\circ}-4 \tan ^2 30^{\circ}}{2 \sin 30^{\circ} \cdot \cos 30^{\circ}+\tan 45^{\circ}}\) + cos0°
= \(\frac{17+6 \sqrt{3}}{6(\sqrt{3}+2)}\) 3
Answer:

Question 31.
Find the value of the height (h) in the given figure, at which the tennis ball must be hit, so that it will just pass over the net and land 7 m away from the base of the net.
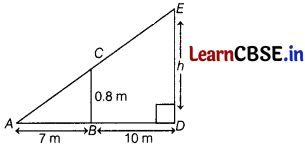
Answer:
Since the height (h) is measured vertically.
So, ∠EDA is a right angle.
We assume that the net (i.e. CB) is vertical.
Here, ∆ADE and ∆ABC are similar.
[by AA similarity criterion]
∴ \(\frac{D E}{B C}=\frac{A D}{A B}\)
\(\frac{h}{0.8}=\frac{17}{7}\)
h = \(\frac{17 \times 0.8}{7}\)
h = 1.94 m
Hence, the height at which the ball should be hit is 19.4 m.
![]()
Section – D
Section D consists of 4 questions of 5 marks each
Question 32.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see figure). Find the distance travelled by the ballon during the interval.

The shadow of a vertical tower on level ground increases by 16 m, when the altitude of the Sun changes from angles of elevation 60° to 45°. Find the height of the tower, correct to one place of decimal. (Use √3 = 1.73). 5
Answer:
In the figure, let C be the position of the girl. A and P are two positions of the balloon. CD is the horizontal line from the eyes of the girl.

Thus, the required distance between the two positions of the balloon is 58√3 m.
OR
Let AB represent the tower of height ‘h’ metres.
AS1, AS2 be, is shadows when sun’s attitude is 60° and 45° respectively.
∴ S1S2 = 16 m
From Δ S1AB,
\(\frac{\mathrm{AB}}{\mathrm{S}_1 \mathrm{~A}}\) = tan 60°

⇒ \(\frac{h}{\mathrm{~S}_1 \mathrm{~A}}=\sqrt{3}\)
⇒ S1A = \(\frac{h}{\sqrt{3}}\) …….. (i)
From Δ S2AB,
\(\frac{\mathrm{AB}}{\mathrm{S}_2 \mathrm{~A}}\) = tan 45°
⇒ \(\frac{h}{16+S_1 A}\) = 1
⇒ 16 + S1A = h ………… (ii)
Subtracting eqn. (i) from (ii), we have
16 = h – \(\frac{h}{\sqrt{3}}\)
= h(1 – \(\frac{1}{\sqrt{3}}\))

= 37.8 metres.
Question 33.
A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Answer:
Let r be the radius of cone and hemisphere and H be the height of the toy.
Given, radius of the conical and hemispherical portion,
r = 3.5 cm
and total height of the toy, H = 15.5 cm
∴ Height of conical portion,
h = Total height – Radius of hemispherical portion
= 15.5 – 3.5 = 12 cm
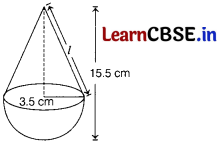
∴ Slant height of the cone,
l = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(12)^2+(3.5)^2}\)
= \(\sqrt{144+12.25}\)
= \(\sqrt{156.25}\)
l = 12.5 cm
Now, total surface area of the toy = Curved surface area of conical portion + Curved surface area of hemispherical portion
= πrl + 2πr2
= \(\frac{22}{7}\) × 3.5 × (12.5 + 2 × 3.5)
= \(\frac{22}{7}\) × 3.5 × 19.5
= 214.5 cm2
Hence, the total surface area of the toy is 214.5 cm2
![]()
Question 34.
Find the median marks for the following frequency distribution:
| Marks | Number of Students |
| 0 – 20 | 7 |
| 20 – 40 | 12 |
| 40 – 60 | 23 |
| 60 – 80 | 18 |
| 80 – 100 | 10 |
Answer:
| Marks | Frequency | Cumulative Frequency |
| 0 – 20 | 7 | 7 |
| 20 – 40 | 12 | 19 |
| 40 – 60 | 23 | 42 |
| 60 – 80 | 18 | 60 |
| 80 – 100 | 10 | 70 |
Here, N = 70,
∴ \(\frac{N}{2}\) = 35
Cumulative frequency just greater than 35 is 42 which belongs to class 40 – 60.
So, the median class is 40 – 60.
For this class,
l = 40, h = 20, c.f. = 19 and f = 23
So, Median = l + \(\frac{\frac{N}{2}-c . f}{f}\) × h
= 40 + \(\frac{35-19}{23}\) × 20
= 40 + 13.9 (approx.)
= 53.9 (approx.)
Question 35.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the cable tower.
Answer:
Let AD = 7 m be the height of the building and
BC = h m be the height of the cable tower.
From the top of the building D, the angles of elevation
and depression are ∠CDE = 60° and ∠EDB = 45°.
From the point D, draw a line DE II AB.
Then, ∠EDB = ∠ABD = 45° [alternate angles]
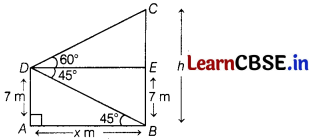
In right angled ∆BAD,
tan 45° = \(\frac{AD}{AB}\)
[∵ tan θ = Perpendicular / Base]
⇒ 1 = \(\frac{7}{x}\)
[∵ tan 45° = 1]
⇒ x = 7m ……………(i)
Now, in right angled ∆CED,
tan 60° = \(\frac{C E}{D E}\)
= \(\frac{C B-B E}{A B}\)
⇒ √3 = \(\frac{h-7}{x}\)
[∵ tan 60° = √3]
⇒ h – 7 = x√3
⇒ h = x√3 + 7
⇒ h = 7√3 +7 [from Eq. (i)]
⇒ h = 7(√3 + 1) m
Hence, the height of the cable tower is 7 (√3 + 1) m.
![]()
Section – E
Case study based questions are compulsory
Question 36.
Raghav and his family went on vacation to Rajasthan. There they had a stay in the tent for a night. Raghav found that the tent in which they stayed was in the form of a cone surmounted by a cylinder. The total height of the tent is 35 m. The diameter of the base is 56 m and the height of the cylinder is 14 m.

Based on the above information, answer the following questions:
(A) If each person need 176 m of floor, then how many persons can be accommodated in the tent? 1
(B) Find total surface area of cone. 1
(C) How much canvas is needed to make the tent?
OR
Find the volume of the tent. 2
Answer:
(A) Area of floor = πr2 = \(\frac{22}{7}\) × 28 × 28
= 2464 m2
Number of persons that can be accommodated in the tent = \(\frac{2464}{176}\) = 14
(B) Total surface area of a cone = curved surface area of a cone + area of circular base
= πrl + πr2 = πr(l + r)
[Since, slant height of cone,
l = \(\sqrt{r^2+h^2}=\sqrt{(28)^2+(21)^2}\)
= \(\sqrt{784+441}=\sqrt{1225}\) = 35 m
= \(\frac{22}{7}\) × 28 (35 + 28) = 5544 m2
(C) Required area of canvas = curved surface area of cone + curved surface area of cylinder

= πrl + 2πrh
= πr(l + 2 h)
= \(\frac{22}{7}\) × 28 (35 + 28)
= 5544 m2
OR
Volume of tent = Volume of cone + Volume of cylinder
= \(\frac{1}{3}\) × π × r2 × 21 + πr2 × 14
= πr2(7 + 14)
= \(\frac{22}{7}\) × 28 × 28 × 21
= 51744 m3
![]()
Question 37.
Ram asks the labour to dig a well up to a depth of 15 m. Labour charges ₹ 100 for first metre and increase ₹ 25 for each subsequent metres. As labour was uneducated, he claims ₹ 400 for the whole work.
Based on above information, answer the following questions.
(i) Find the AP sequence that is formed by the labour charge.
Answer:
For first metre. the charge is ₹ 100
i.e. first term, a = 100
As, there is increasing of ₹ 25 for each subsequent
metres, therefore common difference, d = 25
So, the AP thus formed is 100, 125, 150, ………………
(ii) What is the third term of the AP sequence thus formed.
Answer:
The third term of the AP sequence is 150
Or
Find the sum of AP sequence that is formed by the labour charge.
Answer:
We know that
Sn = \(\frac{n}{2}\) [2a + (n – 1) d]
Sum of 15 terms,
S15 = \(\frac{15}{2}\) [2 × 100 + 14 × 25]
= \(\frac{15}{2}\) [200 + 350]
= \(\frac{15}{2}\) × 550
= 4125
(iii) Find the labour charge to dig the well.
Answer:
Labour charge to dig the well is the 15th term of AP
We know, an = a + (n – 1) d
∴ a15 = 100 + (15 – 1) × 25
= 100 + 14 × 25 = 450
∴ Labour charge = ₹ 450
![]()
Question 38.
Shweta is a baker. She has chocolates and pancakes which together are 40 in number. If she has 50 more pancakes and 50 less pancakes, then number of pancakes would become 4 times the number of chocolates. Denote original number of chocolates and pancakes by x and y respectively.

Based on the above information, answer the following questions:
(A) Represent algebraically the above situations. 1
(B) Which type of solution, the given system of equations has?
OR
Find out the number of chocolates and pancakes that Shweta is having. 2
(C) If cost of 1 chocolates is ₹ 20 and cost of 1 pancake is ₹ 3, then find the total cost of the chocolate and pancake that
Shweta had originally.
Answer:
(A) Since, every student get one chocolate.
So, number of chocolates Rohit has = Number of students in the class = 54
Let, number of milk chocolates Rohit has = x
Probability of distributing milk chocolates = \(\frac{1}{3}\)
⇒ \(\frac{x}{54}=\frac{1}{3}\)
⇒ x = \(\frac{54}{3}\) = 18
(B) Let number of dark chocolates Rohit has = y
Probability of distributing dark chocolates = \(\frac{4}{9}\)
⇒ \(\frac{y}{54}=\frac{4}{9}\)
⇒ y = \(\frac{4 \times 54}{9}\) = 24
OR
Number of white chocolates Rohit has
= 54 – (18 + 24) = 12
∴ Required probability = \(\frac{12}{54}\) = \(\frac{2}{9}\)
(C) Total number of milk and white chocolates
= 18 + 12 = 30
∴ Required probability = \(\frac{30}{54}\) = \(\frac{5}{9}\)