Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 7 are designed as per the revised syllabus.
CBSE Sample Papers for Class 10 Maths Basic Set 12 with Solutions
Time : 3 hrs
Max. Marks : 80
General Instructions:
- This question paper has 5 Sections A, B, C, D and E.
- Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
- Section B has 5 Short Answer-I (SA-I) Type Questions carrying 2 marks each.
- Section C has 6 Short Answer-II (SA-II) Type Questions carrying 3 marks each.
- Section D has 4 Long Answer (LA) Type Questions carrying 5 marks each.
- Section E has 3 Case Based integrated units of assessment (4 marks each).
- All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
- Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
Section – A
Section A consists of 20 questions of 1 mark each
Question 1.
An acute angle θ, for which sin θ + cos θ takes the greatest value, is
(a) 30°
(b) 90°
(c) 60°
(d) 45°
Answer:
(d) 45°
For θ = 45°
sin 45° + cos 45° = \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}\)
= √2 = 1.414 [greatest value]
Question 2.
If 3 chairs and 1 table cost ₹ 1500 and 6 chairs and 1 table costs ₹ 2400, then the linear equations to represent this situation is
(a) x + 3y = 1500 and 6x – y = 2400
(b) 3x – y = 1500 and 6x – y = 2400
(c) 3x + y = 1500 and 6x + y = 2400
(d) x – y = 1500 and x + y = 2400
Answer:
(c) 3x + y = 1500 and 6x + y = 2400
We have, the cost of 1 chair = ₹ x
and the cost of 1 table = ₹ y
Then, according to the given situation
3x + y = 1500
and 6x + y = 2400
Question 3.
The rcth term of an AP 4, 1,- 2 , – 5, is
(a) 3w – 8
(b) 3n – 7
(c) 7 – 3n
(d) 8 – 3n
Answer:
(b) 3n – 7
Given, sequence is 4, 1, – 2, – 5, ……………
Here a = 4 and d = 1 – 4 = – 3
We know,
an = a + (n – 1) d
⇒ an = 4 + (n – 1) (- 3)
⇒ an = 4 + 3 – 3n = 7 – 3n.
![]()
Question 4.
One card is drawn at random from a well-shuffled deck of 52 cards. The probability of selecting a card is
(a) \(\frac{1}{2}\)
(b)1
(c) \(\frac{1}{52}\)
(d) 0
Answer:
(c) \(\frac{1}{52}\)
Total number of possible outcomes in a deck of cards = 52
Number of favourable outcomes of selecting a card = 1
∴ Required probability = \(\frac{1}{52}\)
Question 5.
If in two triangles ∠DEF and ∠PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
(a) \(\frac{E F}{P R}=\frac{D F}{P Q}\)
(b) \(\frac{D E}{P Q}=\frac{E F}{R P}\)
(c) \(\frac{D E}{Q R}=\frac{D F}{P Q}\)
(d) \(\frac{E F}{R P}=\frac{D E}{Q R}\)
Answer:
(b) \(\frac{D E}{P Q}=\frac{E F}{R P}\)
Given, ∠D = ∠Q
and ∠R = ∠E
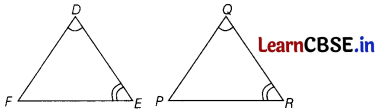
∴ ∆DEF ~ ∆QRP [by AA Rule]
∴ \(\frac{D F}{Q P}=\frac{E D}{R Q}=\frac{F E}{P R}\)
Hence, except option (b), all options are true.
Question 6.
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, the length of each tangent is equal to
(a) 3 cm
(b) 6 cm
(c) \(\frac{\sqrt{3}}{2}\) cm
(d) 3√3 cm
Answer:
(d) 3√3 cm
(d) In ∆POR and ∆OQR
OP = OQ [radius of circle]
∠OPR = ∠OQR [each 90°]
and PR = QR
[∵ pair of tangents drawn from a outside point to a circle are equal in length]
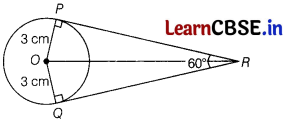
So, ∆POR and ∆QOR are congruent. [by SAS congruency]
Therefore, ∠QRO = \(\frac{60^{\circ}}{2}\) = 30°
In right angled ∆OPR,
tan 30° = \(\frac{O P}{P R}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{3}{P R}\)
⇒ RP = 3√3 cm = QR
![]()
Question 7.
The value of sin 60° cos 30° + cos 60° sin 30° is
(a) 1
(b) √3
(c) \(\frac{\sqrt{3}{2}\)
(d) \(\frac{1}}{2}\)
Answer:
(a) 1
sin 60° cos 30° + cos 60° sin 30° = \(\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}+\frac{1}{2} \times \frac{1}{2}\)
= \(\frac{3}{4}+\frac{1}{4}=\frac{4}{4}\) = 1
Question 8.
The system of equations 3x – 6y + 9 = 0 and – 12x + 24y + 36 = 0 has
(a) a unique solution
(b) exactly two solutions
(c) infinitely many solutions
(d) no solution
Answer:
(d) no solution
Here, \(\frac{a_1}{a_2}=\frac{3}{-12}=\frac{-1}{4}\),
\(\frac{b_1}{b_2}=\frac{-6}{24}=\frac{-1}{4}\)
and \(\frac{c_1}{c_2}=\frac{9}{36}=\frac{1}{4}\)
As \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Hence, the given system has no solution.
Question 9.
The equation 12x2 + 4kx + 3 = 0 has real and equal roots, if
(a) k = ± 2
(b) k = ± 9
(c) k = 4
(d) k = ± 3
Answer:
(d) k = ± 3
Here a = 12, b = 4k and c = 3
The given equation has real and equal roots.
∴ Discriminant, D = b2 – 4ac = 0
⇒ (4k)2 – 4 (12) (3) = 0
⇒ 16k2 – 144 = 0
⇒ k2 = 9
⇒ k = ± 3
![]()
Question 10.
If the distance between the points (4, p) and (1,0) is 5 units, then the value of p is
(a) ± \(\sqrt{20}\) units
(b) ± 4 units
(c) 0 unit
(d) ± 3 units
Answer:
(b) ± 4 units
Distance between (4, p) and (1, 0)
\(\sqrt{(4-1)^2+(p-0)^2}\) = 5 units
On squaring both sides, we get
(4 – 1)2 + p2 = 25
9 + p2 = 25
p2 = 25 – 9 = 16
p = ± 4
Question 11.
A sector is cut from a circle of diameter 21 cm, If the angle of the sector is 150°, then its area is
(a) 27.5 cm2
(b) 144 cm2
(c) 55 cm2
(d) 288 cm2
Answer:
(b) 144 cm2
Given, radius of the circle, r = \(\frac{21}{2}\) cm
and angle of sector, θ = 150°
∴ Area of the sector = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr²
= \(\frac{150^{\circ}}{360^{\circ}} \times \frac{22}{7} \times\left(\frac{21}{2}\right)^2\)
= \(\frac{5}{12} \times \frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\)
= 144.38
= 144 cm2
Question 12.
If (x – 3) is a factor of the polynomial 3x2 + 2x – k, then value of k is
(a) 31
(b) 32
(c) 33
(d) 30
Answer:
(c) 33
(C) Let p(x) = 3x2 + 2x – k
Since, (x – 3) is a factor of p(x).
∴ p(3) = 0
⇒ (3)2 + 2(3) – k = 0
⇒ 27 + 6 – k = 0
⇒ k = 33
![]()
Question 13.
If one of the zeroes of the quadratic polynomial x2 – 3x + k is 2, then the value of k is
(a) 10
(b) 2
(c) – 7
(d) – 2
Answer:
(b) 2
Let p(x) = x2 – 3x + k
2 is a zero of p(x).
∵ f(2) = 0
⇒ (2)2 – 3(2) + k = 0
⇒ 4 – 6 + k = 0
⇒ k = 2
Question 14.
If P(x, 6) is the mid-point of the line segment joining A (6, 5) and B (4, y), then the value of y is
(a) 6
(b) 5
(c) 7
(d) 8
Answer:
(c) 7
We have, P is the mid-point of A and B.
∴ \(\left(\frac{6+4}{2}, \frac{5+y}{2}\right)\) = (x, 6)
⇒ (5, \(\frac{5+y}{2}\)) = (x, 6)
⇒ x = 5 and \(\frac{5+y}{2}\) = 6
⇒ x = 5 and y = 7
Question 15.
If the volume of a cube is 1728 cm3, the length of its edge is equal to
(a) 7 cm
(b) 12 cm
(c) 18 cm
(d) 19 cm
Answer:
We know, volume of a cube with edge, a = a3
⇒ a3 =1728
⇒ a = \(\sqrt[3]{1728}\)
⇒ a = 12 cm
![]()
Question 16.
Two triangles are similar, if their corresponding angles are ……………… and their corresponding sides are in the same ……………
(a) equal, equal
(b) equal, ratio
(c) not equal, ratio
(d) None of these
Answer:
(b) equal, ratio
Two triangles are similar, if their corresponding angles are equal and their corresponding sides are in the same ratio.
Question 17.
If a, b, c are in AP, then \(\frac{a-b}{b-c}\) is equal to
(a) \(\frac{b}{a}\)
(b) 1
(c) \(\frac{a}{c}\)
(d) \(\frac{c}{a}\)
Answer:
(b) 1
Since, a, b, c are in AP
∴ b – a = c – b
⇒ \(\frac{b-a}{c-b}\) = 1
⇒ \(\frac{a-b}{b-c}\) = 1
Question 18.
Which of the following is not a quadratic equation?
(a) x2 + 5x – 3 = 0
(b) x2 + x3 + 7 = 0
(c) 3 + x + x2 = 0
(d) x2 – 36 = 0
Answer:
(b) x2 + x3 + 7 = 0
Since, equation x2 + x3 + 7 = 0 has degree 3, this is not a quadratic equation.
![]()
Directions : In the question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.
Question 19.
Assertion (A) : All equilateral triangle are similar.
Reason (R) : Two triangle are said to be similar, if their corresponding angles are equal and length of corresponding sides are proportional.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true but Reason (R) is false
(d) Assertion (A) is false but Reason (R) is true
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A)
Two equilateral triangle are similar, if their sides are proportional.
∵ In equilateral triangle, each angle are equal and sides are also equal
Therefore, all equilateral triangle are similar.
∴ Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Question 20.
Assertion (A) : Pair of linear equations : 3x + 4y + 6 = 0, 9x + 12y + 18 = 0 have infinitely many solutions.
Reason (R) : Pair of linear equations a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 have infinitely many solutions, if \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\).
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true but Reason (R) is false
(d) Assertion (A) is false but Reason (R) is true
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
From the given equations, we have
\(\frac{3}{9}=\frac{4}{12}=\frac{6}{18}\)
\(\frac{1}{3}=\frac{1}{3}=\frac{1}{3}\)
i.e., \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
![]()
Section – B
Section B consists of 5 questions of 2 marks each
Question 21.
Prove that \(\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}\) = tan θ
Answer:
LHS = \(\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}\)
= \(\frac{\sin \theta\left(1-2 \sin ^2 \theta\right)}{\cos \theta\left(2 \cos ^2 \theta-1\right)}\)
= tan θ . \(\frac{\left[1-2\left(1-\cos ^2 \theta\right)\right]}{\left(2 \cos ^2 \theta-1\right)}\)
[∵ sin2 A = 1 – cos2 A]
= tan θ . \(\frac{\left(2 \cos ^2 \theta-1\right)}{\left(2 \cos ^2 \theta-1\right)}\)
= tan θ
= RHS
Question 22.
Calculate the airthmetic mean for the following data.

Answer:
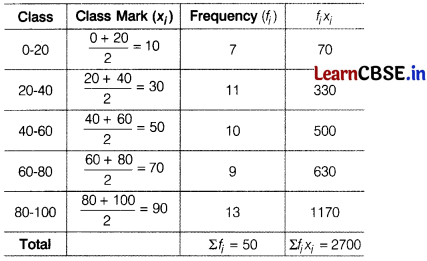
Here, Σfi = 50
and Σfixi =2700
∴ Mean \((\bar{x})=\frac{\Sigma f_i x_i}{\Sigma f_i}\)
= \(\frac{2700}{50}\) = 54
Or
Given below is a cumulative frequency distribution showing the marks secured by 50 students of a class.

Form the frequency distribution table for the above data.
Answer:
Here, we observe that, 17 students have scored marks below 20, it lies between class interval 0 – 20 and 22 students have scored marks below 40, so 22 – 17 = 5 students lies in the class interval 20 – 40, continuing in the same manner, we get the frequency distribution table for above data as follows
| Marks | Number of students |
| 0 – 20 | 17 |
| 20 – 40 | 22 – 17 = 5 |
| 40 – 60 | 29 – 22 = 7 |
| 60 – 80 | 37 – 29 = 8 |
| 80 – 100 | 50 – 37 = 13 |
Question 23.
Find the LCM and HCF of 28, 35 and 343 by applying the prime factorisation method.
Answer:
The prime factors of 28, 35 and 343 are
28 = 2 × 2 × 7 = 22 × 7
35 = 5 × 7
and 343 = 7 × 7 × 7 = 73
∴ HCF = (28, 35, 343) = 7
and LCM (28, 35, 343) = 22 × 5 × 73 = 6860
![]()
Question 24.
Which term of the AP 3, 15, 27, 39, ……….. will be 120 more than its 21st term?
Answer:
Here, a = 3 and d = 15 – 3 = 12
∴ 21st term is given by
T21 = a + (21 – 1) d
[∵ Tn = a + (n – 1)d]
= a + 20d
= 3 + 20 x 12 = 243
∴ Required term = 243 + 120 = 363
Let it be nth term.
Then, Tn = 363
⇒ a + (n – 1) d = 363
⇒ 3 + (n -1) × 12 = 363
⇒ 3 + 12n – 12 = 363
⇒ 12n – 9 = 363
⇒ 12n = 372
∴ n = 31
Hence, 31st term is the required term.
Question 25.
Without solving the following quadratic equation, find the value of m for which the given equation has real and equal roots.
x2 + (m – 1) x + 2 (m + 5) = 0
Answer:
Given, quadratc equation is x2 + (m – 1) x + 2 (m + 5) = 0
On comparing it with ax2 + bx + c = 0 we get
a = 1, b = m – 1 and c = 2 (m + 5)
Since, the given equation has real and equal roots.
So, the discriminant will be zero.
i.e. b2 – 4ac = 0
⇒ [(m – 1)2] – 4 × 1 × 2 (m + 5) = 0
⇒ m2 + 1 – 2m – 8 (m + 5) = 0
[(a – b)2 = a2 + b2 – 2ab]
⇒ m2 + 1 – 2m- 8m – 40 = 0
⇒ m2 – 10m – 39 = 0
⇒m2 – 13m + 3m – 39 = 0
[splitting the middle term]
⇒ m (m – 13) + 3 (m – 13) = 0
⇒ (m + 3) (m – 13) = 0
⇒ m + 3 = 0 or m – 13 = 0
∴ m = – 3 or m = 13
Hence the values of m are – 3 and 13.
Or
For what value(s) of ‘a’ quadratic equation 30ax2 – 6x + 1 = 0 has no real roots?
Answer:
Given, quadratic equation is 30ax2 – 6x + 1 = 0.
On comparing with Ax2 + Bx + C = 0, we get
A = 30a, B = – 6 and C = 1
The condition that given roots have no real value
i.e. B2 – 4AC < 0
⇒ (- 6)2 – 4x3Oaxl< 0
⇒ 36 – 120a < 0
⇒ 120a > 36
⇒ a > \(\frac{36}{120}\)
⇒ a > \(\frac{3}{10}\)
![]()
Section – C
Section C consists of 6 questions of 3 marks each
Question 26.
Three different coins are tossed together. Find the probability of getting
(i) exactly two heads
Answer:
Total outcomes, {HHH, HHT HTH, THH, TTH, THT HTT TTT}
∴ Total number of outcomes = 8
The outcomes favourable to event are {HHT HTH, THH}
∴ P(exactly two heads) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}\)
= \(\frac{3}{8}\)
(ii) atleast two heads
Answer:
The outcomes favourable to event are {HHH, HHT, HTH, THH}
∴P(at least two heads) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}\)
= \(\frac{4}{8}=\frac{1}{2}\)
(iii) atleast two tails
Answer:
The outcomes favourable to event are {TTH, THT, HTT, TTT}
∴ P(atleast two tails) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}\)
= \(\frac{4}{8}=\frac{1}{2}\)
Question 27.
Find the zeroes of the quadratic polynomial x2 – 4x – 5 and verify the relationship between the zeroes and its coefficients.
Answer:
Let f(x) = x2 – 4x – 5
= x2 – 5x + x – 5
= x (x – 5) + 1(x – 5)
= (x + 1) (x – 5)
For zeroes of f(x),
f(x) = 0
⇒ (x + 1) (x – 5) = 0
⇒ x + 1 = 0 and x – 5 = 0
⇒ x = – 1 and x = 5
So, the zeroes of f(x) are – 1, 5
Now, sum of zeroes = – 1 + 5 = 4
= \(\frac{-(-4)}{1}\)
= \(-\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\)
and product of zeroes = (- 1) (5) = \(\frac{(-5)}{1}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
Hence, the relationship between the zeroes and coefficients is verified.
Question 28.
In the figure, quadrilateral ABCD is circumscribing a circle with centre O and AD ⊥ AB. If radius of incircle is 10 cm, then find the value of x.
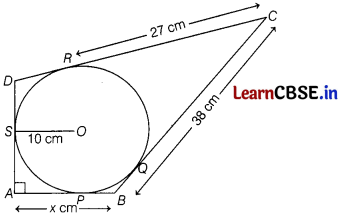
Answer:
Given, inradius of circle, r = 10 cm.
Draw a line perpendicular from centre to the tangent line AB.
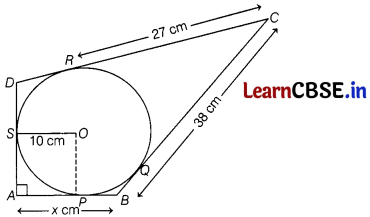
∠A = ∠OPA = ∠OSA = 90°
[∵ all lines in quadriateral ∆POS are perpendicular]
Hence, ∠SOP = 90°
Also, AP = AS
[∵ pair of tangents drawn from an outside point to a circle are equal in length]
Hence, OSAP is a square.
AP = OS = 10 cm
CR = CQ = 27 cm
Now, BQ = BC – CQ
= 38 – 27 = 11
Here, BP = BQ = 11 cm
∴ x = AB = AP + BP
= 10 + 11 = 21 cm
Or
If PQ = 28 cm, then find the perimeter of ∆PLM.
Answer:
We have, PQ = 28 cm
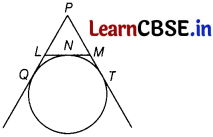
By using the theorem, that the pair of tangents drawn from an external point to a circle are equal in lengths.
∴ PQ = PT, LQ = LN
and NM = MT
Consider, PQ = PT
⇒ PL + LQ = PM + MT
⇒ PL + LN= PM + NM [usingEq.(i)] …………(ii)
Now, perimeter of ∆PLM = PL + LM + PM
= PL + LN + NM + PM
= PL + LN + PL + LN [using Eq.(ii)]
= 2 (PL + LN)
= 2 × (PQ)
[∵ PL + LN = PL + LQ = PQ]
= 2 × 28 = 56 cm
![]()
Question 29.
Find the area of the sector of a circle with radius 7 cm and of angle 90°. Also, find the area of the corresponding major sector. [take π = 3.14]
Answer:
Area of the sector = \(\frac{\theta}{360^{\circ}}\) × πr²
= \(=\frac{90^{\circ}}{360^{\circ}}\) × 3.14 × 7 × 7
= 38.47 cm2
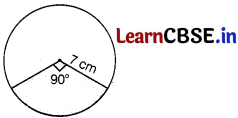
∴ Area of the corresponding major sector = πr² – area of sector
= 3.14 × 7 × 7 – 387
= 153.86 – 38.47
= 115.39 cm2
Question 30.
At the foot of a mountain the elevation of its summit is 45°. After ascending 1000 m towards the mountain up a slope of 30° inclination, the elevation is found to be 60°. Find the height of the mountain.
Answer:
Let AD be the height of the mountain and B be the point on the foot of mountain.
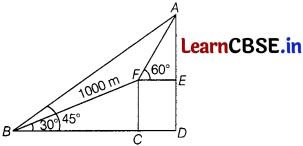
Or
Also, given BF = 1000 m,
∠CBF = 30° and ∠ABO = 45°
∴ ∠ABF=45° – 30° = 15°
In ∆AFE,
∠FAE = 180° – (90° + 60°) = 30°
In ∆ABD,
∠BAD = 180°- (90° + 45°)
⇒ ∠BAF + ∠FAE = 180° – 135° = 45°
⇒ ∠BAF = 45° – 30° = 150 [∵ ∠FAE = 30°]
∴ AF = FB = 1000 m
[since. FAB is an isosceles triangle]
Now, in ∆CBF,
sin 30° = \(\frac{C F}{F B}\)
⇒ \(\frac{1}{2}=\frac{C F}{1000}\)
⇒ CF = \(\frac{1000}{2}\) = 50 cm
Again, in ∆EAF,
sin 60°= \(\frac{A E}{F A}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{A E}{1000}\)
⇒ AE = \(\frac{1000 \sqrt{3}}{2}\) = 5oo√3 m
For height of mountain,
AD = AE + DE
= 500√3 + 500 [∵ DE = FC]
= 500 (√3 + 1)
= 500 × 2.73
= 1365 [√3 = 1.73]
Hence, the height of mountain is 1365 m.
The two palm trees are of equal heights and are standing opposite each other on either side of the river, which is 80 m wide. From a point 0 between them on the river the angles of elevation of the top of the trees are 60° and 30°, respectively. Find the height of the trees and the distances of the point 0 from the trees.
Answer:
Let AB and CD be the positions of palm trees having equal height
i.e. AB = CD = h
Let the width of the river be BD = 80 m. (given)
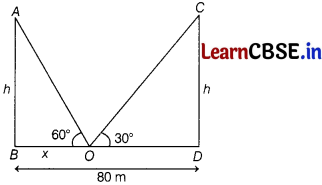
Let BO = x
Then, BD – OD = x
⇒ OD = 80 – x
In ∆ABO,
tan 60° =h/x
√3 = h/x
h = √3x
and in ∆CDO,
tan 30° = h / (80 – x)
⇒ 1/√3 = h / (80 – x)
⇒ h = \(\frac{80-x}{\sqrt{3}}\)
From Eqs. (i) and (ii), we get
√3x = \(\frac{80-x}{\sqrt{3}}\)
⇒ 3x + x = 80
⇒ x = 20
On putting x = 20 in Eq. (i), we get
h = √3 × 20
= 1.73 × 20 = 346 m
∴ The height of the trees, h = 346 m
Also, BO = x = 20 m
Now, DO = 80 – x = 80 – 20 = 60 m
Hence height of the tree is 34.6 and distance of the point O from the trees are 20 m and 60 m.
Question 31.
Sides AB and BC and median AD of ∆ABC are respectively proportional to sides PQ and QR and median PM of APQR. Show that ∆ABC ~ ∆PQR.
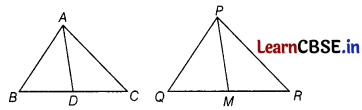
Answer:
Given : ∆ABC and ∆PQR in which AD and PM are their medians respectively and \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A D}{P M}\)
To prove : ∆ABC ~ ∆PQR
Proof : We have, \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A D}{P M}\) [given]
⇒ \(\frac{A B}{P Q}=\frac{\frac{1}{2} B C}{\frac{1}{2} Q R}=\frac{A D}{P M}\)
[multpying numerator and denominator of middle term by \(\frac{1}{2}\)]
⇒ \(\frac{A B}{P Q}=\frac{B D}{Q M}=\frac{A D}{P M}\)
[∵medians AD and PM bisect the lines BC and OR, respectively, i.e. BD = \(\frac{1}{2}\) BC and QM = \(\frac{1}{2}\) QR]
⇒ ∆ADB ~ ∆PMQ [by SSS similarity criterion]
∴ ∠B = ∠Q ………….(i)
In ∠ABC and ∆PQR.
\(\frac{A B}{P Q}=\frac{B C}{Q R}\) [given]
and ∠B = ∠Q [from Eq. (i)]
∴ ∆ABC ~ ∆PQR
[by SAS similarity criterion]
Hence proved.
![]()
Section – D
Section D consists of 4 questions of 5 marks each
Question 32.
If 3 cot A = 4, check whether \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos2 A – sin2 A or not.
Answer:
Given, 3 cot A = 4
⇒ cot A = \(\frac{4}{3}\)
Let AB = 4k, BC = 3k
In right angled ∆ABC,
AC2 = AB2 + BC2 [by Pythagoras theorem]
= (3k)2 + (4k)2
= 9k2 + 16k2
= 25k2
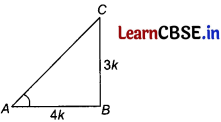
∴ AC = 5k
[∵ side cannot be -ve]
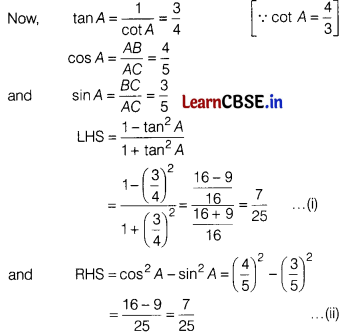
From Eqs. (i) and (ii), we get
LHS = RHS
Or
Prove that (tan2 A – tan2 B) = \(\frac{\left(\sin ^2 A-\sin ^2 B\right)}{\cos ^2 A \cos ^2 B}\) = \(\frac{\cos ^2 B-\cos ^2 A}{\cos ^2 B \cos ^2 A}\)
Answer:
LHS = tan2 A – tan2 B
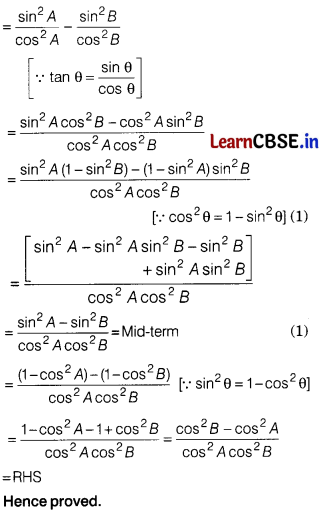
Question 33.
In the given figure, ∠AEF = ∠AFE and E is the mid-point of CA. Prove that \(\frac{B D}{C D}=\frac{B F}{C E}\).
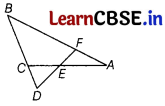
Answer:
Given ∠AEF = ∠AFE and E is the mid-point of CA
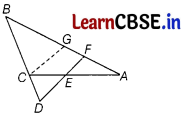
To prove : \(\frac{B D}{C D}=\frac{B F}{C E}\)
Construction : Draw a line CG parallel to DF.
Proof : Given, ∠AEF = ∠AFE and E is mid-point of CA
∴ CE = AE = \(\frac{A C}{2}\)
In ∆BDF, CG || DF
By basic propoilionality theorem,
\(\frac{B D}{C D}=\frac{B F}{G F}\) …………….(ii)
In ∆AFE, ∠AEF = ∠AFE [given]
⇒ AF = AE
[since, sides opposite to equal angles are equal]
⇒ AF = AE = CE [from Eq. (i)] …………(iii)
In ∆ACG, E s the mid-point of AC and EF || CG.
⇒ FG = AF [∵ AE = CE] ……….. (iv)
From Eqs. (ii), (iii) and (iv),
\(\frac{B D}{C D}=\frac{B F}{C E}\)
[∵ GF = AF = CE]
Hence proved.
![]()
Question 34.
Rachel, an engineering student was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, then find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Answer:
Given, model is a combination of a cylinder and two cones.
Clearly, volume of the air will be equal to the sum of the volumes of two cones and one cylinder.
We have, diameter of the model, BC = ED = 3cm
∴ Radius of cone = Radius of cylinder,
r = \(\frac{3}{2}\) = 1.5 cm
Length of cone, h1 = 2 cm
Total length of the mode’, AF = 12 cm
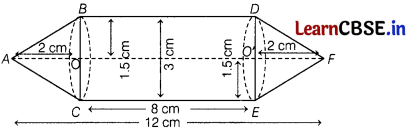
∴ Length of the cylinder, OO’ = AF – (AO + O’F)
= 12 – (2 + 2)
= 8
= h2
Now, volume of the air inside the model = Volume of air inside (cone + cylinder + cone)
= \(\left(\frac{1}{3} \pi r^2 h_1+\pi r^2 h_2+\frac{1}{3} \pi r^2 h_1\right)\)
= \(\frac{1}{3}\) (h1 + 3h2 + h1)
= \(\frac{1}{3} \times \frac{22}{7}\) × 1.5 × 1.5 (2 + 3 × 8 + 2)
= \(\frac{22}{7} \times \frac{2.25}{3}\) × (2 + 24 + 2)
= \(\frac{22}{7}\) × 0.75 × 28
= 22 × 3
= 66 cm3
Or
Two same conical hole have been made on both ends of a solid right circular cylinder. The height of the cylinder is 10 cm and the diameter of its base is 8 cm. If the diameter and depth of the hole are 6 cm and 4 cm respectively, then find the total surface area of remaining solid.
Answer:
For cylinder, diameter of base = 8 cm
∴ Radius of base (R) = \(\frac{\text { Diameter }}{2}=\frac{8}{2}\) = 4 cm
and height (H) = 10 cm
∴ Curved surface area of cylinder = 2πRH
= 2π × 4 × 10
= 80π cm2
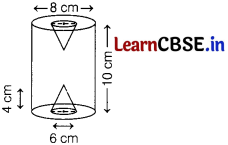
For cone, diameter of base = 6 cm
∴ Radius of base (r) = \(\frac{\text { Diameter }}{2}=\frac{6}{2}\) = 3 cm
Depth of conical hole, h = 4 cm
∴ Slant height, l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{3^2+4^2\)
= \(\sqrt{9+16}\)
= \(\sqrt{25}\)
= 5 cm
CSA of cone = πrl
= π × 3 × 5 = 15π cm2
Area of remaining ends of cylinder = 2 (Area of base of cylinder – Area of base of cone)
= 2(πR2 – πr2)
= 2π [R2 – r2]
= 2π (42 – 32)
= 14π cm2
Total surface area of remaining solid shape = CSA of cylinder + CSA of both cones + Area of remaining ends of cylinder
= 80π + 2 × 15π +2 × 7π
= 80π + 30π + 14π
= 1247π cm2
Question 35.
Find the mode of the following distribution.

Answer:
Given distribution table is
| Marks | Number of Students |
| 0 – 10 | 4 |
| 10 – 20 | 6 |
| 20 – 30 | 7(f0) |
| 30 – 40 | 12(f1) |
| 40 – 50 | 5(f2) |
| 50 – 60 | 6 |
The highest frequency n the given distribution is 12,
whose corresponding class is 30 – 40
Thus, 30 – 40 is the required modal class.
Here, l = 30, f1 = 12, f0 = 7, f2 = 5 and h = 10
∴ Mode = l + \(\frac{f_1-f_0}{2 f_1-f_0-f_2}\) × h
= 30 + \(\frac{12-7}{2 \times 12-7-5}\) × 10
= 30 + \(\frac{50}{24-12}\)
= 30 + \(\frac{50}{12}\)
= 30 + 4.17 = 34.17
Hence, the mode of the given distribution is 34.17.
![]()
Section – E
Case study based questions are compulsory
Question 36.
Raman and Vishnu are friends living on the same street in Laxmi Nagar. Vishnu’s house is at the intersection of one street with another street on which there is a cafe. They both work in the same office and that is not far from Vishnu’s house. Suppose the office is situated at the point 0, i.e. the origin. Raman’s house is at point A. Vishnu’s house is at point B and cafe is at point C.
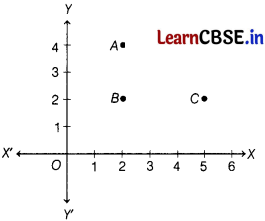
Based on the above information, answer the following questions:
(i) How far is Raman’s house from Vishnu’s house?
Answer:
Coordinates of A (2, 4)
Coordinates of B = (2, 2)
Coordinates of C = (5, 2)
∴ AB = 4 – 2 = 2 units
(ii) How far is the office from cafe?
Answer:
OC = \(\sqrt{(5-0)^2+(2-0)^2}\)
= \(\sqrt{25+4}\)
= [/latex]\sqrt{29}[/latex] units
(iii) Find the perimeter of the triangle formed by Raman’s, Vishnu’s house and the cafe.
Answer:
AB = 2 units
BC = 5 – 2 = 3 units
and AC = \(\sqrt{(5-2)^2+(2-4)^2}\)
= \(\sqrt{(3)^2+(-2)^2}\)
= \(\sqrt{9+4}=\sqrt{13}\) units
Perimeter of ABC = AB + BC + CA
= 2 + 3 + \(\sqrt{13}\)
= 5 + \(\sqrt{13}\) units
Or
There is a tower between the line joining A and C which divides AC in the ratio 2 : 3. Find the coordinates of the tower.
Answer:
Using section formula, coordinates of tower are \(\left(\frac{2 \times 5+3 \times 2}{2+3}, \frac{2 \times 2+3 \times 4}{2+3}\right)\)
= \(\left(\frac{10+6}{5}, \frac{4+12}{5}\right)\)
= \(\left(\frac{16}{5}, \frac{16}{5}\right)\)
![]()
Question 37.
A seminar is being conducted by an Educational Organisation, where the participants will be educators of different subjects. The number of participants in Hindi, English and Mathematics are 60, 84 and 108 respectively.

Based on the above information answer the following questions
(i) In each room the same number of participants are to be seated and all of them being in the same subject, hence find maximum number participants that can accommodated in each room.
Answer:
Given, number of students in each subject are
Hindi = 60,
English = 84
and Mathematics = 108
The prime factors of number of students in each subject are
60 = 2 × 2 × 3 × 5 = 22 × 3 × 5
84 = 2 × 2 × 3 × 7 = 22 × 3 × 7
108 = 2 × 2 × 3 × 3 × 3 = 22× 33
The maximum number of participants that can accommodated in each room = HCF (60, 84, 108)
= Product of the smallest power of each common pnme factor involved in the numbers
= 22 × 3 = 12
(ii) What is the minimum number of rooms required during the event?
Answer:
The minimum number of rooms required during the event is
\(\frac{\text { Total number of participants }}{12}=\frac{252}{12}\) = 21
(iii) Find the product of HCF and LCM of 60, 84 and 108.
Answer:
LCM of (60, 84, 108) = Product of the greatest power of each prime factor involved in the numbers with highest power
= 22 × 33 × 5 × 7
= 4 × 27 × 35 = 3780
Now, HCF (60, 84, 108) × LCM (60, 84, 108)
= 12 × 3780
= 45360
Or
What is the largest number that divides 70 and 125, having remainder 5 and 8 respectively?
Answer:
Let the largest number be x.
Then, the number Will completely divide (70 – 5) and (125 – 8) i.e. 65 and 117.
65 = 13 × 5
⇒ 117 = 13 × 3 × 3
∴ x = HCF (65 and 117) = 13.
![]()
Question 38.
Amit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is 95 sq m.
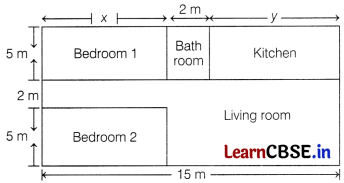
Based on the above information, answer the following questions:
(i) Form the pair of linear equations in two variables from this situation.
Answer:
From the given figure we see that area of two bedrooms = 2(5x) = 10x m2
Area of kitchen 5 × y = 5y m2
According to the question,
Area of the two bedrooms and area of kitchen = 95 m2
∴ 10x + 5y = 95
⇒ 2x + y = 19 [divide both sides by 5] ………….. (i)
Also, length of the home = 15 m
∴ x + 2 + y = 15
⇒ x + y = 13 …………..(ii)
Hence, the pair of linear equations is 2x + y = 19 and x + y = 13.
(ii) Find the length of the outer boundary of the layout.
Answer:
The length of the outer boundary of the layout = 2 (l + b)
= 2 (15 + 12) [∵ b = 5 + 2 + 5 = 12 m]
= 2 (27) = 54 m
(iii) Find the area of living room in the layout.
Answer:
On solving Eqs. (i) and (ii), we get x = 6 and y = 7
∴ Area of each bed room = 5 × x
= 5 × 6 = 30 m2
Area of living room = 15 × (5 + 2) – Area of Bedroom
= 15 × 7 – 5 × 6
= 105 – 30
= 75 m2
Or
Find the cost of laying tiles in kitchen at the rate of ₹ 50 per sq m.
Answer:
Since, area of kitchen = 5 × y = 5 × 7 = 35 m2
But, it is also given, the cost of laying tiles in kitchen at the rate of ₹ 50 per m2
∴ Total cost of laying tiles in the kitchen = 35 × 50 = ₹ 1750