CBSE Sample Papers for Class 10 Maths Basic Set 11 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 11 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Basic Set 11 with Solutions

Time : 3 hrs
Max. Marks : 80

General Instructions:

1. This question paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) Type Questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) Type Questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) Type Questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section – A
Section A consists of 20 questions of 1 mark each

Question 1.
A tangent intersects the circle at
(a) one point
(b) two distinct points
(c) at the circle
(d) does not intersect
Answer:
(a) one point

A tangent touches the circle on its boundary at only one point.

Question 2.
In the given figure, the value of BP is

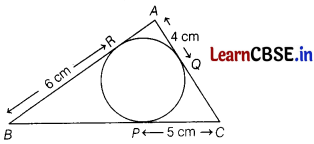
(a) 9 cm
(b) 8 cm
(c) 6 cm
(d) 11 cm
Answer:
(c) 6 cm

Since, tangents drawn from an external point to a circle are equal in length.
∴ BP = BR
⇒ BP = 6 cm

Question 3.
A coin is tossed once. What is the probability of getting a head?
(a) \(\frac{3}{4}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{4}\)
Answer:
(b) \(\frac{1}{2}\)

When a coin is tossed once, possible outcomes are H and T.
Total number of possible outcomes = 2
The favourable outcomes = 1
P(H) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{1}{2}\)

Question 4.
If in a lottery, there are 5 prizes and 20 blanks, then the probability of getting a prize is
(a) \(\frac{2}{5}\)
(b) \(\frac{4}{5}\)
(c) \(\frac{1}{5}\)
(d) 1
Answer:
(c) \(\frac{1}{5}\)

Total number of outcomes = 5 + 20 = 25
Number of favourable outcomes = 5
∴ Required probability = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{5}{25}=\frac{1}{5}\)

Question 5.
Find the coordinates of the point which divides the line segment joining the points (8, – 3) and (4, 5) in the ratio 4 : 2 internally
(a) \(\left(\frac{3}{16}, \frac{3}{7}\right)\)
(b) \(\left(\frac{10}{3}, \frac{4}{3}\right)\)
(c) \(\left(\frac{8}{3}, \frac{13}{7}\right)\)
(d) \(\left(\frac{16}{3}, \frac{7}{3}\right)\)
Answer:
(d) \(\left(\frac{16}{3}, \frac{7}{3}\right)\)

Let P (x, y) be the required point using the section formula, we get
x = \(\frac{4 \times 4+2 \times 8}{4+2}\)
= \(\frac{32}{6}=\frac{16}{3}\)

and y = \(\frac{4 \times 5+2 \times(-3)}{4+2}\)
= \(\frac{20-6}{6}\)
= \(\frac{14}{6}=\frac{7}{3}\)
Therefore, \(\left(\frac{16}{3}, \frac{7}{3}\right)\) is the required point.

Question 6.
The sum and the product of the zeroes of polynomial 6x² – 5, respectively are
(a) 0 and \(\frac{-6}{5}\)
(b) 0 and \(\frac{6}{5}\)
(c) 0 and \(\frac{5}{6}\)
(d) 0 and \(\frac{-5}{6}\)
Answer:
(d) 0 and \(\frac{-5}{6}\)

Given, polynomial is 6x² – 5
∴ Sum of zeroes = – \(\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\)
= – \(\frac{0}{6}\) = 0
Product of zeroes = \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
= \(\frac{-5}{6}\)

Question 7.
If ∆ABC ~ ∆DEF, such that DE = 3 AB and BC = 6 cm, then the length of EF is
(a) 8 cm
(b) 16 cm
(c) 18 cm
(d) 26 cm
Answer:
(c) 18 cm

Since, ∆ABC ~ ∆DEF
∴ \(\frac{A B}{D E}=\frac{B C}{E F}\) [by BPT]
⇒ \(\frac{A B}{3 A B}=\frac{6}{E F}\)
⇒ EF = 3 × 6 = 18 cm

Question 8.
If the distance between the points (4, p) and (1, 0) is 5 units, then the value of p is
(a) 3
(b) 4
(c) 5
(d) 6
Answer:
(b) 4

Let the given coordinates be A (4, p) and B (1. 0)
∴ AB = 5
⇒ \(\sqrt{(4-1)^2+(p-0)^2}\) = 5
⇒ 9 + p² = 25
⇒ p² = 16
⇒ p = \(\sqrt{16}\) = 4

Question 9.
If arithmetic mean of a, a + 2, a + 4, a + 6 and a + 8 is 12, then a is equal to
(a) 10
(b) 8
(c) 5.6
(d) 10.4
Answer:
(b) 8

We know that, AM = \(\frac{\text { Sum of terms }}{\text { Number of terms }}\)
⇒ \(\frac{a+a+2+a+4+a+6+a+8}{5}\) = 12
⇒ 5a + 20 = 60
⇒ 5a = 40
⇒ a = 8

Question 10.
The value of sin⁴ θ – cos⁴ θ is
(a) 1 – 2 cos² θ
(b) 1 – sin² θ
(c) 2 cos² θ – 1
(d) 2 cos² θ
Answer:
(a) 1 – 2 cos² θ

Given, sin⁴ θ – cos⁴ θ
= (sin² θ + cos² θ) (sin² θ – cos² θ)
= 1 (1 – cos² θ – cos² θ) [∵ sin² A = 1 – cos² A]
= 1 – 2 cos² θ

Question 11.
For any two similar triangles, which of the following statements are valid?
(a) Their sides are proportional
(b) Their sides are equal
(c) Their sides are parallel
(d) None of the above
Answer:
(a) Their sides are proportional

Two triangles are said to be similar, it
(I) their corresponding angles are equal.
(ii) their corresponding sides are proportional.

Question 12.
A card is drawn from a deck of 52 cards. The event E is that card which is not an ace of heart. The number of outcomes favourable to E is
(a) 4
(b) 13
(c) 48
(d) 51
Answer:
(d) 51

In a deck of 52 cards, there are 13 cards of heart and 1 of them is ace of heart.
So, number of favourable outcomes to E = 52 – 1 = 51

Question 13.
For what values of k, the pair of linear ‘ equations x + 2 y – 3 and 5x + ky + 7 = 0 represents intersecting lines?
(a) R
(b) R – {10}
(c) 10
(d) None of these
Answer:
(b) R – {10}

Given, pair of linear equations is
x + 2y = 3 and 5x + ky + 7 = 0
On comparing with standard equations, we get
a1 = 1, b1 = 2, c1 = – 3
and a2 = 5, b2 = k, c2 = 7
The condition for intersecting lines is
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
∴ \(\frac{1}{5} \neq \frac{2}{k}\)
⇒ k ≠ 10
Hence, the value of k is R – {10}.

Question 14.
The values of x and y in the given figure are

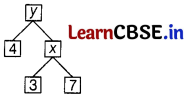
(a) 10 and 14
(b) 21 and 84
(c) 21 and 25
(d) 10 and 40
Answer:
(b) 21 and 84

Given,

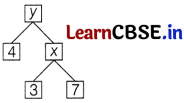
Here,
x = 3 × 7 = 21
and y = 4 × x = 4 × 21 = 84

Question 15.
The sum of the exponents of the prime factors in the prime factorisation of 196, is
(a) 3
(b) 4
(c) 2
(d) 5
Answer:
(b) 4

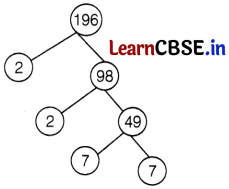
∴ 196 = 2² × 7²
∴ Required sum = 2 + 2 = 4

Question 16.
1 + cot² θ is equal to
(a) sin² θ
(b) tan² θ
(c) cosec² θ
(d) sec² θ
Answer:
(c) cosec² θ

We know, by trigonometric identities,
1 + cot² θ = cosec² θ

Question 17.
If we cut a cone in two parts by a plane parallel to the base, then the bottom part left over is the
(a) cone
(b) frustum of cone
(c) cylinder
(d) sphere
Answer:
(b) frustum of cone

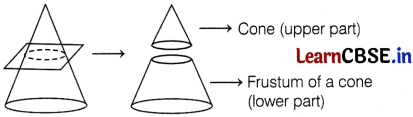
Question 18.
The HCF of 3 × 5³ and 3² × 5² is
(a) 3² × 5²
(b) 3 × 5
(c) 3² × 5³
(d) 3 × 5²
Answer:
(d) 3 × 5²

HCF of 3 × 5³ and 3² × 5²
= Product of each common prime factor which contain smallest power in the numbers
= 3 × 5²

Directions : In the question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) : Class width = Upper class limit – Lower class limit
Reason (R) : Class mark = (Upper class limit + Lower class limit)/2
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Question 20.
Assertion (A) : Angles in the same segment of a circle are equal.
Reason (R) : In cyclic quadrilateral, opposite angles are complementary.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(c) Assertion (A) is true but Reason (R) is false.

Reason (R) is not true, as in cyclic quadrilateral, opposite angles are supplementary i.e. sum of opposite angles is equal to 180° .

Section – B
Section B consists of 5 questions of 2 marks each

Question 21.
Find the solution of the equation
\(\frac{16}{x}\) – 1 = \(\frac{15}{x+1}\), x ≠ 0, – 1
Answer:
Given, equation is \(\frac{16}{x}\) – 1 = \(\frac{15}{x+1}\), x ≠ 0, – 1
⇒ \(\frac{16-x}{x}=\frac{15}{x+1}\)
⇒ (16 – x) (x + 1) = 15x
⇒ 16x + 16 – x² – x = 15x
⇒ x² = 16
⇒ x = ± 4

Question 22.
Prove that \(\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}\) = tan θ
Answer:
We have,
LHS = \(\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}\)
= \(\frac{\sin \theta\left(1-2 \sin ^2 \theta\right)}{\cos \theta\left(2 \cos ^2 \theta-1\right)}\)
= \(\frac{\tan \theta\left[1-2\left(1-\cos ^2 \theta\right)\right]}{\left(2 \cos ^2 \theta-1\right)}\)
[∵ sin² θ + cos² θ = 1]
= tan θ . \(\frac{\left(2 \cos ^2 \theta-1\right)}{\left(2 \cos ^2 \theta-1\right)}\)
= tan θ
= RHS

Or

Prove that \(\frac{1}{1+\sin \theta}+\frac{1}{1-\sin \theta}\) = 2 sec² θ
Answer:
We have,
LHS = \(\frac{1}{1+\sin \theta}+\frac{1}{1-\sin \theta}\)
= \(\frac{(1-\sin \theta)+(1+\sin \theta)}{(1+\sin \theta)(1-\sin \theta)}\)
= \(\frac{2}{1-\sin ^2 \theta}\)
= \(\frac{2}{\cos ^2 \theta}\)
= 2 sec² θ
= RHS
Hence proved.

Question 23.
In two concentric circles, prove that a chord of larger circle which is tangent to smaller circle is bisected at the point of contact.
Answer:
Let O be the common centre of two concentric circles,
and let AB be a chord of the larger circle touching the smaller circle at P.
Join OP.

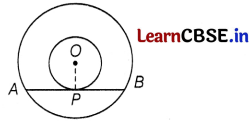
Since, OP is the radius of the smaller circle and AB is a tangent to this circle at a point P.
∴ OP ⊥ AB
We know that, the perpendicular drawn from the centre of a circle to any chord of the circle, bisects the chord.
So, AP ⊥ BP
Hence, AB is bisected at P.
Hence proved.

Question 24.
If the perimeter of a semi-circular protractor is 108 cm, find the diameter of the protractor.
Answer:
Let the radius of the semi-circular protractor ber cm.
Then, its perimeter = 2πr + 2r
∴ πr + 2r = 108 [given]
⇒ \(\frac{22}{7}\) r + 2r = 108
⇒ 36r = 108 × 7
r = 21
∴ Diameter of the serrv-circular protractor = 2r
= (2 × 21) = 42 cm

Question 25.
17 cards numbered 1,2, 3, …………… , 17 are put in a box and mixed thoroughly. One person drawns a card from the box. Find the probability that the number on card is divisible by 3 and 2 both.
Answer:
Out of 17 cards, in the box, one card can be drawn in 17 ways.
∴ Total number of possible outcomes = 17
If a number is divisible by both 3 and 2, then it is a multiple of 6. In cards bearing number 1, 2, 3, ……………, 17, there are only 2 cards which bear a number multiple of 6, i.e. 6 and 12.
Number of favourable outcomes = 2
∴ Hence, required probability = \(\frac{2}{17}\)

Or

Two unbiased coins are tossed simultaneously. Find the probability of getting atleast one head.
Answer:
If two unbiased coins are tossed simultaneously we obtain any one of the following as an outcome.
HH, HT, TH, TT
∴ Total number of elementary events = 4
Atleast one head is obtained, if any one of the following elementary events happens:
HH, HT, TH
∴ Favourable number of elementary events = 3
Hence, required probability = \(\frac{3}{4}\)

Section – C
Section C consists of 6 questions of 3 marks each

Question 26.
On diwali, Pawan purchases a decorative block as shown in figure is made of two solids; a cube and a hemisphere. The base .of the block is the H 5 cm H
cube with edge of 5 cm and the hemisphere attached on the top has a diameter of 4.2 cm. If the block is to be painted, then find the total area to be painted by him. [take, π = 22/7]

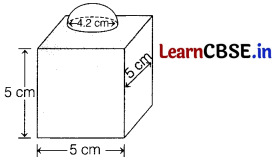
Answer:
Given, edge of cube = 5 cm
and diameter of hemisphere = 4.2 cm
Clearly, total surface area of the cube = 6 (Edge)²
= 6 × 5 × 5
= 150 cm²
Now, area to be painted on the cube = Total surface area of cube – Base area of hemisphere
= 150 – πr²
= 150 – \(\frac{22}{7} \times \frac{4.2}{2} \times \frac{4.2}{2}\)
= 150 – 13.86
= 136.14 cm²
Area to be painted on the hemisphece = Curved surface area of hemisphere
= 2πr²
= 2 × \(\frac{22}{7} \times \frac{4.2}{2} \times \frac{4.2}{2}\)
= 27.72 cm²
Total area to be painted = Area to be painted on the cube + Area to be painted on the hemisphere
= 136.14 + 27.72
163.86 cm²

Question 27.
In a two-digit number, the ten’s digit is three times the unit’s digit. When the number is decreased by 54, the digits are reversed. Find the number.
Answer:
Let the digit in unit’s place be x and the digit in ten’s place be y.
Then, number = 10y + x
According to thegiven condition,
y = 3x …………….(i)
Number obtained by reversing the digits = 10x + y
It the number is decreased by 54, the digits are reversed,
⇒ 10y + x – 54 = 10x + y
⇒ 9x – 9y = – 54
⇒ x – y = – 6 [dividing both sides by 9]
On putting y = 3x from Eq. (i) in Eq. (ii), we get
x – 3x = – 6
⇒ x = 3
On putting x = 3 in Eq. (i), we get
y = 9
Hence, number = 10y + x
= 10 × 9 + 3 = 93

Question 28.
In ∆ABC, points P and Q are on CA and CB respectively, such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
Answer:
Given, CQ = 25 cm,
CB = 30 cm,
CP = 10 cm
and CA = 16 cm

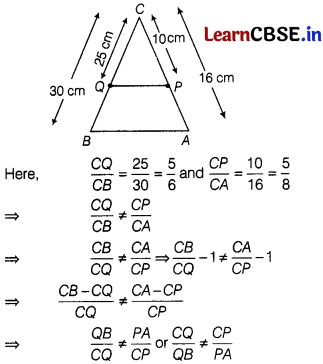
Hence, by converse of basic proportionality theoem,
PQ is not parallel to AB.

Or

In the given figure of ∆ABC, DE || AC. If DC || AP, where point P lies on BC produced, then prove that \(\frac{B E}{E C}=\frac{B C}{C P}\).

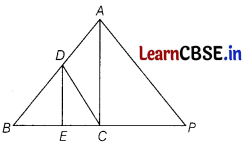
Answer:
Given, in ∆ABC, DE || AC [given]
So, \(\frac{B E}{E C}=\frac{B D}{D A}\) ………..(i)
[by basic proportionality theorem]
Also, in ∆ABP, DC || AP [given]
So, \(\frac{B C}{C P}=\frac{B D}{D A}\) ………….(ii)
[by basic proportionality theorem]
From Eqs. (i) and (ii), we get
\(\frac{B E}{E C}=\frac{B C}{C P}\)
Hence proved.

Question 29.
Find the roots of the quadratic equation 3x² + 2√6x + 2 = 0.
Answer:
We have, 3x² + 2√6x + 2
= 3x – √6x – √6x + 2
= √3x (√3x – √2) – √2 (√3x – √2)
= (√3x – √2) (√3x – √2)
So, the roots of the equation
(√3x – √2) (√3x – √2) = 0
Now, √3x – √2 = 0
⇒ x = \(\sqrt{\frac{2}{3}}\)
Similarly, √3x – √2 = 0
⇒ x = \(\sqrt{\frac{2}{3}}\)
Thecetore, the roots of 3x² + 2√6x + 2 = 0 are \(\sqrt{\frac{2}{3}}\) , \(\sqrt{\frac{2}{3}}\).

Question 30.
Evaluate \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-\ {cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\).
Answer:
\(\frac{\sin 30^{\circ}+\tan 45^{\circ}-\ {cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)

Or

Evaluate \(\frac{\tan ^2 60^{\circ}+4 \tan ^2 45^{\circ}+3 \sec ^2 30^{\circ}+5 \cos ^2 90^{\circ}}{\ {cosec} 30^{\circ}+\sec 60^{\circ}-\cot ^2 30^{\circ}}\)
Answer:
\(\frac{\tan ^2 60^{\circ}+4 \tan ^2 45^{\circ}+3 \sec ^2 30^{\circ}+5 \cos ^2 90^{\circ}}{\ {cosec} 30^{\circ}+\sec 60^{\circ}-\cot ^2 30^{\circ}}\)
= \(\frac{(\sqrt{3})^2+4 \times(1)^2+3\left(\frac{2}{\sqrt{3}}\right)^2+5 \times(0)^2}{\left\{2+2-(\sqrt{3})^2\right\}}\)
= \(\frac{3+4 \times 1+3 \times \frac{4}{3}+5 \times 0}{2+2-3}\)
= \(\frac{3+4+4+0}{1}\)
= 11

Question 31.
For which values of p does the pair of equation given below has unique solution
8x + py + 8 = 0
4x + 4y + 4 = 0
Answer:
Here, a₁ = 8, a₂ = 4
b₁ = p, b₂ = 4
and c₁ = 8, c₂ = 4
Now, for unique solution
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{8}{4} \neq \frac{p}{4}\)
∴ p ≠ 8
Therefore, for all value of p, expect 8, the given pair of equations will have a unique solution.

Section – D
Section D consists of 4 questions of 5 marks each

Question 32.
Find the sum of first 50 terms of an AP, whose second and third terms are 14 and 18 respectively.
Answer:
Let a and d be the first term and common difference of an AP respectively.
Given, a₁₂ = 14 and a₃ = 18
⇒ a + (2 – 1) d = 14 and a + (3 – 1) d = 18
⇒ a + d = 14 …………….(i)
and a + 2d = 18 ………….(ii)
On subtracting Eq. (i) from Eq. (ii), we get
d = 18 – 14
⇒ d = 4
On putting d = 4 in Eq. (i), we get
a + 4 = 14
a = 14 – 4 = 10
Now, sum of first 50 terms of an AP is
S₅₀ = \(\frac{n}{2}\) [2a + (n – 1) d]
= [2 × 10 + (50 – 1) × 4]
= 25 [20 + 49 × 4]
= 25 (20 + 196]
= 25 × 216
= 5400

Or

If the 5 th term of an AP is 31 and 25 th term is 140 more than 5th term, find the AP.
Answer:
Let a and d be the first term and common ditference of an AP respectively.
Given, a₅ = 31
and a₂₅ = 140 + a₅
⇒ a + (5 – 1) d = 31
and a + (5 – 1) d = 140 + 31
a + 4o = 31
and a + 24d = 171 …………….(ii)
On subtracting Eq. (i) from Eq. (ii), we get
⇒ 20d = 171 – 31
⇒ 20d = 140
⇒ d = 7
On putting d = 7 in Eq. (i), we get
a + 4 × 7 = 31
⇒ a = 31 – 28 = 3
The AP series is a, a + d, a + 2d, a + 3d
i.e. 3, 3 + 7, 3 + 2 × 7, 3 + 3 × 7, ………… or 3, 10, 17, 24, ………..

Question 33.
Find the median for the following data.

Class – Interval	Frequency
130 – 139	4
140 – 149	9
150 – 159	18
160 – 169	28
170 – 179	24
180 – 189	10
190 – 199	7

Answer:
Here, given the frequency distribution table is not in continuous classes, so we convert it into continuous classes for finding, the median.
For this, subtract 0.5 from lower limit of each class interval and add 0.5 to upper limit of each class interval as shown in the table given below

Class – Interval	Frequency	Cumulative frequency
129.5 – 139.5	4	4
139.5 – 149.5	9	13
149.5 – 159.5	18	31 (cl)
159.5 – 169.5	28 (f)	59
169.5 – 179.5	24	83
179.5 – 189.5	10	93
189.5  – 199.5	7	100

Here, N = 100
⇒ \(\frac{N}{2}=\frac{100}{2}\) = 50
The cumulative frequency just greater than 50 is 59
and its corresponding class is 159.5 – 169.5.
Now, l = 159.5, t = 28, cf = 31 and h = 10
∴ Median = l + \(\left(\frac{N / 2-c f}{f}\right)\) × h
= 159.5 + \(\frac{50-31}{28}\) × 10
= 159.5 + \(\frac{19}{28}\) × 10
= 159.5 + 679
= 166.29

Question 34.
BL and CM are medians of AABC right angled at A.
Prove that 4 (BL² + CM²) = 5 BC²
Answer:
Given : BL and CM are medians of ∆ABC right angled at A.

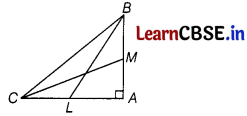
To show 4(8L² + CM²) = 58C²
Proof : Since, SL and CM are medians, so the lines BL and CM divide AC and AB respectively, into two equal parts.
∴ CL = AL = \(\frac{AC}{2}\) …………….(i)
and AM = BM= \(\frac{AB}{2}\) ………….(ii)
In ∆BAC, ∠A = 90°
Using Pythagoras theorem, we get
BC² = AB² + AC² ……….(iii)
In ∆BAL, ∠A = 90°
Using Pythagoras theorem, we get
⇒ BL² = AB² + AL²
⇒ BL² = AB² + (\(\frac{A C}{2}\))² [from Eq. (i)]
⇒ BL² = AB² + \(\frac{A C^2}{4}\)
⇒ 4BL² = 4AB² + AC² ……….(iv)
In ∆ABC, ∠A = 90°
Using Pythagoras theorem, we get
CM² = AC² + AM²
⇒ CM² = AC² + (\(\frac{A B}{2}\))² [from Eq. (ii)]
⇒ 4 CM² = 4AC² + 2 ………….(v)
On adding Eqs. (iv) and (v), we get
4 (BL² + CM²)= 5 (AC² + AB²)
⇒ 4 (BL² + CM²) = 5 BC² [from Eq. (iii)]
Hence proved.

Or

In right angled ∆ ABC, ∠B = 90°. If D is mid-point of side BC, prove that AC² = 4 AD² – 3 AB².
Answer:
Given, ∆ ABC is a right anglel triangle,
∠B = 90° and BD = DC.

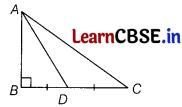
To show AC² = 4AD² – 3AB²
Proof : In ∆ ABC,
AC² = AB² + BC²
[by Pythagoras theorem] …………. (i)
Now, BD =DC (given]
∴ BD = DC = \(\frac{1}{2}\) BC
⇒ BC = 2BD ……………(ii)
On putting BC = 2BD in Eq. (i), we get
AC² – AB² + (2BD)² = AB² + 4BD²
⇒ 4BD² = AC² – AB² ………(iii)
In ∆ABD,
AD² = AB² + BD²
⇒ BD² = AD² – AB² …………… (iv)
⇒ 4BD² = 4AD² – 4AB²
From Eqs. (iii) and (iv), we get
⇒ AC² = AB² + 4AD² – 4AB²
∴ AC² = 4AD² – 3AB²
Hence proved.

Question 35.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After sometime, the angle of elevation reduces to 30° (see the figure). Find the distance travelled by the balloon during the interval.

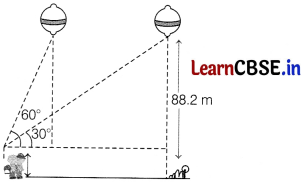
Answer:
Let AD = 1.2 m be the height of girl standing on the horizontal line AB
and let FH = EB = 88.2 m be the height of balloon from the line AB.
At the eyes of the girl, the angles of elevation are
∠FDC = 60°
and ∠EDC = 30°.

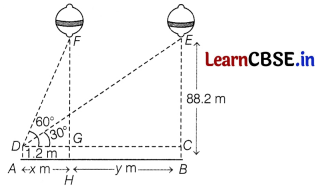
Now, FG = EC = 88.2 – 1.2 = 87 m
Let the distance travelled by the balloon,
HB = y m and AH = x m.
∴ DG = AH = x m
and GC = HB = y m
In right angled ∆FGD,
tan 60° = \(\frac{F G}{D G}\)
⇒ √3 = \(\frac{87}{x}\)
⇒ x = \(\frac{87}{\sqrt{3}}\) ……………(i)
[∵ tan 60° = √3]
In right angled ∆ECD,
tan 30° = \(\frac{E C}{D C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{87}{D G+G C}\)
[∵ tan 30° = \(\frac{1}{\sqrt{3}}\) and DC = DG +GC]
⇒ \(\frac{1}{\sqrt{3}}=\frac{87}{x+y}\)
⇒ x + y = 87√3 ……………(ii)
On putting x = \(\frac{87}{\sqrt{3}}\) from Eq. (i) ¡fl Eq. (ii), we get
\(\frac{87}{\sqrt{3}}\) + y = 87√3
⇒ y = 87 (√3 – \(\frac{1}{\sqrt{3}}\))
⇒ y = \(\frac{87(3-1)}{\sqrt{3}}\)
= \(\frac{87 \times 2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{87 \times 2 \sqrt{3}}{3}\) [rationalising]
= 29 × 2√3 = 58√3 m.

Section – E
Case study based questions are compulsory

Question 36.
Mathematics teacher of a school took her X standard students for drill practice. Teacher interest for students are standing in rows and columns in their playground for a drill practice. A, B, C and D are the positions of four students as shown in figure.

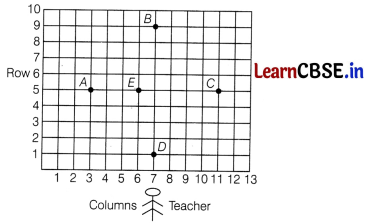
Considering O as origin.

On the basis of above information, answer the following questions.

(i) What are the coordinates of A?
Answer:
The coordinates of A are (3, 5).

(ii) What is the ratio in which E divides AC?
Answer:
AE = 6 – 3 = 3 units
and EC = 11 – 6 = 5 units
∴ Required ratio = \(\frac{A E}{E C}=\frac{3}{5}\)

Or

Find the coordinates of mid-point of DC.
Answer:
Coordinates of C are (11, 5)
and coordinates of D are (7, 1).
Coordinates of mid-point of DC = \(\left(\frac{11+7}{2}, \frac{5+1}{2}\right)\) = (9, 3)

(iii) Find the distance between A and D.
Answer:
Coordinates of D are (7, 1)
and coordinates of A are (3, 5)
AD = \(\sqrt{(7-3)^2+(1-5)^2}\)
= \(\sqrt{16+16}\)
= \(\sqrt{32}\)
= \(4 \sqrt{2}\) units

Question 37.
Heena hold a Japanese fan in her hand as shown in the figure.

It is shaped like a sector of a circle and made of a thin material such as paper or feather. The inner and outer radii are 6 cm and 10 cm respectively. The fan has three colours i.e. Pink, Blue and Black.

On the basis of above information, answer the following questions.

(i) If the region containing blue colour makes an angle of 80° at the centre, then find the area of the region having blue colour.
Answer:
From the figure,
Area of the region having blue colour = \(\frac{80^{\circ}}{360^{\circ}} \pi(10)^2-\frac{80^{\circ}}{360^{\circ}} \times \pi(6)^2\)
= \(\frac{80^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × [(10)² – (6)²]
= \(\frac{80^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 16 × 4
[∵ a² – b² = (a + b) (a – b)]
= \(\frac{112640}{2520}\)
= 44.698 cm²

(ii) If the region containing black colour makes an angle of 40° at the centre, then find the area of the region having black colour.
Answer:
Similarly,
Area of the region having black colour = \(\frac{40^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 16 × 4
= \(\frac{56320}{2520}\)
= 22.35 cm²

(iii) If the region containing pink colour makes an angle of 30° at the centre, then find the perimeter of the region containing pink colour.
Answer:
Similarly,
Perimeter of the region having pink colour = 2 (10 – 6) + length of arc having radius 6 cm + length of arc having radius 10 cm.

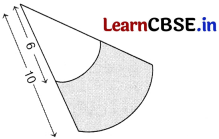
= 8 + \(\frac{30^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7}\) × 6 + \(\frac{30^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7}\) × 10
= 8 + \(\frac{7920}{2520}+\frac{13200}{2520}\)
= 8 + 3.142 + 5238
= 16.38 cm

Or

Find the area of the region having radius 6 cm.
Answer:
Total angle = 80° + 40° + 30° = 150°
∴ Area of the region = \(\frac{150^{\circ}}{360^{\circ}} \times \frac{22}{7}\) x 6 x 6
= \(\frac{118,800}{2520}\)
= 47.14 cm²

Question 38.
Due to heavy storm an electric wire got bent as shown in the figure. It followed a mathematical shape.

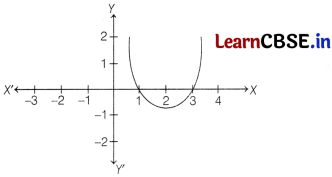
(i) Name the shape in which the wire is bent.
Answer:
Wire is bent in the shape of parabola.

(ii) Find the zeroes of the polynomial.
Answer
Since, graph intersects X-axis at points 1 and 3, so zeroes are 1 and 3.

(iii) What will be the expression of the polynomial?
Answer:
Expression of the polynomial,
p(x) = (x – 1) (x – 3)
= x² – 3x – x + 3
= x² – 4x + 3

Or

If one zero of 3x² + 8x + k be the reciprocal of the other, then find the value of k.
Answer:
Given, polynomial is 3x² + 8x + k
Let one zero of given polynomial is α, then other zero will be \(\frac{1}{\alpha}\).
∵ Product of zeroes = \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
∴ α × \(\frac{1}{\alpha}\) = \(\frac{k}{3}\)
⇒ k = 3.