Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 10 are designed as per the revised syllabus.
CBSE Sample Papers for Class 10 Maths Basic Set 10 with Solutions
Time : 3 hrs
Max. Marks : 80
General Instructions:
- This question paper has 5 Sections A, B, C, D and E.
- Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
- Section B has 5 Short Answer-I (SA-I) Type Questions carrying 2 marks each.
- Section C has 6 Short Answer-II (SA-II) Type Questions carrying 3 marks each.
- Section D has 4 Long Answer (LA) Type Questions carrying 5 marks each.
- Section E has 3 Case Based integrated units of assessment (4 marks each).
- All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
- Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
Section – A
Section A consists of 20 questions of 1 mark each
Question 1.
If one root of the equation 5x2 + 15x + \(\frac{25}{4}\) = 0 is – \(\frac{1}{2}\), then the other root is
(a) – \(\frac{5}{2}\)
(b) \(\frac{1}{2}\)
(c) – \(\frac{2}{2}\)
(d) – \(\frac{3}{2}\)
Answer:
(a) – \(\frac{5}{2}\)
Given, quadratic equation
5x2 + 15x + \(\frac{25}{4}\) = 0
On comparing it with ax2 + bx + c = 0, we get
a = 5, b = 15 and c = \(\frac{25}{4}\).
We know that if α and β are roots of quadratic equation, then
α + β = – \(\frac{b}{a}\)
Here, α = – \(\frac{1}{2}\)
Then, α + β = – \(\frac{15}{5}\) = – 3
β = – 3 + \(\frac{1}{2}\)
∴ β = – \(\frac{5}{2}\)
Question 2.
The product of the HCF and LCM of the smallest prime number and the smallest composite number is
(a) 2
(b) 4
(c) 6
(d) 8
Answer:
(d) 8
Smallest prime number = 2
Smallest composite number = 4
Since, product of HCF and LCM = Product of numbers
∴ HCF × LCM = 2 × 4 = 8
![]()
Question 3.
The probability that it will rain tomorrow is 0.3. What is the probability that it will not rain tomorrow?
(a) 0.3
(b) 0.2
(c) 0.7
(d) 0.07
Answer:
(c) 0.7
Let A be the event of rain tomorrow.
Then, P(A) = 0.3
We know that
P(A) + \(P(\bar{A})\) = 1
Then, probability that it will not rain tomorrow = 1 – 0.3 = 0.7
Question 4.
If one of the zeroes of a quadratic polynomial (k – 1) x2 + kx + 1 is – 3, then the value of k is
(a) 1
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{4}{3}\)
Answer:
(d) \(\frac{4}{3}\)
Let p(x) = (k – 1) x2 + kx + 1
Since, – 3 is a zero of polynomial.
∴ P (- 3) = 0
∴ (k – 1) (- 3)2 + k (- 3) + 1 = 0
⇒ 9 (k – 1) – 3k + 1 = 0
⇒ 9k – 9 – 3k + 1 = 0
⇒ 6k – 8 = 0
⇒ 6k = 8
∴ k = \(\frac{6}{8}\)
⇒ k = \(\frac{4}{3}\)
Question 5.
The area of a quadrant of a circle whose circumference is 20 cm, is
(a) \(\frac{400}{\pi}\) cm2
(b) \(\frac{100}{\pi}\) cm2
(c) \(\frac{200}{\pi}\) cm2
(d) \(\frac{800}{\pi}\) cm2
Answer:
(a) \(\frac{400}{\pi}\) cm2
Given, the circumference of a quadrant of circle is 20 cm.
⇒ \(\frac{2 \pi r}{4}\) = 20
⇒ πr = 40
⇒ r = \(\frac{40}{\pi}\)
Now, area of a quadrant = \(\frac{\pi r^2}{4}=\frac{\pi}{4} \times\left(\frac{40}{\pi}\right)^2\)
= \(\frac{\pi}{4} \times \frac{1600}{\pi^2}\)
= \(\frac{400}{\pi}\) cm2
![]()
Question 6.
Given that sin A = \(\frac{\sqrt{3}}{2}\) and cos B = \(\frac{\sqrt{3}}{2}\), the value of (A + B) is
(a) 60°
(b) 105°
(c) 75°
(d) 90°
Answer:
(d) 90°
Given, sin A = \(\frac{\sqrt{3}}{2}\) and cos B = \(\frac{\sqrt{3}}{2}\)
⇒ sin A = sin 60°
[∵ sin 60° = \(\frac{\sqrt{3}}{2}\)]
and cos B = cos 30°
[∵ cos 30° = \(\frac{\sqrt{3}}{2}\)]
⇒ A = 60° and B = 30°
∴ A + B = 60° + 30° = 90°
Question 7.
In a throw of a die, the probability of getting a prime number, is
(a) \(\frac{2}{3}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{5}{6}\)
Answer:
(b) \(\frac{1}{2}\)
Total number of possible outcomes = 1, 2, 3, 4, 5, 6
Let E = Event of getting a prime number = 2, 3, 5
∴ P(E) = \(\frac{3}{6}=\frac{1}{2}\)
Question 8.
In ∆ABC it is given that, \(\frac{A B}{A C}=\frac{B D}{D C}\), if ∠B = 60° and ∠C = 60°, then ∠BAD is equal to
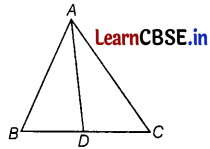
(a) 30°
(b) 40°
(c) 45°
(d) 50°
Answer:
(a) 30°
Given, in ∆ABC,
\(\frac{A B}{A C}=\frac{B D}{D C}\)
∠B = 60° and ∠C = 60°
We know that sum of angles of a triangle is 180°
In ∆ABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 60° + 60° = 180°
⇒ ∠A = 180° – 120° = 60°
Now, \(\frac{A B}{A C}=\frac{B D}{D C}\) [given]
Therefore, AD bisects BC. [by Angle Bisector theorem]
Then, ∠BAC = \(\frac{1}{2}\) ∠A = 30°.
Hence, the value of ∠BAD is 30°.
![]()
Question 9.
In the given figure, PQ || BC, then the value of AQ is
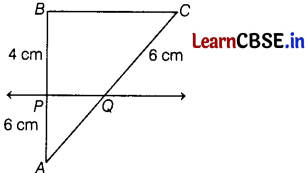
(a) 3.5 cm
(b) 4.5 cm
(c) 9 cm
(d) 9.5 cm
Answer:
(c) 9 cm
In ∆ABC, we have PQ || BC
\(\frac{A Q}{Q C}=\frac{A P}{P B}\) [by Thale’s theorem]
\(\frac{A Q}{6}=\frac{6}{4}\)
AQ = \(\frac{6 \times 6}{4}\)
= 9 cm
Question 10.
The median and mode of a frequency distribution are 32 and 38 respectively, then the mean is
(a) 34
(b) 29
(c) 20
(d) 35
Answer:
(b) 29
∵ Mode = 3 Median – 2 Mean
⇒ 38 = 3 × 32 – 2 × Mean
⇒ 2 Mean = 3 × 32 – 38
= 96 – 38 = 58
⇒ Mean = \(\frac{58}{2}\) = 29
Question 11.
The angle of elevation of the sun when the shadow of a 10 m long pole is 10√3 m is
(a) 60°
(b) 30°
(c) 45°
(d) None of these
Answer:
(b) 30°
Let the angle of elevation of the sun be θ from the point p.
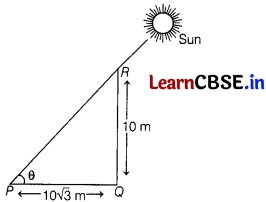
In ∆PQR,
tan θ = \(\frac{Q R}{Q P}\)
= \(\frac{10}{10 \sqrt{3}}\)
= \(\frac{1}{\sqrt{3}}\)
θ = 30°
![]()
Question 12.
In the given figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then, AT is equal to
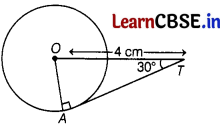
(a) 4 cm
(b) 2 cm
(c) 2√3 cm
(d) 4√3 cm
Answer:
(c) 2√3 cm
In right ∆OAT (having right angle at A), we have
cos (∠OTA) = \(\frac{A T}{O T}\)
⇒ cos 30° = \(\frac{A T}{4}\)
⇒ AT = \(\frac{\sqrt{3}}{2}\) × 4
⇒ AT = 2√3 cm
Question 13.
For which values of p does the pair of equations given below has unique solution?
Ax + py + 8 = 0
2x + 2y + 2 = 0
(a) 2
(b) 3
(c) 4
(d) All real values except 4
Answer:
(d) All real values except 4
Here, a1 = 4, a2 = 2
and b1 = p, b2 = 2
Now, for the given pair to have a unique solution
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{4}{2} \neq \frac{p}{2}\)
⇒ p ≠ 4
Therefore, for all value of p except 4, the pair of equations will have a unique solution.
Question 14.
What are the values of a and b such that the number a, 9, b, 25 form an AP?
(a) 1 and 17
(b) 2 and 12
(c) 4 and 5
(d) 6 and 5
Answer:
(a) 1 and 17
Since, the numbers a, 9, b, 25 form an AP, we have
9 – a = b – 9 = 25 – b
Now, b – 9 = 25 – b
⇒ 2b = 34
⇒ b = 17
and 9 – a = b – 9
⇒ a + b = 18
⇒ a + 17 = 18
⇒ a = 1 and b = 17
![]()
Question 15.
The smallest number by which \(\sqrt{27}\) should be multiplied, so as to get a rational number is
(a) \(\sqrt{27}\)
(b) 3√3
(c) √3
(d) 3
Answer:
(c) √3
As, \(\sqrt{27}\) = \(\sqrt{3 \times 3 \times 3}\) = 3√3
So, if we multiply it by √3 it will become
3√3 √3 = 3 × 3 = 9
i.e. a rational number.
Question 16.
If 0° < 0 < 90°, then the value of θ in tan 5θ = 1 is
(a) 6°
(b) 12°
(c) 9°
(d) 0°
Answer:
(c) 9°
We have,
tan 5θ = 1
⇒ tan 5θ = tan 45°
⇒ 5θ = 45°
⇒ θ = \(\frac{45^{\circ}}{5}\) = 9°
Question 17.
The roots of the given equation (x + 2) (3x – 5) = 0 is
(a) 5, 1
(b) 4, \(\frac{3}{2}\)
(c) – 2, \(\frac{5}{3}\)
(d) 1, 1
Answer:
(c) – 2, \(\frac{5}{3}\)
We have,
(x + 2) (3x – 5) = 0
⇒ x + 2 = 0 or 3x – 5 = 0 5
⇒ x = – 2 or x = \(\frac{5}{3}\)
Hence, the roots of given equation are – 2 and \(\frac{5}{3}\).
![]()
Question 18.
If the product of zeroes of the polynomial f(x) = ax3 – 6x2 + 11x – 6 is 4, then the value of a is
(a) \(\frac{3}{2}\)
(b) \(\frac{11}{4}\)
(c) 3
(d) None of these
Answer:
(a) \(\frac{3}{2}\)
Let α, β, γ are the zeroes of the polynomial f(x).
Now, we have
αβγ = 4
⇒ \(\frac{-(-6)}{a}\) = 4
∴ a = \(\frac{6}{4}=\frac{3}{2}\)
Directions : In the question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.
Question 19.
Assertion (A) : If the median of the given data 26, 29, 42, 53, x, x + 4, 70, 75, 80, 92 is 68, then the value of x is 66.
Reason (R) : When the number of observations (n) is odd, the median is the \(\frac{n+1}{2}\)th observation.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
Given, number of observations is 10 (even).
∴ Median = \(\frac{x+(x+4)}{2}\)
⇒ \(\frac{2 x+4}{2}\) = x + 2
⇒ 68 = x + 2
⇒ x = 66
So, Assertion (A) is true.
Clearly, Reason (R) is also true. But Reason (R) is not the correct explanation of Assertion (A).
Question 20.
Assertion (A) : Frequency is the number of times a particular observation occurs in data.
Reason (R) : Data can be grouped into class intervals such that all observations in that range belong to the class.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(b) Both Assertion (A) and Reason (R) are correct but Reason (R) is not the correct explanation of Assertion (A).
![]()
Section – B
Section B consists of 5 questions of 2 marks each
Question 21.
Two buildings ABC and PQR are constructed in triangular shapes are similar as shown in the below figure
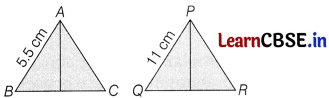
If perimeter of ∆ABC is 70 cm, then find the perimeter of ∆PQR.
Answer:
Given, ∆ABC ~ ∆PQR with AB = 5.5 cm and PQ = 11 cm.
Since, ∆ABC ~ ∆PQR, so corresponding sides are proportional.
∴ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\)
⇒ \(\frac{5.5}{11}=\frac{55}{110}=\frac{1}{2}\)
⇒ \(\frac{A B}{P Q}=\frac{1}{2}\),
\(\frac{B C}{Q R}=\frac{1}{2}\)
and \(\frac{A C}{P R}=\frac{1}{2}\)
⇒ AB = \(\frac{1}{2}\) PQ,
BC = \(\frac{1}{2}\) QR
and AC = \(\frac{1}{2}\) PR
Also, given perimeter of ∆ABC = 70 cm
⇒ AB + BC + CA = 70
⇒ \(\frac{1}{2}\) PQ + \(\frac{1}{2}\) QR + \(\frac{1}{2}\) PR = 70
∴ PQ + QR + PR = 140 cm
Hence, the perimeter of ∆PQR is 140 cm.
Question 22.
Find the type of triangle formed by the points P (- 5, 6), Q (- 4, – 2) and R (7, 5).
Answer:
Given, vertices of triangle are P (- 5, 6), Q (- 4, – 2) and R (7, 5).
Now, PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\) [by distance formula]
= \(\sqrt{(-4+5)^2+(-2-6)^2}\)
= \(\sqrt{1+64}\)
= \(\sqrt{65}\) units
QR = \(\sqrt{(7+4)^2+(5+2)^2}\)
= \(\sqrt{121+49}\)
= \(\sqrt{170}\) units
and PR = \(\sqrt{(7+5)^2+(5-6)^2}\)
= \(\sqrt{144+1}\)
= \(\sqrt{145}\) units
Here, PQ ≠ QR ≠ PR
Hence, the given triangle is a scalene triangle.
Or
A parallelogram has vertices P (1, 4), Q (7, 11), R (a, 4) and S (1, – 3). Find the value of a.
Answer:
Let P (1, 4), Q (7, 1 1), R (a, 4) and S (1, – 3) be the vertices of a parallelogram PQRS, respectively.
Join PR and OS.
Let PR and QS intersect at the point T.
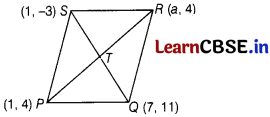
We know that the diagonals of a parallelogram bisect each other.
So, T is the mid-point of PR as well as that of QS.
∴ Mid-point of PR = Mid-point of QS
⇒ \(\left(\frac{1+a}{2}, \frac{4+4}{2}\right)=\left(\frac{7+1}{2}, \frac{11-3}{2}\right)\)
⇒ \(\left(\frac{1+a}{2}, 4\right)\) = (4, 4)
On comparing x-coocdinate from both sides, we get
\(\frac{1+a}{2}\) = 4
⇒ 1 + a = 8
⇒ a = 7
Hence, the value of a is 7.
Question 23.
A bag contains 5 red balls and some blue balls.If the probability of drawing a blue ball from the bag is thrice that of a red ball, then find the number of blue balls in the bag.
Answer:
Let the number of blue balls be y.
Then, total number of balls = (5 + y)
Given, P (blue ball) = 3 × P (red ball)
∴ \(\frac{y}{(5+y)}=3 \times \frac{5}{(5+y)}\)
⇒ y = 15
Hence, the number of blue balls is 15.
![]()
Question 24.
If α and β are the zeroes of the quadratic polynomial f (x) = x2 – 4x + 3, then find the value of (α4β2 + β4α2).
Answer:
On comparing f(x) with ax2 + bx + c, we get
a = 1, b = – 4 and c = 3
∴ α + β = \(\frac{-b}{a}\)
= \(\frac{-(-4)}{1}\) = 4
and αβ = \(\frac{c}{a}=\frac{3}{1}\) = 3
∴ α4β2 + α2β4 = α2β2 (α2 + β2)
= (3)2 [(α + β) – 2 (αβ)]
= 32 × [(4)2 – (2 x 3)]
= 9 × 10 = 90
Question 25.
A circus artist is climbing a 40 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 60°.
Answer:
Let BC be the vertical pole and AB be the rope which is tightly stretched and tied from the top of pole to the ground.
Then, AB = 40 m
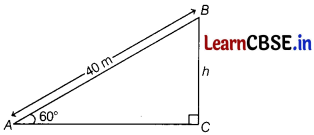
Let h m be the height of the vertical pole BC.
Then, angle of elevation = ∠BAC = 60° [given]
From right angled ∆ABC, we get
sin 60° = \(\frac{B C}{A B}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{h}{40}\)
⇒ h = 20√3
Hence, the height of the pole is 20√3 m.
Or
A kite is flying at a height of 30 m from the level ground, attached to string inclined at 30° to the horizontal. Find the length of the string.
Answer:
Let P be the kite and the height of the kite, MP = 30 m.
Let the string be held at the point O,
then ∠MOP = 30° [given]
and OP is the length of the string.
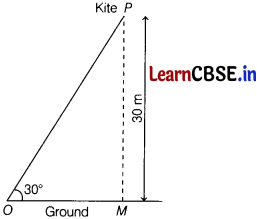
From right angled ∆OMP,
sin 30° = \(\frac{M P}{O P}\)
⇒ \(\frac{1}{2}=\frac{30}{O P}\)
⇒ OP = 60 m
Hence, the length of the string is 60 m.
![]()
Section – C
Section C consists of 6 questions of 3 marks each
Question 26.
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 10 cm each and the slant height of the cone is 13 cm.
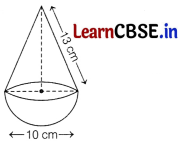
Calculate
(i) the height of the cone.
(ii) the volume of the solid.
Answer:
Given, diameter of the base (d) = 10 cm
∴ Radius of the base (r) = \(\frac{10}{2}\) = 5 cm
Slant height of the cone (l) = 13 cm
(i) Let the height of the cone = h
We know that
l2 = r2 + h2 [using Pythagoras theorem]
⇒ (13)2 = (5)2 + h2
⇒ 169 = 25 + h2
⇒ 169 = 25 + h2
⇒ h2 = 169 – 25 = 144
∴ h = \(\sqrt{144}\) = 12 cm [taking positive square root]
Hence, height of the cone is 12 cm.
(ii) Volume of solid = Volume of hemisphere + Volume of cone
= \(\frac{2}{3}\) πr3 + \(\frac{1}{3}\) πr2h
= \(\frac{1}{3}\) πr2 (2r + h)
= \(\frac{1}{3} \times \frac{22}{7}\) × 5 × 5 (2 × 5 + 12)
[∵ r = 5 cm and h = 12 cm]
= \(\frac{22 \times 25}{21}\) (10 + 12)
= \(\frac{22 \times 25}{21}\) (22)
= \(\frac{12100}{21}\)
= 576.19 cm3
Hence, the volume of solid is 576.19 cm3 .
Question 27.
Calculate the mode for the following frequency distribution

Answer:
As the class 40 – 50 has maximum frequency, so it is the modal class.
∴ l = 40, h = 10,
f1 = 28, f0 = 12
and f2 = 20
Mode, M0 = l + \(\left\{h \times \frac{f_1-f_0}{\left(2 f_1-f_0-f_2\right)}\right\}\)
= 40 + \(\left\{10 \times \frac{(28-12)}{(2 \times 28-12-20)}\right\}\)
= 40 + \(\left\{10 \times \frac{16}{24}\right\}\)
= 40 + \(\frac{20}{3}\)
= 40 + 6.67
= 46.67
Hence, mode is 46.67.
Question 28.
Solve the following quadratic equation by factorisation \(\frac{1}{x+4}-\frac{1}{x+7}=\frac{3}{10}\), x ≠ – 4, – 7
Answer:
Given, \(\frac{1}{x+4}-\frac{1}{x+7}=\frac{3}{10}\)
⇒ \(\frac{x+7-(x+4)}{(x+7)(x+4)}=\frac{3}{10}\)
⇒ \(\frac{3}{\left(x^2+11 x+28\right)}=\frac{3}{10}\)
⇒ \(\frac{1}{x^2+11 x+28}=\frac{1}{10}\)
⇒ x2 + 11x + 28 = 10
⇒ x2 + 11x + 28 = 10
⇒ x2 + 11x + 18 = 0
⇒ x2 + 9x + 2x + 18 = 0
⇒ x (x + 9) + 2 (x + 9) = 0
⇒ (x + 9) (x + 2) = 0
⇒ x = – 9, – 2
Or
Using quadratic formula, solve for x 9x2 – 3 (a + b) x + ab = 0.
Answer:
Given, equation is 9x2 – 3(a + b) x + ab = 0
On comparing with Ax2 + Bx + C = 0, we get
A = 9, B = – 3 (a + b) and C = ab
Discriminant, D = B2 – 4AC
= 9 (a + b)2 – 4(9) (ab)
= 9 {(a + b)2 – 4ab}
= 9 (a – b)2
[∵ (a + b)2 – 4ab = (a – b)2]
Therefore, the two real roots of the equation are given by
x = \(\frac{-B \pm \sqrt{D}}{2 A}\) [by quadratic formula]
= \(\frac{3(a+b) \pm 3(a-b)}{18}\)
= \(\frac{(a+b) \pm(a-b)}{6}\)
⇒ x = \(\frac{(a+b)+(a-b)}{6}\) or x = \(\frac{(a+b)-(a-b)}{6}\)
⇒ x = \(\frac{2 a}{6}\) or x = \(\frac{2 b}{6}\)
∴ x = \(\frac{a}{3}\) or x = \(\frac{b}{3}\)
Hence, the two roots are and x = \(\frac{a}{3}\) and x = \(\frac{b}{3}\).
![]()
Question 29.
In a circle of radius 21 cm, an arc subtends an angle of 45° at the centre. Find the length of the arc and using it, find the area of the sector.
Answer:
Given, r = 21 cm and θ = 45°
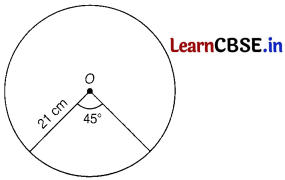
∴ Arc length = \(\frac{\theta}{360^{\circ}}\) × 2πr
= \(\frac{45^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × 21
= \(\frac{1}{4}\) × 22 × 3
= 16.5 cm
Now, area of sector = \(\frac{1}{2}\) × l × r [where l = arc length]
= \(\frac{1}{2}\) × 16.5 × 21
= 173.25 cm2
Question 30.
Find the largest positive integer that will divide 398, 436 and 542 leaving remainders 7, 11 and 15, respectively.
Answer:
It is given that when dividing 398 by the required number, then there is a remainder of 7.
This means that 398 – 7 = 391 is exactly divisible by the required number In othe words, required number is a factor of 391.
Similarly, the required positive integer is a factor of 436 – 11 = 425 and 542 – 15 = 527.
Clearly, required number is the HCF of 391, 425 and 527.
Now, prime factorisations of 391, 425 and 527 are as follows
391 = 17 × 23,
425 = 52 × 17
and 527 = 17 × 31
∴ HCF of 391, 425 and 527 = 17
Hence. 17 is the required number.
Or
There are 156, 208 and 260 students in groups A,B and C, respectively. Buses are to be hired to take them for a field trip. Find the minimum number of buses to be hired, if the same number of students should be accommodated in each bus.
Answer:
Given numbers are 156, 208 and 260.
The prime factor of given numbers are
156 = 22 × 3 × 13,
208 = 24 × 13
and 260 = 22 × 5 × 13
∴ HCF of (1 56, 208 260) = 22 × 13 = 52
Thus, HCF of 156. 208 and 260 is 52.
Hence, the minimum number of buses = \(\frac{156}{52}+\frac{208}{52}+\frac{260}{52}\)
= 3 + 4 + 5 = 12
Question 31.
Prove that \(\frac{(1+\cot A+\tan A)(\sin A-\cos A)}{\sec ^3 A-\ {cosec}^3 A}\) = sin2 A – cos2 A.
Answer:
LHS = \(\frac{(1+\cot A+\tan A)(\sin A-\cos A)}{\sec ^3 A-\ {cosec}^3 A}\)

![]()
Section – D
Section D consists of 4 questions of 5 marks each
Question 32.
If D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC, then prove that CA2 = CB × CD.
Answer:
Draw ∆ABC such that D is a point on BC and join AD.
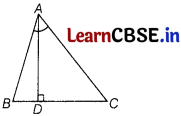
In ∆ABC and ∆DAC, we have
∠BAC = ∠ADC [given]
and ∠ACB = ∠DCA [common anglej
∴ ∆ABC ~ ∆DAC [by AA similarity criterion]
⇒ \(\frac{A C}{D C}=\frac{C B}{C A}\)
[since, corresponding sides of two simiiar triangles are poporional]
or \(\frac{C A}{C D}=\frac{C B}{C A}\)
⇒ CA × CA = CB × CD
⇒ CA2 = CB × CD
Hence proved.
Or
In a ∆ABC, AD is the median of DC and D is the mid-point of AD. If BE produced, it meets AC in F. Prove that AF = \(\frac{1}{3}\) AC.
Answer:
Given : In ∆ABC, mid-point of BC is D and mid-point of AD is E.
Construction : Draw DG || BF.
To Prove : AF = \(\frac{1}{3}\) AC
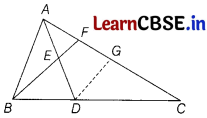
Proof : In ∆CBF,
DG || BF
∴ \(\frac{C G}{G F}=\frac{C D}{B D}\)
[by Basic Proportionality theorem]
⇒ \(\frac{C G}{G F}\) = 1 [∵ D is mid-point of BC]
⇒ CG = GF …………..(i)
In ∆ADG,
EF || DG
∴ \(\frac{A E}{E D}=\frac{A F}{F G}\)
[by Basic Proportionality theorem]
⇒ 1 = \(\frac{A F}{F G}\) [∵ E is mid-point of AD]
⇒ AF = FG …………..(ii)
From Eqs. (i) and (ii), we get
AF = FG = CG
∴ AF = \(\frac{1}{3}\) AC
Hence proved.
Question 33.
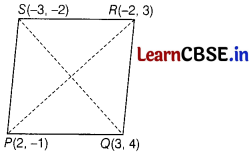
If P (2, – 1), Q (3, 4), R (- 2, 3) and S(- 3, – 2) be four points in a plane, then show that PQRS is a rhombus but not a square. Also, find the area of the rhombus.
Answer:
The given points are P (2, – 1), Q (3, 4), R (- 2, 3) and S (- 3, – 2)
Now, the distance between the two points is given by \(\)
∴ PQ = \(\sqrt{(3-2)^2+(4+1)^2}\)
= \(\sqrt{1^2+5^2}\)
= \(\sqrt{26}\) Units
OR = \(\sqrt{(-2-3)^2+(3-4)^2}\)
= \(\sqrt{(-5)^2+(-1)^2}\)
= \(\sqrt{26}\) units
RS = \(\sqrt{(-3+2)^2+(-2-3)^2}\)
= \(\sqrt{(-1)^2+(-5)^2}\)
= \(\sqrt{26}\) units
and SP = \(\sqrt{(-3-2)^2+(-2+1)^2}\)
= \(\sqrt{(-5)^2+1^2}\)
= \(\sqrt{26}\) units
∴ PQ = QR = RS = SP = units
Now,
PR = \(\sqrt{(-2-2)^2+(3+1)^2}\)
= \(\sqrt{(-4)^2+4^2}\)
= \(\sqrt{32}\)
= \(4 \sqrt{2}\) units
and QS = \(\sqrt{(-3-3)^2+(-2-4)^2}\)
= \(\sqrt{(-6)^2+(-6)^2}\)
= \( \sqrt{72}\)
= \( 6 \sqrt{2}\) units
∴ Diagonal PR ≠ Diagonal QS
∴ PQRS is a rhombus but not a square.
∴Area of the rhombus PQRS = \(\frac{1}{2}\) x (Product of diagonal)
= (\(\frac{1}{2}\) × PR × QS)
= (\(\frac{1}{2}\) × 4√2 × 6√2) sq unit
= 24 sq units.
![]()
Question 34.
The angle of depressions of two consecutive kilometre stones of the road, which are situated on opposite sides of an aeroplane, from an aeroplane fly vertically of the horizontal road are α and β. Prove that height of an aeroplane is \(\frac{\tan \alpha \cdot \tan \beta}{\tan \alpha+\tan \beta}\).
Answer:
Answer:
Let A be an aeroplane flying above h km from the road and angles of depressions a and b are on both sides of aeroplane at points B and C. respectively.
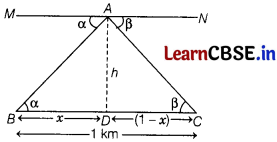
∵ Distance between two stones B and C = 1 km
Now, MN || BC
∴ ∠MAB = ∠ABD = α [alternate angles]
and ∠NAC = ∠ACO = β [alternate angles]
Let BD = x km, then DC = (1 – x) km
In right angled ∆ADB,
tan α = \(\frac{\text { Perpendicular }}{\text { Base }}=\frac{A D}{B D}\)
⇒ tan α = \(\frac{h}{x}\)
⇒ h = x tan α
[using cross-multiplication] ………….(i)
In right angled ∆ADC,
tan β = \(\frac{\text { Perpendicular }}{\text { Base }}=\frac{A D}{D C}\)
⇒ tan β = \(\frac{h}{(1-x)}\)
⇒ tan β = \(\frac{x \tan \alpha}{(1-x)}\) [from Eq. (1)]
⇒ tan β (1 – x) = x tan α [using cross-multiplication]
⇒ tan β – x tan β = x tan α
⇒ tan β = x tan α + x tan β [on transposition]
⇒ tan β = x (tan α + tan β)
⇒ x = \(\frac{\tan \beta}{\tan \alpha+\tan \beta}\) ………….(ii)
On putting the value of x in Eq. (i), we get
h = \(\frac{\tan \beta}{\tan \alpha+\tan \beta}\) . tan α
= \(\frac{\tan \alpha \cdot \tan \beta}{\tan \alpha+\tan \beta}\)
Hence, the height of aeroplane is \(\frac{\tan \alpha \cdot \tan \beta}{\tan \alpha+\tan \beta}\).
Or
An aeroplane is flying above two houses and minimum distance between houses is 300 m. If at any time from the one side of aeroplane, the angle of depressions of two houses are 45° and 60°, respectively, then find how much is the height of the aeroplane?
Answer:
Let D be an aeroplane flying at height h m.
A and B are two houses and distance between them is AB = 300 m.
The angles of depression from D to A and B are 45° and 60°, respectively.
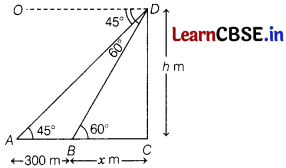
∴ ∠ODA = 45° and ∠ODB = 60°
Now, draw OD || AC.
Then, ∠BAC = ∠ODA = 45° [alternate angles]
and ∠DBC = ∠ODB = 60° [alternate angles]
Again, Let BC = x m.
Then, AC = AB + BC = (300 + x) m
In right angled ∆DCB,
tan 60° = \(\frac{D C}{B C}\)
[∵ tan θ = Perpendicular / Base]
⇒ √3 = \(\frac{h}{x}\) [∵ tan 60° = √3]
⇒ x = \(\frac{h}{\sqrt{3}}\) ……….(i)
In right angled ∆DCA,
tan 45° = \(\frac{D C}{A C}\)
⇒ 1 = \(\frac{D C}{A B+B C}\)
⇒ 1 = \(\frac{h}{300+x}\) [∵ tan 45° = 1]
⇒ 300 + x = h [using cross-multiplication]
On putting the value of x from Eq. (i), we get
300 + \(\frac{h}{\sqrt{3}}\) = h
⇒ 300 = h – \(\frac{h}{\sqrt{3}}\) [on transposition]
⇒ \(\frac{\sqrt{3} h-h}{\sqrt{3}}\) = 300
⇒ \(\frac{h(\sqrt{3}-1)}{\sqrt{3}}\) = 300
∴ h = \(\frac{300 \sqrt{3}}{(\sqrt{3}-1)}\)
= \(\frac{300 \sqrt{3}}{(\sqrt{3}-1)} \times \frac{(\sqrt{3}+1)}{(\sqrt{3}+1)}\) [on rationalisation]
= \(\frac{300 \sqrt{3}(\sqrt{3}+1)}{(\sqrt{3})^2-(1)^2}\)
[∵ (a – b) (a + b) = a2 – b2]
= \(\frac{300 \sqrt{3}(\sqrt{3}+1)}{3-1}\)
= \(\frac{300(3+\sqrt{3})}{2}\)
= 150 (3 + 1.732)
= 150 × 4.732 [∵ √3 = 1.732]
= 709.800 ≅ 709.8
Question 35.
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O’P are two perpendicular tangents to the two circles. Find the length of the common chord PQ.
Answer:
Here, two circles of radii
OP = 3 cm and PO’ = 4 cm
These two circles intersect at P and Q.
Here, OP and PO’ are two tangents drawn at point P.
But, these two tangents make an angle 90°.
Join OO’ and PN
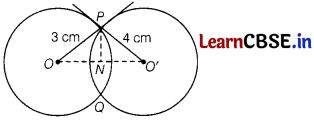
In right ∆OPO’,
(OO’)2 = (OP)2 + (PO’)2 [by Pythagoras theorem]
= (3)2 + (4)2 = 25
⇒ OO’ = 5 cm
Also, PN ⊥ OO’
Let ON = x, then NO’ = 5 – x
In right angled ∆OPN,
(OP)2 = (ON)2 + (NP)2
⇒ (NP)2 = 32 – x2 ………..(i)
and in right angled ∆PNO’,
(PO’)2 = (PN)2 + (NO’)2
⇒ (4)2 = (PN)2 + (5 – x)2
⇒ (PN)2 = 16 – (5 – x)2 …………(ii)
From Eqs. (i) and (ii), we get
9 – x2 = 16 – (5 – x)2
= 7 + x2 – 5 + x2 – 10x = 0
⇒ 10x = 18
⇒ x = 1.8
Again, in right angled ∆OPN,
OP2 = ON2 + NP2
⇒ 32 = (1.8)2 – NP2
⇒ NP2 = 9 – 3.24 = 5.76
⇒ NP = 2.4
∴ Length of common chord,
PQ = 2PN
= 2 × 2.4 = 4.8 cm
![]()
Section – E
Case study based questions are compulsory
Question 36.
India’s literacy rate has increased six times, since the end of the British rule in 1947. From 12% to 74% in recent times. Yet India has the world’s largest population of illiterate people according to a report of oxfam.
Ram asks the labour to dig a well up to a depth of 10 m. Labour charges ₹ 150 for first metre and ₹ 50 for each subsequent metres. As labour was uneducated, he claims ₹ 550 for the whole work.
On the basis of above information, answer the following questions.
(i) What should be the actual amount to be paid to the labour?
Answer:
Labour charges for each subsequent metres are 150, 150 + 50, 150 + 2 × 50 + 150 + 3 × 50
i.e. 150, 200, 250, 300 ………..
Thus, amount of labour charge form an AP with
a = 150 and d = 50
Total depth = 10m
∴ Labour charge for 10 m depth = 150 + (10 – 11) × 50 = 600
Hence, 600 should be paid to the labour.
(ii) If the nth term of an AP is (4n – 10), then find its 16th term.
Answer:
First term a = 4(1) – 10 = 4 – 10 = – 6
Second term, b = 4(2) – 10 = 8 – 10 = – 2
∴ Common difference, d = b – a = – 2 – (- 6)
= – 2 + 6 = 4
So, 16th term = a + (n – 1) d
= – 6 + (16 – 1) × 4
= – 6 + 60 = 54
Or
Find the middle term of the AP 10, 7, 4, ……………., (- 62).
Answer:
Given, nth term of the AP = – 62
Here, a = 10, d = 7 – 10 = – 3
∴ a + (n – 1) d = – 62
⇒ 10 + (n – 1) (- 3) = – 62
⇒ 10 – 3n + 3 = – 62,
⇒ 3n = 13 + 62
⇒ n = \(\frac{75}{3}\) = 25
So, there are total 25 terms.
Middle term of the AP = \(\left(\frac{25+1}{2}\right)\) th term
= 13th term
So, 13th term = 10 + (13 – 1) × (- 3)
= 10 – 36 = – 26
(iii) How much money will Ram save, if labour agrees with ₹ 550?
Answer:
Ram saves = 600 – 500 = ₹ 50
![]()
Question 37.
Mathematics teacher of class X of a school organized a colouring activity to understand geometrical figures. He is interested to make decorative block that shown in the following figure, which is made up of two solids, a cube and a hemisphere.
The base of the block is a cube with edge 12 cm and the hemisphere fixed on the top has a diameter of 4.2 cm. [take, π = \(\frac{22}{7}\)]
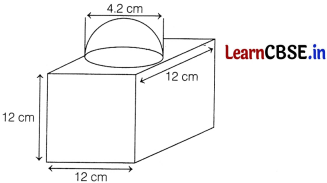
On the basis of above information, answer the following questions.
(i) Find the base area of the cube.
Answer:
Base area of cube = (Side)2 = (12)2 = 144 cm2
(ii) What is the radius of hemispherical portion?
Answer:
Radius of hemispherical portion = \(\frac{4.2}{2}\) = 2.1 cm
(iii) Find the total surface area of hemisphere and total surface area of the cube.
Answer:
Total surface area of hemisphere = 3πr²
= 3 × \(\frac{22}{7}\) × (2.1)2
= 3 × \(\frac{22}{7}\) × 2.1 × 2.1
= 41.58 cm2
Total surface area of cube = 6 (edge)2
= 6 × (12)2
= 6 × 144
= 864 cm2
Or
Find the total surface area to be covering the packing paper.
Answer:
Total surface area to covering the packing pape of the decorative block = Total surface area of cube – Area of base of hemisphere block + Curved surface area of hemisprere
= 864 – πr² + 2πr²
= 864 + πr²
= 864 + \(\frac{22}{7}\) × (2.1)2
= 864 + \(\frac{22}{7}\) × 2.1 × 2.1
= 864 + 13.86
= 877.86 cm2
![]()
Question 38.
Palak went to a mall with her mother and enjoys rides on the giant wheel and plays hoopla (a game in which you throw a ring on the items kept in stall and if the ring covers any object completely you get it). The number of times she played hoopla is half the number of times she rides the giant wheel. If each ride costs ₹ 3 and a game of hoopla costs ₹ 4 and she spent ₹ 20 in the fair.
On the basis of above information, answer the following questions.
(i) Write the representation of given statement algebraically.
Answer:
Let x be the number of rides on the giant wheel and
y be the number of times hoopla played by Palak.
Then, y = \(\frac{x}{2}\)
and 3x + 4y = 20
Rewrite the above equations to represent algebraically
x – 2y = 0 …………..(i)
3x + 4y = 20 ………..(ii)
(ii) Graphically, if the pair of equations intersect at one point, then the pair is consistent or inconsistent.
Answer:
If the pair of equations intersect at only one point.
Then the pair of equations has a unique solution and henœ consistent.
(iii) Find the intersection point of two lines.
Answer:
From Eq. (i), x = 2y
On putting x =2y in Eq. (ii), we get
3 (2y) + 4y = 20
10y = 20
⇒ y = 2
⇒ x = 2 × 2 = 4
Hence, the intersection point is (4, 2).
Or
Find the intersection points of the line 3x + 4y = 20 on X and Y-axes.
Answer:
For intersection point of the line 3x + 4y = 20 on X-axis.
On putting y = 0 in Eq. (ii), we get
3x + 0 = 20
x = \(\frac{20}{3}\)
∴ The intersection point is (\(\frac{20}{3}\), 0)
For intersection point of the line 3x + 4y = 20 on Y-axis.
On putting x = 0 in Eq. (ii), we get
0 + 4y = 20
⇒ y = 5
∴ The intersection point is (0, 5).