CBSE Previous Year Question Papers Class 12 Physics 2015 Outside Delhi
Section-A
Question 1.
Define the term ‘self-inductance’ of a coil. Write its S.I. unit. [1]
Answer:
Self-inductance of a coil is numerically equal to the amount of magnetic flux linked with the coil when unit current flows through the coil. The S.I. unit of self inductance is Henry (H) or Weber per ampere.
\(1 \mathrm{H}=1 \mathrm{Wb} / \mathrm{A}\)
Question 2.
Why does bluish color predominate in a clear sky ? (1]
Answer :
While light from the sun reaches the atmosphere that is comprised of the tiny particles of the atmosphere. These act as a prism and cause the different components to scatter. As blue light travels in shorter and smaller waves in comparison to the other colors of the spectrum, it is scattered the most, causing the sky to appear bluish.
Question 3.
I-V graph for a metallic wire at two different temperatures, T1 and T2 is as shown in the figure. Which of the two temperature is lower and why ? [1]
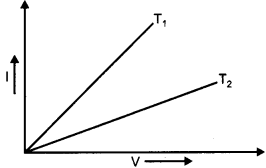
Answer :
The slope of a V-I graph is given by the formula \(\frac{I}{V}=\frac{1}{R}\) Thus, the smaller the slope larger is the resistance. As the resistance of a metal increases with the increase in temperature, so resistance at T2 is higher and T1 is lower.
Question 4.
Which basic mode of communication is used for telephonic communication ? [1]
Question 5.
Why do the electrostatic field lines not form closed loops ? [1]
Answer :
Electrostatic field lines never form loops because they do not converge at only one point as in the case with magnetic field lines. They depend on +ve and -ve charges that can extend to infinity in any particular direction.
Section-B
When an electron in hydrogen atom jumps from the third excited state to the ground state, how would the de-Broglie wavelength associated with the electron change ? Justify your answer. [2]
Answer :
de-Broglie wavelength associated with a moving charge particle having a K.E. ‘K’ can be given as
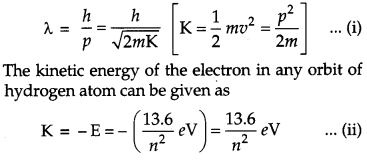
Let K1 and K4 be the K.E. of the electron in ground state and third excited state, where n1 = 1 shows ground state and n2 = 4 shows third ecited state. Using the concept of equations (i) and (ii), we have
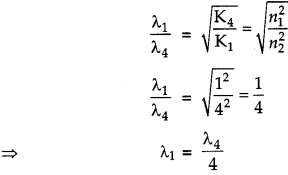
i.e., the wavelength in the ground state will decrease
Question 7.
Write two factors which justify the need of modulating a low frequency signal into high frequencies before transmission. [2]
Question 8.
Use Kirchhoff’s rules to determine the potential difference between the points A and D when no current flows in the arm BE of the electric network shown in the figure. [2]
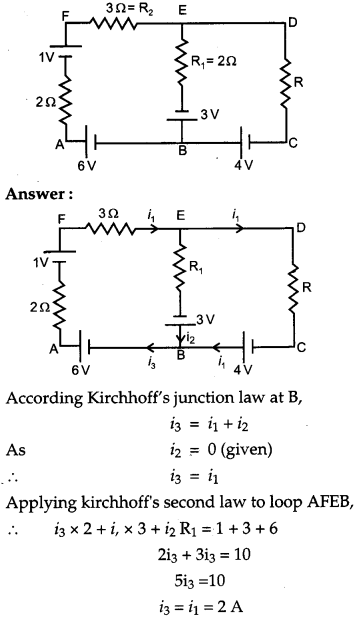
The potential difference between A to D along the branch AFD,
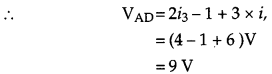
Question 9.
You are given two converging lenses of focal lengths 1.25 cm and 5 cm to design a compound microscope. If it is desired to have a magnification of 30, find out the separation between the objective and the eyepiece. [2]
OR
A small telescope has an objective lens of focal length 150 cm and eye-piece of focal length 5 cm. What is the magnifying power of the telescope for viewing distant objects in normal adjustment ?
If this telescope is used to view a 100 m tall tower 3 km away, what is the height of the image of the tower formed by the objective lens ?



Question 10.
Calculate the shortest wavelength in the Balmer series of hydrogen atom. In which region (infrared, visible, ultraviolet) of hydrogen spectrum does this wavelength lie ? [2]
Answer :
The formula for wavelength (λ) in Balmer series is:

Section-C
Question 11.
Calculate the potential difference and the energy stored in the capacitor C2 in the circuit shown in the figure. Given potential at A is 90 V, C1 = 20 μF, C2 = 30 μF and C3 = 15 μF. [3]
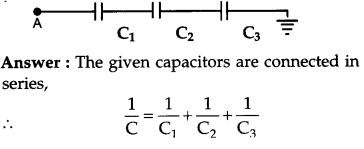

Question 12.
Find the relation between drift velocity and relaxation time of charge carriers in a conductor. A conductor of length L is connected to a d.c. source of emf ‘E’. If the length of the conductor is tripled by stretching it, keeping ‘E’ constant, explain how its drift velocity would be affected. [3]
Answer:
All free electrons suffer collisions with the heavy fixed ions inside the conductor. After collisions, these electrons again emerge with the same speed, but in random directions. So, at given time, net velocity of the electrons is zero
i.e,
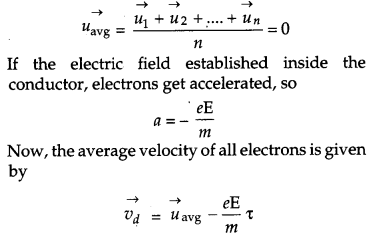
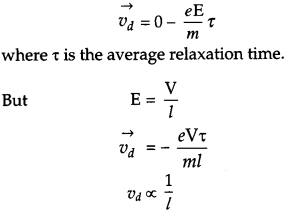
As the drift velocity is inversely proportional to length of conductor, so the drift velocity would be reduced by one third if the length of the conductor is tripled.
Question 13.
State clearly how an unpolarised light gets linearly polarized when passed through a Polaroid. [3]
(i) Unpolarised light of intensity Io is incident on a Polaroid Pi which is kept near another Polaroid P2 whose pass axis is parallel to that of P1. How will the intensities of light, I1 and I2, transmitted by the Polaroids P1 and P2 respectively, change on rotating P1 without disturbing P2 ?
(ii) Write the relation between the intensities I1 and I2.
Answer :
Polaroid filters are made of a special material that is capable of blocking of the two planes of vibration of an electromagnetic wave. In this sense, a polaroid acts as a device that filter out half of the vibrations on transmission of the light through the filter. When unpolarised light . is transmitted through a polaroid filter, it emerge with one-half the intensity and with vibrations in a single plane; it emerges as polarised light.
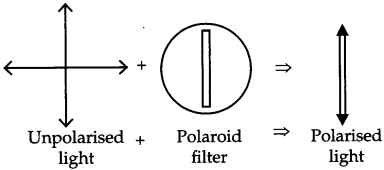
(i) When an unpolarised light of intensity I0 is incident on a polaroid P1 of the light intensity I1 will become half of the incident intensity.
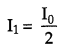
and when it will pass through P2 polaroid kept near P. whose pass axis is parallel to that of P, then, there is no change in the intensity but the angle will change by cos2 θ
![]()
(ii) The relation between I1 and I2 is given by
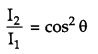
Question 14.
Define modulation index. Why is its value kept, in practice, less than one ?
A carrier wave of frequency 1.5 MHz and amplitude 50 V is modulated by a sinusoidal wave of frequency 10 kHz producing 50% amplitude modulation. Calculate the amplitude of the AM wave and frequencies of the side bands produced. [3]
Question 15.
A uniform magnetic field B is set up along the positive X-axis. A particle of charge ‘q’ and mass ‘m’ moving with a velocity v enters the field at the origin in X-Y plane such that it has velocity components both along and perpendicular to the magnetic field B. Trace, giving reason, the trajectory followed by the particle. Find out the expression for the distance moved by the particle along the magnetic field in one rotation. [3]
Answer :
If component vx of the velocity vector is along the magnetic field, and remain constant, the charge particle will follow a helical trajectory; as shown in figur.
If the velocity component vy is perpendicular to the magnetic field B, the magnetic force acts like a centripetal force qvy B.
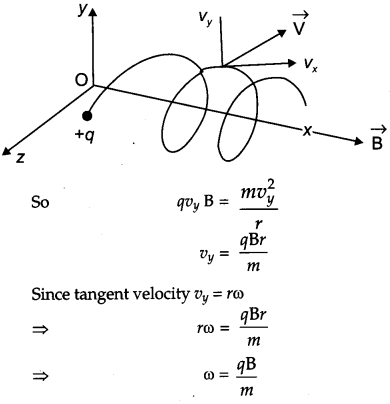

Question 16.
(a) Determine the value of phase difference between the current and the voltage in the given series LCR circuit.
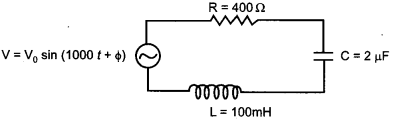
(b) Calculate the value of the additional capacitor which may be joined suitably to the capacitor C that would make the power factor of the circuit unity. [3]
(b) The power factor of the circuit is unity. It means that the given circuit is in resonance. It is possible, if another capacitor C is used in the circuit.

Question 17.
Write the expression for the generalized form of Ampere’s circuital law. Discuss its significance and describe briefly how the concept of displacement current is explained through charging/discharging of a capacitor in an electric circuit. [3]
Answer :
Generalized form of Ampere circuital law:
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_{0}\left(\mathrm{I}_{c}+\varepsilon_{o} \frac{d \phi}{d t}\right)\)
It signifies that the source of magnetic field is not just due to the conduction electric current due to flow of charge but also due to the time rate of change of electric field called displacement current.
During charging and discharging of a capacitor the electric field between the plates will change, because of which there will be a change of electric flux (displacement current) between the plates.
Question 18.
Use Huygens’s principle to show how a plane wavelength propagates from a denser to rarer medium. Hence verify Snell’s law of refraction. [3]
Answer:
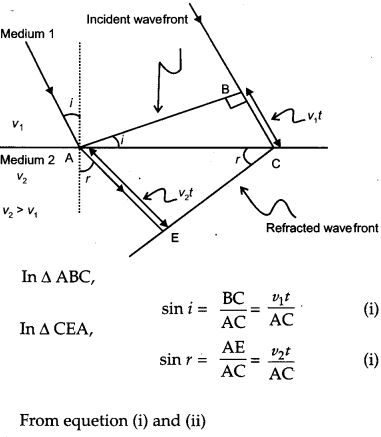
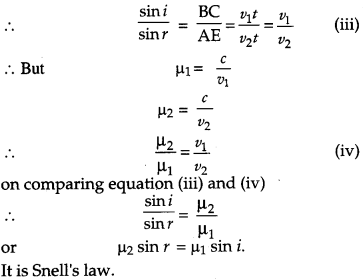
Question 19.
Identify the gates P and Q shown in the figure. Write file truth table for the combination of the gates shown.
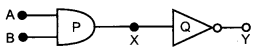
Name the equivalent gate representing this circuit and write its logic symbol. [3]
Question 20.
Draw a circuit diagram of a C.E. transistor amplifier. Briefly explain its working and write the expression for
(i) current gain,
(ii) voltage gain of the amplifier. [3]
Question 21.
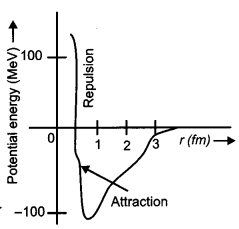
(a) Write three characteristic properties of nuclear force.
(b) Draw a plot of potential energy of a pair of nucleons as a function of their separation. Write two important conclusions that can be drawn from the graph. [3]
Answer :
(a) 1. Nuclear forces are short range forces;
2. Nuclear forces are primarily attractive and extremly strong;
3. Nuclear forces are charge independent.
(b)
Question 22.
(a) Describe briefly three experimentally observed features in the phenomenon of photoelectric effect.
(b) Discuss briefly how wave theory of light cannot explain these features. [3]
OR
(a) Write the important properties of photons which are used to establish Einstein’s photoelectric equation.
(b) Use this equation to explain the concept of
(i) threshold frequency and
(ii) stopping potential.
Answer :
(a) 1. The photoelectric effect will not occur when the frequency of the incident light is less than the threshold frequency. Different materials have different threshold frequencies and most elements have threshold frequencies in the ultraviolet region of the electromagnetic spectrum.
2. The maximum KE of a stream of photo electrons increases linearly with the frequency of the incident light above the threshold frequency.
3. The rate at which photo electrons are emitted from a photosensitive surface is directly proportional to the intensity of incident light when the frequency is constant.
(b) Classical wave theory cannot explain :
- The existence of threshold frequency because it predicts that electrons would absorb enough energy to escape and there would not be any threshold frequency.
- The almost immediate emission of photo electrons as, according to this theory, electrons require a period of time before sufficient energy is absorbed by it to escape from the metal; however, such a thing does not happen practically.
- It cannot explain why maximum KE is dependent on the frequency and independent of intensity.
OR
(a) The important property of photons that is useful in establishing Einstein’s photoelectric equation is their ability to
hold on to the electrons of an atom by their forces of attraction.
(b) Einstein’s photoelectric equation states that:

Section-D
Question 23.
One morning an old man walked bare-foot to replace the fuse wire in kit kat fitted with power supply mains for his house. Suddenly he screamed and collapsed on the floor. His wife cried loudly for help. His neighbor’s son Anil heard the cries and rushed to the place with shoes on. He took a wooden baton and used it to switch off the main supply. [4]
Answer the following questions:
(i) What is the voltage and frequency of mains supply in India ?
(ii) These days most of the electrical devices we use require a.c. voltage. Why ?
(iii) Can a transformer be used to step up d.c. voltage ?
(iv) Write two qualities displayed by Anil by his action.
Answer:
(i) The voltage and frequency of mains supply in India are 240 V and frequency is 50 Hz.
(ii) Most electrical devices require a.c. voltage because a.c. is available by default through the mains supply and also because d.c., is actually a one-way current and is available only through batteries.
(iii) No, a transformer cannot be used to step- up d.c. voltage because induced emf in the secondary coil of the transformer is only due to of change of magnetic flux in primary coil.
Section – E
Question 24.
(a) Define electric flux. Write its S.I. unit.
“Gauss’s law in electrostatics is true for any . closed surface, no matter what its shape or size is”. Justify this statement with the help of a suitable example.
(b) Use Gauss’s law to prove that electric field inside a uniformly charged spherical shell is zero. [5]
OR
(a) Derive the expression for the energy stored in a parallel plate capacitor. Hence obtain the expression for the energy density of the electric field.
(b) A fully charged parallel plate capacitor is connected across an uncharged identical capacitor. Show that the energy stored in the combination is less than that stored initially in the single capacitor.
Answer :
(a) The electric flux through an area is defined as the electric field multiplied by the area of the surface projected on a plane, perpendicular to the field. Its S.I. unit is voltmeter (Vm) or Newton meter square per coulomb (Nm2 C-1). The given statement is justified because while measuring the flux, the surface area is more important than its volume or its size.
(b) To prove that the electric field inside a uniformly charged spherical shell is zero, we place a single positive point charge ‘q’ at the center of an imaginary spherical surface with radius R. The field lines of this point radiate outside equally in all directions. The magnitude E of the electric field at every point on the surface
\(\text { is given by } \mathrm{E}=\frac{1}{4 \pi \varepsilon_{0}} \times \frac{q}{\mathrm{R}^{2}}\)
At each point on the surface, \(\vec{E}\) is ⊥ to the surface and its magnitude is the same.
Thus, the total electric flux (ΦE) is the product of their field magnitude E and the A.
Hence, \(\begin{aligned} \phi_{\mathrm{E}} &=\mathrm{EA} \\ &=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{\mathrm{R}^{2}}\left(4 \pi \varepsilon \mathrm{R}^{2}\right) \\ &=\frac{q}{\varepsilon_{0}} \end{aligned}\)
If the sphere is uniformly charged, then there is zero charge inside the sphere, according to Gauss’s law
When \(q=0, \phi_{\mathrm{E}}=\frac{0}{\varepsilon_{0}}=0\)
OR
(a) Consider a capacitor of capacitance C. Initial charge on capacitor is zero. Initial potential difference between capacitor plates is zero. Let a charge Q be given to it in small steps. When charge is given to capacitor, the potential difference between its plates increases. Let at any instant when charge on capacitor be q, the potential difference between its plates
\(\mathrm{v}=\frac{q}{\mathrm{c}}\)
Now work done in giving an additional infinitesimal charge dq to capacitor
\(d \mathrm{W}=\mathrm{V} d q=\frac{q}{\mathrm{C}} d q\)
The total work done in giving charge from 0 to Q will be equal to the sum of all such infinitesimal works, which may be obtained by integration. Therefore, total work done.

Energy density : Consider a parallel plate capacitor consisting of plates, each of area A, separated by a distance d. If space between the plates is filled with a medium of dielectric constant K, then

(b) Initially, if we consider a charged capacitor, then its charge would be Q = CV
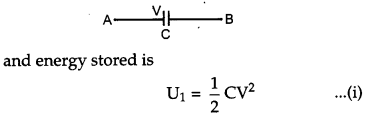
Then, this charged capacitor is connected to uncharged capacitor.
Let the common potential be V. The charge flows from first capacitor to the other capacitor unless both the capacitors attain common potential.
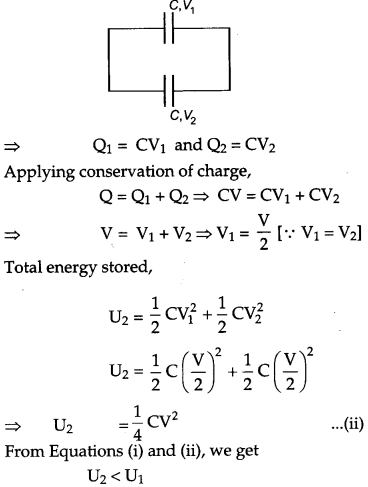
Question 25.
Explain, using a labelled diagram, the principle and working of a moving coil galvanometer. What is the function of
(i) uniform radial magnetic field,
(ii) soft iron core ?
Define the terms
(i) current sensitivity and
(ii) voltage sensitivity of a galvanometer. Why does increasing the current sensitivity not necessarily increase voltage sensitivity ? [5]
OR
(a) Write using Biot-Savart law, the expression for the magnetic field \(\overrightarrow{\mathbf{B}}\) due to an element \(\overrightarrow{\mathbf{dl}}\)carrying current I at a distance \(\overrightarrow{\mathbf{r}}\) from it in a vector form. Hence derive the expression for the magnetic field due to a current carrying loop of radius R at a point P distant X from its centre along the axis of the loop.
(b) Explain how Biot-Savart law enables one to express the Ampere’s circuital law in the integral form
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_{0} \mathrm{I}\)
Where I is the total current passing through the surface.
Answer :
The basic principle of a moving coil galvanometer is that when a current carrying coil is placed in a magnetic field, it experiences a torque.
When the current I is passed through the coil, the torque experienced is given by
T= NIAB sin θ
Where N = No. of turns of the coil,
A = Area of the coil
B = Magnetic field and
θ = Angle between normal of coil and magnetic field
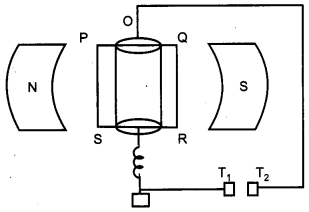
(i) The uniform radial magnetic field is used to make the scale linear.
(ii) The soft iron core increases the strength of the magnetic field.
The current sensitivity is defined as the deflection produced in the galvanometer, while passing a current of 1 ampere. (1 amp), through it
Thus, current sensitivity \(\left(\frac{\alpha}{\mathrm{I}}\right)=\frac{\mathrm{NBA}}{\mathrm{K}}\)
The voltage sensitivity is defined as the deflection produced in the galvanometer when a potential difference of IV is applied to the coil.
Thus, voltage sensitivity \(\left(\frac{\alpha}{\mathrm{V}}\right)=\frac{\mathrm{NBA}}{\mathrm{KR}}\)
Where R is the resistance.
Increasing the current sensitivity does not necessarily increase the voltage sensitivity as there is an increase in the resistance as well.
OR
a) Suppose we have a conductor of length l in which current i is flowing. We need to calculate the magnetic field at a point P in vacuum. If \(\overrightarrow{i d l}\) is one of the infinitely small current element, the magnetic field \(\overrightarrow{dB}\) at point P is given by
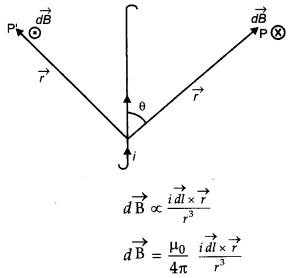
Where µ0/4π is a proportionality constant.
Suppose there is a circular coil of radius R carrying a current i. Let P be a point at the axis of the coil at a distance x from the centre, at which the field in required.
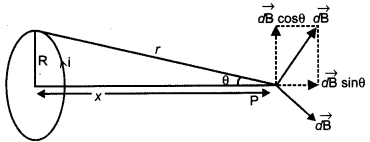
Consider a conducting element dl of the loop. The magnetic field due to dl is given by the Biot- Savart law,
\(\begin{array}{l}{d \mathrm{B}=\frac{\mu_{0}}{4 \pi} \frac{i|\vec{d}| \times \vec{r} |}{r^{3}}} \\ {d \mathrm{B}=\frac{\mu_{0}}{4 \pi} \frac{i d l}{\left(\mathrm{R}^{2}+x^{2}\right)}}\end{array}\)
The direction of dB is perpendicular to the plane formed by dl and r. It has an X-component dBx and a component perpendicular to X-axis, dB⊥y. When the components perpendicular to the X-axis are summed over, they cancel out and we obtain null result. Thus, only the X-component survives.
So the resultant field \(\overrightarrow{\mathbf{B}} \) at P in given by

Question 26.
(a) Consider two coherent sources S1 and S2 producing monochromatic waves to produce interference pattern. Let the displacement of the wave produced by S1 be given by Y1 = a cos ωt and the displacement by S2 be Y2 = a cos (ωt + Φ). Find out the expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be I = 4a2 cos2 Φ/2. Hence establish the conditions for constructive and destructive interference.
(b) What is the effect on the interference fringes in Young’s double slit experiment when
(i) the width of the source slit is increased;
(ii) the monochromatic source is replaced by a source of white light. [5]
OR
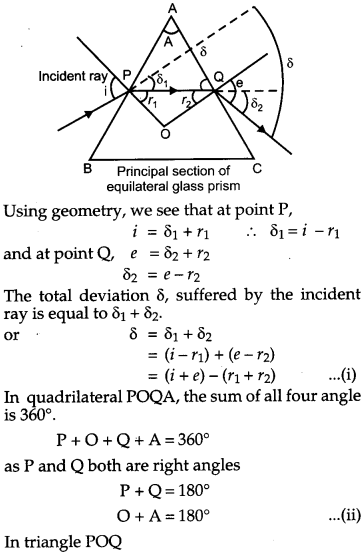
(a) A ray ‘PQ’ of light is incident on the face AB of a glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that ∠i + ∠e = ∠A + ∠δ . When δ and e denote the angle of deviation and angle of emergence respectively.
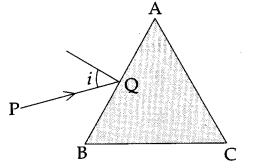
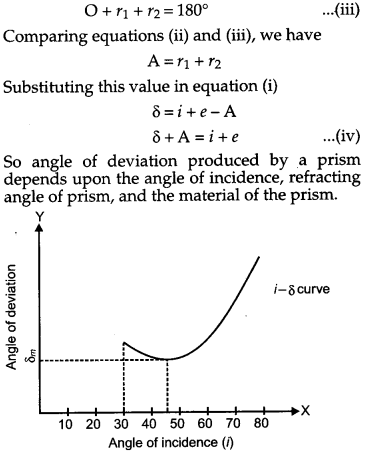
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. State the condition under which ∠δ is minimum.
(b) Find out the relation between the refractive index (μ) of the glass prism and ∠A for the case when the angle of prism (A) is equal to the angle of minimum deviation (δm). Hence obtain the value of the refractive index for angle of prism A = 60°.
Answer :
(a) Let S be a narrow slit illuminated by a monochromatic source of light and S1 and S2 two similar parallel slits very close together and equidistant from S.
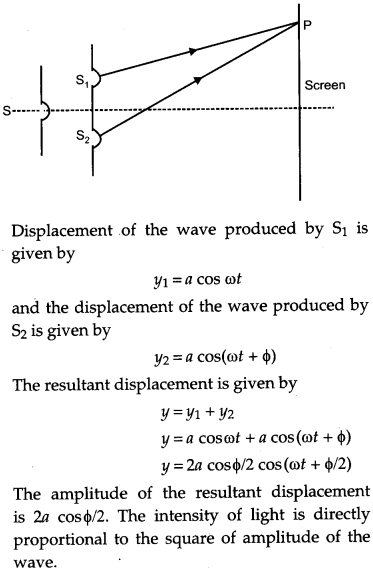


(ii) The different colors of white light will produce different interference patterns but the central bright fringes due to all colors are at the same positions. Therefore, the central bright fringe is white in color. Since the wavelength of the blue light is smallest, the fringe closed on the either side of the central white fringe is blue and farthest is red. Beyond a few fringes, no clear fringe pattern is visible.
OR
(a) Let the incident ray meet refracting face AB of the prism at point P. Ray PQ is the refracted ray inside the prism and δ2 and r1 are the angle of the deviation and refraction at interface AB. At interface AC the ray goes out of the prism. Let e be the angle of emergence. The angle of deviation at point Q is δ2 as shown in figure.

Note: All questions of Outside Delhi Set II are from Outside Delhi Setl and Outside Delhi Set III are from Set I and Set II.