CBSE Previous Year Question Papers Class 12 Physics 2015 Delhi
Section-A
Question 1.
Define capacitor reactance. Write its S.I. units. [1]
Answer :
Capacitor reactance is the resistance offered by a capacitor to the flow of a.c. It is given by

Question 2.
What is the electric flux through a cube of side 1 cm which encloses an electric dipole ? [1]
Answer:
The electric flux through a cube of side 1 cm which encloses an electric dipole will be zero, as net charge enclosed by a cube is zero.
Question 3.
A concave lens of refractive index 1.5 is immersed in a medium of refractive index 1.65. What is the nature of the lens ? [1]
Answer:
Since μg lens < μm surroundings. It behaves like a converging lens.
Question 4.
How are side bands produced ? [1]
Question 5.
Graph showing the variation of current versus voltage for a material Ga As is shown in the figure. Identify the region of: [1]
(i) negative resistance
(ii) where Ohm’s law is obeyed.
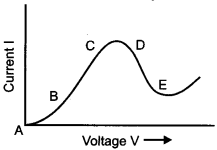
Answer:
(i) DE is the region of negative resistance because the slope of curve in this part is negative,
(ii) BC is the region where Ohm’s law is obeyed because in this part, the current varies linearly with the voltage.
Section-B
Question 6.
A proton and an a-particle have the same de-Broglie wavelength. Determine the ratio of
(i) their accelerating potentials
(ii) their speeds. [2]
Answer :
(i) The de-Broglie wavelength of a particle is given by


Question 7.
Show that the radius of the orbit in hydrogen atom varies as n2. Where n is the principal quantum number of the atom. [2]
Answer :
According to the Bohr’s theory of hydrogen atom, the angular momentum of a revolving electron is given by

Here, m = Mass of the electron
v = Velocity of the electron
r = Radius of the orbit
h = Planck’s constant
n = Principal quantum number of the atom
If an electron of mass m and velocity v is moving in a circular orbit of radius r, then the centripetal force required is given by
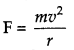
Also, if the charge on the nucleus is Ze, then the force of electrostatic attraction between the nucleus and the electron will provide the necessary centripetal force.

Question 8.
Distinguish between ‘intrinsic’ and ‘extrinsic’ semiconductors. [2]
Answer:
| Intrinsic semiconductor | Extrinsic semiconductor |
| 1. It is pure semiconducting material with no impurity atoms added to it. | 1. It is prepared by doping small quantity of impurity atoms to the pure semiconductor. |
| 2. The number of free electrons in the conduction band and the number of holes in valence band is exactly equal. | 2. The number of free electrons and holes is neve equal. There is an excess of electrons in n-type semiconductors and an excess of holes p-type semiconductors. |
| 3. Its electrical conductivity is a function of temperature alone. | 3. Its electrical conductivity depends upon the temperature and the amount of impurity added in them, to it. |
Question 9.
Use the mirror equation to show that an object placed between f and 2f of a concave mirror produces a real image beyond 2f. [2]
OR
Find an expression for intensity of transmitted light when a Polaroid sheet is rotated between two crossed Polaroids. In which position of the Polaroid sheet will the transmitted intensity be maximum ?
Answer:
mirror equation is
\(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Where u is the distance of object from the mirror, v is the distance of image from the mirror and f is the focal length of the mirror. For a concave mirror f is negative i.e. f < 0, u < 0 For a real object (on the left of mirror)
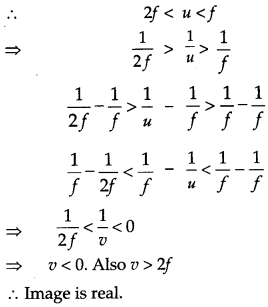
This implies that v is negative and greater than 2f This means that the image lies beyond 2f.
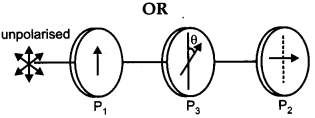
Let us consider two crossed polarisers P1 and P2 with a polaroid sheet P3 placed between them. Let I0 be the intensity of polarised light after passing through the first polarizer P1. If θ is the angle between the axes of P1 and P3, then the intensity of the polarized light after passing through P3 will be I = I0 cos2 θ .
As P1 and P2 are crossed. The angle between the axes of P1 and P2 = 90°.
Angle between the axes of P1 and P3 = (90° – θ) The intensity of light emerging from P2 will be given by

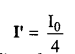
Question 10.
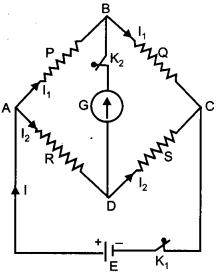
Use Kirchhoff’s rules to obtain conditions for the balance condition in a Wheatstone bridge. [2]
Answer :
Let us consider a Wheatstone bridge arrangement as shown below :
Wheatstone bridge is a special bridge type circuit which consists of four resistances, a galvanometer and a battery. It is used to determine unknown resistance.
In figure four resistance P, Q, R and S are connected in the form of four arms of a quadrilateral. Let the current given by battery in the balanced position be I. This current on reaching point A is divided into two parts I1 and I2 . As there is no current in galvanometer in balanced state, therefore, current in resistances P and Q is Ii and in resistances R and S it is I2 .

Section-C
Question 11.
Name the parts of the electromagnetic spectrum which is
(a) suitable for radar systems used in aircraft navigation
(b) used to treat muscular strain
(c) used as a diagnostic tool in medicine
Write in brief, how these waves can be produced.
Answer :
(a) Microwaves are suitable for radar systems that are used in aircraft navigation. These rays are produced by special vacuum tubes, namely klystrons, magnetrons and Gunn diodes.
(b) Infrared waves are used to treat muscular strain. These rays are produced by hot bodies and molecules.
(c) X-rays are used as a diagnostic tool in medicine. These rays are produced when high energy electrons are stopped suddenly on a metal of high atomic number.
Question 12.
(i) A giant refracting telescope has an objective lens of focal length 15 m. If an eye-piece of focal length 1.0 cm is used. What is the angular magnification of the telescope ?
(ii) If this telescope is used to view the moon. What is the diameter of the image of the moon formed by the objective lens ? The diameter of the moon is 3.48 x 106 m and the radius of lunar orbit is 3.8 x 108 m. [3]
Answer:
(i) Let
f0 = Focal length of the objective lens = 15 m = 1500 cm
fe = Focal length of the eye lens = 1.0 cm
Angular magnification of the giant refracting telescope is given by
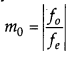

Question 13.
Write Einstein’s photoelectric equation and mention which important features in photoelectric effect can be explained with the help of this equation.
The maximum kinetic energy of the photo electrons gets doubled when the wavelength of light incident on the surface changes from λ1 to λ1. Derive the expressions for the threshold wavelength λ0 and work function for the metal surface. [3]
Answer :
Einstein’s photoelectric equation is given by

- If v < v0, then the maximum kinetic energy is negative, which is impossible. Hence, photoelectric emission does not take place for the incident radiation below the threshold frequency. Thus, the photoelectric emission can take place if v > v0.
- The maximum kinetic energy of emitted photo electrons is directly proportional to the frequency of the incident radiation. This means that maximum kinetic energy of photo electron depends only on the frequency of incident light not on the intensity According to the photoelectric equation,
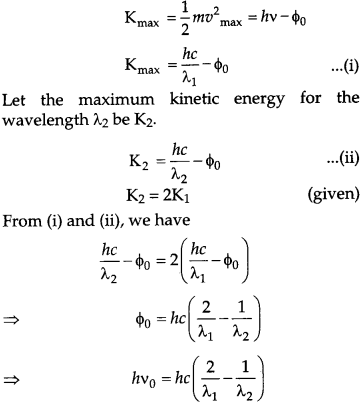
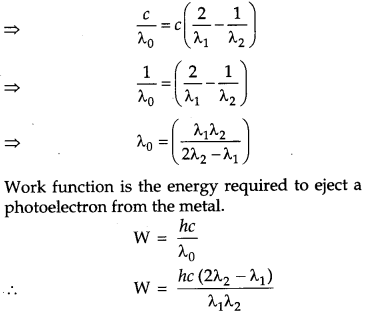
Question 14.
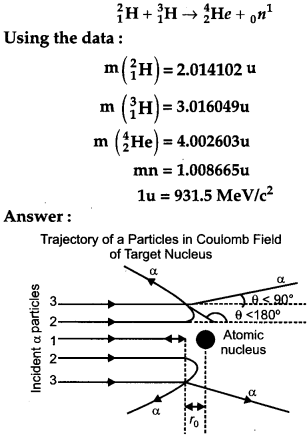
In the study of Geiger-Marsdon experiment on scattering of α-particles by a thin foil of gold, draw the trajectory of α-particles in the Coulomb field of target nucleus. Explain briefly how one gets the information on the size of the nucleus from this study.
From the relation R = R0 A1/3, where R0 is constant and A is the mass number of the nucleus, show that nuclear matter density is independent of A. [3]
OR
Distinguish between nuclear fission and fusion. Show how in both these processes energy is released. Calculate the energy release in MeV in the deuterium-tritium fusion reaction:
From this experiment, the following is observed:
- Most of the alpha particles pass straight through the gold foil. It means that they do not suffer any collision with gold atoms.
- About one alpha particle in every 8000 alpha particles deflects by more than 90°.As most of the alpha particles go undeflected and only a few get deflected, this shows that most of the space in an atom is empty and at the center of the atom, there exists a nucleus. By the number of the alpha particles deflected, the information regarding size of the nucleus can be known.
If m is the average mass of a nucleon and R is the nuclear radius, then mass of nucleus = mA, where A is the mass number of the element

![]()
This shows that the nuclear density is independent of A.
OR
Nuclear fission: Nuclear fission is a disintegration process, in which a heavier nucleus gets split up into two lighter nuclei, with the release of a large amount of energy.
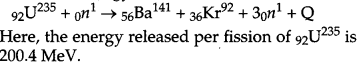
Nuclear fusion : When two or more light nuclei combine to form a heavy stable nuclide, part of mass disappears in the process and is converted into energy. This phenomenon is called nuclear fusion.

Question 15.
Draw a block diagram of a detector for AM signal and show, using necessary processes and the wave forms, how the original message signal is detected from the input AM wave. [3]
Answer:
Question 16.
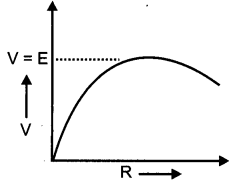
A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable load resistor R. Draw the plots of the terminal voltage V versus
(i) R and
(ii) the current i.
It is found that when R = 4Ω the current is 1 A when R is increased to 9 Ω, the current reduces to 0.5 A. Find the values of the emf E and internal resistance r. [3]
Answer:
(i) Graph between terminal voltage (V) and resistance (R):
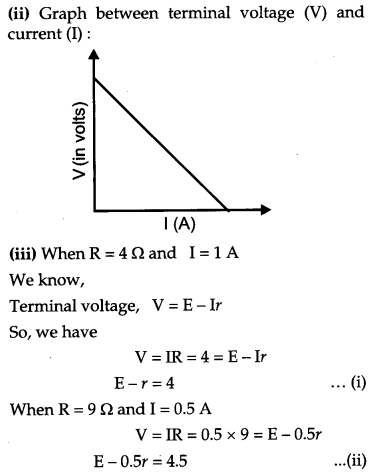
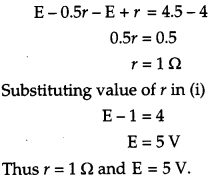
Question 17.
Two capacitors of unknown capacitance’s C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also calculate the charge on each capacitor in parallel combination. [3]
Answer :
When the capacitors are connected in parallel.

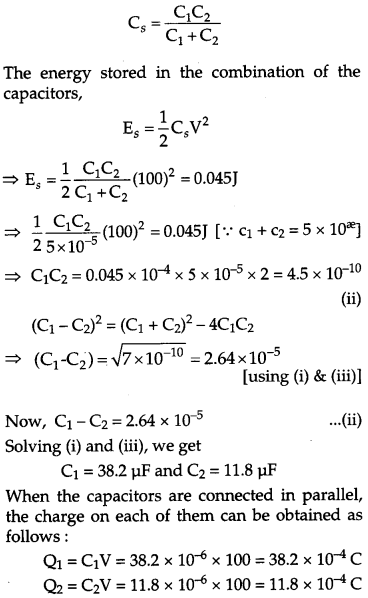
Question 18.
State the principle of working of a galvanometer. A galvanometer of resistance G is converted into a voltmeter to measure upto V volts by connecting a resistance R1 in series with the coil. If a resistance R2 is connected in series with it, then it can measure up to V/2 volts. Find the resistance, in terms of R1 and R2, required to be connected to convert it into a voltmeter that can read up to 2 V. Also find the resistance G of the galvanometer in terms of R1 and R2. [3]
Answer :
Principle : When a current-carrying coil is placed in a magnetic field, it experiences a torque. From the measurement of the deflection of the coil, the strength of the current can be computed. A high resistance is connected in series with the galvanometer to convert it into voltmeter. The value of the resistance is given by


Question 19.
With what considerations in view, a photo diode is fabricated ? State its working with the help of a suitable diagram.
Even though the current in the forward bias is known to be more than in the reverse bias, yet the photo diode works in reverse bias. What is the reason ? [3]
Answer :
A photo diode is used to observe the change in current with change in the light intensity under reverse bias condition.
In fabrication of photo diode, material chosen should have band gap -1.5 eV or lower so that solar conversion efficiency is better. This is the reason to choose Si or GaAs material.
Working : It is a p-n junction fabricated with a transparent window to allow light photons to fall on it. These photons generate electron hole pairs upon absorption. If the junction is reverse biased using an electrical circuit, these electron hole pair move in opposite directions so as to produce current in the circuit. This current is very small and is detected by the micro ammeter placed in the circuit.
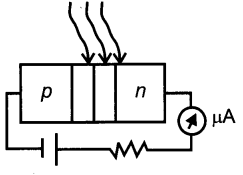
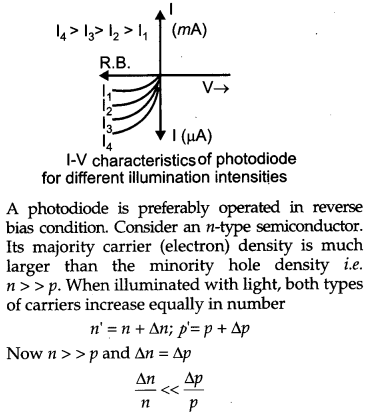
That is, the fractional increase in majority carriers is much less than the fractional increase in minority carriers. Consequently, the fractional change due to the photo-effects on the minority carrier dominated reverse bias current is more easily measurable than the fractional change in the majority carrier dominated forward bias current. Hence, photo diodes are preferably used in the reverse bias condition for measuring light intensity.
Question 20.
Draw a circuit diagram of a transistor amplifier in CE configuration.
Define the terms:
(i) Input resistance and
(ii) Current amplification factor. How are these determined using typical input and output characteristics? [3]
Question 21.
Answer the following questions : [3]
(a) In a double slit experiment using light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
(b) Light of wavelength 5000 A propagating in air gets partly reflected from the surface of water. How will the wavelengths and frequencies of the reflected and refracted light be affected ?
Answer :
(a) Angular width (θ) of fringe in
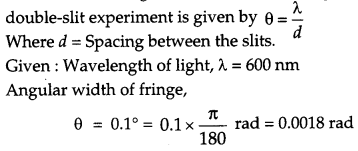

Question 22.
An inductor L of inductance XL is connected in series with a bulb B and an ac source. How would brightness of the bulb change when
(i) number of turn in the inductor is reduced.
(ii) an iron rod is inserted in the inductor and
(iii) a capacitor of reactance XC = XL is inserted in series in the circuit. Justify your answer in each case. [3]
Answer:
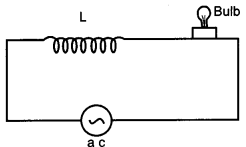
(i) When the number of turns in the inductor is reduced, its reactance XL decreases. The current in the circuit increases and hence brightness of the bulb increases.
(ii) When an iron rod is inserted in the inductor, the self inductance increases. Consequently, the inductive reactance XL = ωL increases. This decreases the current in the circuit and the bulb glows dimmer.
(iii) With capacitor of reactance XC=XL, the impedance
\(Z=\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}=R\)
becomes minimum, the current in circuit becomes maximum. Hence, the bulb glows with maximum brightness.
Section-D
Question 23.
A group of students while coming from the school noticed a box marked “Danger H.T. 2200 V” at a substation in the main street. They did not understand the utility of such a high voltage, while they argued the supply was only 220 V. They asked their teacher this question the next day. The teacher thought it to be an important question and therefore, explained to the whole class. [4]
Answer the following questions:
(i) What device is used to bring the high voltage down to low voltage of a.c. current and what is the principle of its working ?
(ii) Is it possible to use this device for bringing down the high dc voltage to the low voltage? Explain.
(iii) Write the values displayed by the students and the teacher.
Answer:
(i) The device that is used to bring high voltage down to low voltage of an a.c. current is a transformer. It works on the principle of mutual induction of two winding’s or circuits. When current in one circuit changes, emf is induced in the neighboring circuit.
(ii) The transformer cannot convert d.c. voltages because it works on the principle of mutual induction. When the current linked with the primary coil changes the magnetic flux linked with the secondary coil also changes. This change in flux induces emf in the secondary coil. If we apply a direct current to the primary coil the current will remain constant. Thus, there is no mutual induction and hence no emf is induced.
Section-E
Question 24.
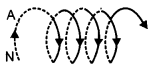
(a) State Ampere’s circuital law. Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius, having ‘n’ turns per unit length and carrying a steady current I.
(b) An observer to the left of a solenoid of N turns each of cross section area A observes that a steady current I in it flows in the clockwise direction. Depict the magnetic field lines due to the solenoid specifying its polarity and show that it acts as a bar magnet of magnetic momentum M = NIA. [5]
OR
(a) Define mutual inductance and write its S.I. units.
(b) Derive an expression for the mutual inductance of two long co-axial solenoids of same length wound one over the other
(c) In an experiment two coils C1 and C2 are placed close to each other. Find out the expression for the emf induced in the coil C1 due to a change in the current through the coil C2.
Answer :
(a) Ampere’s circuital law in electromagnetism is analogous to Gauss’ law in electrostatics. This law states that “The line integral of resultant. magnetic field along a closed plane curve is equal to μ0 time the total current crossing the area bounded by the closed curve provided the electric field inside the loop
remains constant. Thus \(\oint B . d l=\mu_{0} \mathrm{I}_{e n c}\) where μ0 is permeability of free space and Ienc is the net current enclosed by the loop. A toroid is a hollow circular ring on which a large number of turns of a wire are closely wound. Consider an air-cored toroid (as shown below) with center O.
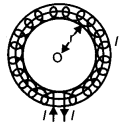
Given :
r = Average radius of the toroid
I = Current through the solenoid
n = Number of turns per unit length
To determine the magnetic field inside the toroid, we consider three amperian loops (loop 1, loop 2 and loop 3) as shown in the figure below.
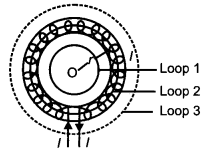
According to Ampere’s circuital law, we have
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_{0} \mathrm{I}_{\mathrm{enc.}}(\text { Total current })\)
Total current for loop 1 is zero because no current is passing through this loop
So, for loop 1
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_{0}(\text { Total current })\)
For loop 3
According to Ampere’s circuital law, we have
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_{0}(\text { Total current })\)
Total current for loop 3 is zero because net current coming out of this loop is equal to the net current going inside the loop.
For loop 2:

This is the expression for magnetic field inside air-cored toroid.
(b) Given that the current flows in the clockwise direction for an observer on the left side of the solenoid. This means that left face of the solenoid acts as south pole and right face acts as north pole. Inside a bar magnet the magnetic field lines are directed from south to north. Therefore, the magnetic field lines are directed from left to right in the solenoid.
Magnetic moment of single current carrying loop is given by m = IA
where
I = Current flowing through the loop
A = Area of the loop
So, Magnetic moment of the whole solenoid is given by
M = Nm = N(IA)
OR
(a) Mutual inductance is the property of two coils by the virtue of which each opposes any change in the value of current flowing through the other by developing an induced emf. The SI unit of mutual inductance is henry and its symbol is H.
(b) Consider two long solenoids S1 and S2 of same length l such that solenoid S2 surrounds solenoid S1 completely.
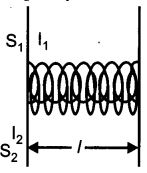
Let:
n1 = Number of turns per unit length of S1
n2 = Number of turns per unit length of S2
I1 = Current passed through solenoid S1
Φ21 = Flux linked with S2 due to current flowing through S1
Φ21 ∝ I1
Φ21 = M21I1
where M21 = Coefficient of mutual induction of the two solenoids .
When current is passed through solenoid S1, an emf is induced in solenoid S2.
Magnetic field produced inside solenoid S1 on passing current through it is given by
B1 = μ0n1I1
Magnetic flux linked with each turn of solenoid S2 will be equal to B1 times the area of cross section of solenoid S1.
Magnetic flux linked with each turn of the solenoid Φ21 = B1A .
Therefore, total magnetic flux linked with the solenoid S2 is given by
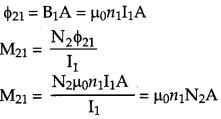
where N2 is total number of turns wound over the secondary coil.
∴ M21 = μ0n1N2A
Similarly the mutual inductance between the two solenoids when current is passed through solenoid S2 and induced emf is produced in solenoid Si is given by
M12 = μ0N1n2A
where N1 total numbers of turns wound over primary coil.
(c) It is found that,
Φ ∝I
Φ = MI
Where, I is the strength of current in coil 2, and Φ is the total amount of magnetic flux linked with coil 1.
E.m.f. induced in neighbouring coil C1 is,
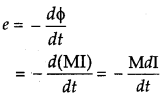
Question 25.
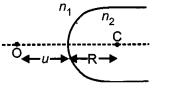
(a) A point object ‘O’ is kept in a medium of refractive index n in front of a convex spherical surface of radius of curvature R which separate the second medium of refractive index n2 from the first one as shown in the figure. Draw the ray diagram showing the image formation and deduce the relationship between the object distance and the image distance in terms of n1, n2 and R.
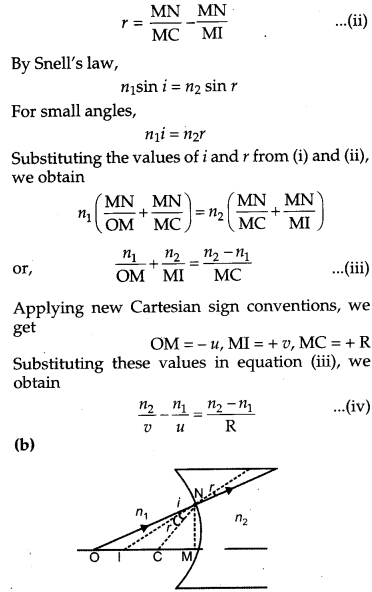
(b) When the image formed above acts as a virtual object for a concave spherical surface separating the medium n2 from n1 (n2 > n1) draw this ray diagram and write the similar (similar to (a)) relation. Hence obtain the expression for the Lens Maker’s formula. [5]
Answer :
(a) Let a spherical surface separate a rarer medium of refractive index n1 from second medium of refractive index n2. Let C be the centre of curvature and R = MC be the radius of the surface.
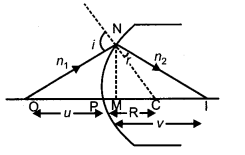
Consider a point object O lying on the principal axis of the surface. Let a ray starting from O incident normally on the surface along OM and pass straight. Let another ray of light incident on NM along ON and refract along NI.
From M, draw MN perpendicular to OI.
The above figure shows the geometry of formation of image I of an object O and the principal axis of a spherical surface with centre of curvature C and radius of curvature R.
Let us make the following assumptions :
- The aperture of the surface is small as compared to the other distance involved.
- The object consists only of a point lying on the principal axis of the spherical refracting surface


Question 26.
(a) An electric dipole of dipole moment \(\vec{p}\) consists of point charges +q arid – q separated by a distance 2a apart. deduce the . expression for the electric field \(\vec{E}\) due to the dipole at a distance x from the centre of the dipole on its axial line in terms of the dipole moment \(\vec{p}\). Hence show that in the limit
\(x>>a, \overrightarrow{\mathrm{E}} \rightarrow \frac{2 \overrightarrow{\mathrm{p}}}{4 \pi \varepsilon_{0} x^{3}}\)
(b) Given the electric field in the region \(\overset { \rightarrow }{ E } =2\overset { \wedge }{ x } l\), find the net electric flux through the cube and the charge enclosed by it. [5]
OR
(a) Explain, using suitable diagrams, the difference in the behavior of a
(i) conductor and
(ii) dielectric in the presence of external electric field.
Define the terms polarization of a dielectric and write its relation with susceptibility.
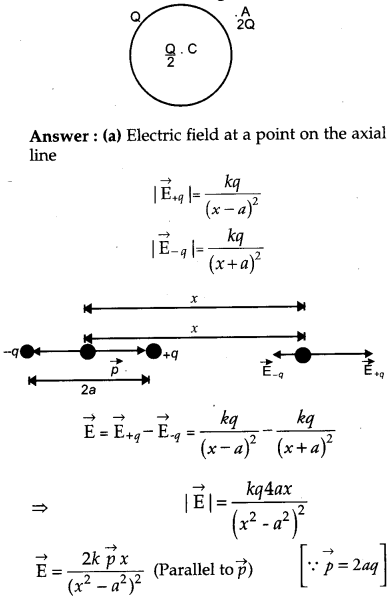
(b) A thin metallic spherical shell of radius carries a charge Q on its surface. A point
charge Q/2 is placed at its center C and another charge +2Q is placed outside the shell at a distance x from the center as shown in the figure. Find
(i) the force on the charge at the center of shell and at the point A,
(ii) the electric flux through the shell.

OR
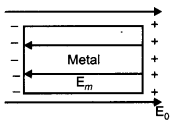
(a) (i) Conductor:
Let E0 = external field, and
Em= internal field created by the redistribution of electrons inside the metal.
When a conductor like a metal is subjected to external electric field, the electrons experience a force in the opposite direction collecting on the left hand side.
A positive charge is therefore induced on the right hand side. This creates an opposite electric field (Em) that balances out (E0).
.’. The net electric field inside the conductor becomes zero.
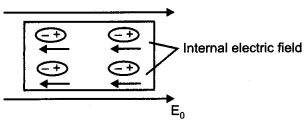
When an external electric field is applied, dipoles are created (in case of non-polar dielectrics). The placement of dipoles is as shown in the given figure. An internal electric field is created which reduces the external electric field.
Polarization of dielectric (P) is defined as the dipole moment per unit volume of the polarized dielectric.

Note: All questions of Delhi Set 11 are from Delhi Set I and Delhi Set III are from Set I and Set 11.