CBSE Previous Year Question Papers Class 12 Physics 2013 Outside Delhi
CBSE Previous Year Question Papers Class 12 Physics 2013 Outside Delhi Set-I
Question 1.
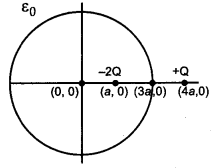
Two charges of magnitudes -2Q and +Q are located at point (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its center at the origin ?
Answer:
Gauss’s theorem states that the electric flux through a closed surface enclosing a charge
is equal to \(\frac{1}{\varepsilon_{0}}\) times the magnitude of the charge enclosed. The sphere encloses a charge of -2Q thus \(\phi=\frac{2 \mathrm{Q}}{\varepsilon_{0}}\)
Question 2.
How does the mutual inductance of a pairs of coils change when
(i) distance between the coils is increased and
(ii) number of turns in the coils is increased ? [1]
Answer :
(i) As Φ = MI, with the increase in the distance between the coils, the magnetic flux linked with the stationary coil decreases and hence the mutual inductance of the two coils will decrease.
(ii) Mutual inductance of two coils can be found out by
M = μ0 n1 n2 AI
i.e., M ∝ n1 n2 so with the increase in number of turns, mutual inductance increases. turns mutual inductance increases.
Question 3.
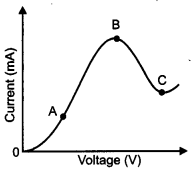
The graph shown in the figure represents a plot of current versus voltage for given semiconductor. Identify the region, if any, over which the semiconductor has a negative resistance. [1]
Answer :
Resistance of a material can be found out by the slope of the V-I curve. Part BC of the curve shows the negative resistance as with the increase in voltage, current decreases.
Question 4.
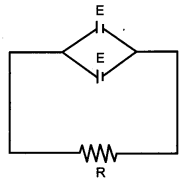
Two identical cells, each of emf E , having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance ? [1]
Answer :
The cells are arranged as shown in the circuit diagram. As the internal resistance is negligible,
so total resistance of the circuit = R.
So, current through the resistance, I = E/R.
Question 5.
The motion of copper plate is damped when it is allowed to oscillate between the two poles of a magnet. What is the cause of this damping ? [1]
Answer :
As the copper plates oscillate in the magnetic field between the two poles of the magnet, there is a continuous change of magnetic flux linked with the copper plate. Due to this, eddy currents are set up in the copper plate which try to oppose the motion of the plate according to the Lenz’s law and finally bring it to rest.
Question 6.
Define the activity of a given radioactive substance. Write its S.I. unit. [1]
Answer :
Activity of a radioactive substance is defined as number of radioactive disintegrations taking place in one second in the sample.
S. I. unit of activity is Becquerel (Bq).
1 Becquerel = 1 Bq = 1 decay per second.
Question 7.
Welders wear special goggles or face masks with glass windows to protect their eyes from electromagnetic radiations. Name the radiations and write the range of their frequency. [1]
Answer:
Welders wear special goggles with glass windows to protect the eyes from ultraviolet rays (UV rays). The range of frequency of UV rays is 8 x 1014 Hz to 3 x 1016 Hz.
Question 8.
Write the expression for the de-Broglie wavelength associated with a charged particle having charge ‘q’ and mass ‘m’, when it is accelerated by a potential V. [1]
Answer:
Let v be the velocity gained by the given charge particle when it is accelerated through a potential difference of ‘V’ volts.
Kinetic energy of the particle \(=\frac{1}{2} m v^{2}\)
Kinetic energy of the particle = Work done on the particle by electric field.
\(\begin{aligned} \therefore \quad \frac{1}{2} m v^{2} &=q \mathrm{V} \\ \frac{p^{2}}{2 m} &=q \mathrm{V} \\ p &=\sqrt{2 m q \mathrm{V}} \end{aligned}\)
de-Broglie wavelength (λ,) associated with the particle,
\(\lambda=\frac{h}{p}=\frac{h}{\sqrt{2 m q V}}\)
Question 9.
Draw a typical output characteristics of an n-p-n transistor in CE configuration. Show how these characteristics can be used to determine output resistance. [1]
Question 10.
A parallel beam of light of 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is at a distance of 2.5 mm from the center of the screen. Calculate the width of the slit. [5]
Answer :
The distance of the nth minimum from the center of the screen is, \(x_{n}=\frac{n \mathrm{D} \lambda}{a}\)
Where, D = distance of slit from screen = 1 m
λ = wavelength of the light = 500 x 10-9 m
a = width of the slit
For first minimum, n = 1
Thus, \(\begin{aligned} 2.5 \times 10^{-3} &=\frac{1(1)\left(500 \times 10^{-9}\right)}{a} \\ a &=2 \times 10^{-4} \mathrm{m} \\ a &=0.2 \mathrm{mm} \end{aligned}\)
Question 11.
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor. [2]
Answer:
Initially when there is vacuum between the two plates, the capacitance of the two parallel plate is
\(\mathrm{C}_{0}=\frac{\varepsilon_{0} \mathrm{A}}{d}\)
Where, A is the area of parallel plates.
Suppose that the capacitor is connected to a battery, an electric field Eo is produced.
Now, if we insert the dielectric slab of thickness
t = d/2 the electric field reduces to E.
Now, the gap between plates is divided in two parts, for distance t there is electric field E and for the remaining distance (d -t) the electric field is E0
If V is the potential difference between the plates of the capacitor, then V = Et + E0 (d-t).
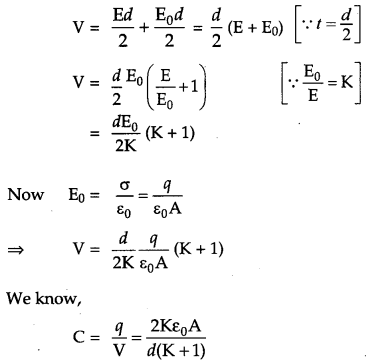
Question 12.
A capacitor, made of two parallel plates each of plate area A and separation d, being charged by an external ac source. Show that the displacement current inside the capacitor is same as the current charging the capacitor. [2]
Answer :
Let the alternating emf charging the plates of capacitor be E = E0 sin ωt.
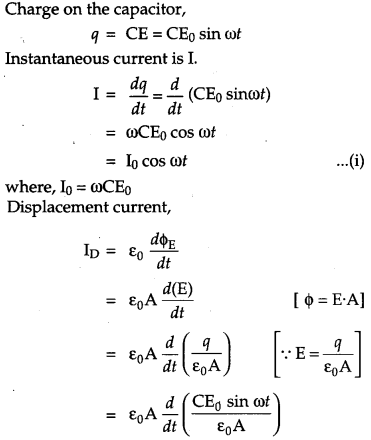

From equations (i) and (ii), the displacement current inside the capacitor is same as the current charging the capacitor.
Question 13.
Explain the term ‘drift velocity’ of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’. [3]
OR
Describe briefly, with the help of a circuit diagram, how a potentiometer is used to determine the internal resistance of a cell.
Answer :
Drift velocity of electrons in a conductor : Metals contain a large number of free electrons. These electrons are in continuous random motion. Due to the random motion, the free electrons collide with positive metal ions with high frequency and undergo change in direction at each collision. So the average velocity for the electrons in a conductor is zero. Now, when this conductor is connected to a source of emf, an electric field is established in the conductor, such that
\(\mathrm{E}=\frac{\mathrm{V}}{\mathrm{L}}\)
Where, V = potential difference across the conductor and,
L = length of the conductor.
The electric field exerts an electrostatic force ‘-Ee’ on each free electron in the conductor. The acceleration of each electron is given by
\(\vec{a}=-\frac{e \overrightarrow{\mathrm{E}}}{m}\)
Where, e = electric charge on the electron and
m = mass of electron.
The negative sign indicates the force and hence the acceleration is in a direction opposite to the direction of the electric field. Due to this acceleration, the electrons attain a velocity in addition to thermal velocity in the direction opposite to that of electric field. The average velocity of all the free electrons in the conductor is called the drift velocity of free electrons of the conductor.
Thus, the expression for the drift velocity in electric field (E)
\(\vec{v}=\frac{e \overrightarrow{\mathrm{E}}}{m} \tau\) ………. (i)
Where T= relaxation time between two successive collision,
Let n = number density of electrons in the conductor.
No. of free electrons in the conductor = nALe
Total charge on the conductor, q = nALe. Time taken by this charge to cover the length L of the conductor,
\(\begin{aligned} t &=\frac{\mathrm{L}}{v_{d}} \\ \text { Current } \quad & \mathrm{I}=\frac{q}{t} \\ &=\frac{n \mathrm{AL} e}{\mathrm{L}} \times v_{d} \\ &=n \mathrm{Aev}_{d} \end{aligned}\)
OR
Measurement of internal resistance of a cell using potentiometer is shown in figure. The cell of emf, E is connected across a resistance box (R) through key K2 .
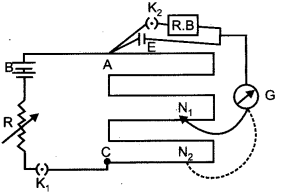
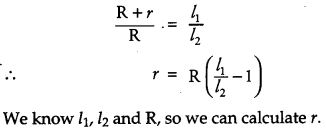
Question 14.
A convex lens of focal length f1 is kept in contact with a concave lens of focal length f2 . Find the focal length of the combination. [2]
Answer:
For convex lens, focal length, f = f1 and for concave lens, the focal length,f= – f2
The equivalent focal length of a combination of convex lens and concave lens is given as :
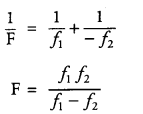
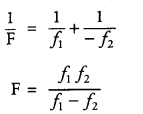
Question 15.
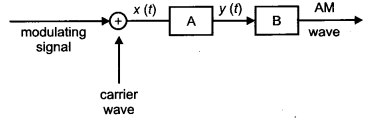
In the block diagram of a simple modulator for obtaining an AM signal, shown in the figure, identify the boxes A and B. Write their functions. [2]
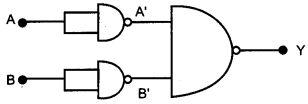
Question 16.
In the circuit shown in the figure, identify the equivalent gate of the circuit and make its truth table. [2]
Question 17.
(a) For a given a.c., i = im sin ωt show that the average power dissipated in a resistor R over a complete cycle is
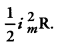
(b) A light bulb is rated at 100 W for a 220 V a.c. supply. Calculate the resistance of the bulb. [2]
Answer:
(a) The average power dissipated
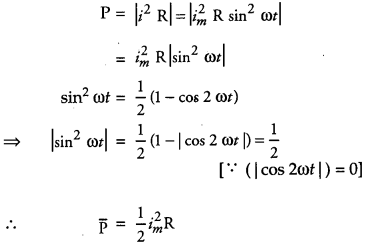
(b) Power of the bulb, P = 100 W and voltage, V= 220 V.
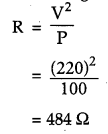
Question 18.
A rectangular conductor LMbfO is placed in a uniform magnetic field of 0.5 T. The field is directed perpendicular to the plane of the conductor. When the arm MN of length of 20 cm is moved towards left with a velocity of 10 ms-1, calculate the emf induced in the arm. Given the resistance of the arm to be 5 Ω (assuming that other arms are of negligible resistance) find the value of the current in the arm. [2]
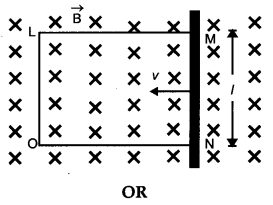
A wheel with 8 metallic spokes each 50 cm long is rotated with a speed of 120 rev/min in a plane normal to the horizontal component of the Earth’s magnetic field. The Earth’s magnetic field at the place is 0.4 G and the angle of dip is 60°. Calculate the emf induced between the axle and the rim of the wheel. How will the value of emf be affected if the number of spokes were increased ?
Answer:
Let ON be x at same instant the emf induced in the loop = e.
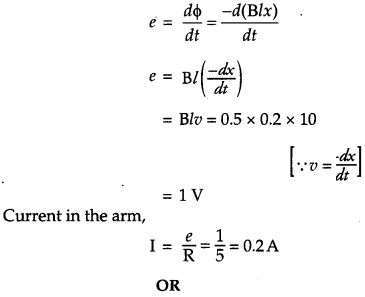

The value of emf induced is independent of the number of spokes as the emf across the spokes are in parallel. So, the emf will be unaffected with the increase in spokes.
Question 19.
Define the current sensitivity of a galvanometer. Write S.I. unit. Figure shows two circuits each having a galvanometer and a battery of 3 V. When the galvanometers in each arrangement do not show any deflection, obtain the ratio R1/R2. [2]
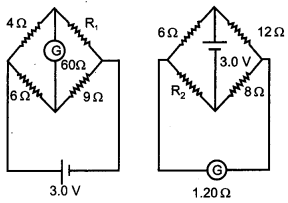
Answer :
Current sensitivity of a galvanometer is defined as the deflection in galvanometer per unit current. Its SI unit is radians/ampere.
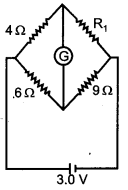
For balanced Wheatstone bridge, there will. _ no deflection in the galvanometer.
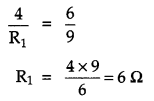
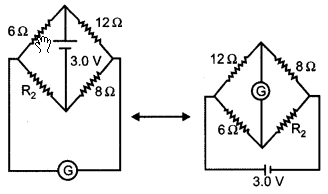
For the equivalent circuit, when the Wheatstone bridge is balanced, there will be no deflection in the galvanometer.
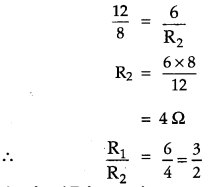
Question 20.
A wire AB is carrying a steady current 12 A and is lying on the table. Another wire CD carrying 5 A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms-2]. [2]
Answer :
Force per unit length between the current carrying wires is given as :
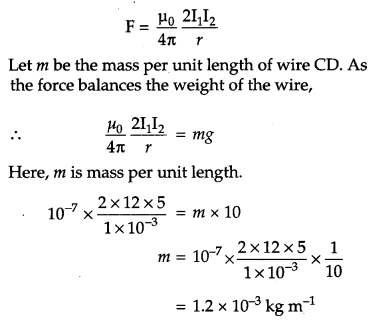
The direction of current in CD is opposite to the direction of current AB. because in this they will repel each other and CD will remain suspended.
Question 21.
Draw V-I characteristics of a p-n junction diode. Answer the following questions, giving reasons:
(i) Why is the current under reverse bias almost independent of the applied potential up to a critical voltage ?
(ii) Why does the reverse current show a sudden increase at the critical voltage ?
Name any semiconductor device which operates under the reverse bias in the breakdown region. [3]
Answer:
V-I characteristics of p-n junction diode:
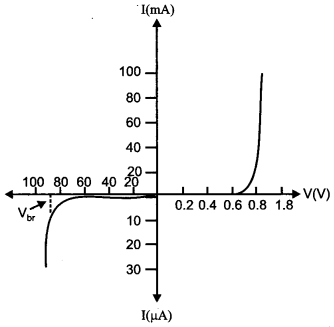
(i) Under the reverse bias condition, the holes of p-side are attracted towards the negative terminal of the battery and the electrons of the n-side are attracted towards the positive terminal of the battery. This increases the depletion layer and the potential barrier. However the minority charge carriers are drifted across the junction producing a small current. At any temperature the number of minority carriers is constant and very small so there is the small current at any applied potential. This is the reason for the current under reverse bias to be almost independent of applied potential. At the critical voltage, avalanche break down takes place which results in a sudden flow of large current.
(ii) At the critical voltage, the holes in the n-side and conduction electrons in the p-side are accelerated due to the reverse-bias voltage. These minority carriers acquire sufficient kinetic energy from the electric field and collide with valence electrons. Thus, the bond is finally broken and the valence electrons move into the conduction band resulting in enormous flow of electrons and thus result in formation of hole-electron pairs. Thus, there is a sudden increase in the current at the critical voltage.
Zener diode is a semiconductor device which operates under the reverse bias condition in the breakdown region.
Question 22.
Draw a labelled ray diagram of a refracting telescope. Define its magnifying power and write the expression for it.
Write two important limitations of a refracting telescope over a reflecting type telescope. [3]
Answer:
Refracting telescope :
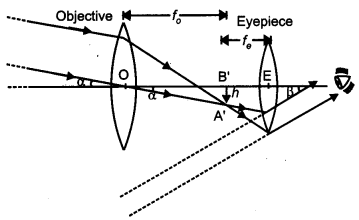
Magnifying power : The magnifying power is the ratio of the angle (3 subtended at the eye by the final image to the angle a which the object subtends at the lens or the eye.
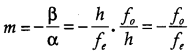
Limitations of refracting telescope over reflecting type telescope:
(i) Refracting telescope suffers from chromatic aberration as it uses large sized lenses.
(ii) The requirement of big lenses tend to be very heavy and therefore, difficult to make and support by their edges.
Question 23.
Write Einstein’s photoelectric equation and point out any two characteristic properties of photons on which this equation is based.
Briefly explain the three observed features which can be explained by this equation. [4]
Answer:
Einstein’s photoelectric effect equation:
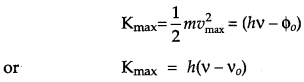
The two characteristics properties of the photon on which this equation is based :
(i) The light travel in the form of photons i.e. small packet of enery and each photon has energy hv.
(ii) Each photon interact with one electron. Three observed features that can be explained by this equation.
(i) When v < v0, Kmax becomes negative. The negative value of K./E. has no physical significance. Hence, no photoelectric effect is possible below there shold frequency.
(ii) When v > v0/ Kmax ∝ v, i.e. max. K.E. of the emitted photo electrons depends linearly on the frequency of incident radiations.
(iii) It is clear from the photoelectric equation that the maximum K.E. of photo electrons is independent of intensity of incident reactions.
Question 24.
Name the type of waves which are used for line of sight (LOS) communication. What is the range of their frequencies ?
A transmitting antenna at the top of a tower has a height of 20 m and the height of the receiving antenna is 45 m. Calculate the maximum distance between them for satisfactory communication in LOS mode. (Radius of the Earth = 6.4 x 106m) [5]
Question 25.
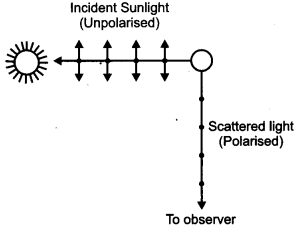
(a) What is linearly polarized light. Describe briefly using a diagram how sunlight is polarized.
(b) Unpolarised light is incident on a Polaroid. How would the intensity of transmitted light change when the Polaroid is rotated ? [5]
Answer:
(a) The light in which the vibrations of electric vector are restricted to a particular plane, is called plane polarized light.
The incident sunlight is unpolarised. The dot and double arrows show the polarization in the perpendicular and in the plane of the figure respectively. Under the influence of the electric field of the incident wave, the electrons in the molecules of the atmosphere acquire components of motion in both these directions. For an observer looking at 90° to the direction of the sun, the charges accelerating parallel to the double arrows do not radiate energy towards this observer since their acceleration has no transverse component. The radiation scattered by the molecule is therefore, represented by dots. It is linearly polarized light perpendicular to the plane of the figure.
(b) If the unpolarised light is incident on a Polaroid, the intensity is reduced by half. Even if the Polaroid is rotated by angle θ the average
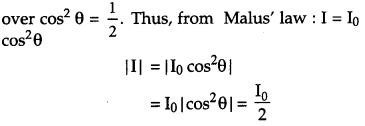
Thus, the intensity of the transmitted light remains unchanged when the Polaroid is rotated.
Question 26.
One day Chetan’s mother developed a severe stomach ache all of a sudden. She rushed to the doctor who suggested for an immediate endoscopy test and gave an estimate of expenditure for the same. Chetan immediately contacted his class teacher and shared the information with her. The class teacher arranged for the money and rushed to the hospital. On realizing that Chetan belonged to a below average income group family, even the doctor offered concession for the test fee. The test was conducted successfully. Answer the following questions based on the above information: [5]
(a) Which principle in optics is made use of in endoscopy ?
(b) Briefly explain the values reflected in the action taken by the teacher.
(c) In what way do you appreciate the response of the doctor on the given situation ?
Answer:
(a) Endoscopy is based on total internal reflection principle. It has tubes which are made up of optical fibres and are used for transmitting and receiving electrical signals, which are converted into light by suitable transducer.
(c) Doctor gave monetary help to Chetan by understanding his poor financial condition
Question 27.
(a) Using Biot-Savart’s law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of ? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero. [5]
OR
(a) Draw a schematic sketch of a cyclotron. Explain clearly the role of crossed electric and magnetic field in accelerating the charge. Hence derive the expression for the kinetic energy acquired by the particles.
(b) An α-particle and a photon are released from the center of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency ? Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit of the dees ?
Answer:
(a) Magnetic field on the axis of a circular loop
I → Current
R → Radii
X → Axis
x → Distance of OP
dl → Conducting element of the loop
According to Biot-Savart’s law, the magnetic field at P is
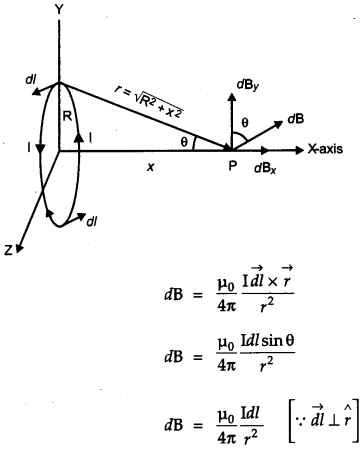
dB has two components dBx and dBy. d.By components being in opposite direction cancel out each other and dBx component being in same direction added up.
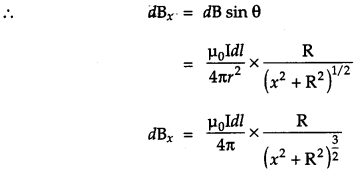
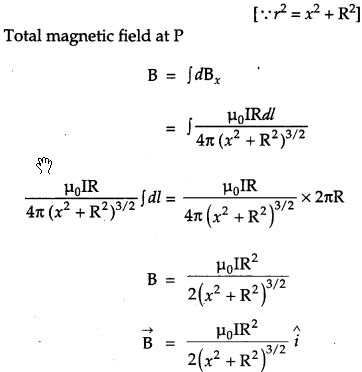
(b) Toroid is a hollow circular ring on which a large number of turns of a wire are closely wound. Figure shows a sectional view of the toroid. The direction of the magnetic field inside is clockwise as per the right-hand thumb rule for circular loops. Three circular Amperian loops 1, 2 and 3 are shown by dashed lines.
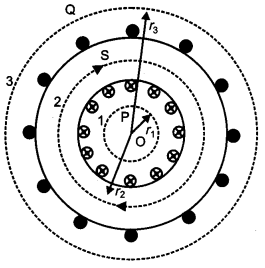
By symmetry, the magnetic field should be tangential to each of them and constant in magnitude for a given loop.
Let the magnetic field inside the toroid be B. Then by Ampere’s circuital law,
\(\overrightarrow{\int B} \cdot \overrightarrow{d l}=\mu_{0} I \Rightarrow B L=\mu_{0} N I\)
Where, L is the length of the loop for which B is tangential, I is the current enclosed by one loop and N is the number of turns.
We find, L = 2πr
The current threads the ring as many times are there are turns in the solenoid, therefore total current in the solenoid is NI.
\(\mathbf{B}(2 \pi r)=\mu_{0} \mathrm{NI}\)
\(\text { or } \quad \mathrm{B}=\frac{\mu_{0} \mathrm{NI}}{2 \pi r}\)
Open space inside the toroid encloses no current thus,
I= 0.
Hence, B = 0
Open space exterior to the toroid :
Each turn of current carrying wire is cut twice by the loop 3. Thus, the current coming out of the plane of the paper is cancelled exactly by the current going into it. Thus,
1= 0, and B = 0
OR
(a) Schematic sketch of cyclotron :
The combination of crossed electric and magnetic field is used to increase the energy of the charged particle. Cyclotron uses the fact that the frequency of revolution of the charged particle in a magnetic field is independent of its energy. Inside the dees particle is shielded from the electric field and magnetic field acts on the particle and makes it to go round in a circular path. Every time the particle moves from one dee to the other it comes under the influence of electric field which ensures to increase the energy of the particles as the sign of the electric field changed alternately. The increase in energy increases the radius of the circular path so the accelerated particle moves in a spiral path.
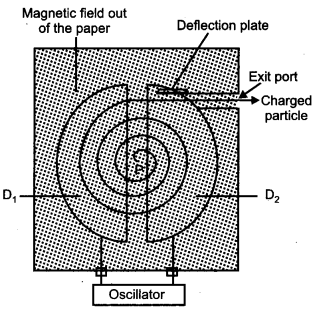


Thus, particles will not exit the dees with same velocity. The velocity of proton is twice the velocity of alpha particle.
Question 28.
(a) Define electric dipole moment. Is it a scalar or a vector ? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero. [5]
OR
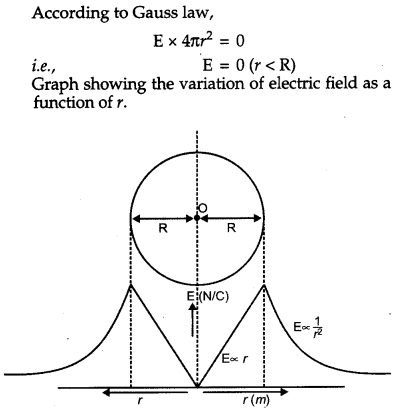
Using Gauss’ law deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point
(i) outside and
(ii) inside the shell.
Plot a graph showing variation of electric field as a function of r > R and r < R. (r being the distance from the center of the shell)
Answer :
(a) Electric dipole moment : Electric dipole moment is defined as the product of magnitude of either charges and the distance between the positive and negative charge of the electric dipole. The strength of any electric dipole is measured by the magnitude of its electric dipole moment
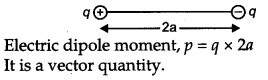
In vector form it is written as \(\vec{p}=q \times \overrightarrow{2 a}\) where
the direction of \(\vec{a}\) is from negative charge to positive charge.
Electric Field of dipole at points on the equatorial plane:
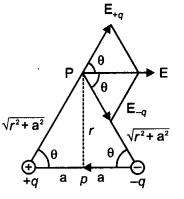
Let P be the point on the equatorial plane of the dipole where electric field is to be calculated. Let its distance from either charge be r. The magnitude of the electric field due to the two charges +q and -q at P is given by
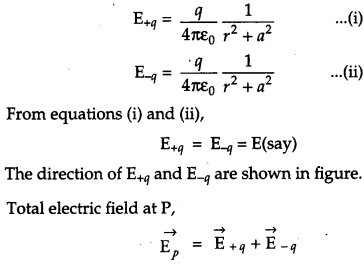
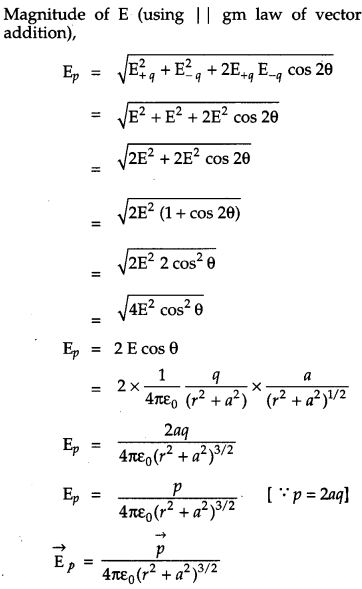
(b) Equipotential surface due to electric dipole:
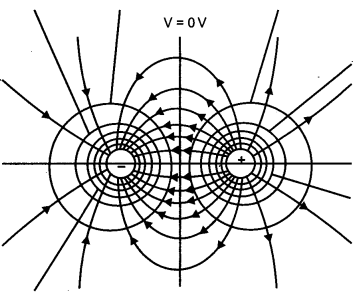
The potential due to the dipole is zero at the line bisecting the dipole length.
OR
Electric field due to a uniformly charged thin spherical shell:
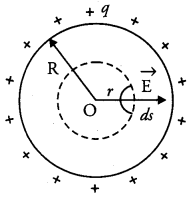
- When point P lies outside the spherical shell : Consider a spherical shell of radius R and center O. Let q be the charge on the spherical shell. Suppose that we have to calculate electric field at the point P at a distance r (r > R) from its center. Draw the Gaussian surface through point P so as to enclose the charged spherical shell. The Gaussian surface is a spherical shell of radius r and centre O.
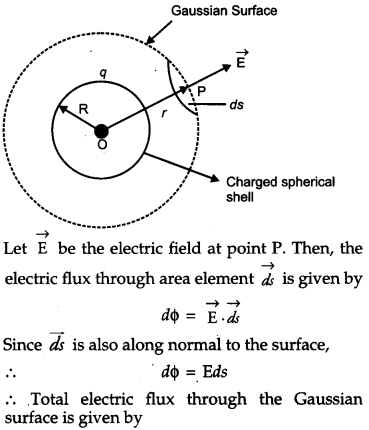

- When point P lies inside the spherical shell : In such a case the Gaussian surface encloses no charge
Question 29.
Using Bohr’s postulates, derive the expression for the frequency of radiation emitted when electron in hydrogen atom undergoes transition from higher energy state (quantum number ni)to the lower state, (nf).
When electron in hydrogen atom jumps from energy state ni = 4 to nf = 3, 2, 1, identify the spectral series to which the emission lines belong. [5]
OR
(a) Draw the plot of binding energy per nucleon (BE/A) as a function of mass number. Write two important conclusions that can be drawn regarding the nature of nuclear source.
(b) Use this graph to explain the release of energy in both the processes of nuclear fusion and fission.
(c) Write the basic nuclear process of neutron undergoing P-decay. Why is the detection of neutrinos found very difficult ?
Answer:
In the hydrogen atom,

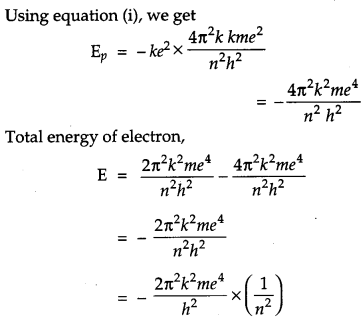
Now, according to Bohr’s frequency condition when electron in hydrogen atom undergoes transition from higher energy state to the lower energy state (nf) is,


![]()
(a) Plot of binding energy per nucleon as the function of mass number A is given as below:
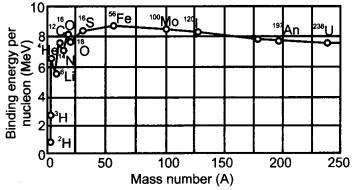
Following are the two conclusion that can be drawn regarding the nature of the nuclear force:
- The force is attractive and strong enough to produce a binding energy of few MeV per nucleon.
- The constancy of the binding energy in the range 30 < A < 170 is a consequence of the fact that the nuclear force is short range force.
(b) Nuclear fission : A very heavy nucleus (say, A = 240) has lower binding energy per nucleon as compared to the nucleus with A = 120. Thus, if the heavier nucleus breaks to tire lighter nucleus with high binding energy per nucleon, nucleons are tightly bound. This implies that energy will be released in the process which justifies the energy release in fission reaction.
Nuclear fusion: When two light nuclei (A < 10) are combined to form a heavier nuclei, the binding energy of the fused heavier nuclei is more than the binding energy per nucleon of the lighter nuclei. Thus the final system is more tightly bound than the initial system. Again the energy will be released in fusion reaction.
(c) The basic nuclear process of neutron undergoing (3-decay is given as :
\(n \rightarrow p+e^{-}+\overline{\mathbf{v}}\)
Neutrinos are mass less and charge less particles. Neutrinos interact very weakly with matter that it becomes very difficult to detect them. That’s why the detection of neutrinos is found very difficult.
CBSE Previous Year Question Papers Class 12 Physics 2013 Outside Delhi Set-II
Note : Except for the following questions, all the remaining questions have been asked in previous Set.
Question 1..
Two charges of magnitudes -3Q and +2Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘5a’ with its center at the origin. [1]
Answer: According to Gauss’ theorem, the electric flux through a closed surface enclosing a charge is equal to \(\frac{1}{\varepsilon_{o}} \)times the magnitude of the charge enclosed.
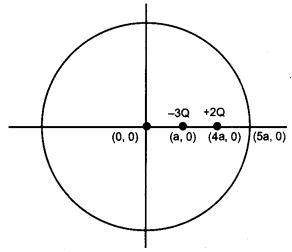
The sphere enclose charge = -3Q + 2Q = -Q
∴ Total electric flux, \(\phi=\frac{Q}{\varepsilon_{0}}\)
Question 2.
A light metal disc on the top of an electromagnet is thrown up as the current is switched on. Why ? Give reason. [2]
Answer :
A light metal disc on the top of an electromagnet is thrown up as the current is switched on because when the current flows through the electromagnet, the magnetic flux through the disc increases which leads in setting up an eddy current in the disc in the same direction of the electromagnetic current. So the upper surface of electromagnet and the lower surface of the disc acquire same polarity. Since body with same polarity repels, therefore, the disc is thrown up.
Question 3.
In the circuit shown in the figure, identify the equivalent gate of the circuit and make its truth table. [2]
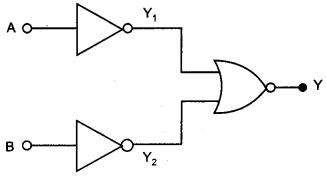
Question 4.
A parallel beam of light of 600 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1.2 m away. It is observed that the first minimum is at a distance of 3 mm from the centre of the screen. Calculate the width of the slit. [3]
Answer :
The distance of the nth minimum from the centre of the screen is, \(x_{n}=\frac{n \mathrm{D} \lambda}{a}\)
where, D= distance of slit from screen
λ = wavelength of the light
a = width of the slit
For first minimum, n = 1
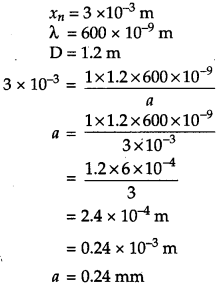
Question 5.
A wire AB is carrying a steady current of 10 A and is lying on the table. Another wire CD canying 6 A is held directly above AB at a height of 2 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms-2] [3]
Answer :
Force per unit length between the current carrying wires is given as :
\(\mathbf{F}=\frac{\mu_{0}}{4 \pi} \frac{2 I_{1} I_{2}}{r}\)
where
The current in wire AB, I1 = 10 A
The current in wire CD, I2 = 6 A
The distance between wires, r = 2 mm = 2 x 10-3 m
Let m be the mass per unit length of wire CD.
As this force balances the weight of the wire CD
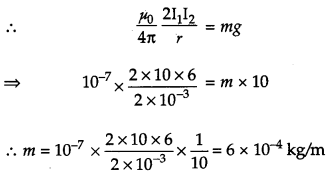
The direction of current in CD w.r.t. AB is opposite (anti parallel) because in this condition both the wires will repel each other.
Question 6.
Name the type of waves which are used for line of sight (LOS) communication. What is the range of their frequencies ?
A transmitting antenna at the top of a tower has a height of 45 m and the height of the receiving antenna is 80 m. Calculate the maximum distance between them for satisfactory communication in LOS mode. (Radius of the Earth = 6.4 × 106 m) [4]
Question 24.
(a) For a given a.c., i = im sin ωt, show that the average power dissipated in a resistor R over a complete cycle is \(\frac{1}{2} i_{m}^{2} \mathrm{RR} \)
(b) A light bulb is rated at 120 W for a 240 V a.c. supply. Calculate the resistance of the bulb. [5]
Answer:
(a) The average power dissipated

CBSE Previous Year Question Papers Class 12 Physics 2013 Outside Delhi Set-III
Note: Except (or the following questions all the remaining question have been asked in previous Sets.
Question 1.
Write the expression for the de-Broglie wavelength associated with a charged particle having charge ‘q’ and mass ‘m’, when it is ‘ accelerated by a potential V. [1]
Answer :
de-Broglie wavelength associated with the particle,
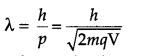
Question 2.
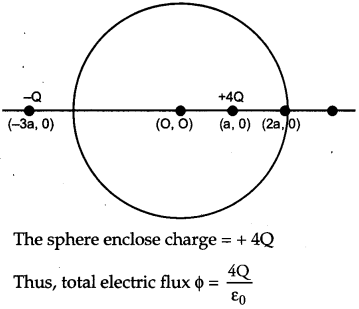
Two charges of magnitudes + 4Q and -Q are located at points (a, 0) and (-3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘2a’ with its center at the origin ? [1]
Answer :
Gauss’s theorem states that the electric flux through a closed surface enclosing
a charge is equal to \(\frac{1}{\varepsilon_{0}}\) times the magnitude of the charge encl0sed.
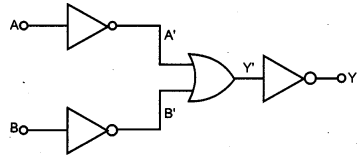
Question 3.
In the circuit shown in the figure, identify the equivalent gate of the circuit and make its truth table. [1]
Question 4.
A parallel beam of light of 450 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1.5 m away. It is observed that the first minimum is at a distance of 3 mm from the center of the screen. Calculate the width of the slit. [2]
Answer :
The distance of the nth minimum from the center of the screen,

Question 5.
A wire AB is carrying a steady current of 6 A and is lying on the table. Another wire CD carrying 4 A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms-2] [3]
Answer :
Force per unit length between the current carrying wire is given as :
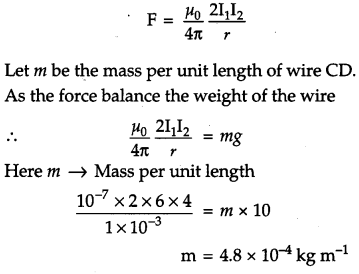
The current in CD is in opposite direction to that in AB than they will repel each other and CD wire remain suspended in air.
Question 6.
A light bulb is rated at 125 W for a 250 V a.c. supply. Calculate the resistance of the bulb. [3]
Answer:
Power of the bulb, P = 125 W Voltage,
V = 250 V The resistance of the bulb is given as
\(R=\frac { { V }^{ 2 } }{ p } =\frac { { 250 }^{ 2 } }{ 125 } =500\Omega \)
Question 7.
Name the type of waves which are used for line of sight (LOS) communication. What is the range of their frequencies ?
A transmitting antenna at the top of a power has a height of 45 m and the receiving antenna is on the ground. Calculate the maximum distance between them for satisfactory communication in LOS mode. (Radius of the Earth = 6.4 x 106 m) [5]