CBSE Previous Year Question Papers Class 12 Maths 2019 Outside Delhi

CBSE Previous Year Question Papers Class 12 Maths 2019 Outside Delhi

Time allowed: 3 hours
Maximun marks : 100

General Instructions:

• All questions are compulsory.
• The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
• All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
• There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
• Use of calculators is not permitted. You may ask for logarithmic tables, if required.

**Answer is not given due to the change in present syllabus

CBSE Previous Year Question Papers Class 12 Maths 2019 Outside Delhi Set I

Section – A

Question 1.
If A is a square matrix satisfying A’ A = I, write the value of |A|. [1]
Solution:
Given, A’ A= I

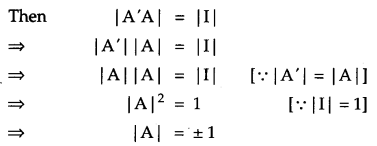
Question 2.
If y = x | x |, find \(\frac{d y}{d x}\) for x < 0. [1]
Solution:
If y = x | x |

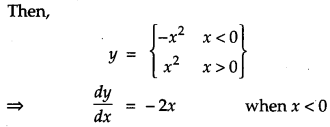
Question 3.
Find the order and degree (if defined) of the differential equation [1]

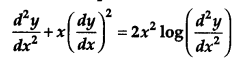
Solution:

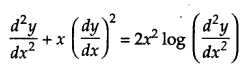
Order of this equation is 2.
Degree of this equation is not defined.

Question 4.
Find the direction consines of a line which makes equal angles with the coordinate axes. [1]
Solution :
Let the direction cosines of the line make an angle a with each of the coordinate axes and direction cosines be l, m and n.

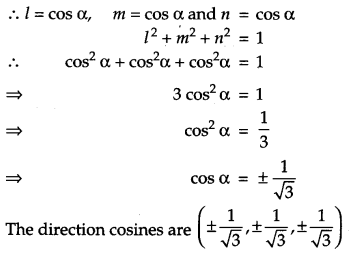
A line passes through the point with position vector \(2 \hat{i}-\hat{j}+4 \hat{k}\) and is in the direction of the vector \(\hat{i}+\hat{j}-2 \hat{k}\). Find the equation of the line in cartesian form.
Solution:
The line passes through a point (2, -1, 4) and has direction ratios proportional to (1, 1, – 2).
Cartesian equation of the line

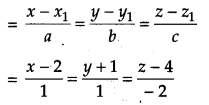
Section – B

Question 5.
Examine whether the operation * defined on R, the set of all real numbers, by \(a * b=\sqrt{a^{2}+b^{2}}\) is a binary operation or not, and if it is a binary operation, find whether it is associative or not.** [2]

Question 6.
If A = \(\left[\begin{array}{cc}{4} & {2} \\ {-1} & {1}\end{array}\right]\), show that (A – 2I)(A – 3I) = 0. [2]
Solution:
Given,

Question 7.
Find: [2]

Solution:

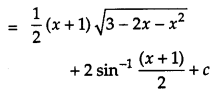
Question 8.
Find: [2]

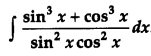
Solution:

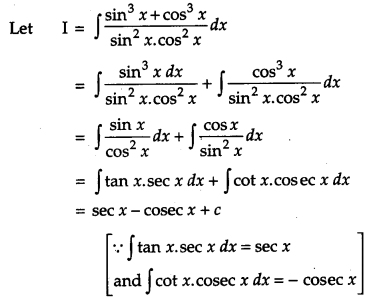
OR
Find:

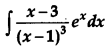
Solution:

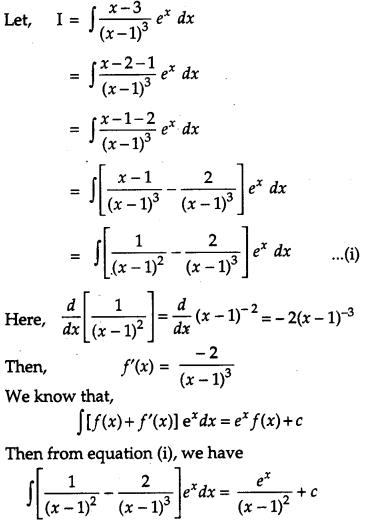
Question 9.
Find the differential equation of the family of curves y = Ac^2x + Be^-2x, where A and B are arbitrary constants. [2]
Solution:
Given, y = Ae^2x + Be^-2x (i)
On differentiating equation (i) w.r.t. x, we get

Question 10.
If \(|\vec{a}|=2,|\vec{b}|\) and \(\vec{a} \times \vec{b}=3 \hat{i}+2 \hat{j}+6 \hat{k}\), find the angle between \(\vec{a}\) and \(\vec{b}\) . [2]
Solution:
Given,

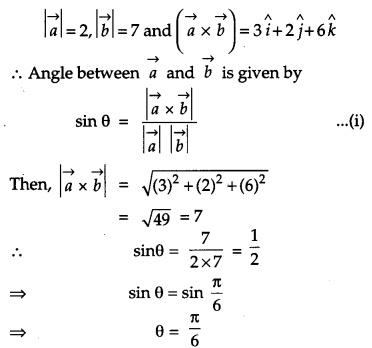
Or
Find the volume of a cuboid whose edges are given by \(-3 \hat{i}+7 \hat{j}+5 \hat{k},-5 \hat{i}+7 \hat{j}-3 \hat{k}\) and \(7 \hat{i}-5 \hat{j}-3 \hat{k}\).
Solution:
If a, b, c are edges of a cuboid.

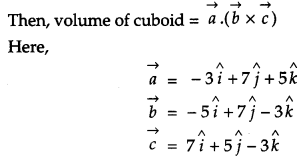
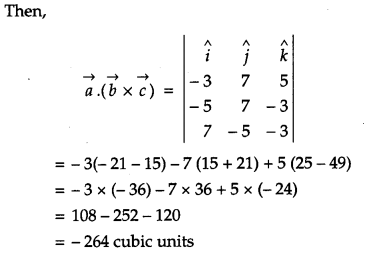
Question 11.
If P(not A) = 0·7, P(B) = 0·7 and P(B/A) = 0·5, then find P(A∆B). [2]
Solution:

Question 12.
A coin is tossed 5 times. What is the probability of getting (i) 3 heads, (ii) at most 3 heads? [2]
Solution:


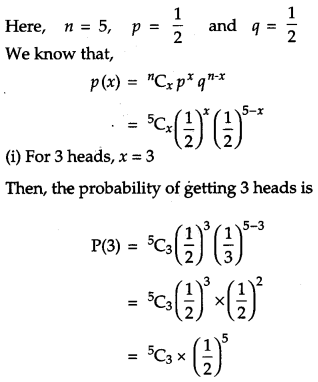
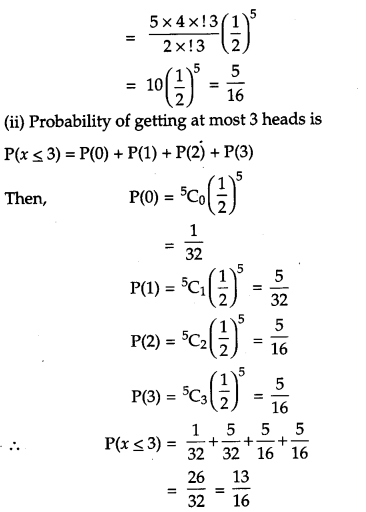
OR
Find the probabilty distribution of X, the number of heads in a simultaneous toss of two coins.
Solution:
If we toss two coins simultaneously then sample space is given by (HH, HT, TH, IT)
Then probability distribution is,

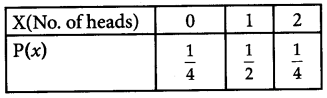
Section – C

Question 13.
Check whether the relation R defined on the set A = {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive. [4]
Solution:
Here, R = {(a, b): b = a +1}
∴ R = {(a, a + 1): a, a + 1 ϵ (1, 2, 3, 4, 5 ,6)}
⇒ R = {(1, 2,) (2, 3), (3, 4), (4, 5), (5, 6)}
(i) R is not reflexive as {a, a} ∉ R∀a
(ii) R is not symmetric as (1, 2) ϵ R but (2, 1) ∉ R
(iii) R is not transitive as (1, 2) ϵ R, (2, 3) ϵ R but (1, 3) ϵ R
OR
Let f: N → Y be a function defined as
f(x) = 4x + 3,
where Y = {y ϵ N : y = 4x + 3, for some x ϵ N}.
Show that f is invertible. Find its inverse.
Solution:
Consider an arbitrary element of Y. By the definition of y, y = 4x + 3, for some x in the domain N.

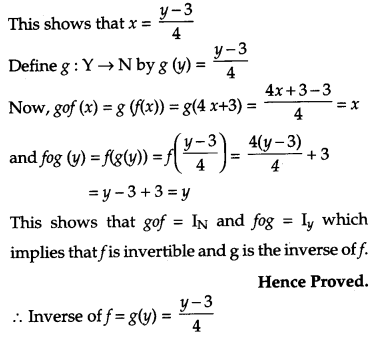
Question 14.
Find the value \(\left(\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}\right)\) [4]
Solution:
\(\left(\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}\right)\)

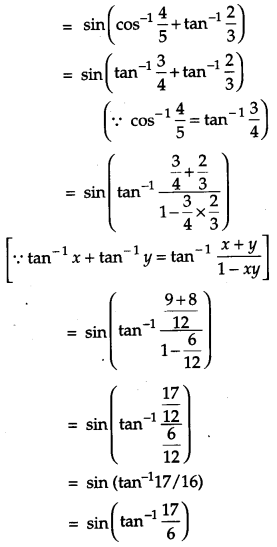
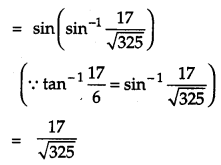
Question 15.
Using properties of determinants, show that [4]

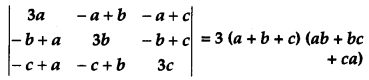
Solution:

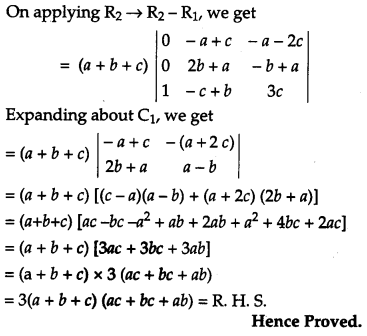
Question 16.
If \(x \sqrt{1+y}+y \sqrt{1+x}\) = 0 and x ≠ y, prove that \(\frac{d y}{d x}=-\frac{1}{(x+1)^{2}}\) [4]
Solution:

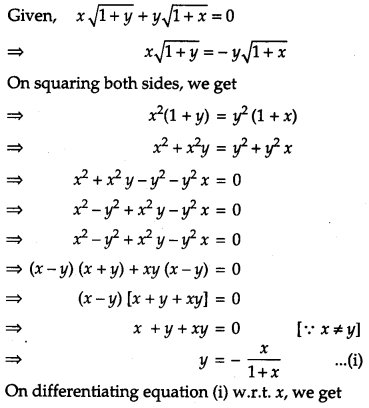
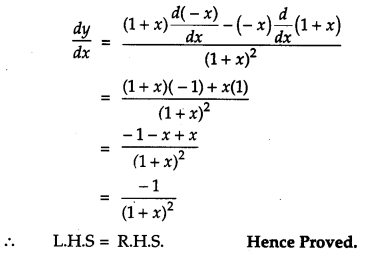
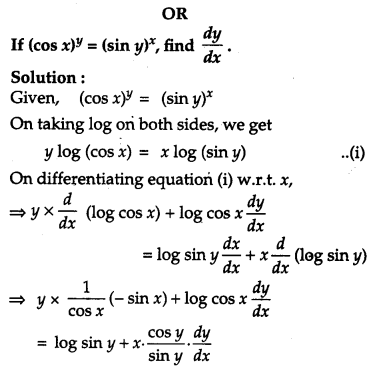
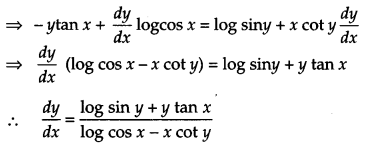
Question 17.
If If (x – a)² + (y – b)² = c², for some c > 0, prove that \(\frac{\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{3 / 2}}{\frac{d^{2} y}{d x^{2}}}\) is a constant independent of a and b. [4]
Solution:

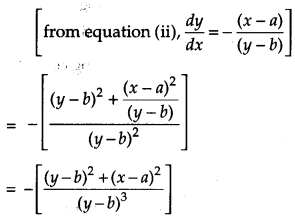
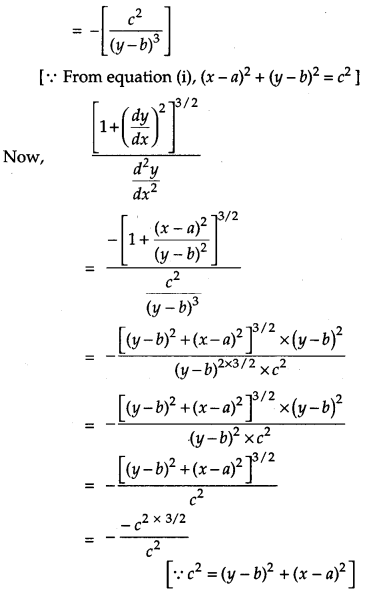
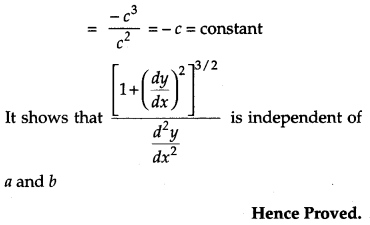
Question 18.
Find the equation of the normal to the curve x² = 4y which passes through the point (-1, 4). [4]
Solution:
Suppose the normal at P(x₁, y₁) on the parabola x² = 4y passes through (-1, 4)
Since, P(x₁, y₁) lies on x² = 4y
∴ \(x_{1}^{2}\) = 4y₁
The equation of curve is x² = 4y
Differentiating with respect to x, we have
2x = 4 \(\frac{d y}{d x}\)

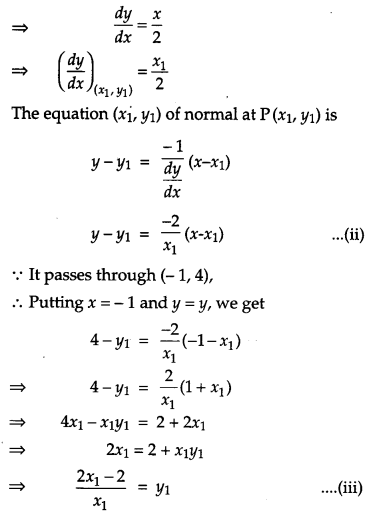
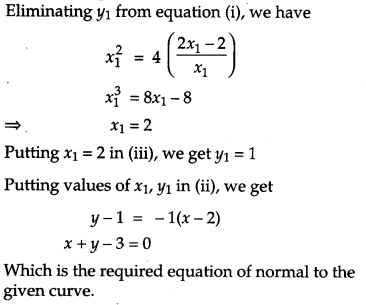
Question 19.
Find: [4]

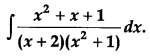
Solution:

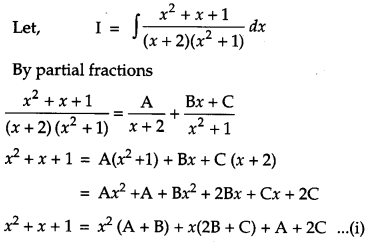
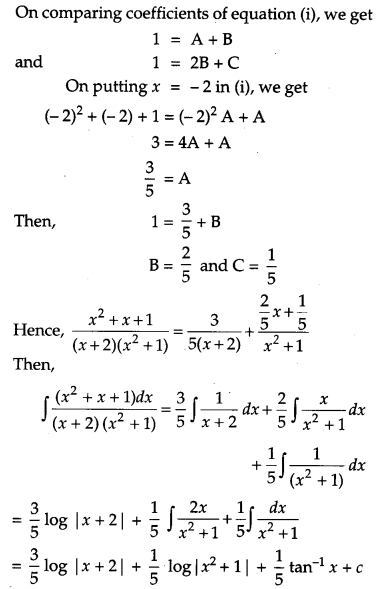
Question 20.
Prove that : \(\int_{0}^{a} f(x) d x=\int_{0}^{a} f(a-x) d x\) and hence evaluate \(\int_{0}^{\pi / 2} \frac{x}{\sin x+\cos x} d x\). [4]
Solution:

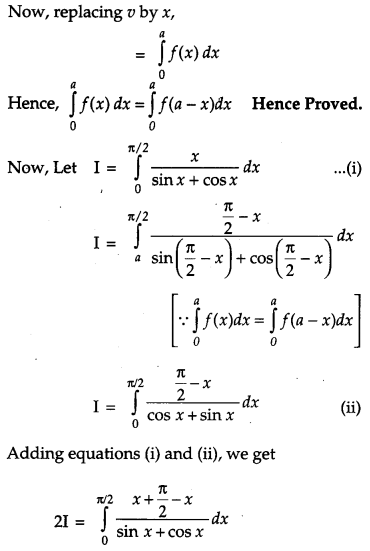
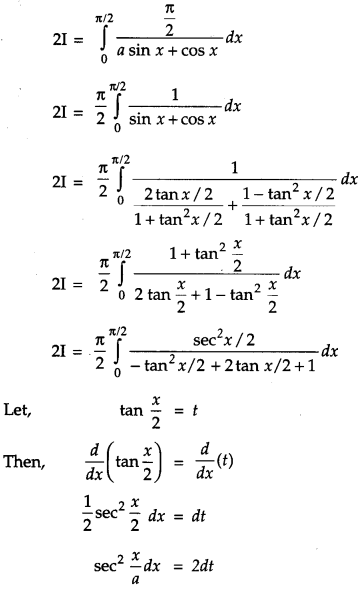
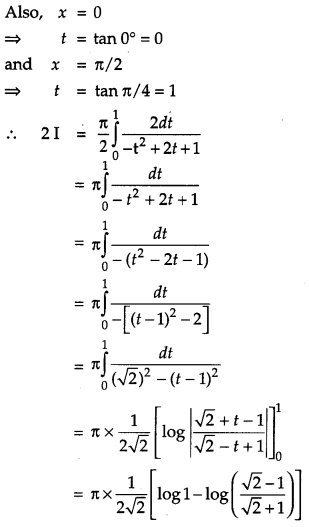
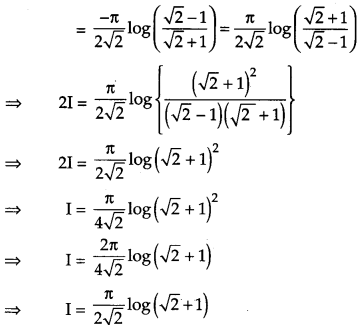
Question 21.
Solve the differential equation: [4]

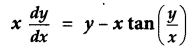
Solution:

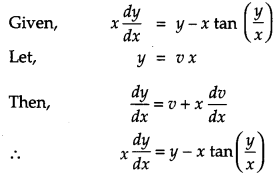
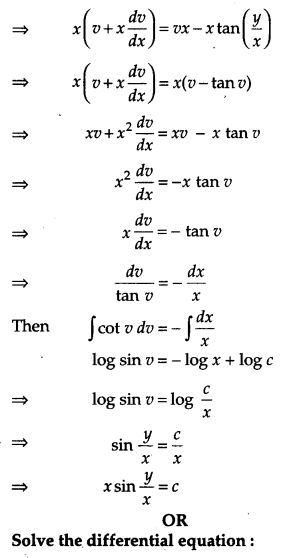
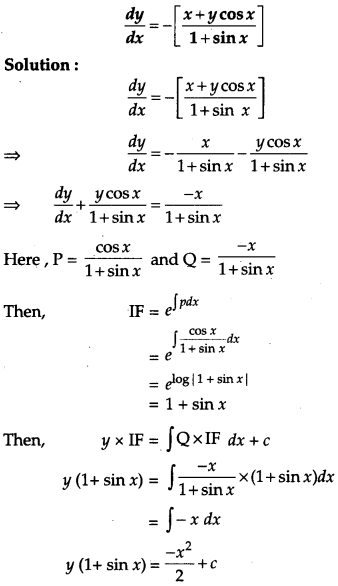
Question 22.
The scalar product of the vector \(\vec{a}=\hat{i}+\hat{j}+\hat{k}\) with a unit vector along the sum of the vectors \(\vec{b}=2 \hat{i}+4 \hat{j}-5 \hat{k}\) and \(\vec{c}=\lambda \hat{i}+2 \hat{j}+3 \hat{k}\) is equal to 1. Find the value of λ and hence find the unit vector along \(\vec{b}+\vec{c}\). [4]
Solution:

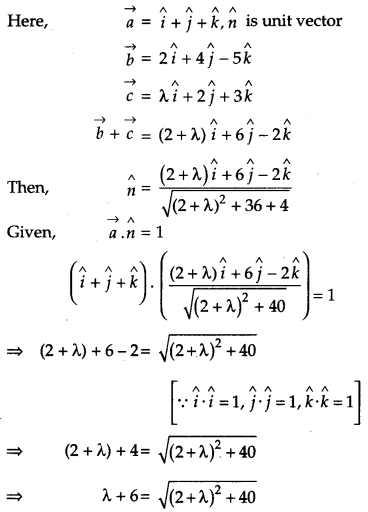
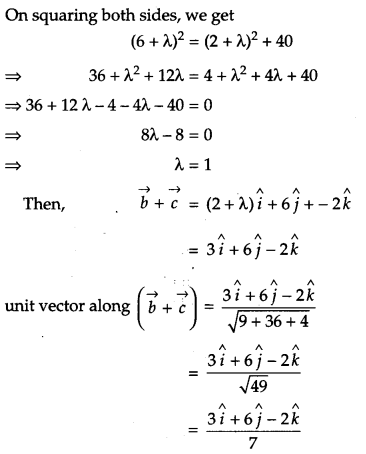
Question 23.
If the lines \(\frac{x-1}{-3}=\frac{y-2}{2 \lambda}=\frac{z-3}{2}\) and \(\frac{x-1}{3 \lambda}=\frac{y-1}{2}=\frac{z-6}{-5}\) are perpendicular, find the value of λ. Hence find whether the lines are intersecting or not. [4]
Solution:

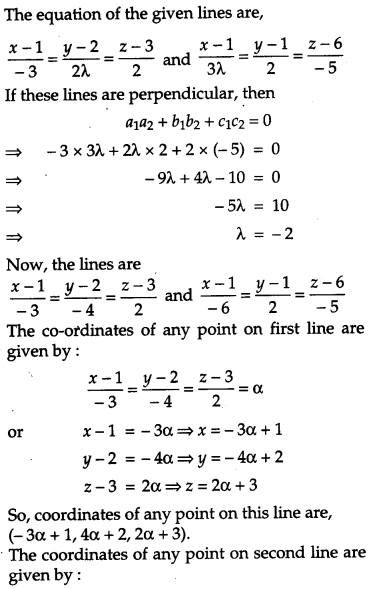
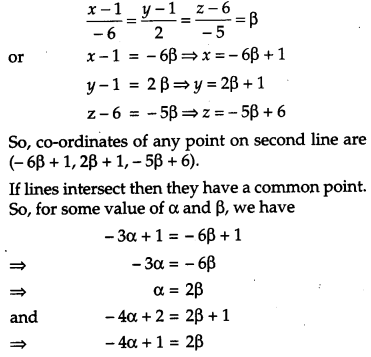
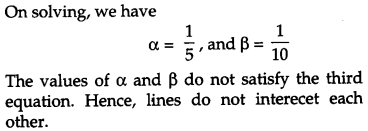
Section – D

Question 24.
If A = \(\left[\begin{array}{lll}{1} & {3} & {4} \\ {2} & {1} & {2} \\ {5} & {1} & {1}\end{array}\right]\), find A^-1 [6]
Hence solve the system of equations
x + 3y + 4z = 8
2x + y + 2z = 5
and 5x + y + z = 7
Solution:




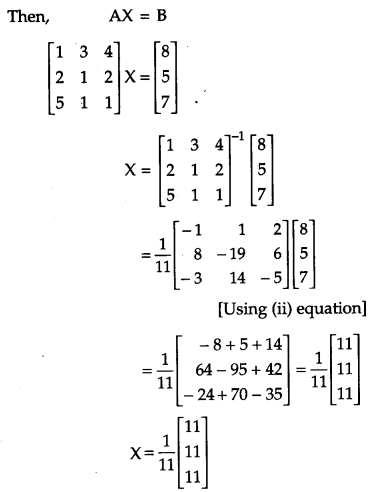
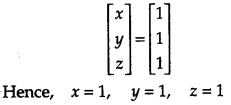
OR
Find the inverse of the following matrix, using elementary transformation:
A = \(\left[\begin{array}{ccc}{2} & {0} & {-1} \\ {5} & {1} & {0} \\ {0} & {1} & {3}\end{array}\right]\)
Solution:

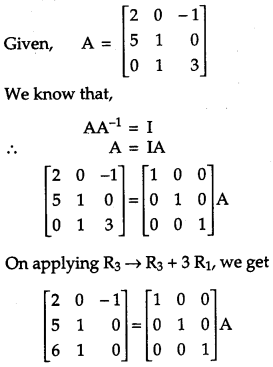
Question 25.
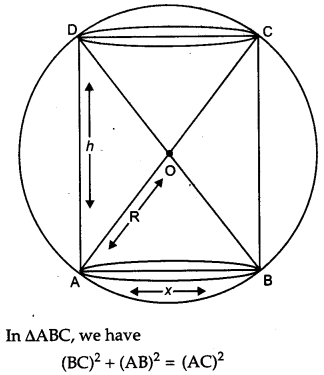
Show that the height the cylinder of maximum volume that can inscribed in a sphere of radius R is \(\frac{2 R}{\sqrt{3}}\). Also find the maximum volume. [6]
Solution:
Let, ‘x’ be the diameter of the base of the cylinder and let ‘h’ be height of the cylinder.

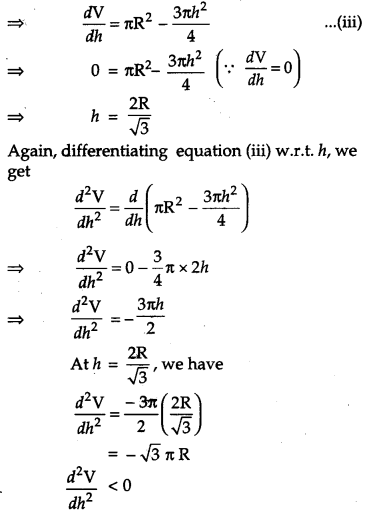
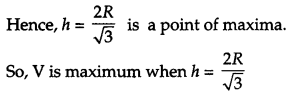
Question 26.
Using method of integration, find the area of the triangle whose vertices are (1, 0), (2, 2) and (3, 1). [6]
Solution:
A(1, 0), B(2, 2) and C(3, 1)


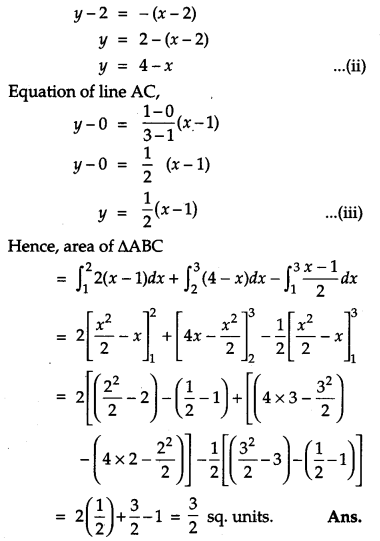
OR
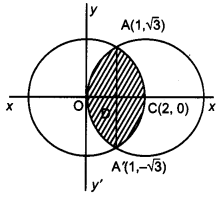
Using method of integration, find the area of the region enclosed between two circles x² + y² = 4 and (x – 2)² + y² = 4.
Solution:
Equations of the given circles are,
x² + y² = 4 …(i)
(x – 2)² + y² = 4 …(ii)
Equation (i) is a circle with centre O at the origin and radius 2. Equation (ii) is a circle with centre C (2, 0) and radius 2.
Solving equation (i) and (ii) we have
(x – 2)² + y² = x² + y²
or x² – 4x + 4 + y² = x² + y² or x = 1 which gives y = ±\(\sqrt{3}\)
Thus, the points of intersection of the given circles are A (1, \(\sqrt{3}\) ) and A'(1, \(\sqrt{3}\) )

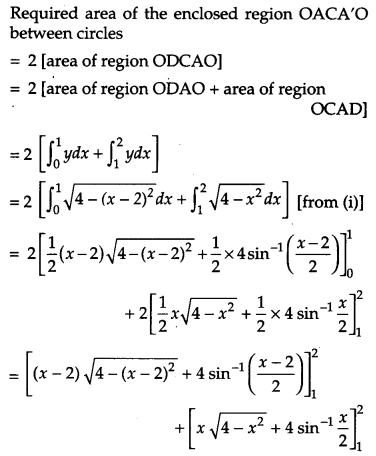
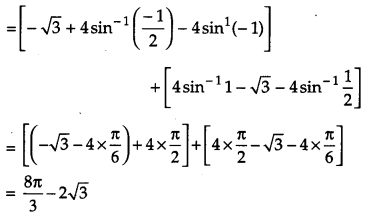
Question 27.
Find the vector and cartesian equations of the plane passing through the points having position vectors \(\hat{i}+\hat{j}-2 \hat{k}, 2 \hat{i}-\hat{j}+\hat{k}\) and \(\hat{i}+2 \hat{j}+\hat{k}\). Write the equation of a plane passing through a point (2, 3, 7) and parallel to the plane obtained above. Hence, find the distance between the two parallel planes. [6]
Solution :
Let A, B, C be the points with position




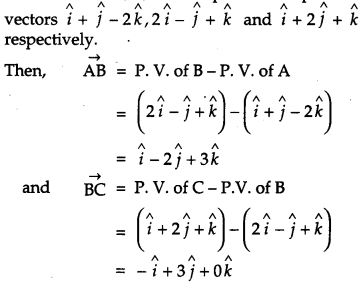
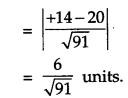
OR
Find the equation of the line pasing through (2, -1, 2) and (5, 3, 4) and of the plane passing through (2, 0, 3), (1, 1, 5) and (3, 2, 4). Also, find their point of intersection.
Solution:
We know that the equation of line passing through points (x₁, y₁, z₁) and(x₂, y₂, z₂) is given by

Question 28.
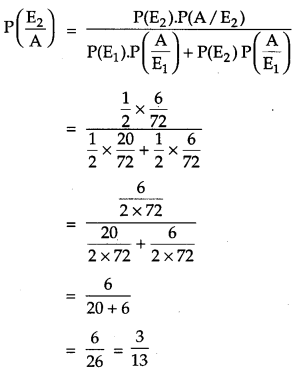
There are three coins. One is a two-headed coin, another is a biased coin that comes up heads 75% of the time and the third is an unbiased coin. One of the three coins is chosen at random and tossed. If it shows heads, what is the probability that it is the two-headed coin? [6]
Solution:
Given, there are three coins.
Let,
E₁ = coin is two headed
E₂ = biased coin
E₃ = unbiased coin
A = shows only head

Question 29.
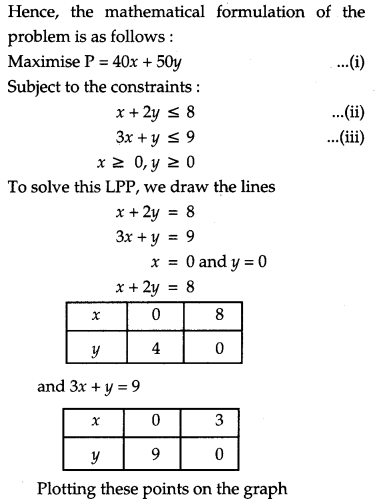
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requries 3g of silver and 1 g of gold while that of type B requires 1 g of silver and 2g of gold. The company can use at the most of 9 g of silver and 8 of gold. If each unit of type A brings a profit of ₹ 40 and that of type B ₹ 50, find the number of units of each type that the company should produce to maximize profit. Formulate the above LPP and solve it graphically and also find the maximum profit [6]
Solution:
There are two types of goods, A and B and let units of type A be x and units of type B be y.

CBSE Previous Year Question Papers Class 12 Maths 2019 Outside Delhi Set II

Section – A

Question 1.
Find | AB |, if A = \(\left[\begin{array}{rr}{0} & {-1} \\ {0} & {2}\end{array}\right]\) anf B = \(\left[\begin{array}{ll}{3} & {5} \\ {0} & {0}\end{array}\right]\). [1]
Solution:

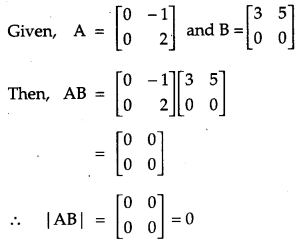
Question 2.
Differentiate \(e^{\sqrt{3 x}}\), with respect to x. [1]
Solution:

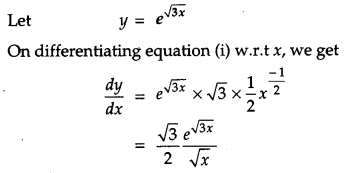
Section – B

Question 6.
If A = \(\left[\begin{array}{ll}{p} & {2} \\ {2} & {p}\end{array}\right]\) and | A³| = 125, the find the value of p. [2]
Solution:

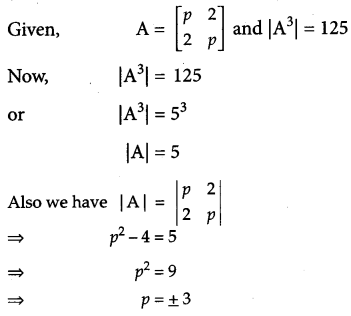
Question 12.
Find the general solution of the differential equation \(\frac{d y}{d x}=e^{x+y}\). [2]
Solution:

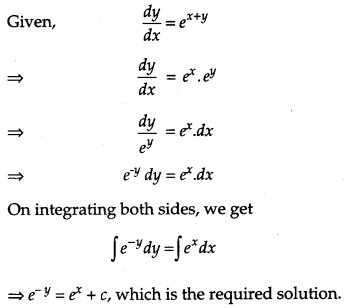
Section – C

Question 21.
If (a + bx)e^y/x = x, then prove that [4]

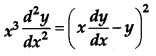
Solution:
We have

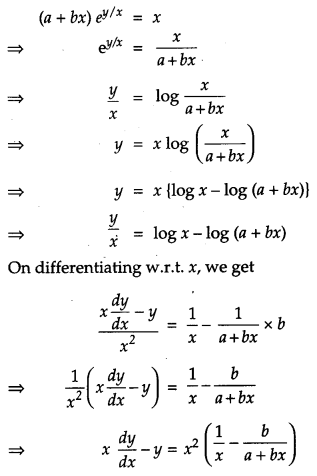
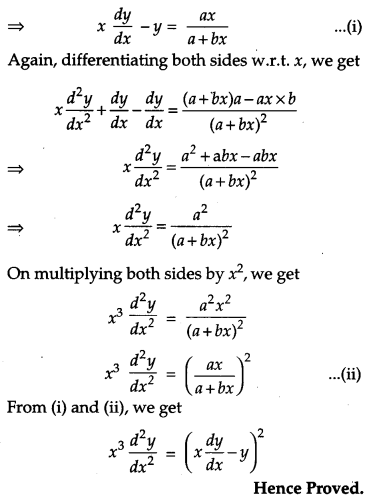
Question 22.
The volume of a cube is increasing at the rate of 8 cm³/s. How fast is the surface area increasing when the length of its edge is 12 cm? [4]
Solution:
Let x be the length of side, V be the volume and S be the surface area of cube.
Then, V = x³ and S = 6x², where x is a function of time t

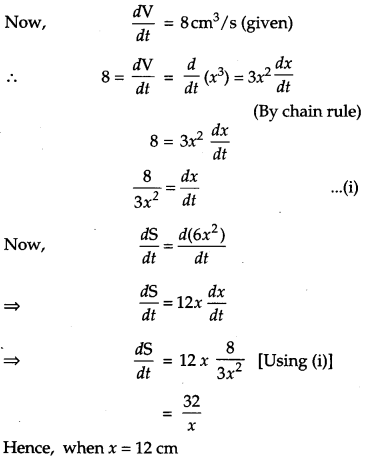
Question 23.
Find the cartesian and vector equations of the plane passing through the point A(2, 5, – 3), B(- 2, – 3, 5) and C(5, 3, – 3). [4]
Solution:
We know that the general equation of the plane passing through three points (x₁, y₁, z₁) (x₁, y₁, Z₁), (x₃, y₃, z₃)

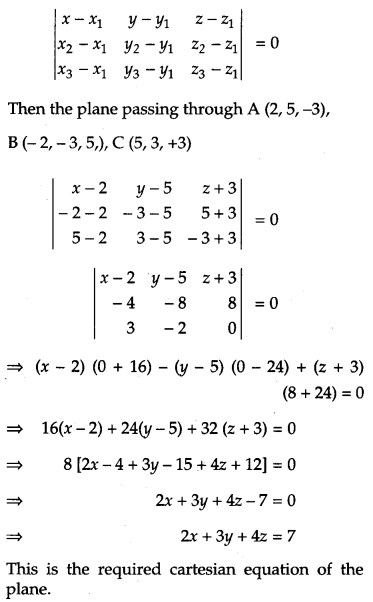
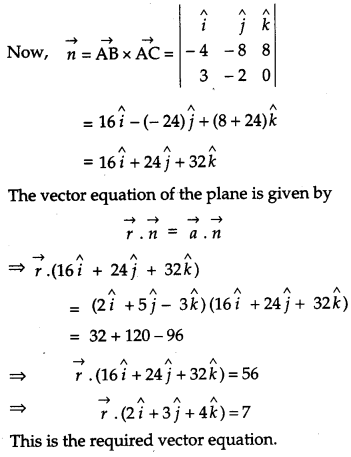
Section – D

Question 24.
Find the point on the curve y² = 4x, which is nearest to the point (2, – 8). [6]
Solution:
Given curve is of the form, y² = Ax and let p(x, y) is a point on the curve which is nearest to the point (2, – 8).

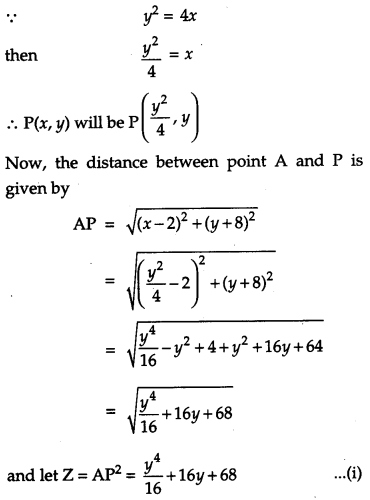
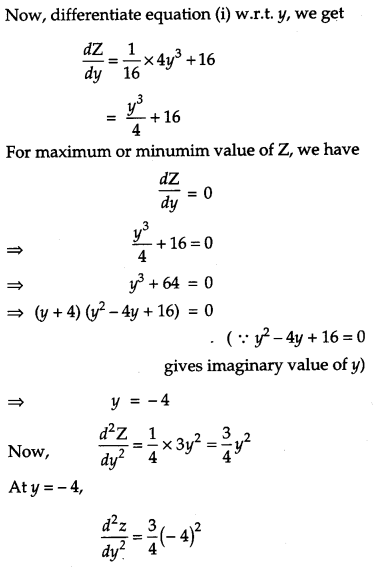
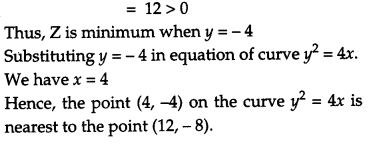
Question 25.
Find \(\int_{1}^{3}\left(x^{2}+2+e^{2 x}\right)\) as the limit of sums. [6]
Solution:
We have




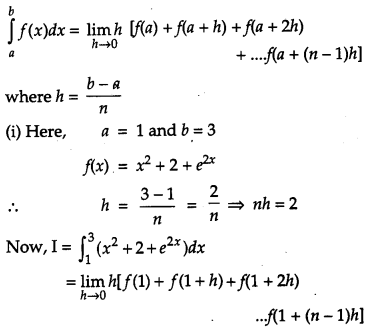
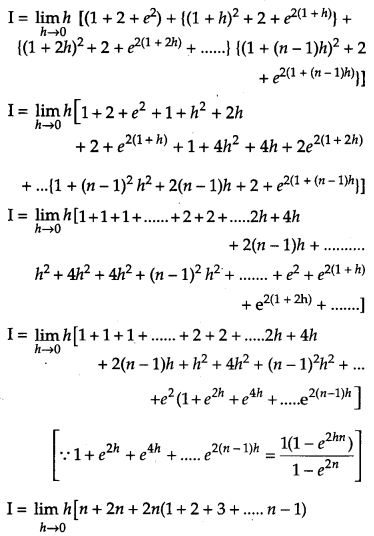
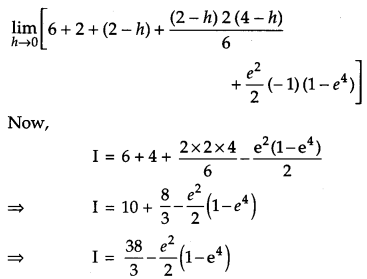
OR
Using integration, find the area of the triangular region whose sides have the equation y = 2x + 1, y = 3x + 1 and x = 4.
Solution:
The equations of sides of triangle are
y = 2x + 1, …(i)
y = 3x + 1 …(ii)
and x = 4 …(iii)

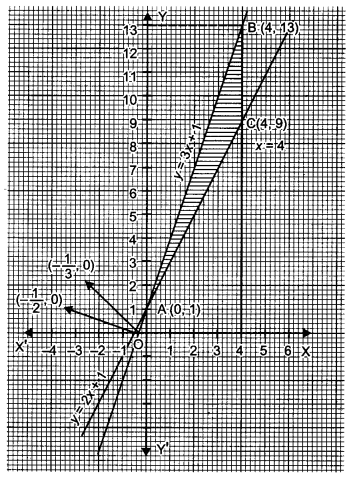
The equation y = 2x + 1 meets x and y axes at \(\left(-\frac{1}{2}, 0\right)\) and (0, 1). By joining these two points we obtain the graph of x + 2y = 2. Similarly, graphs of other equations are drawn.
Solving equation (i), (ii) and (iii) in pairs, we obtain the coordinates of verticies of ∆ABC are A(0, 1), B (4, 13) and C (4, 9).
Then, area of ∆ABC = Area (OLBAO) – Area (OLCAO)

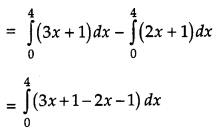
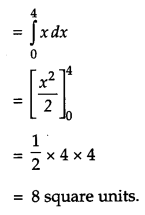
CBSE Previous Year Question Papers Class 12 Maths 2019 Outside Delhi Set III

Section – A

Question 1.
Find the differenital equation representing the family of curves y = ae^2x + 5, where a is an arbitrary constant. [1]
Solution:
Given, y = ae^2x + 5
On differentiating w.r.t. x, we get

Question 2.
If y = cos\(\sqrt{3 x}\), then find \(\frac{d y}{d x}\). [1]
Solution:

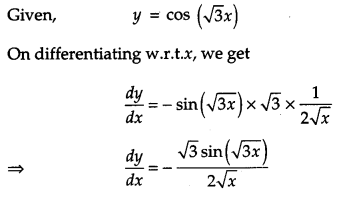
Section – B

Question 5.
Show that the points \(\mathbf{A}(-2 \hat{i}+3 \hat{j}+5 \hat{k})\), \(\mathbf{B}(\hat{i}+2 \hat{j}+3 \hat{k})\) and \(\mathbf{c}(7 \hat{i}-\hat{k})\) are collinear. [2]
Solution:

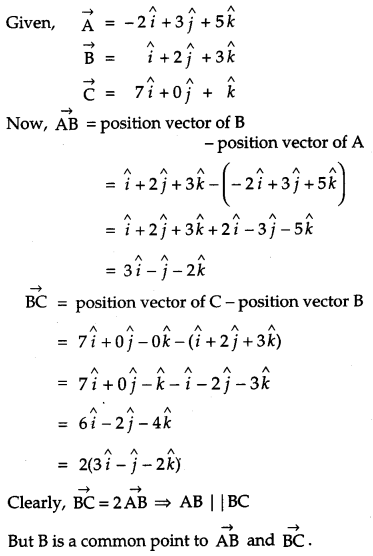
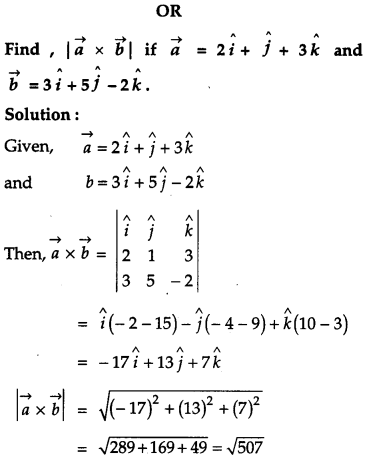
Question 6.
Find:[2]

Solution:

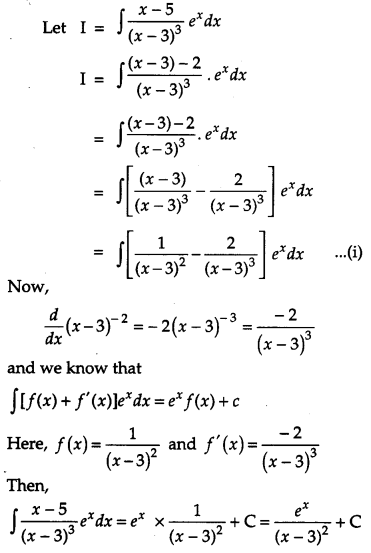
Section – C

Question 13.
Solve for x: tan^-1 + tan^-1(x – 1) = tan^-1\(\left(\frac{8}{31}\right)\). [4]
Solution:

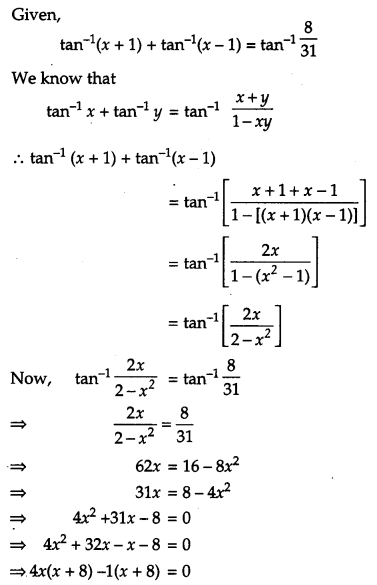
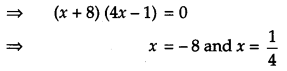
Question 14.
If x = ae^t (sin t + cost t) and y = ae^t (sin t – cos t), then prove that \(\frac{d y}{d x}=\frac{x+y}{x-y}\). [4]
Solution:



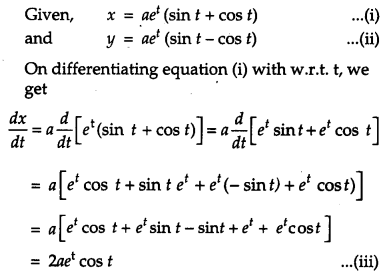
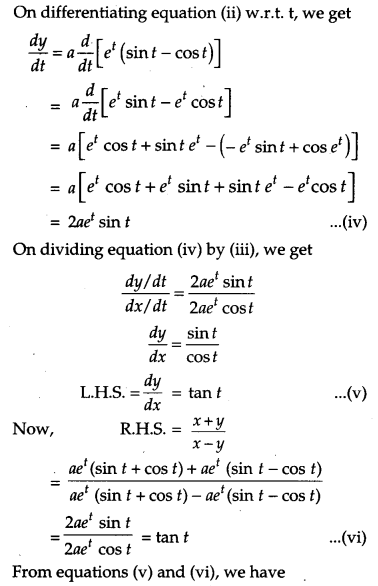
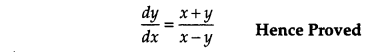
OR
Differentiate x^sinx + (sinx)^cosx with respect to x.
Solution:

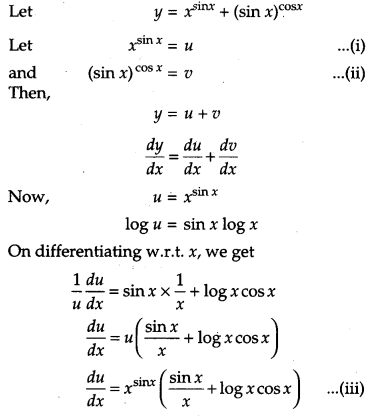
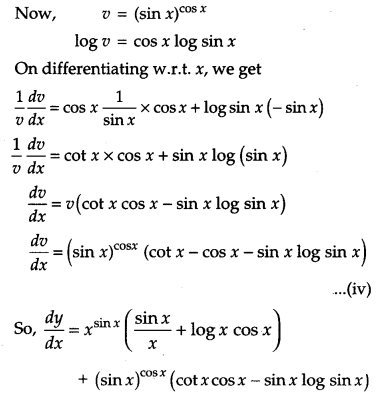
Question 15.
Find: [4]

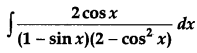
Solution:

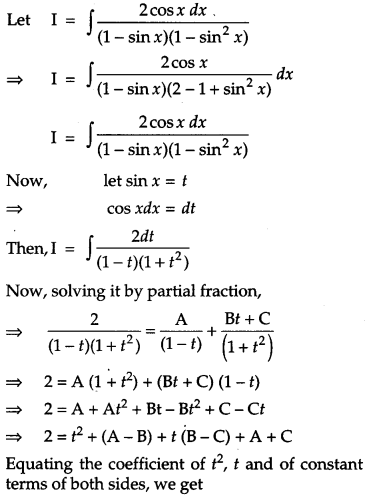
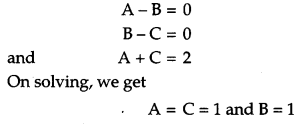
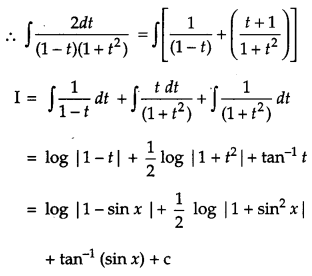
Section – D

Question 24.
Show that for the matrix A = \(\left[\begin{array}{rrr}{1} & {1} & {1} \\ {1} & {2} & {-3} \\ {2} & {-1} & {3}\end{array}\right]\), A³ – 6A² + 5A + 111 = 0. Hence, find A ^-1.
Solution:






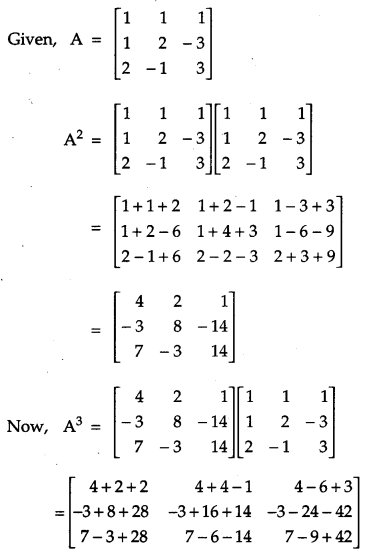
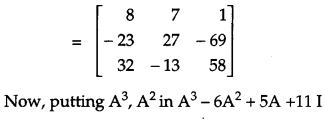
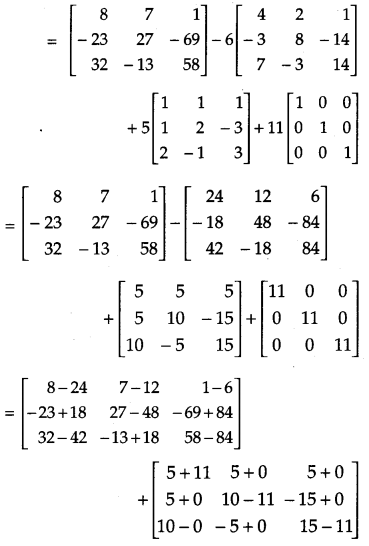
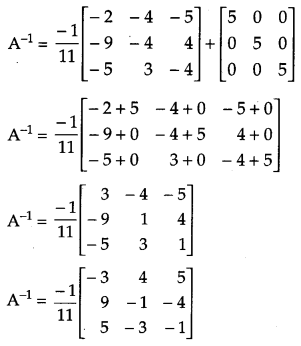
OR
Using matrix method, solve the following system of equations:
3x – 2y + 3z = 8
2x + y – z = 1
4x – 3y + 2z = 4
Solution:
The given equations are
3x – 2y + 3z = 8
2x + y – z = 1
4x – 3y + 2z = 4
These equations can be written in the form AX = B, where

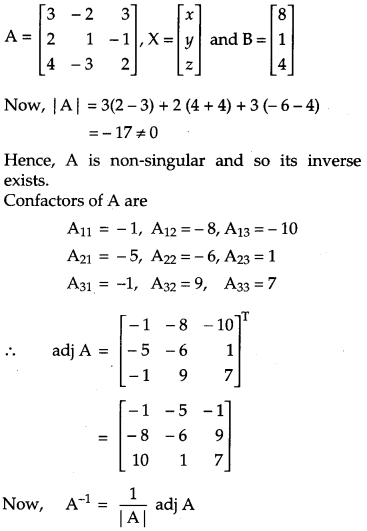
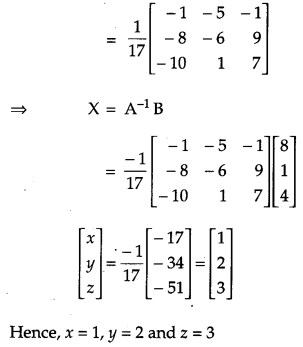
Question 26.
A bag contains 5 red and 4 black balls, a second bag contains 3 red and 6 black balls. One of the two bags is selected at random and two balls are drawn at random (without replacement) both of which are found to be red. Find the probability that the balls are drawn from the second bag. [6]
Solution:
Let E₁ be the event of choosing the bag I, E₂ be the event of choosing the bag II and A be the event of drawing a red ball.
Then,

CBSE Previous Year Question Papers