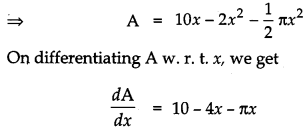CBSE Previous Year Question Papers Class 12 Maths 2017 Outside Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
**Answer is not given due to the change in present syllabus
CBSE Previous Year Question Papers Class 12 Maths 2017 Outside Delhi Set I
Section – A
Question 1.
If for any 2 × 2 square matrix A, A(adj A) = \(\left[\begin{array}{ll}{8} & {0} \\ {0} & {8}\end{array}\right]\) then write the value of | A |. [1]
Solution:
We have,
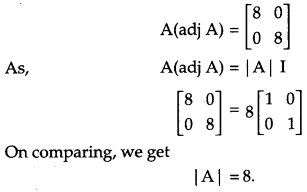
Question 2.
Determine the value of ‘k’ for which the following function is continuous at x = 3 [1]
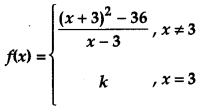
Solution:
Given,
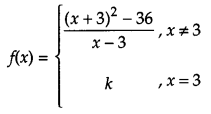
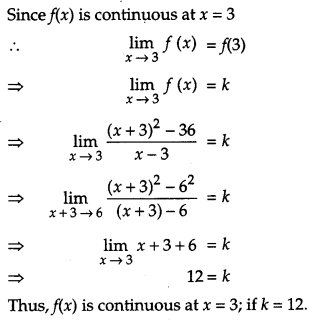
Question 3.
Find: \(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin x \cos x} d x\). [1]
Solution:
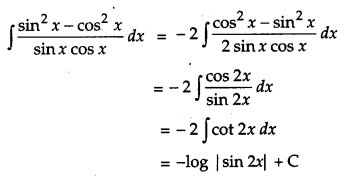
Question 4.
Find the distance between the planes 2x – y + 2z = 5 and 5x – 2.5y + 5z = 20. [1]
Solution:
Since, the direction ratios of the normal to the given planes are proportional.
i.e., \(\frac{2}{5}=\frac{-1}{-2.5}=\frac{2}{5}\)
Thus, the given planes are parallel.
Now, let P(x1, y1, z1) be any point on 2x – y + 2z – 5 = 0
Then, 2x1 – y1 + 2z1 – 5 = 0
or 5x1 – 2.5y1 + 5z1 – 12.5 = 0 …(i)
The length of the perpendicular from P(x1, y1, Z1) to 5x – 2.5y + 5z – 20 = 0,
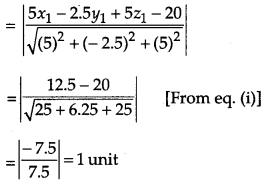
Therefore, the distance between the given planes is 1 unit.
Section – B
Question 5.
If A is a skew-symmetric matrix of order 3, then prove that det A = 0. [2]
Solution :
Given, A is a skew-symmetric matrix of order 3.
So, AT = -A
Now, |AT| = |-A |
|AT| = (-1 )3|A| [1 |kA | = kn | A | where n is order of A]
|A | = – | A| [ | AT | = | A | ]
⇒ |A| + |A| =0
∴ 2|A| = 0 or |A| = 0.
i.e., det A = 0 Hence Proved.
Question 6.
Find the value of c in Rolle’s theorem for the function f(x) = x2 – 3x in [-\( \sqrt{{3}} \), 0] [2]
Solution:
We know that the polynomial function f(x) = x2 – 3x is everywhere continuous and differentiable.
So, f(x) is continuous on [-\( \sqrt{{3}} \),0].
Also, f(x) is differentiable on(-\( \sqrt{{3}} \),0)
Now, f(-\( \sqrt{{3}} \)) = (-\( \sqrt{{3}} \))3 – 3 (-\( \sqrt{{3}} \))

Question 7.
The volume of a cube is increasing at the rate of 9 cm3/s. How fast is its surface area increasing when the length of an edge is 10 cm ? [2]
Solution:
Let, the side of the cube be a cm then, volume of cube (V) = a3
Differentiating V w.r.t.t, we get
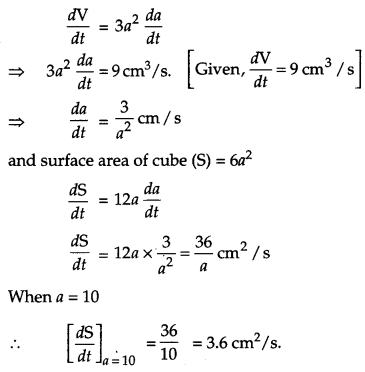
Question 8.
Show that the function f(x) = x3 – 3x2 + 6x – 100 is increasing on R. [2]
Solution:
We have,
f(x) = x3 – 3x2 + 6x – 100
then, f'(x) = 3x2 – 6x + 6
= 3(x2 – 2x + 1) + 3
= 3 (x – 1)2 + 3 > 0 for all x ϵ R.
Hence, the function f(x) is increasing on R.
Hence Proved
Question 9.
The x-coordinate of a point on the line joining the points P( 2, 2, 1) and Q (5, 1, – 2) is 4. Find its z-coordinate. [2]
Solution :
Given, the points P(2, 2, 1) and Q (5, 1, – 2) of a line.
Then, equation of line PQ,
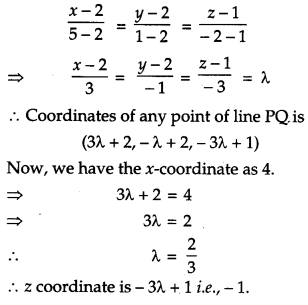
Question 10.
A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events. [2]
Solution:
Since, A be the event of number obtained is even then, A = {2, 4, 6}
and B be the event of number obtained is red

Hence, the events A and B are not independent events.
Question 11.
Two tailors, A and B earn ₹ 300 and ₹ 400 per day respectively. A can stitch 6 shirts and 4 pairs of trousers while B can stitch 10 shirts and 4 pairs of trousers per day. To find how many days should each of them work if it is desired to produce at least 60 shirts and 32 pairs of trousers at a minimum labour cost, formulate this as an LPP. [2]
Solution:
Let x and y be the number of days for which the tailors A and B work respectively.
Total cost per day = ₹ (300x + 400y)
Let Z denote the total cost in rupees, then,
Z = 300₹ + 400y
Since in one day 6 shirts are stitched by tailor A and 10 shirts are stitched by tailor B and it is desired to produce atleast 60 shirts.
∴ 6₹ + 10y ≥ 60
It is given that 4 pairs of trousers are stitched by each tailor A and B per day to produce atleast 32 pairs of trousers.
∴ 4₹ + 4y ≥ 32
Finally, the no. of shirts and pair of trousers cannot be negative.
∴ x ≥ 0, y ≥ 0
Thus, mathematical formulation of the given LPP is as follows:
Minimize Z = 300x + 400y
Subject to constraints:
6x + 10y ≥ 60
4x + 4y ≥ 32
x ≥ 0, y ≥ 0
Question 12
Find: \(\int \frac{d x}{5-8 x-x^{2}}\). [2]
Solution:
We have,
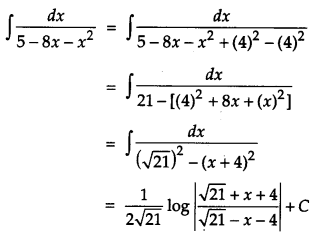
Section – C
Question 13.
If \(\tan ^{-1} \frac{x-3}{x-4}+\tan ^{-1} \frac{x+3}{x+4}=\frac{\pi}{4}\), then find the value of x.
Solution:
We have,
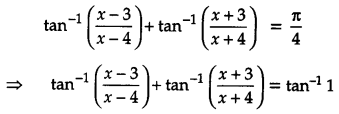
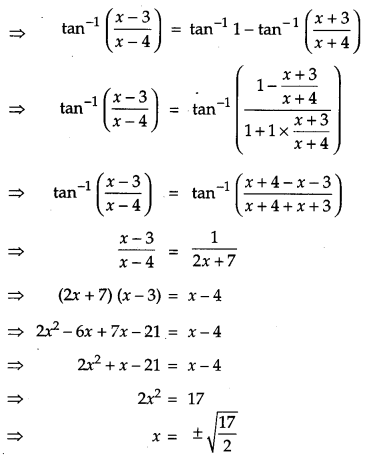
Question 14.
Using properties of determinants, prove that [1]
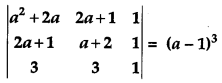
Solution:

OR
Find matrix A such that
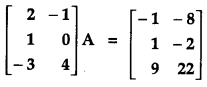
Solution:
We have,

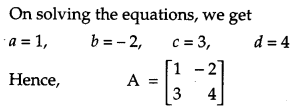
Question 15.
If xy + yx = ab, then find \(\frac{d y}{d x}\). [4]
Solution:
We have, xy + yx = ab
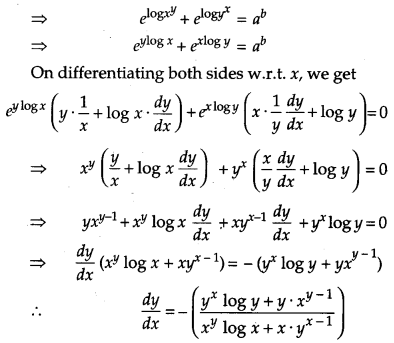
OR
If ey(x + 1) = 1, then show that \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\).
Solution:
We have,
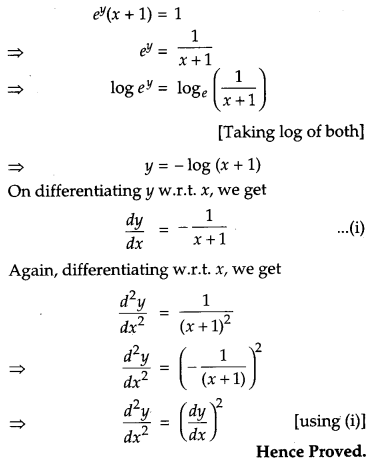
Question 16.
Find: [4]
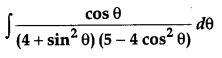
Solution:

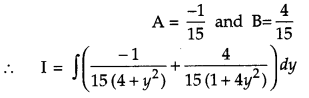
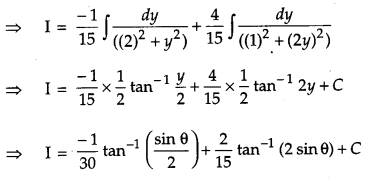
Question 17.
Evaluate: [4]
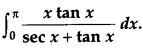
Solution:
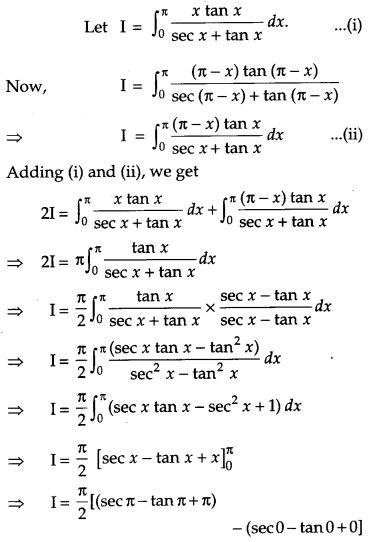
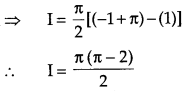
OR
Evaluate : \(\int_{1}^{4}\{|x-1|+|x-2|+|x-4|\} d x\)
Solution:
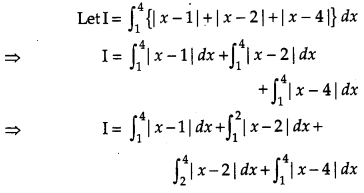
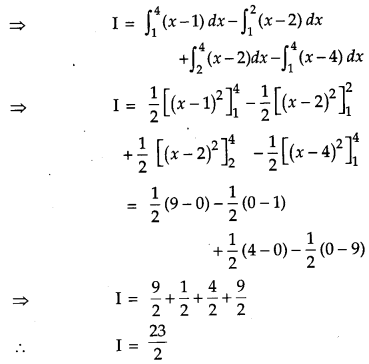
Question 18.
Solve the differential equation \(\left(\tan ^{-1} x-y\right) d x=\left(1+x^{2}\right) d y\) [4]
Solution:
We have,

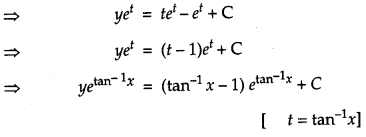
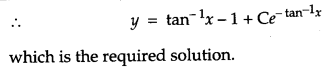
Question 19.
Show that the points A, B, C with position vectors \(2 \hat{i}-\hat{j}+\hat{k}, \quad \hat{i}-3 \hat{j}-5 \hat{k} \quad \text { and } \quad 3 \hat{i}-4 \hat{j}-4 \hat{k}\) respectively, are the vertices of a right-angled triangle. Hence, find the area of the triangle. [4]
Solution:
Given, the position vectors of the points A, B and C are \(2 \hat{i}-\hat{j}+\hat{k}, \quad \hat{i}-3 \hat{j}-5 \hat{k} \quad \text { and } \quad 3 \hat{i}-4 \hat{j}-4 \hat{k}\) respectively.
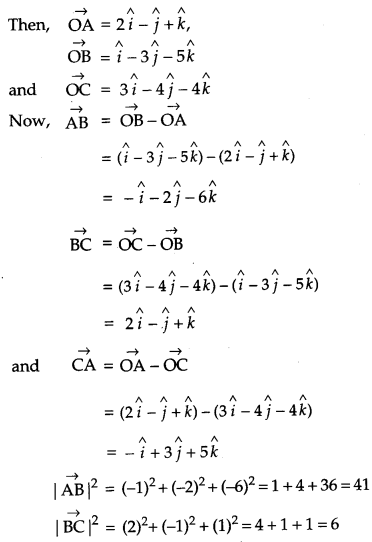

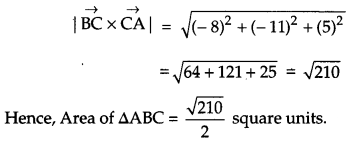
Question 20.
Find the value of X, if four points with position vectors \(3 \hat{i}+6 \hat{j}+9 \hat{k}, \hat{i}+2 \hat{j}+3 \hat{k}, 2 \hat{i}+3 \hat{j}+\hat{k}\) and \(4 \hat{i}+6 \hat{j}+\lambda \hat{k}\) are coplanar. [4]
Solution:
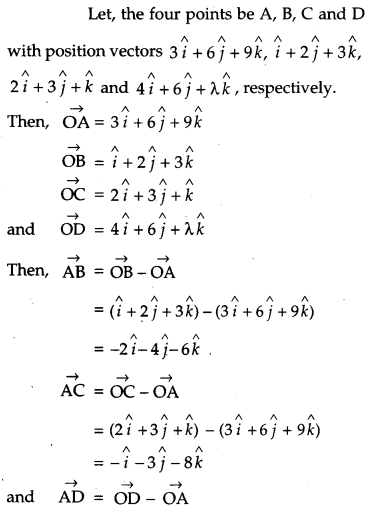
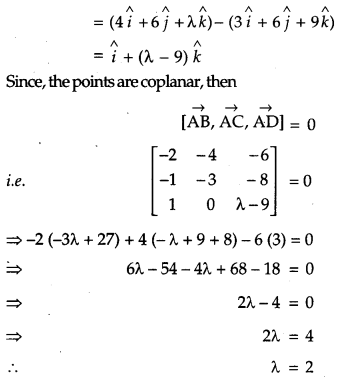
Question 21.
There are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean and variance of X. [4]
Solution:
Given, X denote the sum of the numbers on the two drawn cards.
Then, X can take values 4, 6, 8,10,12 and sample space (S) = {(1, 3), (1, 5), (1, 7), (3, 1), (3, 5), (3, 7), (5, 1), (5, 3), (5, 7), (7, 1), (7, 3), (7, 5)]
So, the probability distribution of X is as given below:
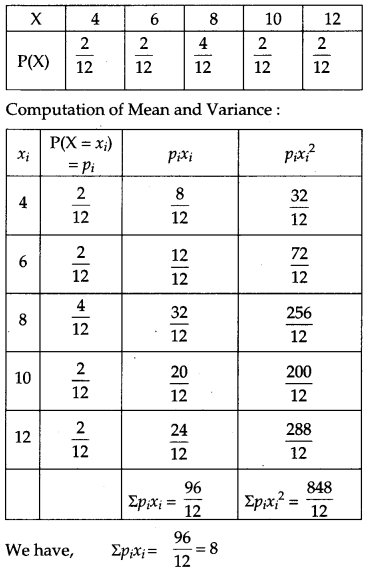
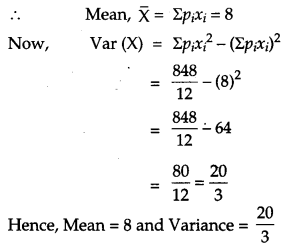
Question 22.
Of the students in a school, it is known that 30% have 100% attendance and 70% students are irregular. Previous year results report that 70% of all students who have 100% attendance attain A grade and 10% irregular students attain A grade in their annual examination. At the end of the year, one student is chosen at random from the school and he was found to have an A grade. What is the probability that the student has 100% attendance ? Is regularity required only in school ? Justify your answer. [4]
Solution:
Consider the following events:
A : the student has grade A.
E1 : the student has 100% attendance.
E2 : the student is irregular.
Then, probability of the students having 100% attendance:
P(E1) = 30% = 0.3
Similarly, P(E2) = 70% = 0.7
Now, by previous year report, the probability of the students having grade A who have 100% attendance:
P(A/E1) = 70% = 0.7
and the probability of the students having grade A who are irregular :
P(A/E2) = 10% = 0.1
Then, the probability of the student having 100% attendance who already has attain A grade = P(E1/A)
By Bayes’ theorem,
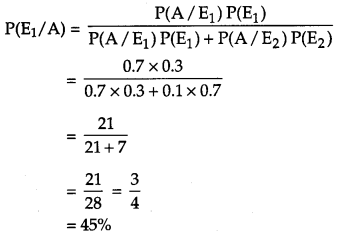
No, regularity is required in school as well as in life.
It helps to be disciplined in every aspect of life. Or, when you work regularly, inspiration strikes regularly.
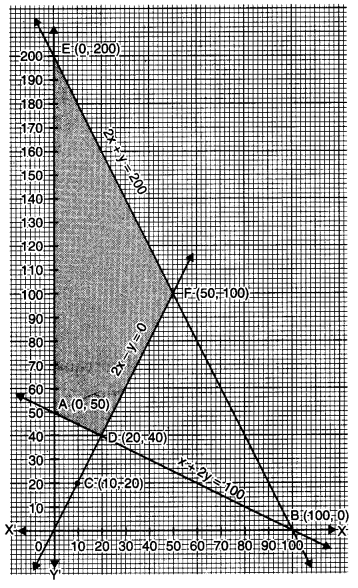
Question 23.
Maximise Z = x + 2y
subject to the constraints :
x + 2y ≥ 100 2x – y ≤ 0
2x + y ≤ 200 x, y ≥ 0
Solve the above LPP graphically. [4]
Solution:
Given,
Maximise Z = x + 2y
Subject to the constraints :
x + 2y ≥ 100 2x – y ≤ 0
2x + y ≤ 200 x, y ≥ 0
Converting the inequations into equations we obtain the lines
x + 2y = 100,
2x – y = 0,
2 x + y = 200.
Then, x + 2y = 100

Plotting these points on the graph, we get the shaded feasible region i.e., ADFEA.

Section – D
Question 24.
Determine the product: \(\left[\begin{array}{rrr}{-4} & {4} & {4} \\ {-7} & {1} & {3} \\ {5} & {-3} & {-1}\end{array}\right]\left[\begin{array}{rrr}{1} & {-1} & {1} \\ {1} & {-2} & {-2} \\ {2} & {1} & {3}\end{array}\right]\) and use it to solve the system equations x – y + z = 4, x – 2y – 2z = 9, 2x + y + 3z = 1. [6]
Solution:
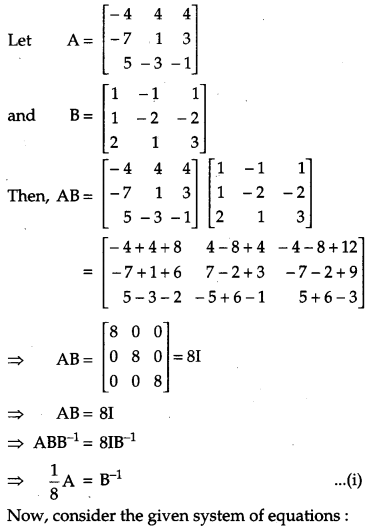
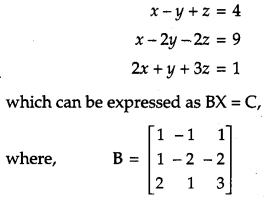
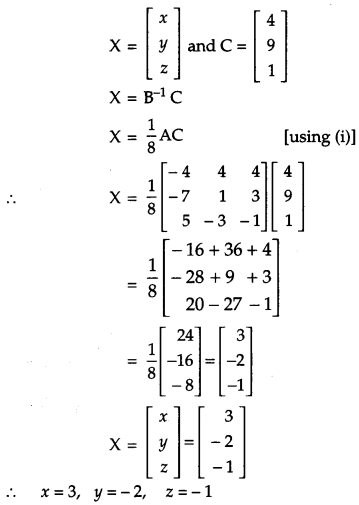
Question 25.
Consider f : \(\mathbf{R}-\left\{-\frac{4}{3}\right\} \rightarrow \boldsymbol{R}-\left\{\frac{\mathbf{4}}{3}\right\}\) given by \(f(x)=\frac{4 x+3}{3 x+4}\). Show that f is bijective. Find the inverse of f and hence find f-1(0) and x such that f-1(x) = 2. [6]
Solution:
For one-one:

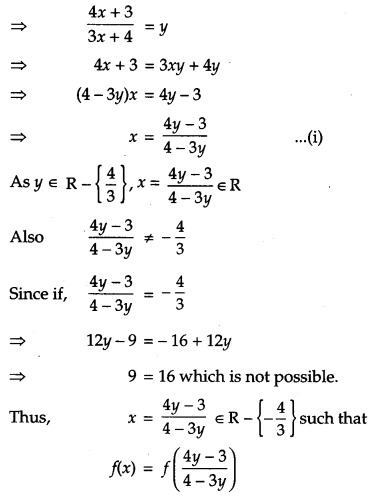

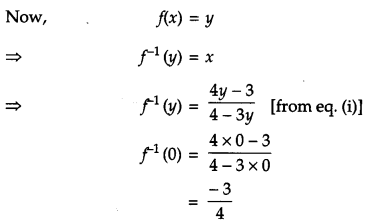
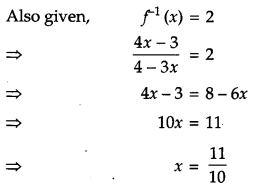
OR
Let A = Q × Q and let * be a binary operation on A defined by (a, b) * (c, d) = (ac, b + ad) for (a, b), (c, d) ϵ A. Determine, whether * is commutative and associative. Then, with respect to * on A.**
(i) Find the identity element in A
(ii) Find the invertible elements of A.
Question 26.
Show that the surface area of a closed cuboid with square base and given volume is minimum, when it is a cube. [6]
Solution:
Let the length and breadth of the cuboid of square base be x and height be y.

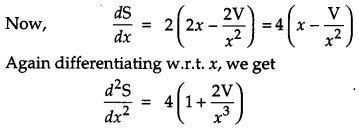
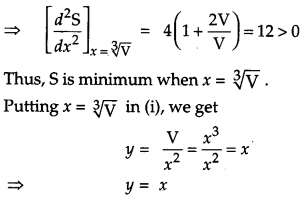
Hence, it is a cube since the length, breadth and height of a cube are equal. Hence Proved.
Question 27.
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4). [6]
Solution:
We have, A(4, 1), B (6, 6) and C(8, 4) as the vertices of a triangle ABC.
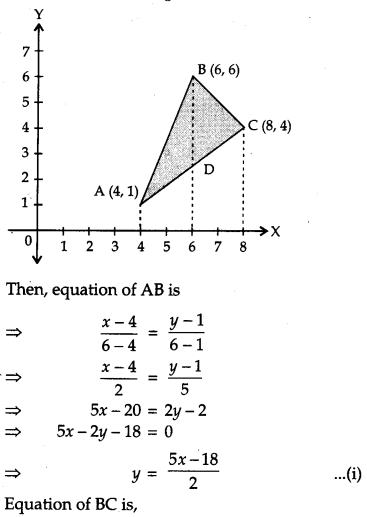


OR
Find the area enclosed between the parabola 4y = 3x2 and the straight line 3x – 2y + 12 = 0.
Solution :
Given, the equation 4y = 3x2 and 3x – 2y + 12 = 0.
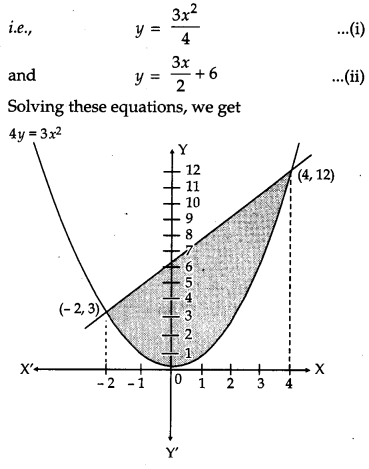

Question 28.
Find the particular solution of the differential equation (x – y)\(\frac{d y}{d x}\) = (x + 2y), given that y = 0 when x = 1. [6]
Solution:
We have,

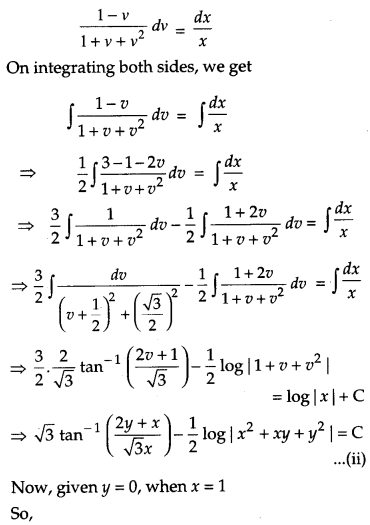
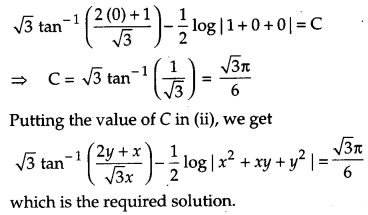
Question 29.
Find the coordinates of the point where the line through the points (3, -4, -5) and (2, – 3, 1), crosses the plane determined by the points (1, 2, 3),(4, 2, -3) and (0, 4, 3). [6]
Solution:
Equation of the plane determined by the points (1, 2, 3), (4, 2, – 3) and (0, 4, 3) is
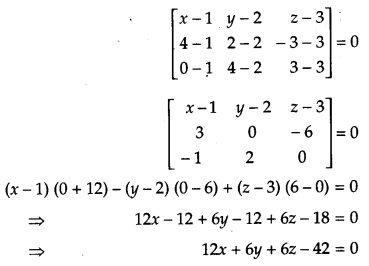

OR
A variable plane which remains at a constant distance 3p from the origin cuts, the coordinate axes at A, B, C. Show that the locus of the centroid of triangle ABC is
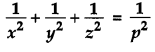
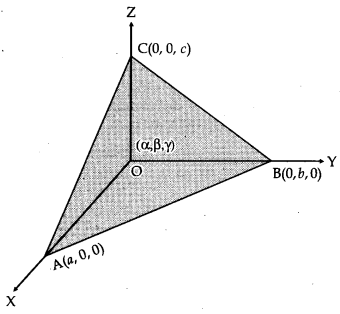
Solution:
Let the coordinates of A, B, C are (a, 0,0), (0, b, 0) and (0,0, c)


CBSE Previous Year Question Papers Class 12 Maths 2017 Outside Delhi Set II
Note : Except for the following questions, all the remaining questions have been asked in previous set.
Section – B
Question 12.
The length x, of a rectangle is decreasing at the rate of 5 cm/minute and the width y, is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rate of change of the area of the rectangle. [2]
Solution:
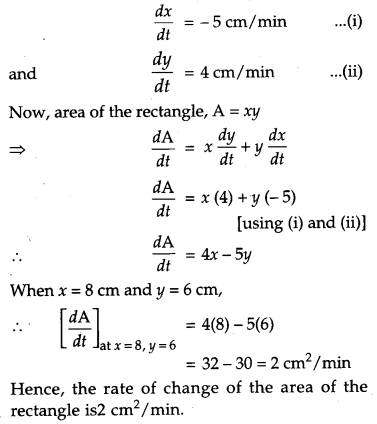
Section – C
Question 20.
Find: \(\int \frac{\sin \theta d \theta}{\left(4+\cos ^{2} \theta\right)\left(2-\sin ^{2} \theta\right)}\). [4]
Solution:
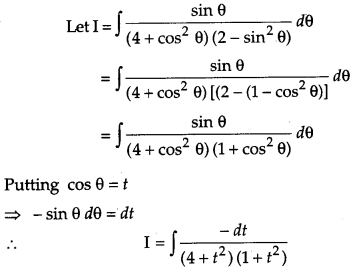

Question 21.
Solve the following linear programming problem graphically:
Maximise Z = 34x + 45y
under the following constraints
x + y ≤ 300
2x + 3y ≤ 70
x ≥ 0, y ≥ 0 [4]
Solution:
We have,
Maximise Z = 34x + 45y
Subject to the constraints :
x + y ≤ 300
2x + 3y ≤ 70
x ≥ 0, y ≥ 0
Converting the given inequalities into equations, we obtain the following equations :
x + y = 300
2x + 3y = 70
Then, x + y = 300
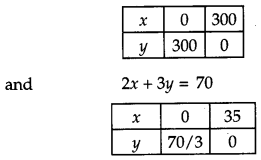
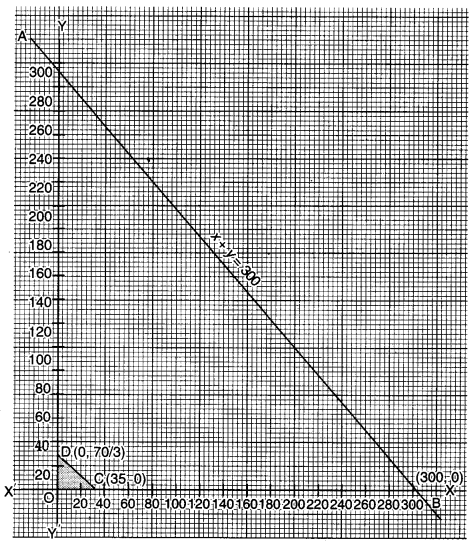
Plotting these points on the graph, we get the shaded feasible region i.e., OCDO.
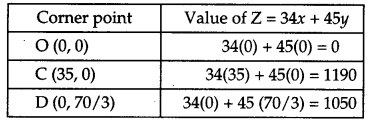
Clearly, the maximum value of Z is 1190 at (35, 0).
Question 22.
Find the value of x such that the points A (3, 2, 1), B (4, x, 5), C(4, 2, – 2) and D (6, 5, – 1) are coplanar. [4]
Solution:
Given, the points A(3, 2, 1), B (4, x, 5), C (4, 2, – 2) and D (6, 5, -1).
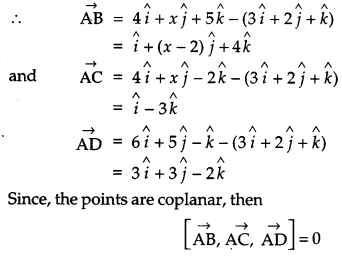
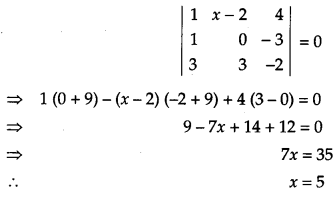
Question 23.
Find the general solution of the differential equation:
y dx – (x + 2y2) dy = 0 [4]
Solution:
We have,
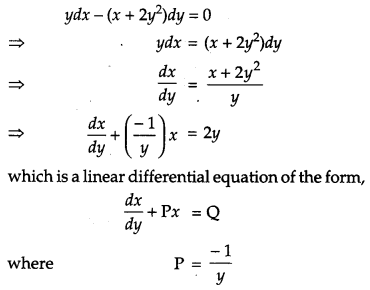
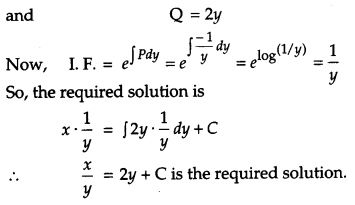
Section – D
Question 28.
AB is the diameter of a circle and C is any point on the circle. Show that the area of triangle ABC is maximum, when it is an isosceles triangle. [6]
Solution:
Let r be the radius of the circle then,
AB = 2 r ( AB is diameter)
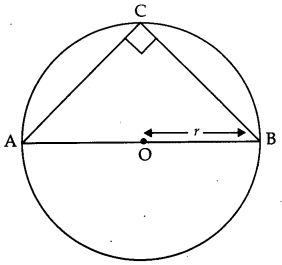
Let, BC = x units
We know that angle subtended by diameter in a circle is right angle
∴ ∠C = 90°



Question 29.
If A = \(\left[\begin{array}{rrr}{2} & {-3} & {5} \\ {3} & {2} & {-4} \\ {1} & {1} & {-2}\end{array}\right]\) , find A-1. Hence using A-1 solve the system of equations 2x – 3y + 5z = 11, 3x + 2y – 4z = -5, x + y – 2z = -3.
Solution:
We have,
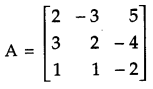
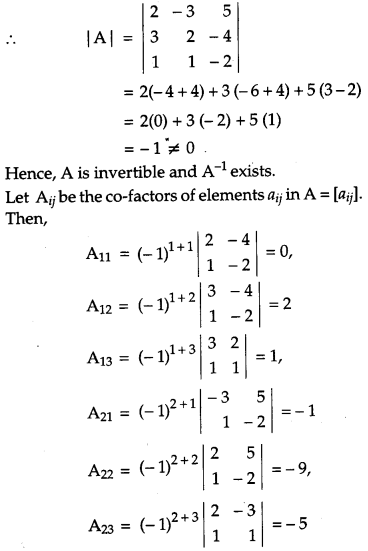
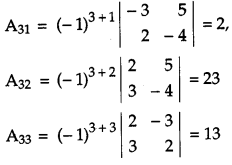

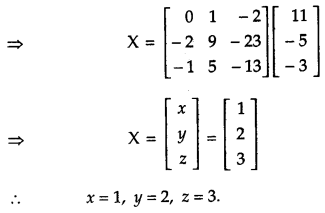
CBSE Previous Year Question Papers Class 12 Maths 2017 Outside Delhi Set III
Note : Except for the following questions, all the remaining questions have been asked in previous sets.
Section – B
Question 12.
The volume of a sphere is increasing at the rate of 8 cm3/s. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm. [2]
Solution:
We have,
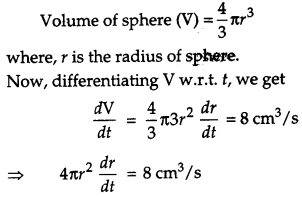

Section – C
Question 20.
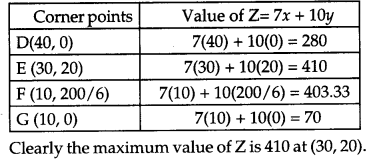
Solve the following linear programming problem graphically: [4]
Maximise Z = 7x + 10y
subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Solution:
We have,
Maximise Z = 7x + 10y
Subject to the constraints :
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Converting the given inequalities into equations, we obtain the following equations :
4x + 6y = 240
6x + 3y = 240
x = 10
Then, 4x + 6y = 240

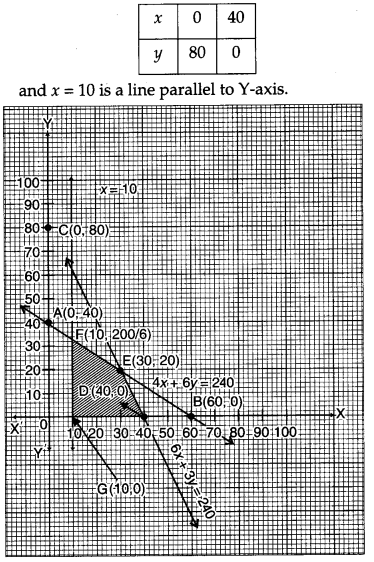
Plotting these points on the graph, we get the shaded feasible region i.e., DEFGD.
Question 21.
Find: \(\int \frac{e^{x} d x}{\left(e^{x}-1\right)^{2}\left(e^{x}+2\right)}\) [4]
Solution:
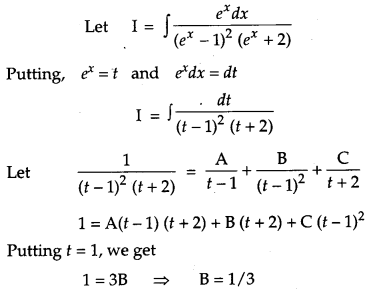
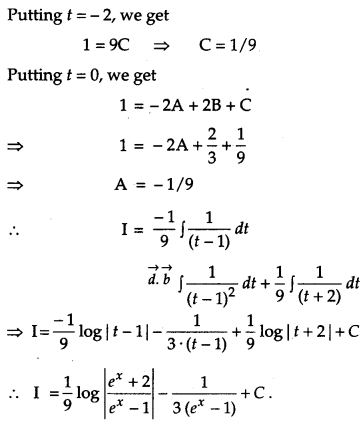
Question 22.
If \(\vec{a}=2 \hat{i}-\hat{j}-2 \hat{k} \text { and } \vec{b}=7 \hat{i}+2 \hat{j}-3 \hat{k}\) then express \(\vec{b}\) in the form of \(\vec{b}=\overrightarrow{b_{1}}+\overrightarrow{b_{2}}\), where \(\overrightarrow{b_{1}}\) is parallel to \(\vec{a} \text { and } \vec{b}_{2}\) is perpendicular to \(\vec{a}\). [4]
Solution:
We have,
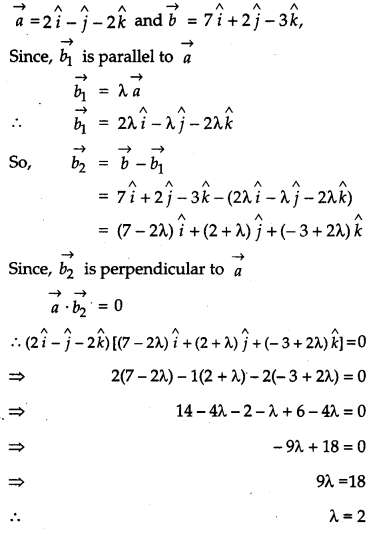
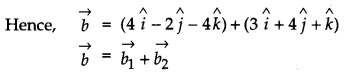
Question 23.
Find the general solution of the differential equation \(\frac{d y}{d x}\) – y = sin x. [4]
Solution:
We have,

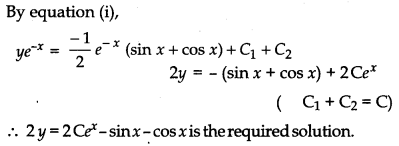
Section – D
Question 29.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening. [6]
Solution:
Let ABCD be a window of rectangular form surmounted by a semicircle with diameter AB.