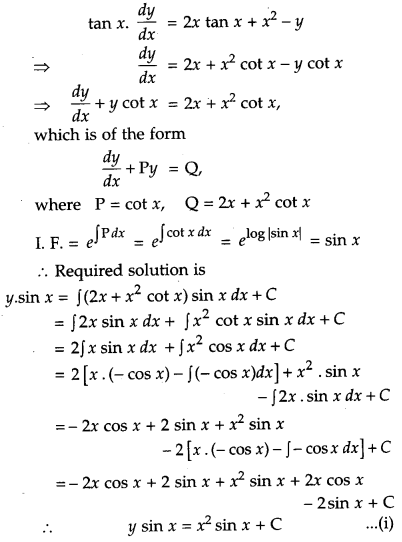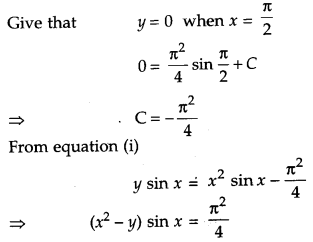CBSE Previous Year Question Papers Class 12 Maths 2017 Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
**Answer is not given due to the change in present syllabus
CBSE Previous Year Question Papers Class 12 Maths 2017 Delhi Set I
Section – A
Question 1.
If A is a 3 × 3 invertible matrix, then what will be the value of k if det (A-1) = (det A)k. [1]
Solution:
Given, A is an invertible matrix.
∴ A. A-1 = I
⇒ det (A.A-1) = det (I)
⇒ det (A).det(A-1) = 1 [ ∵ det(I) = 1]
⇒ det (A), (det A)k = 1 [∵ det(A-1)=(det A)k]
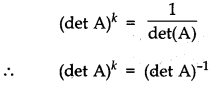
on comparing both sides, we get
k = -1
Question 2.
Determine the value of the constant ‘k’ so that the function f(x) = \(\left\{\begin{array}{l}{\frac{k x}{|x|}, \text { if } x<0} \\ {3, \text { if } x \geq 0}\end{array}\right.\) is continuous at x = 0. [1]
Solution:
Given, that the function is continuous
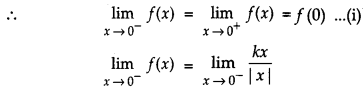
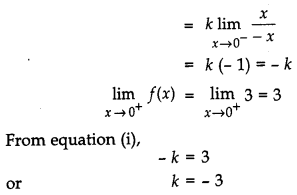
Question 3.
Evaluate: \(\int_{2}^{3} 3^{x} d x\). [1]
Solution:

Question 4.
If a line makes angles 90° and 60° respectively with the positive directions of X and Y-axes, find the angle which it makes with the positive direction of Z-axis. [1]
Solution:
We know that:
l2 + m2 + n2 = 1 …(i)
and l = cos α, m = cos β, n = cos γ
Given, α = 90°, β = 60°
∴ cos α = cos 90° = 0 and cos β = cos 60° = \(\frac{1}{2}\)
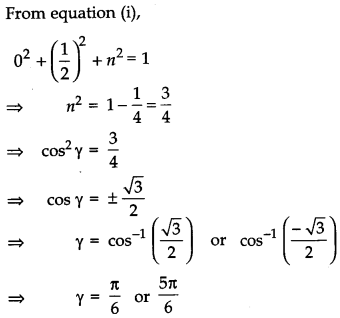
Section – B
Question 5.
Show that all the diagonal elements of a skew symmetric matrix are zero. [2]
Solution:
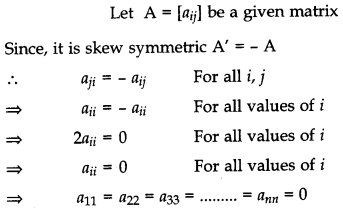
Hence, all the diagonal elements of a skew, symmetric matrix are zero (as diagonal elements are : a11; a22, …….. ann). Hence Proved.
Question 6.
Find \(\frac{d y}{d x}\) at x = 1, y = \(\frac{\pi}{4}\) if sin2 y + cos xy = K. [2]
Solution:
Given, sin2 y + cos xy = K
Differentiating both sides w.r.t x, we get
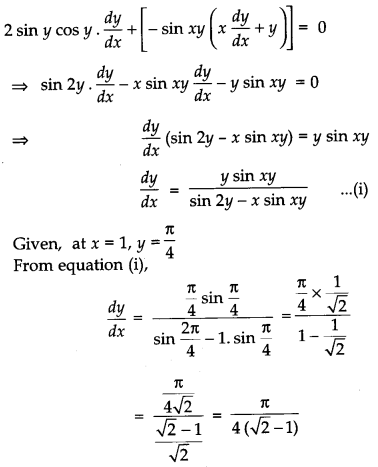
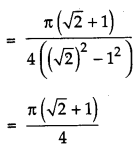
Question 7.
The volume of a sphere is increasing at the rate of 3 cubic centimetre per second. Find the rate of increase of its surface area, when the radius is 2 cm. [2]
Solution:
Let V be the volume and r be the radius of sphere at any time t.

∴ Rate of increase of surface area of the sphere is 3 square centimetre per second.
Question 8.
Show that the function f(x) = 4x3 – 18x2 + 27x – 7 is always increasing on R. [2]
Solution:
Given, f(x)= 4x3 – 18x2 + 27x – 7
Differentiating f(x) w.r.t. x, we get
f'(x) = 12x2 – 36x + 27 = 3(4x2 – 12x + 9)
= 3(2x – 3)2 for any x ϵ R
3 > 0 and (2x – 3)2 ≥ 0
∴ f'(x) ≥ o
⇒ The fimction is always increasing on R.
Question 9.
Find the vector equation of the line passing through the point A(1, 2, -1) and parallel to the line 5x – 25 = 14 – 7y = 35z. [2]
Solution:
Given line is 5x – 25 = 14 – 7y = 35z
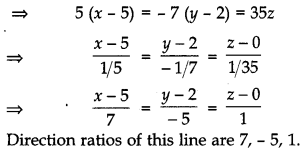
∴ Vector equation of the line which passes through the point A (1, 2, – 1) and its direction ratio are proportional to 7, – 5, 1 is
![]()
Question 10.
Prove that if E and F are independent events, then the events E and F’ are also independent. [2]
Solution:
Since E and F are independent events :
P(E ∩ F) = P (E) . P (F) …(i)
P(E ∩ F’) = P (E) – P (E ∩ F)
= P (E) – P (E) P (F) [From (i)]
= P(E)(1 – P(F))
= P (E) P (F’)
∴ E and F’ are also independent. Hence Proved.
Question 11.
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is ₹ 100 and that on a bracelet is ₹ 300. Formulate an L.P.P. for finding how many of each should be produced daily to maximize the profit ? It is being given that at least one of each must be produced. [2]
Solution:
Let the manufacturer produces x pieces of necklaces and y pieces of bracelets.
Since total number of necklaces and bracelets that can be handle per day are 24.
so, x + y ≤ 24 …(i)
To make bracelet one needs one hour and half an hour is need to make necklace and maximum time available is 16 hours
so, \(\frac{1}{2}\)x + y ≤ 16 ….(ii)
Now, let Z be the profit and we have to maximize it, so our LPP will be
Maximize Z = 100x + 300y
Subject to constraints :
x + y ≤ 24
\(\frac{1}{2}\) x + y ≤ 16
or x + 2y ≤ 32
and x, y ≥ 1
Question 12.
Find: \(\int \frac{d x}{x^{2}+4 x+8}\). [2]
Solution:
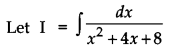
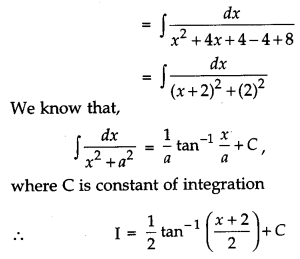
Section – C
Question 13.
Prove that [4]
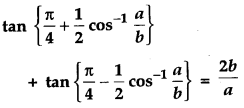
Solution:
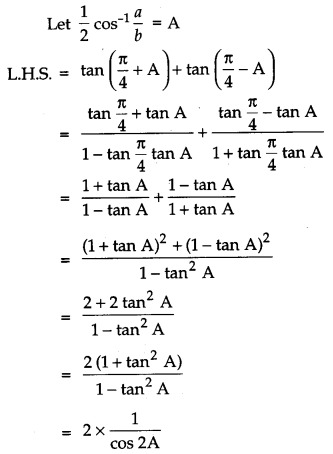
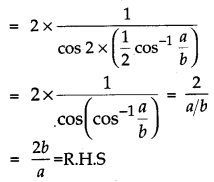
Question 14.
Using properties of determinants, prove that: [4]
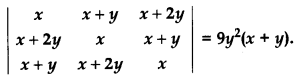
Solution:
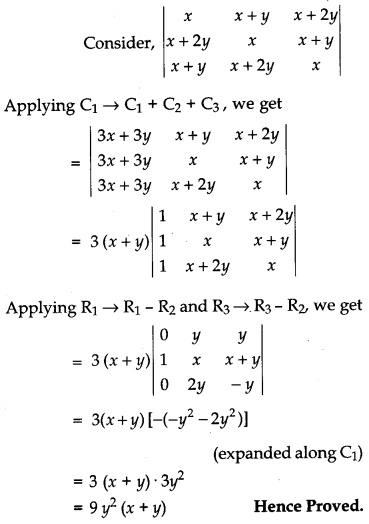
OR
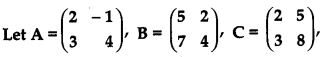
find the matrix D such that CD – AB = 0.
Solution:
Let D be the matrix of order 2 × 2,
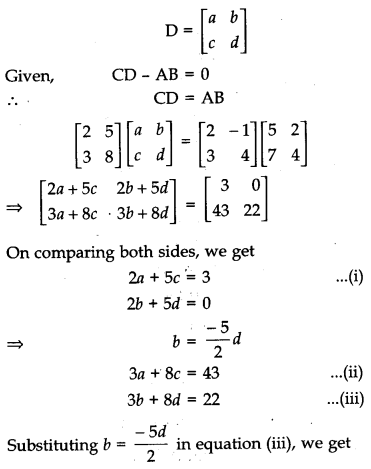

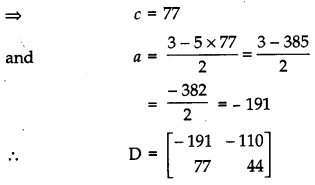
Question 15.
Differentiate the function (sin x)x + sin-1 \(\sqrt{x}\) with respect to x.
Solution:
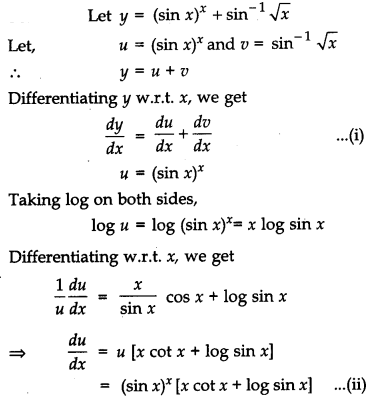
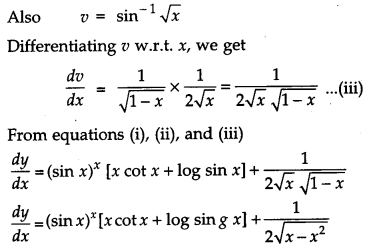
OR
IF xmyn = (x + y)m+n, prove that \(\frac{d^{2} y}{d x^{2}}\) = 0.
Solution:
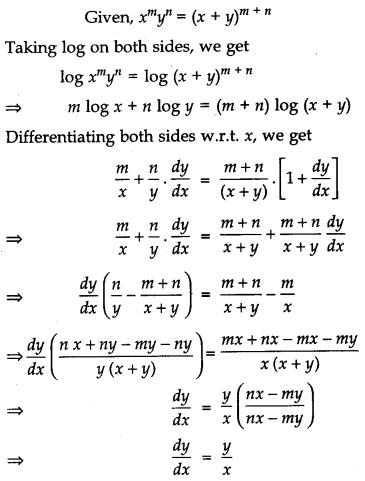
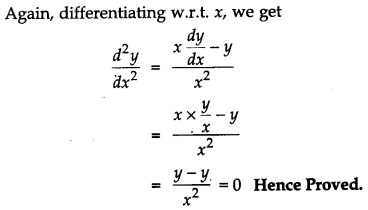
Question 16.
Find [4]
![]()
Solution:
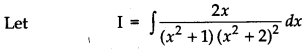


Question 17.
Evaluate: [4]
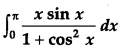
Solution:
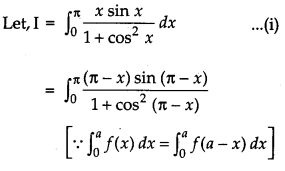
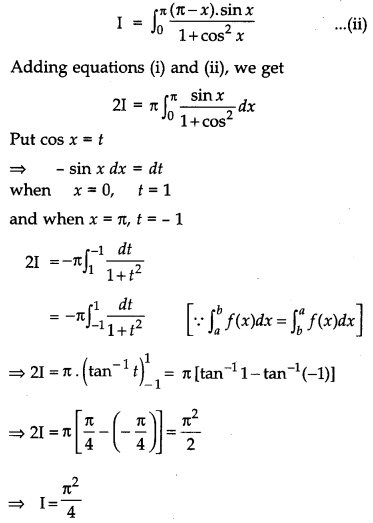
OR
Evaluate: ![]()
Solution:
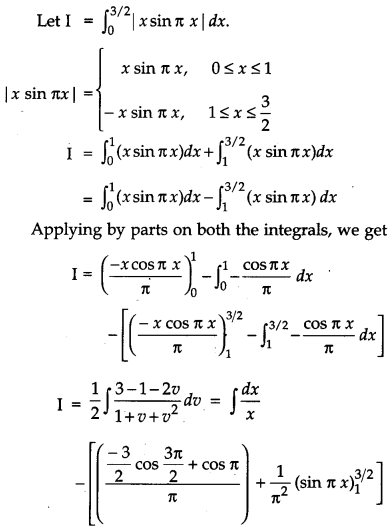
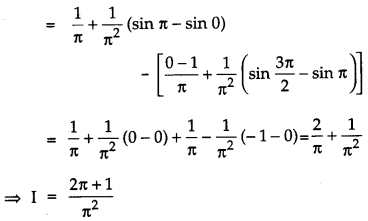
Question 18.
Prove that x2 – y2 = c(x2 +y2)2 is the general solution of the differential equation (x3 – 3xy2) dx = (y3 – 3x2y) dy, where c is a parameter. [4]
Solution:
Given differential equation is,



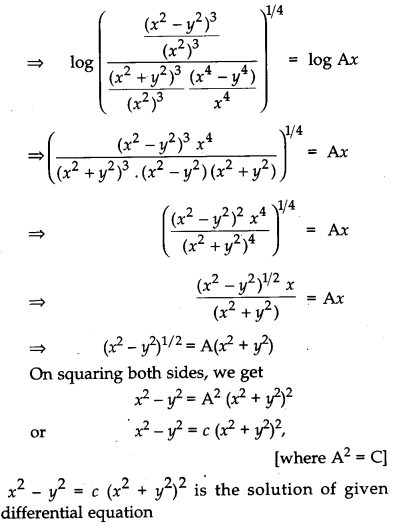
Question 19.
Let \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=\hat{i} \text { and } \vec{c}=c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}\) then:
(a) Let c1 = 1 and c2 = 2, find c3 which makes \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar.
(b) If c2 = – 1 and c3 = 1, show that no value of c1 can make \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar. [4]
Solution:
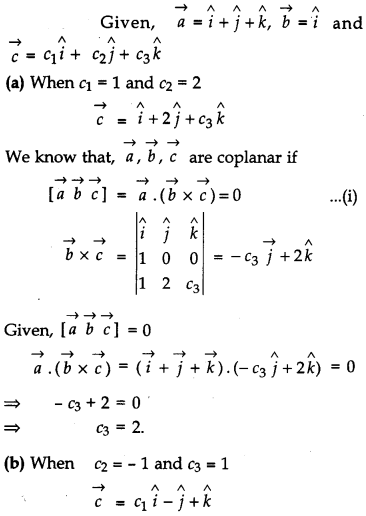
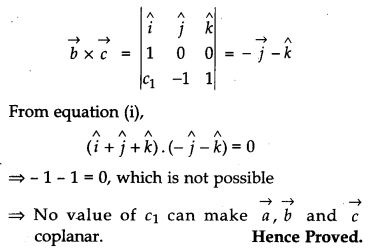
Question 20.
If \(\vec{a}, \vec{b}, \vec{c}\) are mutually perpendicular vectors of equal magnitudes, show that the vector \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined to \(\vec{a}, \vec{b} \text { and } \vec{c}\). Also, find the angle which \(\vec{a}+\vec{b}+\vec{c}\) makes with \(\vec{a} \text { or } \vec{b} \text { or } \vec{c}\). [4]
Solution:
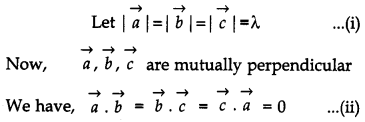
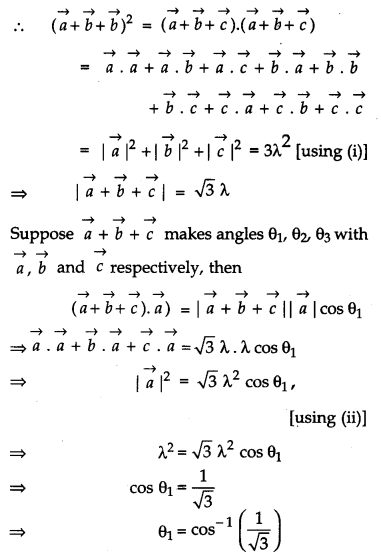
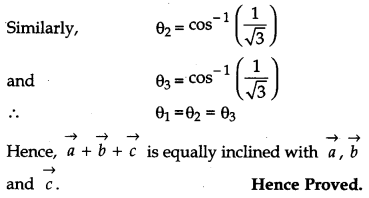
Question 21.
The random variable X can take only the values 0, 1, 2, 3. Given that P (X = 0) = P (X = 1) = p and P(X = 2) = P(X = 3) such that Σpixi2 = 2Σpixi , find the value of p. [4]
Solution:
Given, P(X = 0) = P(X = 1) = p and P(X = 2) = P (X = 3)
Let P (X = 2) = P(X = 3) = k
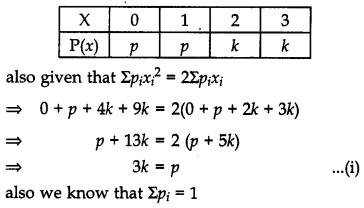
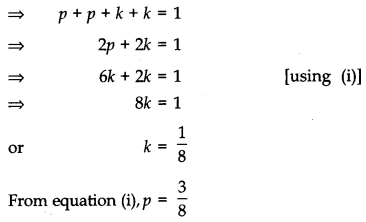
Question 22.
Often it is taken that a truthful person commands, more respect in the society. A man is known to speak the truth 4 out of 5 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
Do you also agree that the value of truthfulness leads to more respect in the society ? [4]
Solution:
Let E1, E2 and A be the events defined as follows:
E1 = Six appears on throwing a die.
E2 = Six does not appear on throwing a die.
and A = the man reports that it is a six We have,
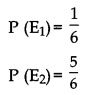
Now P(A/E1) = Probability that the man reports that there is a six on the die given that six has occurred on the die = 4/5 (probability that the man speaks truth)
and P(A/E2) = Probability that the man reports that there is a six on the die given that six has not occurred on the die (probability that the man does not speak truth).
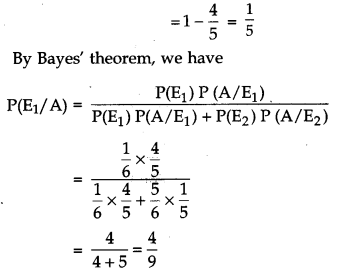
Yes, truthfulness always leads to more respect in the society as truth always wins.
Question 23.
Solve the following L.P.P. graphically : Minimise Z = 5x + 10y Subject to constraints
x + 2y ≤ 120
x + y ≥ 60
x – 2y ≥ 0
and x, y ≥ 0 [4]
Solution:
We have,
Minimise Z = 5x + 10y
Subject to the constraints :
x + 2y ≤ 120
x + y ≥ 60
x – 2y ≥ 0
and x, y ≥ 0
Converting the given inequalities into equations, we obtain the following equations :
x + 2y = 120
x + y = 60
x – 2y = 0
Then, x + 2y = 120
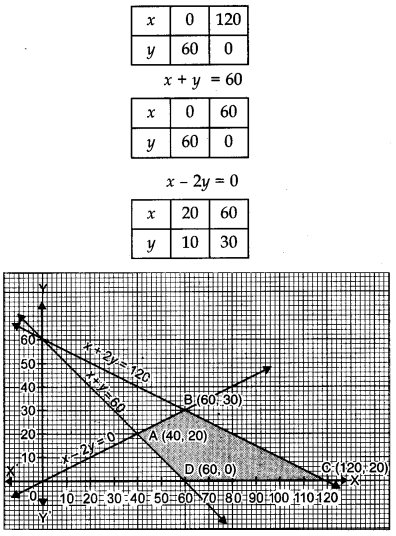
The shaded region ABCD represented by the given constraints is the feasible region. Comer points of the common shaded region are A (40, 20), B (60, 30), C (120, 0) and D (60, 0). Value of Z at each corner point is given as :

Hence, minimum value of Z is 300 at (60, 0).
Section – D
Question 24.
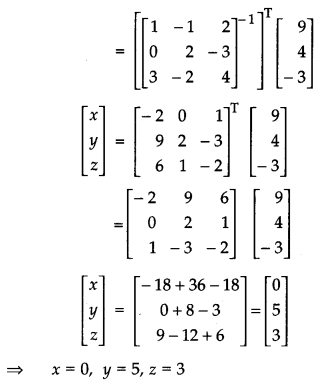
Use product \(\left[\begin{array}{rrr}{1} & {-1} & {2} \\ {0} & {2} & {-3} \\ {3} & {-2} & {4}\end{array}\right]\left[\begin{array}{rrr}{-2} & {0} & {1} \\ {9} & {2} & {-3} \\ {6} & {1} & {-2}\end{array}\right]\) to solve the system of equations x + 3z = 9, – x + 2y – 2z = 4, 2x – 3y + 4z = 3. [6]
Solution:
Consider,

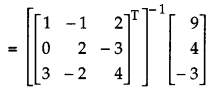
Question 25.
Consider f : R+ → [- 5, ∞), given by f(x) = 9x2 + 6x – 5. Show that f is invertible with f-1(y) = \(\left(\frac{\sqrt{y+6}-1}{3}\right)\). [6]
hence find:
(i) f-1(10)
(ii) y if f-1(y) = \(\frac{4}{3}\),
where R+ is the set of all non-negative real numbers.
Solution:
For one-one :
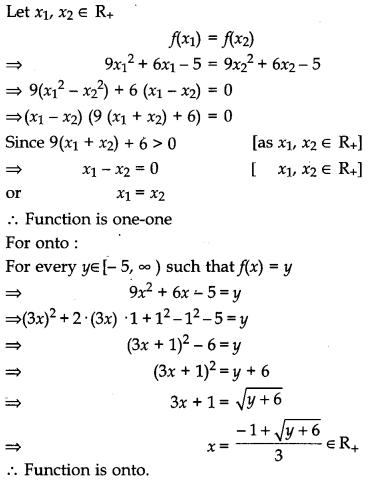

OR
Discuss the commutativity and associativity of binary operation defined on A = Q – {1} by the rule a * b = a – b + ab for all, a, b ϵ A. Also find the identity element of * in A and hence find the invertible elements of A.**
Question 26.
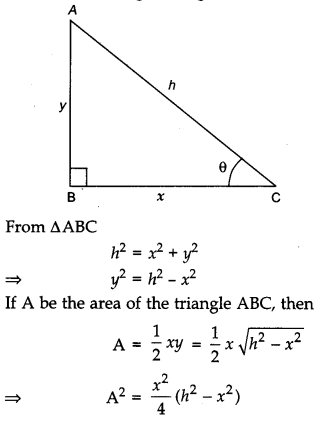
If the sum of lengths of the hypotenuse and a side of a right angled triangle is given, show that the area of the triangle is maximum, when the angle between them is \(\frac{\pi}{3}\).
Solution:
Let h, x and y be the length of hypotenuse and sides of the right triangle ABC.
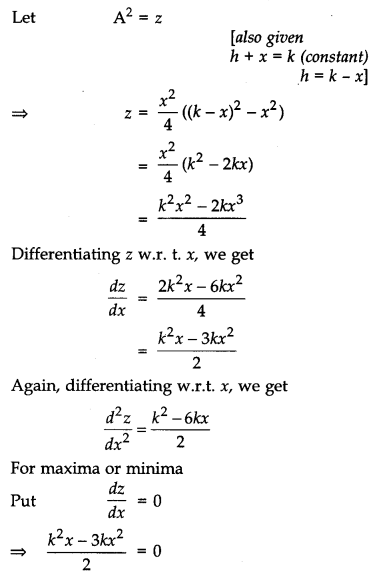
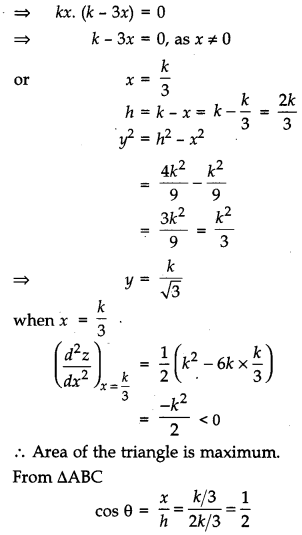
![]()
Question 27.
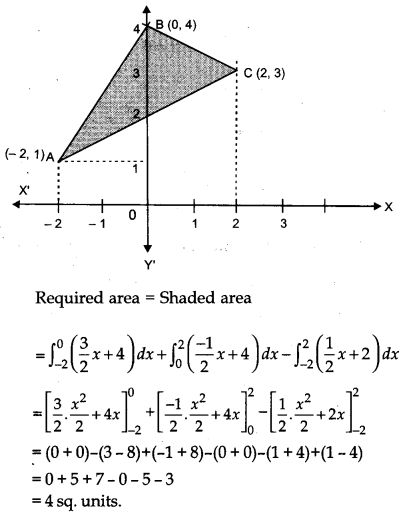
Using integration, find the area of region bounded by the triangle whose vertices are (- 2, 1), (0, 4) and (2, 3). [6]
Solution:
The vertices of the ∆ABC are A(- 2, 1), B(0, 4) and C(2, 3).
Equation of the side AB is

OR
Find the area bounded by the circle x2 + y2 = 16 and the line \( \sqrt{{3}} \)y = x in the first quadrant, using integration.
Solution:
Given, x = \( \sqrt{{3}} \)y
and x2 + y2 = 16,
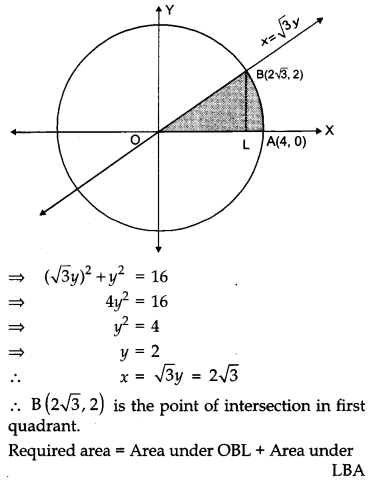
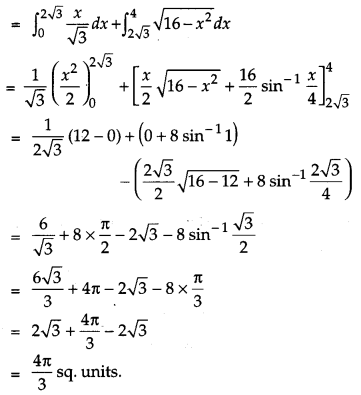
Question 28.
Solve the differential equation x\(\frac{d y}{d x}\) + y = x cos x + sin x, given that y = 1 when x = \(\frac{\pi}{2}\).[6]
Solution:
Given differential equation is :
![]()

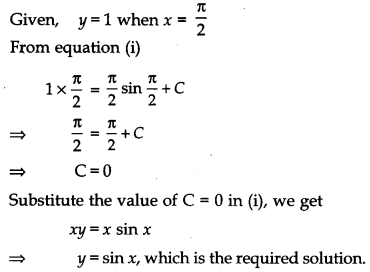
Question 29.
Find the equation of the plane through the line of intersection of \(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+4 \hat{k})=1\) and \(\vec{r} \cdot(\hat{i}-\hat{j})+4=0\) and perpendicular to the plane \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})+8=0\). Hence find whether the plane thus obtained contains the line x – 1 = 2y – 4 = 3z – 12. [6]
Solution:
The equation of the plane passing through the line of intersection of the given planes is :
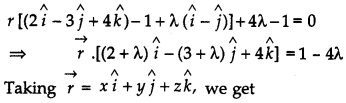


OR
Find the vector and Cartesian equations of a line passing through (1, 2, – 4) and perpendicular to the two lines \(\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}\) and \(\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}\).
Solution:
Cartesian equation of the line passing through (1, 2, – 4) is
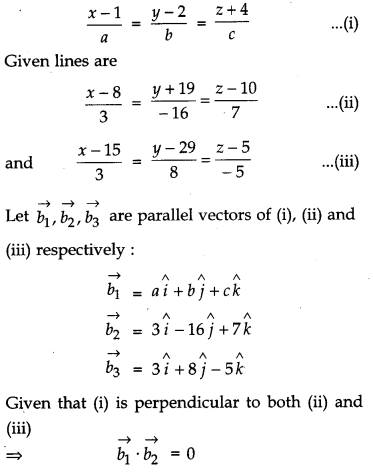
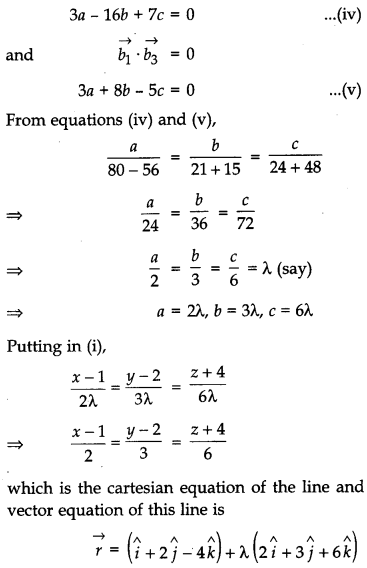
CBSE Previous Year Question Papers Class 12 Maths 2017 Delhi Set II
Note : Except for the following questions, all the remaining questions have been asked in previous set.
Section – B
Question 12.
For the curve y = 5x – 2x3, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when 2 = 3. [2]
Solution:
Given curve is,
y = 5x – 2x3
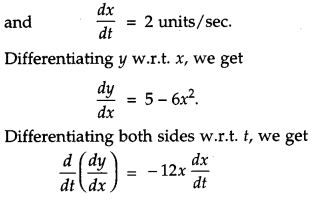
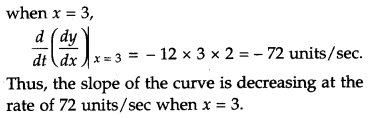
Section – C
Question 20.
The random variable X can take only the values 0, 1, 2, 3. Given that P(2) = P(3) = p and P(0) = 2P(1). If Σpixi2 = 2Σpixi, find the value of p. [4]
Solution:
Given, P(2) = P(3) = p
and P(0) = 2P(1)
Let P(1) = k
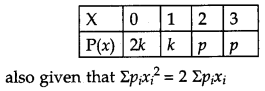
⇒ 0 + k + 4p + 9p = 2(0 + k + 2p + 3p)
⇒ k + 13p = 2k + 10p
or 3p = k ….(i)
also we know that
Σpi = 1
⇒ 2k + k + p + p = l
⇒ 3k + 2p = 1
⇒ 9p + 2p = 1 [using (i)]
⇒ 11p = 1
or P = \(\frac{1}{11}\)
Question 21.
Using vectors find the area of triangle ABC with vertices A(1, 2, 3), B(2, – 1, 4) and C (4, 5, – 1). [4]
Solution:
Vertices of the given ∆ABC are A(1, 2, 3) B(2, – 1, 4) and C(4, 5, – 1)

Question 22.
Solve the following L. P. P. graphically
Maximise Z = 4x + y
Subject to following constraints :
x + y ≤ 50,
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0 [4]
Solution:
We have,
Maximise Z = 4x + y
Subject to the constraints :
x + y ≤ 50
3x + y ≤ 90
x ≥ 10
x, y ≥ 0
Converting the given inequalities into equations, we obtain the following equations :
x + y = 50
3x + y = 90
x = 10
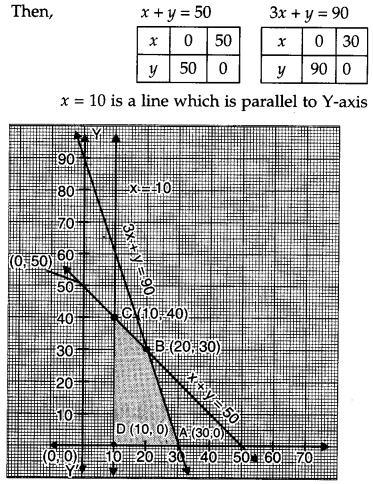
Plotting these points on the graph, we get the shaded feasible region i.e., ABCD.

Question 23.
Find: [4]
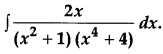
Solution:
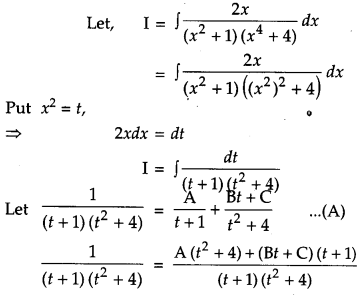


Section – D
Question 28.
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs ₹ 5 per cm2 and the material for the sides costs ₹2.50 per cm2. Find the least cost of the box. [6]
Solution:
Let the length, breadth and height of the metal box be x cm, x cm and y cm respectively. It is given that,
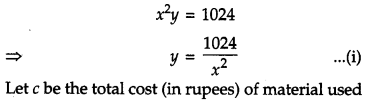
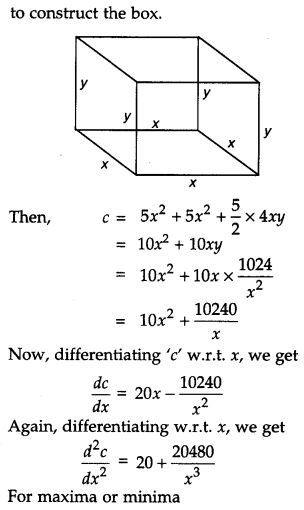

Question 29.
If A = \(\left(\begin{array}{rrr}{2} & {3} & {10} \\ {4} & {-6} & {5} \\ {6} & {9} & {-20}\end{array}\right)\), find A-1. Using A-1 solve the system of equations: [6]
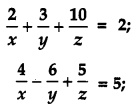
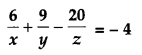
Solution:



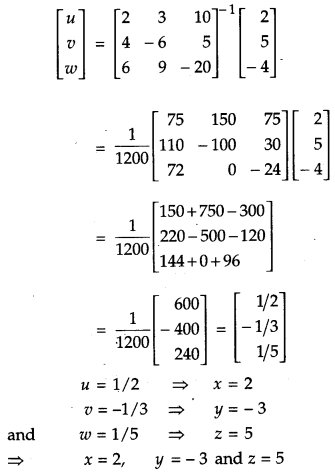
CBSE Previous Year Question Papers Class 12 Maths 2017 Delhi Set III
Section – B
Question 12.
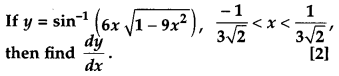
Solution:
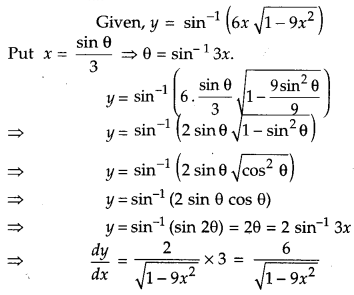
Section – C
Question 20.
Solve the following L.P.P. graphically :
Maximise Z = 20x + 10y
Subject to the following constraints :
x + 2y ≤ 28,
3x + y ≤ 24,
x ≥ 2
x, y ≥ 0 [4]
Solution:
We have
Maximise Z = 20x + 10y
Subject to the constraints :
x + 2y ≤ 28
3x + y ≤ 24
x ≥ 2
x, y ≥ 0
Converting the given inequalities into equations, we obtain the following equations :
x + 2y = 28
3x + y = 24
x = 2
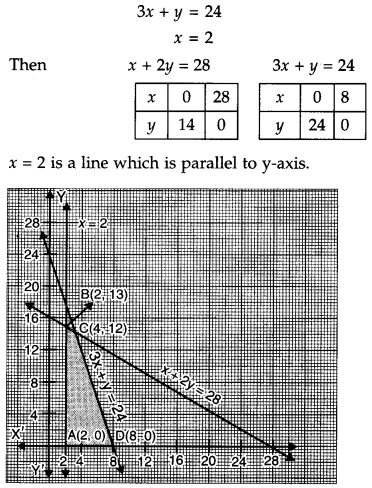
Plotting these points on the graph, we get the shaded feasible region i.e., ABCD

Question 21.
Show that the family of curves for which \(\frac{d y}{d x}=\frac{x^{2}+y^{2}}{2 x y}\), is given by x2 – y2 = cx. [4]
Solution:
Given family of curve,
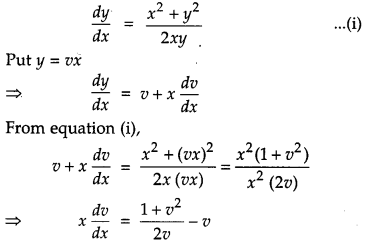
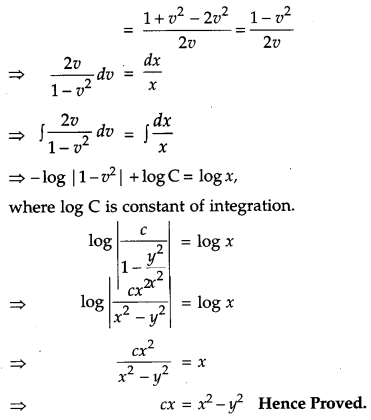
Question 22.
Find: [4]
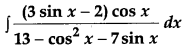
Solution:
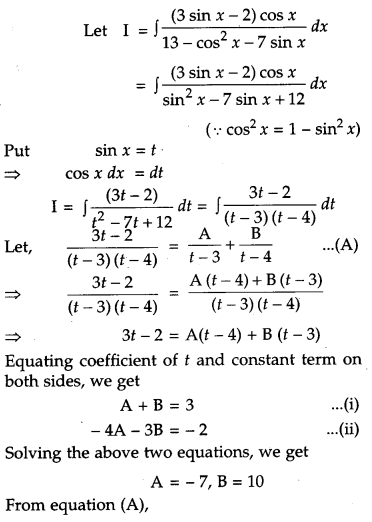
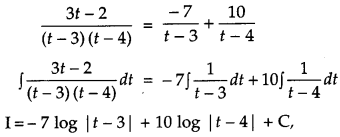
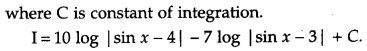
Question 23.
Solve the following equation for x : cos (tan-1x) = sin (cot-1\(\frac{3}{4}\)) [4]
Solution:
Given equation is,
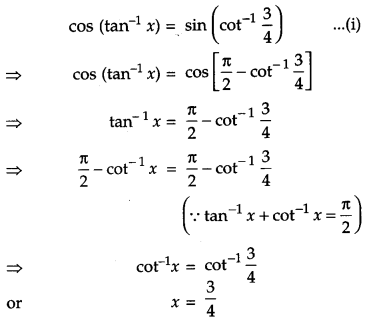
Section – D
Question 28.
If A = \(\left[\begin{array}{ccc}{2} & {3} & {1} \\ {1} & {2} & {-2} \\ {-3} & {1} & {-1}\end{array}\right]\) find A-1 and hence solve the system of equations 2x + y – 3z = 13, 3x + 2y + z = 4, x + 2y – z = 8 [6]
Solution:
Given,
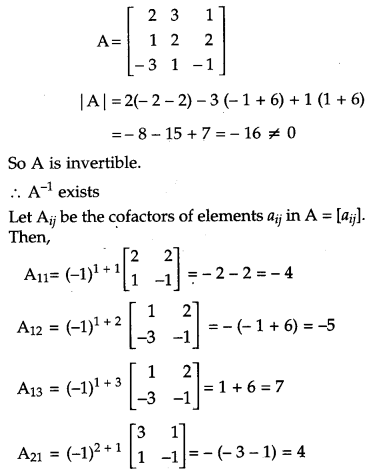
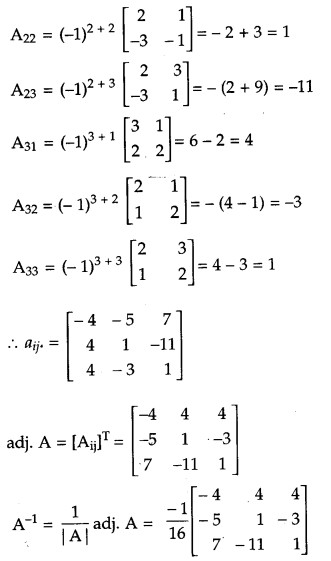
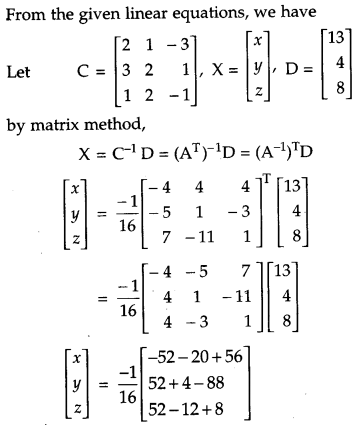
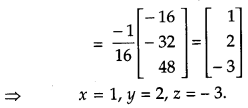
Question 29.
Find the particular solution of the differential equation. tan x · \(\frac{d y}{d x}\) = 2x tan x + x2 – y; (tan x ≠ 0) given that y = 0 when x = \(\frac{\pi}{2}\). [ 6]
Solution:
Given differential equation is,