CBSE Previous Year Question Papers Class 12 Maths 2016 Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
CBSE Previous Year Question Papers Class 12 Maths 2016 Delhi Set I
Section – A
Question 1.
Find the maximum value of [1]
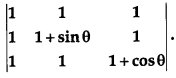
Solution:
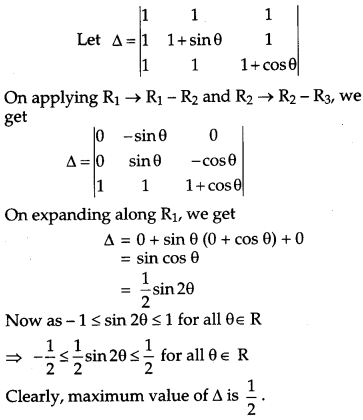
Question 2.
If A is a square matrix such that A2 = I, then find the simplified value of (A – I)3 + (A + I)3 – 7A. [1]
Solution:
Given,
(A – I)3 + (A + I)3 – 7A
= A3 – I3 – 3A2I + 3AI2 + A3 + I3 + 3A2I
= 2A3 + 6AI2 – 7A
= 2A.A2 + 6AI2 – 7A
= 2AI + 6AI – 7A
= 8A – 7A = A
Question 3.
Matrix A = \(\left[\begin{array}{rrr}{0} & {2 b} & {-2} \\ {3} & {1} & {3} \\ {3 a} & {3} & {-1}\end{array}\right]\) is given to be symmetric, find values of a and b. [1]
Solution:
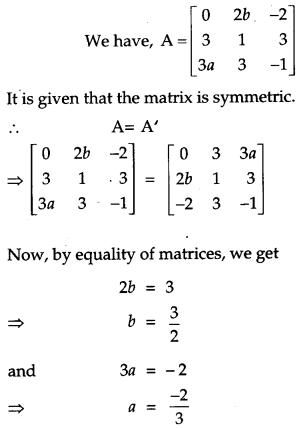
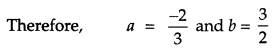
Question 4.
Find the position vector of a point which divides the join of points with position vectors \(\vec{a}-2 \vec{b}\) and \(2 \vec{a}+\vec{b}\) externally in the ratio 2 : 1. [1]
Solution:
Let A and B be the given points with

Question 5.
The two vectors \(\hat{j}+\hat{k} \text { and } 3 \hat{i}-\hat{j}+4 \hat{k}\) represent the two sides AB and AC, respectively of a ∆ABC. Find the length of the median through A. [1]
Solution:
In ∆ABC,
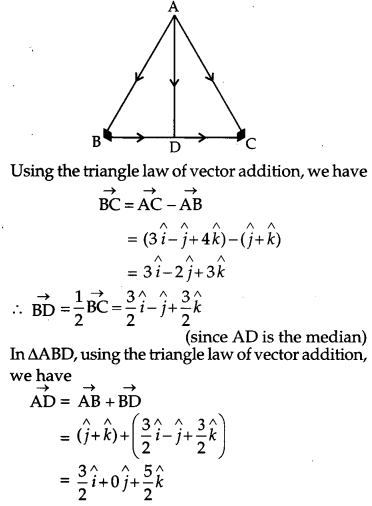
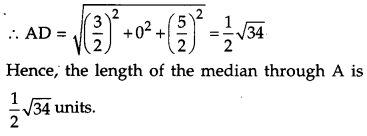
Question 6.
Find the vector equation of a plane which is at a distance of 5 units from the origin and its normal vector is \(2 \hat{i}-3 \hat{j}+6 \hat{k}\). [1]
Solution:
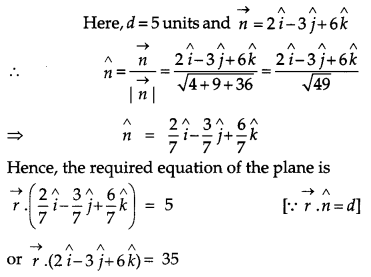
Section – B
Question 7.
Prove that: [4]
![]()
Solution:
LHS =
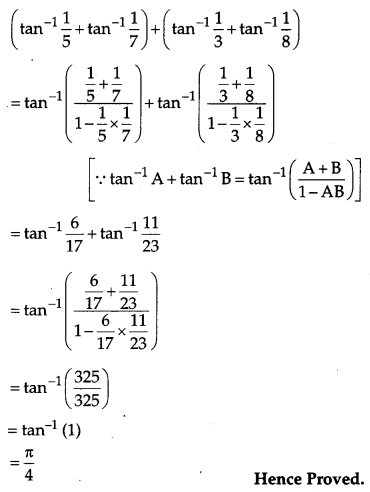
OR
Solve for x : 2 tan-1(cos x) = tan-1(2 cosec x)
Solution:
Given, 2 tan-1(cos x) = tan-1(2 cosec x)
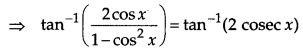
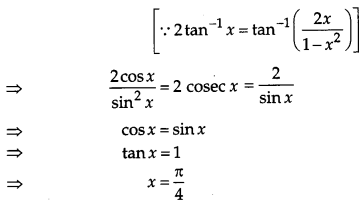
Question 8.
The monthly incomes of Aryan and Babban are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves ₹ 15,000 per month, find their monthly incomes using matrix method. This problem reflects which value ? [4]
Solution:
Let the monthly incomes of Aryan and Babban be 3x and 4x respectively.
Suppose their monthly expenditures are 5y and 7y respectively.
Since each saves ₹ 15,000 per month.
Monthly saving of Aryan : 3x – 5y = 15,000
Monthly saving of Babban : 4 x – 7y = 15,000
The above system of equations can be written in the matrix form as follows:
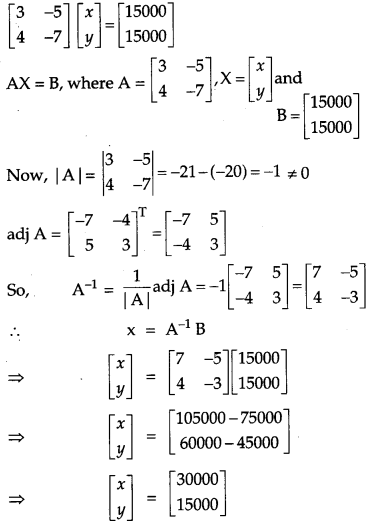
⇒ x = 30,000 and y = 15,000
Therefore,
Monthly income of Aryan = 3 × 30,000 = ₹ 90,000
Monthly income of Babban = 4 × 30,000 = ₹ 1,20,000
Value : Saving in good time helps us to survive in bad times.
Question 9.
If x = a sin 2t (1 + cos 2t) and y = b cos 2t (1 – cos 2t), find the values of \(\frac{d y}{d x} \text { at } t=\frac{\pi}{4} \text { and } t=\frac{\pi}{3}\). [4]
Solution:
We have, x = a sin 2t (1 + cos 2t)
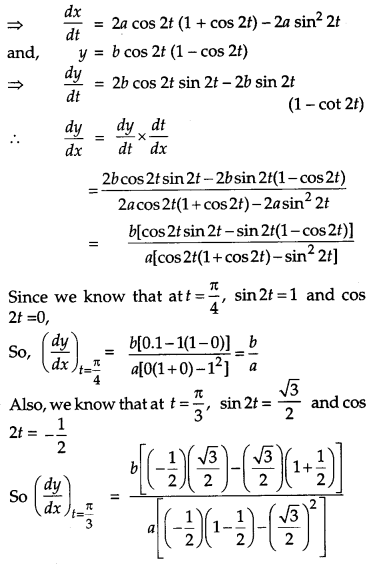
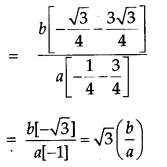
OR
If y = xx prove that \(\frac{d^{2} y}{d x^{2}}-\frac{1}{y}\left(\frac{d y}{d x}\right)^{2}-\frac{y}{x}=0\).
Solution:
Given, y = xx
Taking log on both sides, we get
log y = log(xx)
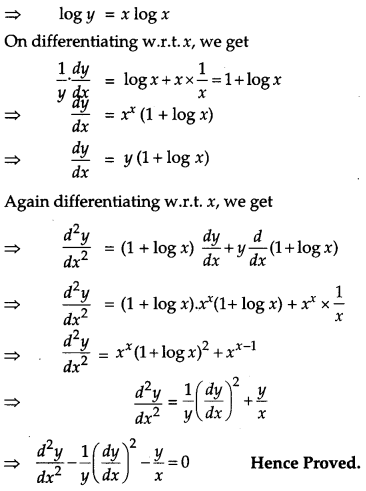
Question 10.
Find the values of p ans q for which [4]
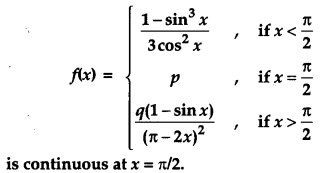
Solution:
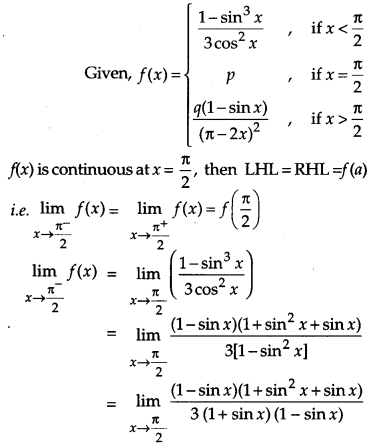
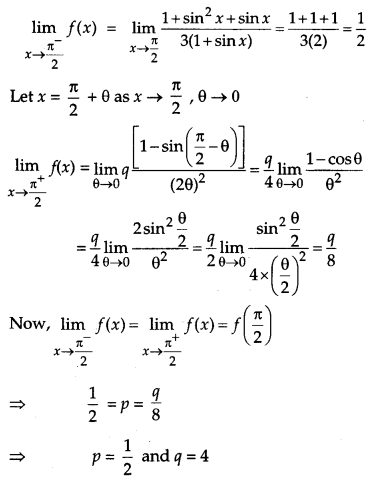
Question 11.
Show that the equation of normal at any point on the curve x = 3 cos t – cos3 t and y = 3 sin t- sin3 is 4(y cos3 t – x sin3t) = 3 sin 4 t. – sin3 t is [4]
Solution:
Given,

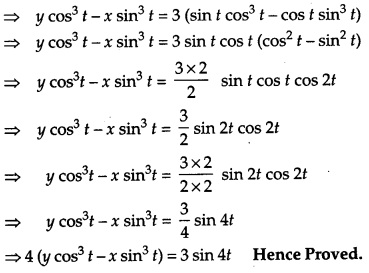
Question 12.
Fimd: [4]
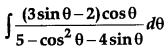
Solution:

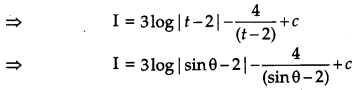
OR
Evaluate
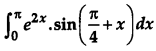
Solution:
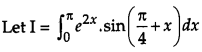
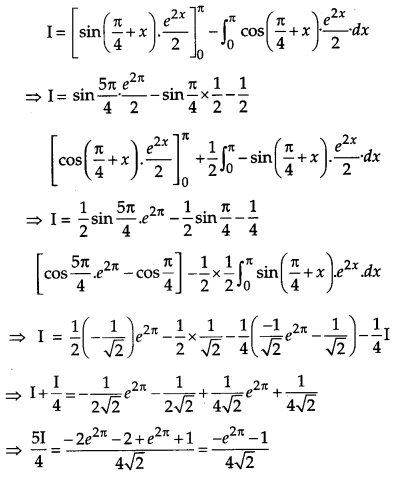
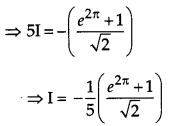
Question 13.
Find: [4]
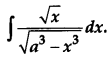
Solution:
Question 14.
Evaluate : [4]
![]()
Solution:
![]()
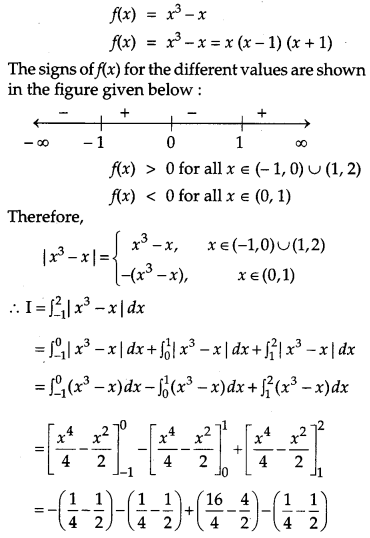
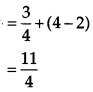
Question 15.
Find the particular solution of the differential equation (1 – y2) (1 + logx) dx + 2xy dy=0, given that y = 0 when x = 1. [4]
Solution:
The given differential equation is,
(1 – y2) (1 + log x).dx + 2xy dy = 0
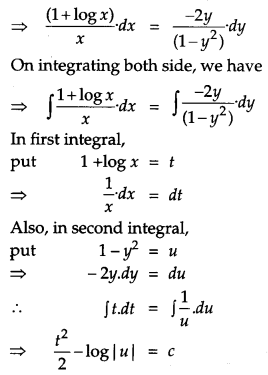
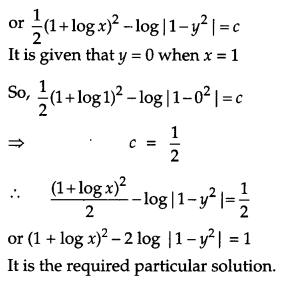
Question 16.
Find the general solution of the following differential equation: [4]
![]()
Solution:
The given differential equation is,

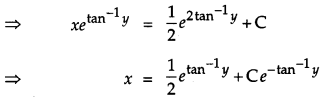
Question 17.
Show that the vectors \(\vec{a}, \vec{b} \text { and } \vec{c}\) are coplanar if \(\vec{a}+\vec{b}, \vec{b}+\vec{c} \text { and } \vec{c}+\vec{a}\) are coplanar. [4]
Solution:
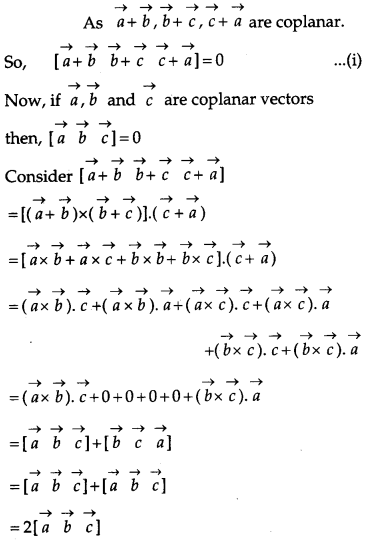

Question 18.
Find the vector and cartesian equations of the line through the point (1, 2, – 4) and perpendicular to the two lines.
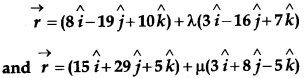
Solution:
The equations of the given lines are


Question 19.
Three persons A, B and C apply for a job of Manager in a Private Company. Chances of their selection (A, B and C) are in the ratio 1 : 2 : 4. The probabilities that A, B and C can introduce changes to improve profits of the company are 0.8, 0.5 and 0.3 respectively. If the change does not take place, find the probability that it is due to the appointment of C. [4]
Solution:
Let E1, E2 and E3 be the events denoting the selection of A, B and C as managers respectively.
P(E1) = Probability of selection of A = \(\frac{1}{7}\)
P(E2) = Probability of selection of B = \(\frac{2}{7}\)
P(E3) = Probability of selection of C = \(\frac{4}{7}\)
Let A be the event denoting the change not taking place.
P(A/E1) = Probability that A does not introduce change = 0.2
P(A/E2) = Probability that B does not introduce change = 0.5
P(A/E3) = Probability that C does not introduce change 0.7 .
∴ Required probability = P(E3/A)
By Bayes’ theorem, we have
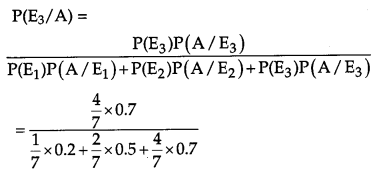
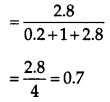
OR
A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B wins the game if he gets a total of 10. If A starts the game, then find the probability that B wins.
Solution:
Total of 7 on the dice can be obtained in the following ways :
(1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3)



Section – C
Question 20.
Let f : N → N be a function defined as f(x) = 9x2 + 6x – 5. Show that f : N → S, where S is the range off, is invertible. Find the inverse of f and hence find f-1 (43) and f-1 (163). [6]
Solution:
Given,

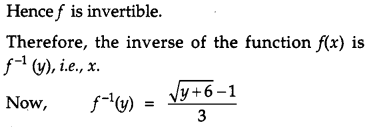
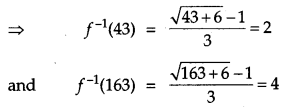
Question 21.
Prove that \(\left|\begin{array}{lll}{y z-x^{2}} & {z x-y^{2}} & {x y-z^{2}} \\ {z x-y^{2}} & {x y-z^{2}} & {y z-x^{2}} \\ {x y-z^{2}} & {y z-x^{2}} & {z x-y^{2}}\end{array}\right|\) is visible by (x + y + z) and hence find the quotient. [6]
Solution:
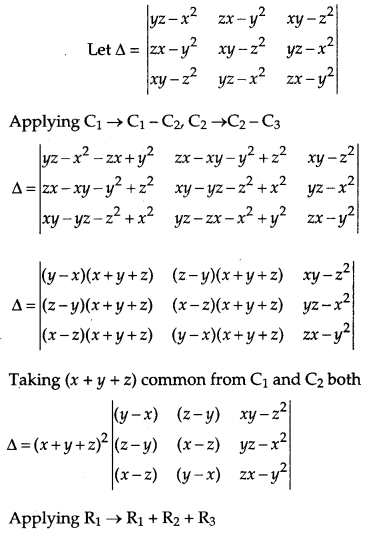
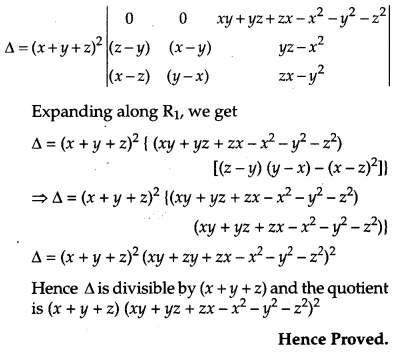
OR
Using elementary transformations, find the inverse of the matrix A = \(\left[\begin{array}{lll}{8} & {4} & {3} \\ {2} & {1} & {1} \\ {1} & {2} & {2}\end{array}\right]\) and use it to solve the following system of linear equations:
8x + 4y + 3z = 19
2x + y + z = 5
x + 2y + 2z = 7
Solution:
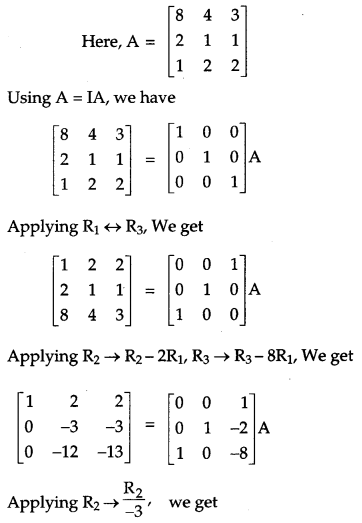

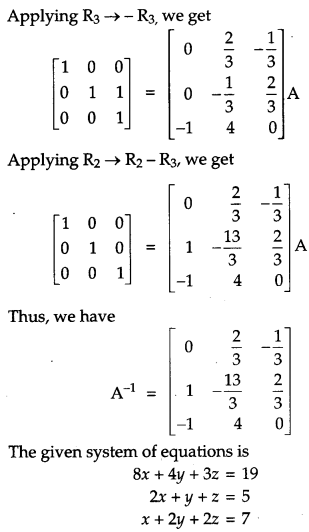

Question 22.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is \(\frac{4 r}{3}\). Also find maximum volume in terms of volume of the sphere. [6]
Solution:
A sphere of fixed radius (r) is given. Let R and h be the radius and the height of the cone respectively.

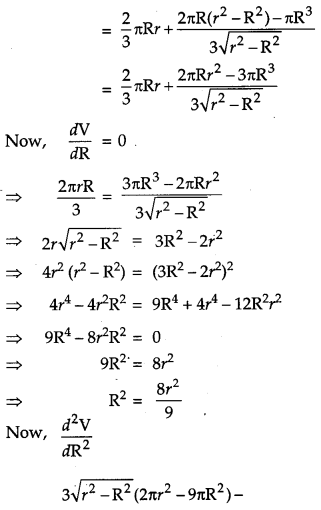
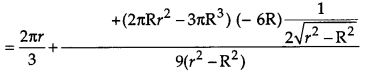

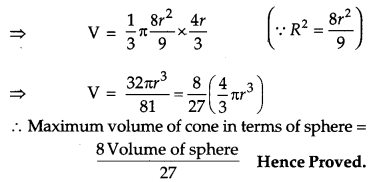
OR
Find the intervals in which f(x) = sin 3x – cos 3x, 0 < x < π, is strictly increasing or strictly decreasing.
Solution:
Consider the function
f(x) = sin 3x – cos 3x
⇒ f'(x) = 3 cos 3x + 3 sin 3x
= 3 (sin 3x + cos 3x)
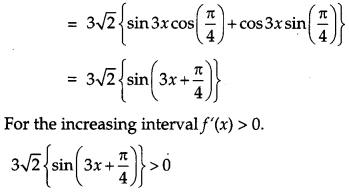


Question 23.
Using integration find the area of the region {(x, y) : x2 + y2 ≤ 2ax, y2 ≥ ax, x, y ≥ 0} [6]
Solution:
We have, {(x, y) : x2 + y2 ≤ 2ax, y2 ≥ ax, x, y ≥ 0}
Consider x2 + y2 = 2ax
y2 = ax …9ii)
x = 0, y = 0
Solving equation (i) and (ii), we get
x2 + ax = 2ax
⇒ x2 – ax = 0
⇒ x(x – a) = 0
∴ x = 0, a
So, points of intersections of (i) and (ii) are (0, 0) and (a, ± a). Also, equation (i) can be written as, (x – a)2 + (y – 0)2 = a2 whose centre is at (a, 0) and radius is of ‘a’ units.

Question 24.
Find the coordinate of the point P where the line through A(3, -4, -5) and B (2, – 3, 1) crosses the plane passing through three points L (2, 2, 1), M (3, 0, 1) and N (4, – 1, 0). Also, find the ratio in which P divides the line segment AB. [6]
Solution:
The equation of the plane passing through three given points can be given by
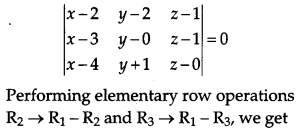
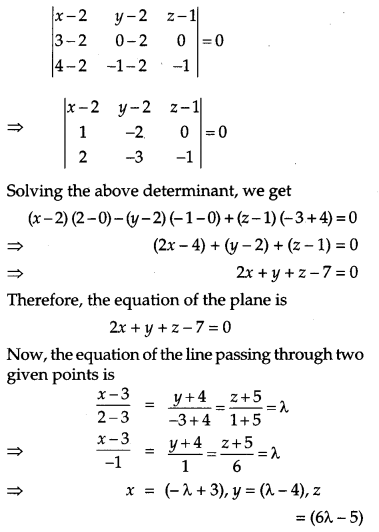
At the point of intersection, these points satisfy the equation of the plane 2x + y + z – 7 = 0
Putting the values of x, y and z in the equation of the plane, we get the value of λ
2(-λ + 3) + (λ – 4) + (6λ – 5) – 7 = 0
⇒ -2λ + 6 + λ – 4 + 6λ – 5 – 7 = 0
⇒ 5λ =10
⇒ λ = 2
Thus, the point of intersection is P (1, – 2, 7). Now, let P divide the line AB in the ratio m : n.
By the section formula, we have
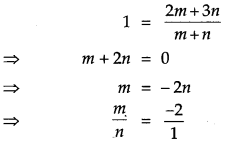
Hence, P divides externally the line segment AB in the ratio 2 : 1.
Question 25.
An urn contains 3 white and 6 red balls. Four balls are drawn one by one with replacement from the urn. Find the probability distribution of the number of red balls drawn. Also find mean and variance of the distribution. [6]
Solution:
Let X denote the total number of red balls when four balls are drawn one by one with replacement.


Question 26.
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at ₹ 7 profit and B at a profit of ₹ 4. Find the production level per day for maximum profit graphically.
Solution:
Let the numbers of units of products A and B to be produced be x and y, respectively.

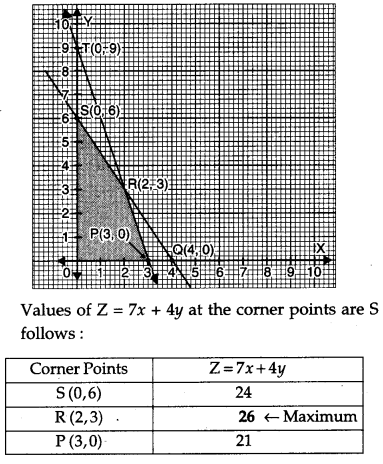
Therefore, the manufacturer has to produce 2 units of product A and 3 units of product B for the maximum profit of ₹ 26.
All questions are same in Outside Delhi Set II and Set III