CBSE Previous Year Question Papers Class 12 Maths 2015 Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
CBSE Previous Year Question Papers Class 12 Maths 2015 Delhi Set I
Section – A
Question 1.
If \(\vec{a}=7 \hat{i}+\hat{j}-4 \hat{k} \text { and } \hat{b}=2 \hat{i}+6 \hat{j}+3 \hat{k}\), then find the projection of \(\vec{a} \text { on } \vec{b}\). [1]
Solution:
Given,
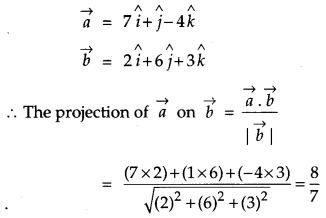
Question 2.
Find λ, if the vectors \(\vec{a}=\hat{i}+3 \hat{j}+\hat{k}, \vec{b}=2 \hat{i}-\hat{j}-\hat{k}\) and \(\vec{c}=\lambda \hat{j}+3 \hat{k}\) are coplanar. [1]
Solution:
Since, the given vectors are coplanar.
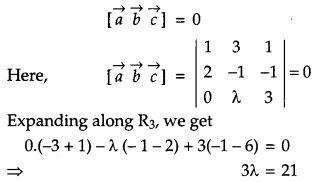
∴ λ = 7
Question 3.
If a line makes angles 90°, 60° and θ with x, y and z-axis respectively, where θ is acute, then find θ. [1]
Solution:
Given,
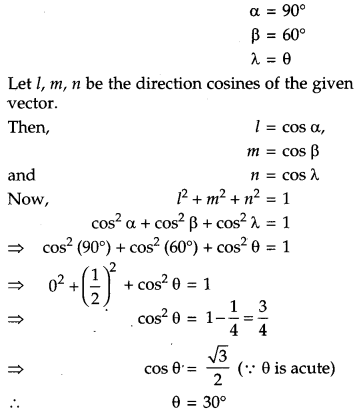
Question 4.
Write the element a23 of a 3 × 3 matrix A = (aij) whose elements aij are given be aij = \(\frac{|i-j|}{2}\). [1]
Solution:
Given,
aij = \(\frac{|i-j|}{2}\)
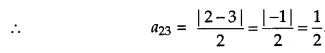
Question 5.
Find the differential equation representing the family of curves v = \(\frac{\mathbf{A}}{r}\) + B, where A and B are arbitrary constants. [1]
Solution:
We have,
v = \(\frac{\mathbf{A}}{r}\) + B …(i)
Since, the given equation contains two arbitrary constants, we shall differentiate it two times. Now, differentiating (i) w.r.t. r, we get
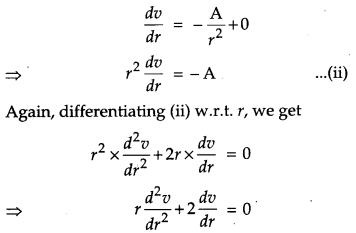
This is the required differential equation representing the family of the given curve.
Question 6.
Find the integrating factor of the differential equation \(\left(\frac{e^{-2 \sqrt{x}}}{\sqrt{x}}-\frac{y}{\sqrt{x}}\right) \frac{d x}{d y}=1\). [1]
Solution:
We have,
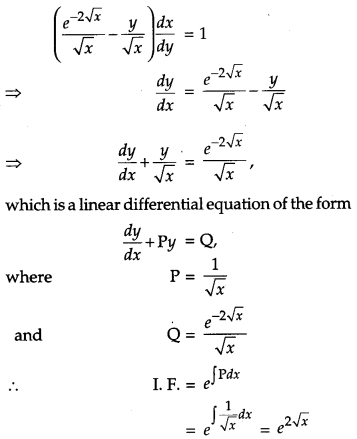
Section – B
Question 7.
If A = \(\left[\begin{array}{ccc}{2} & {0} & {1} \\ {2} & {1} & {3} \\ {1} & {-1} & {0}\end{array}\right]\), find A2 – 5A + 4I and hence find a matrix X such that A2 – 5A + 4I + X = 0. [4]
Solution:
We have,
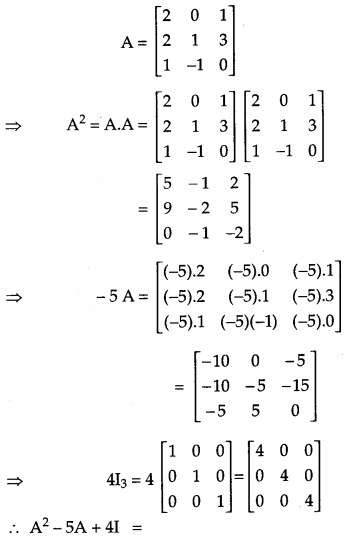
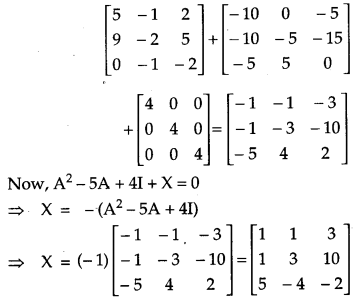
OR
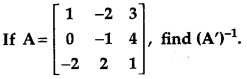
Solution:
Given,

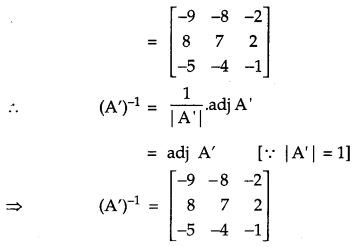
Question 8.
If f(x) = \(\left[\begin{array}{ccc}{a} & {-1} & {0} \\ {a x} & {a} & {-1} \\ {a x^{2}} & {a x} & {a}\end{array}\right]\), using properties of determinants find the value of f(2x) – f(x). [4]
Solution:
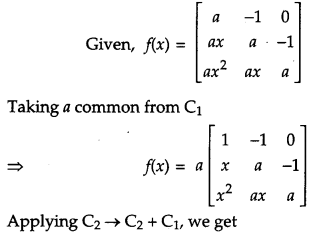

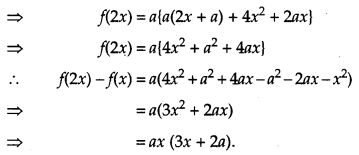
Question 9.
Find: [4]
![]()
Solution:
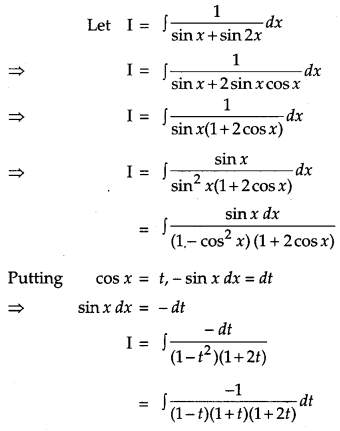

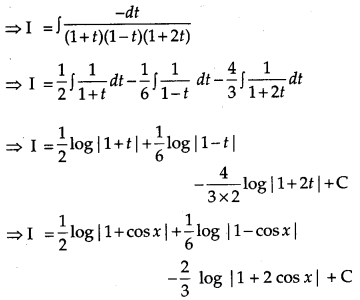
OR
Integrate the following w.r.t. x: \(\frac{x^{2}-3 x+1}{\sqrt{1-x^{2}}}\).
Solution:
Given,
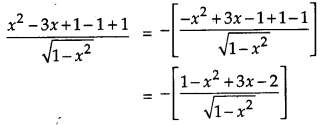
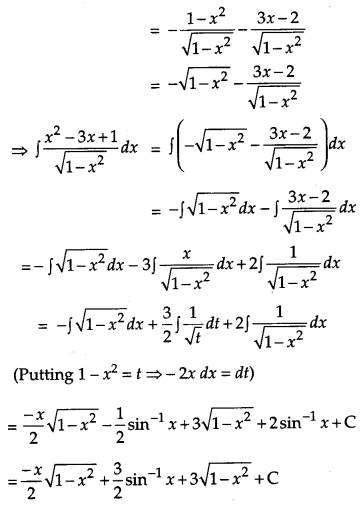
Question 10.
Evaluate: [4]
![]()
Solution:
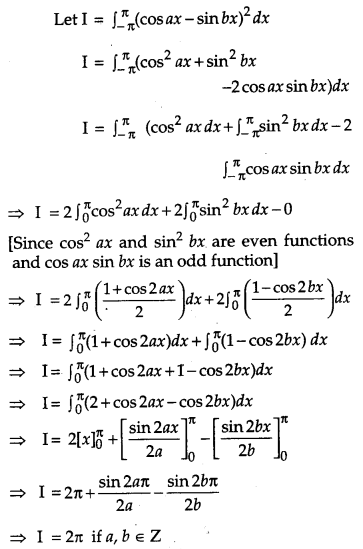
Question 11.
A bag ‘A’ contains 4 black and 6 red balls and bag ‘B’ contains 7 black and 3 red balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise bag B. If two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black. [4]
Solution:
Consider the following events :
E1 = Getting 1 or 2 on die.
E2 = Getting 3, 4, 5 or 6 on die.
E = One of the ball drawn is red and another is black.

OR
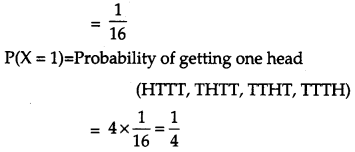
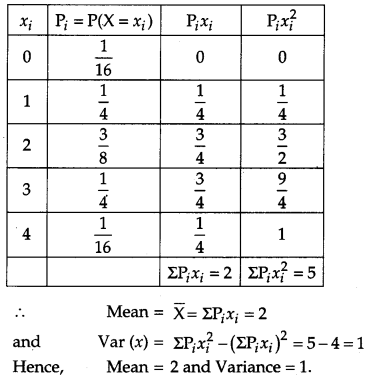
An unbiased coin is tossed 4 times. Find the mean and variance of the number of heads obtained.
Solution:
Let X denote the number of heads in the four tosses of the coin, then X is a random variable that can have values 0, 1, 2, 3, 4.
P(X = 0) = Probability of getting no head (TTTT)

Question 12.
If \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\), find \((\vec{r} \times \hat{i}) \cdot(\vec{r} \times \hat{j})\) + xy. [4]
Solution:
Given,
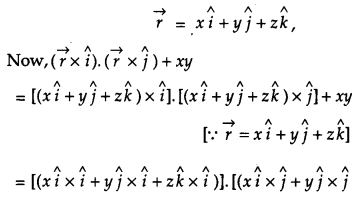
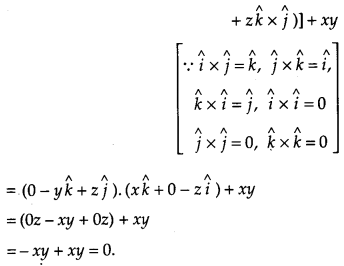
Question 13.
Find the distance between the point (- 1, – 5, – 10) and the point of intersection of the line \(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{12}\) and the plane x – y + z = 5. [4]
Solution:



Question 14.
If sin [cot-1 (x + 1)] = cos(tan-1 x), then find x. [4]
Solution:
Given, sin [cot-1 (x +1)] = cos(tan-1 x)
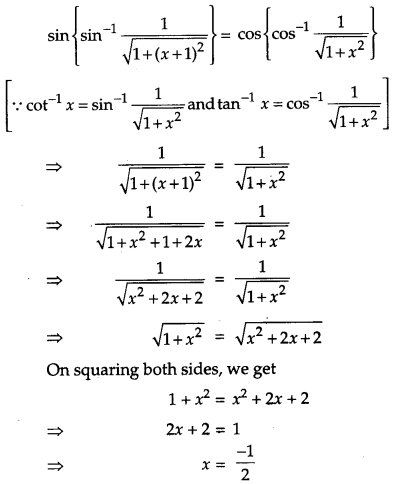
OR
If (tan-1 x)2 + (cot-1 x)2 = \(\frac{5 \pi^{2}}{8}\), then find x.
Solution:
Given, (tan-1 x)2 + (cot-1 x)2 = \(\frac{5 \pi^{2}}{8}\)
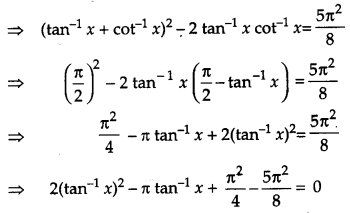
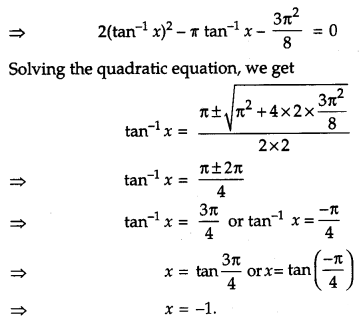
Question 15.
If y = tan-1\(\left(\frac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)\), x2 ≤ 1, then find \(\frac{d y}{d x}\). [4]
Solution:
Given,
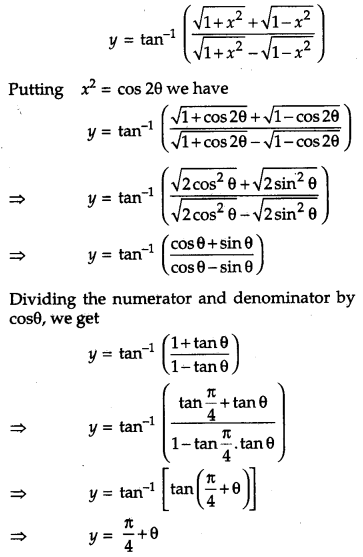
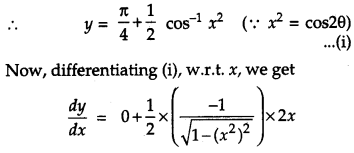
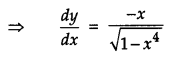
Question 16.
IF x = a cos θ + b sin θ, y = a sin θ – b cos θ, show that \(\frac{y^{2} d^{2} y}{d x^{2}}-\frac{x d y}{d x}+y=0\). [4]
Solution:
We have,
x = a cos θ + b sin θ …(i)
y = a sin θ – b cos θ …(ii)
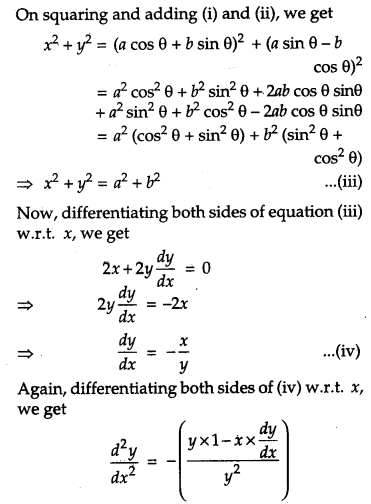
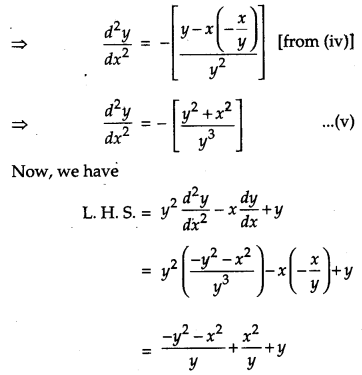
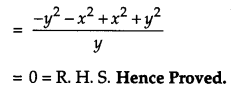
Question 17.
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ? [4]
Solution:
We know that, Area of an equilateral triangle,
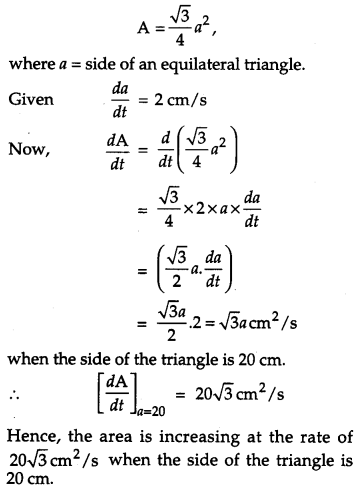
Question 18.
Find \(\int(x+3) \sqrt{3-4 x-x^{2}} d x\). [4]
Solution:
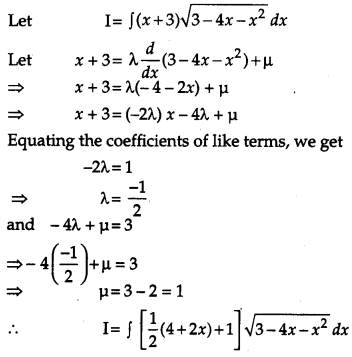
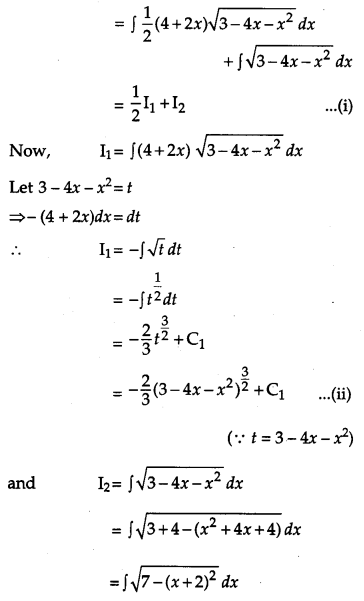
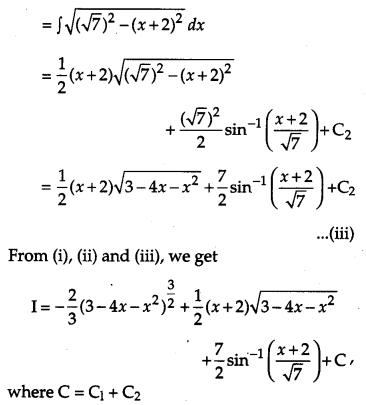
Question 19.
Three schools A, B and C organised a mela for collecting funds for helping the rehabilitation of flood victims. They sold handmade fans, mats and plates from recycled material at a cost of ₹ 25, ₹ 100 and ₹ 50 each. The number of articles sold are given below:
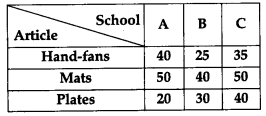
Find the fund collected by each school separately by selling the above articles. Also find the total funds collected for the purpose. Write one value generated by the above situation. [4]
Solution:
The number of articles sold by each school can be represented by the 3 × 3 matrix
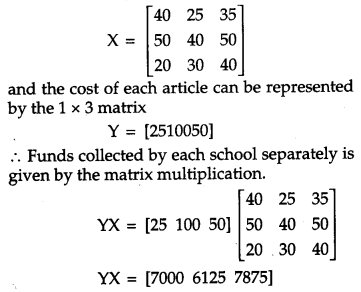
Hence, the funds collected by schools A, B and C are ₹ 7,000, ₹ 6,125 and ₹ 7,875 respectively.
The total funds collected for flood victims
= ₹ (7,000 + 6,125 + 7,875)
= ₹ 21,000
The above situation exhibits the helping nature of students.
Section – C
Question 20.
Let N denote the set of all natural numbers and R be the relation on N × N defined by (a, b) R (c, d) if ad(b + c) = bc(a + d). Show that R is an equivalence relation. [6]
Solution:
We know that relation R will be an equivalence relation, if we prove it as a reflexive, symmetric and transitive relation.
(i) Reflexivity:
Let (a, b), be an arbitrary element of N × N
then, (a, b) ϵ N × N
a, b ϵ N
⇒ ab(b + a) = ba(a + b)
⇒ (a, b) R (a, b)
(a, b) R (a, b) ∀ (a, b) ϵ N × N.
(ii) Symmetry:’
Let (a, b), (c, d) be ah arbitrary element of N × N such that (a, b) R (c, d)
⇒ ad(b + c) = bc(a + d)
⇒ cb(d + a) = da(c + b)
⇒ (c, d) R (a, b)
∴ (a, b) R (c, d) ⇒ (c, d) R (a, b) ∀ (a, b), (c, d) ϵ N × N So, R is symmetric on N × N.
(iii) Transitivity:
Let (a, b), (c, d), (e, f) be an arbitrary element of N × N such that (a, b) R (c, d) and (c, d) R then (a, b) R (c, d)
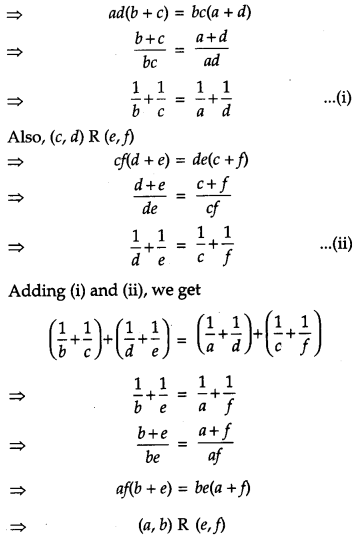
Thus, (a, b) R (c, d) and (c, d) R (e, f) ⇒ (a, b) R (e, f). ∀ (a, b) (c, d) (e, f) ϵ N × N
So, R is transitive on N × N.
Hence, R being reflexive, symmetric and transitive, is an equivalence relation on N × N.
Hence Proved.
Question 21.
Using integration find the area of the triangle formed by positive x-axis and tangent and normal to the circle x2 + y2 = 4 at (1, \( \sqrt{{3}} \)). [6]
Solution:
The equation of the given circle is x2 + y2 = 4. The equation of the normal to the circle at (1, \( \sqrt{{3}} \)) is same as the line joining the points (1, \( \sqrt{{3}} \)) and (0, 0) which is given by
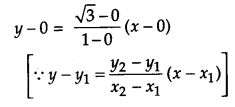

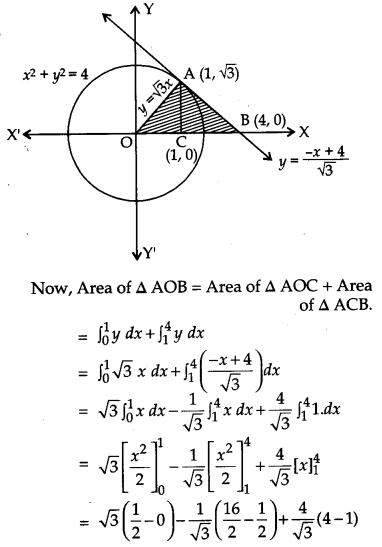
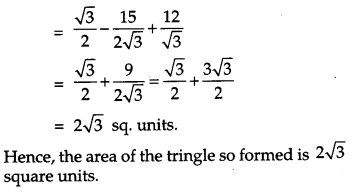
OR
Evaluate \(\int_{1}^{3}\left(e^{2-3 x}+x^{2}+1\right)\) dx as a limit of a sum.
Solution:
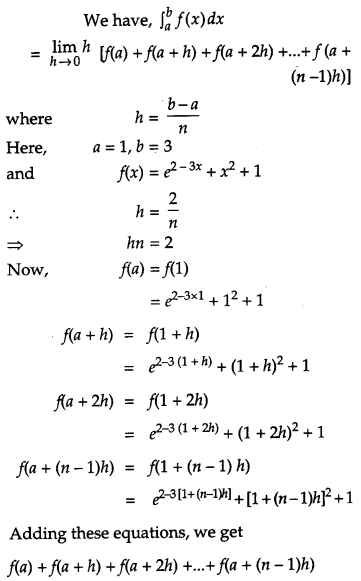


Question 22.
Solve the differential equation: (tan-1 y – x) dy = (1 + y2) dx. [6]
Solution:
Same as solution Q. 23 (OR) Set 1 (Outside Delhi) upto eq. x = tan-1 y – 1 + c etan-1 y
OR
Find the particular solution of the differential equation \(\frac{d y}{d x}=\frac{x y}{x^{2}+y^{2}}\) given that y = 1, when x = 0.
Solution:

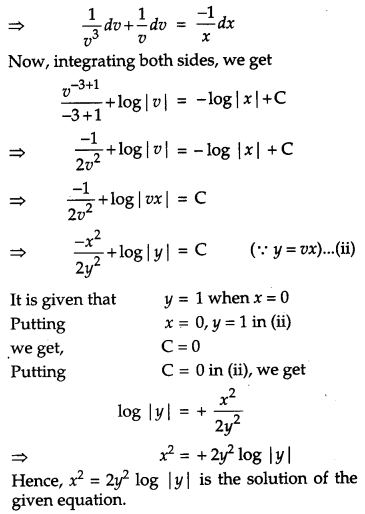
Question 23.
If lines \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4} \text { and } \frac{x-3}{1}=\frac{y-k}{2}=\frac{z}{1}\) intersect, then find the value of k and hence find the equation of the plane containing these lines. [6]
Solution:
The coordinates of any point on first line are

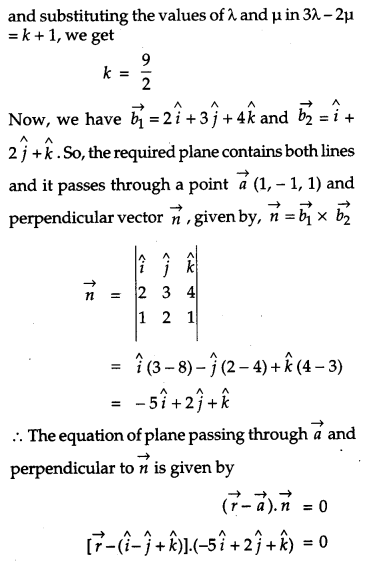
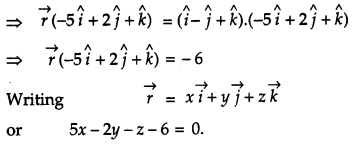
Question 24.
If A and B are two independent events such that P(\(\overline{\mathbf{A}}\) ∩ B) = \(\frac{2}{15}\) and P(A ∩ \(\overline{\mathbf{B}}\)) = \(\frac{1}{6}\) then find P(A) and P(B). [6]
Solution:
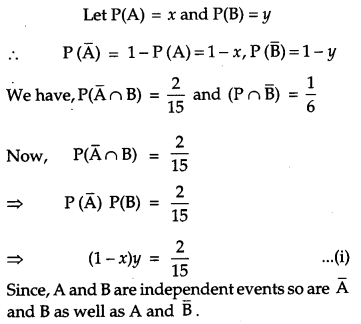
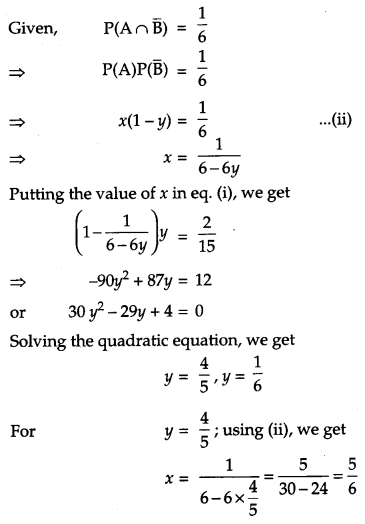
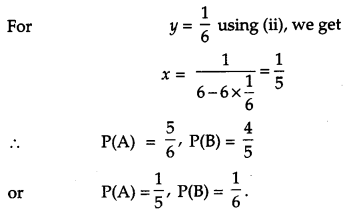
Question 25.
Find the local maxima and local minima of the function f(x) = sin x – cos x, 0 < x < 2π. Also find the local maximum and local minimum values. [6]
Solution:
We have,/(x) = sin x – cos x, 0 < x < 2π.
⇒ f'(x) – cos x + sin x
For local maximum or minimum, we have
⇒ f'(x) = o
⇒ cos x + sin x = 0
⇒ cos x = – sin x
⇒ tan x = -1
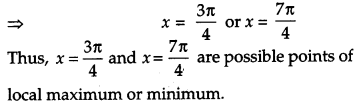
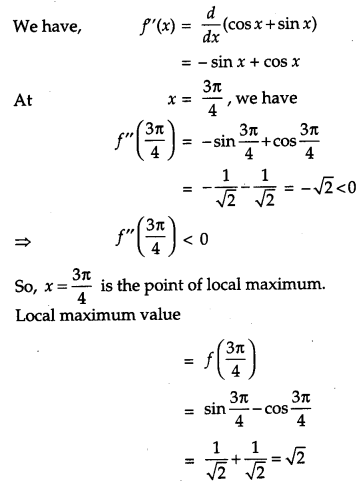

Question 26.
Find graphically, the maximum value of z = 2x + 5y, subject to constraints given below: [6]
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≤ 0
Solution:
We first convert the inequalities into equations to obtain lines
2x + 4y = 8 ….(i)
3x + y = 6 …..(ii)
x + y = 4 —(iii)
x = 0
and y = 0.
We need to maximize the objective function z = 2x + 5y
These lines are drawn and the feasible region of the L.P.P. is the shaded region :
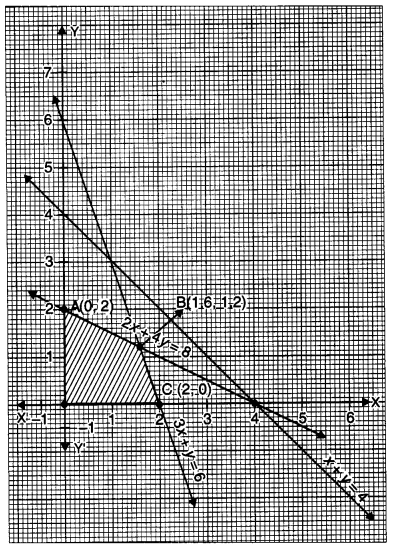
The point of intersection of (i) and (ii) is B (1.6, 1.2)
The coordinates of the corner points of the feasible region are 0(0, 0), A(0, 2), B (1.6, 1.2) and C(2, 0).
The value of the objective function at these points are given in the following table:
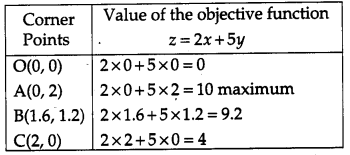
Out of these values of z, the maximum value of z is 10 which is attained at the point (0, 2). Thus the maximum value of z is 10.
All questions are same in Delhi Set II and Set III