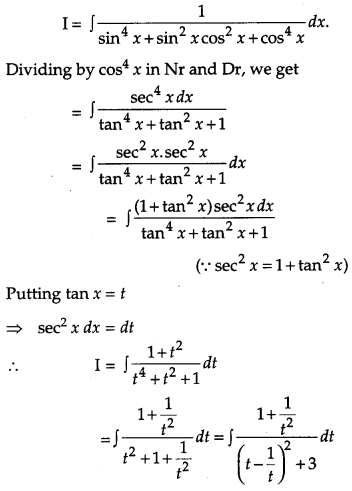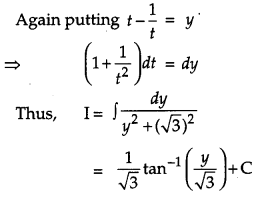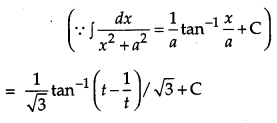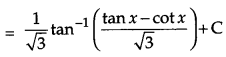CBSE Previous Year Question Papers Class 12 Maths 2014 Outside Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
CBSE Previous Year Question Papers Class 12 Maths 2014 Outside Delhi Set I
Section – A
Question 1.
If R = [(x, y): x + 2y = 8] is a relation on N, write the range of R. [1]
Solution:
The given relation on N is
R = [(x, y): x + 2y = 8]
Since both x, y ϵ N
x can take values 2, 4, 6 for other values of y ϵ N.
For x = 2, 2 + 2y = 8
⇒ y = 3
For x = 4, 4 + 2y = 8
⇒ y = 2
For x = 6, 6 + 2y = 8
⇒ y = 1
∴ R = {(2, 3), (4, 2), (6, 1)}
∴ The range of R = Set of second element’s
= {1, 2, 3}.
Question 2.
If tan-1 x + tan-1 y =\(\frac{\pi}{4}\), xy < 1, then write the value of x + y + xy. [1]
Solution:
Given,
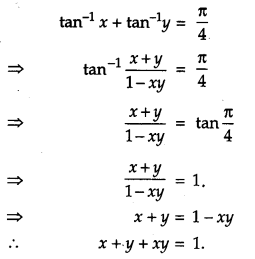
Question 3.
If A is a square matrix such that A2 = A, then write the value of 7A – (I + A)3, where I is an identity matrix. [1]
Solution:
7A – (I + A)3 = 7A – (I3 + A3 + 3I2A + 3IA2)
[ ∵ (a + b)3 = a3 + b3 + 3a2b + 3ab2]
= 7A – (I + A2. A + 3IA + 3IA2) [ v In = I ∀ n ϵ N]
= 7A – (I + A2 + 3A + 3IA) [∵ A2 = A, IA = A]
= 7A – (I + A + 3A + 3A)
= 7A – 1 – 7A = -1.
Question 4.
If \(\left[\begin{array}{cc}{x-y} & {z} \\ {2 x-y} & {w}\end{array}\right]=\left[\begin{array}{cc}{-1} & {4} \\ {0} & {5}\end{array}\right]\), find the value of x + y. [1]
Solution:
Given,
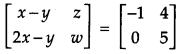
Comparing the corresponding elements, we get
x – y = -1, z = 4
2x – y = 0, w = 5
Solving these equations, we get
x = 1, y = 2
x + y = 1 + 2 = 3.
Question 5.
If \(\left|\begin{array}{cc}{3 x} & {7} \\ {-2} & {4}\end{array}\right|=\left|\begin{array}{cc}{8} & {7} \\ {6} & {4}\end{array}\right|\), find the value of x. [1]
Solution:
Given,
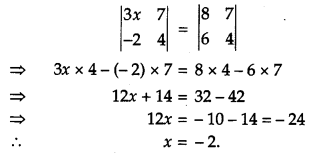
Question 6.
If f(x) = \(\int_{0}^{x} t \sin t d t\), then write the value of f'(x). [1]
Solution:
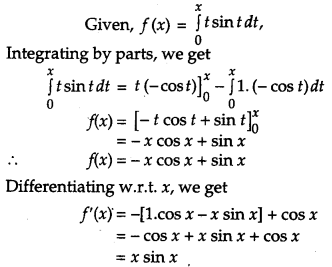
Question 7.
Evaluate: [1]
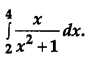
Solution:
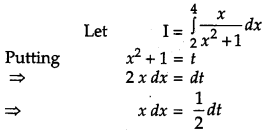
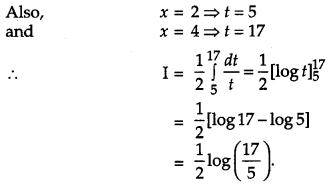
Question 8.
Find the value of ‘p’ for which the vectors \(3 \hat{i}+2 \hat{j}+9 \hat{k} \text { and } \hat{i}-2 p \hat{j}+3 \hat{k}\) are parallel. [1]
Solution:
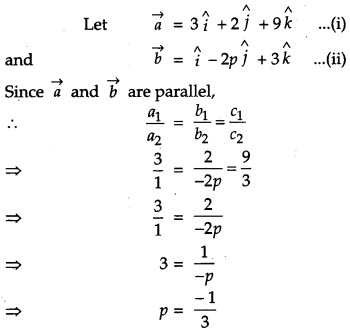
Question 9.
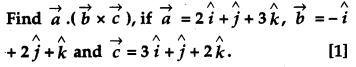
Solution:
Given,
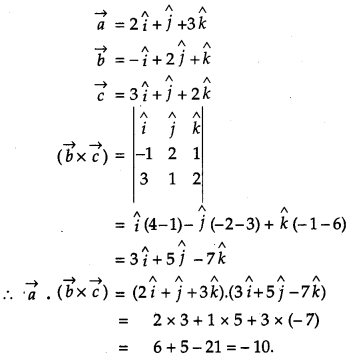
Question 10.
If the Cartesian equations of a line are \(\frac{3-x}{5}=\frac{y+4}{7}=\frac{2 z-6}{4}\) write the vector equation for the line. [1]
Solution:
The Cartesian equations of a line are
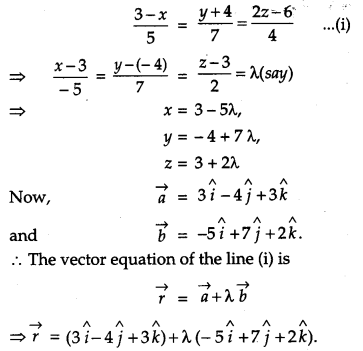
Section – B
Question 11.
If the function f : R→R be given by f(x) = x2 + 2, and : R→R be given by g(x) = \(\frac{x}{x-1}\), x ≠ 1, find fog ang gof and hence find fog(2) and gof(-3). [4]
Solution:
Given, f : R→R
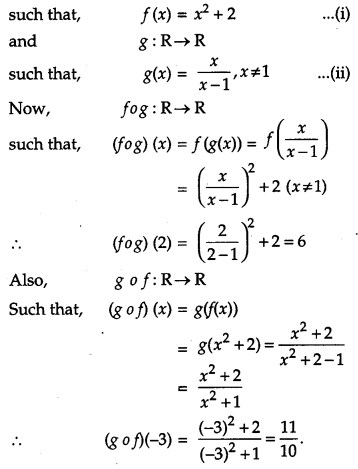
Question 12.
Prove that:
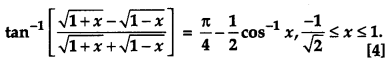
Solution:
L. H. S
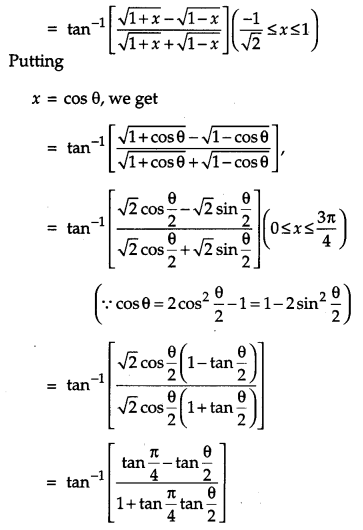
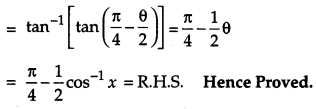
OR
If \(\tan ^{-1}\left(\frac{x-2}{x-4}\right)+\tan ^{-1}\left(\frac{x+2}{x+4}\right)=\frac{\pi}{4}\), find the value of x.
Solution:
Given,
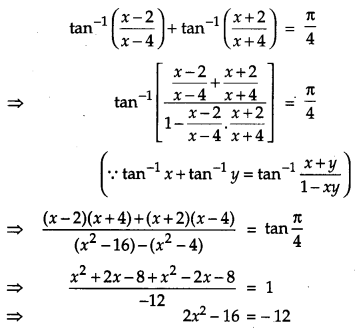

Question 13.
Using properties of determinants, prove that: [4]
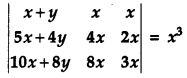
Solution:
Taking L.H.S
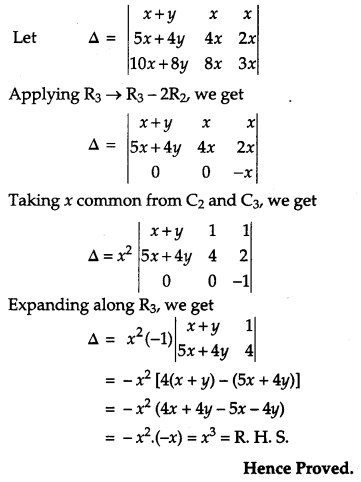
Question 14.
Find the value of \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{4}\) if x = aeθ(sin θ – cos θ) and y = aeθ(sin θ + cos θ). [4]
Solution:
Given,
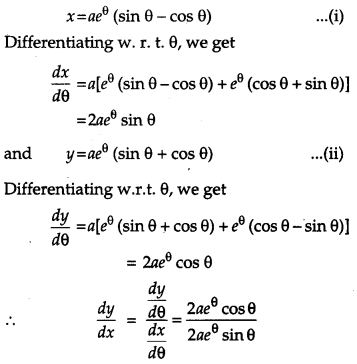
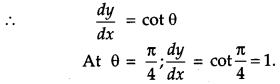
Question 15.
If y = Peax + Qebx, Show that [4]
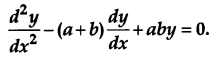
Solution:
Given,
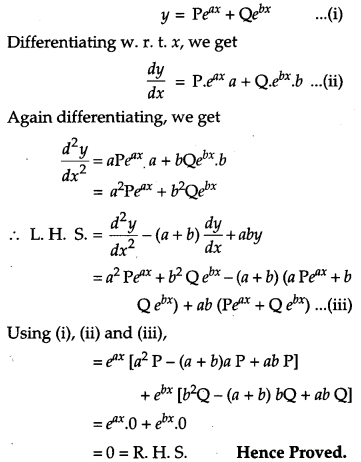
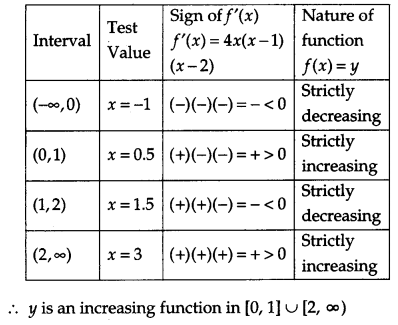
Question 16.
Find the value (s) of x for which y = [x(x – 2)]2 is an increasing function.
Solution:
Given
y=[x(x- 2)]2
=> y = x2 (x- 2)2
= f(x) (Let)
Differentiating w.r.t. x, we get
f'(x) = \(\frac{d y}{d x}\)
2x(x – 2)2 + 2x2(x- 2)
= 2x(x – 2) (x – 2 + x1)
= 4x(x – 1)(x – 2).
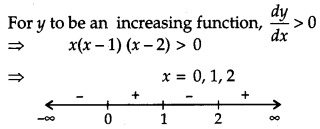
OR
Find the equations of the tangent and normal to the curve \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) at the point (\( \sqrt{{2}} \) a, b).
Solution:
The given curve is

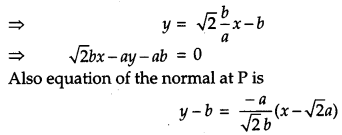
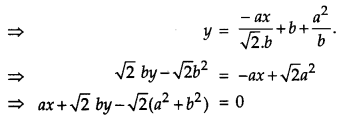
Question 17
Evaluate: [4]
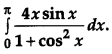
Solution:

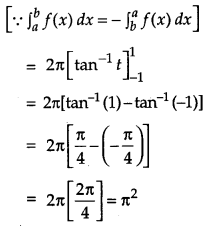
OR
Evaluate:
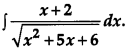
Solution:
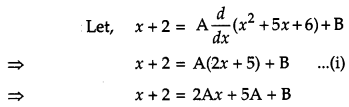
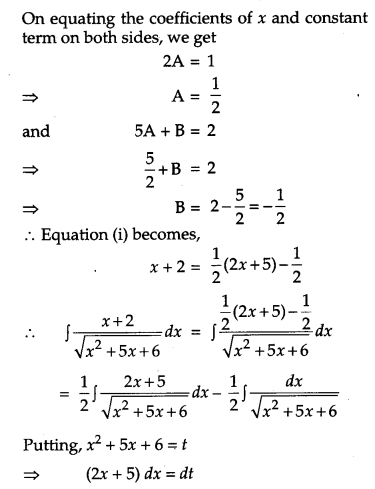
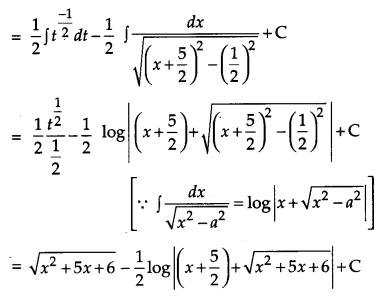
Question 18.
Find the particular solution of the differential equation \(\frac{d y}{d x}\) = 1 + x + y + xy, given that y = 0 when x = 1. [4]
Solution:
The given differential equation is
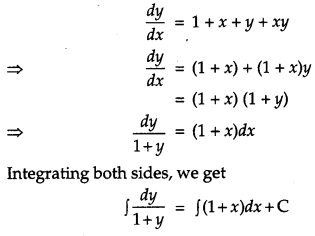
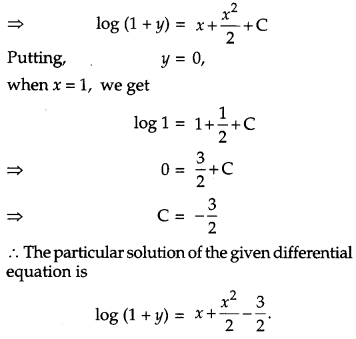
Question 19.
Solve the differential equation (1 + x2)\(\frac{d y}{d x}\) + y = etan-1x. [4]
Solution:
The given differential equation is

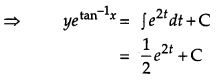
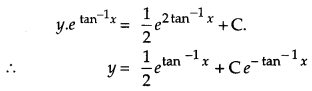
Question 20.
Show that the four points A, B, C and D with position vectors \(\hat{4} \hat{i}+5 \hat{j}+\hat{k}, \quad-\hat{j}-\hat{k}\) \(3 \hat{i}+9 \hat{j}+4 \hat{k} \text { and } 4(-\hat{i}+\hat{j}+\hat{k})\) respectively are coplanar. [4]
Solution:
Given the position vectors are

The given points A, B, C and D are coplanar.
Hence Proved
OR
The scalar product of the vector \(\vec{a}=\hat{i}+\hat{j}+\hat{k}\) with a unit vector along the sum of vectors \(\vec{b}=2 \hat{i}+4 \hat{j}-5 \hat{k} \text { and } \vec{c}=\lambda \hat{i}+2 \hat{j}+3 \hat{k}\) is equal to one. Find the value of λ and hence find the unit vector along \(\vec{b}+\vec{c}\).
Solution:
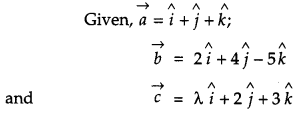
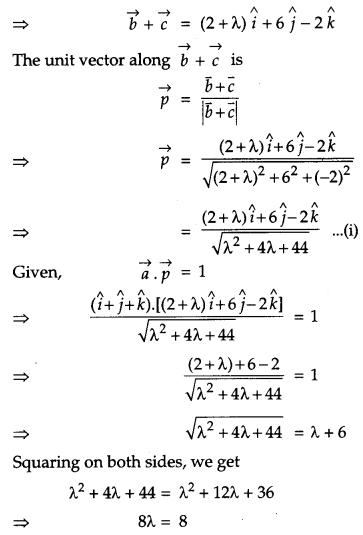

Question 21.
A line passes through (2, -1, 3) and is perpendicular to the lines \(\vec{r}=(\hat{i}+\hat{j}-\hat{k})+\)\(+\lambda(2 \hat{i}-2 \hat{j}+\hat{k}) \text { and } \vec{r}=(2 \hat{i}-\hat{j}-3 \hat{k})+\mu\)\((\hat{i}+2 \hat{j}+2 \hat{k})\). Obtain its equation in vector and Cartesian form. [4]
Solution:
The given lines are
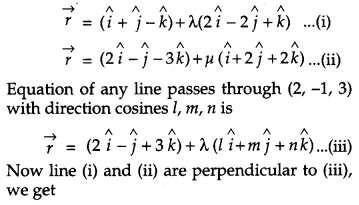
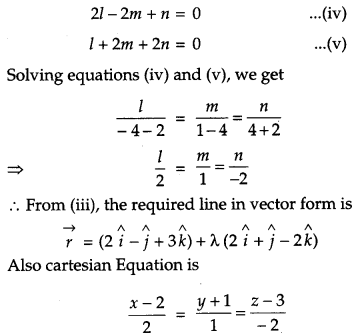
Question 22.
An experiment succeeds thrice as often as it fails. Find the probability that in the next five trials, there will be at least 3 successes. [4]
Solution:
Let, p = Probability of success

Section – C
Question 23.
Two schools A and B want to award their selected students on the values of sincerity, truthfulness and helpfulness. The school A wants to award ₹ x each, ₹ y each and ₹ z each for the three respective values to 3, 2 and 1 students respectively with a total award money of ₹ 1,600. School B wants to spend ₹ 2,300 to award its 4,1 and 3 students on the respective values (by giving the same award money to the three values as before). If the total amount of award for one prize on each value is ₹ 900, using matrices, find the award money for each value. Apart from these three values, suggest one more value which should be considered for award. [6]
Solution:
Given the awards for sincerity, truthfulness and helpfulness are ₹ x, ₹ y and ₹ z respectively.
3x + 2y + z = 1,600
4x + y + 3z = 2,300
x + y + z = 900
The given equation can be written in matrix form,
AX = B …(i)
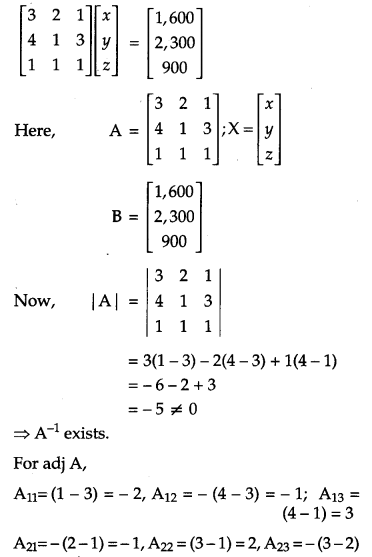
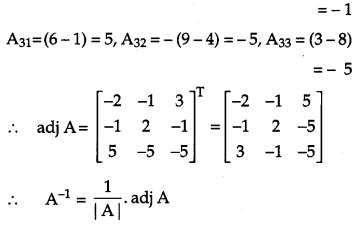

Apart from the three values, sincerity, truthfulness and helpfulness, another value for award should be discipline
Question 24.
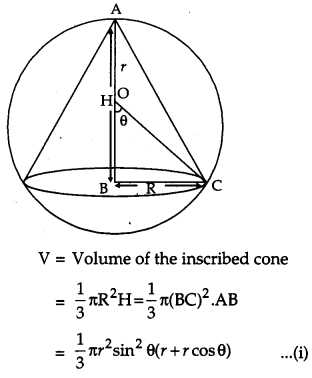
Show that the altitude of the right circular cone of maximum volume that can be described in a sphere of radius r is \(\frac{4 r}{3}\). Also show that the maximum volume of the cone is \(\frac{8}{27}\) of the volume of the sphere. [6]
Solution:
From the figure OA = OC = r (Radius of the sphere)
From right angled ∆ OBC,
BC = r sin θ,
OB = r cos θ

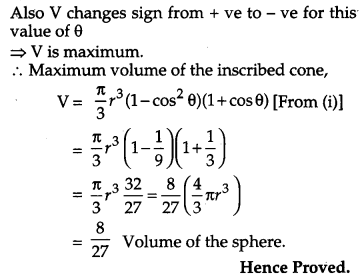
Question 25.
Evaluate: [6]
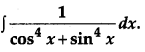
Solution:
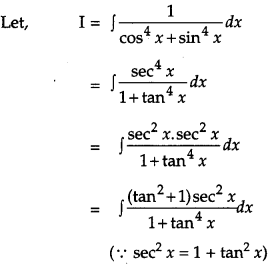
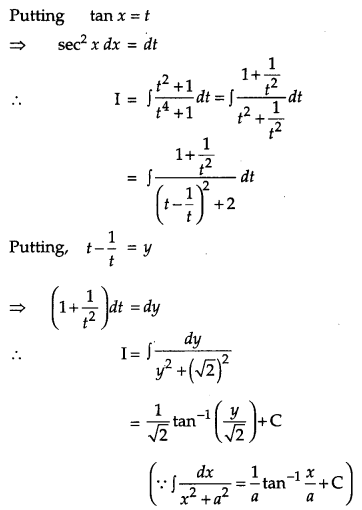
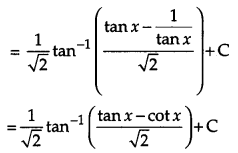
Question 26.
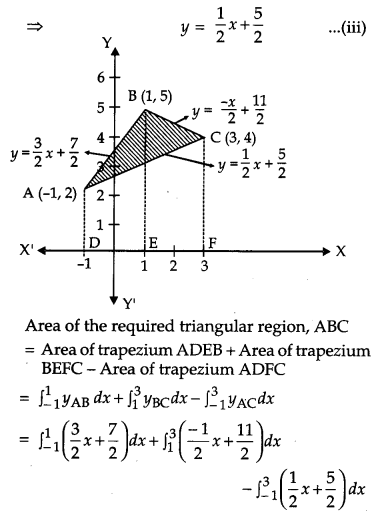
Using integration, find the area of the region bounded by the triangle whose vertices are (-1, 2), (1, 5) and(3, 4). [6]
Solution:
Let A (-1, 2); B (1, 5) and C (3, 4) Equation of AB is
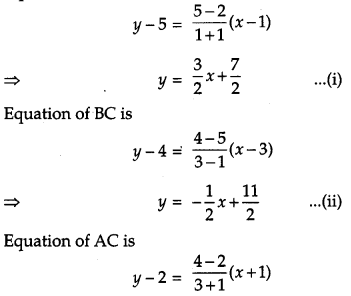
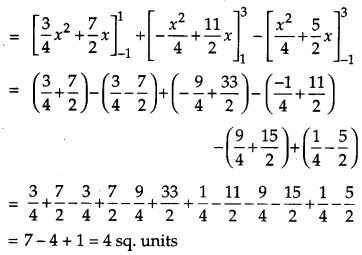
Question 27.
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0. Also find the distance of the plane obtained above, from the origin. [6]
Solution:
Equation of any plane through the line of intersection of the planes.
x + y + z – 1 = 0
and 2x + 3y + 4z – 5=0
x + y + z – 1 + λ(2x + 3y + 4z – 5) = 0
⇒ (1 + 2λ)x + (1 + 3λ)y + (1 + 4λ)z – (1 + 5λ) = 0 ……(i)
This plane is perpendicular to the plane
x – y + z = 0
∴ (1 + 2λ). 1 + (1 + 3λ)(- 1) + (1 + 4λ). 1 = 0
⇒ 1 + 2λ – 1 – 3λ + 1 + 4λ = 0
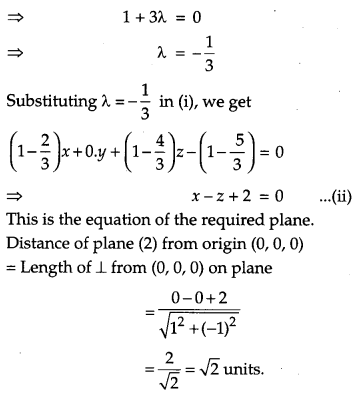
OR
Find the distance of the point (2, 12, 5) from the point of intersection of the line \(\vec{r}=2 \hat{i}-4 \hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+2 \hat{k})\) and the plane \(\vec{r} \cdot(\hat{i}-2 \hat{j}+\hat{k})=0\).
Solution:
The given line is

Question 28.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours of fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of ‘ 80 on each piece of type A and ₹ 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit ? Make it as an LPP and solve graphically. What is the maximum profit per week ? [6]
Solution:
Let x and y be the number of teaching aids of type A and B respectively. Then the LPP is
Maximize Z = 80x + 120y Subject to constraints:
9x + 12y ≤ 180
x + 3y ≤ 30
and x ≥ 0, y ≥ 0,
First we draw the lines AB and CD whose equations are
9x + 12y = 180
⇒ 3x + 4y = 60 …(i)
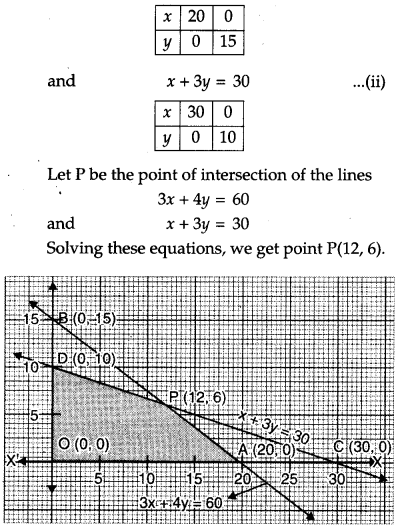
The feasible region is OAPDO which is shaded in the figure.
The vertices of the feasible region are O (0, 0), A (20, 0), P(12, 6) and D (0, 10)
The value of objective function Z = 80x + 120y as follows :

∴ The profit is maximum at P(12, 6) i.e., when the teaching aids of types A and B are 12 and 6 respectively.
Also maximum profit = ₹ 1680 per week.
Question 29.
There are three coins. One is a two-headed coin (having head on both faces), another is a biased coin that comes up heads 75% of the times and third is also a biased coin that comes up tails 40% of the times. One of the three coins is chosen at random and tossed, and it shows heads. What is the probability that it was the two-headed coin ? [6]
Solution:
Let A be the two headed coin, B be the biased coin showing up heads 75% of the times and C be the biased coin showing up tails 40% (i.e., showing up heads 60%) of the times.
Let E1, E2 and E3 be the events of choosing coins of the type A, B, C respectively. Let S be the event of getting a head. Then,

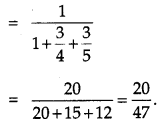
OR
Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of the random variable X, and hence find the mean of the distribution.
Solution:
Sample space
S = {1, 2, 3, 4, 5, 6}
Number of ways of selecting any two members of S is
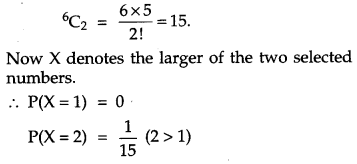

CBSE Previous Year Question Papers Class 12 Maths 2014 Outside Delhi Set II
Note: Except for the following questions, all the remaining questions have been asked in previous set.
Section – A
Question 9.
Evaluate: [1]
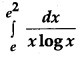
Solution:
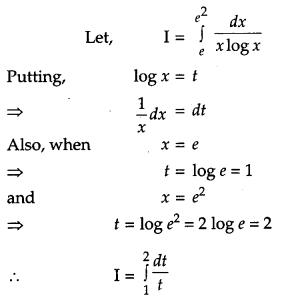
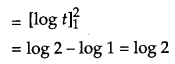
Question 10.
Find a vector \(\vec{a}\) of magnitude \(5 \sqrt{2}\), making an angle of \(\frac{\pi}{4}\) with x-axis, \(\frac{\pi}{2}\) with y-axis and an acute angle θ wirh z-axis. [1]
Solution:
Here,
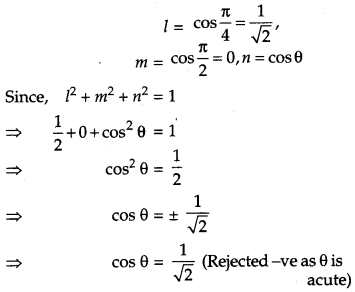
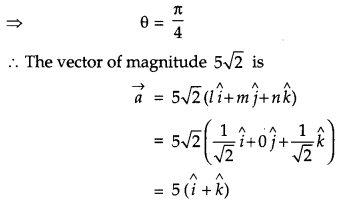
Section – B
Question 19.
Using properties of determinants, prove that [4]

Solution:
Taking L. H. S
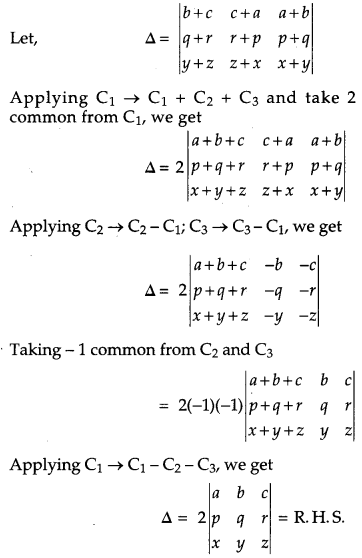
Hence Proved.
Question 20.
If x = a sin 2t (1 + cos 2t) and y = b cos 2t (1 – cos 2t), show that at t = \(\frac{\pi}{4},\left(\frac{d y}{d x}\right)=\frac{b}{a}\). [4]
Solution:
Here,
x = a sin 2t (1 + cos 2t) …(i)
y = b cos 2t (1 – cos 2t) …(ii)
Differentiating (i) w. r. t. ‘t’, we get

Question 21.
Find the particular solution of the differential equation x(1 + y2) dx – y( 1 + x2) dy = 0, given that y = 1 when x = 0. [4]
Solution:
The given differential equation is
x(1 + y2)dx – y(1 + x2) dy = 0 …(i)
Separate the given differential equation, we get

Question 22.
Find the vector and Cartesian equations of the line passing through the point (2, 1, 3) and perpendicular to the lines \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{3}\) and \(\frac{x}{-3}=\frac{y}{2}=\frac{z}{5}\). [4]
Solution:
Let the equation of any line passing through (2, 1, 3) and perpendicular to the lines

Section – C
Question 28.
Evaluate: [6]
![]()
Solution:
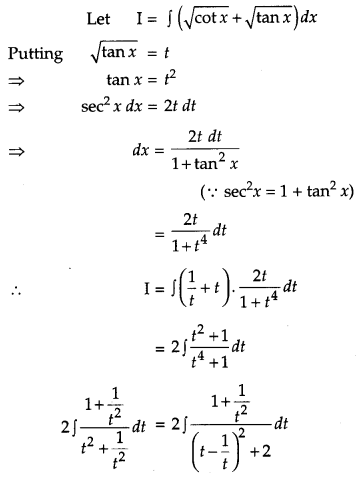
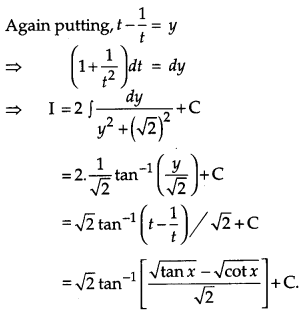
Question 29.
Prove that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is \(\frac{2 \mathbf{R}}{\sqrt{3}}\). Also find the maximum volume. [6]
Solution:
From the figure,
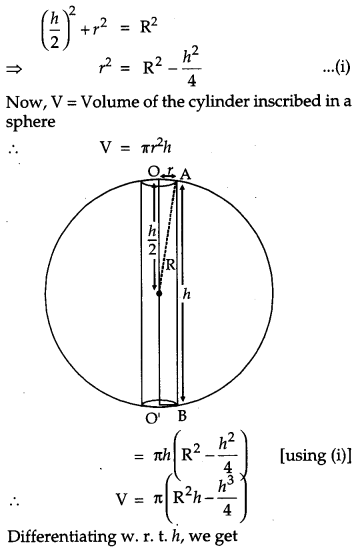
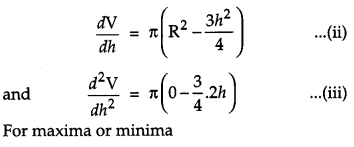
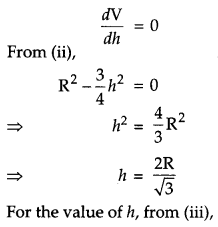
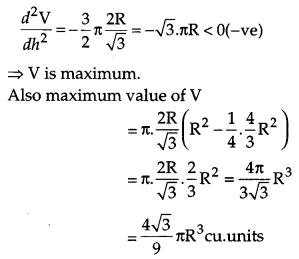
CBSE Previous Year Question Papers Class 12 Maths 2014 Outside Delhi Set III
Note: Except for the following questions, all the remaining questions have been asked in previous sets.
Section – A
Question 9.
If \(\int_{0}^{a} \frac{1}{4+x^{2}} d x=\frac{\pi}{8}\), find the value of a. [1]
Solution:
Given,
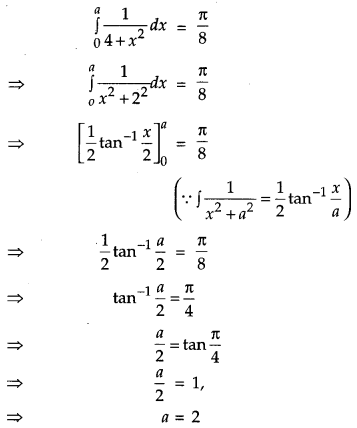
Question 10.
If \(\vec{a} \text { and } \vec{b}\) are perpendicular vectors, \(|\vec{a}+\vec{b}|=13 \text { and }|\vec{a}|=5\) find the value of \(|\vec{b}|\). [1]
Solution:
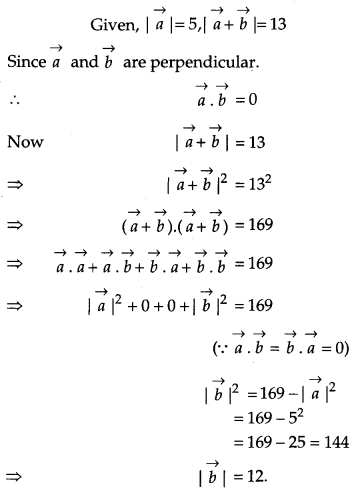
Section – B
Question 19.
Using properties of determinants, prove that: [4]
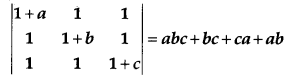
Solution:
Taking L. H. S
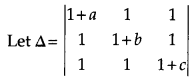

![]()
Question 20.
If x = cos t (3 – 2 cos2 t) and y = sin t (3 – 2 sin2t), find the value of \(\frac{d y}{d x} \text { at } t=\frac{\pi}{4}\). [4]
Solution:
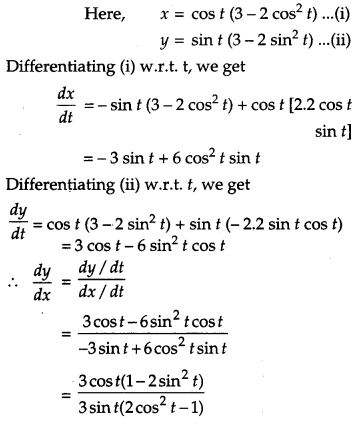
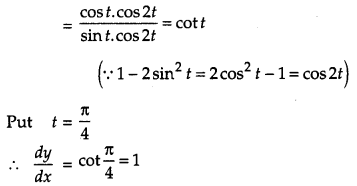
Question 21.
Find the particular solution of the differential equation log \(\left(\frac{d y}{d x}\right)\) = 3x + 4y, given that y = 0 when x = 0. [4]
Solution:
The given differential equation is
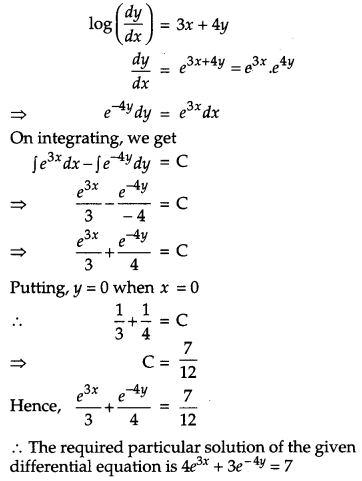
Question 22.
Find the value of p, so that the lines l1 : \(\frac{1-x}{3}\)
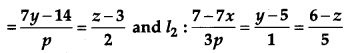
are perpendicular to each other. Also find the equations of a line passing through a point (3, 2, – 4) and parallel to line l1. [4]
Solution:
The given lines are
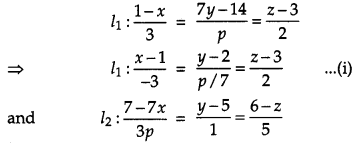

Section – C
Question 28.
If the sum of the lengths of the hypotenuse and a side of a right triangle is given, show that the area of the triangle is maximum, when the angle of between them is 60°. [6]
Solution:
Let ∆ ABC be right angled with side a and hypotenuse l be
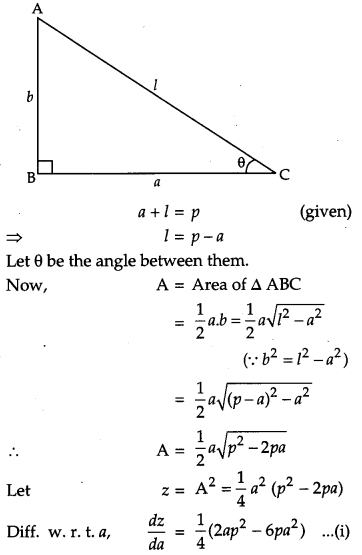
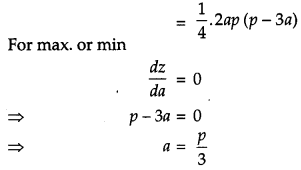
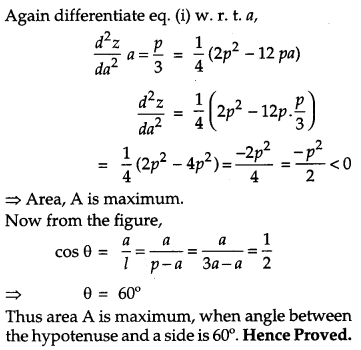
Question 29.
Evaluate: [6]
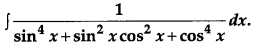
Solution:
Let